A&A 406, 213-219 (2003)
DOI: 10.1051/0004-6361:20030787
S. Araujo-Betancor1,![]() -
B. T. Gänsicke1,
-
B. T. Gänsicke1,![]() -
H.-J. Hagen2 -
P. Rodriguez-Gil1 -
D. Engels2
-
H.-J. Hagen2 -
P. Rodriguez-Gil1 -
D. Engels2
1 - Department of Physics and Astronomy, University of Southampton,
Southampton SO17 1BJ, UK
2 -
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112,
21029 Hamburg, Germany
Received 1 April 2003 / Accepted 30 April 2003
Abstract
We report the identification of the cataclysmic variable
1RXS J062518.2+733433 as an intermediate polar. The orbital period of
the system is determined to be
![]() min from the radial
velocity variation of
min from the radial
velocity variation of
![]() ,
measured in an extensive set of
time-resolved spectra. Differential optical photometry obtained
over a base line of three weeks reveals the presence of coherent
variability with a period of
,
measured in an extensive set of
time-resolved spectra. Differential optical photometry obtained
over a base line of three weeks reveals the presence of coherent
variability with a period of
![]() min, which we suggest
to be the white dwarf spin period. The power spectrum of our
photometry also contains a strong signal near the spectroscopically-determined orbital period. The emission lines in
1RXS J062518.2+733433 display a complex multicomponent structure. In
the trailed spectrogram of He I
min, which we suggest
to be the white dwarf spin period. The power spectrum of our
photometry also contains a strong signal near the spectroscopically-determined orbital period. The emission lines in
1RXS J062518.2+733433 display a complex multicomponent structure. In
the trailed spectrogram of He I ![]() 6678 we detect a narrow
component with a radial velocity semi-amplitude of
6678 we detect a narrow
component with a radial velocity semi-amplitude of ![]() 140 kms,
consistent with a possible origin on the irradiated face of the secondary. The
absence of eclipses gives an upper limit on the binary inclination of
140 kms,
consistent with a possible origin on the irradiated face of the secondary. The
absence of eclipses gives an upper limit on the binary inclination of
![]() .
.
Key words: stars: binaries: close - stars: individual: 1RXS J062518.2+733433 - stars: novae, cataclysmic variables
There are currently a number of large-scale surveys for CVs underway that pursue this aim (e.g. Marsh et al. 2002; Szkody et al. 2002). Among these projects, our selection of CVs based on their spectroscopic properties in the Hamburg Quasar Survey (HQS; Hagen et al. 1995) has been especially prolific, resulting in the discovery of more than 50 new bright CVs (e.g. Nogami et al. 2001; Gänsicke et al. 2002a,b,2000).
In this paper, we report follow-up observations of
1RXS J062518.2+733433, henceforth RX J0625, an object originally
identified as a CV on the basis of its X-ray emission
and optical spectrum (Wei et al. 1999). We have
independently selected RX J0625 as a CV candidate because of the
noticeable Balmer emission in its HQS data. The strong
He II ![]() 4686 emission detected in the identification spectrum
of RX J0625, along with coherent optical variability observed on a
time scale of
4686 emission detected in the identification spectrum
of RX J0625, along with coherent optical variability observed on a
time scale of ![]() 20 min, immediately reveal the intermediate polar
nature of this CV. In Sect. 2 we describe the observational data and
its reduction. We then derive the orbital period from the radial
velocity variation of the emission lines and the spin period from
differential photometry in Sect. 3. Finally, in Sect. 4 we discuss
the behaviour of the strongest emission lines in detail and summarise
our findings in Sect. 5.
20 min, immediately reveal the intermediate polar
nature of this CV. In Sect. 2 we describe the observational data and
its reduction. We then derive the orbital period from the radial
velocity variation of the emission lines and the spin period from
differential photometry in Sect. 3. Finally, in Sect. 4 we discuss
the behaviour of the strongest emission lines in detail and summarise
our findings in Sect. 5.
On April 29 2001 we obtained a single identification spectrum of
RX J0625 at the Calar Alto 2.2 m telescope with the CAFOS focal
reductor spectrograph, using the standard SITe CCD (Table 1). We used
the B-200 grism and a slit width of
![]() ,
resulting in a useful
wavelength range of 3500-7000 Å and a spectral resolution of
4.7 Å (Fig. 1). A flux standard (BD+75
,
resulting in a useful
wavelength range of 3500-7000 Å and a spectral resolution of
4.7 Å (Fig. 1). A flux standard (BD+75![]() 325) was
observed with the same set-up in order to correct for the instrumental
response. The identification spectrum contains noticeable Balmer,
He I and He II and N/C Bowen emission lines. The
strength of He II
325) was
observed with the same set-up in order to correct for the instrumental
response. The identification spectrum contains noticeable Balmer,
He I and He II and N/C Bowen emission lines. The
strength of He II ![]() 4686 is comparable to
4686 is comparable to
![]() ,
indicating the
presence of a strong source of ionising photons in RX J0625,
typical of either magnetic CVs or novalike variables.
In order to determine the orbital period of RX J0625, we obtained 45
higher resolution spectra, again with CAFOS at the Calar Alto 2.2 m telescope
(Table 1). This time the G-100 grism was used in conjuction with a
,
indicating the
presence of a strong source of ionising photons in RX J0625,
typical of either magnetic CVs or novalike variables.
In order to determine the orbital period of RX J0625, we obtained 45
higher resolution spectra, again with CAFOS at the Calar Alto 2.2 m telescope
(Table 1). This time the G-100 grism was used in conjuction with a
![]() slit which gave a wavelength range of 4240-8300 Å and
a spectral resolution of 2.1 Å. The higher resolution spectra were
obtained over a period of 3 weeks, optimising the sampling for an
efficient period determination.
slit which gave a wavelength range of 4240-8300 Å and
a spectral resolution of 2.1 Å. The higher resolution spectra were
obtained over a period of 3 weeks, optimising the sampling for an
efficient period determination.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms3806.f1}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg18.gif) |
Figure 1: Identification spectrum of RX J0625 obtained on 2001 April 29. |
| Open with DEXTER | |
Table 1: Log of observations.
Table 2: Equivalent widths and line widths (corrected for the instrumental resolution) of the strongest emission lines measured from the average of the 45 spectra obtained in December 2002.
All spectra were reduced in a standard manner using the Figaro package within the Starlink software collection. The frames were corrected for the bias level by subtracting the mean of a series of bias images taken at the start and end of each observing night. Dome flat-fields were used to remove pixel to pixel variations of the chip. The spectra were then optimally extracted (Horne 1986) and sky line subtracted using Tom Marsh's Pamela package. Especial care was taken to account for the tilt of the spectra in order to maximise the signal-to-noise ratio. The wavelength calibration was performed using mercury-cadmium, helium-argon and rubidium arcs. Uncertainties on every data point calculated from photon statistics are rigorously propagated through every stage of the data reduction. We did not attempt to flux-calibrate the higher resolution spectra as it was not required for the radial velocity analysis described below.
Table 2 gives the equivalent widths and line widths of the main emission lines detected in the average of the 45 high resolution spectra.
We obtained differential V-band and filter-less photometry of
RX J0625 during 6 nights in December 2002 with the CAFOS SITe CCD
camera on the Calar Alto 2.2m telescope (Table 1). In
order to achieve a high time resolution (![]() 30 s), only a small
window of the chip (
30 s), only a small
window of the chip (![]()
![]() )
was read out. The
data were bias-subtracted and flat-fielded in a standard fashion using
the ESO-MIDAS package, and aperture magnitudes were extracted
with the sextractor (Bertin & Arnouts 1996). The V magnitudes of
RX J0625 were derived relative to the HST Guide Star GSC 0437000234
(
)
was read out. The
data were bias-subtracted and flat-fielded in a standard fashion using
the ESO-MIDAS package, and aperture magnitudes were extracted
with the sextractor (Bertin & Arnouts 1996). The V magnitudes of
RX J0625 were derived relative to the HST Guide Star GSC 0437000234
(
![]() ), located
), located
![]() southwards of RX J0625.
This comparison star was saturated in a number of the filter-less
CCD images obtained on December 14/15, and, hence, we used
GSC 0437000998 (
southwards of RX J0625.
This comparison star was saturated in a number of the filter-less
CCD images obtained on December 14/15, and, hence, we used
GSC 0437000998 (
![]() ), located
), located
![]() northwards of RX J0625 for the reduction of these
images. RX J0625 was found at an average magnitude of
northwards of RX J0625 for the reduction of these
images. RX J0625 was found at an average magnitude of
![]() throughout the nights in which we used the V band
filter. The light curves of RX J0625 clearly reveal the presence of
variability with a period of
throughout the nights in which we used the V band
filter. The light curves of RX J0625 clearly reveal the presence of
variability with a period of ![]() 20 min and an amplitude of
20 min and an amplitude of
![]()
![]() mag throughout all nights (Fig. 2). In
addition to this short-term variation the light curve of RX J0625
displays a modulation on time scales of several hours.
mag throughout all nights (Fig. 2). In
addition to this short-term variation the light curve of RX J0625
displays a modulation on time scales of several hours.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3806.f2}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg39.gif) |
Figure 2: Differential CCD V-band (V) and filter-less (C) photometry obtained at the Calar Alto 2.2 m observatory. Note the different scales of the filter-less and V band data. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.2cm,clip]{ms3806.f3}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg40.gif) |
Figure 3:
Continuum-subtracted and
normalised
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3806.f4}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg41.gif) |
Figure 4:
Period analysis of the radial velocities
measured from a Gauss-fit to the
|
| Open with DEXTER | |
The primary aim of our time-resolved spectroscopy of RX J0625 is to
measure its orbital period from the radial velocity variations of the
emission lines. The line profiles clearly display a complicated
multicomponent structure (Fig. 3). In a first attempt,
we used a single Gaussian least square fitting procedure to determine
the radial velocity variations of
![]() ,
,
![]() and
He II
and
He II ![]() 4686. The radial velocity data were then subjected to
the following period analysis methods: (a) the phase dispersion method
(Stellingwerf 1978), (b) the analysis of variance
(Schwarzenberg-Czerny 1989,
as implemented in the
MIDAS context TSA), (c) and a sine wave
4686. The radial velocity data were then subjected to
the following period analysis methods: (a) the phase dispersion method
(Stellingwerf 1978), (b) the analysis of variance
(Schwarzenberg-Czerny 1989,
as implemented in the
MIDAS context TSA), (c) and a sine wave ![]() fitting procedure, using chisq in the Starlink package
period. The resulting periodograms for
fitting procedure, using chisq in the Starlink package
period. The resulting periodograms for
![]() are shown in
Fig. 4. The orbital frequency (period) is inferred
from the three independent techniques in a consistent way to be
are shown in
Fig. 4. The orbital frequency (period) is inferred
from the three independent techniques in a consistent way to be
![]()
![]() (
(
![]() min), where the
error is computed from the
min), where the
error is computed from the ![]() sine wave fitting (
sine wave fitting (![]() ,
4
interesting parameter). A slightly more conservative error estimate
based on the results obtained from all three methods gives
,
4
interesting parameter). A slightly more conservative error estimate
based on the results obtained from all three methods gives
![]() min. The analysis of
min. The analysis of
![]() and He II
and He II ![]() 4686
provides consistent results for
4686
provides consistent results for
![]() ,
but with significantly larger
errors. The robustness of our period determination is shown in
Fig. 5 were we folded the
,
but with significantly larger
errors. The robustness of our period determination is shown in
Fig. 5 were we folded the
![]() radial velocities over
the orbital period. The radial velocity measurements from this fit are
provided in Table 3.
radial velocities over
the orbital period. The radial velocity measurements from this fit are
provided in Table 3.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms3806.f5}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg49.gif) |
Figure 5:
Radial velocities measured from a
Gauss-fit to the
|
| Open with DEXTER | |
Table 3:
Radial velocities of the
![]() emission line determined from
a single-Gaussian fit to the line profile (corrected for the
heliocentric velocity).
emission line determined from
a single-Gaussian fit to the line profile (corrected for the
heliocentric velocity).
For comparison purposes we measured the radial velocities of
![]() cross-correlating the observed line profile with a single Gaussian of
fixed width of 300
cross-correlating the observed line profile with a single Gaussian of
fixed width of 300
![]() (Schneider & Young 1980).
The resulting orbital period is identical to that derived from the
single Gaussian fit to the
(Schneider & Young 1980).
The resulting orbital period is identical to that derived from the
single Gaussian fit to the
![]() profiles, but the radial velocity
variation displays an amplitude larger by a factor of
profiles, but the radial velocity
variation displays an amplitude larger by a factor of ![]() 2.
2.
Finally, we attempted to fit the
![]() emission with a blend of a
narrow and a broad Gaussian component to model more accurately the
complex structure of the observed profiles. Unfortunately, this
procedure did not provide unambiguous results because of the limited
spectral resolution of our data. Due to the multicomponent structure
of the lines profile (see Fig. 3) it is difficult to
interpret the radial velocity variation obtained from either the
single Gaussian fit (Fig. 5) or the Gauss correlation to
emission with a blend of a
narrow and a broad Gaussian component to model more accurately the
complex structure of the observed profiles. Unfortunately, this
procedure did not provide unambiguous results because of the limited
spectral resolution of our data. Due to the multicomponent structure
of the lines profile (see Fig. 3) it is difficult to
interpret the radial velocity variation obtained from either the
single Gaussian fit (Fig. 5) or the Gauss correlation to
![]() .
The behaviour of the most important emission lines is discussed
in more detail in Sect. 4 on the basis of
trailed spectrograms.
.
The behaviour of the most important emission lines is discussed
in more detail in Sect. 4 on the basis of
trailed spectrograms.
In order to analyse the periodicities observed in the light curve of
RX J0625 (Fig. 2), we have computed from the entire
photometric data set both a Scargle (1982) periodogram (as
implemented in the MIDAS context TSA) as well as a periodogram using
the Phase Dispersion Method (PDM) of Stellingwerf (1978).
Because the lengths of our individual photometric observations are of
the order of or shorter than the orbital period, subtracting the
nightly mean from the data would introduce erroneous signals in the
low-frequency range of the periodograms. Considering that RX J0625
does not exhibit noticeable night-to-night variability, we
decided to subtract from the V filter and white light data the mean
of all measurements obtained in the corresponding band prior to the
computation of the periodograms. The resulting periodograms
(Figs. 6 and 7) contain strong
signals concentrated in the frequency ranges
![]() and
and
![]() .
The nature of the signals detected in these two
separate frequency regimes is discussed below.
.
The nature of the signals detected in these two
separate frequency regimes is discussed below.
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm,clip]{ms3806.f6}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg56.gif) |
Figure 6:
Scargle periodogram of the differential
CCD photometry shown in Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms3806.f7}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg57.gif) |
Figure 7:
Period analysis near the presumed
white dwarf spin. Top panel: Scargle periodogram. Bottom panel: phase
dispersion periodogram. The black lines are computed from the observed
data. The gray lines are computed from a sinusoid assuming a period of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3806.f8}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg58.gif) |
Figure 8: The photometric data points from Fig. 2 mean-subtracted and folded over: a) The spin period of 19.788 min, using Eq. (1). b) The beat period of 21.275 min. c) The orbital period of 283.0 min, using Eq. (2). |
| Open with DEXTER | |
Coherent variability on time scales of a several minutes to several
tens of minutes has been detected in the optical light curves of a
number of intermediate polars (e.g. Patterson 1994), and is
interpreted as the spin period of the accreting magnetic white
dwarf. We conclude from the spectral appearance of RX J0625 and from
the detected coherent optical variability that RX J0625 is indeed a
new member of the small class of intermediate polars. We
suggest that the detected frequency (period) of 72.772
![]() (19.788 min) is the white dwarf spin frequency
(19.788 min) is the white dwarf spin frequency ![]() (period
(period
![]() ). From the combined V band and filter-less
photometry, we derive the following spin ephemeris:
). From the combined V band and filter-less
photometry, we derive the following spin ephemeris:
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm]{ms3806.f9}
\end{figure}](/articles/aa/full/2003/28/aa3806/Timg62.gif) |
Figure 9:
Trailed spectrograms of
|
| Open with DEXTER | |
Another hallmark of intermediate polars is the detection of beat
frequencies between the white dwarf spin frequency ![]() and the
orbital frequency
and the
orbital frequency ![]() ,
which arise from the reprocession of
X-rays emitted from close to white dwarf surface on, e.g., the
secondary star. Such sideband signals have been detected in different
systems at
,
which arise from the reprocession of
X-rays emitted from close to white dwarf surface on, e.g., the
secondary star. Such sideband signals have been detected in different
systems at
![]() ,
,
![]() ,
,
![]() ,
,
![]() (see Warner 1986 for an interpretation of
these frequencies). In RX J0625, the only unambiguous detection of a
sideband signal is
(see Warner 1986 for an interpretation of
these frequencies). In RX J0625, the only unambiguous detection of a
sideband signal is
![]() (see Fig. 6). The
photometric data folded over this beat period of 21.275 min
are shown in Fig. 8b. While we are
confident that our identifications of the spin and beat period are
correct we mention as a note of caution that time-resolved X-ray
and/or polarimetric data are necessary to unambigously confirm this
interpretation.
(see Fig. 6). The
photometric data folded over this beat period of 21.275 min
are shown in Fig. 8b. While we are
confident that our identifications of the spin and beat period are
correct we mention as a note of caution that time-resolved X-ray
and/or polarimetric data are necessary to unambigously confirm this
interpretation.
As already mentioned in Sect. 3.1, the line profiles
clearly display a multicomponent structure (Fig. 3),
which makes the interpretation of the determined radial velocity
variations rather ambiguous (Fig. 5). To explore the
behaviour of the emission lines in more detail, we constructed trailed
spectra of
![]() ,
,
![]() ,
He I
,
He I ![]() 6678, and He II
6678, and He II ![]() 4686,
which are shown in Fig. 9. These diagrams were
computed from the continuum-normalised spectra after binning into 15
phase intervals. The He I
4686,
which are shown in Fig. 9. These diagrams were
computed from the continuum-normalised spectra after binning into 15
phase intervals. The He I ![]() 6678 line clearly shows two
emission components: a narrow one with a radial velocity
semi-amplitude of
6678 line clearly shows two
emission components: a narrow one with a radial velocity
semi-amplitude of ![]() 140
140
![]() and a wider one with velocity
reaching
and a wider one with velocity
reaching ![]()
![]()
![]() .
Both components are not in phase, the
phase offset being
.
Both components are not in phase, the
phase offset being ![]() 0.15. The trailed spectra shown in
Fig. 9 were phased according to the following
orbital ephemeris
0.15. The trailed spectra shown in
Fig. 9 were phased according to the following
orbital ephemeris
In analogy to the narrow emission lines observed in many magnetic CVs,
this narrow emission line component may have its origin on the
irradiated face of the secondary star. In order to test this
hypothesis, we performed the following simple calculation. The
secondary mass was estimated from the mass-period relation derived by
Smith & Dhillon (1998), which gives a value of
![]()
![]() .
For the primary mass we adopted M1=0.8
.
For the primary mass we adopted M1=0.8 ![]() (the average white dwarf mass in long-period CVs determined
by Smith & Dhillon 1998), resulting in a mass ratio
(the average white dwarf mass in long-period CVs determined
by Smith & Dhillon 1998), resulting in a mass ratio
![]() .
Assuming a disc radius of
.
Assuming a disc radius of
![]() ,
the lack of
eclipses in the optical light curve of RX J0625 sets an upper limit
on the orbital inclination of
,
the lack of
eclipses in the optical light curve of RX J0625 sets an upper limit
on the orbital inclination of
![]() .
The projected
velocity of the secondary is given by:
.
The projected
velocity of the secondary is given by:
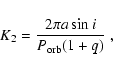 |
(3) |
Taken at face value, the behaviour of the narrow emission line components detected in our (admittedly rather low resolution) phase-resolved spectroscopy are consistent with an origin on the irradiated face of the secondary.
As we mentioned above, the broad component of the He I ![]() 6678
line displays a phase offset of
6678
line displays a phase offset of ![]() 0.15 with respect to the narrow
one, reaching a velocity of
0.15 with respect to the narrow
one, reaching a velocity of ![]() -500
-500
![]() at its maximum
excursion to the blue. The phasing with respect to the narrow
component (and assuming that our above interpretation of the origin of
the narrow component is correct) indicates that the broad emission is
not coming from an axisymmetric structure around the white
dwarf. Nevertheless, the high velocity dispersion observed in the
broad component clearly points towards an origin close to the white
dwarf. The maximum velocity to the blue is reached at phase
at its maximum
excursion to the blue. The phasing with respect to the narrow
component (and assuming that our above interpretation of the origin of
the narrow component is correct) indicates that the broad emission is
not coming from an axisymmetric structure around the white
dwarf. Nevertheless, the high velocity dispersion observed in the
broad component clearly points towards an origin close to the white
dwarf. The maximum velocity to the blue is reached at phase ![]() 0.4-0.5. A similar high-velocity S-wave has been observed in the
intermediate polars EX Hya (Hellier et al. 1989) and V1025 Cen
(Hellier et al. 2002). The same components are also characteristic
of the SW Sextantis stars, which have been recently proposed to be
magnetic systems (Rodríguez-Gil et al. 2001). In all these systems,
it is believed that these high-velocity S-waves form in the vicinity
of the primary's magnetosphere.
0.4-0.5. A similar high-velocity S-wave has been observed in the
intermediate polars EX Hya (Hellier et al. 1989) and V1025 Cen
(Hellier et al. 2002). The same components are also characteristic
of the SW Sextantis stars, which have been recently proposed to be
magnetic systems (Rodríguez-Gil et al. 2001). In all these systems,
it is believed that these high-velocity S-waves form in the vicinity
of the primary's magnetosphere.
The trailed spectra of He II ![]() 4686 seem to exhibit the same
two emission components, with the narrow one also dominating and the same
velocity amplitudes as in He I
4686 seem to exhibit the same
two emission components, with the narrow one also dominating and the same
velocity amplitudes as in He I ![]() 6678. Also the trailed spectra
of
6678. Also the trailed spectra
of
![]() and
and
![]() clearly show a multicomponent structure, even though
their narrow components are less obvious than in He I
clearly show a multicomponent structure, even though
their narrow components are less obvious than in He I ![]() 6678. In
order to securely identify the different line components with physical
emission sites in the binary, it will be necessary to obtain
time-resolved spectroscopy spanning several consecutive binary
orbits with better spectral resolution.
6678. In
order to securely identify the different line components with physical
emission sites in the binary, it will be necessary to obtain
time-resolved spectroscopy spanning several consecutive binary
orbits with better spectral resolution.
We have observed RX J0625 as part of our ongoing search for new CVs
selected on the basis of their spectroscopic properties from the
Hamburg Quasar Survey. From the radial velocity variations measured in
![]() ,
we determined an orbital period of
,
we determined an orbital period of
![]() min. The
detection of coherent optical variations clearly classifies RX J0625
as a member of the small class of intermediate polars. The
period of these variations is
min. The
detection of coherent optical variations clearly classifies RX J0625
as a member of the small class of intermediate polars. The
period of these variations is
![]() min which is
most likely the spin period of the white dwarf. In terms of its
orbital and spin period, RX J0625 is very similar to FO Aqr
(
min which is
most likely the spin period of the white dwarf. In terms of its
orbital and spin period, RX J0625 is very similar to FO Aqr
(
![]() min, and
min, and
![]() min). Our phase-resolved
spectroscopy clearly shows that the emission lines are multicomponent,
and we identify a narrow component with a radial velocity
semi-amplitude of
min). Our phase-resolved
spectroscopy clearly shows that the emission lines are multicomponent,
and we identify a narrow component with a radial velocity
semi-amplitude of ![]() 140 kms, which might originate from the
irradiated face of the secondary. Extensive photometric monitoring,
phase-resolved high-resolution spectroscopy and pointed X-ray
observations of RX J0625 are strongly encouraged.
140 kms, which might originate from the
irradiated face of the secondary. Extensive photometric monitoring,
phase-resolved high-resolution spectroscopy and pointed X-ray
observations of RX J0625 are strongly encouraged.
![]() :
After submission of this paper, we became
aware of an independent photometric study of RX J0625 by
Staude et al. (2003) that confirms the likely white dwarf spin
period and shows that the low-frequency photometric signal detected in
RX J0625 is consistent with our spectroscopic orbital period within
the errors of the measurements. Furthermore, the referee drew our
attention to the fact that an orbital period for RX J0625 was
included on December 13 2002 in the online catalogue of
Downes et al. (2001), which is consistent with our value.
:
After submission of this paper, we became
aware of an independent photometric study of RX J0625 by
Staude et al. (2003) that confirms the likely white dwarf spin
period and shows that the low-frequency photometric signal detected in
RX J0625 is consistent with our spectroscopic orbital period within
the errors of the measurements. Furthermore, the referee drew our
attention to the fact that an orbital period for RX J0625 was
included on December 13 2002 in the online catalogue of
Downes et al. (2001), which is consistent with our value.
Acknowledgements
SAB thanks PPARC for a studentship. BTG was supported by a PPARC Advanced Fellowship, the HQS was supported by the Deutsche Forschungsgemeinschaft through grants Re 353/11 and Re 353/22. We thank Ana Guijarro for obtaining part of the Calar Alto observations. We are grateful to Christian Knigge for suggesting the use of chisq in the Starlink period package for the analysis of the radial velocity data - and for pointing out that the latest version of period does not work properly. Tom Marsh is thanked for providing his reduction and analysis packages. Patrick Woudt is acknowldedged for his prompt referee report and for a number of useful suggestions.