A&A 406, 7-13 (2003)
DOI: 10.1051/0004-6361:20030728
Research Note
Signatures of highly inclined accretion disks in galactic black hole candidates and AGNs
A. F. Zakharov1,2,3 - S. V. Repin4
1 - National Astronomical Observatories, Chinese Academy of Sciences, 100012
Beijing, PR China
2 - Institute of Theoretical and Experimental Physics,
25, B. Cheremushkinskaya st., Moscow 117259, Russia
3 - Astro Space Centre of Lebedev Physics Institute, 84/32,
Profsoyuznaya st.,
Moscow 117810, Russia
4 - Space Research Institute, 84/32,
Profsoyuznaya st.,
Moscow 117810, Russia
Received 7 March 2003 / Accepted 18 April 2003
Abstract
Recent X-ray observations of microquasars and Seyfert galaxies
reveal broad emission lines in their spectra, which can arise in
the innermost parts of accretion disks. Simulations indicate that
at low inclination angle the line is measured by a distant
observer as characteristic two-peak profile. However, at high
inclination angles (>
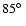 )
two additional peaks arise.
This phenomenon was discovered by Matt et al. (1993) using the
Schwarzschild black hole metric to analyze such effect. They
assumed that the effect is applicable to a Kerr metric far beyond
the range of parameters that they exploited. We check and confirm
their hypothesis about such a structure of the spectral line shape
for the Kerr metric case. We use no astrophysical assumptions
about the physical structure of the emission region except the
assumption that the region should be narrow enough.
Positions and heights of these extra peaks drastically
depend on both the radial coordinate of the emitting region
(circular hot spot) and the inclination angle. We find that the
best conditions to observe this effect are realized at
)
two additional peaks arise.
This phenomenon was discovered by Matt et al. (1993) using the
Schwarzschild black hole metric to analyze such effect. They
assumed that the effect is applicable to a Kerr metric far beyond
the range of parameters that they exploited. We check and confirm
their hypothesis about such a structure of the spectral line shape
for the Kerr metric case. We use no astrophysical assumptions
about the physical structure of the emission region except the
assumption that the region should be narrow enough.
Positions and heights of these extra peaks drastically
depend on both the radial coordinate of the emitting region
(circular hot spot) and the inclination angle. We find that the
best conditions to observe this effect are realized at
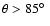 and
and
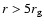 and may exist in microquasars or
low-mass black holes in X-ray binary systems, because there is
some precession (and nutation of accretion disks) with not very
long time periods (see, for example, the SS433 binary system). The
line profiles for different inclination angles and radial
coordinates are presented. To analyze the influence of disk
models on the spectral line shapes we simulate the line profiles
for the Shakura-Sunyaev disk model for accretion disks with the
high inclination.
and may exist in microquasars or
low-mass black holes in X-ray binary systems, because there is
some precession (and nutation of accretion disks) with not very
long time periods (see, for example, the SS433 binary system). The
line profiles for different inclination angles and radial
coordinates are presented. To analyze the influence of disk
models on the spectral line shapes we simulate the line profiles
for the Shakura-Sunyaev disk model for accretion disks with the
high inclination.
Key words: black hole physics - line: profiles - X-rays
individuals: SS433
More than ten years ago it was predicted that profiles of lines
emitted by AGNs and X-ray binary systems![[*]](/icons/foot_motif.gif) could have an asymmetric double-peaked shape
(e.g. Chen et al. 1989; Matt et al. 1993; Dumont & Collin-Souffrin 1990; Robinson et al. 1990; Fabian et al. 1989).
Generation of the broad
could have an asymmetric double-peaked shape
(e.g. Chen et al. 1989; Matt et al. 1993; Dumont & Collin-Souffrin 1990; Robinson et al. 1990; Fabian et al. 1989).
Generation of the broad 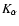 fluorescence lines as a result
of irradiation of a cold accretion disk was discussed by many
authors
(see, for example, Matt et al. 1991, 1992a; Matt & Perola 1992; Matt et al. 1993; Bao 1993; Martocchia et al. 2002 and references therein).
Recent X-ray observations of Seyfert galaxies, microquasars
and binary systems
(Fabian et al. 1995; Tanaka et al. 1995; Nandra et al. 1997a,b; Malizia et al. 1997; Sambruna et al. 1998; Yaqoob et al. 2001; Ogle et al. 2000; Miller et al. 2002 and references therein) confirm these
considerations in general and reveal broad emission lines in their
spectra with characteristic two-peak profiles.
A comprehensive
review by Fabian et al. (2000)
summarizes the detailed discussion of
theoretical aspects of possible scenarios for generation of broad
iron lines in AGNs. These lines are assumed to arise in the
innermost parts of the accretion disk, where the effects of
General Relativity (GR) must be taken into account, otherwise it
appears very difficult to find a natural explanation for observed
line profile.
fluorescence lines as a result
of irradiation of a cold accretion disk was discussed by many
authors
(see, for example, Matt et al. 1991, 1992a; Matt & Perola 1992; Matt et al. 1993; Bao 1993; Martocchia et al. 2002 and references therein).
Recent X-ray observations of Seyfert galaxies, microquasars
and binary systems
(Fabian et al. 1995; Tanaka et al. 1995; Nandra et al. 1997a,b; Malizia et al. 1997; Sambruna et al. 1998; Yaqoob et al. 2001; Ogle et al. 2000; Miller et al. 2002 and references therein) confirm these
considerations in general and reveal broad emission lines in their
spectra with characteristic two-peak profiles.
A comprehensive
review by Fabian et al. (2000)
summarizes the detailed discussion of
theoretical aspects of possible scenarios for generation of broad
iron lines in AGNs. These lines are assumed to arise in the
innermost parts of the accretion disk, where the effects of
General Relativity (GR) must be taken into account, otherwise it
appears very difficult to find a natural explanation for observed
line profile.
Numerical simulations of the line structure
are be found in a number of papers
(Ma 2002; Laor 1991; Fanton et al. 1997; Kojima 1991; Pariev & Bromley 1998,1997; Pariev et al. 2001; Bromley et al. 1997; Bao et al. 1994; Rauch & Blandford 1994; Bao & Stuchlik 1992; Bao 1993; Rauch & Blandford 1993; Ruszkowski M. 2000). They indicate that the accretion disks in Seyfert
galaxies are usually observed at the inclination angle 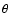 close to
close to
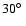 or less. This occurs because according to the
Seyfert galaxy models, an opaque dusty torque surrounds the
accretion disk which does not allow us to observe the disk at
larger inclination angles.
or less. This occurs because according to the
Seyfert galaxy models, an opaque dusty torque surrounds the
accretion disk which does not allow us to observe the disk at
larger inclination angles.
However, at inclination angles
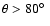 ,
new
observational manifestations of GR could arise. (Matt et al. 1993 discovered such phenomenon for a Schwarzschild black hole,
moreover the authors predicted that their results could be
applicable to a Kerr black hole over the range of parameters
exploited.)
The authors mentioned that this problem was not
analyzed in detail for a Kerr metric case and it would be
necessary to investigate this case. Below we do not use a specific
model on surface emissivity of accretion (we only assume that the
emitting region is narrow enough). But general statements (which
will be described below) can be generalized to a wide disk case
without any problem. Therefore, in this paper we check and confirm
their hypothesis for the Kerr metric case and for a Schwarzschild
black hole using other assumptions about surface emissivity of
accretion disks. In principle, such a phenomenon could be observed
in microquasars and X-ray binary systems where there are neutron
stars and black holes with stellar masses.
,
new
observational manifestations of GR could arise. (Matt et al. 1993 discovered such phenomenon for a Schwarzschild black hole,
moreover the authors predicted that their results could be
applicable to a Kerr black hole over the range of parameters
exploited.)
The authors mentioned that this problem was not
analyzed in detail for a Kerr metric case and it would be
necessary to investigate this case. Below we do not use a specific
model on surface emissivity of accretion (we only assume that the
emitting region is narrow enough). But general statements (which
will be described below) can be generalized to a wide disk case
without any problem. Therefore, in this paper we check and confirm
their hypothesis for the Kerr metric case and for a Schwarzschild
black hole using other assumptions about surface emissivity of
accretion disks. In principle, such a phenomenon could be observed
in microquasars and X-ray binary systems where there are neutron
stars and black holes with stellar masses.
In Sect. 3 we discuss disk models used for
simulations. In Sect. 4 we present the results of simulations
with two extra peaks in the line profile. These extra peaks exist
because of the gravitational lens effect in the strong field
approximation of GR. In Sect. 5 we discuss results of
calculations and present some conclusions.
We used an approach discussed in detail in papers by
Zakharov (1991,1994), Zakharov & Repin (1999,20002a), Zakharov & Repin (2003,2002b), Zakharov et al. (2002).
The approach was used in particular to simulate spectral line
shapes. For example, Zakharov et al. (2002) used this approach to simulate
the influence of a magnetic field on spectral line profiles. This
approach is based on results of a qualitative analysis
(which was done by Zakharov 1986, 1989 for different types of geodesics near a Kerr black hole).
The equations of photon motion in the Kerr metric are reduced to
the following system of ordinary differential equations
in dimensionless Boyer-Lindquist coordinates
(Zakharov 1991,1994; Zakharov & Repin 1999):
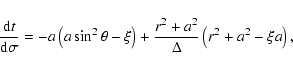 |
(1) |
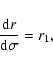 |
(2) |
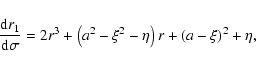 |
(3) |
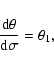 |
(4) |
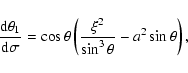 |
(5) |
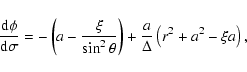 |
(6) |
where
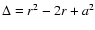 ;
;
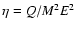 and
and
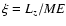 are the Chandrasekhar constants (Chandrasekhar 1983) which are
derived from the initial conditions of the emitted quantum in the
disk plane.
The system (1)-(6) has two first
integrals
are the Chandrasekhar constants (Chandrasekhar 1983) which are
derived from the initial conditions of the emitted quantum in the
disk plane.
The system (1)-(6) has two first
integrals
which can be used for the accuracy control of computation.
Solving Eqs. (1)-(6) for
monochromatic quanta emitted by a ring we can calculate a specral
line shape
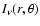 which is registered by a distant
observer at inclination angle
which is registered by a distant
observer at inclination angle 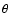 .
.
The numerical integration has been performed using
the combination of the Gear and Adams methods (Gear 1971) and
realized as the standard package by
Hindmarsh (1983), Petzold (1983), Hiebert & Shampine (1980). We obtain the entire disk
spectrum by summation of sharp ring spectra.
To simulate the structure of the emitted line it is necessary
first to choose a model for the emissivity of an accretion disk.
We exploit two different models, namely we consider a narrow and
thin disk moving in the equatorial plane near a Kerr black hole as
the first model and as we analyze the inner wide part of an
accretion disk with a temperature distribution which is chosen
according to the Shakura & Sunyaev (1973) with fixed inner and outer radii
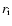 and
and 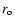 as the second model.
Usually a power law is
used for wide disk emissivity
(see, for example, Laor 1991; Martocchia et al. 2002; Martocchia & Matt 1996; Matt et al. 1991; Martocchia et al. 2000). However, other models for
emissivity can not be excluded for such a wide class of accreting
black holes, therefore, to demonstrate how another emissivity law
could change line profiles we investigate such a emissivity law.
as the second model.
Usually a power law is
used for wide disk emissivity
(see, for example, Laor 1991; Martocchia et al. 2002; Martocchia & Matt 1996; Matt et al. 1991; Martocchia et al. 2000). However, other models for
emissivity can not be excluded for such a wide class of accreting
black holes, therefore, to demonstrate how another emissivity law
could change line profiles we investigate such a emissivity law.
First, we assume that the source of the emitting quanta is a
narrow thin disk rotating in the equatorial plane of a Kerr black
hole. We also assume that the disk is opaque to radiation, so that
a distant observer situated on one disk side cannot measure the
quanta emitted from its other side.
For the sake of computational simplicity we suggest that the
spectral line is monochromatic in its co-moving frame. It can
really be adopted because even at T = 108 K the thermal line
width
appears to be much less than the Doppler line width associated
with the Kepler velocity of the disk rotation.
For second case of the Shakura-Sunyaev disk model, we assume
that the local emissivity is proportional to the surface element
and and T4, where T is a local temperature.
The emission intensity of the ring is proportional to its area.
The area of the emitting ring (width 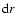 )
differs in the Kerr
metric from its classical expression
)
differs in the Kerr
metric from its classical expression
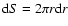 and should
be replaced with
and should
be replaced with
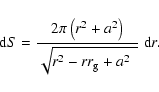 |
(9) |
Thus, the total flux density emitted by the disk and
registered by a distant observer is proportional to the integral
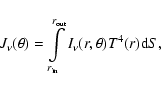 |
(10) |
where
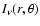 is obtained from the solution of
Eqs. (1)-(6), T(r) - from the
appropriate dependence for a hot disk and dS - from
Eq. (10).
is obtained from the solution of
Eqs. (1)-(6), T(r) - from the
appropriate dependence for a hot disk and dS - from
Eq. (10).
For simulation purposes we assume that
the emitting region lies entirely in the innermost region of the
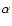 -disk (zone a) from
-disk (zone a) from
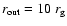 to
to
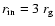 and the emission is monochromatic in the co-moving
frame
and the emission is monochromatic in the co-moving
frame![[*]](/icons/foot_motif.gif) .
The frequency of this emission set as unity
by convention.
.
The frequency of this emission set as unity
by convention.
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{MS3699f1.eps}
\end{figure}](/articles/aa/full/2003/28/aa3699/Timg40.gif) |
Figure 1:
Line profiles for
high inclination angles,
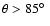 ,
due to
gravitational lens effects in the strong gravitational
field approach. The Kerr (rotation) parameter was
chosen as
a = 0.9981. The radii decrease
from top to bottom, the inclination angles increase from
left to right; their values are shown in each panel along
with the number of quanta included in the spectrum. ,
due to
gravitational lens effects in the strong gravitational
field approach. The Kerr (rotation) parameter was
chosen as
a = 0.9981. The radii decrease
from top to bottom, the inclination angles increase from
left to right; their values are shown in each panel along
with the number of quanta included in the spectrum. |
Spectral line profiles of a narrow ring observed at large inclination
angles
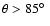 and different radii r are shown in
Fig. 1 (a Kerr metric generalization of Fig. 1 from
Matt et al. 1993 which was drawn using calculations for the
Schwarzschild case). The ring is assumed to move in the equatorial
plane of a Kerr black hole with an almost extreme rotation
parameter
a = 0.9981. The inclination angle increases from left
to right and the radial coordinate from bottom to top. The figure
indicates that there are practically no new specific features of
profiles, thus, the line profile remains one-peaked with a
maximum close to
and different radii r are shown in
Fig. 1 (a Kerr metric generalization of Fig. 1 from
Matt et al. 1993 which was drawn using calculations for the
Schwarzschild case). The ring is assumed to move in the equatorial
plane of a Kerr black hole with an almost extreme rotation
parameter
a = 0.9981. The inclination angle increases from left
to right and the radial coordinate from bottom to top. The figure
indicates that there are practically no new specific features of
profiles, thus, the line profile remains one-peaked with a
maximum close to
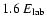 and a very long red wing without
any significant details.
and a very long red wing without
any significant details.
For the lowest radii there are no signatures of multiple peaks of
spectral line shapes even for high inclination angles (the bottom
row in Fig. 1 which corresponds to
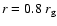 ).
).
Increasing the radius to
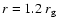 ,
an additional
blue peak arises in the vicinity of the blue maximum at the
highest inclination angle
,
an additional
blue peak arises in the vicinity of the blue maximum at the
highest inclination angle
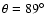 .
The red maximum
is so small that no details can be distinguished in its
structure. At lower inclination angles
.
The red maximum
is so small that no details can be distinguished in its
structure. At lower inclination angles
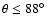 the blue maximum also has no details and the entire line
profile remains essentially one-peaked.
the blue maximum also has no details and the entire line
profile remains essentially one-peaked.
For
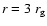 additional details in the blue peak
appear for
additional details in the blue peak
appear for
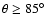 .
Thus, for
.
Thus, for
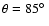 we
have a fairly clear bump, at
we
have a fairly clear bump, at
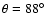 it changes into a
small complementary maximum and for
it changes into a
small complementary maximum and for
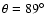 this
maximum becomes well-distinguished. Its position in the last case
differs significantly from the main maximum:
this
maximum becomes well-distinguished. Its position in the last case
differs significantly from the main maximum:
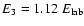 ,
,
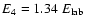 .
.
When further increasing the radius the red maximum also
bifurcates. This effect becomes visible for
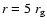 and
and
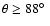 .
Thus, for
.
Thus, for
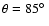 we have only a
faintly discernible (feebly marked) bump, but for
we have only a
faintly discernible (feebly marked) bump, but for
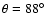 both complementary maxima (red and blue) arise. For
both complementary maxima (red and blue) arise. For
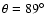 we have already four maxima in the line
profile:
we have already four maxima in the line
profile:
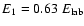 ,
,
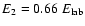 ,
,
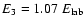 ,
,
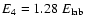 .
Note that the splitting for
the blue and red maxima is not equal, moreover,
.
Note that the splitting for
the blue and red maxima is not equal, moreover,
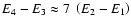 .
.
For
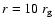 the profile becomes more narrow,
but the complementary peaks appear very distinctive. We have a
four-peak structure for
the profile becomes more narrow,
but the complementary peaks appear very distinctive. We have a
four-peak structure for
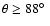 .
It is interesting
to note that for
.
It is interesting
to note that for
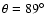 the energy of the blue
complementary peak is close to its laboratory value.
the energy of the blue
complementary peak is close to its laboratory value.
Note that the effect almost disappears when the radial coordinate
becomes less than 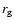 ,
i.e. for the orbits which could exist
only near a Kerr black hole.
,
i.e. for the orbits which could exist
only near a Kerr black hole.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{MS3699f2.eps}
\end{figure}](/articles/aa/full/2003/28/aa3699/Timg62.gif) |
Figure 2:
Details of a hot spot line profile for the most
distinctive case with
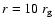 and
a = 0.9981 (see the top row of Fig. 1).
The images of all orders are counted. The left panel includes
all the quanta, registered at infinity with
and
a = 0.9981 (see the top row of Fig. 1).
The images of all orders are counted. The left panel includes
all the quanta, registered at infinity with
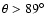 .
The right panel includes the quanta with .
The right panel includes the quanta with
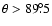 . . |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{MS3699f3.eps}
\end{figure}](/articles/aa/full/2003/28/aa3699/Timg63.gif) |
Figure 3:
Details of the line structure for an 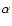 -disk in
the Schwarzschild metric with outer and inner edges of
emitting region equal to -disk in
the Schwarzschild metric with outer and inner edges of
emitting region equal to
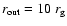 and
and
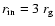 ,
respectively. The left panel includes all
the quanta, registered at infinity with ,
respectively. The left panel includes all
the quanta, registered at infinity with
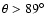 .
The right panel includes the quanta with .
The right panel includes the quanta with
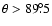 . . |
Figure 2 demonstrates the details of the spectrum
presented in the top row in Fig. 1. Thus, the left
panel includes all the quanta emitted by a hot spot at
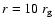 with
with
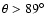 at infinity (the mean value could
be counted as
at infinity (the mean value could
be counted as 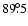 if the quanta distribution would be
uniform there) but with much higher resolution than in
Fig. 1. The spectrum has four narrow distinctive
maxima separated by lower emission intervals. In the right panel,
which includes all the quanta with
if the quanta distribution would be
uniform there) but with much higher resolution than in
Fig. 1. The spectrum has four narrow distinctive
maxima separated by lower emission intervals. In the right panel,
which includes all the quanta with
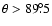 ,
the right complementary maxima is even higher
than the main one. The blue complementary maxima still remains
lower than its main counterpart, but it increases rapidly its
intensity with increasing inclination angle. It follows
immediately from the comparison of the left and right panels. The
"oscillation behavior" of the line profile between the maxima has
a pure statistical origin and is not caused by the physics
involved.
,
the right complementary maxima is even higher
than the main one. The blue complementary maxima still remains
lower than its main counterpart, but it increases rapidly its
intensity with increasing inclination angle. It follows
immediately from the comparison of the left and right panels. The
"oscillation behavior" of the line profile between the maxima has
a pure statistical origin and is not caused by the physics
involved.
As an illustration, a spectrum of an entire accretion disk at
high inclination angles in the Schwarzschild metric is shown in
Fig. 3. (In reality we have calculated geodesics for
the quanta trajectories in the Schwarzschild metric using the same
Eqs. (1)-(6) as for a Kerr metric, but assuming
there a = 0.01.) The emitting region (from 3 to
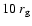 )
lies
as a whole in the innermost region of the
)
lies
as a whole in the innermost region of the 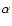 -disk
(the detailed description of this model was given by Lipunova & Shakura 2002; Shakura & Sunyaev 1973).
-disk
(the detailed description of this model was given by Lipunova & Shakura 2002; Shakura & Sunyaev 1973).
As follows from Fig. 3, the blue peak may consist of the two
components, whereas the red one remains unresolved.
The complicated structure of the line profile at large inclination
angles is explained by the multiple images of some pieces of the
hot ring. We point out that the result was obtained in the
framework of GR without any extra physical and astrophysical
assumptions about the character of the radiation etc. For a Kerr
black hole we assume only that the radiating ring is circular and
narrow.
The problem of multiple images in the accretion disks and extra
peaks was first considered by Matt et al. (1993)
(see also Bao & Stuchlik 1992; Bao 1993; Bao et al. 1994, 1996). Using numerical simulations
Matt et al. (1993) proved the statement for the Schwarzschild metric and
suggested that the phenomenon is applicable to a Kerr metric over
the range of parameters that the authors have analyzed. They noted
also that it is necessary to perform detailed calculations to
confirm their hypothesis. We verified and confirmed their
conjecture without any assumptions about a specific distribution
of surface emissivity or accretion disk model (see Figs. 1 and
2).
We confirmed also their conclusion that extra peaks
are generated by photons which are emitted by the far side of the
disk, therefore we have a manifestation of gravitational lensing
in the strong gravitational field approach for GR.
Some possibilities to observe considered features of spectral
line profiles were considered by Matt et al. (1993), Bao (1993). The authors
argued that there are non-negligible chances to observe such
phenomenon in some AGNs and X-ray binary systems. For example,
Bao (1993) suggested that NGC 6814 could be a candidate to
demonstrate such a phenomenon
(but Madejski et al. 1993 found that
the peculiar properties of NGC 6814 are caused by a cataclysmic
variable like an AM Herculis System).
However, it is clear that in general the probability to observe
objects where one could find such features of spectral lines is
small. Moreover, even if the inclination angle is very close to
 ,
the thickness of the disk (shield or a torus around
an accretion disk) may not allow us to look at the inner part of
accretion disk. Here, discuss astrophysical situations when the
the inclination angle of the accretion disk is high enough.
,
the thickness of the disk (shield or a torus around
an accretion disk) may not allow us to look at the inner part of
accretion disk. Here, discuss astrophysical situations when the
the inclination angle of the accretion disk is high enough.
About 1% of all AGN or microquasar systems could have an
inclination angle of the accretion disk >
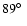 .
For
example, Kormendy et al. (1996) found that NGC 3115 has a very high
inclination angle about of
.
For
example, Kormendy et al. (1996) found that NGC 3115 has a very high
inclination angle about of
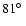 (Kormendy & Richstone 1992 discovered a
massive dark object
(Kormendy & Richstone 1992 discovered a
massive dark object
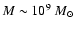 (probably a massive black
hole) in NGC 3115). Perhaps we have a much higher probability to
observe such a phenomenon in X-ray binary systems where black
holes with stellar masses could be. Taking into account the
precession which is actually observed for some X-ray binary
systems (for example, there is a significant precession of the
accretion disk for the SS433 binary system
(Cherepashchuk 2002)
(probably a massive black
hole) in NGC 3115). Perhaps we have a much higher probability to
observe such a phenomenon in X-ray binary systems where black
holes with stellar masses could be. Taking into account the
precession which is actually observed for some X-ray binary
systems (for example, there is a significant precession of the
accretion disk for the SS433 binary system
(Cherepashchuk 2002)![[*]](/icons/foot_motif.gif) , moreover since the
inclination of the orbital plane is high (
, moreover since the
inclination of the orbital plane is high (
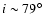 for
this object) sometimes we may observe almost edge-on accretion
disks of such objects. Observations indicated that there is a
strong evidence that the optically bright accretion disk in SS433
is in a supercritical regime of accretion. The first description
of a supercritical accretion disk was given by Shakura & Sunyaev (1973). Even
now such a model is discussed to explain observational data for SS433 (Cherepashchuk 2002). We used the temperature distribution from
the Shakura-Sunyaev model (Lipunova & Shakura 2002; Shakura & Sunyaev 1973) for the inner
part of accretion disk to simulate shapes of lines which could be
emitted from this region (Fig. 3). Therefore, we
should conclude that the properties of spectral line shapes
discovered by Matt et al. (1993) are confirmed also for such emissivity
(temperature) distributions which correspond to the Shakura-Sunyaev model.
for
this object) sometimes we may observe almost edge-on accretion
disks of such objects. Observations indicated that there is a
strong evidence that the optically bright accretion disk in SS433
is in a supercritical regime of accretion. The first description
of a supercritical accretion disk was given by Shakura & Sunyaev (1973). Even
now such a model is discussed to explain observational data for SS433 (Cherepashchuk 2002). We used the temperature distribution from
the Shakura-Sunyaev model (Lipunova & Shakura 2002; Shakura & Sunyaev 1973) for the inner
part of accretion disk to simulate shapes of lines which could be
emitted from this region (Fig. 3). Therefore, we
should conclude that the properties of spectral line shapes
discovered by Matt et al. (1993) are confirmed also for such emissivity
(temperature) distributions which correspond to the Shakura-Sunyaev model.
Thus, such properties of spectral line shapes are robust enough
with respect to wide variations of rotational parameters of black
holes and the surface emissivity of accretion disks as it was
predicted by Matt et al. (1993). In this work their conjecture was
confirmed not only for the Kerr black hole case but also for other
dependences of surface emissivity of the accretion disk.
Acknowledgements
A.F.Z. is grateful to E. F. Zakharova for the kindness and
support necessary to complete this work. AFZ would like to thank
Dipartimento di Fisica Universita di Lecce, INFN, Sezione di Lecce
and the National Astronomical Observatories of the Chinese Academy
of Sciences
for a hospitality and profs. F. DePaolis,
G. Ingrosso, J. Wang and Dr. Z. Ma for very useful discussions.
S.V.R. is very grateful to Prof. E. Starostenko,
Dr. A. Salpagarov and Dr. O. Sumenkova for the possibility of
working on this problem.
This work was supported by the National Natural Science Foundation
of China, No. 10233050. This work has been partly supported also
by the Russian Foundation for Basic Research, grant 00-02-16108.
The authors thank the anonymous referee for useful remarks.
-
Bao, G. 1993, ApJ, 409, L41
NASA ADS
-
Bao, G., Hadrava, P., & Ostgaard, E. 1994,
ApJ, 435, 55
NASA ADS
-
Bao, G., & Stuchlik, Z. 1992, ApJ, 400, 163
NASA ADS
-
Bao, G., Hadrava, P., & Ostgaard, E. 1996,
ApJ, 464, 684
NASA ADS
-
Bromley, B. C., Chen, K., & Miller, W. A. 1997, ApJ, 475, 57
NASA ADS
-
Carter, B. 1968, Phys. Rev. D, 174, 1559
-
Chandrasekhar, S. 1983, Mathematical Theory of Black Holes
(Oxford: Clarendon Press)
-
Chen, K., Halpern, J. P., & Filippenko, A. V. 1998,
ApJ, 344, 115
NASA ADS
-
Cherepashchuk, A. M. 2002, Space Sci. Rev., 102, 23
NASA ADS
-
Cui, W., Zhang, S. N., & Chen, W. 1998,
ApJ, 492, L53
NASA ADS
-
Cunningham, C. T., & Bardeen, J. M. 1973, ApJ, 183, 237
-
Cunningham, C. T. 1975, ApJ, 202, 788
NASA ADS
-
Dumont, A. M., & Collin-Souffrin, S. 1990, A&AS, 83, 71
NASA ADS
-
Fabian, A. C., Rees, M., Stella, L., & White, N. E. 1989,
MNRAS, 238, 729
NASA ADS
-
Fabian, A. C., Nandra, K., Reynolds, C. S., et al. 1995,
MNRAS, 277, L11
NASA ADS
-
Fabian, A. C., Iwazawa, K., Reynolds, C. S., & Young, A. J. 2000,
PASP, 112, 1145
NASA ADS
-
Fanton, C., Calvani, M., de Felice, F., & Cadez, A. 1997,
PASJ, 49, 159
NASA ADS
-
Gear, C. W. 1971, Numerical Initial Value Problems in Ordinary
Differential Equations (Englewood Cliffs, NY: Prentice Hall)
-
Greiner, J. 2000, in Cosmic Explosions, Proc. of 10th
Annual Astrophysical Conf. in Maryland, ed. S. Holt, &
W. W. Zang, AIP Conf. Proc., 522, 307 [astro-ph/9912326]
-
Hiebert, K. L., & Shampine, L. F. 1980, Implicitly Defined Output
Points for Solutions of ODE-s. Sandia report sand80-0180
-
Hindmarsh, A. C. 1983,
ODEpack, a systematized collection of ODE solvers,
in Scientific Computing, ed. R. S. Stepleman (Amsterdam: North-Holland),
55
-
Karas, V., Vokrouhlický, D., & Polnarev, A. G. 1992,
MNRAS, 259, 569
NASA ADS
-
Kojima, Y. 1991, MNRAS, 250, 629
NASA ADS
-
Kormendy, J., & Richstone, D.
1992, ApJ, 393, 559
NASA ADS
-
Kormendy, J., Bender, R., Richstone, D., et al.
1996, ApJ, 459, L57
NASA ADS
-
Landau, L. D., & Lifshitz, E. M. 1971, The classical theory of fields
(Oxford: Pergamon)
-
Laor, A. 1991, ApJ, 376, 90
NASA ADS
-
Lipunova, G. V., & Shakura, N. I.
2002, Astron. Rep., 46, 366
NASA ADS
-
Ma, Zhen-Guo 2002, Chin Phys. Lett., 19, 1537
-
Madejski, G. M., Done, C., Turner, T. J., et al. 1993,
Nature, 365, 626
NASA ADS
-
Malizia, A., Bassani, L., Stephen, J. B., et al.
1997, ApJSS, 113, 311
-
Martocchia, A., & Matt, G. 1996,
MNRAS, 282, L53
NASA ADS
-
Martocchia, A., Karas, V., & Matt, G. 2000,
MNRAS, 312, 817
NASA ADS
-
Martocchia, A., Matt, G., & Karas, V. 2002,
A&A, 383, L23
NASA ADS
-
Martocchia, A., Matt, G., & Karas, V., et al. 2002,
A&A, 387, 215
NASA ADS
-
Matt, G., Fabian, A. C., & Ross, R. R. 1993,
MNRAS, 262, 179
NASA ADS
-
Matt, G., Perola, G. C., & Piro, L. 1991,
A&A, 267, 643
NASA ADS
-
Matt, G., & Perola, G. C. 1992,
MNRAS, 259, 63
NASA ADS
-
Matt, G., Perola, G. C., Piro, L., & Stella, L. 1992a,
A&A, 257, 63
NASA ADS
-
Matt, G., Perola, G. C., Piro, L., & Stella, L. 1992b,
A&A, 263, 453
NASA ADS
-
Matt, G, Perola, G. C., & Stella, L. 1993,
A&A, 267, 643
NASA ADS
-
Miller, J. M., Fabian, A. C., Wijnands, R., et al. 2002,
ApJ, 570, L69
NASA ADS
-
Mirabel, I. F. 2001, Ap&SS, 276, 319
-
Mirabel, I. F., & Rodriguez, L. F. 2002, Sky & Telescope, May, 33
-
Misner, C. W., Thorne, K. S., & Wheeler, J. A. 1973, Gravitation
(San Francisco: W. H. Freeman and Company)
-
Nandra, K., George, I. M., Mushotzky, R. F., et al.
1997a, ApJ, 476, 70
NASA ADS
-
Nandra, K., George, I. M., Mushotzky, R. F., et al.
1997b, ApJ, 477, 602
NASA ADS
-
Novikov, I. D., & Thorne, K. S. 1973,
in Black Holes, ed. C. De Witt, & B. S. DeWitt (New York: Gordon & Breach), 334
-
Ogle, P. M., Marshall, H. L., Lee, J. C., et al. 2000,
ApJ, 545, L81
NASA ADS
-
Pariev, V. I., & Bromley, B. C. 1997,
Line Emission from an Accretion Disk around Black Hole: Effects
of the Disk Structure, in Proc. of the 8th Annual October
Astrophysics Conference in Maryland
Accretion Processes in Astrophysical Systems: Some Like it
Hot!
College Park, MD, October 1997,
ed. S. S. Holt, & T. R. Kallman, AIP Conf. Proc. 431, 273
[astro-ph/9711214]
-
Pariev, V. I., & Bromley, B. C. 1998, ApJ, 508, 590
NASA ADS
-
Pariev, V. I., Bromley, B. C., & Miller, W. A. 2001,
ApJ, 547, 649 [astro-ph/0010318]
NASA ADS
-
Paul, B., Agrawal, P. C., Rao, A. R., et al.
1998, ApJ, 492, L63
NASA ADS
-
Petzold, L. R. 1983, SIAM J. Sci. Stat. Comput., 4, 136
-
Rauch, K. P., & Blandford, R. D. 1993, Caltech Preprint GRP-334
-
Rauch, K. P., & Blandford, R. D. 1994, ApJ, 421, 46
NASA ADS
-
Robinson, A., Perez, E., & Binette, L. 1990, MNRAS, 246, 349
NASA ADS
-
Romanova, M. M., Ustyugova, G. V., Koldoba, A. V.,
et al.
1998, ApJ, 500, 703
NASA ADS
-
Ruszkowski, M. 2000,
MNRAS, 315, 1
NASA ADS
-
Sambruna, R. M., George, I. M., Mushotsky, R. F.,
et al.
1998, ApJ, 495, 749
NASA ADS
-
Shakura, N. I. 1972, AZh, 49, 921
NASA ADS
-
Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337
NASA ADS
-
Sharp, N. A. 1981, J. Comput. Phys., 41, 295
NASA ADS
-
Sulentic, J. W., Marziani, P., Zwitter, T.,
et al.
1998a, ApJ, 501, 54
NASA ADS
-
Sulentic, J. W., Marziani, P., & Calvani, M. 1998b,
ApJ, 497, L65
NASA ADS
-
Tanaka, Y., Nandra, K., Fabian, A. C.,
et al.
1995, Nature, 375, 659
NASA ADS
-
Weawer, K. A., Krolik, J. H., & Pier, E. A. 1998, ApJ, 498, 213
NASA ADS
-
Yaqoob, T., Serlemitsos, P. J., Turner, T. J., et al.
1996, ApJ, 470, L27
NASA ADS
-
Yaqoob, T., McKernan, B., Ptak, A.,
et al.
1997, ApJ, 490, L25
NASA ADS
-
Yaqoob, T., George, I. M., Nandra, K., et al. 2001,
ApJ, 546, 759
NASA ADS
-
Zakharov, A. F. 1986,
Sov. Phys. - Journ. Experim. and Theor.
Phys., 64, 1
-
Zakharov, A. F. 1989,
Sov. Phys. - Journ. Experimental and Theoretical
Phys., 68, 217
-
Zakharov, A. F. 1991, SvA, 35, 147
NASA ADS
-
Zakharov, A. F. 1993, Preprint MPA 755
-
Zakharov, A. F. 1994, MNRAS, 269, 283
NASA ADS
-
Zakharov, A. F. 1995, On the Hot Spot near a Kerr Black Hole,
In 17th Texas Symposium on Relativistic Astrophysics, Ann. NY
Academy of Sciences, 1995, 759, 550
-
Zakharov, A. F., & Repin, S. V. 1999, Astron. Rep., 43, 705
NASA ADS
-
Zakharov, A. F., & Repin, S. V. 2002a, Astron. Rep., 46, 360
NASA ADS
-
Zakharov, A. F., & Repin, S. V. 2002b,
in Proc. of the
Eleven Workshop
on General Relativity and Gravitation in Japan, ed. J. Koga, T. Nakamura, K. Maeda, & K. Tomita (Tokyo: Waseda University), 68
-
Zakharov, A. F., Kardashev, N. S., Lukash, V. N., & Repin, S. V. 2002, MNRAS, accepted
[astro-ph/0212008]
-
Zakharov, A. F., & Repin, S. V. 2003, Adv. in Space Res., accepted
Copyright ESO 2003
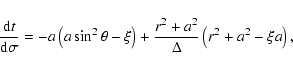
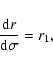
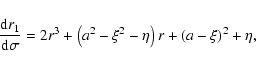
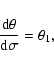
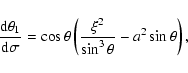
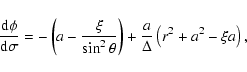
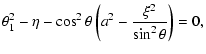
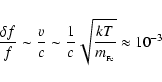
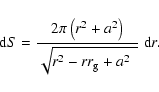
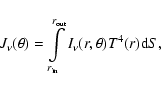
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{MS3699f1.eps}
\end{figure}](/articles/aa/full/2003/28/aa3699/Timg40.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{MS3699f2.eps}
\end{figure}](/articles/aa/full/2003/28/aa3699/Timg62.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{MS3699f3.eps}
\end{figure}](/articles/aa/full/2003/28/aa3699/Timg63.gif)