References: (1) Bruch & Diaz (1998), (2) this work,
Sect. 7, (3) Perryman et al. (1998), (4)
Abell (1966), (5) Cahn & Kaler (1971), (6) Maciel (1984),
(7) Cahn et al. (1992), (8) Vennes & Thorstensen (1996), (9)
Wood & Marsh (1991), (10) Walton et al. (1993), (11)
Pottasch (1996).
Analysing PCEBs is not only interesting in itself, it is also
important in the context of CV formation and evolution (see Sects. 1
and 2). Discussing the properties of our sample of PCEBs in the
framework of the present-day CV population requires to select
those systems which are representative for the former progenitors of
the current CV population. Only PCEBs which will evolve into CVs in
less than the Hubble time (assuming
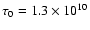 yrs yrs![[*]](/icons/foot_motif.gif) )
satisfy this condition. To distinguish these systems from the PCEBs
which are different from the former progenitors of the present CVs we
refer to them as pre-CVs (see also Sect. 1). )
satisfy this condition. To distinguish these systems from the PCEBs
which are different from the former progenitors of the present CVs we
refer to them as pre-CVs (see also Sect. 1).
Applying this selection criterion, we find 14 (16) pre-CV candidates in
our sample (Table 2) when assuming
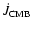 ( (
 ). Although ). Although
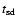 depends strongly on the assumed AML for some
individual systems (e.g. EG UMa, Fig. 6; see also
Fig. 8), the number of pre-CVs among the PCEB sample is
nearly independent on it (see Table 2,
Fig. 8). From the sample of pre-CVs 5 (3) will
initiate mass transfer at orbital periods >3 h whereas the other 9
(13) systems will start their CV life in or below the orbital period
gap. This finding is in good agreement with the prediction of
King et al. (1994) that
depends strongly on the assumed AML for some
individual systems (e.g. EG UMa, Fig. 6; see also
Fig. 8), the number of pre-CVs among the PCEB sample is
nearly independent on it (see Table 2,
Fig. 8). From the sample of pre-CVs 5 (3) will
initiate mass transfer at orbital periods >3 h whereas the other 9
(13) systems will start their CV life in or below the orbital period
gap. This finding is in good agreement with the prediction of
King et al. (1994) that 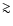 67% of CVs will start mass transfer
near or below the period gap. Possible observational selection effects
will be discussed in Sect. 9. 67% of CVs will start mass transfer
near or below the period gap. Possible observational selection effects
will be discussed in Sect. 9.
A further test on whether the current pre-CV population is a
representative sample of progenitors for the present CV population
comes from comparing their space density to that of CVs. An estimate
of the space density of PCEBs/pre-CVs requires obviously the knowledge
of their distances.
7 Distance estimates
We estimate the distances to the systems in Table 1 for
which no previous distance determination has been available in the
literature using the following methods.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{3351f9.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg258.gif) |
Figure 9:
The HST/STIS echelle spectrum of HZ9 along with the best-fit
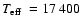 K pure hydrogen white dwarf model, assuming K pure hydrogen white dwarf model, assuming
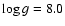 .
The sharp "absorption dips'' at the red end of the spectrum
are due to gaps between the echelle orders. .
The sharp "absorption dips'' at the red end of the spectrum
are due to gaps between the echelle orders. |
For all but one system without a published distance estimate
ultraviolet (UV) spectroscopy is available in the public archives of
the International Ultraviolet Explorer (IUE) and the
Hubble Space Telescope. We fitted the UV data listed by
Table 3 with pure-hydrogen white dwarf model spectra computed with
the code described by Gänsicke et al. (1995), fixing
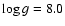 ,
i.e. ,
i.e.
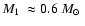 .
The free parameters of this fit were,
hence, the white dwarf temperature .
The free parameters of this fit were,
hence, the white dwarf temperature
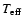 and the scaling factor
and the scaling factor
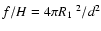 ,
with f the observed flux and H the Eddington
flux of the model spectra. The results from our fits are given in
Table 3. Overall, the white dwarf temperatures that we derived here
are in good agreement with the published values. ,
with f the observed flux and H the Eddington
flux of the model spectra. The results from our fits are given in
Table 3. Overall, the white dwarf temperatures that we derived here
are in good agreement with the published values.
Fixing the surface gravity (= white dwarf mass) in the fit
introduces a systematic uncertainty in the derived distances, as the
white dwarf radius obviously depends on the assumed mass. However, it
is important to notice that also the white dwarf temperature derived
from the fit depends on the assumed mass, with higher (lower)
temperatures resulting for higher (lower) 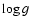 .
This effect
compensates to some extent the .
This effect
compensates to some extent the
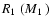 dependence, and the error
in the spectroscopic parallaxes is
dependence, and the error
in the spectroscopic parallaxes is
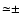 15% for an assumed
range 15% for an assumed
range
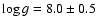 (i.e.
(i.e.
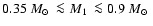 ),
which covers probably most of the analysed objects.
The Hyades member HZ 9 can be used to estimate the robustness of our
distance estimate and error analysis. From our model fit to
unpublished HST STIS spectroscopy, we find a temperature
which is slightly below the low end of the range quoted by
Guinan & Sion (1984), which was based on the analysis of
IUE spectroscopy. However, the much better HST data
available now clearly shows the 1400 Å quasimolecular H2+absorption which indicates a temperature <20 000 K
(Fig. 9). We derive from the scaling factor of the model a
distance of ),
which covers probably most of the analysed objects.
The Hyades member HZ 9 can be used to estimate the robustness of our
distance estimate and error analysis. From our model fit to
unpublished HST STIS spectroscopy, we find a temperature
which is slightly below the low end of the range quoted by
Guinan & Sion (1984), which was based on the analysis of
IUE spectroscopy. However, the much better HST data
available now clearly shows the 1400 Å quasimolecular H2+absorption which indicates a temperature <20 000 K
(Fig. 9). We derive from the scaling factor of the model a
distance of 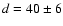 pc, which is entirely consistent with the
Hipparcos-measured parallax (Perryman et al. 1998). pc, which is entirely consistent with the
Hipparcos-measured parallax (Perryman et al. 1998).
For GK Vir, we had to fix the temperature to the value derived by
Fulbright et al. (1993) as the temperature-sensitive
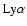 absorption
line is entirely blended with geocoronal emission in the available IUE
spectrum.
absorption
line is entirely blended with geocoronal emission in the available IUE
spectrum.
A final note concerns the distance of LM Com. Orosz et al. (1999)
quote a distance of 290-308 pc, which they base on a lengthy
discussion of the white dwarf contribution to the observed R band
magnitude. However, as the contamination of the M-dwarf is lowest in
the blue, we re-examined the distance of LM Com scaling a
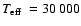 K, K,
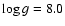 model to
model to
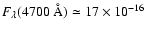
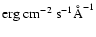 (measured from
Orosz et al. 1999, Fig. 7), and find d=170 pc.
(measured from
Orosz et al. 1999, Fig. 7), and find d=170 pc.
Considering the rather similar properties of the sdB primaries in
HW Vir, HS 0705+6700, PG 1017-086, and NY Vir ( , ,
 ,
see
Table 1), we computed (crude) distances estimates by scaling the
distance of HW Vir (d=171 pc, V=10.6; Wood & Saffer 1999)
to the observed V magnitudes of the other sdB PCEBs (HS 0705+6700:
V=14.8; PG 1017-086: V=14.4; NY Vir: V=13.2). This estimate
ignores possible extinction as well as differences in ,
see
Table 1), we computed (crude) distances estimates by scaling the
distance of HW Vir (d=171 pc, V=10.6; Wood & Saffer 1999)
to the observed V magnitudes of the other sdB PCEBs (HS 0705+6700:
V=14.8; PG 1017-086: V=14.4; NY Vir: V=13.2). This estimate
ignores possible extinction as well as differences in
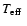 and
and
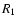 . .
Table 3:
Distance estimates for PCEBs, see text.
|
Object |
Instrument |
Dataset |
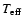 [K] [K] |
d [pc] |
|
EG UMa |
HST/FOS |
y16u0502t |
13 400 |
32 |
| HR Cam |
HST/STIS |
o6gj02020 |
20 800 |
72 |
| UZ Sex |
IUE |
swp27393 |
17 200 |
35 |
| BPM 6502 |
IUE |
swp27351 |
21 400 |
25 |
| HZ 9 |
HST/STIS |
o5dma6010 |
17 400 |
40 |
| CC Cet |
IUE |
swp27392 |
25 000 |
89 |
| GK Vir |
IUE |
swp07459 |
48 800* |
350 |
*Temperature fixed to the value given by
Fulbright et al. (1993).
![\begin{figure}
\par\includegraphics[angle=270,width=12.3cm,clip]{3351f10.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg274.gif) |
Figure 10:
The currently known populations of single
white dwarfs (top) and PCEBs (bottom) as a function of their effective
temperature. Here, we follow McCook & Sion (1999) and plot the
spectral temperature index,
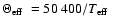 ,
which is a direct indicator of the age of the white dwarfs. The grey
shaded histograms represent systems which have been found in the PG
survey. Obviously, there exists a population of cool single white
dwarfs whereas PCEBs white dwarfs are generally hot and young. ,
which is a direct indicator of the age of the white dwarfs. The grey
shaded histograms represent systems which have been found in the PG
survey. Obviously, there exists a population of cool single white
dwarfs whereas PCEBs white dwarfs are generally hot and young. |
8 Space densities
Inspection of Table 2 shows that 12 PCEBs from our
sample are within 100 pc (including RE 1016-053,
d=75-109 pc).
This gives an "observed'' space density of
(=
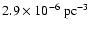 )
which can be considered to be a
conservative lower limit on the PCEB space density as
the presently known PCEB sample is systematically dominated by young
PCEBs (see Sect. 5.1, Table 2). Accounting for this
bias, we estimate the true PCEB space density to be: )
which can be considered to be a
conservative lower limit on the PCEB space density as
the presently known PCEB sample is systematically dominated by young
PCEBs (see Sect. 5.1, Table 2). Accounting for this
bias, we estimate the true PCEB space density to be:
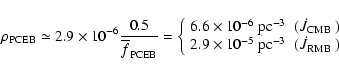 |
(12) |
where
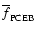 is the mean fractional PCEB
life time that the systems have already passed through.
The substantial difference between the estimates of
is the mean fractional PCEB
life time that the systems have already passed through.
The substantial difference between the estimates of
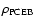 for the two AML prescriptions results from the
fact that the mean evolution time scale is significantly longer for
for the two AML prescriptions results from the
fact that the mean evolution time scale is significantly longer for
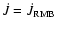 and, thus, the existence of more old and yet undetected PCEBs is
predicted. However,
even the higher value of
and, thus, the existence of more old and yet undetected PCEBs is
predicted. However,
even the higher value of
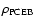 ,
assuming ,
assuming
 ,
is
still significantly below the theoretical predictions of de Kool & Ritter (1993,
their Fig. 4) indicating that our sample is
probably not only biased towards young systems (see
Sect. 9.3). ,
is
still significantly below the theoretical predictions of de Kool & Ritter (1993,
their Fig. 4) indicating that our sample is
probably not only biased towards young systems (see
Sect. 9.3).
Requiring
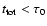 for PCEBs which can be considered
pre-CVs, we find 6 (
for PCEBs which can be considered
pre-CVs, we find 6 (
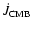 )
and 7 ( )
and 7 (
 )
of these systems within 100 pc,
resulting in lower limits on their space density )
of these systems within 100 pc,
resulting in lower limits on their space density
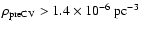 (
(
 )
and )
and
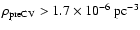 (
(
 ).
We estimate the actual pre-CV space density, again taking into account
age and evolution time scale and find ).
We estimate the actual pre-CV space density, again taking into account
age and evolution time scale and find
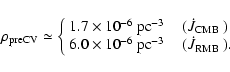 |
(13) |
Our estimate of the current pre-CV space density allows an
estimate for the present CV space density. Considering the average of
the pre-CV lifetime (
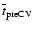 )
of the systems
we find within 100 pc and following Politano (1996) in assuming
that the CV birthrate has been constant since )
of the systems
we find within 100 pc and following Politano (1996) in assuming
that the CV birthrate has been constant since
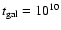 yrs we get yrs we get
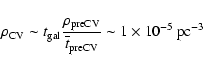 |
(14) |
for both angular momentum loss prescriptions.
Considering the assumptions involved and the small number statistics
of the known pre-CV sample, this result has to be regarded as a rather
rough estimate. Nevertheless, our estimate for
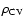 is
in agreement with the high end of current observational estimates
(see Gänsicke et al. 2002) but below theoretical predictions:
is
in agreement with the high end of current observational estimates
(see Gänsicke et al. 2002) but below theoretical predictions:
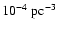 (de Kool 1992) to
(de Kool 1992) to
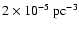 (Politano 1996). As we will
discuss in Sect. 9.4, the presently known sample
of PCEBs/pre-CVs is very likely incomplete not only with respect to
those systems containing cold white dwarfs, but also to those systems
containing an early-type secondary. Hence, we would like to stress
that all the space densities derived above should be regarded as lower
limits to the true values.
(Politano 1996). As we will
discuss in Sect. 9.4, the presently known sample
of PCEBs/pre-CVs is very likely incomplete not only with respect to
those systems containing cold white dwarfs, but also to those systems
containing an early-type secondary. Hence, we would like to stress
that all the space densities derived above should be regarded as lower
limits to the true values.
Considering the binary age postulate (BAP) of
King & Schenker (2002) outlined in Sect. 2 we note that assuming
reduced magnetic braking indeed leads to an increase of the averaged
evolution time scale for pre-CVs but the presently known PCEB population is too
small and too strongly biased to prove or disprove the BAP scenario.
9 Observational selection effects
We have shown that the known population of PCEBs is dominated by young
hot systems (Sect. 5.1), and that, applying the
current theories of (pre-)CV evolution, the majority of them will
remain in a detached configuration for many 108 yrs to several
109 yrs (Sect. 6) - sufficiently long for their
white dwarf primaries to cool - depending on
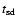 and
and 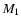 - to
temperatures - to
temperatures
 K (see
Fig. 7)
These findings strongly suggest that - if the reality about AML in
PCEBs is somewhere bracketed between the prescriptions of K (see
Fig. 7)
These findings strongly suggest that - if the reality about AML in
PCEBs is somewhere bracketed between the prescriptions of
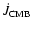 and
and
 - the currently known population of PCEBs is highly
incomplete. - the currently known population of PCEBs is highly
incomplete.
As a test for possible selection effect, we compare the effective
temperature distribution of the white dwarfs in our PCEB sample to
that of field white dwarfs.
9.1 The known PCEB population vs. the McCook & Sion (1999)
white dwarf population
McCook & Sion (1999) present a catalogue of 1793 spectroscopically
identified white dwarfs, including information on the white dwarf
temperatures where available. The temperature distribution of the
McCook & Sion white dwarf sample peaks at temperatures
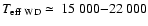 K (top panel of
Fig. 10) with a mean effective temperature of K (top panel of
Fig. 10) with a mean effective temperature of
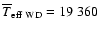 K. Also shown in
Fig. 10 (bottom panel) is the temperature
distribution of the PCEB white dwarf primaries from our sample
(Table 1),
which also peaks in the range K. Also shown in
Fig. 10 (bottom panel) is the temperature
distribution of the PCEB white dwarf primaries from our sample
(Table 1),
which also peaks in the range
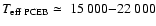 K, but lacks the
low-temperature tail seen in the McCook & Sion sample.
The average temperature of the white dwarfs in our PCEB sample is K, but lacks the
low-temperature tail seen in the McCook & Sion sample.
The average temperature of the white dwarfs in our PCEB sample is
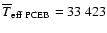 K.
Using K.
Using 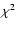 statistics, the significance that two distributions are
different is
statistics, the significance that two distributions are
different is
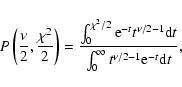 |
(15) |
where 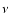 is the number of degrees of freedom, i.e. the number of bins, and
is the number of degrees of freedom, i.e. the number of bins, and
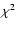 is given by:
is given by:
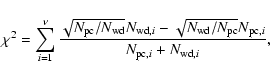 |
(16) |
with Ni the number of objects in bin i,
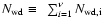 and
and
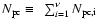 .
We obtain
for the probability that the two distributions are different: .
We obtain
for the probability that the two distributions are different:
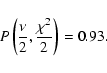 |
(17) |
It appears, hence, likely that the PCEB white dwarfs are indeed on
average hotter - and therefore younger - than the single field white
dwarfs of (McCook & Sion 1999).
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{3351f11.ps}\hspace*{0.2cm}
\includegraphics[angle=270,width=8.8cm,clip]{3351f11b.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg302.gif) |
Figure 11:
Simulated colours for PCEBs containing
a white dwarf with
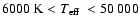 and a companion with a
spectral type in the range K0 to M6. The left panel shows in gray the
PCEB parameter space that do not fulfill the selection
criterion of the PG survey (U-B<0.46).
and a companion with a
spectral type in the range K0 to M6. The left panel shows in gray the
PCEB parameter space that do not fulfill the selection
criterion of the PG survey (U-B<0.46). |
9.2
PCEB and field white dwarfs in the Palomar Green survey
Whereas the McCook & Sion (1999) is a heterogenous catalogue of
white dwarfs identified by various means, it is of fundamental
interest to compare the properties of white dwarfs in PCEBs and of
field white dwarfs drawn from a single survey. Inspection of
Table 1 shows that five of our PCEBs with a white dwarf
primary are contained in the Palomar-Green (PG) survey
(Green et al. 1986): UZ Sex, CC Cet, LM Com, GK Vir and
NN Ser. Figure 10 shows the temperature distribution
of both the field white dwarfs (upper panel) and of the PCEB white
dwarfs (bottom panel) from the PG survey. The mean values of the
effective temperatures for PCEB white dwarfs and single white dwarfs
contained in the PG survey are
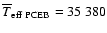 K and K and
 K, respectively.
The mean effective temperature of the white dwarfs in PCEBs
is again somewhat higher than that of their field relatives.
As there are only five PCEBs with a white dwarf primary
included in the PG-survey, the statistic is very poor but for completeness
we give the probability that the difference of the two distributions (see the
shaded histograms in Fig. 10) can be explained by
chance K, respectively.
The mean effective temperature of the white dwarfs in PCEBs
is again somewhat higher than that of their field relatives.
As there are only five PCEBs with a white dwarf primary
included in the PG-survey, the statistic is very poor but for completeness
we give the probability that the difference of the two distributions (see the
shaded histograms in Fig. 10) can be explained by
chance
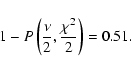 |
(18) |
Obviously, from this subset of systems we can neither say
that the white dwarfs in PCEBs are
systematically hotter and younger than their field relatives nor can
we exclude that this is the case.
In the next section we will discuss observational selection effects.
This will give us a hint which possibility is more likely.
Notice, the probabilities given by Eqs. (17) and (18) are calculated by
neglecting the very few detected extremely old single white dwarfs,
i.e. using only 9 (Eq. (17)) respectively 5 (Eq. (18)) bins.
9.3 Finding PCEBs
Based on the presently available data (Sects. 9.1 and
9.2), we can not exclude that the white dwarfs in PCEBs
are - on average - systematically hotter (and younger) than
single white dwarfs. This statement may be entirely based on selection
effects skewing the temperature/age distribution of the white dwarfs
in the known PCEB population. It is, however, very difficult to assess
this bias quantitatively. We list in Appendix A for the PCEBs from our
sample in Table 1 (1) the way that they were discovered
in the first place, and (2) the way that their binarity has been
identified. Inspection of these notes shows that the vast majority of the
known PCEBs have been identified in the first place because
of their white dwarf component - either as blue object or X-ray
source. Obviously, the presence of a late-type companion may
significantly affect the colour of a PCEB: the cooler the white dwarf
and/or the earlier the companion are, the less blue the system
will appear. This may affect different candidate samples in different
ways, depending on how the criterion blue has been defined.
We have computed the colours expected for PCEBs containing a white
dwarf with
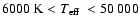 K and an ZAMS companion with
spectral type K0 to M6, the results for U-B and B-V are shown in
Fig. 11. Comparing these simulated colours to the
selection criterion of the PG survey, U-B<0.46(Green et al. 1986), it becomes apparent that PCEBs containing a
cool ( K and an ZAMS companion with
spectral type K0 to M6, the results for U-B and B-V are shown in
Fig. 11. Comparing these simulated colours to the
selection criterion of the PG survey, U-B<0.46(Green et al. 1986), it becomes apparent that PCEBs containing a
cool (
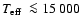 K) white dwarf will be included in the PG
survey only if their companions are of spectral type K) white dwarf will be included in the PG
survey only if their companions are of spectral type 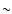 M4 or
later. Similarly, for such PCEBs B-V>0.5, which will most likely
prevent their selection as white dwarf candidates. As an example for
the "historic'' white dwarf searches, Giclas et al. (1965) used a
Lowell colour class -1 or 0 (corresponding to B-V<0.0 or
B-V<+0.2, and U-B<-0.78 or U-B<-0.60) as selection
criterion. Consequently, the GD lists will contain only those PCEBs
containing moderately hot white dwarfs and late type secondaries, such
as HR Cam and MS Peg. M4 or
later. Similarly, for such PCEBs B-V>0.5, which will most likely
prevent their selection as white dwarf candidates. As an example for
the "historic'' white dwarf searches, Giclas et al. (1965) used a
Lowell colour class -1 or 0 (corresponding to B-V<0.0 or
B-V<+0.2, and U-B<-0.78 or U-B<-0.60) as selection
criterion. Consequently, the GD lists will contain only those PCEBs
containing moderately hot white dwarfs and late type secondaries, such
as HR Cam and MS Peg.
PCEBs which were not initially selected as white dwarf candidates are:
(1) the planetary nebulae; (2) high proper motion objects (RR Cae,
BPM 6502, and BPM 71214) - interestingly enough, RR Cae is the
PCEB containing the coldest white dwarf in our sample; and (3) variable
stars (V471 Tau: spectroscopic; BE UMa: photometric). In the case of
V471 Tau the optical emission is largely dominated by the K2V
companion, and with
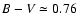 the system does clearly not
qualify as a white dwarf candidate.
the system does clearly not
qualify as a white dwarf candidate.
9.4 The lack of early companions
So far we have focussed much of our attention on the temperatures of
the white dwarfs in our PCEB sample, as this parameter is a direct
measure of the age of these systems. However, Table 1
suggests that this sample is also biased with respect to the
mass of the companion stars. The average mass of the
companion in our PCEB sample is
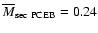 ,
whereas CVcat
(Kube et al. 2002) lists the masses for 80 CVs with ,
whereas CVcat
(Kube et al. 2002) lists the masses for 80 CVs with
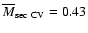 .
A direct consequence of this
dominance of low mass companion stars in the known PCEB sample is that
the majority of these systems evolve into contact at short orbital
periods (Sect. 6, Fig. 5). .
A direct consequence of this
dominance of low mass companion stars in the known PCEB sample is that
the majority of these systems evolve into contact at short orbital
periods (Sect. 6, Fig. 5).
The shortage of PCEBs with massive/early-type donor stars
(
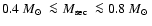 ), i.e. the progenitors of
long-period CVs, is subject to the selection effect which we just
discussed in Sect. 9.3: in PCEBs with an early-type
companion the secondary contributes significantly to the total optical
emission of the system, and, consequently, such binaries do not
qualify as white dwarf candidates (Fig. 11), the
major discovery channel for PCEBs. ), i.e. the progenitors of
long-period CVs, is subject to the selection effect which we just
discussed in Sect. 9.3: in PCEBs with an early-type
companion the secondary contributes significantly to the total optical
emission of the system, and, consequently, such binaries do not
qualify as white dwarf candidates (Fig. 11), the
major discovery channel for PCEBs.
As a result of the (very likely) incompleteness of known PCEBs with an
early-type donor the space density estimates presented in
Sect. 8 should be considered to be lower limits
to the true
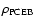 and
and
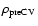 . .
We have presented the properties of the currently known sample of
well-observed PCEBs and have calculated their past and future
evolution based on two different assumptions for the angular
momentum loss mechanism, adopting either the "classical'' disrupted
magnetic braking prescription (
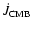 )
or the AML prescription derived
by Sills et al. (2000) ( )
or the AML prescription derived
by Sills et al. (2000) (
 ). The results from this study are: ). The results from this study are:
- 1.
- The presently known PCEB population is dominated by young
systems most of which have evolved only through a small fraction of
their lifetime as detached binaries. On average, the white dwarfs in
PCEBs are hotter than field white dwarfs.
- 2.
- While the evolution of an individual system strongly depends on
whether we assume
 or
or
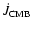 ,
the total number of pre-CVs within the PCEB sample, i.e. systems which will
start mass transfer within a Hubble time, is nearly the same for both
prescriptions. Considering the time scale on which the PCEBs will evolve into
semi-detached CVs we predict the existence
of a large population of old PCEBs containing cold white dwarfs. The
present lack of such systems is very likely the result of
observational biases, as the majority of the known PCEBs were
initially selected as blue objects. ,
the total number of pre-CVs within the PCEB sample, i.e. systems which will
start mass transfer within a Hubble time, is nearly the same for both
prescriptions. Considering the time scale on which the PCEBs will evolve into
semi-detached CVs we predict the existence
of a large population of old PCEBs containing cold white dwarfs. The
present lack of such systems is very likely the result of
observational biases, as the majority of the known PCEBs were
initially selected as blue objects.
- 3.
- An additional consequence of the observational selection effects
involved in the discovery of PCEBs is a shortage of systems containing
a "massive''/early-type companion
(
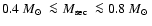 ) - which are the progenitors of
long-period CVs. Indeed, our calculations predict that most of the
pre-CVs among the PCEBs in our sample will evolve into CVs with short
orbital periods ( ) - which are the progenitors of
long-period CVs. Indeed, our calculations predict that most of the
pre-CVs among the PCEBs in our sample will evolve into CVs with short
orbital periods (
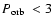 h). h).
- 4.
- The space density of PCEBs estimated from the currently known
sample is
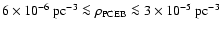 ,
depending on the assumed AML
prescription. Taking into account the age as well as the evolution
time scale of the pre-CVs in our sample and assuming that the
birthrate of PCEBs remained unchanged we derive for the CV space
density ,
depending on the assumed AML
prescription. Taking into account the age as well as the evolution
time scale of the pre-CVs in our sample and assuming that the
birthrate of PCEBs remained unchanged we derive for the CV space
density
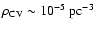 ,
nearly independent
on whether we assume ,
nearly independent
on whether we assume
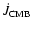 or or
 .
This value is somewhat higher
than current observational estimates but below theoretical
predictions. However, due to the observational bias working against
the discovery of PCEBs containing an early-type companion our
estimates should be considered to be lower limits to the true values
of .
This value is somewhat higher
than current observational estimates but below theoretical
predictions. However, due to the observational bias working against
the discovery of PCEBs containing an early-type companion our
estimates should be considered to be lower limits to the true values
of
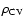 and
and
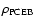 . .
Acknowledgements
We thank for support by an individual Marie-Curie Fellowship (MRS) and
a PPARC Advanced Fellowship (BTG).
 :
After the submission of our paper,
Raymond et al. (2003) have published a list of 109 PCEBs found in
the Sloan Digital Sky Survey. The average white dwarf temperature of
this sample (16 000 K) is significantly lower than that of our sample of
PCEBs with known orbital period (Table 1), and
demonstrates that more sophisticated selection criteria (compared to
pure "blue'' surveys) can successfully identify PCEBs containing rather
cold white dwarfs. Unfortunately, only a single system in the
list of Raymond et al. (2003) has an orbital period
measurement - determining the periods of their PCEBs harbouring white
dwarfs with :
After the submission of our paper,
Raymond et al. (2003) have published a list of 109 PCEBs found in
the Sloan Digital Sky Survey. The average white dwarf temperature of
this sample (16 000 K) is significantly lower than that of our sample of
PCEBs with known orbital period (Table 1), and
demonstrates that more sophisticated selection criteria (compared to
pure "blue'' surveys) can successfully identify PCEBs containing rather
cold white dwarfs. Unfortunately, only a single system in the
list of Raymond et al. (2003) has an orbital period
measurement - determining the periods of their PCEBs harbouring white
dwarfs with
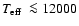 K provides a direct test for our
prediction (2) above. K provides a direct test for our
prediction (2) above.
RR Cae: Discovered as high proper motion object by
Luyten (1955), DA white dwarf plus Balmer emission line spectrum
noted by Rodgers & Eggen (1974), late-type nature for the companion
suggested by Bessell & Wickramasinghe (1979), discovery of eclipses
and orbital period measurement (photometric) by
Krzeminski (1984). Two comprehensive studies by
Bruch & Diaz (1998) and Bruch (1999).
EG UMa: Discovered as a white dwarf on Schmidt prism plates
by Stephenson (1960), emission lines noted by
Greenstein (1965), orbital period (spectroscopic) by
Lanning (1982). Recent comprehensive study by
Bleach et al. (2000).
EC 13471-1258: Discovered in the Edinburgh-Cape faint blue
object survey of high galactic latitudes, binarity revealed through
the detection of eclipses (Kilkenny et al. 1997).
Recent study by Kawka et al. (2002).
BPM 71214: Discovered as a high proper motion object
(Luyten 1963).
Recent study by Kawka et al. (2002).
HR Cam: Listed as WD candidate by Giclas et al. (1970),
spectroscopic confirmation of WD nature by Wills & Wills (1974),
detection of a red companion by Zuckerman & Becklin (1992), orbital
period (spectroscopic and photometric) from the comprehensive studies
of Maxted et al. (1998); Marsh & Duck (1996).
UZ Sex: Discovered in the PG survey, listed as a
DA/composite spectral type by Green et al. (1986), orbital period
(spectroscopic) from the comprehensive study of
Saffer et al. (1993), see also the recent analyses by
Bleach et al. (2000); Bruch & Diaz (1999).
BPM 6502: Discovered as a high proper motion star by
Luyten (1957a), listed as WD candidate by Eggen (1969),
spectroscopically confirmed as a WD by Wegner (1973), detection
of companion and orbital period (spectroscopic) by
Kawka et al. (2000).
HZ 9: Discovered in a search for faint blue stars by
Humason & Zwicky (1947), mentioned as a DA+dMe candidate by
Greenstein (1958), orbital period (spectroscopic) measured by
Lanning & Pesch (1981).
MS Peg: Listed as WD candidate by Giclas et al. (1965),
spectroscopic confirmation of WD nature by Greenstein (1969),
emission lines and radial velocity variations detected by
Tytler & Rubenstein (1989) and Schultz et al. (1993), orbital
period (spectroscopic) measured by Schmidt et al. (1995).
HS 0705+6700: Classified in the Hamburg Quasar Survey
(Hagen et al. 1995) as hot star candidate, eclipses discovered and
orbital period measured by Drechsel et al. (2001).
HW Vir: Listed as ultraviolet-bright star by
Carnochan & Wilson (1983) and classified as likely sdB star by
Berger & Fringant (1980), discovery of eclipses and orbital period
(photometric) by Menzies (1986).
LM Com: Listed as blue object by
Iriarte & Chavira (1957), also detected in the PG survey
(Green et al. 1986), and identified as DA+dM binary by
Ferguson et al. (1984),
 emission detected by
Orosz et al. (1997), orbital period (spectroscopic) and
comprehensive study by Orosz et al. (1999).
emission detected by
Orosz et al. (1997), orbital period (spectroscopic) and
comprehensive study by Orosz et al. (1999).
PG 1017-086: Discovered in the PG survey, classified as
sdB star by Green et al. (1986), variability discovered and orbital
period measured by Maxted et al. (2002).
CC Cet: Discovered in the PG survey, listed as a
DA/composite spectral type by Green et al. (1986), orbital period
(spectroscopic) from the comprehensive study of
Saffer et al. (1993), see also Somers et al. (1996).
V471 Tau: The brightest and best-studied pre-CV. Listed as a
spectroscopic binary by Wilson (1953), discovery of eclipses,
spectral classification as DA+dK binary, and measurement of the
orbital period (photometric) by Nelson & Young (1970).
PG 1336-018: Discovered in the PG survey, classified as
sdB star by Green et al. (1986), eclipses discovered and orbital
period measured by Kilkenny et al. (1998).
AA Dor: Listed as faint blue star by Luyten (1957b) and
as spectroscopically variable object in the foreground of the LMC
by Feast et al. (1960), discovery of eclipses and measurement of the
orbital period (photometric) by Kilkenny et al. (1978).
RE 2013+400: Discovered as bright EUV source during the
ROSAT Wide Field Camera all-sky survey and listed as a WD by
Pounds et al. (1993), variable Balmer emission was noted by
Barstow et al. (1993), the orbital period (spectroscopic) was
measured by Thorstensen et al. (1994).
GK Vir: Discovered in the PG survey, eclipse discovered and
orbital period (photometric) measured by Green et al. (1978).
MT Ser: Classified as PN on the Palomar Sky Survey plates
by Abell (1955), variability suggested by Abell (1966),
recurrent photometric variability was detected by
Grauer & Bond (1983) who also suggested the sdO+dM nature of the
system, for a more comprehensive photometric study, see
Bruch et al. (2001).
IM CMa: Discovered as bright EUV source during the
ROSAT Wide Field Camera all-sky survey and listed as a WD by
Pounds et al. (1993), Balmer emission detected and orbital period
(spectroscopic) measured by Vennes & Thorstensen (1994).
NN Ser: Discovered as a CV candidate in the PG survey by
Green et al. (1986), discovery of deep eclipses, classification as
DA+dM binary and measurement of the orbital period (photometric) by
Haefner (1989).
RE 1016-053: Discovered as bright EUV source during the
ROSAT Wide Field Camera all-sky survey and listed as a WD by
Pounds et al. (1993), classified as DA+dM by
Jomaron et al. (1993), orbital period (spectroscopic)
measured by Tweedy et al. (1993).
V477 Lyr: Classified as PN on the Palomar Sky Survey plates by
Abell (1955), variability suggested by Abell (1966),
eclipse discovered and period (photometric) measured by Bond (1980).
Abell 65: Classified as PN on the Palomar Sky Survey plates
by Abell (1966), an estimate of the orbital period (photometric)
was published by Bond & Livio (1990).
KV Vel: Listed as luminous star in the list of
Stephenson & Sanduleak (1971), planetary nebula nature suggested by
Holmberg et al. (1978), spectroscopically identified as sdO star
within a planetary nebula by Drilling (1983). Photometric
variability discovered and orbital period (photometric) measured by
Drilling & Bravo (1984).
UU Sge: Classified as PN on the Palomar Sky Survey plates by
Abell (1955), variability suggested by Abell (1966),
eclipses discovered and orbital period (photometric) measured by
Miller et al. (1976).
HS 1136+6646: Classified in the Hamburg Quasar Survey
(Hagen et al. 1995) as hot star candidate, identified as a
spectroscopic binary by Heber et al. (1996), orbital period
(spectroscopic) measured by Sing et al. (2001).
BE UMa: Identified as variable star and orbital period
(photometric) by Kurochkin (1971,1964), recovered as
emission line star in the PG survey by Ferguson et al. (1981).
-
Abell, G. O. 1955, PASP, 67, 258
NASA ADS
-
Abell, G. O. 1966, ApJ, 144, 259
NASA ADS
-
Althaus, L. G., & Benvenuto, O. G. 1997, ApJ, 477, 313
NASA ADS
-
Andronov, N., Pinsonneault, M., & Sills, A. 2003, ApJ, 582, 358
NASA ADS
-
Barstow, M. A., Hodgkin, S. T., Pye, J. P., et al. 1993, in White
Dwarfs: Advances in Observation and Theory, ed. M. A. Barstow, NATO ASIC
Proc. No. 403 (Dordrecht: Kluwer), 433
-
Bell, S. A., Pollacco, D. L., & Hilditch, R. W. 1994, MNRAS, 270, 449
NASA ADS
-
Berger, J., & Fringant, A.-M. 1980, A&A, 85, 367
NASA ADS
-
Bergeron, P., Wesemael, F., Beauchamp, A., et al. 1994, ApJ, 432, 305
NASA ADS
-
Bessell, M. S., & Wickramasinghe, D. T. 1979, ApJ, 227, 232
NASA ADS
-
Bleach, J. N., Wood, J. H., Catalán, M. S., et al. 2000, MNRAS,
312, 70
NASA ADS
-
Bond, H. E. 1980, IAU Circ., 3480
-
Bond, H. E., & Livio, M. 1990, ApJ, 355, 568
NASA ADS
-
Bragaglia, A., Renzini, A., & Bergeron, P. 1995, ApJ, 443, 735
NASA ADS
-
Bruch, A. 1999, AJ, 117, 3031
NASA ADS
-
Bruch, A., & Diaz, M. P. 1998, AJ, 116, 908
NASA ADS
-
Bruch, A., & Diaz, M. P. 1999, A&A, 351, 573
NASA ADS
-
Bruch, A., Vaz, L. P. R., & Diaz, M. P. 2001, A&A, 377, 898
NASA ADS
-
Cahn, J. H., & Kaler, J. B. 1971, ApJS, 22, 319
NASA ADS
-
Cahn, J. H., Kaler, J. B., & Stanghellini, L. 1992, A&AS, 94, 399
NASA ADS
-
Carnochan, D. J., & Wilson, R. 1983, MNRAS, 202, 317
NASA ADS
-
Catalan, M. S., Davey, S. C., Sarna, M. J., Connon-Smith, R., &
Wood, J. H. 1994, MNRAS, 269, 879
NASA ADS
-
Cayrel, R., Hill, V., Beers, T. C., et al. 2001, Nature, 409, 691
NASA ADS
-
Chen, A., O'Donoghue, D., Stobie, R. S., et al. 1995, MNRAS, 275, 100
NASA ADS
-
Clemens, J. C., Reid, I. N., Gizis, J. E., & O'Brien, M. S. 1998, ApJ,
496, 352
NASA ADS
-
de Kool, M. 1992, A&A, 261, 188
NASA ADS
-
de Kool, M., & Ritter, H. 1993, A&A, 267, 397
NASA ADS
-
Downes, R. A. 1986, ApJ, 307, 170
NASA ADS
-
Drechsel, H., Heber, U., Napiwotzki, R., et al. 2001, A&A, 379, 893
NASA ADS
-
Driebe, T., Blöcker, T., Schönberner, D., & Herwig, F. 1999, A&A,
350, 89
NASA ADS
-
Driebe, T., Schoenberner, D., Bloecker, T., & Herwig, F. 1998, A&A,
339, 123
NASA ADS
-
Drilling, J. S. 1983, ApJ, 270, L13
NASA ADS
-
Drilling, J. S., & Bravo, J. 1984, IAU Circ., 3939
-
Dubus, G., Taam, R. E., & Spruit, H. C. 2002, ApJ, 569, 395
NASA ADS
-
Eggen, O. J. 1969, ApJ, 157, 287
NASA ADS
-
Eggleton, P. P. 1983, ApJ, 268, 368
NASA ADS
-
Feast, M. W., Thackeray, A. D., & Wesselink, A. J. 1960, MNRAS, 121, 337
NASA ADS
-
Ferguson, D. H., Green, R. F., & Liebert, J. 1984, ApJ, 287, 320
NASA ADS
-
Ferguson, D. H., Liebert, J., Haas, S., Napiwotzki, R., & James,
T. A. 1999, ApJ, 518, 866
NASA ADS
-
Ferguson, D. H., McGraw, J. T., Spinrad, H., Liebert, J., & Green,
R. F. 1981, ApJ, 251, 205
NASA ADS
-
Ferreras, I., Melchiorri, A., & Silk, J. 2001, MNRAS, 327, L47
NASA ADS
-
Fontaine, G., Brassard, P., & Bergeron, P. 2001, PASP, 113, 409
NASA ADS
-
Fujimoto, M. Y., & Iben, I. J. 1989, ApJ, 341, 306
NASA ADS
-
Fulbright, M. S., Liebert, J., Bergeron, P., & Green, R. 1993, ApJ,
406, 240
NASA ADS
-
Gänsicke, B. T. 2000, Reviews of Modern Astronomy, 13, 151
NASA ADS
-
Gänsicke, B. T., Beuermann, K., & de Martino, D. 1995, A&A, 303, 127
NASA ADS
-
Gänsicke, B. T., Hagen, H. J., & Engels, D. 2002, On the
space density of cataclysmic variables, ed. B. T. Gänsicke,
K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 190
-
Giclas, H. L., Burnham, R., & Thomas, N. G. 1965, Lowell Obs. Bull.,
125, 155
-
Giclas, H. L., Burnham, R., & Thomas, N. G. 1970, Lowell Obs. Bull., 153, 183
-
Grauer, A. D., & Bond, H. E. 1983, ApJ, 271, 259
NASA ADS
-
Green, R. F., Liebert, J., & Wesemael, F. 1984, ApJ, 280, 177
NASA ADS
-
Green, R. F., Richstone, D. O., & Schmidt, M. 1978, ApJ, 224, 892
NASA ADS
-
Green, R. F., Schmidt, M., & Liebert, J. 1986, ApJS, 61, 305
NASA ADS
-
Greenstein, J. L. 1958, Handbuch der Physik, vol. 50 (Berlin: Springer), 161
-
Greenstein, J. L. 1965, in First Conference on Faint Blue Stars, ed.
W. Luyten (Minneapolis: University of Minnesota Press), 97
-
Greenstein, J. L. 1969, ApJ, 158, 281
NASA ADS
-
Guinan, E. F., & Sion, E. M. 1984, AJ, 89, 1252
NASA ADS
-
Haefner, R. 1989, A&A, 213, L15
NASA ADS
-
Hagen, H. J., Groote, D., Engels, D., & Reimers, D. 1995, A&AS, 111,
195
NASA ADS
-
Heber, U., Dreizler, S., & Hagen, H.-J. 1996, A&A, 311, L17
NASA ADS
-
Herrero, A., Manchado, A., & Mendez, R. H. 1990, Ap&SS, 169, 183
NASA ADS
-
Hilditch, R. W., Harries, T. J., & Hill, G. 1996, MNRAS, 279, 1380
NASA ADS
-
Holmberg, E. B., Lauberts, A., Schuster, H. E., & West, R. M. 1978,
A&AS, 31, 15
NASA ADS
-
Howell, S. B., Nelson, L. A., & Rappaport, S. 2001, ApJ, 550, 897
NASA ADS
-
Howell, S. B., Rappaport, S., & Politano, M. 1997, MNRAS, 287, 929
NASA ADS
-
Humason, M. L., & Zwicky, F. 1947, ApJ, 105, 85
NASA ADS
-
Iben, I. J., & Tutukov, A. V. 1993, ApJ, 418, 343
NASA ADS
-
Iriarte, B., & Chavira, E. 1957, Boletin de los Observatorios Tonantzintla
y Tacubaya, 2, 3
-
Jomaron, C. M., Raymont, G. B., Bromage, G. E., et al. 1993, MNRAS,
264, 219
NASA ADS
-
Kawka, A., Vennes, S., Dupuis, J., & Koch, R. 2000, AJ, 120, 3250
NASA ADS
-
Kawka, A., Vennes, S., Koch, R., & Williams, A. 2002, AJ, 124, 2853
NASA ADS
-
Kepler, S. O., & Nelan, E. P. 1993, AJ, 105, 608
NASA ADS
-
Kilkenny, D., Hilditch, R. W., & Penfold, J. E. 1978, MNRAS, 183, 523
NASA ADS
-
Kilkenny, D., O'Donoghue, D., Koen, C., Lynas-Gray, A. E., & van Wyk, F. 1998, MNRAS, 296, 329
NASA ADS
-
Kilkenny, D., O'Donoghue, D., Koen, C., Stobie, R. S., & Chen, A.
1997, MNRAS, 287, 867
NASA ADS
-
King, A. R. 1988, QJRAS, 29, 1
NASA ADS
-
King, A. R., Frank, J., Kolb, U., & Ritter, H. 1995, ApJ, 444,
L37
NASA ADS
-
King, A. R., & Kolb, U. 1995, ApJ, 439, 330
NASA ADS
-
King, A. R., Kolb, U., De Kool, M., & Ritter, H. 1994, MNRAS, 269, 907
NASA ADS
-
King, A. R., Osborne, J. P., & Schenker, K. 2002, MNRAS, 329, L43
NASA ADS
-
King, A. R., & Schenker, K. 2002, in The Physics of Cataclysmic Variables
and Related Objects, ed. B. T. Gänsicke, K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 233
-
Koester, D. 2002, A&AR, 11, 33
-
Koester, D., Schulz, H., & Weidemann, V. 1979, A&A, 76, 262
NASA ADS
-
Kolb, U. 2002, in The Physics of Cataclysmic Variables and Related Objects,
ed. B. T. Gänsicke, K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261,
180
-
Kolb, U., & Baraffe, I. 1999, MNRAS, 309, 1034
NASA ADS
-
Kolb, U., King, A. R., & Ritter, H. 1998, MNRAS, 298, L29
NASA ADS
-
Krishnamurthi, A., Pinsonneault, M. H., Barnes, S., & Sofia, S. 1997,
ApJ, 480, 303
NASA ADS
-
Krzeminski, W. 1984, IAU Circ., 4014
-
Kube, J., Gänsicke, B., & Hoffmann, B. 2002, in The Physics of
Cataclysmic Variables and Related Objects, ed. B. T. Gänsicke,
K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 678
-
Kudritzki, R. P., Simon, K. P., Lynas-Gray, A. E., Kilkenny, D., &
Hill, P. W. 1982, A&A, 106, 254
NASA ADS
-
Kurochkin, N. E. 1964, Peremnye Zvezdy (Academy Sci. U.S.S.R., Var. Star
Bull), 15, 77
-
Kurochkin, N. E. 1971, Peremnye Zvezdy (Academy Sci. U.S.S.R., Var. Star Bull), 18, 85
-
Lanning, H. H. 1982, ApJ, 253, 752
NASA ADS
-
Lanning, H. H., & Pesch, P. 1981, ApJ, 244, 280
NASA ADS
-
Livio, M., & Pringle, J. E. 1994, ApJ, 427, 956
NASA ADS
-
Luyten, W. J. 1955, Luyten's Five Tenths (Minneapolis: Lund Press)
-
Luyten, W. J. 1957a, A catalogue of 9867 stars in the Southern Hemisphere
with proper motions exceeding
 annually (Minneapolis: Lund Press)
annually (Minneapolis: Lund Press)
-
Luyten, W. J. 1957b, A Search for Faint Blue Stars (Minneapolis: University
of Minnesota)
-
Luyten, W. J. 1963, Bruce proper motion survey. The general catalogue, Vol. I, II
-
Maciel, W. J. 1984, A&AS, 55, 253
NASA ADS
-
Marsh, T. R., Dhillon, V. S., & Duck, S. R. 1995, MNRAS, 275, 828
NASA ADS
-
Marsh, T. R., & Duck, S. R. 1996, MNRAS, 278, 565
NASA ADS
-
Maxted, P. F. L., Marsh, T. R., Heber, U., et al. 2002, MNRAS, 333, 231
NASA ADS
-
Maxted, P. F. L., Marsh, T. R., Moran, C., Dhillon, V. S., &
Hilditch, R. W. 1998, MNRAS, 300, 1225
NASA ADS
-
McCook, G. P., & Sion, E. M. 1999, ApJS, 121, 1
NASA ADS
-
Menzies, J. W. 1986, Ann. Rep. SAAO, 1985, 20
-
Miller, J. S., Krzeminski, W., & Priedhorsky, W. 1976, IAU Circ., 2974
-
Nelson, B., & Young, A. 1970, PASP, 82, 699
NASA ADS
-
O'Brien, M. S., Bond, H. E., & Sion, E. M. 2001, ApJ, 563, 971
NASA ADS
-
Orosz, J., Wade, R. A., & Harlow, J. J. B. 1997, AJ, 114, 317
NASA ADS
-
Orosz, J. A., Wade, R. A., Harlow, J. J. B., et al. 1999, AJ, 117, 1598
NASA ADS
-
Paczynski, B., & Sienkiewicz, R. 1983, ApJ, 268, 825
NASA ADS
-
Patterson, J. 1984, ApJS, 54, 443
NASA ADS
-
Patterson, J. 1998, PASP, 110, 1132
NASA ADS
-
Perryman, M. A. C., Brown, A. G. A., Lebreton, Y., et al. 1998, A&A,
331, 81
NASA ADS
-
Pinsonneault, M. H., Andronov, N., & Sills, A. 2002, in The Physics of
Cataclysmic Variables and Related Objects, ed. B. T. Gänsicke,
K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 208
-
Politano, M. 1996, ApJ, 465, 338
NASA ADS
-
Pollacco, D. L., & Bell, S. A. 1993, MNRAS, 262, 377
NASA ADS
-
Pollacco, D. L., & Bell, S. A. 1994, MNRAS, 267, 452
NASA ADS
-
Pottasch, S. R. 1996, A&A, 307, 561
NASA ADS
-
Pounds, K. A., Allan, D. J., Barber, C., et al. 1993, MNRAS, 260, 77
NASA ADS
-
Prialnik, D., & Livio, M. 1985, MNRAS, 216, 37
NASA ADS
-
Rappaport, S., Joss, P. C., & Verbunt, F. 1983, ApJ, 275, 713
NASA ADS
-
Rauch, T. 2000, A&A, 356, 665
NASA ADS
-
Raymond, S. N., Szkody, P., Hawley, S. L., et al. 2003, AJ, 125, 2621
NASA ADS
-
Ringwald, F. A. 1996, in Cataclysmic Variables and Related Objects, ed.
A. Evans, & J. H. Wood, IAU Coll. No. 158 (Dordrecht: Kluwer), 89
-
Ritter, H. 1986, A&A, 169, 139
NASA ADS
-
Ritter, H., & Kolb, U. 1998, A&AS, 129, 83
NASA ADS
-
Rodgers, A. W., & Eggen, O. J. 1974, PASP, 86, 742
NASA ADS
-
Saffer, R. A., Wade, R. A., Liebert, J., et al. 1993, AJ, 105, 1945
NASA ADS
-
Schenker, K., & King, A. R. 2002, in The Physics of Cataclysmic Variables
and Related Objects, ed. B. T. Gänsicke, K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 242
-
Schmidt, G. D., Smith, P. S., Harvey, D. A., & Grauer, A. D. 1995, AJ,
110, 398
NASA ADS
-
Schultz, G., Zuckerman, B., Becklin, E. E., & Barnbaum, C. 1993, BAAS,
25, 824
NASA ADS
-
Sills, A., Pinsonneault, M. H., & Terndrup, D. M. 2000, ApJ, 534, 335
NASA ADS
-
Sing, D. K., Holberg, J. B., Howell, S., Barstow, M. A., & Burleigh,
M. 2001, American Astronomical Society Meeting, 199
-
Somers, M. W., Lockley, J. J., Naylor, T., & Wood, J. H. 1996, MNRAS,
280, 1277
NASA ADS
-
Spruit, H. C., & Ritter, H. 1983, A&A, 124, 267
NASA ADS
-
Spruit, H. C., & Taam, R. E. 2001, ApJ, 548, 900
NASA ADS
-
Stauffer, J. R. 1987, AJ, 94, 996
NASA ADS
-
Stephenson, C. B. 1960, PASP, 72, 387
NASA ADS
-
Stephenson, C. B., & Sanduleak, N. 1971, Luminous stars in the Southern
Milky Way, Vol. 1 (Publications of the Warner & Swasey Observatory)
-
Thorstensen, J. R., Vennes, S., & Shambrook, A. 1994, AJ, 108, 1924
NASA ADS
-
Townsley, D. M., & Bildsten, L. 2002, in The Physics of Cataclysmic
Variables and Related Objects, ed. B. T. Gänsicke, K. Beuermann, &
K. Reinsch, ASP Conf. Ser., 261, 31
-
Tweedy, R. W., Holberg, J. B., Barstow, M. A., et al. 1993, AJ, 105,
1938
NASA ADS
-
Tytler, D., & Rubenstein, E. 1989, in White dwarfs, ed. G. Wegner, IAU
Coll. No. 158 (Heidelberg: Springer), 524
-
Vennes, S., & Thorstensen, J. R. 1994, ApJ, 433, L29
NASA ADS
-
Vennes, S., & Thorstensen, J. R. 1996, AJ, 112, 284
NASA ADS
-
Vennes, S., Thorstensen, J. R., & Polomski, E. F. 1999, ApJ, 523, 386
NASA ADS
-
Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7
NASA ADS
-
Walsh, J. R., & Walton, N. A. 1996, A&A, 315, 253
NASA ADS
-
Walton, N. A., Walsh, J. R., & Pottasch, S. R. 1993, A&A, 275, 256
NASA ADS
-
Warner, B. 1995, Cataclysmic Variable Stars (Cambridge: Cambridge University
Press)
-
Wegner, G. 1973, MNRAS, 163, 381
NASA ADS
-
Weidemann, V. 2000, A&A, 363, 647
NASA ADS
-
Wills, D., & Wills, B. J. 1974, MNRAS, 167, 79P
NASA ADS
-
Wilson, R. E. 1953, General Catalogue of Stellar Radial Velocities
(Carnegie Institute Washington D.C. Publication)
-
Wood, J. H., & Marsh, T. R. 1991, ApJ, 381, 551
NASA ADS
-
Wood, J. H., Robinson, E. L., & Zhang, E.-H. 1995, MNRAS, 277, 87
NASA ADS
-
Wood, J. H., & Saffer, R. 1999, MNRAS, 305, 820
NASA ADS
-
Wood, M. A. 1995, in White Dwarfs, ed. D. Koester, & K. Werner, LNP No.
443 (Heidelberg: Springer), 41
-
Zuckerman, B., & Becklin, E. E. 1992, ApJ, 386, 260
NASA ADS
Copyright ESO 2003
|
![\begin{figure}
\par\includegraphics[angle=-90,width=8.25cm,clip]{3351f1.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg60.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{3351f2.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg62.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{3351f3.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg173.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=10.5cm,clip]{3351f4.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg181.gif)
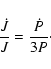
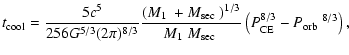
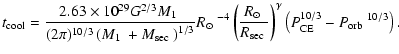
![$\displaystyle t_{{\rm cool}}=b{\Biggl [}\frac{3\left(1+aP^{4/3}\right)}{4a\left...
...{-5/3}+aP^{-1/3}\right)P^{5/3}}}\Biggr]^{\mbox{$P_{\rm orb}$ }}_{P_{{\rm CE}}},$](/articles/aa/full/2003/28/aa3351/img200.gif)
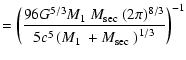
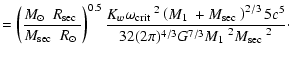
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{3351f5.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg212.gif)
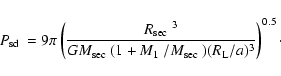
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{3351f6.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg228.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{3351f7.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg233.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3351f8.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg235.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{3351f9.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg258.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=12.3cm,clip]{3351f10.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg274.gif)
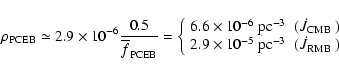
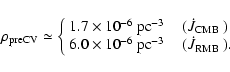
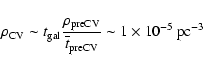
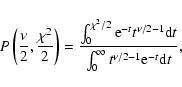
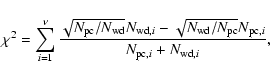
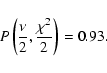
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{3351f11.ps}\hspace*{0.2cm}
\includegraphics[angle=270,width=8.8cm,clip]{3351f11b.ps}
\end{figure}](/articles/aa/full/2003/28/aa3351/Timg302.gif)