A&A 405, 959-967 (2003)
DOI: 10.1051/0004-6361:20030678
J. Scharwächter1 - A. Eckart1 - S. Pfalzner1 - J. Moultaka1 - C. Straubmeier1 - J. G. Staguhn2
1 - I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
2 -
NASA/Goddard Space Flight Center, Building 21, Code 685, Greenbelt, MD 20771, USA
Received 28 January 2003 / Accepted 28 April 2003
Abstract
The paper presents an analysis of the nearby QSO host
I Zw 1
based on new J-band
imaging data, obtained
with ISAAC at the Very Large Telescope (VLT) of the European
Southern Observatory (ESO).
As one of the best-studied QSOs with
exceptional properties lying between those of QSOs, narrow-line
Seyfert 1s, and ultraluminous infrared galaxies,
I Zw 1 is a
prime candidate for a detailed case study of a QSO host.
With its high angular resolution and sensitivity, the new J-band image
provides strong evidence for an interaction between I Zw 1 and
the western companion galaxy.
We present a procedure for subtracting the QSO nucleus from the
I Zw 1 image to obtain an undisturbed view on the underlying host
galaxy. Based on the derived surface brightness profile and the gas
rotation curve, the host is classified as a
high-surface-brightness Freeman type I galaxy with a central disk surface
brightness significantly larger than that of normal spirals.
The surface-brightness profile
is decomposed into a Plummer bulge and a Kuzmin disk with similar luminosities
and a bulge-to-disk scale length ratio of 0.29, comparable to that of
nearby spiral hosts with active galactic
nuclei (AGN). Different models for the
decomposition of the gas rotation curve are discussed. The
resulting J-band mass-to-light ratio
(M/L) of
![]() for the disk component
suggests a mean solar-type stellar population with a tendency towards young
stars.
The bulge exhibits a lower M/L of
for the disk component
suggests a mean solar-type stellar population with a tendency towards young
stars.
The bulge exhibits a lower M/L of
![]() ,
which
supports previous findings of enhanced starburst
activity
in the nuclear and circumnuclear region.
,
which
supports previous findings of enhanced starburst
activity
in the nuclear and circumnuclear region.
Key words: galaxies: individual: I Zw 1 - galaxies: active - galaxies: photometry - galaxies: structure - methods: observational
Due to their extreme properties in many physical respects, active galactic nuclei have attracted much interest for a long time. Thanks to improvements in sensitivity and angular resolution, the host galaxies have become a new focal point (e.g. McLeod 1995; Bothun et al. 1984; Lowenthal et al. 1995; Hunt et al. 1999; Márquez et al. 2000), as host disks are considered as the fuel reservoirs for their embedded active nuclei (e.g. Shlosman et al. 1990; Pogge & Martini 2002; Evans et al. 2001). Structures and stellar populations of the hosts seem to be closely entangled with the evolution and types of their active nuclei (Storchi-Bergmann et al. 2001). In order to minimize the effects of dust extinction, stellar properties of host galaxies are preferentially observed in the near-infrared (NIR). Nevertheless, the measured nuclear and circumnuclear fluxes are still dominated by the high energy output of the embedded active nucleus. As an unresolved source, the active nucleus is usually removed by subtracting an appropriately scaled point-spread function (PSF). Most statistical studies of AGN hosts, however, lack an exact knowledge of the AGN flux contribution so that the scaling is often rather arbitrary. It is determined either by assuming the residual central stellar component of the host to be flat or by applying some fitting algorithm (e.g. Bahcall et al. 1995; Hunt et al. 1999; Percival et al. 2001). In contrast to these statistical approaches, this paper focusses on a detailed study of one nearby representative of QSO hosts, the QSO host I Zw 1, for which some basic data are listed in Table 1.
|
|
|
Falco et al. (1999) |
|
|
|
Falco et al. (1999) |
|
|
|
Schinnerer et al. (1998) |
|
|
|
Schinnerer et al. (1998) |
|
|
0.0611 | Solomon et al. (1997) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2001-08-19 | 08:05:06-08:13:17 |
|
4 | 1.26 |
|
|
2001-08-19 | 06:14:20-06:16:57 |
|
5 | 1.33-1.34 |
|
Characteristics of the ISAAC J-band filter: central wavelength
|
This case study benefits from the fact that
a reliable subtraction procedure for the I Zw 1 AGN
can be deduced from
known flux fractions. By two independent methods,
Eckart et al. (1994) and Schinnerer et al. (1998)
find a stellar fraction of 15% in the total nuclear K-band
flux and a stellar fraction of ![]() % in the total nuclear H-band flux.
Both results refer to a non-extincted QSO component surrounded by a stellar
component which is extincted by 10 to 20 mag.
The first method (Eckart et al. 1994) is
based on a comparison of the nuclear NIR colours of
I Zw 1 with the colours of a mean zero-redshift QSO
(Hyland & Allen 1982), while the second method
(Schinnerer et al. 1998) investigates the depths of
stellar absorption lines in the NIR spectra.
The large stellar flux contribution seems to be connected with the strong
activity of a
% in the total nuclear H-band flux.
Both results refer to a non-extincted QSO component surrounded by a stellar
component which is extincted by 10 to 20 mag.
The first method (Eckart et al. 1994) is
based on a comparison of the nuclear NIR colours of
I Zw 1 with the colours of a mean zero-redshift QSO
(Hyland & Allen 1982), while the second method
(Schinnerer et al. 1998) investigates the depths of
stellar absorption lines in the NIR spectra.
The large stellar flux contribution seems to be connected with the strong
activity of a
![]() yr-old decaying starburst
(Schinnerer et al. 1998), probably located in the
circumnuclear molecular ring which has
recently been resolved in 12CO(1-0)
maps (Staguhn et al. 2001) and shows a radius of about 1 kpc.
yr-old decaying starburst
(Schinnerer et al. 1998), probably located in the
circumnuclear molecular ring which has
recently been resolved in 12CO(1-0)
maps (Staguhn et al. 2001) and shows a radius of about 1 kpc.
Since I Zw 1 shows properties of high-redshift QSOs, like the
blueshifted nuclear emission lines of
[C IV]
![]() ,
[Si VI]
,
[Si VI]
![]() ,
and
[Al IX]
,
and
[Al IX]
![]() (Buson & Ulrich 1990; Schinnerer et al. 1998), this case study
implies interesting consequences for
evolutionary scenarios.
With properties lying inbetween those of QSOs, narrow-line Seyfert 1s, and
ultraluminous infrared galaxies,
I Zw 1 is discussed as a possible transition object
from the QSO to the
ultraluminous infrared stage (Canalizo & Stockton 2001) regarding the
original evolutionary scheme for AGN (Sanders et al. 1988).
According to its nuclear blue magnitude of
(Buson & Ulrich 1990; Schinnerer et al. 1998), this case study
implies interesting consequences for
evolutionary scenarios.
With properties lying inbetween those of QSOs, narrow-line Seyfert 1s, and
ultraluminous infrared galaxies,
I Zw 1 is discussed as a possible transition object
from the QSO to the
ultraluminous infrared stage (Canalizo & Stockton 2001) regarding the
original evolutionary scheme for AGN (Sanders et al. 1988).
According to its nuclear blue magnitude of
![]() mag
(Smith et al. 1986, adopted for H0=75 km s-1 Mpc-1),
I Zw 1 just belongs to the QSO class
defined by
mag
(Smith et al. 1986, adopted for H0=75 km s-1 Mpc-1),
I Zw 1 just belongs to the QSO class
defined by
![]() mag
(
mag
(
![]() ,
Veron-Cetty & Veron 1998),
although the host galaxy is visible.
I Zw 1 has a radio-quiet AGN
(Kukula et al. 1995; Barvainis & Antonucci 1989) whose radio
source has not been resolved at the
observed angular resolutions so far (see Kukula et al. 1995).
Its narrow-line Seyfert 1 characteristics are prototypical of this class,
like the narrow
H
,
Veron-Cetty & Veron 1998),
although the host galaxy is visible.
I Zw 1 has a radio-quiet AGN
(Kukula et al. 1995; Barvainis & Antonucci 1989) whose radio
source has not been resolved at the
observed angular resolutions so far (see Kukula et al. 1995).
Its narrow-line Seyfert 1 characteristics are prototypical of this class,
like the narrow
H![]() line with a FWHM of 1240 km s-1
(Boller et al. 1996), the low line ratio
of [O III]/H
line with a FWHM of 1240 km s-1
(Boller et al. 1996), the low line ratio
of [O III]/H![]() of 0.49
(Hutchings & Crampton 1990), and the many Fe II multiplets
(Hutchings & Crampton 1990; Vestergaard & Wilkes 2001; Oke & Lauer 1979).
With an infrared luminosity of
of 0.49
(Hutchings & Crampton 1990), and the many Fe II multiplets
(Hutchings & Crampton 1990; Vestergaard & Wilkes 2001; Oke & Lauer 1979).
With an infrared luminosity of
![]() (Canalizo & Stockton 2001), I Zw 1 just fails to be
an ultraluminous
infrared galaxy but it still belongs to the luminous infrared objects.
(Canalizo & Stockton 2001), I Zw 1 just fails to be
an ultraluminous
infrared galaxy but it still belongs to the luminous infrared objects.
The host of I Zw 1 consists of an extended rotating disk as
supported by the double-horned line profiles of H I
(Condon et al. 1985) and
CO (Barvainis et al. 1989), the spiral arms in the
optical and NIR
images, and the 12CO(1-0) velocity field
(Schinnerer et al. 1998).
The fuelling mechanisms which are responsible for driving the gas from
the gas-rich host towards the AGN
are unclear, even on large scales. On the one hand, there is certainly
no large-scale bar
component as can be seen from the disk images as well as the symmetric
12CO(1-0) isovelocity diagram (Schinnerer et al. 1998).
On the other hand, the blue disk colours of
B- V=0.6-0.7
(Hutchings & Crampton 1990)
indicate enhanced star formation in the disk which can be modelled for
the north-western spiral arm by either
a young decaying starburst (
![]() yr) or an old (1010 yr)
constant starburst (Schinnerer et al. 1998). Together with slight tidal
features in the H I distribution (Lim & Ho 1999) and in the
B*-band image (Canalizo & Stockton 2001) this suggests that an interaction
with the nearby western companion galaxy may trigger the nuclear activity.
However, the evidence for an interaction is weak (Canalizo & Stockton 2001)
and it remains
controversial whether I Zw 1 is undergoing a minor merger process.
yr) or an old (1010 yr)
constant starburst (Schinnerer et al. 1998). Together with slight tidal
features in the H I distribution (Lim & Ho 1999) and in the
B*-band image (Canalizo & Stockton 2001) this suggests that an interaction
with the nearby western companion galaxy may trigger the nuclear activity.
However, the evidence for an interaction is weak (Canalizo & Stockton 2001)
and it remains
controversial whether I Zw 1 is undergoing a minor merger process.
The new J-band data complement the knowledge about I Zw 1, which is already one of the best-studied QSO hosts. Observations, data reduction, and data analysis are described in Sect. 2. The resulting surface-brightness profile is presented together with the derived gas rotation curve in Sect. 3. After an introduction to the applied gravitational potential models, the surface-brightness profile and the gas rotation curve are decomposed into structural components in Sect. 3.4. The obtained parameters are discussed in Sect. 4 and compared to the reviewed properties of the I Zw 1 host. A summary of the results is presented in Sect. 5.
NIR imaging data in the J-band have been obtained with the ISAAC camera at the VLT of ESO on Cerro Paranal in Chile. All processed data of this paper - the object frames as well as the standard star frames for photometric calibration - were observed within two consecutive hours. Basic parameters of the observation runs and the corresponding air masses are listed in Table 2.
Four object frames are
available in J-band,
in each of which the object has a different position on the
detector.
The images are reduced by means of standard procedures of the
IRAF software package.
Since I Zw 1 only occupies a small fraction of the total field
of view in an else uncrowded environment, sky and dark current are removed by
subtracting the object frames from each other for all possible
permutations.
Some modifications of the reduction steps turn out
to optimize the final background noise:
First, the flatfield shows variations of less than 1% - measured in several
![]() pixel boxes in the region of interest - so that a flatfield
correction is ignored.
Second, the sky-subtracted and aligned images are combined, using a median
algorithm. The advantage of this algorithm over the average algorithm is that
residual stars in the sky-subtracted images are effectively
removed during combination.
pixel boxes in the region of interest - so that a flatfield
correction is ignored.
Second, the sky-subtracted and aligned images are combined, using a median
algorithm. The advantage of this algorithm over the average algorithm is that
residual stars in the sky-subtracted images are effectively
removed during combination.
A standard star from the catalogue of the faint NIR LCO/Palomar
NICMOS standards (Persson et al. 1998) was observed for photometric
calibration.
The match between these standards
and the ISAAC filters has not yet been experimentally
verified but the colour terms are expected to be close to zero.
Observed in the same acquisition modes, the calibration frames
are reduced parallel to the object frames.
The flux
of the star is measured at all five different detector positions in the
unaligned frames to account for detector variations.
Mean and standard deviation of the five values are used for the final
zero-point determination and the calibration
error, respectively.
The derived zero-point is corrected for air mass with the canonical
average value of
![]() given for J in the ISAAC manual.
given for J in the ISAAC manual.
In order to investigate the host galaxy of I Zw 1, the non-stellar brightness contribution of the QSO has to be subtracted. For a two-dimensional subtraction, the PSF of the original J-band image is built with a Gaussian using the IRAF task PSF. To account for asymmetries, the residuals of the fit are stored in an additional lookup table. In order to subtract only the non-stellar portion of nuclear flux, the PSF has to be appropriately scaled. Without any prior assumptions about bulge shape or fitting constraints, the scaling is determined from the known stellar contributions to the total nuclear H- and K-band fluxes (Eckart et al. 1994; Schinnerer et al. 1998) as mentioned in Sect. 1. The corresponding J-magnitude is computed using the JHK colours of a mean zero-redshift QSO (Hyland & Allen 1982). The QSO turns out to be 0.08 mag fainter than the total nuclear J-magnitude starting from the K-band estimate and 0.19 mag fainter starting from the H-band estimate. As expected, both results are similar and the mean value of 0.13 mag is used for the final scaling of the PSF.
The analysis of the I Zw 1 host is restricted to a one-dimensional fitting of radial profiles. A one-dimensional decomposition turns out to be sufficient for the goals of this NIR study, since (i) spiral arms are not as pronounced in the NIR as in the optical and (ii) I Zw 1 is seen nearly face-on so that its brightness distribution is radially symmetric to a good approximation - the latter being supported by a previous NIR investigation of I Zw 1 (Peletier et al. 1999) in which ellipse fitting resulted in an almost constant ellipticity of about 0.1 throughout the disk. The radial surface-brightness profile is determined by measuring the flux per arcsec2 along circles around the centre of I Zw 1 using the IRAF task PRADPROF. Error bars are computed as the standard deviation of numerous values along neighbouring circles in radially logarithmic bins. Neglecting the slight ellipticity of the isophotes adds radial smearing to the measured profile. To estimate the amount of smearing, the radially averaged profile is cross-checked with a direct cut along the kinematic major axis. Both curves agree well within the error bars.
Since the minimum integration time of the ISAAC detector was increased by a
factor of 2 on July 24th, 2001, the nuclear J-band flux in a few central pixels
exceeds the analog-to-digital-units (ADU) level above
which non-linearity of the array occurs.
To make sure that no nuclear flux
is lost in the J-band images, the formula
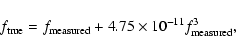 |
(1) |
According to the relative photometric calibration based on the
LCO/Palomar NICMOS system
(Persson et al. 1998), the surface brightness is given in units of
mag arcsec-2.
In order to obtain an absolute calibration in units of
Watt m-2 Hz-1, the UKIRT absolute flux calibration
(Beckwith et al. 1976) is used, taking into account the
slight zero-point offset of
![]() (Hawarden et al. 2001).
The resulting conversion formula is given by
(Hawarden et al. 2001).
The resulting conversion formula is given by
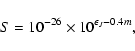 |
(2) |
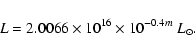 |
(3) |
The typical characteristics of the I Zw 1 environment - like the
two-armed spiral structure, the northern foreground star, and
the nearby western galaxy - can be seen in the
reduced and calibrated J-band image
(Fig. 1).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4270f1.eps}}
\end{figure}](/articles/aa/full/2003/27/aah4270/Timg57.gif) |
Figure 1: Contour J-band image of the I Zw 1 host. The displayed contour levels are 21.16, 20.63, 20.38, 20.16, 19.97, 19.51, 18.83, 18.41, 17.88, 17.25, 16.64, and 14.65 mag arcsec-2. The position of the tidal bridge and the tidal tail in the interaction zone is indicated. |
The derived J-band surface brightness profile is presented in
Fig. 2 together with the PSF,
as measured for a nearby star,
and the ![]() limiting surface brightness.
The profile is compared to the J-band data
previously measured by Peletier et al. (1999). Both curves agree well,
even within the
FWHM of the PSF of the ISAAC observations.
limiting surface brightness.
The profile is compared to the J-band data
previously measured by Peletier et al. (1999). Both curves agree well,
even within the
FWHM of the PSF of the ISAAC observations.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4270f2.eps}}
\end{figure}](/articles/aa/full/2003/27/aah4270/Timg60.gif) |
Figure 2:
Comparison between the VLT/ISAAC J-band
surface-brightness profile
of I Zw 1, corrected for detector non-linearity,
and earlier data from
Peletier et al. (1999). Both profiles show a
good agreement, even within
the FWHM of the PSF (
|
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4270f3.eps}}
\end{figure}](/articles/aa/full/2003/27/aah4270/Timg61.gif) |
Figure 3: Comparison of the original J-band surface-brightness profile of the I Zw 1 host and the profile from which the QSO nucleus is subtracted. |
The original profile and the QSO-subtracted profile of the I Zw 1 host are compared in Fig. 3. Although the subtraction method does not rely on a certain shape of the host bulge, the residual stellar component shows a flat light distribution within the error bars. An exponential disk is fitted to the calibrated and QSO-subtracted surface-brightness profile in Fig. 4 in order to model the clearly evident extended rotating disk of I Zw 1.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4270f4.eps}}
\end{figure}](/articles/aa/full/2003/27/aah4270/Timg62.gif) |
Figure 4: J-band surface-brightness profile of I Zw 1 calibrated in solar luminosities. An exponential disk component is fitted to emphasize the Freeman type I of the profile. |
This fit shows that an additional bulge component is needed to describe the
whole profile consistently.
Bulge and disk components can be clearly distinguished,
as it is typical of Freeman type I galaxies (Freeman 1970).
The host belongs to the high-surface-brightness galaxies which, per
definition, have a central blue disk surface brightness of
![]() mag arcsec-2 (Freeman 1970).
The exponential disk of I Zw 1
has a central surface brightness of about
mag arcsec-2 (Freeman 1970).
The exponential disk of I Zw 1
has a central surface brightness of about
![]() arcsec-2 or
arcsec-2 or
![]() mag arcsec-2. Assuming that the central part of the
galaxy shows almost the same colours as the outer parts of the disk, this
corresponds to
mag arcsec-2. Assuming that the central part of the
galaxy shows almost the same colours as the outer parts of the disk, this
corresponds to
![]() mag arcsec-2, which is
brighter than the canonical Freeman value.
Here, a B-J of
mag arcsec-2, which is
brighter than the canonical Freeman value.
Here, a B-J of
![]() for the I Zw 1 host is used as
derived from the broad band spectrum
in Fig. 9 of Schinnerer et al. (1998) and the B-V
colour of 0.6 to 0.7
(Hutchings & Crampton 1990).
The high central disk surface brightness of the I Zw 1 host
reflects the finding
by Hunt et al. (1999) that exponential disks of
Seyfert galaxies tend to
be brighter than normal spirals. With
for the I Zw 1 host is used as
derived from the broad band spectrum
in Fig. 9 of Schinnerer et al. (1998) and the B-V
colour of 0.6 to 0.7
(Hutchings & Crampton 1990).
The high central disk surface brightness of the I Zw 1 host
reflects the finding
by Hunt et al. (1999) that exponential disks of
Seyfert galaxies tend to
be brighter than normal spirals. With
![]() mag arcsec-2
the I Zw 1 disk is
significantly brighter than the mean B-band surface brightness of
21.44 mag arcsec-2 of normal spirals shown in Fig. 6 of
Hunt et al. (1999).
mag arcsec-2
the I Zw 1 disk is
significantly brighter than the mean B-band surface brightness of
21.44 mag arcsec-2 of normal spirals shown in Fig. 6 of
Hunt et al. (1999).
The composite rotation curve, plotted in
Fig. 5 together with 5![]() error bars,
is corrected for the I Zw 1 disk inclination of
error bars,
is corrected for the I Zw 1 disk inclination of
![]() under the assumption of purely circular gas motions.
Gas velocities at outer radii are taken from a VLA H I map
(Lim & Ho 1999).
These observations have an angular resolution of about
under the assumption of purely circular gas motions.
Gas velocities at outer radii are taken from a VLA H I map
(Lim & Ho 1999).
These observations have an angular resolution of about
![]() .
For the inner rotation curve,
gas velocities are derived from 12CO(1-0) maps
(Schinnerer et al. 1998, Fig. 5), measured with the Plateau de Bure
interferometer at angular resolutions of
.
For the inner rotation curve,
gas velocities are derived from 12CO(1-0) maps
(Schinnerer et al. 1998, Fig. 5), measured with the Plateau de Bure
interferometer at angular resolutions of
![]() and
and
![]() .
The inner slope
is verified by a comparison with 12CO(1-0) BIMA
observations taken at a
higher resolution of about
.
The inner slope
is verified by a comparison with 12CO(1-0) BIMA
observations taken at a
higher resolution of about
![]() (Staguhn et al. 2001).
The good agreement of the different observations indicates that
the inner rise of the rotation curve is not yet affected by the mass
concentration of the active nucleus at these resolutions. The single
deviating data point corresponds to an isolated peak in the 12CO(1-0)
position-velocity diagrams (Schinnerer et al. 1998) and is interpreted as
a giant molecular cloud complex by the same authors. The deviation from the
general circular velocity at this radius corresponds to a cloud orbit which is
inclined by
(Staguhn et al. 2001).
The good agreement of the different observations indicates that
the inner rise of the rotation curve is not yet affected by the mass
concentration of the active nucleus at these resolutions. The single
deviating data point corresponds to an isolated peak in the 12CO(1-0)
position-velocity diagrams (Schinnerer et al. 1998) and is interpreted as
a giant molecular cloud complex by the same authors. The deviation from the
general circular velocity at this radius corresponds to a cloud orbit which is
inclined by
![]() with respect to the I Zw 1 disk.
with respect to the I Zw 1 disk.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4270f5.eps}}
\end{figure}](/articles/aa/full/2003/27/aah4270/Timg73.gif) |
Figure 5:
Rotation curve of I Zw 1 corrected for a constant
inclination of
|
Like the surface-brightness profile, the gas rotation curve supports the classification of the I Zw 1 host as a high-surface-brightness galaxy. It shows the characteristic steep increase at the inside and slight decrease at the outside found for the universal rotation curve of high surface-brightness galaxies by Persic et al. (1996). The overall shape of the rotation curve of the I Zw 1 host is also similar to the rotation curve of the Milky Way (Sofue et al. 1999, Fig. 1) and agrees with the mean rotation curve, presented for galaxies with disk rotation velocities between 200 km s-1 and 250 km s-1 in the same article (Fig. 5). According to the authors, the central peak, the broad disk component, and the high velocities at large radii characterize the I Zw 1 host as a massive Sb or Sc galaxy. A similar classification of the I Zw 1 host as a Sc galaxy is given by Jansen et al. (2000).
In order to derive structural information about the underlying galaxy of the I Zw 1 QSO, the host is decomposed into contributions from bulge, disk, and dark halo components. Taking one potential model for each component, the one-dimensional decomposition has six free parameters, i.e. the scale lengths and the M/L ratios of the bulge and disk potentials as well as, where required, the scale length and mass contribution of a dark halo. The bulge and disk scale lengths which are used to model the rotation curve are derived from the distribution of luminous matter as traced by the surface brightness profile. This approach results in mean M/Ls for the bulge and disk components and is straightforward for the purpose of discussing general trends in M/L. However, the reader should be aware that M/Ls - even in the NIR - are local observables which vary due to effects of dust and stellar populations. Decompositions of the rotation curve are usually not unique (e.g. Bottema & Verheijen 2002; van Albada & Sancisi 1986) so that four different solutions will be presented and discussed. All fits are performed with an implementation of the non-linear least-squares method.
|
|
|
|
|
X | |||
| disk only | 3.50 | - | 1.33 | 49.18 | 28.00 | - | - |
| max disk | - | 0.26 | 1.11 | 49.03 | 26.58 | 100 | 0.9 |
| free a | 1.51 | 0.34 | 0.64 | 44.38 | 19.17 | 76 | 1.5 |
| free b | 0.11 | 0.56 | 0.30 | 43.02 | 15.91 | 52 | 3.2 |
The rotation curve and the surface-brightness profile are decomposed with a
Plummer model for the bulge component and a thin-disk Kuzmin model for the
disk component. These models are chosen due to mathematical
convenience, since both are consistently described by the Miyamoto-Nagai
gravitational potential (Miyamoto & Nagai 1975)
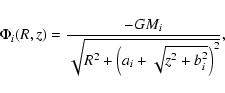 |
(4) |
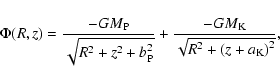 |
(5) |
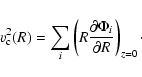 |
(6) |
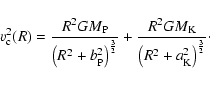 |
(7) |
As the I Zw 1 host is a Freeman Type I galaxy (Sect. 3.2), its profile can best be described by a combination of bulge and disk component.
A decomposition of the J-band surface-brightness profile, consisting of the
two-component model with Plummer bulge and Kuzmin disk, is shown
in Fig. 6. In this decomposition,
the Kuzmin model is fitted to that part of the profile where
possible residua of an unclean
QSO subtraction do certainly not bias the profile shape. The remaining
surface brightness is ascribed to the Plummer bulge.
The decomposition defines the scale lengths of bulge and disk as
![]() and
and
![]() ,
respectively, which corresponds
to a bulge-to-disk scale length ratio of about 0.29.
The luminosity of the bulge results in
,
respectively, which corresponds
to a bulge-to-disk scale length ratio of about 0.29.
The luminosity of the bulge results in
![]() and is roughly half as large
as the luminosity
of the disk of
and is roughly half as large
as the luminosity
of the disk of
![]() .
.
Figure 7
shows four decomposition models for the
gas rotation curve of I Zw 1.
Each fit is obtained under different contraints
for the model components.
The final parameters are listed in Table 3. The
resulting ![]() is added for these cases in which the fitting
procedure allows a specification.
is added for these cases in which the fitting
procedure allows a specification.
![\begin{figure}
\par\mbox{\subfigure[]{
\resizebox{8.6cm}{!}
{\includegraphics[...
... \resizebox{8.6cm}{!}
{\includegraphics[clip]{h4270f10.eps}} }}
\end{figure}](/articles/aa/full/2003/27/aah4270/Timg93.gif) |
Figure 7:
Four examples of a decomposition of the I Zw 1 gas rotation curve.
The model curve (solid line) is shown together with the individual
contributions of bulge (dotted line), disk (dashed line), and dark halo
(dash-dot line). a) Fit with only
a disk and a dark halo (disk only). b)
Maximum-disk fit (max disk).
c), d) All fitting parameters are unconstrained and
fitted simultaneously.
The left panel shows a case in which more weight is put
on the steep increase at the inside
of the rotation curve by confining the lower limit of
the fitting region to
|
As a cross-validation of the two-component decomposition of the
surface-brightness profile,
Fig. 7a shows a fit in which
only a disk and a dark halo model are used while
the bulge component is left out (disk only).
The high ![]() indicates
that the peak of the rotation curve at small radii
cannot sufficiently be described by
such a model. In order to obtain a good fit of the rotation curve with only
a disk and dark-matter model, the disk scale length would have to be chosen
very small (
indicates
that the peak of the rotation curve at small radii
cannot sufficiently be described by
such a model. In order to obtain a good fit of the rotation curve with only
a disk and dark-matter model, the disk scale length would have to be chosen
very small (![]()
![]() ). Such a Kuzmin disk, however, does not yield
a good fit of the surface-brightness profile at large radii.
). Such a Kuzmin disk, however, does not yield
a good fit of the surface-brightness profile at large radii.
Figure 7b presents a maximum-disk fit
(max disk) with bulge, disk, and dark halo component.
The four parameters (Table 3) are determined by the
following procedure: first, only the disk M/L is adjusted to the rotation
curve in order to obtain a maximum contribution of the disk component.
Bulge and dark halo are added in a second and third step to finetune the
total velocity profile.
Since the
fitting is done in individual steps, it is not possible to
give a general ![]() for this procedure.
for this procedure.
The lower panels of Fig. 7 show two least-squares
minima for a non-maximum-disk fit in which all four parameters
(Table 3) are fitted simultaneously.
In Fig. 7c,
more weight is put on the steep increase
of the rotation curve at small radii
by giving a lower limit of
![]() for the fitting
region (free a) whereas the fit in Fig. 7d
is confined to a region starting at
for the fitting
region (free a) whereas the fit in Fig. 7d
is confined to a region starting at
![]() (free b).
The first procedure results in a disk component
whose circular velocities amount to 76% of the corresponding circular
velocities of the maximum disk.
The second procedure yields a more massive bulge
component and a dominant dark matter contribution within the disk region of the
I Zw 1 host. Here, only 52% of the maximum disk circular velocities
are attributed to the disk component.
(free b).
The first procedure results in a disk component
whose circular velocities amount to 76% of the corresponding circular
velocities of the maximum disk.
The second procedure yields a more massive bulge
component and a dominant dark matter contribution within the disk region of the
I Zw 1 host. Here, only 52% of the maximum disk circular velocities
are attributed to the disk component.
By comparing the decompositions of the J-band surface-brightness profile and the gas rotation curve it becomes obvious that at least two components of luminous matter - a bulge and a disk - are necessary to model the I Zw 1 host. The surface-brightness fit results in a bulge and a disk with almost equal luminosities and a bulge-to-disk scale length ratio of 0.29. This is in good agreement with the relations presented by Márquez et al. (2000) for nearby AGN spiral hosts, who found a bulge-to-disk scale length ratio of about 0.2.
| Component | Gas mass | J-band extinction |
|
|
| Disk | 0.4 |
|
||
| Bulge | 0.02 |
|
The maximum-disk assumption
(van Albada & Sancisi 1986) is often applied to have a
criterion for unique rotation curve fits.
Maximum-disk fits seem to provide satisfying
models for Freeman type I as well as Freeman type II galaxies
(Palunas & Williams 2000), although this may only be true for
high-surface-brightness galaxies (de Blok & McGaugh 1997). As a
high-surface-brightness galaxy of Freeman type I, the maximum-disk fit should,
therefore, provide a good estimation of the M/Ls of the I Zw 1
host components.
However, Bottema (1993) argues that, for realistic disk
scale heights, stellar velocity dispersion only allows disk components
with circular velocities of about 63% of the observed maximum velocities.
Such a Bottema disk is close to the two results
presented in Figs. 7c and 7d
with disk components of 76% and 52% of the maximum disk.
I Zw 1 is an interacting galaxy so that the observed two-armed
spiral structure could be driven by the companion. However, assuming
swing amplification
(see Fuchs 2001; Athanassoula 1984; Toomre 1981)
as the underlying mechanism for the
amplification of the I Zw 1 spiral, the disk surface density ![]() at radius R can be obtained from the relation
at radius R can be obtained from the relation
The discussion so far has only concentrated on dynamical M/Ls of the I Zw 1 host components, ignoring any effects of gas contributions and dust extinction. The real stellar M/Ls, however, are certainly lower than the given values, since the mass contributed by gas has to be subtracted from the measured dynamical mass and the light absorbed by dust has to be added to the measured luminosity. With at maximum 7% of total cold gas mass (Eckart et al. 1994), the mass correction for the disk component is negligible and within the error bars. As the disk is seen nearly face-on, the extinction correction is also assumed to be low with a maximum mean J-band extinction of 0.5 mag. The effects on the M/L of the bulge are probably much stronger. With a gas fraction of 20% in the bulge (Schinnerer et al. 1998), the stellar bulge M/L amounts to 80% of the dynamical bulge M/L. The visual extinction of the stellar component in the circumnuclear region is reported to be about 10 mag (Eckart et al. 1994; Schinnerer et al. 1998, and Sect. 1), which corresponds to a J-band extinction of about 3 mag, according to the standard interstellar extinction law (Rieke & Lebofsky 1985). This is certainly an upper limit, since the high visual extinction of 10 mag is most likely confined to the starburst ring, i.e. to radii smaller than 1 kpc, while the fitted bulge model reflects mean properties of a region extending far beyond 1 kpc. Applying these corrections results in estimates about the lower limits for the M/L (Table 4).
Measured J-band M/Ls are very rarely found in literature but
Palunas & Williams (2000) report bulge and disk M/Ls for a sample of
74 spirals in the I-band. For comparison, the bulge and disk M/Ls of the
I Zw 1 host have to be multiplied by a factor of about 2.3,
according to
the host I- J colour of roughly 0.9 mag
(Schinnerer et al. 1998, Fig. 9). The M/Ls for the I Zw 1
host are similar to the majority of M/Ls found by
Palunas & Williams (2000),
since most of their disk M/Ls are in the range of
![]() to
to
![]() and most of their bulge M/Ls are significantly lower
with values below
and most of their bulge M/Ls are significantly lower
with values below
![]() .
.
As the M/Ls increase with increasing age of the underlying stellar population,
the derived M/Ls for the I Zw 1 host
can be used to estimate the mean stellar population in the disk and the bulge
component.
The derived M/L of the disk of
![]()
![]() is slightly sub-solar.
It indicates a predominance of normal stars with a tendency towards a slightly
increased fraction of younger stars. Such a tendency could be explained
by the enhanced star formation activity found for the north-western
spiral arm (Schinnerer et al. 1998).
The M/L of the bulge of
is slightly sub-solar.
It indicates a predominance of normal stars with a tendency towards a slightly
increased fraction of younger stars. Such a tendency could be explained
by the enhanced star formation activity found for the north-western
spiral arm (Schinnerer et al. 1998).
The M/L of the bulge of
![]()
![]() is much lower and
hints at a young stellar population with a significant fraction
of hot stars and supergiants. Such an interpretation is supported by
the finding of strong starburst activity
in the circumnuclear region of I Zw 1 (Staguhn et al. 2001; Schinnerer et al. 1998).
is much lower and
hints at a young stellar population with a significant fraction
of hot stars and supergiants. Such an interpretation is supported by
the finding of strong starburst activity
in the circumnuclear region of I Zw 1 (Staguhn et al. 2001; Schinnerer et al. 1998).
As a nearby QSO, yet showing many properties of high-redshift counterparts, and as a likely transition object in the original evolutionary scheme for AGN, I Zw 1 is a very interesting candidate for a detailed case study of a QSO host. This paper presents new results from J-band imaging of the I Zw 1 host with ISAAC at the VLT - the first investigations in a series, turning I Zw 1 into one of the best-studied QSO hosts.
The analysis shown here provides first-time results focussing on the structure of the underlying host galaxy of I Zw 1, since the host is uncovered by a reliable subtraction of the QSO nucleus from the J-band images. By the structural decomposition of the surface brightness profile and the gas rotation curve the host is characterized as a Freeman-type-I high surface brightness galaxy. It is shown that the radial distribution of luminous matter is similar to that found for nearby AGN spiral hosts. Different solutions for the decomposition of the rotation curve are discussed assuming swing amplification as the prevailing mechanism for the amplification the two-armed spiral structure in the I Zw 1 disk. The resulting M/Ls indicate a tendency towards a younger stellar population in the disk and a predominance of young hot stars and supergiants in the bulge. This interpretation aims at the same direction as previous findings about enhanced star formation in the north-western spiral arm and strong starburst activity in the circumnuclear molecular ring of I Zw 1. New evidence for a tidal interaction between I Zw 1 and the nearby western companion galaxy is found in the sensitive high-resolution ISAAC J-band image, which shows an elongation of the companion as well as a tidal bridge and tail. Without a large-scale bar in the I Zw 1 host, this interaction seems to be the major mechanism for triggering the inflow of gas which is needed to fuel the circumnuclear starburst as well as the QSO. The anticipated merger process would be a further argument for I Zw 1 to be a transitional object in the original evolutionary scheme.
Acknowledgements
We would like to thank the observer who carried out the VLT observations in service mode. We also thank Prof. Dr B. Fuchs for helpful comments and suggestions. J. Scharwächter is supported by a scholarship for doctoral students of the "Studienstiftung des deutschen Volkes''.