A&A 405, 999-1012 (2003)
DOI: 10.1051/0004-6361:20030440

Unidentified infrared bands in the interstellar medium across the Galaxy^,

J. Kahanpää¹ - K. Mattila¹ - K. Lehtinen¹ - C. Leinert² - D. Lemke²

1 - Observatory, University of Helsinki, PO Box 14, 00014 Helsingin yliopisto, Finland
2 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany

Received 26 September 2002 / Accepted 18 March 2003

Abstract
We present a set of 6-12  ISOPHOT-S spectra of the general interstellar medium of the Milky Way. This part of the spectrum is dominated by a series of strong, wide emission features commonly called the Unidentified Infrared Bands. The sampled area covers the inner Milky Way from l = -60$^\circ$ to +60$^\circ$ with a ten-degree step in longitude and nominal latitudes b = 0$^\circ$, $\pm$1$^\circ$. For each grid position the actual observed direction was selected from IRAS 100  maps to minimize contamination by point sources and molecular clouds. All spectra were found to display the same spectral features. Band ratios are independent of band strength and Galactic coordinates. A comparison of total observed flux in band features and IRAS 100  emission, a tracer for large interstellar dust grains, shows high correlation at large as well as small (1$^\prime$) scales. This implies a strong connection between large dust grains and the elusive band carriers; the evolutionary history and heating energy source of these populations must be strongly linked. The average mid-infrared spectrum of the Milky Way is found to be similar to the average spectrum of spiral galaxy NGC 891 and the spectra of other spirals. The common spectrum can therefore be used as a template for the 6-12  emission of late-type spiral galaxies. Finally, we show that interstellar extinction only weakly influences the observed features even at $\lambda = 10$  , where the silicate absorption feature is strongest.

Key words: ISM: lines and bands - ISM: dust, extinction - infrared: ISM - Galaxy: disk - galaxies: ISM

1 Introduction

The 3-13  spectra of diffuse objects such as H II regions, planetary and reflection nebulae and Milky Way cirrus clouds include a series of emission bands collectively known as the unidentified infrared bands (UIR bands or UIBs). These structures have also been observed in external galaxies. Since the first detection of the 11.3  band by Gillett et al. (1973) more than a dozen bands have been identified in various astronomical spectra. Main bands always occur together, at 3.3, 6.2, 7.7, 8.6, 11.3 and 12.7  . Sometimes fainter companions at 3.4, 5.25, 5.65, 6.9, 9.7, 13.6, 14.1 and 16.5  are seen. The relative strengths of bands depend on the observed object. This variation is probably related to changes in age and chemical abundances in carrier molecules since band ratios do not depend strongly on strength or hardness of the local UV field (Chan et al. 2001; Uchida et al. 2000).

The exact nature of the carriers of the UIR bands is still unknown. It is generally agreed that the main bands are caused by bending and stretching modes of carbon-carbon and carbon-hydrogen bonds in large organic molecules; Holmlid (2000) has, however, proposed an alternative scenario based on de-excitation of Rydberg matter. All details of the chemical structure of UIB carriers are still obscure. The polyaromatic hydrocarbon (PAH) model, originally proposed by Léger & Puget (1984) and Allamandola et al. (1985) is frequently used for analysis of the observed band widths and band ratios but other proposed carriers like coal (Papoular et al. 1989), hydrogenated amorphous carbon (Duley & Williams 1981) and quenched carbonaceous composite (Sakata et al. 1984) can not be ruled out at present.

In 1985, Puget et al. proposed that the IRAS 12  excess, first reported by Boulanger et al. (1985), is caused by a UIB component in the diffuse Galactic emission. This hypothesis was supported by detections of the 3.3 and 6.2  bands in the Galactic emission with a balloon-borne instrument, AROME (Giard et al. 1988; Ristorcelli et al. 1994) and later confirmed by detailed spectrophotometry by the ISO and IRTS satellites (Mattila et al. 1996; Onaka et al. 1996; Tanaka et al. 1996) and by the detection of UIB emission from a single high-latitude cloud (Lemke et al. 1998). It has hence become clear that the UIB carriers are also common in the low-density (0.01-100  H atoms per cm^-3), low energy density regions known collectively as the diffuse interstellar medium. Further support is provided by detection of the interstellar 6.2  band in absorption in the IR spectra of Wolf-Rayet stars (Schutte et al. 1998)

Most studies of properties of the UIBs and their carriers are based on observations of high-density and high energy density environments such as reflection or planetary nebulae, where the UIB carriers are expected to be newly formed. The diffuse ISM provides us with a complementary set of properties: there the UIB carriers are expected to be old and all volatile species should have evaporated. The low energy density limits the number of possible carrier species. As equilibrium temperatures are not high enough to produce these bands, transient heating of very small particles by single photons must be considered (Greenberg 1968; Lemke et al. 1998; Boulanger et al. 1998b).

In this paper we present the results of an ISO guaranteed time project on the distribution and properties of UIB carriers in the general interstellar matter of the Galactic disk. Our aim is to answer the following questions:
1) What is the projected distribution of UIR band emission in the inner Milky Way?
2) Do the band ratios, band widths or scale height of the emitting layer change with Galactic longitude?
3) How does the UIB emission from the diffuse interstellar matter relate to other dust components (represented by IRAS 25, 60 and 100  emission maps) and neutral or molecular gas?

Table 1: Summary of observed positions. Five leading columns give the name and equatorial and galactic coordinates for each position; the remaining columns give the UIR line intensities. The unit used is . Statistical errors for all intensities are also shown.

   
2 Observations and data reduction

The dataset consists of 49 small raster maps made with the ISOPHOT-S spectrometer (Lemke et al. 1996) onboard the Infrared Space Observatory (ISO) (Kessler et al. 1996). This low-resolution ( $R \approx 60$, $\Delta\lambda \approx 0.1$  ) instrument covers the wavelength range $\lambda = 2.5{-}11.6$  with a small gap at 4.9-5.8  . Observations spanned a large part of the lifetime of ISO; the first dataset was recorded during revolution 81 (2/1996) and the last during revolution 840 (3/1998). The equatorial and galactic coordinates of the observed positions are listed in Table 1. ISO Target Dedicated Time (TDT) numbers for each observation are listed in Table 2, available only in electronic form at the CDS. The observed fields sampled the inner Milky Way at $\emph{l}\approx \pm 5\hbox{$^\circ$ }, \pm 15\hbox{$^\circ$ }, \pm 30\hbox{$^\circ$ }, \pm 45\hbox{$^\circ$ }$ and $\pm$ $60\hbox{$^\circ$ }$. For each nominal longitude, five latitudes were observed: two reference measurements (OFF-positions) at $\emph{b}\approx +5\hbox{$^\circ$ }$ and -5$^\circ$ in order to check the zodiacal emission and three ON-positions at $\emph{b}\approx 0, \pm 1\hbox{$^\circ$ }$. A single position included in the original grid, G-60-1, was not observed due to observing time constraints.

All observations at a given Galactic longitude were done within the same ISO revolution to minimize variations in the zodiacal emission foreground due to changes in solar aspect angle. The contribution of Galactic emission in the OFF-positions was minimized by choosing the darkest positions in IRAS 12 and 100  maps close to the nominal (l, b) positions. For the ON-positions the IRAS maps were checked for point sources and the exact positions were then selected in regions with no known Galactic or extragalactic IR sources. CO maps were also consulted and regions with major molecular gas complexes were avoided. The resulting positions should be a reasonable sample of the general ISM: emission from the tenuous diffuse ISM dominates even if regions with molecular gas can never be completely avoided in this kind of sampling.

Each observation consists of a small raster map made with ISO Astronomical Observing Template P40 (see Laureijs et al. 2000); a standard 32-s dark current and memory effect checking integration was followed by 64-s sky measurements arranged in a small raster map. For the ON-positions the map size was $2 \times 2$ pixels, for OFF-positions $2 \times 1$ pixels. The distance between raster points was equal to the PHT-S aperture size ( $24\hbox{$^{\prime\prime}$ }\times\ 24\hbox{$^{\prime\prime}$ }$).

Figure 1: Data reduction steps of the PHT-S spectrum of G+30+0. a) Charge accumulation rate (mV/s) for the four individual pointings. Data for all four pixels is shown. b) Median of surface brightness ( ). Zodiacal emission surface brightness at c) b =  $+5\hbox {$^\circ $ }$ and d) b =  $-5\hbox {$^\circ $ }$. e) Average the of the zodiacal spectrum at b = $\pm$5$^\circ$ and a polynomial fit to the data. f) Final foreground-subtracted spectrum.

Open with DEXTER

	Figure 2: Zodiacal foreground emission for selected OFF-positions. A 2nd degree polynomial fit to the data is shown with a solid line and a model prediction of zodi_emit (see Sect. 2) with a dashed line. In the case of G+5$\pm$5 the two lines completely coincide.
Open with DEXTER

Data reduction was done with the ISOPHOT Interactive Analysis (PIA) program version 9.0.1.

A few observations were first processed manually to find the optimal reduction procedure and the PIA batch processing mode was then used to create a homogeneous set of calibrated spectra. Figure 1 illustrates the reduction procedure. The following reduction steps were applied:

1.

2-threshhold deglitching (i.e. detecting and removing cosmic ray events from raw data).

2.

Fitting ramps. Using the ramps subdivision technique tripled the number of usable data points and made the next step feasible.

3.

Removal of deviating points caused by detector glitches. The first 15 s of each measurement were always discarded as values in this range are strongly affected by drift of the detector.

4.

Subtraction of dark current. We used the default orbital position-dependent dark current model as the dark measurement in the P40 observing mode is dominated by memory effects. The top panel a in Fig. 1 shows the resulting spectrum for each of the four pixels in the G+30+0  $2 \times 2$ raster map.

5.

Calibration from instrumental (V/s) to physical units ( $\ensuremath{\rm {10^{-10}~W~cm^{-2}~\ensuremath{\rm {\mu m}}^{-1}~sr^{-1}}}$). The default calibration scheme in PIA 9.0.1 was used. The P40 observing mode is well suited for use of the new ISO dynamic calibration method, but since all observed fields are very faint, the resulting calibration was practically independent of the chosen calibration method.

6.

Each $2 \times 2$ raster map was checked for pixels with systematically higher values in either the short- or the long-wavelength part of the spectrum. If such a discrepancy was found the deviating pixel was rejected from further analysis. Only one position (G-15+1) had signs of point source contamination in one of the four pixels.

7.

The final search point in the (l, b)-grid was obtained by averaging over all good pixels in the raster maps. The second panel b in Fig. 1 presents the calibrated spectrum for G+30+0 in physical units ( ).

8.

The contribution from zodiacal dust was estimated from the OFF-position spectra at $\emph{b}= \pm 5\hbox{$^\circ$ }$. We fitted a 2nd degree polynomial to the foreground emission measurements and subtracted the resulting smooth approximation of the zodiacal emission spectrum from the ON-position spectra. Panels c and d in Fig. 1 show the individual spectra at b = 30$^\circ$, l = +5$^\circ$ and -5$^\circ$, respectively. The next panel e shows the average together with the polynomial fit and the last panel f displays the final, calibrated and foreground-subtracted mid-IR spectrum at position G+30+0.

The error estimate for our data includes several components. Error bars in Fig. 3 show the statistical errors in each spectrum. The uncertainty of the continuum level is mostly affected by the accuracy of the zodiacal foreground subtraction, which we estimate to be better than 10% of the foreground level or less than $0.15~\times$  . Observed zodiacal light levels at the OFF-positions were compared with model predictions by the zodi_emit method in the ISO Spectral Analysis Package (ISAP). The excellent match of both intensity and shape of the observed foreground spectra and the models is shown in Fig. 2. The absolute calibration accuracy of ISOPHOT-S is known to be around 10% and relative accuracy of feature intensity within the spectrum is 20% (Laureijs et al. 2000) Finally, it should be noted that the random noise pattern is slightly, but definitely non-Gaussian with a preference for high values. This effect is probably caused by only partial correction for minor cosmic ray hits during exposures.

A few spectra are also affected by one to three systematically deviating detector pixels; these pixels were identified by the very high dark current and ignored in the analysis.

According to Tanaka et al. (1996) and Giard et al. (1989) the 3.3  band peak intensity in the plane of the Milky Way is 0.1-1 $\times$  - less than the 1-$\sigma$ noise level of our spectra at 3.3  . No signs of the 3.3  peak were found in the short-wavelength part. The short-wavelength parts of the spectra were not analyzed further.

Figure 3a: UIB spectra of the general interstellar matter. The southern quarter of the inner Milky Way (l = -60$^\circ$--5$^\circ$). For each position the observed spectrum is shown as a histogram line and a fit using four Cauchy profiles and a linear continuum as a continuous line. For G-15+0 the linear component with 1-$\sigma$ error limits is also displayed separately as a dashed line.

Figure 3b: UIB spectra of the general interstellar matter. The northern quarter of the inner Milky Way (l = +5$^\circ$-+60$^\circ$). Data and fit as in Fig. 3a.

3 Results

Visual inspection of the resulting spectra presented in Fig. 3 reveals a number of common properties:

• The 6.2, 7.7 and 11.3  UIR bands are widespread in the diffuse ISM. All observed fields within $\emph{l}< 45\hbox{$^\circ$ }$ display these bands. At G+60+0 and G-60+0 the bands are clearly visible, but the off-plane positions at these longitudes display only traces of UIR bands.
• The flux level of all bands at $\emph{b}= \pm1\hbox{$^\circ$ }$ is roughly one half of the flux at $\emph{b}= 0\hbox{$^\circ$ }$. If this relation also holds for the outer longitudes the lack of a reliable detection of band structures at G$\pm$60$\pm$1 is caused by the limited sensitivity of the spectrometer.
• The 8.6 band is visible at most positions. Spectra with high S/N ratio clearly shows this feature as a well-defined bump on the shoulder of the broad 7.7  band. No fainter bands are detected.
• The spectra are similar to those observed in molecular clouds (Boulanger et al. 1985; Cesarsky et al. 1996b), reflection nebulae (Cesarsky et al. 1996a), spiral (Mattila et al. 1999) and starburst galaxies (Lutz et al. 1999).
• The widths, shapes, relative strengths and positions of the main bands are seemingly uncorrelated with Galactic position or with the total UIR band flux.
• No position displays the clear continuum seen in hot sources such as the M17 H II region (see Cesarsky et al. 1996a). Flux levels in the 9-11 range are very low in all spectra. The average spectrum in Fig. 6 sets the upper limit of continuum emission near 10  to <10% of the 7.7  band peak flux. The contribution from stellar atmospheres, which is clearly seen in the short-wavelength (2.5-4.9  ) part of the spectrum (Fig. 1a), is negligible in the long-wavelength part of the spectrum.
• Position G-15+0 displays seemingly aberrant behavior: the flux levels at the Galactic plane are only slightly higher than those at b = $\pm$1$^\circ$ while all other longitudes behave in a consistent fashion. Closer examination of the IRAS 100  map reveals a very dark spot exactly at the observed position. It seems clear that we have in this case inadvertently selected a line-of-sight with little interstellar matter.

3.1 Band widths and central wavelengths

The UIR bands are frequently approximated and modelled with Cauchy profiles:

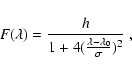$$F(\lambda) = \frac{h} {1 + 4(\frac{\lambda-\lambda_0}{\sigma})^2}~ ,$$ (3)

where h is the height of the band and $\sigma$ is the full width at half maximum (FWHM), superimposed on a linear continuum component (see Boulanger et al. 1998a). We adopted this method and fitted all ON-position spectra with a combination of four Cauchy profiles and a linear component using the curvefit function in IDL. No significant variability in the central wavelengths or band widths as a function of band strength or Galactic position was detected during the first round of modeling. These two parameters for each band were then fixed to the average values (listed in Table 3). Widths are comparable to other published values (see Table 7 in Li & Draine 2001 and references therein); the sparse literature on band widths in the diffuse ISM is summarized in Table 4. These values are also in agreement with the quantitative PAH model by Li & Draine if instrumental broadening is taken into account. The central wavelengths are somewhat shifted compared to values listed in Mattila et al. (1999); this is not a true difference between NGC 891 and the Milky Way, but caused by a change in the official ISOPHOT-S wavelength calibration. Final UIR band modeling used only the height of each band and the slope and zero point of the linear background as free parameters, giving a total of six free parameters. Figure 3 shows the fits (solid lines) overplotted on original data.

The infrared continuum component is minimal in all spectra. As an example, the continuum component for position G-15+0 is shown in Fig. 3a. The dashed continuum line is flanked by the steepest and flattest continuum (dotted lines) allowed within 1-$\sigma$ error limits. Note that this fit and the error margins are all within $0.15~\times$  of zero and thus within the estimated error of our foreground subtraction accuracy. Our foreground subtraction method would eliminate a Galactic continuum emission component from our spectra, if and only if such a continuum had a very broad latitudinal distribution at 6-11  with essentially the same values at $\emph{b}= \pm 5\hbox{$^\circ$ }$ and at  $\emph{b}= 0\hbox{$^\circ$ }$. No such Galactic component is seen in the COBE-DIRBE or IRAS 12  all-sky maps. It is therefore clear that no significant, mid-IR continuum at 6-11  is present in the sampled area.

Table 2: UIR band widths and central wavelengths in the diffuse interstellar matter.

Table 3: Published UIR band widths (FWHM, in ) in the diffuse interstellar medium.

3.2 Band ratios and correlations

We define the band area or band intensity as the total area of the Cauchy profile, which can easily be calculated from band parameters: $A = 0.5 \pi h \sigma$. The total band area is then defined as the sum of band areas of the four bands seen in our ISOPHOT-S data. Any systematic changes in the relative band strengths with the total strength of the UIR bands should be observable as displacements or nonlinearities in Fig. 5, which displays the 6.2 and 11.3  band areas as a function of the 7.7  band area. No such structures can be seen in either one of the band ratio plots. Least-squares fits (shown in Fig. 5 as solid lines) to the band ratios yield average ratios of 0.21 and 0.27 for the 6.2/7.7  and 11.3/7.7  band pairs, respectively. The uncertainty for each ratio is $\pm$0.01. The standard deviations of individual ratios are 0.07 and 0.13.

The two lower panels in Fig. 5 show the behavior of band ratios as a function of the 7.7  band strength for individual points. 11.3/7.7  flux ratios do not seem to have any systematic trends except the expected decrease of noise towards higher intensities, while the 6.2/7.7  flux ratios suggests that there may be a trend towards higher 6.2/7.7  ratio values at small intensities.

	Figure 4: a) 6.2  vs. 7.7  band area ( ). b) 11.3  vs. 7.7  band area. c) 6.2/7.7  band ratio vs. 7.7  band area. d) 11.3/7.7  band ratio vs. 7.7  band area. The solid lines in panels  a) and  b) show a least-square fit to the data. The resulting band ratios are 0.21 and 0.27 for the 6.2/7.7  and 11.3/7.7  pairs.
Open with DEXTER

	Figure 5: a) The average of six points with strongest emission (b = 0$^\circ$, l = $\pm$5$^\circ$, $\pm$15$^\circ$and $\pm$30$^\circ$) together with a four-band fit to the average; the residual shown has been shifted downwards by  $-0.5~\times$   and multiplied by a factor of 5 for clarity. b) The average over all spectra at Galactic latitude $\emph {b}= \pm 1$$^\circ$.
Open with DEXTER

3.3 Weak UIR bands

We searched for the fainter UIR bands at 6.9 and 9.7  in an average spectrum encompassing the points between +30$^\circ$ and -30$^\circ$ Galactic longitude and b = 0$^\circ$. The resulting low-noise spectrum (shown in Fig. 6) was fitted with the same combination of four Cauchy profiles and a linear continuum as the individual spectra. The residual does not reveal any clear structures; this sets the upper limit for these bands at 0.3 $\times$  , a value much larger than the upper limit calculated by Onaka et al. (1996) from a larger data set covering some 100 square degrees around l = 50$^\circ$, b = 0$^\circ$.

Some excess is present near 6.9  but it might also be caused by a non-Lorentzian shape of the 7.7  band. Any signal at 9.7  is masked by the noise. For comparison Fig. 6 also shows the average of all off-plane spectra (b = $\pm$1$^\circ$); no difference in the band shapes between on-plane and off-plane positions is seen.

   
3.4 Distribution of UIB emission within the Milky Way

The longitudinal distribution of the UIB emission is sampled at ten positions by our dataset: at each longitude three latitudes (b = 0, $\pm$1$^\circ$) were probed. The resulting on-plane and off-plane longitude profiles of the UIR bands and band ratios are shown in Fig. 7. The on-plane profile shows a strong concentration towards the central 90$^\circ$ of the Galactic plane and strong variability within this region. The off-plane profile mimics the on-plane values but displays less variation in the central region. No warp of the diffuse dust layer is seen; the behavior of the b = +1$^\circ$ and b = -1$^\circ$ profiles is identical in the outer (l > 30$^\circ$) part of the sampled area. However, there is a clear systematic asymmetry between the outer parts of the Galaxy: both on-plane and off-plane emission is weaker at l = +45$^\circ$-+60$^\circ$ than at l = -45$^\circ$--60$^\circ$. This asymmetry is also seen in the large dust grain distribution (COBE-DIRBE 240  data) and stellar radiation (see Drimmel & Spergel 2001 and references therein).

The variation of band ratios seen in Fig. 7 does not deviate from a noise pattern since the statistical errors for individual band ratios are close to the standard deviation of the distribution of the ratios and no clear longitudal pattern is seen.

In order to estimate the angular height of the UIB-emitting layer at each sampled Galactic longitude we fitted a Gaussian profile to the three observed points at each nominal longitude. Due to the limited number of observations, the FWHM and the peak flux at the Galactic plane were the only free parameters while the center of the distribution was assumed to be on the Galactic plane. No statistically significant trends were found in the longitudinal distribution of FWHM values except the high FWHM value at l = -15$^\circ$ caused by the anomalously low flux at G-15+0. Our average FWHM value for the UIB component, 1.49$^\circ$ $\pm 0.08$$^\circ$ is close to the FWHM value (1.6$^\circ$) found by Ristorcelli et al. (1994) for the 6.2  band in the inner Milky Way and the IRAS 12  FWHM value ($1.5\pm0.1$$^\circ$). The deviating longitude l = -15$^\circ$ was excluded from the average.

The latitude distribution of 3.3 band emission has two components: a narrow one with a FWHM of 1.6$^\circ$ and a wide one with a 9-degree FWHM (Giard et al. 1989). The present observations do not allow us to exclude the possibility of a wide component in UIR bands between 5.8 and 11.6  . The OFF-position measurements at $\pm$5$^\circ$ provide only an upper limit (<0.1 $\times$  ) for the flux levels at higher latitudes.

Figure 6: Galactic distribution of UIB bands: a) Total area of the four main bands. b) 6.2/7.7  band ratio. c) 8.6/7.7  band ratio. d) 11.3/7.7  band ratio. e) 11.3/6.2  band ratio. In each panel stars and a line are used for values at the Galactic plane and triangles for b = $\pm$1$^\circ$. A dotted line traces the average of values at b = $\pm$1$^\circ$. For clarity error bars are plotted only for Galactic plane values.

Open with DEXTER

4 Discussion

The diffuse ISM provides us with a test laboratory where the properties of all interstellar components are uniform. Due to the high age of the diffuse component, we expect to see little large-scale variation in the properties of the UIB emitters and this is indeed what is observed. Variations caused by evolution of dust grains and strong UV fields have been diluted away. Another stabilising effect is the independence of shape of UIBs of the intensity of the heating UV field. This is a general property of all models that rely on single-photon heating; it holds as long as the UV flux does not ionize or otherwise permanently modify the carrier particles. These properties combine to form a universal template spectrum of old UIB carrier populations in cool environments, which is observed over and over again in the diffuse ISM of our own Galaxy and in other quiescent spiral galaxies. Unfortunately, the general insensitivity of UIB carriers to nuances of ISM conditions make the bands rather useless as probes of physical conditions of the diffuse interstellar matter.

Because of the diffuse, but still inhomogeneous nature of the general ISM, each one of our observations samples a range of environments. A typical line-of-sight will pass through several small molecular clouds in addition to the tenuous intercloud medium. The very existence of a template spectrum - i.e. a spectrum that matches all positions - proves that cloud-to-cloud variation of the spectral shape must be small. This has already been pointed out by Chan et al. (2001), who analysed a larger sample of observations which did not specifically target the diffuse component.

4.1 Correlation with other ISM components

Figure 7: Total UIB flux in the 5.8-11.6  range versus a) IRAS 100 and b) IRAS 12  flux from ISSA. Each panel shows also a least-squares fit to the data (dashed line) and one-sigma errors for the fit (dotted lines). Diamonds mark Galactic plane positions and crosses b = $\pm$1$^\circ$ values. Values for NGC 891 (from Mattila et al. 1996) are marked for comparison with a triangle with error bars. Data for NGC 891 have been arbitrarily scaled (while preserving the ratio) to typical Milky Way values.

Open with DEXTER

Figure 8 presents the total 5.8-11.6  UIB emission plotted against the IRAS 100 and 12  fluxes. In both cases linear least-squares fits to the data and one-sigma error estimates are also shown. A high correlation with the IRAS/ISSA 12  flux is expected, as the flux in this band is dominated by UIB structures (Puget et al. 1985; Giard et al. 1989; Mattila et al. 1996) and a high correlation is indeed found: the Pearson correlation coefficient of the IRAS 12  flux and the total UIR band flux is 0.96. The correlation with the IRAS 100  flux measured on the IRAS Galaxy Atlas (IGA) is equally good, with a correlation coefficient of 0.95. A similar value (0.96) was found by Onaka et al. 1996 for the correlation between UIB (7.7  band) and IRAS 100  fluxes in a larger set of observations, which sampled only a small sector of the Galaxy ( $44\hbox{$^\circ$ }< \emph{l}< 54\hbox{$^\circ$ }$, $\vert\emph{b}\vert \le 5\hbox{$^\circ$ }$). These correlation coefficients can thus be considered typical for the general interstellar matter. Previously published figures of the UIB/IRAS correlation show a deviation towards lower UIB flux at high IRAS 100  fluxes (Tanaka et al. 1996; Onaka et al. 1996). This effect is explained by heating of large dust grains by intense radiation fields. Using the total FIR flux as a dust measure instead of using the 100  flux corrects for this effect (Onaka 2000). A trend towards low UIB to FIR ratios is still evident at very high radiation densities ( $G_0 > 10^3 - 10^4\;G_{\odot}$, where $G_{\odot}$ is the total radiation density in the solar vicinity), but such conditions are never seen in the general interstellar medium. Most of the UIB flux included in our plots is emitted by the 7.7  band; we see no change of slope in the UIB/100  relation up to 100  flux of 1700 MJy/sr.

A comparison of the longitudinal profile of UIBs with profiles for several other interstellar components is shown in Fig. 9. Dense gas and dust tracers ( ¹²CO and IRAS far-infrared fluxes) follow the general UIB distribution as described in Sect. 3.4, but the profile for atomic gas (H I and C II) displays a much less concentrated profile with a central minimum. The strong correlation with molecular gas provides a tool for further analysis of the properties and general distribution of UIB carriers in the Milky Way: the molecular gas tracers can be used for distance estimation. It should be noted that the resolution of Galactic plane surveys in the radio and infrared domains is generally less than our field of view (1$^\prime$) and thus the details of the profiles should not be compared.

Figure 8: Comparison of UIB emission distribution with a) diffuse gas (C II, 158  , Nakagawa et al. 1998); b) molecular gas ( 12CO, Dame et al. 2001); c) neutral hydrogen (H I column density, Dickey & Lockman 1990); d) IRAS 12  flux; e) IRAS 25  flux; f) IRAS 100  flux. The UIB data is marked with filled circles and have been scaled to match the outer parts of the comparison profile in all panels.

Open with DEXTER

Our data probes the correlation between 100  and UIR band emission in the general ISM at two very different angular scales, the largest scale being defined by the grid step and the smallest by the size of the ISOPHOT-S pixel, i.e. 24 $^{\prime\prime}$. Large-scale correlation between 100  emission and UIBs is proved by point-by-point comparison of the fluxes in Fig. 8. There is no obvious reason why the 100  and UIR band emission should be so strongly correlated at any scales in the general ISM. The IRAS 100  band is dominated by thermal emission of large, cool dust grains, while the UIB spectrum stems from much smaller, thermally fluctuating particles. The conclusion is that formation and subsequent evolution and dynamics of the UIB carriers and large dust grains in the ISM must follow similar lines. The observed correlation also constrains the energy budget of UIB carriers: the heating source for UIBs and large grains must be the same or at least the energy sources for UIBs and FIR emission be strongly correlated. Heating of large grains in the general ISM is dominated by the visible - near infrared part of the interstellar radiation field. The same part of the interstellar radiation field must thus be important for the heating of UIB carriers. According to Sodroski et al. (1997), the relative abundance of UIB carriers with respect to large grains rises by a factor of two at Galactic radii larger than 8.5 kiloparsecs. This change should be seen in the UIB to 100  ratio. Our dataset samples mainly the inner Milky Way: even the G$\pm$60 lines of sight pass within 7.5 kpc from the Galactic center. Only a minor contribution in each spectrum is expected to arise from the outer parts of the Galaxy and thus this dataset cannot be used to limit the variation of the UIB to 100  ratio at Galactic radii larger than 8.5 kpc.

  
4.2 NGC 891 and the Milky Way

The UIB emission of the edge-on spiral galaxy NGC 891 has recently been mapped by Mattila et al. (1999). This study used the same instrument and a similar observing scheme as our Milky Way study. NGC 891 is in many ways similar to our own Galaxy and this similarity is also evident in the UIB spectrum. An average spectrum of NGC 891 was produced by summing all observed spectra within 144 $^{\prime\prime}$ from the center of the galaxy. This average, the corresponding average spectrum of the Milky Way and their difference is shown in Fig. 10. The shapes of the UIB spectra in the 6-12  range are almost identical. This is remarkable especially since the two datasets sample the ISM of the target galaxies in different ways: Our Milky Way dataset targets small fields in the general ISM. In NGC 891 the ISOPHOT pixel size (24 $^{\prime\prime}$) corresponds to 1 kpc and there is no way to separate the contribution from giant molecular clouds or point sources. A survey of UIB spectra of various types of spiral galaxies (Helou et al. 2000) shows that the shape we see in Fig. 10 is typical not only for Milky Way-type spirals, but for spirals in general.

The only, tentative, difference between the spectra of NGC 891 and the Milky Way is the presence of a small excess feature at 7.1  in the difference spectrum of NGC 891 minus the Milky Way average. This bump is also present in the average UIB spectrum of 28 spiral galaxies (Helou et al. 2000) and less clearly in the ISO SWS spectrum of the Galactic center (Lutz et al. 1996). A recent summary of UIR band data (Peeters et al. 2002) reveals that this feature is rather strong in such objects as HD 44179 (the central star of the "Red Rectangle'') while the spectra of low-radiation-density objects lack this band. The presence of the 7.1  bump in the average spectrum of NGC 891 reveals a significant and expected contribution from compact sources, if this feature truly is missing from the spectrum of the diffuse ISM.

The peak and average observed surface brightness of UIR bands are identical in NGC 891 and the plane of the Milky Way (Fig. 10). This must be a coincidence since the viewing geometry and the beam filling factor are not the same for these two targets. In the Milky Way the UIB emission uniformly fills  the small (24 $^{\prime\prime}$) detector beam and a single beam includes sources at both small and large distances. In the case of NGC 891 the distance to the constituent sources is constant, but the real surface brightness varies across a single ISOPHOT-S detector pixel (see Fig. 2 in Mattila et al. 1999).

The ratios of the total UIB flux to the 100  and 12  fluxes of NGC 891 are similar to the ratios for individual lines-of-sight in the Milky Way. Data for NGC 891 are included in Fig. 8 and marked with triangles with error bars. Both UIB/12  and UIB/100  ratios for NGC 891 lie above typical Milky Way values by 30-40%. However, the uncertainty of the ratios ($\pm$30%) is such that the difference is not significant. Not only the shape of the UIB spectrum but also the total intensity compared with other dust components is similar in the Milky Way and in NGC 891. (Note that the units for NGC 891 and the Milky Way data are different, surface brightness versus total flux, and only the ratios can be meaningfully compared here.) The flux values for NGC 891 shown in Fig. 8 were arbitrarily scaled - while preserving the ratio - to fit into the brightness range defined by Galactic values.

In spite of the different sampling of the ISM in the Milky Way and NGC 891 by our PHT-S observations the UIB spectra are almost identical. Therefore, the spectrum in Fig. 10 can be used as a template spectrum for the 6-12  emission of large, late-type spiral galaxies in general until new IR observatories in space enlarge the available data base.

	Figure 9: Comparison of the UIB spectra of NGC 891 and the Milky Way. Solid line: Average of Milky Way spectra. Dashed line: Average of central region of NGC 891 (see Mattila et al. 1999). Dotted line: The difference of the spectra mentioned above, shifted down by $0.5 \times$  .
Open with DEXTER

4.3 Band ratios in the PAH model

The observed band ratios can be converted into physical properties of the emitting particles. This conversion is naturally model-dependent as the radiative properties of very small, solid interstellar particles are still poorly understood. We adopt the PAH model of Draine & Li (2001) for our analysis. The observed mean values for band ratios ( 11.3/7.7 = 0.27, 6.2/7.7 = 0.21) correspond to a somewhat ionised PAH mixture with a typical particle size around 200 carbon atoms heated by an average interstellar radiation field. Draine & Li define band ratios in the same way as we do, i.e. as the ratio of areas of Cauchy-profile fits to the bands. Their model results are directly comparable with the ratios used in this paper. Previous papers on UIR bands have frequently defined the band area as the integrated flux above an estimated baseline. Ratios derived from such estimates are not directly comparable with our results or the model values in Draine & Li since a large part of the intensity in Cauchy profiles lie outside the central peak.

While each of our observations samples several diffuse and molecular clouds, it is to be expected that the conditions in these clouds do not vary wildly and so average values over observed lines-of-sight still represent typical values in the general ISM.

   
4.4 Absorption effects and the 9-11 $\mu$m continuum

Table 4: Effects of extinction in UIR band ratios.

The study of mid- and far-IR continuum emission of low  brightness sources is strongly affected by the zodiacal foreground. We have tried to minimize this error source by using two OFF-position measurements for each longitude. The zodiacal-subtracted spectra include only a trivial continuum component; the remaining flux in the 9-11  range is a product of the wide wings of the 7.7  and 11.3  bands. The lack of flux in this interval could be attributed to a number of phenomena. The most simple is a true lack of emission in this wavelength range from the diffuse ISM. A weak continuum component (less than our detection limit) was reported by Onaka et al. (1996). The Mid-IR Spectrometer (MIRS) of IRTS had a much larger field-of-view than ISOPHOT-S and thus a contribution from compact UIB emitters within the field of view is probably present in the published MIRS spectra of the diffuse ISM.

Another possible cause of the low flux is the broad silicate absorption feature centered at 9.7  . This structure has been observed in the diffuse medium towards the Galactic center (Rieke & Lebowsky 1985) and several local sources (Knacke & Gaustad 1969; Gillett et al. 1975) as well as in nearby spiral galaxies (Glass et al. 1982; Imanishi & Ueno 2000).

We can solve the attenuation caused by the silicate band if we assume spatially constant values for the emissivity ( $\epsilon_{\lambda}$) and the absorption coefficient ( $\kappa_{\lambda}$). In the unobscured case, the surface brightness is simply  $I_0 = \epsilon_{\lambda} r$, where r is the path length. If $\kappa_{\lambda}$ is >0, the intensity is

$$I = \frac{\epsilon_{\lambda}}{\kappa_{\lambda}}(1-{\rm e}^{-\... ...}) = \frac{I_0}{\tau_{\lambda}}(1-{\rm e}^{-\tau_{\lambda}}) .$$ (4)

Optical thickness at the center of the silicate feature can be estimated from A_V: $\tau_{\rm Si}$ is $0.05{-}0.07 \times A_V$(Aitken 1981; Rieke & Lebowsky 1985; van der Hucht et al. 1996); we adopt an average value, 0.052, as calculated in the summary of observations in Mathis (1998). Resulting loss of intensity near the 9.7  minimum is $I/I_0 = 0.8{-}0.5 \; (\tau_{\rm Si} = 0.5{-}1.4)$, as the average optical attenuation is $A_V \approx 1 {\rm ^m kpc^{-1}}$ and a typical path length within the Milky Way is 10-20 kiloparsecs. The total loss of flux at the center of the 9.7  silicate absorption feature is thus only 20-50% and the average unobscured flux in the 9-11  minimum would be less than $0.4 \times \ensuremath{\rm {10^{-10}~W~cm^{-2}~\ensuremath{\rm {\mu m}}^{-1}~sr^{-1}}}$ or <15% of the peak flux in the 7.7  band. It is not surprising that the general ISM displays such a faint continuum component as a steep continuum is typical for sources with high UV energy density and a hard UV spectrum; moderate sources such as reflection nebula NGC 7023 display only a trace of continuum emission at wavelengths shorter than 20  (Moutou et al. 1998).

This analysis can be taken further by using a real extinction law and calculating the change of band profiles with increasing optical depth. The relation between UIB emitters and absorbing particles must then be defined. The high correlation between large dust grains and UIR band strength leads to the conclusion that these populations are well mixed: $\kappa_{\lambda} \propto \epsilon_{\lambda}$. In this case it is not possible to talk about the intensity of unobscured profile as internal extinction will always be present in any UIB-emitting region. The shape of the UIB profile can still be defined as the limiting values when $\tau \to 0$. With these assumptions it is possible to model changes in profile shapes by using the first form of Eq. (4) individually for each wavelength of the spectrum. We adopted  $\tau_{\rm Si}$ as the measure of extinction and calculated optical thickness for other wavelengths from the silicate extinction law in Draine & Li (2001). Finally, the shape of the unobscured spectrum was approximated with the fit to the average of observed spectra, corrected using Eq. (4) and $\tau({\rm Si}) = 1$.

	Figure 10: Absorptions effects in UIR band profiles. Profiles were calculated using the model described in Sect. 4.4 for (from top to bottom) $\tau(9.7~\ensuremath{\rm{\mu m}} ) = 0$, 1, 2, 5 and $\infty$. Each spectrum is normalized to 1.0 at the top of the 7.7  band.
Open with DEXTER

The resulting observable spectra for $\tau = 0$, 1, 2, 5 and $\infty$ are shown in Fig. 11. Each spectrum is normalised to unity at the peak of the 7.7  band. From the first form of Eq. (4) we see that when $\tau = \infty$ the observed intensity is simply $\epsilon_{\lambda} / \kappa_{\lambda}$. Model band ratios were calculated from the modeled profiles. Table 5 lists these band ratios for a range of values of  $\tau_{\rm Si}$. The first row shows the band ratios in the unobscured spectrum and the following rows the observable ratios for $\tau_{\rm Si} = 0.1$, 0.5, 1, 5 and $\infty$. It is clear that the interstellar extinction is a minor contributor to the observed band ratios and band shapes in the diffuse ISM. The shape of the minimum around 10  is also practically unaffected by extinction in this simple test calculation. The changes become apparent only when optical thickness at the center of the silicate feature becomes larger than unity. In such conditions the 8.6  band is strongly damped and the 9-11  minimum becomes deeper; the 11.3/7.7  band ratio is less affected. The 6.2/7.7  band ratio does not change with increasing extinction because the extinction curve is flat in this wavelength range.

5 Conclusions

We have proven that the UIB emission signature of the general ISM is constant in a sample of lines-of-sight covering the inner Milky Way. This independence is indeed what one expects to see if the UIBs in the diffuse component are mainly heated by single-photon events. The observed shape and calculated band ratios are typical for UIB sources with low particle density and a low UV flux. No interstellar continuum emission component is seen in the observed wavelength range. The UIB spectrum of other spiral galaxies differ only slightly from the Milky Way spectrum and the spectrum presented in Fig. 10 can be used as a template for the 6-12  emission of spirals. A weak emission bump around 7.1  , present in the total spectrum of spirals, seems to be lacking in the spectrum of the diffuse ISM. The significance of the observed variability of this feature among galactic objects and galaxies is still unknown.

The distribution of UIB emission in the Galactic ISM follows the general distribution of large dust grains (IRAS 100  emission) and molecular (CO) gas. The same tendency is seen in the high correlation between IRAS 100  and UIB emission at large (10$^\circ$) angular scales. Such a strong correlation links the history and energy budget of UIB carriers directly to the large grain population: the physical processes that are responsible for creating and heating the two particle populations must be closely related.

Finally, we have analyzed the effect of interstellar extinction on our observations and find that the silicate extinction feature centered at 9.7  only contributes weakly to lowering the continuum at 10  if silicates are well mixed with UIB carriers. The extinction effects on band ratios are also found to be negligible as long as the silicon absorption feature is not optically thick.

Acknowledgements

Contributing ISOPHOT Consortium institutes are DSRI, DIAS, RAL, AIP, MPIK, and MPIA. ISOPHOT and the Data Centre at MPIA, Heidelberg, are funded by the Deutsches Zentrum für Luft- und Raumfahrt and the Max-Planck-Gesellschaft.

The ISOPHOT data presented in this paper were reduced using PIA, which is a joint development by the ESA Astrophysics Division and the ISOPHOT Consortium with the collaboration of the Infrared Processing and Analysis Center (IPAC). Contributing ISOPHOT Consortium institutes are DIAS, RAL, AIP, MPIK, and MPIA.

The ISO Spectral Analysis Package (ISAP) is a joint development by the LWS and SWS Instrument Teams and Data Centers. Contributing institutes are CESR, IAS, IPAC, MPE, RAL and SRON.

This study was supported by the Academy of Finland Grants No. 173727 and 174854 and by the Finnish Graduate School for Astronomy and Space Physics.

References

 
• Aitken, D. K. 1981, in Infrared Astronomy, ed. C. G. Wynn-Williams, & D. P. Cruikshank (Dordrecht), Proc. IAU Symp., 96, 207 In the text  
• Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1985, ApJ, 290, L25 In the text NASA ADS  
• Boulanger, F., Baud, B., & van Albada, G.D. 1985, A&A, 144, L9 In the text NASA ADS  
• Boulanger, F., Reach, W. T., Abergel, A., et al. 1996, A&A, 315, L325 In the text NASA ADS  
• Boulanger, F., Boissel, P., Cesarsky, D., et al. 1998a, A&A, 339, 194 In the text NASA ADS  
• Boulanger, F., Abergel, A., Bernard, J. P., et al. 1998b, in Star Formation with ISO, ed. J. L. Yun, & R. Liseau (Astronomical Society of the Pacific), 15 In the text  
• Boulanger, F. 1999, in New Perspectives on the Interstellar Medium, ed. A. R. Taylor, T. L. Landecker, & G. Joncas (Astronomical Society of the Pacific), 173  
• Cesarsky, D., Lequeux, J., Abergel, A., et al. 1996a, A&A, 315, L305 In the text NASA ADS  
• Cesarsky, D., Lequeux, J., Abergel, A., et al. 1996b, A&A, 315, L309 In the text NASA ADS  
• Chan, K.-W., Roellig, T. L., Onaka, T., et al. 2001, ApJ, 546, 273 In the text NASA ADS  
• Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 In the text NASA ADS  
• Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 In the text NASA ADS  
• Draine, B. T., & Li, A. 2001, ApJ, 551, 807 In the text NASA ADS  
• Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 In the text NASA ADS  
• Dudley, W. W., & Williams, D. A. 1981, MNRAS, 196, 269 In the text NASA ADS  
• Gabriel, C., Acosta-Pulido, J., Heinrichsen, I., et al. 1997, in Astronomical Data Analysis Software and Systems (ADASS) VI, ed. G. Hunt, & H. E. Payne (San Francisco: ASP), ASP Conf. Ser., 125, 108  
• Giard, M., Pajot, F., Lamarre, J. M., et al. 1988, A&A, 201, L1 In the text NASA ADS  
• Giard, M., Pajot, F., Lamarre, J. M., et al. 1989, A&A, 215, 92 In the text NASA ADS  
• Gillett, F. C., Kleinmann, D. E., Wright, E. L., et al. 1973, ApJ, 198, L65 In the text NASA ADS  
• Gillett, F. C., Jones, T. W., Merrill, K. M., et al. 1975, A&A, 45, 77 In the text NASA ADS  
• Glass, I. S., Moorwood, A. F. M., & Eichendorf, W. 1982, A&A, 107, 276 In the text NASA ADS  
• Greenberg, J. M. 1968, in Stars and Stellar Systems, vol. VII, ed. B. M. Middlehurst, & L. H. Aller (University of Chicago Press), 221 In the text  
• Helou, G., Lu, Nanyao Y., Werner, M. W., et al. 2000, ApJ, 532, L21 In the text NASA ADS  
• Holmlid, L. 2000, A&A, 358, 276 In the text NASA ADS  
• van der Hucht, K. A., Morris, P. W., Williams, P. M., et al. 1996, A&A, 315, 193 In the text  
• Imanishi, M., & Ueno, S. 2000, ApJ, 535, 626 In the text NASA ADS  
• Knacke, R. F., & Gaustad, J. E. 1969, ApJ, 155, 189 In the text  
• Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 In the text NASA ADS  
• Laureijs, R. J., Klaas, U., Richards, P. J., et al. 2000, The ISO Handbook, vol. V: PHT - The Imaging Photo-Polarimeter, In the text isowww.estec.esa.nl/manuals/HANDBOOK/V/pht_hb/  
• Léger, A., & Puget, J. L. 1984, A&A, 137, L5 In the text NASA ADS  
• Lemke, D., Klaas, U., Abolins, J., et al. 1996, A&A, 315, L64 In the text NASA ADS  
• Lemke, D., Mattila, K., Lehtinen, K., et al. 1998, A&A, 331, 742 In the text NASA ADS  
• Li, A., & Draine, B. T. 2001, ApJ, 554, 778 In the text NASA ADS  
• Lutz, D., Feuchtgruber, H., Genzel, R., et al. 1996, A&A, 315, L269 In the text NASA ADS  
• Lutz, D., Genzel, R., Kunze, D., et al. 1999, Ap&SS, 266, 85 In the text NASA ADS  
• Mathis, J. S. 1998, ApJ, 497, 824 In the text NASA ADS  
• Mattila, K., Lehtinen, K., & Lemke, D. 1999, A&A, 342, 643 In the text NASA ADS  
• Mattila, K., Lemke, D., Haikala, L. K., et al. 1996, A&A, 315, L353 In the text NASA ADS  
• Moutou, C., Sellgren, K., Verstreate, L., et al. 1998, in Star Formation with the Infrared Space Observatory, ed. J. Yun, & R. Liseau, ASP Conf. Ser., 132, 47 In the text NASA ADS  
• Nakagawa, T., Yui, Y. Y., Doi, Y., et al. 1998, ApJS, 115, 259 In the text NASA ADS  
• Onaka, T., Yamamura, I., Tanabé, T., et al. 1996, PASJ, 48, L59 In the text NASA ADS  
• Onaka, T. 2000, Adv. Space Res., 25, 2167 In the text NASA ADS  
• Papoular, R., Conard, J., Giuliano, M., et al. 1989, A&A, 217, 204 In the text NASA ADS  
• Peeters, E., Hony, S., van Kerckhoven, C., et al. 2002, A&A, 390, 1089 In the text NASA ADS  
• Puget, J. L., Léger, A., & Boulanger, F. 1985, A&A, 142, L19 In the text NASA ADS  
• Rieke, G. H., & Lebowsky, M. J. 1985, ApJ, 288, 618 In the text NASA ADS  
• Ristorcelli, I., Giard, M., Mény, C., et al. 1994, A&A, 286, L23 In the text NASA ADS  
• Sakata, A., Wada, S., Tanabé, T., et al. 1984, ApJ, 287, L51 In the text NASA ADS  
• Schutte, W. A., van der Hucht, K. A., & Whittet, D. C. B., et al. 1998, A&A, 337, 261 In the text NASA ADS  
• Sodroski, T. J., Odegard, N., Arendt, R. G., et al. 1997, ApJ, 480, 173 In the text NASA ADS  
• Tanaka, M., Matsumota, T., Murakami, H., et al. 1996, PASJ, 48, L53 In the text NASA ADS  
• Uchida, K. I., Sellgren, K., Werner, M. W., et al. 2000, ApJ, 530, 817 In the text NASA ADS