A&A 405, 455-471 (2003)
DOI: 10.1051/0004-6361:20030470
J. Falcón-Barroso1 - M. Balcells2 - R. F. Peletier1,3 - A. Vazdekis2
1 - School of Physics & Astronomy, University of Nottingham,
Nottingham NG7 2RD, UK
2 -
Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
3 -
CRAL, Observatoire de Lyon, 69561 St-Genis Laval cedex, France
Received 15 November 2002 / Accepted 18 March 2003
Abstract
We present minor axis kinematic profiles for a well-studied sample of
19 early- to intermediate-type disk galaxies. We introduce, for the first time,
the use of single-burst stellar population (SSP) models to obtain stellar velocities,
velocity dispersions and higher order Gauss-Hermite moments (h3, h4) from
galaxy spectra in the near-infrared Ca II triplet region. SSP models,
which employs the synthetic spectra of Vazdekis et al. (2003), provide a means to address
the template-mismatch problem, and are shown to provide as good or better fits
as traditional stellar templates. We anticipate the technique to be of
particular use for high-redshift galaxy kinematics. We give the measurement of
a recently defined CaT* index (Cenarro et al. 2001a), and describe the global
properties of the bulge kinematics as derived from the kinematic profiles. We
detect small-amplitude minor-axis rotation, generally due to inner isophotal
twists as a result of slightly triaxial bulges or misaligned inner disks; such
inner features do not show peculiar colors or distinct CaT* index values.
Velocity dispersion profiles, which extend well into the disk region, show a
wide range of slopes. Flattened bulges tend to have shallower velocity
dispersion profiles. The inferred similarity of bulge and disk radial
velocity dispersions supports the interpretation of these bulges as thickened
disks.
Key words: galaxies: bulges - galaxies: kinematics and dynamics - galaxies: structure - methods: data analysis
The measurement of kinematics in galaxies has been one of the major achievements in astrophysics in the second half of the last century. Our knowledge in this field has evolved from crude kinematic determinations from photographic plates (Burbidge & Burbidge 1968), to high-resolution, detailed measurements of the line-of-sight velocity distributions (hereafter LOSVDs; i.e. Bender et al. 1994; Fisher 1997; Vega Beltrán et al. 2001).
In the seventies, methods were devised to measure velocity dispersions in addition to radial velocities, i.e. cross-correlation (Tonry & Davis 1979), Fourier Quotient (Sargent et al. 1977). In the past decade, with the improved quality of the data, a new set of algorithms were developed allowing us to measure LOSVDs (Fourier Correlation Quotient, Bender 1990), and quantify deviations from pure single Gaussian (van der Marel & Franx 1993) and multiple Gaussian LOSVD with UGD (Kuijken & Merrifield 1993; Prada et al. 1996). Galactic kinematics, however, suffers from an important technical constraint: template mismatching. Stars are observed together with the object which kinematics we are interested in, to be used as spectral templates. However, it is difficult to choose the right star, since galaxy light comes from a wide range of stellar types. Although, for ellipticals in the V-band, it has been found that half of the light comes from G and K giants (Pickles 1985) and, therefore, those stellar types are good templates, this situation may change dramatically from galaxy to galaxy or even within a galaxy. Therefore kinematic parameters will be sensitive to the stellar template used. Much work has been devoted to address the template mismatch problem (González 1993; Statler et al. 1996; Statler & Smecker-Hane 1999; Rix & White 1992).
In the last decade, new evolutionary stellar population synthesis models (Vazdekis et al. 1996; Bruzual A. & Charlot 1993; Buzzoni 1995; Worthey et al. 1994; Tantalo et al. 1996) have helped us to significantly increase our galaxy stellar populations knowledge. These models predict line strengths of a limited number of spectral features, such as those of the Lick/IDS system (i.e. Vazdekis et al. 1996; Worthey et al. 1994). However since these models were unable to predict full SEDs (Spectral Energy Distributions) at high enough resolution, they could not be used as templates for galaxy stellar kinematics. This situation has recently changed with the development of new SSP model SEDs in the blue and visual at resolution 1.8 Å (FWHM) by Vazdekis (1999) and in the near-IR Ca II triplet region at 1.5 Å (Vazdekis et al. 2003). In fact, Vazdekis (1999) and Vazdekis & Arimoto (1999) have shown the potential use of the SSP models as templates for determining the main kinematic parameters in the optical spectral range. In this paper we are for the first time in position to determine galaxy kinematics using SSP templates in the near-IR Ca II spectral range. It is generally assumed, that kinematic stellar templates are required to be obtained with the same instrumental setting as the one used for the galaxy spectra (Sargent et al. 1977; Tonry & Davis 1979). In this paper we show that this is no longer a requirement, at least at the resolutions of the spectra considered here.
This paper intends to be a first step in the exploration of SSP models as templates by comparing velocity profiles, for a sample of 19 galaxies, with those obtained with our best stellar or mixture of stellar templates. We show that in all cases SSP models produce kinematics of at least at the same level of quality, and are quite often better than the best stellar templates. In order to trace correlations between kinematic and population features along the galaxy minor axes, we measure the CaT* index (Cenarro et al. 2001a).
Section 2 summarizes the observations and data reduction. In Sect. 3 we describe the different types of template samples and the way the kinematical profiles have been determined, including a detailed comparison between stellar templates and SSP models. The obtained kinematics is discussed in Sect. 4. Kinematical profiles are graphically presented in Appendix A. Tables containing the numerical values presented in Appendix A will be available in electronic form.
The sample comprises 20 galaxies of types S0-Sbc selected out of the Balcells & Peletier (1994) sample of bulges. The latter is a diameter-limited sample of galaxies with inclinations above 50 degree from the UGC catalog (Nilson 1995); it is has been the subject of several studies on bulges (see Falcón-Barroso et al. 2002 and references therein). The 20 objects were those we had observed with HST/WFPC2 and NICMOS, hence high-spatial resolution images are available for them at B,I,H bands (Peletier et al. 1999). The main properties of the sample are presented in Table 1.
We obtained long-slit spectra for our sample of galaxies at the 4.2-m William
Herschel Telescope of the Observatorio del Roque de los Muchachos at La Palma
between 11 and 13 July 1997. Twenty galaxies were observed between 8360-9170 Å using the ISIS double spectrograph. We discarded NGC 5577 as the
spectra did not have sufficient signal-to-noise. We are thus left with 19 objects (see Table 1). The red arm was equipped with the
Tektronix (1024![]() 1024) TEK2 CCD (0.36
1024) TEK2 CCD (0.36
![]() per 24
per 24 ![]() m pixel) and the
R600R grating, providing a spectral resolution (FWHM of arc lines) of
1.74 Å (59.6 km s-1) with a spectral dispersion of 0.8 Å/pix. We used the
6100 Å dichroic for simultaneous red and blue arm exposures. In this paper
we discuss the red arm spectra only. Typical exposure times per galaxy were
1500 s. The length of the slit was 3.6
m pixel) and the
R600R grating, providing a spectral resolution (FWHM of arc lines) of
1.74 Å (59.6 km s-1) with a spectral dispersion of 0.8 Å/pix. We used the
6100 Å dichroic for simultaneous red and blue arm exposures. In this paper
we discuss the red arm spectra only. Typical exposure times per galaxy were
1500 s. The length of the slit was 3.6![]() .
The slit width was 1.2
.
The slit width was 1.2
![]() ,
matching the seeing at the time of the observations. Arc line exposures
were taken before and after each target exposure. Tungsten continuum lamp
exposures were taken with the red arm after each target exposure, for fringe
calibration. Twilight sky exposures were taken every night for flat fielding.
We also obtained spectra for 11 stellar templates of types A2 to M4, from the Lick list of stars (Worthey et al. 1994), listed in Table 2.
,
matching the seeing at the time of the observations. Arc line exposures
were taken before and after each target exposure. Tungsten continuum lamp
exposures were taken with the red arm after each target exposure, for fringe
calibration. Twilight sky exposures were taken every night for flat fielding.
We also obtained spectra for 11 stellar templates of types A2 to M4, from the Lick list of stars (Worthey et al. 1994), listed in Table 2.
| NGC |
|
Scale | Type |
|
|
B/D | PA | Exp. time | r
|
Best templ. | S/N | ||
| km s-1 | kpc/
|
mag | mag | deg | s |
|
pix-1 | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) |
| 5326 | 2576 | 0.25 | 1 | -22.16 | -21.22 | 0.73 | -138 | 1500 | 0.50 | 0.43 | 5.97 | +0.2, 3.16 | 83 |
| 5389 | 1990 | 0.19 | 0 | -21.32 | -20.70 | 1.30 | 93 | 1500 | 0.80 | 0.46 | 2.85 | M1 III / +0.2, 4.47 | 61 |
| 5422 | 1929 | 0.19 | -2 | -21.96 | -21.33 | 1.28 | 64 | 1500 | 0.80 | 0.35 | 3.33 | +0.2, 7.08 | 68 |
| 5443 | 2060 | 0.20 | 3 | -21.53 | -19.09 | 0.12 | -52 | 1400 | 0.68 | 0.54 | 1.98 | +0.2, 3.16 | 37 |
| 5475 | 1861 | 0.18 | 0 | -20.98 | -18.72 | 0.14 | -101 | 1500 | 0.68 | 0.24 | 2.45 | +0.2, 1.41 | 57 |
| 5587 | 2291 | 0.22 | 0 | -21.07 | -19.43 | 0.29 | 73 | 1500 | 0.70 | 0.47 | 1.51 | -0.4, 14.12 | 36 |
| 5689 | 2290 | 0.22 | 0 | -22.29 | -21.47 | 0.89 | -5 | 1500 | 0.75 | 0.48 | 2.04 | 0.0, 4.47 | 58 |
| 5707 | 2354 | 0.23 | 2 | -21.43 | -20.11 | 0.42 | -59 | 1500 | 0.75 | 0.20 | 3.79 | 0.0, 2.51 | 51 |
| 5719 | 1684 | 0.16 | 2 | -21.60 | -20.00 | 0.30 | 5 | 1500 | 0.64 | 0.61 | 7.71 | K3 Ib / -0.4, 3.55 | 51 |
| 5746 | 1677 | 0.16 | 3 | -22.68 | -21.70 | 0.68 | -99 | 1200 | 0.84 | 0.52 | 2.37 | M1 III / +0.2, 3.16 | 44 |
| 5838 | 1337 | 0.13 | -3 | -21.89 | -20.93 | 0.71 | 134 | 1500 | 0.65 | 0.22 | 8.39 | 0.0, 12.59 | 86 |
| 5854 | 1708 | 0.17 | -1 | -21.43 | -20.18 | 0.46 | -33 | 1500 | 0.70 | 0.32 | 4.85 | -0.7, 6.31 | 64 |
| 5879 | 1065 | 0.10 | 4 | -20.30 | -19.08 | 0.48 | 89 | 1500 | 0.62 | 0.32 | 0.85 | -0.4, 3.16 | 41 |
| 5965 | 3603 | 0.35 | 3 | -22.92 | -21.76 | 0.53 | -38 | 1500 | 0.84 | 0.50 | 2.32 | -0.4, 5.01 | 46 |
| 6010 | 1923 | 0.19 | 0 | -21.57 | -19.88 | 0.27 | 12 | 1500 | 0.75 | 0.28 | 2.70 | 0.0, 14.12 | 67 |
| 6504 | 4680 | 0.46 | 2 | -24.57 | -23.30 | 0.45 | 135 | 1500 | 0.83 | 0.44 | 4.05 | -0.4, 3.16 | 52 |
| 7331 | 1138 | 0.11 | 3 | -- | -- | 0.0011 | 80 | 1500 | 0.631 | 0.62 | 4.57 | -0.4, 15.85 | 117 |
| 7332 | 1550 | 0.15 | -2 | -21.86 | -20.52 | 0.41 | -114 | 1500 | 0.74 | 0.29 | 2.99 | -0.4, 11.22 | 101 |
| 7457 | 1114 | 0.11 | -3 | -20.91 | -20.91 | 10.00 | 35 | 1500 | 0.48 | 0.34 | 3.29 | +0.2, 2.51 | 51 |
|
Notes: Description of the columns: (1): The NGC numbers of the galaxies. (2): Recession velocity of each galaxy in km s-1, corrected to the Local Group (Karachentsev & Makarov 1996), from optical heliocentric velocities given in the Third Reference Catalogue of Bright Galaxies (1991) (hereafter RC3). (3): Scale in kpc/arcsec from Falcón-Barroso et al. (2002). (4): Type index T from the RC3. (5) and (6): Absolute magnitudes, in R-band, from Peletier & Balcells (1997) (H0=50 km s-1 Mpc-1). (7): Bulge-to-disk ratio from an R-band bulge-disk decomposition following Kent's (1984) method (Peletier & Balcells 1997). (8): The position angle, in degrees, (N - E) of the dust-free minor axis (Peletier & Balcells 1997). (9): Integration time, in sec, for each galaxy during the observations. (10): Disk ellipticity from Peletier & Balcells (1997). (11): Effective bulge ellipticity, from HST H-band ellipticity profiles, measured at the geometric effective radius (Balcells et al. 2003). (12): Minor axis bulge radius, derived from Balcells et al. (2003) HST H-band profiles, as the radius at which the contribution from the disk and bulge light are equal, except for NGC 7332 for which a ground-based image was used instead (Peletier & Balcells 1997) (Alister W. Graham, private communication). (13): Best template fit for each galaxy. The metallicity ([m/H]) and age (Gyr) of the best fit SSP models is shown. In those cases where the stellar template performed better, the adopted SSP best template is also given. (14): Signal-to-noise ratio per pixel in the central aperture ( 1 From Prada et al. (1996). |
In Table 2 we list the observed stellar templates. A representative set of spectra is shown in Fig. 1. The wide range of spectral types covered allows us for an exploration of the best templates for matching galaxy spectra. The most apparent variation from top to bottom in Fig. 1 is the decrease of the Paschen lines toward later types. P14, in a region devoid of other features, is a strong discriminant of the presence of stars earlier than G. P13 and P15, when present, give characteristic asymmetric profiles to the second and third lines of the Ca II (Cenarro et al. 2001b). Following previous works in the literature (Hau et al. 1999; Rix & White 1992) we have included in our analysis a mix-template from a linear combination of stars in our sample. However we have used a different approach to derive our optimal mix-template. Given the importance of the continuum shape in this wavelength region (Vazdekis et al. 2003; Cenarro et al. 2001a), we have created an optimal template that provides the best fit to the overall continuum shape of each galaxy (i.e. fitting the regions outside the main Ca II features, but including the TiO bands), before broadening with the appropriate kinematics. It is important to perform this fit using a combination of unconvolved stellar spectra, since any input kinematics comes from a particular template and could bias our result. In most cases the optimal mix-template is formed by G8III, K3Ib and M4V stars. The importance of the M4V star in the final template is justified by its ability to match the TiO molecular bands. As we will show in Sect. 3.4, this mixture of stellar templates helps to alleviate the template mismatch problem and it is an ideal benchmark to test our SSP models.
| Name | Spectral type | MV | ||
| (1) | (2) | (3) | (4) | (5) |
| BARNARD1 | 17 57 48.50 | +04 41 36.2 | M4 Ve | 9.54 |
| GL8182 | 21 05 19.75 | +07 04 09.5 | K6 V | 8.33 |
| HR0072 | 00 18 41.87 | -08 03 10.8 | G0 V | 6.46 |
| HR4521 | 11 46 55.62 | +55 37 41.5 | K3 III | 5.26 |
| HR5340 | 14 15 39.67 | +19 10 56.7 | K3 Ib | 1.23 |
| HR5681 | 15 15 30.16 | +33 18 53.4 | G8 III | 3.47 |
| HR5826 | 15 31 24.93 | +77 20 57.7 | K5 III | 5.00 |
| HR5854 | 15 44 16.07 | +06 25 32.3 | K2 III | 2.64 |
| HR6685 | 17 55 25.19 | +26 03 00.0 | F2 Ibe | 5.47 |
| HR8334 | 21 45 26.93 | +61 07 14.9 | A2 Iab | 4.31 |
| HR8795 | 23 07 00.26 | +09 24 34.2 | M1 III | 4.55 |
|
Notes: (1) HR names from the Bright Star Catalogue (Hoffleit & Warren 1995). (2),(3) J2000 coordinates from SIMBAD. (4) spectral type from Worthey et al. (1994). (5) from SIMBAD (http://simbad.u-strasbg.fr/Simbad). 1 NSV 9910 from the New catalogue of suspected variable stars (Kukarkin & Kholopov 1982). 2 HD 200779 from the Henry Draper Catalogue and Extension (Cannon & Pickering 1993). |
We have used 78 SSP synthetic models at
![]() Å (0.85 Å/pix) in the
Ca II triplet region, corresponding to a single-age, single-metallicity
stellar populations of
Å (0.85 Å/pix) in the
Ca II triplet region, corresponding to a single-age, single-metallicity
stellar populations of
![]() ,
-0.4, 0.0, and +0.2. For each
metallicity, the age varies from 1 to 17 Gyr, except for
,
-0.4, 0.0, and +0.2. For each
metallicity, the age varies from 1 to 17 Gyr, except for
![]() starting
from 6 Gyr and for
starting
from 6 Gyr and for
![]() starting 3 Gyr. These limitations arise from the
limited coverage of atmospheric parameters of the stellar sample used by the
models. More details can be found in Vazdekis et al. (2003). In order to adapt these models
to the instrumental resolution of our data, we have convolved them with a
Gaussian of
starting 3 Gyr. These limitations arise from the
limited coverage of atmospheric parameters of the stellar sample used by the
models. More details can be found in Vazdekis et al. (2003). In order to adapt these models
to the instrumental resolution of our data, we have convolved them with a
Gaussian of
![]() Å. This procedure relies on the assumption that a
Gaussian represents a good match to the instrumental PSF (Point Spread Function)
of the observations. We have tested whether the arclines followed a Gaussian
shape, finding that indeed they do, with only small deviations (below 0.01) in
the h3 and h4 parameters, as described by van der Marel & Franx (1993). If h3 and h4 had been found to be significantly different from 0, we would have had
to convolve the models with the line profile of the arc-lines.
Å. This procedure relies on the assumption that a
Gaussian represents a good match to the instrumental PSF (Point Spread Function)
of the observations. We have tested whether the arclines followed a Gaussian
shape, finding that indeed they do, with only small deviations (below 0.01) in
the h3 and h4 parameters, as described by van der Marel & Franx (1993). If h3 and h4 had been found to be significantly different from 0, we would have had
to convolve the models with the line profile of the arc-lines.
Kinematic profiles were derived from the data in the region of the near-IR Ca II triplet (8498 Å, 8542 Å, 8662 Å). For each galaxy, we generated two sets of coadded galaxy spectra, with minimum signal-to-noise ratios (S/N) of 33 and 20 per pixel, respectively. We made use of the program FOURFIT developed by van der Marel & Franx (1993), available from the first author's website. A Gauss-Hermite fit to the LOSVD was performed to obtain mean radial velocities, velocity dispersions, h3 and h4 moments for the data with signal-to-noise ratio above 33 per pixel. For data with signal-to-noise ratio between 33 and 20 per pixel a pure Gaussian fit was used. The choice of S/N is explained in Sect. 3.5.
We have determined the kinematic profiles for our sample using each of the 90 templates we had available (78 SSP models, 11 stellar templates and the best
mix-template for each galaxy). We have considered as our best fit template the
one that minimized the ![]() ,
as defined in van der Marel & Franx (1993), for the central
position of the galaxy profile, which has a S/N well above 33.
One of the features
of this code is the possibility of filtering the input spectra in Fourier space
so that any remaining low-order component not removed by the continuum subtraction
or high-frequency noise can be filtered out. The resulting
,
as defined in van der Marel & Franx (1993), for the central
position of the galaxy profile, which has a S/N well above 33.
One of the features
of this code is the possibility of filtering the input spectra in Fourier space
so that any remaining low-order component not removed by the continuum subtraction
or high-frequency noise can be filtered out. The resulting ![]() is then
evaluated over a finite range of wavenumbers determined by the filtering parameters.
For our dataset the results from FOURFIT were weakly dependent on the lower cutoff
and insensitive to the choice of the upper cutoff (given that we chose the same upper
cutoff for all the galaxies and that this cut was well above the sigma of the galaxy).
We also reduce the uncertainties in the derived kinematics by flux-calibrating the
data and the template stars before applying the continuum subtraction because the
normalizing polynomia for the data should be very similar to the ones used for the
templates. otherwise, the normalization procedure might introduce non-negligible
variations in the spectra, including in the equivalent widths of the lines.
is then
evaluated over a finite range of wavenumbers determined by the filtering parameters.
For our dataset the results from FOURFIT were weakly dependent on the lower cutoff
and insensitive to the choice of the upper cutoff (given that we chose the same upper
cutoff for all the galaxies and that this cut was well above the sigma of the galaxy).
We also reduce the uncertainties in the derived kinematics by flux-calibrating the
data and the template stars before applying the continuum subtraction because the
normalizing polynomia for the data should be very similar to the ones used for the
templates. otherwise, the normalization procedure might introduce non-negligible
variations in the spectra, including in the equivalent widths of the lines.
We establish whether SSP, stellar templates or mix-template provide better
fits to the galaxy spectra by comparing the global reduced ![]() of the
fits. A typical distribution of
of the
fits. A typical distribution of ![]() values is shown in
Fig. 2. The lines trace reduced
values is shown in
Fig. 2. The lines trace reduced ![]() for the SSP models,
labeled by age and metallicity, while the crosses are the reduced
for the SSP models,
labeled by age and metallicity, while the crosses are the reduced ![]() of
the stellar templates labeled by their spectral types and combined stellar
template. The patterns in this figure are representative of those found for
all the galaxies in the sample. There is a group of stellar templates that do
significantly better than the others; in particular, the A2, F2 and M4
templates consistently yield poor fits in all the galaxies. For the SSP models, the
of
the stellar templates labeled by their spectral types and combined stellar
template. The patterns in this figure are representative of those found for
all the galaxies in the sample. There is a group of stellar templates that do
significantly better than the others; in particular, the A2, F2 and M4
templates consistently yield poor fits in all the galaxies. For the SSP models, the ![]() distributions are fairly flat as a function of age for a
given metallicity, except for ages below
distributions are fairly flat as a function of age for a
given metallicity, except for ages below ![]() 2 Gyr, where the quality of the
fits quickly degrades. This behavior is expected since, at younger ages,
the Ca II equivalent widths significantly decrease and the Paschen series
become noticeable (see Vazdekis et al. 2003). At each age, the fits are sensitive to
metallicity.
2 Gyr, where the quality of the
fits quickly degrades. This behavior is expected since, at younger ages,
the Ca II equivalent widths significantly decrease and the Paschen series
become noticeable (see Vazdekis et al. 2003). At each age, the fits are sensitive to
metallicity.
For the spectrum used in Fig. 2, the best fit is obtained with a
SSP model corresponding to
![]() and 3.16 Gyr. It is worth noting that
this SSP model should not necessarily be considered as the best fit to the
stellar populations of this galaxy (see below). For the entire sample, the
and 3.16 Gyr. It is worth noting that
this SSP model should not necessarily be considered as the best fit to the
stellar populations of this galaxy (see below). For the entire sample, the
![]() for the best SSP model, best stellar template and mix-template are
quite similar, and for 16 of the 19 objects the SSP templates provide marginally
better fits. This result demonstrates that synthetic SSP spectra, convolved to
the resolution of the data, can provide accurate templates for kinematic analysis
of galaxy spectra. The high quality of the SSP fits is most-likely due to their
ability to minimize the template mismatch problem. While the stellar populations
of bulges are likely to contain a mixture of ages and a range of metallicities, the
SSP models provide a better approximation to galaxy spectra than a single stellar
spectrum. Our results indicate that late KIII stars and early M stars provide
a better approximation to the integrated light of bulges than A, F, and G stars
in agreement with Vazdekis et al. (2003). Table 1, Col. 13, lists the
overall best template for each galaxy. Note that, for three galaxies (NGC 5389,
NGC 5719, NGC 5746), the M1III and K3I stellar templates provide the overall
best fit to the galaxy spectra.
for the best SSP model, best stellar template and mix-template are
quite similar, and for 16 of the 19 objects the SSP templates provide marginally
better fits. This result demonstrates that synthetic SSP spectra, convolved to
the resolution of the data, can provide accurate templates for kinematic analysis
of galaxy spectra. The high quality of the SSP fits is most-likely due to their
ability to minimize the template mismatch problem. While the stellar populations
of bulges are likely to contain a mixture of ages and a range of metallicities, the
SSP models provide a better approximation to galaxy spectra than a single stellar
spectrum. Our results indicate that late KIII stars and early M stars provide
a better approximation to the integrated light of bulges than A, F, and G stars
in agreement with Vazdekis et al. (2003). Table 1, Col. 13, lists the
overall best template for each galaxy. Note that, for three galaxies (NGC 5389,
NGC 5719, NGC 5746), the M1III and K3I stellar templates provide the overall
best fit to the galaxy spectra.
In Fig. 3 we plot the central spectrum of NGC 5326 and the best-fitting stellar (M1 III), mix and SSP templates, convolved with their respective kinematic solutions. The SSP model represents a very good fit for the whole sample of galaxies spectrum. Fitted output parameters for the best template stars (G8III, K2III, K3I, K3III, K5III, K6V, M1III), mix-template and best SSP model are shown in Fig. 4 for the entire profile of NGC 5326. The results show an excellent agreement. Therefore we adopt the solution from our best SSP template for each galaxy to obtain kinematic profiles.
A point to remark is that no inferences on the stellar population age and metallicity of the galaxies are presented here from the best-fitting SSP models. The reason is that an important relation has been shown to exist between the continuum shape and the stellar populations in this spectral region (Vazdekis et al. 2003; Cenarro et al. 2003). Since we remove this continuum, as required by FOURFIT, we neglect its valuable information for constraining galaxy stellar populations. Therefore the most useful information left in our spectra is the equivalent width of the Ca II feature, which does not vary much for SSPs of the age and metallicity regimes considered here. The wavelength region that we have used to derive the kinematics excludes the strong TiO molecular bands seen in this spectral range. Therefore we are left with an almost featureless continuum shape which is straightforward to subtract. A different methodology is required to be able to analyze their stellar populations on the basis of the SSP models. Methods for extracting useful information from the full SSP spectra are discussed in Vazdekis (1999) and Vazdekis & Arimoto (1999). The stellar population analysis of this galaxy sample will be presented in a forthcoming paper (Falcón-Barroso et al. 2003).
The use of SSP models has a potential to minimize the template mismatch problems that have traditionally affected galaxy kinematic measurements. Whereas the KIII stellar templates have been shown to provide reasonably good fits to elliptical galaxy spectra in the optical region, one expects that the SSP models should significantly improve the kinematical fits. The blue and visible have been proven to have large sensitivities to the age, metallicity and abundance ratios (Rose et al. 1994; Vazdekis et al. 1996; Vazdekis 1999; Worthey et al. 1994). Our results suggest that the requirement of observing template stars with the same instrumental setting as the galaxies is not compelling. The use of SSP models as templates allows us to use all of the available observing time for the targets, without the need to take spectra of template stars. An important application of SSP models should be in the field of high-redshift galaxy kinematics, where the measurement of the same spectral range in stars and target galaxies would require changing the instrumental setup, and where the redshift of the target objects is not generally known a priori.
The main limitation of the use of SSP models is that it relies on a well designed stellar library to produce the full stellar population synthesis. However, the method is expandable to include combinations of SSP models to account for composite populations. Potential applications are the study of age differences between bulge and disk, or population signatures of kinematically-decoupled cores.
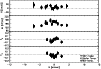 |
Figure 4: Comparison of the profiles obtained with our best stellar templates (G8III, K2III, K3I, K3III, K5III, K6V, M1III), mix-template and best SSP model fit of NGC 5326. |
Although FOURFIT gives the formal errors of the fit, we have performed
simulations to establish the level of confidence the code can produce on
(V, ![]() ,
h3 and h4) at S/N=33 pix-1, and (V,
,
h3 and h4) at S/N=33 pix-1, and (V, ![]() )
at
S/N=20 pix-1.
)
at
S/N=20 pix-1.
For the simulations two different tests have been performed. In the first one we
convolved an SSP model (
![]() ,
t= 5.01 Gyr) with a wide range of LOSVDs to
generate model galaxy spectra. The LOSVDs included several velocities, velocity
dispersions, h3 and h4 mapping a representative parameter space covered by
our sample of galaxies (
,
t= 5.01 Gyr) with a wide range of LOSVDs to
generate model galaxy spectra. The LOSVDs included several velocities, velocity
dispersions, h3 and h4 mapping a representative parameter space covered by
our sample of galaxies (
![]() ,
,
![]() ,300], h3 and
,300], h3 and
![]() ,0.1]). The inclusion of higher velocities (up to 4000 km s-1, to match our
furthest galaxy) doesn't affect our results. Eight different samples of white noise
were added to our model galaxy spectra to yield S/N ratios of 20 and 33 pix-1. For
each one of the noise sample at the two S/N levels the full battery of LOSVDs was
recovered. Given the fact that all SSP models give very similar
,0.1]). The inclusion of higher velocities (up to 4000 km s-1, to match our
furthest galaxy) doesn't affect our results. Eight different samples of white noise
were added to our model galaxy spectra to yield S/N ratios of 20 and 33 pix-1. For
each one of the noise sample at the two S/N levels the full battery of LOSVDs was
recovered. Given the fact that all SSP models give very similar ![]() values, only
a representative subsample of 3 SSP models covering the models parameter space
(
values, only
a representative subsample of 3 SSP models covering the models parameter space
(
![]() ,
,
![]() Gyr;
Gyr;
![]() ,
,
![]() Gyr;
Gyr;
![]() ,
,
![]() Gyr)
was used to perform these simulations. We have simulated both Gaussian and non-Gaussian
LOSVDs, however we only fitted pure Gaussians to the spectra of S/N=20 pix-1, for
which we only modeled the V and
Gyr)
was used to perform these simulations. We have simulated both Gaussian and non-Gaussian
LOSVDs, however we only fitted pure Gaussians to the spectra of S/N=20 pix-1, for
which we only modeled the V and ![]() errors due to LOSVD mismatching in the S/N=20
spectra. In the second test we created the galaxy spectra from a stellar template (K3I).
Spectra from the K3I, K5III and M1III stars were used as kinematic templates. The choice
of these templates is due to their ability to produce, overall, the lowest values of
errors due to LOSVD mismatching in the S/N=20
spectra. In the second test we created the galaxy spectra from a stellar template (K3I).
Spectra from the K3I, K5III and M1III stars were used as kinematic templates. The choice
of these templates is due to their ability to produce, overall, the lowest values of ![]() when fitted to the sample of galaxies. We have convolved the model galaxy
spectra with the same LOSVDs and added the same white noise samples as in the first test.
when fitted to the sample of galaxies. We have convolved the model galaxy
spectra with the same LOSVDs and added the same white noise samples as in the first test.

ratios measured from the simulations (see Sect. 3.5). |
The main results of the simulations are summarised in Table 3. The
table gives the standard deviations of the distributions (parameter
![]() - parameter
- parameter![]() ),
obtained from the simulations in each test, for the full set of parameters and white
noise samples. This is a measurement of the uncertainty when working at the mentioned
S/N ratios. We use the uncertainties obtained from the simulations with the SSP models
and display them as error bars on the right-hand side of each kinematic profile, see
Appendix A. In Fig. 5, the left panels show the distribution of the
recovered LOSVDs compared to the input ones at each sampled value of
),
obtained from the simulations in each test, for the full set of parameters and white
noise samples. This is a measurement of the uncertainty when working at the mentioned
S/N ratios. We use the uncertainties obtained from the simulations with the SSP models
and display them as error bars on the right-hand side of each kinematic profile, see
Appendix A. In Fig. 5, the left panels show the distribution of the
recovered LOSVDs compared to the input ones at each sampled value of ![]() and h4
for each test for
and h4
for each test for
![]() .
The values shown below each histogram represent the median
(within square brackets) and standard deviation of the distribution, found at those values
of
.
The values shown below each histogram represent the median
(within square brackets) and standard deviation of the distribution, found at those values
of ![]() and h4. The right panels, on the other hand, show the total distribution
and standard deviation (i.e. the sum of the individual ones) from which we have obtain
the values shown in Table 3. No significant differences are found
between the distributions obtained from the SSP models and stellar templates. This
result strengthens our approach of using SSP models as kinematic templates.
and h4. The right panels, on the other hand, show the total distribution
and standard deviation (i.e. the sum of the individual ones) from which we have obtain
the values shown in Table 3. No significant differences are found
between the distributions obtained from the SSP models and stellar templates. This
result strengthens our approach of using SSP models as kinematic templates.
The simulations show two effects worth mentioning. First, there is no systematic
underestimate of the velocity dispersion for low input velocity dispersions
(see Fig. 5). This effect, if present, might bias our velocity
dispersion results for our two smallest bulges, see Fig. 8. Such an
effect has been previously reported by Joseph et al. (2001) using a different code (i.e. FCQ),
finding an overestimation of ![]() 10 km s-1 at
10 km s-1 at ![]() km s-1. Second, as we move
towards larger velocity dispersions, the uncertainty in
km s-1. Second, as we move
towards larger velocity dispersions, the uncertainty in ![]() also increases (from 6 km s-1 at
also increases (from 6 km s-1 at ![]() km s-1, to 15 km s-1 between
km s-1, to 15 km s-1 between
![]() km s-1 and 32 km s-1 between
km s-1 and 32 km s-1 between
![]() km s-1). Hence, although the Gauss-Hermite expansion conforms a description of the LOSVD with a set of orthogonal functions and therefore we only expect major
coupling between
km s-1). Hence, although the Gauss-Hermite expansion conforms a description of the LOSVD with a set of orthogonal functions and therefore we only expect major
coupling between ![]() (the peak of the LOSVD) and
(the peak of the LOSVD) and ![]() (Larsen et al. 1983), V and h3, and
(Larsen et al. 1983), V and h3, and ![]() and h4, we have detected other correlations when working at low
signal-to-noise ratios. The expected coupling of V with h3 and
and h4, we have detected other correlations when working at low
signal-to-noise ratios. The expected coupling of V with h3 and ![]() with h4
appears in our simulations. Similar results have been found by authors who have performed
similar tests (Hau et al. 1999; van der Marel & Franx 1993).
with h4
appears in our simulations. Similar results have been found by authors who have performed
similar tests (Hau et al. 1999; van der Marel & Franx 1993).
We have decided to impose a S/N=33 as the minimum level to determine h3 and h4. This is a slightly lower level than that suggested by van der Marel & Franx (1993)
(
![]() pix-1) to give a good estimation of the Gauss-Hermite higher
order moments. Nevertheless in most cases we obtain
pix-1) to give a good estimation of the Gauss-Hermite higher
order moments. Nevertheless in most cases we obtain ![]() for the
profile central position (see Table 1).
for the
profile central position (see Table 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4111F6.eps}
\end{figure}](/articles/aa/full/2003/26/aah4111/Timg54.gif) |
Figure 6: Comparison between our best SSP model fit and Vega Beltrán et al. (2001) for NGC 5854. |
We have measured the recently defined Paschen-free CaT* index
(Cenarro et al. 2001a), that measures the strength of the Ca II lines
corrected from the contamination by Paschen lines, from our flux calibrated
spectra. We have made used of the FORTRAN routine indexfits
(part of the RED uc m E package), kindly made available to us by Javier Cenarro.
No velocity dispersion correction and zero-point offset have been performed.
Errors in the CaT* index include contributions from radial velocity
uncertainties and from S/N. The first one is obtained by the CaT* index from 100 random simulations within the velocity range [
![]() ,
,
![]() ].
The latter is determined using Eq. (A37) from Cenarro et al. (2001a). Both terms are
added in quadrature. The uncertainty from the S/N dominates the CaT* error.
].
The latter is determined using Eq. (A37) from Cenarro et al. (2001a). Both terms are
added in quadrature. The uncertainty from the S/N dominates the CaT* error.
We have compared our best SSP model fits with those in the literature.
Unfortunately, published minor axis kinematic profiles are scarce. We
present the comparison in Figs. 6 and 7
for NGC 5854 and NGC 7332 respectively. An excellent agreement is found for
the two galaxies, with no major systematic deviations, supporting our approach
of using synthetic SSP models. This agreement is particularly good for the
velocity dispersion of NGC 5854, where our results follow the same trend
obtained by Vega Beltrán et al. (2001). The comparison for NGC 7332 reveals also good
agreement with Fisher et al. (1994) and Simien & Prugniel (1997).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4111F7.eps}
\end{figure}](/articles/aa/full/2003/26/aah4111/Timg57.gif) |
Figure 7: Comparison between our best SSP model fit with Fisher et al. (1994) (F94) and Simien & Prugniel (1997) (SP97) for NGC 7332. |
Kinematic profiles for the 19 galaxies in the sample are shown in
Fig. A.1 (Appendix A). For each galaxy we show profiles of mean
heliocentric velocity V, velocity dispersion (![]() ), h3 and h4Gauss-Hermite coefficients, and Ca II triplet index CaT*, along
the galaxy's minor axis. Abscissae are centered on the brightness peak
of the long-slit spectrum, i.e. on the photometric center of the galaxy
since we don't expect large centering errors. Negative abscissae correspond
to the minor axis that projects away from the disk (the "dust-free'' side),
whose position angle on the sky is given at the top next to the galaxy's name.
Circles are measurements derived from S/N > 33 pix-1 spectra, and triangles
are V,
), h3 and h4Gauss-Hermite coefficients, and Ca II triplet index CaT*, along
the galaxy's minor axis. Abscissae are centered on the brightness peak
of the long-slit spectrum, i.e. on the photometric center of the galaxy
since we don't expect large centering errors. Negative abscissae correspond
to the minor axis that projects away from the disk (the "dust-free'' side),
whose position angle on the sky is given at the top next to the galaxy's name.
Circles are measurements derived from S/N > 33 pix-1 spectra, and triangles
are V, ![]() and CaT* derived from
20 < S/N < 33 spectra. Error bars
in each point are the formal error estimates coming from FOURFIT code.
Measurement uncertainties derived from the simulations described in
Sect. 3.5 are shown with vertical bars on the right edge of each
plot for the S/N > 33 spectra and, for V and
and CaT* derived from
20 < S/N < 33 spectra. Error bars
in each point are the formal error estimates coming from FOURFIT code.
Measurement uncertainties derived from the simulations described in
Sect. 3.5 are shown with vertical bars on the right edge of each
plot for the S/N > 33 spectra and, for V and ![]() ,
for
20 < S/N < 33 as well
(longest bar). The contour plot draws isophotes of the HST NICMOS F160W images
(Peletier et al. 1999), drawn to scale. The length of the 1.2 arcsec wide slit delimits the
range along the minor axis profile from which spectra has been binned to obtain a
S/N>20. The high spatial resolution of the NICMOS images (0.075 arcsec/pixel,
,
for
20 < S/N < 33 as well
(longest bar). The contour plot draws isophotes of the HST NICMOS F160W images
(Peletier et al. 1999), drawn to scale. The length of the 1.2 arcsec wide slit delimits the
range along the minor axis profile from which spectra has been binned to obtain a
S/N>20. The high spatial resolution of the NICMOS images (0.075 arcsec/pixel,
![]() arcsec FWHM) provides a clue on the level of substructure existing within the
spectroscopic slit. Due to the lack of a NICMOS image for NGC 7332, a WFPC1 image, retrieved
from the HST archive, has been used instead. Vertical dotted lines indicate the minor axis
bulge radius and center of the galaxy (see Table 1 for more details).
arcsec FWHM) provides a clue on the level of substructure existing within the
spectroscopic slit. Due to the lack of a NICMOS image for NGC 7332, a WFPC1 image, retrieved
from the HST archive, has been used instead. Vertical dotted lines indicate the minor axis
bulge radius and center of the galaxy (see Table 1 for more details).
Owing to the short integration times and the S/N requirements for kinematic extractions derived from the simulations (Sect. 3.5), the kinematic profiles typically extend to 5-10 arcsec from the nucleus only. Only for the large galaxy NGC 7331 do kinematic profiles extend over 20 arcsec on the dust-free side. All profiles are drawn to the same horizontal scale. In the following subsections we briefly address the global behavior of each kinematic parameter.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=90,clip]{H4111F8.eps}}
\end{figure}](/articles/aa/full/2003/26/aah4111/Timg59.gif) |
Figure 8: Velocity dispersion profiles for our sample of galaxies. Bulges with centrally-peaked velocity dispersions profiles are drawn in the top panel, whereas bulges with flat velocity dispersion profiles are plotted in the bottom panel. In the abscissa, radii have been normalized to the minor axis bulge radius (Table 1, Col. 12), defined as the radius along the minor axis where bulge and disk have equal surface brightness. |
As expected for the minor-axis alignment of the slits, mean velocity profiles are fairly flat. However, the profiles are not entirely featureless. We note three types of features.
We detect non-zero rotation in the outer parts of the profiles
(opposite mean velocities at both sides of the center, at the
2-![]() level) in 6 out of the 19 galaxies (NGC 5389, 5689, 5746,
5838, 5854, 7457). Typical rotation amplitudes are in the range
10 <
V < 20 km s-1. Such estimates of velocity amplitude and frequency
of occurrence are highly dependent on the depth of the data. For two
galaxies (NGC 5475, 5587) the profiles do not reach 5 arcsec and
contain no information on rotation at large radii. Brighter galaxies
in which the spectra extend farthest from the center show the highest V at large radii. In most of these cases, the outer velocity
measurements sample disk or bulge-disk transition regions. The
non-zero velocities indicate that our spectroscopic slits were not
perfectly aligned with the line of nodes. The slit was placed
orthogonal to the major axis of the outer isophotes. Hence the
misalignment might reflect an isophote twist in the outer parts
sampled by the spectra, due e.g. to warps or spiral arms, or a
distortion of the inner disk velocity field due to a bar or a spiral
arm. Note that a misalignment of
level) in 6 out of the 19 galaxies (NGC 5389, 5689, 5746,
5838, 5854, 7457). Typical rotation amplitudes are in the range
10 <
V < 20 km s-1. Such estimates of velocity amplitude and frequency
of occurrence are highly dependent on the depth of the data. For two
galaxies (NGC 5475, 5587) the profiles do not reach 5 arcsec and
contain no information on rotation at large radii. Brighter galaxies
in which the spectra extend farthest from the center show the highest V at large radii. In most of these cases, the outer velocity
measurements sample disk or bulge-disk transition regions. The
non-zero velocities indicate that our spectroscopic slits were not
perfectly aligned with the line of nodes. The slit was placed
orthogonal to the major axis of the outer isophotes. Hence the
misalignment might reflect an isophote twist in the outer parts
sampled by the spectra, due e.g. to warps or spiral arms, or a
distortion of the inner disk velocity field due to a bar or a spiral
arm. Note that a misalignment of ![]() or more could easily explain
such amplitudes in velocity.
or more could easily explain
such amplitudes in velocity.
We detect inner minor-axis rotation in 8 galaxies (NGC 5443, 5587, 5689, 5707, 5838, 5965, 6010, 7457) and possibly also in NGC 5389, 5422, 5854. Whenever the profiles extend beyond the nuclear region, inner rotation is delimited by a change in the velocity profile slope. These bulges thus contain kinematically distinct regions (hereafter KDR). We do not intend to set a link between these KDR and counterrotating or otherwise kinematically decoupled cores in ellipticals and bulges; full counterrotation cannot be established from our minor-axis kinematic profiles. Rather, we associate the velocity features to slight variations in the kinematic structure, related to inner components such as disks or bars.
Theoretically the simplest way to explain a minor-axis rotation in a bulge is to assume we are dealing with a triaxial object. In a triaxial object the position angle of the apparent minor axis can be different from that of the projected intrinsic short axis of the object (de Zeeuw & Franx 1991). Moreover, the photometric and kinematic minor axes may be misaligned as a result of the wide range of possible locations of the total angular momentum in a triaxial object (Binney 1985). In practice, whether minor-axis rotation traces a triaxial bulge can only be checked using integral field spectrographs e.g. SAURON (Bacon et al. 2001), or measuring kinematics along different positions angles of the galaxy (Statler & Smecker-Hane 1999).
The typical minor-axis radial extent of the KDR is 2-3 arcsec, or 0.5 kpc
at the median distance for the sample. In all of the eight galaxies listed
above as KDR, isophotal analysis of the HST/NICMOS F160W images (our
work, unpublished) reveals an inflection in the C4 isophotal
coefficient of the
![]() term that measures disky deviations
of the isophotes from pure ellipses (e.g. Jørgensen et al. 1992). C4 amplitudes
of the features are above 1% in all cases. This suggests the presence of
flattened subcomponents in the inner regions of the bulges showing up as
excesses in the bulge surface brightness profiles (Balcells et al. 2003). One
probably sees a mixture of inner disks and inner bars. In four of the eight
cases the isophotal analysis reveals changes in isophote position angle
(
term that measures disky deviations
of the isophotes from pure ellipses (e.g. Jørgensen et al. 1992). C4 amplitudes
of the features are above 1% in all cases. This suggests the presence of
flattened subcomponents in the inner regions of the bulges showing up as
excesses in the bulge surface brightness profiles (Balcells et al. 2003). One
probably sees a mixture of inner disks and inner bars. In four of the eight
cases the isophotal analysis reveals changes in isophote position angle
(
![]() )
at the same radius, which are likely to correspond to
inner bars but could also trace misaligned disks. The small rotation amplitudes
and the lack of isophotes elongated perpendicularly to the disks suggests that none of our
bulges show the type of orthogonal bulge kinematics found in NGC 4698 (Bertola et al. 1999)
and NGC 4672 (Sarzi et al. 2000). The four remaining cases with no isophotal misalignment
probably correspond to inner bars, as an aligned disk has its line of nodes parallel to
the minor axis.
)
at the same radius, which are likely to correspond to
inner bars but could also trace misaligned disks. The small rotation amplitudes
and the lack of isophotes elongated perpendicularly to the disks suggests that none of our
bulges show the type of orthogonal bulge kinematics found in NGC 4698 (Bertola et al. 1999)
and NGC 4672 (Sarzi et al. 2000). The four remaining cases with no isophotal misalignment
probably correspond to inner bars, as an aligned disk has its line of nodes parallel to
the minor axis.
The most prominent nuclear KDR is that of NGC 5838. The nucleus of NGC 5838 harbors an ordered ring or disk of dust and young stars (Peletier et al. 1999), which is oriented orthogonal to the slit. The dust may be responsible for the asymmetric rotation pattern.
It is worth noting that none of the KDR have distinct colors B-I and I-H (Peletier et al. 1999) on the dust-free side of the galaxies, nor do they have corresponding features in the CaT* profiles (Fig. A1). This may suggests that the velocity features are not associated to distinct stellar populations (e.g. Davies et al. 2001).
In two galaxies (NGC 5707, 7331) the velocities at large radii appear offset in the same direction relative to the nuclear velocity. NGC 5707 has a nuclear disk or bar extending over 1 arcsec, which is well aligned with the major axis of the outer disk and partially obscured by a dust lane; the dust might be responsible for the offset velocity measurement at the photometric center of the galaxy. In NGC 7331, the entire region from -4 arcsec to +4 arcsec appears displaced 15-20 km s-1 from the velocities further out. It is unclear whether dust extinction can be responsible for this structure, or whether the bulge might actually wander in the potential of the galaxy. The major-axis kinematics of this galaxy is complex, and its outer spiral structure is asymmetric; this could indicate a recent accretion event and/or the motion of the luminous material within the dark matter halo of the galaxy (Noordermeer et al. 2001). Results on the major-axis kinematics of this galaxy are puzzling. While Prada et al. (1996) reported to have found the bulge in NGC 7331 to counter-rotate, a more recent work by Bottema (1999) contradicts this result.
Velocity dispersion profiles trace the dynamical temperature of the bulges and are key ingredients for dynamical modeling of the bulges. They also provide diagnostics for distinguishing between bulge and disk on the basis of the internal dynamics.
For our galaxies, the minor-axis velocity dispersion profiles show a
wide diversity of shapes, from flat to strongly centrally peaked.
Velocity dispersion gradients, (
![]() per unit minor-axis
per unit minor-axis ![]() )
were computed by fitting linear relations to the
negative-abscissa dispersion profiles of Fig. A.1, which correspond
to the dust-free side of the bulges. Minor-axis
)
were computed by fitting linear relations to the
negative-abscissa dispersion profiles of Fig. A.1, which correspond
to the dust-free side of the bulges. Minor-axis ![]() were derived
using the
were derived
using the ![]() values from Balcells et al. (2003), which derive from
H-band surface brightness profiles from HST-NICMOS images, and
ellipticities at the bulge effective radius
values from Balcells et al. (2003), which derive from
H-band surface brightness profiles from HST-NICMOS images, and
ellipticities at the bulge effective radius
![]() obtained from
the ellipticity profiles in the same paper. Dispersion gradients range
from 0 to -70 km s-1
obtained from
the ellipticity profiles in the same paper. Dispersion gradients range
from 0 to -70 km s-1
![]() ,
with
a median of -21 km s-1
,
with
a median of -21 km s-1
![]() and a mode of
only
and a mode of
only ![]() 10 km s-1
10 km s-1
![]() .
.
Figure 8 displays all the velocity dispersion
profiles, presented on two panels for clarity; the top/bottom panel
shows the half sample with highest/lowest
![]() .
In order
to show whether the profiles sample only the bulge or extend to the
disk region, we normalize each abscissa to
.
In order
to show whether the profiles sample only the bulge or extend to the
disk region, we normalize each abscissa to
![]() ,
the minor-axis
radius where bulge and disk contribute equally to the surface
brightness profile (listed in Col. 12 of Table 1). Most
profiles extend well beyond
,
the minor-axis
radius where bulge and disk contribute equally to the surface
brightness profile (listed in Col. 12 of Table 1). Most
profiles extend well beyond
![]() ,
indicating that the
profiles reach to the region dominated by disk light according to the
bulge-disk decomposition.
,
indicating that the
profiles reach to the region dominated by disk light according to the
bulge-disk decomposition.
Three effects may influence the shape of the minor axis velocity dispersion profiles in our galaxies, (i) the intrinsic velocity structure of the bulge, (ii) the galaxy inclination, which determines which projection of the velocity ellipsoid is sampled by the data, and (iii) the brightness of the disk in the region sampled by the kinematic profiles.
Because most profiles reach the region where the surface brightness is
dominated by the disk (Fig. 8), flat dispersion
profiles imply similar dispersions for bulge and host disk. At the
median inclination of the sample,
![]() ,
minor-axis dispersion
profiles preferentially sample the radial component of the velocity
dispersion ellipsoid. Our flat profiles then indicate a surprisingly
high radial velocity dispersions in the regions dominated by disk
light, and an equally surprising continuity of the radial velocity
dispersions into the region of the bulge. Steep dispersion profiles,
in contrast, indicate distinct radial dispersions in the bulge and host
disk, with dispersions increasing toward the center as is expected in
dynamically hot, self-gravitating ellipsoids.
,
minor-axis dispersion
profiles preferentially sample the radial component of the velocity
dispersion ellipsoid. Our flat profiles then indicate a surprisingly
high radial velocity dispersions in the regions dominated by disk
light, and an equally surprising continuity of the radial velocity
dispersions into the region of the bulge. Steep dispersion profiles,
in contrast, indicate distinct radial dispersions in the bulge and host
disk, with dispersions increasing toward the center as is expected in
dynamically hot, self-gravitating ellipsoids.
The disk central surface brightness influences the velocity dispersion
gradient. Figure 9a shows the distribution of
![]() against the face-on disk central surface brightness
against the face-on disk central surface brightness ![]() .
Bright disks have shallow dispersion profiles, while the
steepest profiles are found in faint disks. We find it unlikely that
this dependency arises from biases in the derivation of the kinematic
profiles. Our simulations (Sect. 3.5) show that
dispersions as low as
.
Bright disks have shallow dispersion profiles, while the
steepest profiles are found in faint disks. We find it unlikely that
this dependency arises from biases in the derivation of the kinematic
profiles. Our simulations (Sect. 3.5) show that
dispersions as low as
![]() km s-1 are well reproduced by the
FOURFIT algorithm. Selection biases would hamper the detection of disk
dispersions for faint disks first, but dispersion gradients of all
values are found for these disks. The lack of steep dispersion
profiles in bright disks appears therefore real.
km s-1 are well reproduced by the
FOURFIT algorithm. Selection biases would hamper the detection of disk
dispersions for faint disks first, but dispersion gradients of all
values are found for these disks. The lack of steep dispersion
profiles in bright disks appears therefore real.
Figure 9b shows the distribution of
![]() against
against
![]() ,
the ellipticity measured at the bulge
effective radius. A trend is found, in the sense that more flattened
bulges show shallower dispersion profiles. This dependence does not
arise from viewing-angle effects: Fig. 9c shows that
,
the ellipticity measured at the bulge
effective radius. A trend is found, in the sense that more flattened
bulges show shallower dispersion profiles. This dependence does not
arise from viewing-angle effects: Fig. 9c shows that
![]() does not depend on the galaxy inclination.
Shallow-profile objects may be kinematically described as thickened disks.
In low-ellipticity bulges, the
does not depend on the galaxy inclination.
Shallow-profile objects may be kinematically described as thickened disks.
In low-ellipticity bulges, the ![]() profiles increase toward the
center, again as expected from hot ellipsoids.
profiles increase toward the
center, again as expected from hot ellipsoids.
Kormendy (1993) discusses that some bulges share strong similarities with
disks, on the basis of their low velocity dispersions, high
![]() for their ellipticity, and nuclear spiral structure.
The disky nature of bulges is usually discussed in relation to
late-type, low-mass bulges (Kormendy 1993). Our dispersion profiles indicate
that this situation affects also early-types, including several S0's.
for their ellipticity, and nuclear spiral structure.
The disky nature of bulges is usually discussed in relation to
late-type, low-mass bulges (Kormendy 1993). Our dispersion profiles indicate
that this situation affects also early-types, including several S0's.
It appears that the disky nature of bulges cannot be established on the basis of spheroid luminosity; our velocity dispersion gradients do not correlate with bulge luminosity or with central velocity dispersion. Gradients do not correlate either with morphological type index, bulge Sérsic index n, bulge and disk scale lengths and bulge effective surface brightness. We have searched for a dependency on the presence of bars or box-peanut shaped bulge isophotes. Such galaxies are depicted with triangles in Fig. 9. While bar detection is difficult at the inclinations of our sample galaxies, it is apparent that barred and box-peanut bulges do not occupy preferred regions in Fig. 9.
The massive bulge of NGC 5746 (Sb) is the only object showing a strongly-defined central velocity dispersion minimum. A weak central minimum is also found in NGC 5443. Central velocity dispersion minima are generally understood as tracing embedded disks, bars, or low-mass spheroids. Therefore, given the abundance of isophotal substructure in the nuclei of these galaxies, it is surprising that central velocity dispersion minima are so infrequent among our objects. As mentioned above, our sample includes six box- or peanut-shaped bulges. For these objects, the bar producing the peanut may not reach the center; or, alternatively, the central dispersion may be affected by the presence of secondary nuclear stellar bars/disks, with dispersion minima in bars being found for given viewing angles only. In NGC 5746 the local central minimum may be due to the main bar reaching all the way to the inner arcsecond, or to the presence of a secondary bar or nuclear disk.
Profiles of the h3 skewness term of the LOSVD are consistent with zero in most cases. In the few cases with significant non-zero h3 (NGC 5475, 6010, 7331), h3 does not have an opposite sign to the mean velocity that is typical of major axis profiles. This is reasonable as any rotation detected in the spectra is due to slight slit misalignment respect to the minor axis.
Similarly, the kurtosis profiles h4 are generally flat and close to zero. In 12 galaxies however, h4 is significantly positive above 0.1 somewhere in the profile, denoting centrally-peaked LOSVDs.
We have measured the CaT* profiles for our sample of galaxies in order to
trace correlations between kinematic and population features along the galaxies
minor axis. Our analysis of the profiles does not show any correlation with either
kinematic (V, ![]() ,
h3, h4) or photometric parameters (from
Balcells et al. 2003). The lack of correlation might be due to the very small
dependence of the CaT* on age and metallicity for the values we expect for
this type of galaxies (Vazdekis et al. 2003).
,
h3, h4) or photometric parameters (from
Balcells et al. 2003). The lack of correlation might be due to the very small
dependence of the CaT* on age and metallicity for the values we expect for
this type of galaxies (Vazdekis et al. 2003).
In a forthcoming paper (Falcón-Barroso et al. 2003) we will present an extensive study of
the near-IR Ca II triplet-![]() relation for our sample of bulges.
In that paper we give measurements of the recently defined near-infrared
Ca II triplet indices (CaT, CaT*), Paschen (PaT) and Magnesium (Mg I) indices (see Cenarro et al. 2001a) for our sample of bulges. We show
that both the CaT* and CaT indices decrease with central velocity dispersion
relation for our sample of bulges.
In that paper we give measurements of the recently defined near-infrared
Ca II triplet indices (CaT, CaT*), Paschen (PaT) and Magnesium (Mg I) indices (see Cenarro et al. 2001a) for our sample of bulges. We show
that both the CaT* and CaT indices decrease with central velocity dispersion ![]() with small scatter. The decrease of CaT and CaT* with
with small scatter. The decrease of CaT and CaT* with ![]() contrasts
with the well-known increase of another
contrasts
with the well-known increase of another ![]() -element index, Mg2, with
-element index, Mg2, with ![]() .
.
We have extracted minor-axis kinematic profiles from spectra in the Ca II near-IR region for a well-studied sample of early - to intermediate-type, inclined galaxies from the Balcells & Peletier (1994) sample. SSP models from Vazdekis et al. (2003) at 1.5 Å resolution have been used in addition to the traditional template stars. We have compared results obtained with the different templates and determined that synthetic models produce slightly better results than those from stellar templates, in the Ca II triplet region. We discuss the advantages/disadvantages of using SSP models instead of stellar templates. Our main conclusion is that synthetic models, when coming from a well constructed stellar library, help to reduce several drawbacks such as the template mismatch problem affecting all the traditional kinematical methods. We find a good agreement withhigh-quality kinematic profiles from the literature. SSP model spectra used as templates have clear applications for kinematic studies of galaxies at high redshift.
We find minor axis rotation in almost half of our galaxy sample. We discuss two types of minor axis rotation: rotation in the outer parts, probably due to slit misalignments, and inner rotation, which are associated to disky deviations of the isophotes from pure ellipses. We also find some cases of kinematically offset nuclei (NGC 5707 and NGC 7331) for which we do not find a clear explanation. We show that flattened bulges tend to show shallow velocity dispersion gradients and similar dispersions in bulge and inner disk, possibly indicating a thickened disk structure for these bulges. Finally, we find that our velocity dispersion gradients correlate with disk central surface brightness and with bulge ellipticity, but do not correlate with disk ellipticity. Gradients do not correlate either with bulge luminosity, bulge central velocity dispersion, bulge Sérsic index n, bulge effective surface brightness, galaxy morphological type, and disk or bulge effective radii.
Acknowledgements
JFB acknowledges the financial support from a PPARC studentship. The William Herschel Telescope is operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. We acknowledge the professional help of the observatory staff in the operation of the WHT and the ISIS spectrograph.
In this section we present kinematic profiles for each galaxy (heliocentric velocity, velocity dispersion, h3, h4), together with an H-band NICMOS (F160W) contour map from Peletier et al. (1999) (except for NGC 7332 for which a WFPC1 image, taken from the archive, is plotted instead). The length of the 1.2 arcsec wide slit delimits the range along the minor axis profile from which spectra has been binned to obtain a S/N>20. The CaT* index (see Sect. 3.6) is shown in the bottom panel. Filled circles represent data points with signal to noise ratio above 33, whereas filled triangles represent data points with signal to noise between 20 and 33. Contour levels have 0.5 mag difference. The left hand side of the profiles, for all galaxies, corresponds the dust-free side, while the right hand side corresponds to the dusty side. The PA (on top of the figure) is the position angle (N-E) of the dust-free minor axis. Error bars determined in the simulation for each S/N (see Sect. 3.5) are located on the right hand side of each panel, S/N=33 (short bar) and S/N=20 (long bar). A dotted line has been drawn, on each panel, at the level of the central value for the velocity, velocity dispersion and CaT* index and it is at the zero value for the h3 and h4 parameters. Vertical dotted lines indicate the minor axis bulge radius and center of the galaxy (see Table 1 for more details).
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -6.78 | 2586 | 13 | 132 | 16 | 0.00 | 0.00 | 0.00 | 0.00 | 7.11 | 0.62 |
| -4.24 | 2572 | 8 | 140 | 9 | 0.00 | 0.00 | 0.00 | 0.00 | 7.36 | 0.58 |
| -2.84 | 2571 | 8 | 173 | 10 | 0.00 | 0.00 | 0.00 | 0.00 | 8.53 | 0.54 |
| -2.37 | 2579 | 6 | 164 | 6 | -0.03 | 0.03 | 0.05 | 0.03 | 7.34 | 0.37 |
| -1.23 | 2581 | 8 | 194 | 8 | -0.08 | 0.03 | -0.01 | 0.04 | 6.79 | 0.37 |
| -0.72 | 2568 | 8 | 155 | 9 | -0.09 | 0.04 | -0.04 | 0.05 | 5.70 | 0.36 |
| -0.36 | 2564 | 7 | 181 | 8 | -0.05 | 0.03 | -0.02 | 0.03 | 7.24 | 0.26 |
| 0.00 | 2568 | 4 | 182 | 5 | -0.01 | 0.02 | -0.09 | 0.02 | 6.95 | 0.24 |
| 0.36 | 2576 | 6 | 178 | 7 | -0.01 | 0.03 | -0.04 | 0.03 | 7.66 | 0.28 |
| 0.72 | 2574 | 10 | 178 | 12 | 0.02 | 0.05 | -0.02 | 0.05 | 7.98 | 0.37 |
| 1.22 | 2569 | 6 | 159 | 6 | 0.01 | 0.03 | 0.06 | 0.03 | 7.90 | 0.37 |
| 2.50 | 2575 | 5 | 147 | 6 | -0.10 | 0.03 | -0.05 | 0.04 | 6.57 | 0.37 |
| 4.22 | 2578 | 10 | 143 | 11 | 0.00 | 0.00 | 0.00 | 0.00 | 6.84 | 0.61 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -7.96 | 1893 | 12 | 134 | 14 | 0.00 | 0.00 | 0.00 | 0.00 | 5.60 | 0.63 |
| -4.75 | 1862 | 12 | 174 | 14 | 0.00 | 0.00 | 0.00 | 0.00 | 7.74 | 0.59 |
| -3.86 | 1872 | 6 | 114 | 4 | -0.05 | 0.04 | 0.26 | 0.05 | 7.30 | 0.37 |
| -1.73 | 1847 | 4 | 112 | 5 | 0.01 | 0.03 | 0.06 | 0.04 | 6.82 | 0.35 |
| -0.87 | 1849 | 5 | 129 | 6 | 0.05 | 0.03 | 0.01 | 0.04 | 6.70 | 0.29 |
| -0.36 | 1862 | 3 | 125 | 4 | 0.05 | 0.02 | 0.01 | 0.03 | 6.49 | 0.35 |
| -0.00 | 1862 | 4 | 132 | 4 | -0.02 | 0.02 | 0.02 | 0.03 | 6.91 | 0.34 |
| 0.51 | 1864 | 4 | 127 | 5 | -0.03 | 0.03 | 0.04 | 0.03 | 6.86 | 0.29 |
| 1.37 | 1865 | 4 | 108 | 4 | -0.03 | 0.03 | 0.13 | 0.03 | 7.88 | 0.35 |
| 3.43 | 1864 | 6 | 134 | 6 | 0.01 | 0.04 | 0.08 | 0.04 | 6.61 | 0.38 |
| 4.36 | 1862 | 10 | 146 | 11 | 0.00 | 0.00 | 0.00 | 0.00 | 6.17 | 0.62 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -6.48 | 1841 | 13 | 144 | 15 | 0.00 | 0.00 | 0.00 | 0.00 | 5.56 | 0.62 |
| -4.86 | 1837 | 7 | 134 | 7 | -0.01 | 0.05 | 0.11 | 0.05 | 6.35 | 0.38 |
| -2.24 | 1854 | 5 | 138 | 5 | -0.02 | 0.03 | 0.06 | 0.03 | 6.82 | 0.36 |
| -1.23 | 1856 | 6 | 155 | 7 | 0.10 | 0.03 | -0.02 | 0.04 | 6.65 | 0.33 |
| -0.72 | 1839 | 7 | 176 | 7 | 0.09 | 0.03 | 0.02 | 0.04 | 7.01 | 0.36 |
| -0.36 | 1838 | 5 | 182 | 6 | 0.04 | 0.02 | -0.01 | 0.02 | 7.20 | 0.31 |
| -0.00 | 1832 | 5 | 187 | 7 | 0.00 | 0.02 | -0.06 | 0.03 | 6.68 | 0.30 |
| 0.36 | 1844 | 7 | 190 | 8 | -0.05 | 0.03 | -0.00 | 0.03 | 6.25 | 0.35 |
| 0.87 | 1827 | 7 | 183 | 7 | 0.03 | 0.03 | 0.08 | 0.03 | 7.18 | 0.32 |
| 1.87 | 1830 | 7 | 165 | 7 | -0.02 | 0.03 | 0.06 | 0.04 | 6.70 | 0.36 |
| 4.51 | 1841 | 7 | 131 | 9 | 0.01 | 0.05 | -0.01 | 0.06 | 6.14 | 0.38 |
| 6.13 | 1843 | 11 | 103 | 13 | 0.00 | 0.00 | 0.00 | 0.00 | 4.61 | 0.65 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -7.47 | 1787 | 13 | 107 | 16 | 0.00 | 0.00 | 0.00 | 0.00 | 7.88 | 0.63 |
| -3.34 | 1739 | 9 | 110 | 11 | 0.00 | 0.00 | 0.00 | 0.00 | 4.69 | 0.61 |
| -1.74 | 1740 | 7 | 121 | 8 | 0.00 | 0.00 | 0.00 | 0.00 | 7.70 | 0.60 |
| -1.23 | 1738 | 5 | 115 | 6 | -0.01 | 0.04 | 0.03 | 0.05 | 7.66 | 0.37 |
| -0.02 | 1758 | 3 | 89 | 4 | -0.07 | 0.03 | 0.05 | 0.04 | 7.43 | 0.33 |
| 1.67 | 1760 | 6 | 112 | 10 | 0.01 | 0.05 | -0.11 | 0.07 | 6.70 | 0.38 |
| 4.36 | 1752 | 11 | 125 | 13 | 0.00 | 0.00 | 0.00 | 0.00 | 5.57 | 0.65 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -4.12 | 1665 | 5 | 55 | 8 | 0.00 | 0.00 | 0.00 | 0.00 | 7.57 | 0.60 |
| -2.48 | 1665 | 5 | 74 | 6 | 0.00 | 0.00 | 0.00 | 0.00 | 6.94 | 0.60 |
| -1.50 | 1660 | 5 | 93 | 7 | 0.10 | 0.05 | 0.01 | 0.05 | 7.04 | 0.38 |
| -0.50 | 1669 | 5 | 111 | 7 | 0.03 | 0.04 | -0.09 | 0.06 | 6.91 | 0.30 |
| 0.00 | 1661 | 3 | 97 | 4 | 0.02 | 0.03 | -0.02 | 0.04 | 7.52 | 0.36 |
| 0.50 | 1674 | 6 | 91 | 7 | -0.05 | 0.05 | 0.04 | 0.06 | 7.40 | 0.32 |
| 1.64 | 1667 | 5 | 89 | 6 | -0.01 | 0.05 | 0.06 | 0.05 | 7.32 | 0.37 |
| 2.12 | 1665 | 5 | 87 | 7 | 0.00 | 0.00 | 0.00 | 0.00 | 6.65 | 0.55 |
| 3.49 | 1671 | 4 | 43 | 6 | 0.00 | 0.00 | 0.00 | 0.00 | 7.33 | 0.61 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -3.82 | 2291 | 6 | 76 | 9 | 0.00 | 0.00 | 0.00 | 0.00 | 6.66 | 0.62 |
| -1.43 | 2311 | 6 | 110 | 9 | -0.06 | 0.05 | -0.06 | 0.06 | 6.24 | 0.37 |
| -0.00 | 2296 | 3 | 100 | 4 | -0.03 | 0.03 | 0.06 | 0.03 | 7.09 | 0.35 |
| 1.57 | 2280 | 6 | 79 | 6 | 0.19 | 0.07 | 0.09 | 0.06 | 7.95 | 0.37 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -9.04 | 2202 | 11 | 96 | 14 | 0.00 | 0.00 | 0.00 | 0.00 | 7.81 | 0.61 |
| -5.86 | 2173 | 9 | 137 | 10 | 0.00 | 0.00 | 0.00 | 0.00 | 6.57 | 0.62 |
| -4.10 | 2195 | 8 | 143 | 10 | 0.00 | 0.00 | 0.00 | 0.00 | 7.51 | 0.59 |
| -3.04 | 2202 | 5 | 138 | 5 | -0.04 | 0.03 | 0.11 | 0.04 | 6.87 | 0.37 |
| -1.37 | 2212 | 5 | 151 | 4 | -0.10 | 0.03 | 0.10 | 0.03 | 7.80 | 0.33 |
| -0.52 | 2214 | 4 | 157 | 5 | -0.07 | 0.02 | -0.05 | 0.03 | 6.84 | 0.28 |
| 0.00 | 2200 | 5 | 158 | 5 | -0.04 | 0.02 | 0.02 | 0.03 | 6.44 | 0.36 |
| 0.36 | 2201 | 5 | 163 | 5 | 0.01 | 0.02 | 0.01 | 0.03 | 7.48 | 0.37 |
| 0.88 | 2192 | 5 | 154 | 5 | -0.03 | 0.02 | 0.04 | 0.03 | 6.88 | 0.30 |
| 1.74 | 2184 | 5 | 158 | 5 | 0.04 | 0.02 | 0.07 | 0.03 | 7.78 | 0.33 |
| 3.38 | 2200 | 6 | 147 | 7 | -0.05 | 0.04 | 0.05 | 0.04 | 7.05 | 0.38 |
| 4.46 | 2211 | 8 | 100 | 10 | 0.00 | 0.00 | 0.00 | 0.00 | 5.70 | 0.62 |
| 6.21 | 2209 | 9 | 125 | 11 | 0.00 | 0.00 | 0.00 | 0.00 | 5.76 | 0.63 |
| 9.29 | 2218 | 9 | 92 | 11 | 0.00 | 0.00 | 0.00 | 0.00 | 7.72 | 0.62 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -5.06 | 2208 | 5 | 71 | 7 | 0.00 | 0.00 | 0.00 | 0.00 | 6.90 | 0.62 |
| -4.33 | 2211 | 5 | 85 | 5 | 0.02 | 0.05 | 0.14 | 0.05 | 7.36 | 0.37 |
| -1.89 | 2193 | 5 | 143 | 6 | 0.03 | 0.03 | -0.05 | 0.04 | 6.51 | 0.35 |
| -0.88 | 2179 | 6 | 154 | 8 | 0.01 | 0.03 | -0.00 | 0.04 | 7.33 | 0.34 |
| -0.01 | 2191 | 3 | 163 | 4 | -0.04 | 0.02 | -0.06 | 0.02 | 7.03 | 0.24 |
| 1.01 | 2200 | 5 | 147 | 6 | -0.04 | 0.03 | 0.02 | 0.03 | 7.56 | 0.34 |
| 2.66 | 2198 | 5 | 119 | 5 | -0.04 | 0.03 | 0.06 | 0.04 | 6.59 | 0.37 |
| 3.20 | 2199 | 6 | 96 | 7 | 0.00 | 0.00 | 0.00 | 0.00 | 6.18 | 0.62 |
| 4.83 | 2210 | 6 | 84 | 8 | 0.00 | 0.00 | 0.00 | 0.00 | 6.24 | 0.62 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -6.63 | 1731 | 8 | 82 | 10 | 0.00 | 0.00 | 0.00 | 0.00 | 7.93 | 0.62 |
| -4.44 | 1723 | 7 | 104 | 8 | 0.00 | 0.00 | 0.00 | 0.00 | 6.94 | 0.62 |
| -3.38 | 1719 | 4 | 83 | 5 | -0.01 | 0.04 | 0.25 | 0.04 | 7.39 | 0.37 |
| -1.75 | 1726 | 5 | 97 | 5 | -0.03 | 0.04 | 0.09 | 0.04 | 6.80 | 0.35 |
| -0.88 | 1719 | 4 | 102 | 4 | -0.02 | 0.03 | 0.17 | 0.03 | 6.86 | 0.33 |
| -0.01 | 1720 | 3 | 113 | 2 | 0.02 | 0.02 | 0.12 | 0.02 | 6.83 | 0.24 |
| 0.87 | 1717 | 5 | 125 | 6 | 0.02 | 0.03 | 0.02 | 0.04 | 7.30 | 0.36 |
| 2.12 | 1723 | 5 | 92 | 5 | -0.02 | 0.04 | 0.13 | 0.04 | 7.11 | 0.37 |
| 3.89 | 1728 | 5 | 72 | 7 | 0.00 | 0.00 | 0.00 | 0.00 | 7.62 | 0.58 |
| 8.01 | 1712 | 15 | 57 | 21 | 0.00 | 0.00 | 0.00 | 0.00 | 7.28 | 0.70 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -13.66 | 1690 | 15 | 161 | 17 | 0.00 | 0.00 | 0.00 | 0.00 | 5.49 | 0.62 |
| -11.52 | 1703 | 11 | 164 | 13 | 0.02 | 0.05 | -0.01 | 0.06 | 5.61 | 0.38 |
| -6.14 | 1719 | 9 | 223 | 10 | -0.01 | 0.03 | -0.02 | 0.04 | 6.43 | 0.37 |
| -3.32 | 1713 | 7 | 215 | 7 | -0.03 | 0.03 | 0.05 | 0.03 | 6.53 | 0.35 |
| -1.76 | 1711 | 7 | 184 | 8 | 0.01 | 0.03 | 0.04 | 0.03 | 6.70 | 0.37 |
| -0.89 | 1713 | 5 | 161 | 5 | -0.05 | 0.03 | 0.04 | 0.03 | 7.04 | 0.37 |
| -0.00 | 1723 | 4 | 160 | 5 | -0.04 | 0.02 | 0.01 | 0.03 | 6.86 | 0.28 |
| 1.03 | 1714 | 6 | 182 | 5 | 0.00 | 0.03 | 0.10 | 0.03 | 7.19 | 0.32 |
| 2.43 | 1691 | 7 | 228 | 7 | -0.02 | 0.02 | 0.06 | 0.03 | 6.74 | 0.36 |
| 6.19 | 1733 | 12 | 202 | 14 | -0.06 | 0.05 | -0.03 | 0.05 | 5.15 | 0.39 |
| 7.14 | 1714 | 18 | 175 | 20 | 0.00 | 0.00 | 0.00 | 0.00 | 4.62 | 0.70 |
| 12.51 | 1727 | 18 | 184 | 21 | 0.00 | 0.00 | 0.00 | 0.00 | 5.47 | 0.68 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -14.62 | 1358 | 16 | 172 | 11 | 0.13 | 0.09 | 0.32 | 0.11 | 8.43 | 0.38 |
| -7.00 | 1341 | 8 | 172 | 8 | 0.03 | 0.04 | 0.06 | 0.04 | 7.04 | 0.37 |
| -4.61 | 1345 | 9 | 220 | 9 | 0.05 | 0.03 | 0.06 | 0.04 | 6.35 | 0.35 |
| -3.21 | 1369 | 9 | 282 | 9 | -0.03 | 0.02 | 0.05 | 0.03 | 6.86 | 0.36 |
| -2.32 | 1332 | 9 | 267 | 12 | 0.03 | 0.03 | -0.06 | 0.03 | 6.73 | 0.36 |
| -1.60 | 1336 | 8 | 267 | 10 | 0.03 | 0.02 | -0.04 | 0.03 | 6.49 | 0.29 |
| -1.08 | 1325 | 11 | 302 | 12 | -0.01 | 0.03 | 0.01 | 0.03 | 6.35 | 0.33 |
| -0.72 | 1328 | 8 | 271 | 9 | 0.03 | 0.02 | -0.02 | 0.03 | 7.01 | 0.29 |
| -0.36 | 1336 | 7 | 278 | 9 | -0.01 | 0.02 | -0.00 | 0.02 | 6.80 | 0.26 |
| 0.00 | 1345 | 7 | 291 | 8 | 0.03 | 0.02 | 0.00 | 0.02 | 6.51 | 0.25 |
| 0.36 | 1382 | 8 | 319 | 10 | 0.04 | 0.02 | -0.03 | 0.02 | 7.81 | 0.25 |
| 0.72 | 1381 | 10 | 295 | 11 | -0.11 | 0.03 | -0.03 | 0.03 | 6.37 | 0.27 |
| 1.08 | 1398 | 11 | 271 | 13 | -0.05 | 0.03 | -0.06 | 0.04 | 6.59 | 0.32 |
| 1.44 | 1365 | 11 | 322 | 14 | -0.05 | 0.03 | -0.03 | 0.03 | 7.01 | 0.37 |
| 1.96 | 1359 | 10 | 295 | 9 | -0.00 | 0.03 | 0.09 | 0.03 | 6.86 | 0.30 |
| 2.68 | 1360 | 10 | 244 | 10 | -0.07 | 0.03 | 0.08 | 0.04 | 6.90 | 0.35 |
| 3.57 | 1298 | 10 | 278 | 10 | 0.03 | 0.03 | 0.06 | 0.03 | 6.53 | 0.35 |
| 4.81 | 1331 | 10 | 227 | 12 | -0.05 | 0.04 | -0.04 | 0.04 | 5.79 | 0.38 |
| 6.71 | 1322 | 9 | 212 | 8 | 0.03 | 0.03 | 0.09 | 0.04 | 7.15 | 0.38 |
| 11.00 | 1327 | 16 | 160 | 22 | 0.02 | 0.08 | -0.10 | 0.11 | 5.26 | 0.39 |
| 11.74 | 1353 | 21 | 157 | 24 | 0.00 | 0.00 | 0.00 | 0.00 | 3.65 | 0.62 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -5.98 | 1682 | 8 | 103 | 9 | 0.00 | 0.00 | 0.00 | 0.00 | 7.97 | 0.60 |
| -4.31 | 1677 | 5 | 67 | 4 | 0.01 | 0.06 | 0.34 | 0.06 | 7.46 | 0.37 |
| -1.88 | 1660 | 4 | 95 | 6 | 0.05 | 0.04 | -0.05 | 0.05 | 6.47 | 0.37 |
| -0.86 | 1659 | 5 | 100 | 6 | 0.05 | 0.04 | -0.03 | 0.05 | 5.96 | 0.31 |
| -0.36 | 1675 | 4 | 107 | 5 | -0.00 | 0.03 | -0.00 | 0.04 | 6.78 | 0.35 |
| 0.00 | 1670 | 3 | 102 | 4 | 0.02 | 0.03 | 0.05 | 0.03 | 6.73 | 0.33 |
| 0.36 | 1676 | 3 | 121 | 5 | -0.03 | 0.02 | -0.04 | 0.03 | 7.75 | 0.33 |
| 0.86 | 1698 | 4 | 108 | 4 | -0.10 | 0.03 | 0.07 | 0.04 | 7.88 | 0.30 |
| 1.88 | 1677 | 4 | 121 | 6 | 0.05 | 0.03 | -0.03 | 0.04 | 7.65 | 0.36 |
| 4.31 | 1659 | 5 | 74 | 5 | 0.01 | 0.05 | 0.10 | 0.05 | 6.55 | 0.38 |
| 5.98 | 1660 | 6 | 73 | 8 | 0.00 | 0.00 | 0.00 | 0.00 | 5.55 | 0.61 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -7.00 | 764 | 10 | 70 | 14 | 0.00 | 0.00 | 0.00 | 0.00 | 4.88 | 0.63 |
| -4.24 | 785 | 4 | 51 | 6 | 0.00 | 0.00 | 0.00 | 0.00 | 6.44 | 0.60 |
| -2.68 | 777 | 5 | 43 | 8 | 0.06 | 0.10 | 0.10 | 0.12 | 6.35 | 0.38 |
| -1.03 | 780 | 5 | 68 | 6 | 0.04 | 0.06 | 0.02 | 0.07 | 6.88 | 0.36 |
| -0.01 | 779 | 3 | 51 | 3 | 0.00 | 0.04 | 0.22 | 0.04 | 6.47 | 0.30 |
| 1.17 | 781 | 4 | 45 | 5 | -0.00 | 0.07 | 0.22 | 0.07 | 7.55 | 0.34 |
| 4.30 | 780 | 14 | 34 | 22 | 0.00 | 0.30 | 0.24 | 0.33 | 6.55 | 0.38 |
| 6.42 | 776 | 10 | 41 | 15 | 0.00 | 0.00 | 0.00 | 0.00 | 4.06 | 0.63 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -5.41 | 3375 | 12 | 148 | 14 | 0.00 | 0.00 | 0.00 | 0.00 | 4.80 | 0.62 |
| -3.08 | 3398 | 9 | 192 | 8 | 0.11 | 0.04 | 0.08 | 0.04 | 5.22 | 0.38 |
| -1.00 | 3411 | 9 | 160 | 7 | -0.01 | 0.05 | 0.19 | 0.06 | 6.18 | 0.37 |
| 0.00 | 3417 | 5 | 191 | 6 | -0.01 | 0.02 | 0.05 | 0.03 | 7.37 | 0.27 |
| 0.99 | 3421 | 10 | 189 | 14 | 0.05 | 0.05 | -0.09 | 0.06 | 7.27 | 0.38 |
| 2.22 | 3368 | 12 | 170 | 15 | 0.00 | 0.00 | 0.00 | 0.00 | 5.19 | 0.61 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -6.51 | 2038 | 22 | 110 | 26 | 0.00 | 0.00 | 0.00 | 0.00 | 7.96 | 0.67 |
| -3.70 | 2028 | 9 | 105 | 11 | 0.00 | 0.00 | 0.00 | 0.00 | 7.76 | 0.60 |
| -2.68 | 2038 | 8 | 123 | 10 | 0.00 | 0.00 | 0.00 | 0.00 | 8.27 | 0.61 |
| -2.23 | 2027 | 7 | 130 | 7 | -0.06 | 0.04 | 0.09 | 0.05 | 7.67 | 0.38 |
| -1.23 | 2013 | 8 | 150 | 9 | -0.06 | 0.04 | -0.03 | 0.05 | 7.61 | 0.34 |
| -0.72 | 1991 | 9 | 160 | 8 | -0.15 | 0.05 | 0.04 | 0.05 | 7.02 | 0.37 |
| -0.36 | 2010 | 5 | 156 | 5 | -0.10 | 0.03 | 0.03 | 0.03 | 7.05 | 0.32 |
| -0.00 | 2020 | 4 | 163 | 5 | -0.02 | 0.02 | -0.02 | 0.02 | 6.21 | 0.31 |
| 0.36 | 2025 | 7 | 177 | 9 | -0.06 | 0.03 | -0.08 | 0.04 | 6.33 | 0.35 |
| 0.87 | 2036 | 7 | 170 | 8 | -0.02 | 0.03 | 0.02 | 0.04 | 7.23 | 0.32 |
| 1.87 | 2015 | 5 | 139 | 6 | 0.05 | 0.03 | 0.04 | 0.04 | 7.12 | 0.36 |
| 2.83 | 2017 | 8 | 119 | 9 | 0.00 | 0.00 | 0.00 | 0.00 | 6.64 | 0.58 |
| 4.47 | 2030 | 11 | 84 | 14 | 0.00 | 0.00 | 0.00 | 0.00 | 7.36 | 0.61 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -4.01 | 4724 | 13 | 191 | 16 | 0.00 | 0.00 | 0.00 | 0.00 | 6.38 | 0.61 |
| -3.12 | 4725 | 8 | 195 | 8 | 0.03 | 0.03 | 0.12 | 0.04 | 7.00 | 0.38 |
| -0.99 | 4740 | 11 | 248 | 14 | -0.00 | 0.04 | -0.05 | 0.04 | 7.47 | 0.34 |
| 0.01 | 4735 | 5 | 213 | 5 | 0.00 | 0.02 | 0.07 | 0.02 | 7.15 | 0.24 |
| 0.87 | 4760 | 8 | 180 | 8 | -0.09 | 0.04 | 0.07 | 0.04 | 6.07 | 0.35 |
| 2.00 | 4732 | 8 | 191 | 9 | 0.01 | 0.03 | 0.03 | 0.04 | 5.99 | 0.37 |
| 2.48 | 4739 | 10 | 187 | 12 | 0.00 | 0.00 | 0.00 | 0.00 | 6.18 | 0.55 |
| 3.86 | 4722 | 12 | 203 | 15 | 0.00 | 0.00 | 0.00 | 0.00 | 7.71 | 0.59 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -22.43 | 771 | 25 | 142 | 29 | 0.00 | 0.00 | 0.00 | 0.00 | 7.15 | 0.83 |
| -19.02 | 781 | 11 | 93 | 14 | 0.00 | 0.00 | 0.00 | 0.00 | 6.86 | 0.64 |
| -17.32 | 807 | 9 | 85 | 9 | -0.11 | 0.09 | 0.34 | 0.09 | 5.93 | 0.37 |
| -13.03 | 804 | 8 | 115 | 7 | -0.04 | 0.06 | 0.17 | 0.06 | 6.38 | 0.37 |
| -10.21 | 816 | 6 | 97 | 5 | -0.01 | 0.05 | 0.27 | 0.05 | 7.34 | 0.37 |
| -8.25 | 810 | 5 | 88 | 4 | 0.01 | 0.05 | 0.27 | 0.05 | 6.19 | 0.36 |
| -6.64 | 811 | 5 | 103 | 4 | -0.11 | 0.04 | 0.19 | 0.04 | 6.66 | 0.36 |
| -5.38 | 816 | 5 | 118 | 5 | -0.09 | 0.04 | 0.15 | 0.04 | 7.53 | 0.37 |
| -4.30 | 822 | 4 | 117 | 4 | -0.02 | 0.03 | 0.16 | 0.03 | 7.26 | 0.32 |
| -3.41 | 834 | 4 | 112 | 4 | -0.12 | 0.03 | 0.09 | 0.03 | 6.91 | 0.34 |
| -2.69 | 828 | 3 | 118 | 3 | -0.04 | 0.02 | 0.15 | 0.03 | 6.27 | 0.30 |
| -2.16 | 846 | 4 | 108 | 3 | -0.05 | 0.03 | 0.20 | 0.03 | 7.39 | 0.37 |
| -1.80 | 827 | 4 | 116 | 6 | -0.01 | 0.03 | -0.07 | 0.05 | 6.60 | 0.34 |
| -1.44 | 835 | 4 | 129 | 5 | 0.08 | 0.03 | -0.05 | 0.04 | 6.65 | 0.30 |
| -1.08 | 821 | 3 | 131 | 5 | -0.03 | 0.02 | -0.04 | 0.03 | 6.50 | 0.26 |
| -0.72 | 817 | 3 | 137 | 4 | 0.02 | 0.02 | -0.04 | 0.03 | 6.54 | 0.22 |
| -0.36 | 821 | 3 | 135 | 3 | -0.03 | 0.02 | 0.01 | 0.02 | 7.06 | 0.18 |
| -0.00 | 821 | 2 | 138 | 3 | -0.02 | 0.01 | 0.03 | 0.02 | 7.65 | 0.18 |
| 0.36 | 833 | 3 | 136 | 3 | -0.04 | 0.02 | 0.08 | 0.02 | 7.37 | 0.20 |
| 0.72 | 830 | 3 | 139 | 4 | -0.05 | 0.02 | 0.02 | 0.02 | 7.60 | 0.24 |
| 1.08 | 828 | 5 | 146 | 5 | 0.01 | 0.03 | 0.10 | 0.03 | 8.43 | 0.29 |
| 1.44 | 817 | 4 | 120 | 4 | 0.06 | 0.03 | 0.14 | 0.03 | 7.07 | 0.35 |
| 1.96 | 820 | 4 | 120 | 4 | 0.01 | 0.03 | 0.09 | 0.03 | 6.78 | 0.30 |
| 2.70 | 814 | 4 | 118 | 4 | -0.04 | 0.03 | 0.09 | 0.03 | 7.18 | 0.34 |
| 3.41 | 808 | 4 | 95 | 5 | 0.09 | 0.04 | 0.06 | 0.04 | 6.52 | 0.37 |
| 4.29 | 826 | 5 | 120 | 5 | -0.06 | 0.03 | 0.11 | 0.04 | 6.76 | 0.36 |
| 5.67 | 802 | 5 | 115 | 5 | -0.02 | 0.04 | 0.13 | 0.04 | 7.29 | 0.36 |
| 7.89 | 806 | 7 | 112 | 6 | -0.15 | 0.05 | 0.15 | 0.05 | 6.23 | 0.36 |
| 11.47 | 794 | 12 | 103 | 9 | -0.30 | 0.12 | 0.25 | 0.11 | 6.27 | 0.40 |
| 15.74 | 704 | 39 | 133 | 46 | 0.00 | 0.00 | 0.00 | 0.00 | 12.04 | 1.21 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -12.21 | 1214 | 13 | 57 | 19 | 0.00 | 0.00 | 0.00 | 0.00 | 3.47 | 0.64 |
| -8.17 | 1224 | 8 | 93 | 10 | 0.00 | 0.00 | 0.00 | 0.00 | 6.41 | 0.60 |
| -6.78 | 1228 | 5 | 88 | 6 | -0.08 | 0.05 | 0.06 | 0.05 | 6.53 | 0.37 |
| -3.87 | 1214 | 4 | 110 | 5 | 0.04 | 0.03 | -0.03 | 0.04 | 5.55 | 0.38 |
| -2.47 | 1219 | 4 | 120 | 5 | -0.04 | 0.03 | -0.01 | 0.04 | 6.10 | 0.36 |
| -1.59 | 1231 | 6 | 122 | 7 | 0.03 | 0.05 | 0.03 | 0.05 | 8.05 | 0.31 |
| -1.08 | 1237 | 4 | 126 | 5 | -0.02 | 0.03 | 0.01 | 0.03 | 7.12 | 0.33 |
| -0.72 | 1230 | 3 | 125 | 4 | -0.01 | 0.02 | 0.06 | 0.03 | 6.77 | 0.26 |
| -0.36 | 1230 | 3 | 131 | 3 | 0.01 | 0.02 | 0.05 | 0.02 | 7.56 | 0.22 |
| 0.00 | 1227 | 2 | 130 | 3 | 0.05 | 0.02 | -0.03 | 0.02 | 6.85 | 0.21 |
| 0.36 | 1223 | 2 | 127 | 3 | 0.02 | 0.02 | 0.04 | 0.02 | 7.62 | 0.21 |
| 0.72 | 1227 | 3 | 123 | 3 | -0.05 | 0.02 | 0.02 | 0.02 | 7.04 | 0.22 |
| 1.08 | 1225 | 3 | 122 | 4 | -0.02 | 0.02 | 0.01 | 0.03 | 7.14 | 0.25 |
| 1.44 | 1227 | 4 | 133 | 5 | -0.01 | 0.03 | -0.03 | 0.03 | 7.01 | 0.32 |
| 1.95 | 1222 | 3 | 116 | 4 | -0.01 | 0.03 | -0.01 | 0.03 | 6.57 | 0.31 |
| 2.83 | 1223 | 5 | 121 | 5 | 0.02 | 0.03 | 0.03 | 0.04 | 6.56 | 0.36 |
| 4.23 | 1230 | 4 | 99 | 4 | 0.03 | 0.04 | 0.07 | 0.04 | 6.61 | 0.38 |
| 7.14 | 1214 | 5 | 94 | 6 | 0.03 | 0.05 | 0.09 | 0.05 | 6.56 | 0.37 |
| 8.53 | 1208 | 7 | 78 | 10 | 0.00 | 0.00 | 0.00 | 0.00 | 5.13 | 0.61 |
| 12.46 | 1223 | 11 | 99 | 14 | 0.00 | 0.00 | 0.00 | 0.00 | 5.26 | 0.62 |
| x[
|
V |
|
h3 | h4 | CaT* | |||||
| -11.00 | 833 | 6 | 45 | 9 | 0.00 | 0.00 | 0.00 | 0.00 | 4.68 | 0.63 |
| -5.98 | 837 | 4 | 60 | 6 | 0.00 | 0.00 | 0.00 | 0.00 | 6.69 | 0.62 |
| -3.31 | 842 | 3 | 59 | 4 | 0.02 | 0.04 | 0.03 | 0.05 | 6.96 | 0.37 |
| -1.00 | 847 | 4 | 59 | 6 | -0.02 | 0.05 | -0.02 | 0.07 | 7.56 | 0.37 |
| 0.01 | 839 | 2 | 59 | 2 | -0.02 | 0.03 | 0.05 | 0.03 | 7.70 | 0.24 |
| 0.88 | 836 | 3 | 66 | 3 | 0.03 | 0.03 | 0.05 | 0.04 | 7.88 | 0.32 |
| 1.85 | 840 | 3 | 71 | 4 | 0.08 | 0.04 | -0.01 | 0.04 | 7.20 | 0.37 |
| 4.97 | 848 | 4 | 52 | 5 | -0.07 | 0.06 | 0.02 | 0.07 | 7.15 | 0.38 |
| 6.68 | 853 | 4 | 47 | 6 | 0.00 | 0.00 | 0.00 | 0.00 | 7.24 | 0.61 |
| 11.63 | 851 | 6 | 54 | 8 | 0.00 | 0.00 | 0.00 | 0.00 | 7.15 | 0.62 |