A&A 405, 409-414 (2003)
DOI: 10.1051/0004-6361:20030511
Cosmological parameter estimation in the quintessence paradigm
M. Douspis1,2 - A. Riazuelo3
- Y. Zolnierowski1,4,5 - A. Blanchard1
1 - Laboratoire d'Astrophysique de l'Observatoire Midi-Pyrénées,
14 avenue E. Belin, 31400 Toulouse, France
2 -
Nuclear and Astrophysics Laboratory, Keble Road, Oxford, OX1 3RH,
UK
3 -
Service de Physique Théorique, CEA/DSM/SPhT, Unité de recherche
associée au CNRS, CEA/Saclay, 91191 Gif-sur-Yvette Cedex, France
4 -
L.A.P.P., IN2P3-CNRS, BP 110, 74941 Annecy-le-Vieux Cedex, France
5 -
Université de Savoie, BP 1104, 73011 Chambéry Cedex, France
Received 6 December 2002 / Accepted 21 March 2003
Abstract
We present cosmological parameter constraints on flat
cosmologies dominated by dark energy using various cosmological data
including the recent Archeops angular power spectrum measurements. A
likelihood analysis of the existing Cosmic Microwave Background data
shows that in the absence of further prior, dark energy is not
required. This comes from the fact that degeneracies exist among the
various cosmological parameters constrained by the Cosmic Microwave
Background. We found that there is a degeneracy in a combination of
the Hubble parameter H0 and of the dark energy equation of state
parameter
 ,
but that
,
but that
 is not correlated with the
primordial index n of scalar fluctuations and the baryon content
is not correlated with the
primordial index n of scalar fluctuations and the baryon content
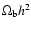 .
The preferred primordial index is
.
The preferred primordial index is
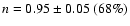 and baryon content
and baryon content
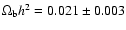 .
Adding constraints on the amplitude of matter fluctuations
on small scales,
.
Adding constraints on the amplitude of matter fluctuations
on small scales, 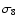 ,
obtained from clusters abundance or weak
lensing data may allow degenaracies to be broken, although present-day
systematic uncertainties do not allow for firm conclusions as
yet. Further addition of the Hubble Space Telescope measurements of
the local distance scale and of the high redshift supernovae data
allow one to obtain tight constraints. When these constraints are
combined we find that the amount of dark energy is
0.7+0.10-0.07 (
,
obtained from clusters abundance or weak
lensing data may allow degenaracies to be broken, although present-day
systematic uncertainties do not allow for firm conclusions as
yet. Further addition of the Hubble Space Telescope measurements of
the local distance scale and of the high redshift supernovae data
allow one to obtain tight constraints. When these constraints are
combined we find that the amount of dark energy is
0.7+0.10-0.07 (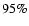 C.L.) and that its equation of state is
very close to those of the vacuum:
C.L.) and that its equation of state is
very close to those of the vacuum:
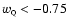 (
(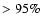 C.L.). In no case do we find that quintessence is prefered over the
classical cosmological constant, although robust data on
C.L.). In no case do we find that quintessence is prefered over the
classical cosmological constant, although robust data on 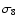 might
rapidly shed light on this important issue.
might
rapidly shed light on this important issue.
Key words: cosmology:
cosmic microwave background - cosmology: cosmological parameters
The determination of cosmological parameters has always been a central
question in cosmology. In this respect the measurements of the
Cosmological Microwave Background (CMB) anisotropies on degree angular
scales has brought one of the most spectacular results in the field:
the flatness of the spatial geometry of the universe, implying that
its density is close to the critical density. Although evidence for
the existence of non-baryonic dark matter has strongly gained in
robustness during the last twenty years, observations clearly favor a
relatively low matter content somewhere between 20 and 50% of the
critical density, thus indicating that the dominant form of the
density of the universe is in an unclustered form.
Furthermore, the
observations of distant supernovae, at cosmological distances, provide
direct evidence for an accelerating universe, which is naturally
explained by the gravitational domination of a component with a
relatively large negative pressure,
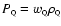 with
with
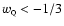 .
The cosmological constant
.
The cosmological constant 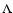 (for
which
(for
which
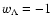 )
is historically the first possibility which
was introduced and satisfies this requirement. However, the presence
of a non-zero cosmological constant is a huge problem in physics: (i)
quantum field theory predicts that
)
is historically the first possibility which
was introduced and satisfies this requirement. However, the presence
of a non-zero cosmological constant is a huge problem in physics: (i)
quantum field theory predicts that 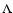 should be the sum of a
number of enormous contributions, so in order to avoid a cosmological
catastrophe, it is usually assumed that a yet unknown mechanism
produces a cancelation between all these contributions; (ii) it is
difficult to think of a mechanism which puts
should be the sum of a
number of enormous contributions, so in order to avoid a cosmological
catastrophe, it is usually assumed that a yet unknown mechanism
produces a cancelation between all these contributions; (ii) it is
difficult to think of a mechanism which puts 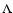 to 0 exactly,
but it is even more difficult to find a mechanism which gives
to 0 exactly,
but it is even more difficult to find a mechanism which gives
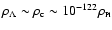 ,
as the
supernovae observations suggest. (Where
,
as the
supernovae observations suggest. (Where
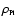 and
and
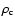 are the Planck energy density and the critical density today
respectively.) For this reason the concept of quintessence, a scalar
field with negative pressure, has recently been proposed as a possible
alternative to a cosmological constant.
are the Planck energy density and the critical density today
respectively.) For this reason the concept of quintessence, a scalar
field with negative pressure, has recently been proposed as a possible
alternative to a cosmological constant.
In this paper we briefly describe the quintessence paradigm and its
effect on some observable quantities. We then summarise the different
sets of data and methods used to constrain cosmological parameters. We
then conclude with our results on quintessence and cosmological
parameters.
The idea of quintessence was proposed in order to allow for the
presence of a non-zero dark energy - as suggested by observations
- without being confronted by the dramatic fine-tuning problem of
the cosmological constant. Indeed, one still assumes that an unknown
mechanism puts the bare cosmological constant is zero, and the
smallness of the dark energy has a dynamical origin, coming from a
scalar field 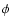 which has not yet reached the minimum of its
potential
which has not yet reached the minimum of its
potential 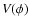 .
.
A large number of quintessence models were already considered in the
literature. Historically, the first proposed quintessence model had an
inverse power law potential,
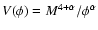 (Ratra & Peebles 1988; Wetterich 1988; Caldwell
et al. 1998), where the exponent
(Ratra & Peebles 1988; Wetterich 1988; Caldwell
et al. 1998), where the exponent 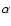 is positive and M is an energy scale fixed so that the scalar field has the correct
energy density today. This unusual shape, which can have some
motivations from particle physics (Binétruy 1999,
2000), insures that regardless of the initial conditions, the
field will reach a so-called "tracking regime'' (Steinhardt et al.
1999), in which its pressure and energy density tend to a
constant ratio given by
is positive and M is an energy scale fixed so that the scalar field has the correct
energy density today. This unusual shape, which can have some
motivations from particle physics (Binétruy 1999,
2000), insures that regardless of the initial conditions, the
field will reach a so-called "tracking regime'' (Steinhardt et al.
1999), in which its pressure and energy density tend to a
constant ratio given by
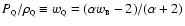 ,
where
,
where
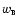 is the pressure
to energy density ratio of the other background matter fluids
(photons, neutrinos, baryons, and cold dark matter). Moreover, since
is the pressure
to energy density ratio of the other background matter fluids
(photons, neutrinos, baryons, and cold dark matter). Moreover, since
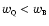 in this regime, the quintessence energy density
decreases more slowly than that of the background fluids and
ultimately the quintessence field will become dominant. When this
occurs, i.e., when its density parameter reaches
in this regime, the quintessence energy density
decreases more slowly than that of the background fluids and
ultimately the quintessence field will become dominant. When this
occurs, i.e., when its density parameter reaches
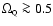 ,
the field slows down in its potential, and
asymptotically reaches
,
the field slows down in its potential, and
asymptotically reaches
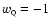 (Steinhardt
et al. 1999). The rate at which one goes from the tracking
regime to the cosmological regime is usually quite slow, so that
unless
(Steinhardt
et al. 1999). The rate at which one goes from the tracking
regime to the cosmological regime is usually quite slow, so that
unless
 is already close to - 1 in the tracking regime, it
will still be significantly different from - 1 when
is already close to - 1 in the tracking regime, it
will still be significantly different from - 1 when
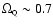 .
For example, if
.
For example, if
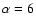 ,
in which case
,
in which case
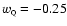 in the tracking regime during the matter-dominated era, one has
in the tracking regime during the matter-dominated era, one has
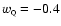 today if
today if
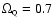 .
This feature leaves
open the hope of distinguishing a quintessence field from a
cosmological constant.
.
This feature leaves
open the hope of distinguishing a quintessence field from a
cosmological constant.
The effect of a quintessence field on CMB anisotropies is twofold
(Brax et al. 2000). First, when the quintessence field
becomes dominant, it modifies the expansion rate of the universe. This
translates into a modification of the angular distance vs. redshift
relation, and hence a shift in the peak structure of the CMB
anisotropies power spectrum, the 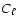 's, for
's, for
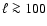 .
Second, the gravitational potentials decay at late time as the
universe is no longer matter-dominated. This produces a so-called
integrated Sachs-Wolfe effect and modifies the
.
Second, the gravitational potentials decay at late time as the
universe is no longer matter-dominated. This produces a so-called
integrated Sachs-Wolfe effect and modifies the 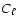 spectrum at
low multipoles (
spectrum at
low multipoles (
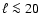 )
as a consequence of the fact that
photons exchange energy with time-varying gravitational potentials.
Both of these effects are also present with a cosmological constant,
but they differ quantitatively with a quintessence field: the shift in
the peak position is smaller, whereas the integrated Sachs-Wolfe
effect can be very different (Caldwell et al. 1998).
)
as a consequence of the fact that
photons exchange energy with time-varying gravitational potentials.
Both of these effects are also present with a cosmological constant,
but they differ quantitatively with a quintessence field: the shift in
the peak position is smaller, whereas the integrated Sachs-Wolfe
effect can be very different (Caldwell et al. 1998).
Most of the CMB experiments do not cover a large fraction of the
sky. On the contrary, the new Archeops data (Benoît et al.
2002; Benoît et al. 2003a) are extremely
precise around
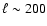 improving by a factor of two the
precision measurements on the location of the first Doppler peak
(Benoît et al. 2003b), whereas at larger angular scales
(low
improving by a factor of two the
precision measurements on the location of the first Doppler peak
(Benoît et al. 2003b), whereas at larger angular scales
(low 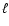 )
the COBE data are limited by a large cosmic variance
(Tegmark 1996). Therefore we can hope to be able to
contrain the quintessence parameters through their influence on the
position of the first Doppler peak rather than through the integrated
Sachs-Wolfe effect. It is well-known that the position of the first
peak is primarily sensitive to the curvature but also to several other
cosmological parameters. It is therefore important to investigate a
wide space of parameters in order to constraint the possible existence
of quintessence in a robust way.
)
the COBE data are limited by a large cosmic variance
(Tegmark 1996). Therefore we can hope to be able to
contrain the quintessence parameters through their influence on the
position of the first Doppler peak rather than through the integrated
Sachs-Wolfe effect. It is well-known that the position of the first
peak is primarily sensitive to the curvature but also to several other
cosmological parameters. It is therefore important to investigate a
wide space of parameters in order to constraint the possible existence
of quintessence in a robust way.
Finally, let us add that quintessence also modifies significantly the
matter power spectrum: as for the cosmological constant, matter
fluctuations stop growing at the onset of quintessence domination.
This has an influence on the normalization of the matter power
spectrum on small scales, 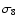 .
This effect of
.
This effect of
 can be
understood as follows: as long as
can be
understood as follows: as long as
 is not too close to 0,
one can roughly consider that the universe has experienced two
distinct epochs since recombination: a first (usual) one where it was
matter-dominated, and a second one where it is
quintessence-dominated. The transition occurs when
is not too close to 0,
one can roughly consider that the universe has experienced two
distinct epochs since recombination: a first (usual) one where it was
matter-dominated, and a second one where it is
quintessence-dominated. The transition occurs when
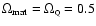 .
If we suppose that
.
If we suppose that
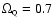 today,
then the transition epoch occured at a redshift of
today,
then the transition epoch occured at a redshift of
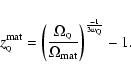 |
(1) |
For
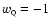 (cosmological constant case), one has
(cosmological constant case), one has
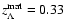 ,
whereas for
,
whereas for
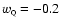 ,
this gives
,
this gives
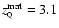 .
If we suppose that perturbations grow as the
scale factor before the transition and stop growing immediately
afterward, then this corresponds to a reduction of
.
If we suppose that perturbations grow as the
scale factor before the transition and stop growing immediately
afterward, then this corresponds to a reduction of
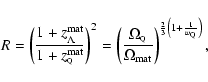 |
(2) |
in the matter power spectrum as compared to the cosmological constant
case. In practice, several factors modify this amount, such as the
fact the the matter perturbation still grow (although slowly) in the
quintessence-dominated era, but the above analysis illustrates the
dramatic change that quintessence can trigger in the matter power
spectrum (see also Benabed & Bernardeau 2001). When
 ,
the situation is even more dramatic as matter never
dominates. In order to understand the value of
,
the situation is even more dramatic as matter never
dominates. In order to understand the value of  ,
one has to
compute the growth of dark matter perturbations when there is a
mixture of matter and quintessence with identical equation of
state. Neglecting the quintessence fluctuations (which are never
subject to any instability), the Jeans equation is rewritten as
,
one has to
compute the growth of dark matter perturbations when there is a
mixture of matter and quintessence with identical equation of
state. Neglecting the quintessence fluctuations (which are never
subject to any instability), the Jeans equation is rewritten as
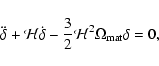 |
(3) |
where 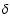 is the matter perturbation density constrast, an
overdot denotes a derivative with respect to conformal time (defined
by
is the matter perturbation density constrast, an
overdot denotes a derivative with respect to conformal time (defined
by
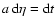 ,
where a is the scale factor and t is
the cosmic time), and
,
where a is the scale factor and t is
the cosmic time), and
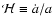 .
The only
difference with the usual matter-dominated case is that we do not have
.
The only
difference with the usual matter-dominated case is that we do not have
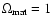 in the above equation. In the matter-dominated era,
in the above equation. In the matter-dominated era,
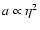 ,
so that
,
so that
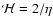 ,
and
,
and
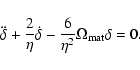 |
(4) |
When
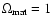 ,
one gets the usual result that the growing
mode goes as
,
one gets the usual result that the growing
mode goes as
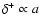 .
If we now suppose that
.
If we now suppose that
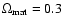 ,
then the growing mode goes as
,
then the growing mode goes as
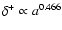 .
If
this regime lasts for several orders of magnitude in redshift, then
this represents an enormous reduction in the matter power spectrum, of
around
.
If
this regime lasts for several orders of magnitude in redshift, then
this represents an enormous reduction in the matter power spectrum, of
around
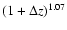 ,
where
,
where 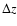 represent the
duration of this regime. This effect will imply that
represent the
duration of this regime. This effect will imply that 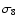 is
drastically reduced when one goes from
is
drastically reduced when one goes from
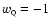 to
to
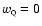 .
In order to illustrate this point we have computed the amplitude
of matter fluctuations
.
In order to illustrate this point we have computed the amplitude
of matter fluctuations 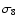 for a family of models which have the
same same cosmological parameters but the equation of state
for a family of models which have the
same same cosmological parameters but the equation of state
 (Fig. 1). As one can see,
(Fig. 1). As one can see, 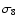 varies dramatically with
varies dramatically with
 and is therefore a very useful quantity to take into
account in order to constrain quintessence.
and is therefore a very useful quantity to take into
account in order to constrain quintessence.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3380.f1}
\end{figure}](/articles/aa/full/2003/26/aa3380/Timg59.gif) |
Figure 1:
The amplitude of matter fluctuations 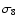 as a
function of a constant
as a
function of a constant
 in cosmological models with
in cosmological models with
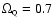 , ,
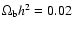 ,
H0 = 66.5, n =
1, and ,
H0 = 66.5, n =
1, and
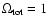 ,
with amplitude normalized to match the COBE
data. ,
with amplitude normalized to match the COBE
data. |
| Open with DEXTER |
In the following, we make use of the most recent CMB data available as
well as data on other relevant cosmological quantities. With these, we
examine the constraints that can be set on the amount of quintessence
present in the universe. We assume Gaussian adiabatic fluctuations and
a flat spatial geometry. Negligible amounts of gravitational waves are
assumed. This contribution has little impact on the position of the
peak, but modifies significantly the relative power between low and
large 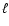 .
Identically, a reionisation effect and a possible hot
dark matter component are neglected. We make the assumption that
.
Identically, a reionisation effect and a possible hot
dark matter component are neglected. We make the assumption that
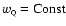 throughout all the epochs of interest. This
assumption is unjustified in realistic quintessence models as one
expects
throughout all the epochs of interest. This
assumption is unjustified in realistic quintessence models as one
expects
 to have varied at the radiation to matter
transition and to be decreasing today. However, if we want to study
the influence of the quintessence field on the position of the Doppler
peaks of the CMB anisotropies, then this is sufficent, and the
constant
to have varied at the radiation to matter
transition and to be decreasing today. However, if we want to study
the influence of the quintessence field on the position of the Doppler
peaks of the CMB anisotropies, then this is sufficent, and the
constant
 has to be seen as some "average'' of a dynamical
has to be seen as some "average'' of a dynamical
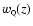 arising in a quintessence scenario.
arising in a quintessence scenario.
In order to use CMB data, we first reconstruct the likelihood function
of the various experiments.
We follow the technique developped in Bartlett et al. (2000),
and used in Douspis et al. (2001) and Benoît et al.
(2003b), by constructing a large 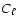 power spectra
database. We investigate six cosmological parameters assuming flat
cosmology (
power spectra
database. We investigate six cosmological parameters assuming flat
cosmology (
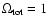 ). The density of the universe is parametrised by
the baryon contribution,
). The density of the universe is parametrised by
the baryon contribution,
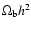 ,
and the dark energy,
,
and the dark energy,
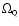 ,
for
which we study various values of its pressure-energy density ratio,
,
for
which we study various values of its pressure-energy density ratio,
 .
.
The Hubble parameter, H0, the spectral index, n, and the
normalisation of the spectra, parametrized in this work by 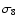 ,
are
the remaining free parameters. Table 1 describes the
corresponding gridding used for the database.
,
are
the remaining free parameters. Table 1 describes the
corresponding gridding used for the database.
We proceed by estimating cosmological parameters from the likelihood
functions reconstructed as described in Benoît et al.
(2003b). We compute the value of the likelihood considering
the actual band powers dataset of the COBE, BOOMERanG, DASI, MAXIMA,
VSA, CBI, Archeops experiments (Tegmark 1996; Netterfield
et al. 2002; Halverson et al. 2002; Lee et al.
2001; Scott et al. 2002; Pearson et al.
2002; Benoît et al. 2003a) on each model of
our grid. In our approach, the best model is estimated as being that
for which the likelihood is maximal
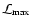 ,
while the 68%
(resp. 95%) 1-parameter interval corresponds to
,
while the 68%
(resp. 95%) 1-parameter interval corresponds to
![$-2 \ln~({\cal L} /
{\cal L}_{\rm max}) \in [0, 1]$](/articles/aa/full/2003/26/aa3380/img64.gif) (resp.
(resp.
![$-2 \ln~({\cal L} / {\cal L}_{\rm max})
\in [0, 4]$](/articles/aa/full/2003/26/aa3380/img65.gif) )
and the 68% (resp. 95%) 2-parameters interval
corresponds to
)
and the 68% (resp. 95%) 2-parameters interval
corresponds to
![$-2 \ln~({\cal L} / {\cal L}_{\rm max}) \in [0, 2.3]$](/articles/aa/full/2003/26/aa3380/img66.gif) (resp.
(resp.
![$-2 \ln~({\cal L} / {\cal L}_{\rm max}) \in [0, 6.18]$](/articles/aa/full/2003/26/aa3380/img67.gif) ). The likelihoods
shown in the following are already marginalized (by maximisation) over
the calibration uncertainties and the amplitude. The results are
presented as 2D contour plots, showing in shades of blue the regions
where the likelihood function for a combination of any two parameters
drops to the levels corresponding to 68%, 95%, and 99%
confidence regions. They would correspond to 1, 2, 3
). The likelihoods
shown in the following are already marginalized (by maximisation) over
the calibration uncertainties and the amplitude. The results are
presented as 2D contour plots, showing in shades of blue the regions
where the likelihood function for a combination of any two parameters
drops to the levels corresponding to 68%, 95%, and 99%
confidence regions. They would correspond to 1, 2, 3 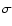 ,
respectively if the likelihood function were Gaussian. Dashed red
contours mark the limits to be projected if confidence intervals are
sought for any one of the parameters. To calculate either 1 or 2D
confidence intervals, the likelihood function is maximized over the
remaining parameters.
,
respectively if the likelihood function were Gaussian. Dashed red
contours mark the limits to be projected if confidence intervals are
sought for any one of the parameters. To calculate either 1 or 2D
confidence intervals, the likelihood function is maximized over the
remaining parameters.
Table 1:
Grid of explored cosmological parameters; for H0 we adopt
a log-periodic binning,
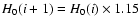 .
.
In order to include other data of cosmological relevance, the
corresponding additional likelihood have to be evaluated.
An interesting useful additional constraint to add is that obtained
from the amplitude of matter fluctuations on small scales: present day
clusters data allow one to constrain
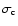 ,
related to
,
related to 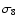 to
a high accuracy of the order of 5% (Blanchard et al.
2000). A similar constraint can be obtained from weak lensing
measurements (Bacon et al. 2000; van Waerbeke et al.
2002). However, significant differences among similar analyses
have appeared in recent works based on clusters as well as on weak
lensing measurements (Jarvis et al. 2003; Brown et al.
2003; Hamana et al. 2002). We have therefore chosen
to use two recent constraints, the differences of which will allow us
to investigate a realistic range of systematic uncertainties. First we
consider a constraint leading to high values of
to
a high accuracy of the order of 5% (Blanchard et al.
2000). A similar constraint can be obtained from weak lensing
measurements (Bacon et al. 2000; van Waerbeke et al.
2002). However, significant differences among similar analyses
have appeared in recent works based on clusters as well as on weak
lensing measurements (Jarvis et al. 2003; Brown et al.
2003; Hamana et al. 2002). We have therefore chosen
to use two recent constraints, the differences of which will allow us
to investigate a realistic range of systematic uncertainties. First we
consider a constraint leading to high values of 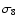 (high
(high 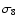 hereafter), in agreement with Pierpaoli et al. (2001):
hereafter), in agreement with Pierpaoli et al. (2001):
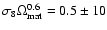 % (68% C.L.). Then, new estimations
from Seljak et al. (2002), Viana et al. (2002),
Reiprich et al. (2002), Hoekstra et al. (2002) leading
to lower values, are considered by taking
% (68% C.L.). Then, new estimations
from Seljak et al. (2002), Viana et al. (2002),
Reiprich et al. (2002), Hoekstra et al. (2002) leading
to lower values, are considered by taking
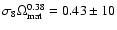 % (68% C.L.), hereafter low
% (68% C.L.), hereafter low 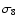 .
The latter error bar
estimates encompass the three above low normalization measurements of
.
The latter error bar
estimates encompass the three above low normalization measurements of 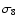 .
.
We also use the recent determination of the Hubble parameter from the
Hubble Space Telescope (HST) Key Project (Freedman et al.
2001):
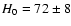 (68% C.L.), assuming Gaussian
uncertainty.
(68% C.L.), assuming Gaussian
uncertainty.
For the distant supernovae constraints we compute the likelihood as
follows. The magnitude-redshift relation of the supernovae is given
by the following relation
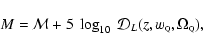 |
(5) |
where M is the observed magnitude and
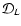 and
and 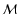 are respectively the "Hubble-parameter-free'' luminosity-distance and
the "Hubble-parameter-free'' absolute magnitude at the maximum of the
supernova.
are respectively the "Hubble-parameter-free'' luminosity-distance and
the "Hubble-parameter-free'' absolute magnitude at the maximum of the
supernova.
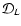 is a function of redshift of the supernova, z, and of the cosmological parameters
is a function of redshift of the supernova, z, and of the cosmological parameters
 and
and
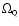 .
In the
case of a flat universe with
.
In the
case of a flat universe with
 as the pressure to energy
density ratio of the quintessence field, the
as the pressure to energy
density ratio of the quintessence field, the
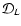 function is
given by
function is
given by
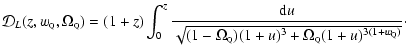 |
|
|
(6) |
With the sample of supernovae from Perlmutter et al.
(1999), we construct the likelihood
 with
the following procedure:
with
the following procedure:
![\begin{displaymath}{\cal L}_{\rm SN}
= C \exp \left[
\sum_i \left( - \frac{( M...
...rm\scriptscriptstyle Q}))^2}
{2 \sigma^2_i} \right) \right] ,
\end{displaymath}](/articles/aa/full/2003/26/aa3380/img80.gif) |
(7) |
where C is an arbitrary constant. We take for measured magnitude
 and uncertainty
and uncertainty 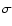 the B-band peak magnitude and the
total uncertainty of the supernovae from Perlmutter et al.
(1999). At each point of the two parameters grid,
the B-band peak magnitude and the
total uncertainty of the supernovae from Perlmutter et al.
(1999). At each point of the two parameters grid,
 and
and
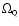 is associated a likelihood value obtained by
maximising it over the absolute magnitude
is associated a likelihood value obtained by
maximising it over the absolute magnitude 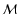 .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3380.f2}\end{figure}](/articles/aa/full/2003/26/aa3380/Timg82.gif) |
Figure 2:
Present CMB dataset likelihood contours in the quintessence
paradigm. The sharpness of contours at
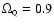 is due to grid
effect.
is due to grid
effect. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.8cm,clip]{3380.f3}
\end{figure}](/articles/aa/full/2003/26/aa3380/Timg83.gif) |
Figure 3:
Likelihood contours with combination of CMB and priors. From
left to right, panels show (i) colored contours corresponding to the
combination CMB + 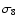 (high), wiht overplotted SN contours; (ii)
colored contours corresponding to the combination CMB +
(high), wiht overplotted SN contours; (ii)
colored contours corresponding to the combination CMB + 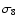 (low),
with overplotted SN contours; (iii) colored contours corresponding to
the combination CMB +
(low),
with overplotted SN contours; (iii) colored contours corresponding to
the combination CMB + 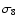 (low) + HST, with overplotted SN
contours; (iv) colored contours corresponding to the combination CMB +
(low) + HST, with overplotted SN
contours; (iv) colored contours corresponding to the combination CMB +
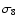 (low) + HST + SN.
(low) + HST + SN. |
| Open with DEXTER |
Constraints given by the CMB on some of our investigated parameters
are shown in Fig. 2. Considering only CMB constraints
leads to degeneracies between parameters. Figure 2 shows
the case of two parameters, n and
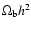 ,
which are not affected by
the assumed equation of state of the dark energy. Their prefered
values and error bars are
,
which are not affected by
the assumed equation of state of the dark energy. Their prefered
values and error bars are
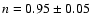 and
and
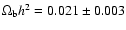 (68% C.L.). Using CMB alone leaves the
2-parameter space (
(68% C.L.). Using CMB alone leaves the
2-parameter space (
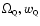 )
almost unconstrained. Finally, 2D
diagrams
)
almost unconstrained. Finally, 2D
diagrams
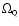 vs. H0 or
vs. H0 or
 vs. H0 show a significant
level of correlation, but with degeneracies. This is illustrated by
the plot
vs. H0 show a significant
level of correlation, but with degeneracies. This is illustrated by
the plot
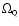 vs. H0 shown in Fig. 2. In our
analysis, we found that with the improvement of CMB data obtained by
the addition of Archeops band powers reduces appreciably the contours
of constraints on the quintessence parameters as well as on
cosmological parameters because the position and the amplitude of the
first acoustic peak are better determined, but still does not allow to
break the degeneracies.
vs. H0 shown in Fig. 2. In our
analysis, we found that with the improvement of CMB data obtained by
the addition of Archeops band powers reduces appreciably the contours
of constraints on the quintessence parameters as well as on
cosmological parameters because the position and the amplitude of the
first acoustic peak are better determined, but still does not allow to
break the degeneracies.
As cluster abundance observations lead to a strong constraint on the
normalization of the matter power spectrum, and 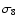 is rather
sensitive to the changing the equation of state, it is natural to
expect that this constraint in combination with constraints from
is rather
sensitive to the changing the equation of state, it is natural to
expect that this constraint in combination with constraints from
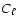 will lead to tight constraints on quintessence scenarios.
Figure 3 (left panels) shows the combination of CMB data with
the two
will lead to tight constraints on quintessence scenarios.
Figure 3 (left panels) shows the combination of CMB data with
the two
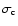 priors described previously. As one can see,
constraints on the amplitude of matter fluctuations on small scales
has the potential to break the degeneracies between
priors described previously. As one can see,
constraints on the amplitude of matter fluctuations on small scales
has the potential to break the degeneracies between
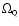 and
and
 .
Only a band-shaped region of the plane is not
excluded. Furthermore, combinations with different priors lead to
different likelihood contours, due to the strong effect of the
equation of state on
.
Only a band-shaped region of the plane is not
excluded. Furthermore, combinations with different priors lead to
different likelihood contours, due to the strong effect of the
equation of state on 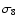 emphasized in Sect. 2. More
specifically, we find that the CMB, combined with the high
normalization leads to a prefered region which is marginally
consistent with the constraints given by high redshift supernovae
(overplotted black lines in Fig. 3). The "concordance
model'' (
emphasized in Sect. 2. More
specifically, we find that the CMB, combined with the high
normalization leads to a prefered region which is marginally
consistent with the constraints given by high redshift supernovae
(overplotted black lines in Fig. 3). The "concordance
model'' (
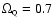 ,
,
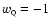 )
lies on the 99%
C.L. contours, and defines the two dataset as inconsistent. The best
model appears then to have
)
lies on the 99%
C.L. contours, and defines the two dataset as inconsistent. The best
model appears then to have
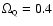 ,
,
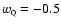 ,
which is
itself outside the 99% confidence region of the supernovae
constraints. The combination of CMB with low normalization leads, on
the other hand, to likelihood contours in agreement with those of
supernovae and HST key project determination of H0.
,
which is
itself outside the 99% confidence region of the supernovae
constraints. The combination of CMB with low normalization leads, on
the other hand, to likelihood contours in agreement with those of
supernovae and HST key project determination of H0.
Due to the form of the joint
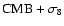 (high or low) contours, a
combination with the HST constraints is expected to give stronger
constraints on both
(high or low) contours, a
combination with the HST constraints is expected to give stronger
constraints on both
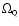 and
and
 .
The corresponding likelihood
contours of Fig. 3 (middle right panel) show that
quintessence is not prefered over classical cosmological constant even
if the degeneracy is not totally broken:
.
The corresponding likelihood
contours of Fig. 3 (middle right panel) show that
quintessence is not prefered over classical cosmological constant even
if the degeneracy is not totally broken:
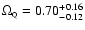 ,
,
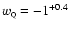 (95% C.L.).
(95% C.L.).
In order to break the degeneracy, it is clearly necessary to consider
the additional information on the angular distance coming from distant
supernovae. Considering a flat cosmology, the information on the
luminosity of the supernovae can be expressed in term of constraints
on the dark energy density and equation of state. Prefered values are
consistent with a cosmological constant, and the likelihood contours
are almost perpendicular to those of CMB, as shown in
Fig. 3. Combining all the priors finally allows to put
strong constraints on both quintessence parameters (Fig. 3,
rightmost panel):
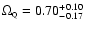 ,
,
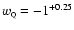 (95% C.L.) and finally breaks the
(95% C.L.) and finally breaks the
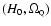 degeneracy, see Fig. 4.
degeneracy, see Fig. 4.
As a main result, it appears that the classical 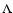 CDM scenario
is still prefered and given the priors we used there is no need for
quintessence to reproduce the present data, although quintessence
models with low
CDM scenario
is still prefered and given the priors we used there is no need for
quintessence to reproduce the present data, although quintessence
models with low
 are still viable, and that good fits to the
data can also be found for models with
are still viable, and that good fits to the
data can also be found for models with
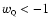 (Melchiorri
et al. 2002)
(Melchiorri
et al. 2002)![[*]](/icons/foot_motif.gif) . However, those correspond to rather
unusual quintessence models.
. However, those correspond to rather
unusual quintessence models.
Going back to typical quintessence models, finding only low values of
 raises some interesting points. If we consider a pure
inverse power law potential, having
raises some interesting points. If we consider a pure
inverse power law potential, having
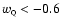 when
when
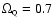 implies a low value of the exponent
implies a low value of the exponent 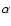 (if
the slope of the potential is too steep, the field does not stop
rapidly when it starts dominating, and
(if
the slope of the potential is too steep, the field does not stop
rapidly when it starts dominating, and
 is too large). This
translates into an annoyingly low value of the energy scale Marising in the potential, since one has
is too large). This
translates into an annoyingly low value of the energy scale Marising in the potential, since one has
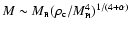 (Brax et al. 2000). For
example, in order to have
(Brax et al. 2000). For
example, in order to have
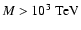 ,
one needs
,
one needs
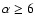 ,
whereas data favor
,
whereas data favor
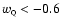 ,
which corresponds to
,
which corresponds to
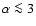 ,
or
,
or
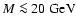 .
There are of
course several quintessence models which predict a lower
.
There are of
course several quintessence models which predict a lower
 .
For example, the SUGRA potential found by Brax & Martin
(1999), is given by
.
For example, the SUGRA potential found by Brax & Martin
(1999), is given by
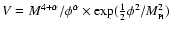 .
The exponential correction
comes from supergravity considerations and insures that the potential
has a local minimum which is almost reached by the field today. For
example, for
.
The exponential correction
comes from supergravity considerations and insures that the potential
has a local minimum which is almost reached by the field today. For
example, for
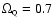 ,
one has
,
one has
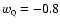 ,
almost
independently of
,
almost
independently of 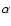 .
This illustrates the fact that it is still
difficult to distinguish some quintessence models from a cosmological
constant with the present state of available data. On the other hand,
the data already allow one to exclude a large number of quintessence
models, among which the simplest.
.
This illustrates the fact that it is still
difficult to distinguish some quintessence models from a cosmological
constant with the present state of available data. On the other hand,
the data already allow one to exclude a large number of quintessence
models, among which the simplest.
We have studied the constraints that can be obtained on cosmological
parameters within the quintessence paradigm by using various
combinations of observational data. For simplicity, only models with
constant
 were examined: given the accuracy of existing
data, we believe this to be a sufficient approximation. For similar
reasons, we neglected possible reionization or non-zero gravitational
wave contributions. This approach has the advantage to helping us to
understand whether quintessence models are favored or not over a
classical cosmological constant, while constraints on more specific
scenarios have to be investigated directly one by one (Douspis et al.
2003). Our analysis method has been to
investigate contours in 2D parameters space. Such an approach allows
one to examine possible degeneracies among parameters which are not
easy to identify when constraints are formulated in term of a single
parameter. For instance, we found that, despite the high precision
data obtained by Archeops, CMB data alone does not require the
existence of a non-zero contribution of quintessence, because of the
degeneracy with the Hubble parameter: in practice CMB data leaves a
large fraction of the
were examined: given the accuracy of existing
data, we believe this to be a sufficient approximation. For similar
reasons, we neglected possible reionization or non-zero gravitational
wave contributions. This approach has the advantage to helping us to
understand whether quintessence models are favored or not over a
classical cosmological constant, while constraints on more specific
scenarios have to be investigated directly one by one (Douspis et al.
2003). Our analysis method has been to
investigate contours in 2D parameters space. Such an approach allows
one to examine possible degeneracies among parameters which are not
easy to identify when constraints are formulated in term of a single
parameter. For instance, we found that, despite the high precision
data obtained by Archeops, CMB data alone does not require the
existence of a non-zero contribution of quintessence, because of the
degeneracy with the Hubble parameter: in practice CMB data leaves a
large fraction of the
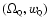 plane unconstrained,
while only a restricted region of the
plane unconstrained,
while only a restricted region of the
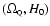 plane is
allowed. On the contrary, we found that almost no correlation exists
with the baryonic content
plane is
allowed. On the contrary, we found that almost no correlation exists
with the baryonic content
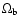 nor the primordial index n. In order to restrict the parameter space of allowed models, we
have applied several different constraints. Interestingly, we found
that the amplitude of the dark matter fluctuations, as measured by
clusters abundance or large scale weak lensing data can potentially
help to break existing degeneracies, although existing uncertainties,
mainly systematics in nature, do not allow for a firm conclusion as
yet. Clearly this will be an important check of consistency in the
future. We have then added constraints from supernovae data as well as
HST estimation of the Hubble parameter in order to break existing
degeneracies. This allows us to infer very tight constraints on the
possible range of equation of state of the dark energy. Probably the
most remarkable result is that no preference for quintessence emerges
from existing CMB data although accurate measurement of the amplitude
of matter fluctuations on scale of
8 h-1 Mpc may change this picture.
nor the primordial index n. In order to restrict the parameter space of allowed models, we
have applied several different constraints. Interestingly, we found
that the amplitude of the dark matter fluctuations, as measured by
clusters abundance or large scale weak lensing data can potentially
help to break existing degeneracies, although existing uncertainties,
mainly systematics in nature, do not allow for a firm conclusion as
yet. Clearly this will be an important check of consistency in the
future. We have then added constraints from supernovae data as well as
HST estimation of the Hubble parameter in order to break existing
degeneracies. This allows us to infer very tight constraints on the
possible range of equation of state of the dark energy. Probably the
most remarkable result is that no preference for quintessence emerges
from existing CMB data although accurate measurement of the amplitude
of matter fluctuations on scale of
8 h-1 Mpc may change this picture.
Acknowledgements
The authors acknowledge the use of the CAMB code (Lewis et al.
2000). M.D. is on a CMBNet fellowship and acknowledges Oxford
Astrophysics group computational facilities and the Archeops
collaboration. Y.Z. acknowledges support from the CNRS. This work
has greatly benefitted from discussions inside the Archeops
collaboration
- Bacon, D. J., Refregier, A. R., & Ellis, R. S. 2000, MNRAS, 318, 625
In the text
NASA ADS
- Bartlett, J. G., Douspis, M., Blanchard, A., &
Le Dour, M. 2000, A&AS, 146, 507
In the text
NASA ADS
- Benabed, K., & Bernardeau, F. 2001,
Phys. Rev. D, 64, 083501
In the text
- Benoît, A., Ade, P., Amblard, A.,
et al. (Archeops collaboration) 2002, Astropart. Phys., 17, 101
In the text
NASA ADS
- Benoît, A., Ade, P., Amblard, A.,
et al. (Archeops collaboration) 2003a, A&A, 399, L19
In the text
NASA ADS
- Benoît, A., Ade, P., Amblard, A.,
et al. (Archeops collaboration) 2003b, A&A,
399, L25
In the text
NASA ADS
- Binétruy, P. 1999, Phys. Rev. D, 60, 063502
In the text
- Binétruy, P. 2000, Int. J. Theor. Phys. 39,
1852
In the text
- Blanchard, A., Sadat, R., Bartlett, J., & Le
Dour, M. 2000, A&A, 362, 809
In the text
NASA ADS
- Brax, P., & Martin, J. 1999, Phys. Lett. B468 40
In the text
- Brax, P., Martin, J., & Riazuelo, A. 2000,
Phys. Rev. D, 62, 103505
In the text
- Brown, M. L., Taylor, A. N., Bacon, D. J.,
et al. 2003, MNRAS, 341, 100
In the text
NASA ADS
- Caldwell, R. R., Dave, R., & Steinhardt, P. 1998, Phys. Rev. Lett., 88, 1582
In the text
- Douspis, M., Blanchard, A., Sadat, R.,
Bartlett, J. G., & Le Dour, M. 2001, A&A, 379, 1
In the text
NASA ADS
- Douspis, M., Riazuelo, A., Blanchard, A.,
& Zolnierowski, Y. 2003, in preparation
In the text
- Freedman, W. L., Madore, B. F., Gibson,
B. K., et al. 2001, ApJ, 553, 47
In the text
NASA ADS
- Halverson, N. W., Leitch, E. M., Pryke, C.,
et al. 2002, MNRAS, 568, 38
In the text
- Hamana, T., Miyazaki, S., Shimasaku, K.,
et al. 2002, ApJ, submitted [astro-ph/0210450]
In the text
- Hoekstra, H., Yee, H., & Gladders, M. 2002,
ApJ, 577, 595
In the text
NASA ADS
- Jarvis, M., Bernstein, G., Jain, B., et al.
2003, AJ,
125, 1014
In the text
NASA ADS
- Lee, A. T., Ade, P., Balbi, A., et al. 2001,
ApJ, 561, L1
In the text
NASA ADS
- Lewis, A., Challinor, A., & Lasenby, A. 2000,
ApJ, 538, 473
In the text
NASA ADS
- Melchiorri, A., Mersini, L., Ödman, C. J.,
& Trodden, M. 2002 [astro-ph/0211522]
In the text
- Netterfield, C. B., Ade, P. A. R., Bock, J. J.,
et al. 2002, ApJ, 571, 604
In the text
NASA ADS
- Pearson, T. J., Mason, B. S., Readhead,
A. C. S., et al. 2002, ApJ, accepted [astro-ph/0205388]
In the text
- Perlmutter, S., Aldering, G., Goldhaber,
G., et al. 1999, ApJ, 517, 565; see also In the text
http://www-supernova.lbl.gov
NASA ADS
- Pierpaoli, E., Scott, D., & White, M. 2001,
MNRAS, 325, 77
In the text
NASA ADS
- Ratra, B., & Peebles, P. J. E. 1988, Phys.
Rev. D, 37, 3406
In the text
NASA ADS
- Reiprich, T. H., & Böhringer, H. 2002,
ApJ, 567, 716
In the text
NASA ADS
- Scott, P. F., Carreira, P., Cleary, K., et al.
2002, MNRAS, in press [astro-ph/0205380]
In the text
- Seljak, U. 2002, MNRAS,
337, 769
In the text
NASA ADS
- Steinhardt, P., Wang, L., & Zlatev, I. 1999,
Phys. Rev. D, 59, 123504
In the text
- Tegmark, M. 1996, ApJ, 464, L35
In the text
NASA ADS
- Van Waerbeke, L., Mellier, Y., Pelló, R., et al.
2002, A&A, 393, 369
In the text
NASA ADS
- Viana, P. T. P., Nichol, R. C., & Liddle,
A. R. 2002, ApJ, 569, L75
In the text
NASA ADS
- Wetterich, C. 1988, Nucl. Phys. B302, 668
In the text
NASA ADS
Copyright ESO 2003
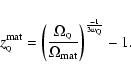
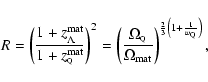
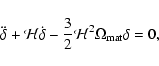
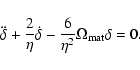
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3380.f1}
\end{figure}](/articles/aa/full/2003/26/aa3380/Timg59.gif)
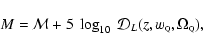
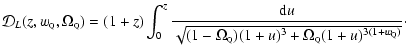
![\begin{displaymath}{\cal L}_{\rm SN}
= C \exp \left[
\sum_i \left( - \frac{( M...
...rm\scriptscriptstyle Q}))^2}
{2 \sigma^2_i} \right) \right] ,
\end{displaymath}](/articles/aa/full/2003/26/aa3380/img80.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3380.f2}\end{figure}](/articles/aa/full/2003/26/aa3380/Timg82.gif)
![\begin{figure}
\includegraphics[width=8.5cm,clip]{3380.f4}
\end{figure}](/articles/aa/full/2003/26/aa3380/Timg106.gif)