A&A 405, 165-174 (2003)
DOI: 10.1051/0004-6361:20030518

Ionization structure in the winds of B[e] supergiants

I. Ionization equilibrium calculations in a H plus He wind

M. Kraus - H. J. G. L. M. Lamers

Astronomical Institute, University of Utrecht, Princetonplein 5, 3584 CC Utrecht, The Netherlands

Received 11 October 2002 / Accepted 3 April 2003

Abstract
The non-spherically symmetric winds of B[e] supergiants are investigated. An empirical density distribution is chosen that accounts for the density concentrations and ratios derived from observations, and our model winds are assumed to contain only hydrogen and helium. We first calculate the approximate ionization radii for H and He and compare the results with the ionization fractions calculated from the more accurate ionization balance equations. We find that winds with a r-2 density distribution turn out to reach a constant ionization fraction as long as the wind density is low, i.e. in polar direction. For the high density equatorial regions, however, we find that the winds become neutral just above the stellar surface of the hot and massive B[e] supergiants forming a disk-like neutral region. In such a disk molecules and dust can form even very near the hot central star.

Key words: supergiants - stars: mass-loss - stars: winds, outflows - H II regions

1 Introduction

B[e] supergiants are massive and luminous post-main sequence stars with strong non-spherically symmetric winds induced probably due to the rapid rotation of the stars. Observations of dust and molecules indicate that there must exist some neutral regions near these stars that are shielded from the ionizing and dissociating stellar radiation field. The goal of this paper is to show that in the equatorial regions where the slow, high density wind forms a disk-like structure, hydrogen becomes neutral just above the stellar surface and can therefore perfectly shield the disk material to allow molecules and dust to be formed near the hot central star.

Photoionization of gas around hot stars is since long a well known process leading to the beautiful observable emission objects like H II regions and planetary nebulae. The central stars thereby ionize the material that has been blown away by the star itself in a more or less dense wind. The sizes of such ionization regions, also called the Strömgren spheres, can be calculated by balancing the number of ionizations by the number of recombinations and usually a very sharp outer edge of the ionized region is found. These calculations are normally performed for nebulae with a constant electron temperature and density (for an overview see Osterbrock 1989 and references therein).

O and B stars have a stellar wind which for a spherically symmetric and steady radial outflow leads to a v(r)-1r-2 wind density distribution. So the calculation of the ionization structure in these winds is more complicated than for a homogeneous cloud. In an early work by Drew (1985) a radiative ionization and thermal equilibrium model for the wind from P Cygni was calculated, and later on e.g. Pauldrach (1987), Drew (1989), MacFarlane et al. (1994), and Pauldrach et al. (1994) calculated in great detail the ionization structure in the spherically symmetric winds of hot luminous stars using the ionization balance equations. In addition, they solved the thermal equilibrium equations to calculate the electron temperature in the wind. For this, line cooling by collisionaly excited heavy elements is the most important cooling mechanism and the authors took a huge amount of different lines into account which results in an enormous set of equations that has to be solved.

In this paper we calculate the ionization structure in the non-spherically symmetric winds of B[e] supergiants. For simplicity, these winds are supposed to contain only hydrogen and helium. We especially focus our investigations on the equatorial regions where we expect to find neutral material near the central star. In our calculations we make use of several approximations which result in an upper limit for the distance of the equatorial neutral region, because we want to show that efficient shielding of dust at larger distances can occur.

  
2 The winds of B[e] supergiants

B[e] supergiants are thought to be post main-sequence stars but their real location within a clear evolutionary sequence is still under debate (see e.g. Schulte-Ladbeck 1997; Lamers et al. 2003). Up to now about 15 B[e] supergiants are known in the Magellanic Clouds, and a few candidates are known in the Milky Way although the classification as a B[e] supergiant in the Milky Way is very difficult due to the lack of good distance and therefore luminosity determinations (Lamers et al. 1998). The situation is more favorable for B[e] supergiants in the Magellanic Clouds for which the distances are known.

The B[e] supergiants in the Magellanic Clouds have been observed in great detail and many spectra in different wavelength regions are nowadays available. Most interesting, these stars were found to have a so-called hybrid spectrum (Zickgraf et al. 1985) which means that on the one hand the UV resonance lines of highly ionized atoms show broad P Cygni profiles indicating a wind of low density and high velocity, while, on the other hand, forbidden and permitted emission lines of low ionized ions and of neutral atoms arising in the optical spectrum indicate a wind of high density and low velocity. The winds of B[e] supergiants must therefore consist of two different components and Zickgraf et al. (1985) proposed a picture of these winds containing a hot and fast radiation-driven CAK-type wind (Castor et al. 1975) in polar direction and a much cooler, slow and dense wind in equatorial direction which might form a disk-like structure. The density contrast between equator and pole is of order 102 - 103, and from the statistical viewpoint a mean opening angle of $20\hbox{$^\circ$ }{-} 40\hbox{$^\circ$ }$ of the disk has been derived (Zickgraf 1990, 1992). The reason for the non-spherically symmetric winds is probably the rapid rotation of these stars. Rotational velocities in the equatorial region of the star of about 40 - 70% of the break-up velocity have been derived from their spectra (Zickgraf et al. 1996). Pelupessy et al. (2000) and Bjorkman (1998) have argued that the disk is probably due to a combination of rotation induced bi-stability and rotation induced wind compression (see Lamers & Casinelli 1999, Chapt. 11).

Other observations confirm the existence of a neutral disk. These are emission from molecules like CO (McGregor et al. 1988a, 1988b) and TiO (Zickgraf et al. 1989) and emission from cool and warm dust with strong contributions to the spectral energy distribution (Zickgraf et al. 1985, 1986, 1989, 1992; Gummersbach et al. 1995). Also some typical dust emission features have been observed (e.g. Waters et al. 1998; Allen 1973; Zickgraf et al. 1986). The dust component in these disks is also confirmed via polarization measurements (Magalh $\tilde{\rm a}$es 1992). Detailed observations of the B[e] supergiants with different inclination angles show that the polarization is strongest for the edge-on systems. In addition, there is a correlation between the polarization and the [H - L] color of the stars, indicating that the observed infrared excess emission is due to circumstellar dust concentrated in the equatorial region. This dust disk is the origin of the major part of the observed intrinsic polarization.

3 The wind model


  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics[clip]{H4034F1.eps}}\end{figure} Figure 1: Angular distribution of the mass flux, velocity and hydrogen density on the stellar surface. The parameters are b1 = 1; b2 = -2; s = 100 (dashed lines); b1 = 0.5; b2 = -1.5; s = 100 (dotted lines); and b1 = 1; b2 = -2; s = 10 (solid lines).
Open with DEXTER

For a star with a stationary spherically symmetric wind, the mass loss rate is related to the density and the velocity at any point in the wind via the equation of mass continuity

 \begin{displaymath} \dot{M} = 4\pi r^{2} \rho(r)~v(r). \end{displaymath} (1)

The mass flux per unit surface area from a spherical star is

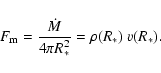\begin{displaymath}F_{\rm m} = \frac{\dot{M}}{4\pi R_{*}^{2}} = \rho(R_{*})~v(R_{*}). \end{displaymath} (2)

For a non-spherically symmetric wind the mass flux is a function of latitude, $F_{\rm m} = F_{\rm m}(\theta)$, and the mass loss rate is

 \begin{displaymath} \dot{M} = 4\pi R_{*}^{2}\int\limits_{0}^{\pi/2}F_{\rm m}(\theta)~\sin(\theta)~{\rm d}\theta \end{displaymath} (3)

where we assumed that the star is a sphere. The hydrogen density distribution in such a wind is

 \begin{displaymath} N_{\rm H}(\theta, r) = \frac{1}{\mu m_{\rm H}}\left(\frac{R_{*}}{r}\right)^{2} \frac{F_{\rm m}(\theta)} {v(\theta,r)} \end{displaymath} (4)

which we parametrize in the following form

 \begin{displaymath} N_{\rm H}(\theta, r) = \frac{1}{\mu m_{\rm H}}\left(\frac{R_... ...F_{\rm m, pol}} {v_{\rm pol}(r)}\times 10^{b(\sin\theta)^{s}}. \end{displaymath} (5)

The term 10b with b = 2 - 3 reflects the density contrast between the equator and the pole, and the term $(\sin\theta)^{s}$ describes the stronger density concentration with increasing s towards the equator.

Table 1: Model wind parameters. Listed are the electron temperature, $T_{\rm e}$, mass fluxes in polar and equatorial direction, $F_{\rm m, pol}$ and $F_{\rm m, eq}$, mass loss rate of the star, $\dot{M}$, terminal velocity in equatorial direction, $v_{\infty ,\rm eq}$, and the resulting equatorial hydrogen density on the stellar surface,  $N_{\rm H, \rm eq}(R_{*})$. The velocity in polar direction is assumed to be in all cases 2000 km s-1 which is a typical value in a CAK-type wind.

The parameters $F_{\rm m, pol}$ and $v_{\rm pol}(r)$are the mass flux and wind velocity in polar direction which can be derived from the observations. Their latitude dependence is taken to

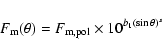\begin{displaymath}F_{\rm m}(\theta) = F_{\rm m, pol}\times 10^{b_{1}(\sin\theta)^{s}} \end{displaymath} (6)

and

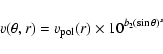\begin{displaymath}v(\theta,r) = v_{\rm pol}(r)\times 10^{b_{2}(\sin\theta)^{s}} \end{displaymath} (7)

with b = b1 - b2. This implies that we have adopted the same shape of the velocity law, $v(r)/v_{\infty}$, for all latitudes. In Fig. 1 we show the variation of the mass flux, velocity and hydrogen density along the stellar surface for different values of b1, b2, and s.

The radial velocity dependence in a stellar wind is normally described by the $\beta$-law

 \begin{displaymath} v(r) \simeq v_{\infty}\left( 1-\frac{R_{*}}{r}\right)^{\beta} \end{displaymath} (8)

where $v_{\infty}$ is the terminal velocity. For hot stars, $\beta$ is typically of order 0.8, and the wind reaches its terminal velocity at a distance of a few stellar radii.

For our calculations we make the following assumptions, whose validity and influence on the results are discussed in Sect. 6:

(i)   we set the electron temperature in the wind constant;
(ii)  we take the velocity in the wind to be independent of distance, i.e. $v(\theta,r) = v_{\infty}(\theta)$.
For this paper we choose a star with a mass of approximately M* = 30 $M_{\odot}$, a radius of R* = 82 $R_{\odot}$, and a radiation temperature of the photosphere in the Lyman continuum of $T_{\rm rad} = 1.7\times 10^{4}$ K which coincides with a Kurucz model atmosphere (Kurucz 1979) for a star with an effective temperature $T_{\rm eff} \simeq 22~500$ K and $\log g = 3$. The luminosity of this star is $L_{*} = 1.5\times 10^{6}~L_{\odot}$ which corresponds to the most luminous B[e] supergiants observed.

For the wind we calculate different models whose parameters are summarized in Table 1.

4 Ionization radii in a wind with non-spherical density distribution

In this section we discuss the calculation of ionization radii. We adopt a similar procedure as for the classical Strömgren sphere calculation but use the non-spherical density distribution given by Eq. (5). We first derive the general formulae. In Sect. 4.2 we discuss the ionization radii in the optically thin case while in Sect. 4.3 the on-the-spot approximation is used. Both models are with the assumption that the ionization is complete within the ionization radii (as usually adopted). This simplification allows us to get a first impression of the overall shape of the ionized region around a B[e] supergiant (Sect. 4.4). The physically more relevant case of partial ionization is discussed in Sect. 5.

4.1 General formulae

We restrict the calculations to a wind containing hydrogen and helium. Since the following equations have the same shape for all angles $\theta$ we skip the angular dependence of the densities and write down the equations only as functions of the radial distance. In addition, we assume that the fraction of He++ is negligible.

The ionization radius is calculated by balancing the number of ionizations which depends an both, the stellar, $J_{\nu}^{\rm s}$, and the diffuse radiation field, $J_{\nu}^{\rm d}$, and the number of recombinations per cm3 and per s. For H and He we can therefore write

 
$\displaystyle N_{\rm H^{0}}(r) \int\limits_{\nu_{0}}^{\infty} a_{\nu}\left({\rm... ...m d}\nu = N_{\rm H^{+}}(r)N_{\rm e}(r) \alpha_{\rm A}\left({\rm H^{0}},T\right)$     (9)


 
$\displaystyle N_{\rm He^{0}}(r) \int\limits_{\nu_{2}}^{\infty} a_{\nu}\left({\r... ...d}\nu = N_{\rm He^{+}}(r)N_{\rm e}(r) \alpha_{\rm A}\left({\rm He^{0}},T\right)$     (10)

with N as the number density of the individual ions and neutral atoms, whereby $N_{\rm He} = y N_{\rm H}$ and y is the He/H ratio by number which we set to 0.1. The terms $\alpha_{\rm A}({\rm H^{0}},T)$ and $\alpha_{\rm A}({\rm He^{0}},T)$ are the radiative recombination coefficients of hydrogen and helium for recombinations into all levels (see Fig. 2), $a_{\nu}({\rm H^{0}})$ and $a_{\nu}({\rm He^{0}})$ are the ionization coefficients, $\nu_{0}$and $\nu_{2}$ are the ionization frequencies of hydrogen and helium, and the electron density, $N_{\rm e}$, is given by $N_{\rm e}(r) = N_{\rm H^{+}}(r) + N_{\rm He^{+}}(r)$.


  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics[clip]{H4034F2.eps}}\end{figure} Figure 2: Hydrogen and helium recombination coefficients. The dots for H refer to values given by Seaton (1959), the dots for He are taken from Osterbrock (1989), and the lines give fits according to interpolation calculations.
Open with DEXTER

Taking into account the absorption of stellar continuum photons along the direction to the star, the mean intensity of the stellar radiation is

 \begin{displaymath} 4\pi J_{\nu}^{\rm s} = 4\pi W(r) B_{\nu}(T_{\rm rad}) {\rm e}^{-\tau_{\nu}} \end{displaymath} (11)

where $W(r) = \frac{1}{2}\left(1-\sqrt{1 - (R_{*}/r)^{2}}\right)$ is the geometrical dilution factor, $T_{\rm rad}$ is the radiation temperature of the photosphere, and $\tau_{\nu}$ is the radial optical depth defined as

 \begin{displaymath} \tau_{\nu}(r) = \int\limits_{R_{*}}^{r}a_{\nu}\left({\rm H^{0}}\right)N_{\rm H^{0}}\left(r'\right) {\rm d}r' \end{displaymath} (12)

for $\nu_{0} \leq \nu < \nu_{2}$ and

 \begin{displaymath} \tau_{\nu}(r) = \int\limits_{R_{*}}^{r}\left( a_{\nu}\left({... ...m He^{0}}\right)N_{\rm He^{0}}\left(r'\right)\right) {\rm d}r' \end{displaymath} (13)

for $\nu_{2} \leq \nu$. We know that Eq. (11) is only correct as long as the star can be considered as a point source. But for our purpose this approximation is also good enough for distances near the star (see Sect. 6).

The diffuse radiation field is much more complicated to calculate because at every point in the wind one must integrate the diffuse radiation over the complete wind zone. To do so, one needs the information of the structure of the wind zone, i.e. information about where in the non-spherically symmetric wind exist neutral regions, what is the absorptivity and emissivity of these neutral regions, etc. Therefore, we restrict our investigations to two extremes: (a) the optically thin case, where all ionizing radiation produced by recombinations leaves the wind zone without being absorbed by a neutral atom, and (b) the optically thick case, better known as the on-the-spot approximation, which states that every ionizing photon produced in the wind via recombination is immediately absorbed by a neutral atom nearby, i.e. on-the spot. In reality the mean intensity will be in between the values predicted for these two extremes.

  
4.2 Non-spherical ionization radii in the optically thin approximation

In this case, the diffuse radiation field is zero, and the ionization equilibrium equations for H and He, Eqs. (9) and (10), reduce to

 
$\displaystyle 4\pi W(r) (1 - q_{\rm H}(r))\int\limits_{\nu_{0}}^{\infty}\frac{B... ...rad})a_{\nu}\left({\rm H^{0}}\right)}{h\nu}~{\rm e}^{-\tau_{\nu}(r)}~{\rm d}\nu$      
$\displaystyle = q_{\rm H}(r)~N_{\rm H}(r)~(q_{\rm H}(r) + yq_{\rm He}(r))~\alpha_{\rm A}\left({\rm H^{0}},T\right)$                                                   (14)

and
 
$\displaystyle 4\pi W(r) (1 - q_{\rm He}(r))\int\limits_{\nu_{2}}^{\infty}\frac{... ...ad})a_{\nu}\left({\rm He^{0}}\right)}{h\nu}~{\rm e}^{-\tau_{\nu}(r)}~{\rm d}\nu$      
$\displaystyle = q_{\rm He}(r)~N_{\rm H}(r)~(q_{\rm H}(r) + yq_{\rm He}(r))~\alpha_{\rm A}\left({\rm He^{0}},T\right)$                                                    (15)

where we replaced the densities by density fractions $N_{\rm H^{+}}(r) = q_{\rm H}(r) N_{\rm H}(r)$ and $N_{\rm H^{0}}(r) = (1 - q_{\rm H}(r)) N_{\rm H}(r)$, and the same for He.

To calculate the distance from the star at which the gas turns from ionized into neutral, i.e. the ionization radius $R_{\rm s}(\theta)$, we assume (as usually adopted in classical Strömgren sphere calculations) that all atoms are ionized whithin the ionization radius, and all atoms are neutral outside, which means that

 \begin{displaymath}q_{\rm H} = \left\{\begin{array}{lcl} 1 & ; & r < R_{\rm s}^{... ...^{\rm He}\\ 0 & ; & r > R_{\rm s}^{\rm He}\end{array}\right.. \end{displaymath} (16)

Integrating now both sides of Eqs. (14) and (15) over the radius, and taking into account the different sizes of the ionized regions for H and He with $R_{\rm s}^{\rm He} \leq R_{\rm s}^{\rm H}$, the ionization balance equations become
 
$\displaystyle 4\pi \int\limits_{R_{\rm s}^{\rm H}}^{\infty}\!\!W(r)\int\limits_... ...imits_{R_{\rm s}^{\rm He}}^{R_{\rm s}^{\rm H}}\!\!N_{\rm H}(r)~{\rm d}r \right]$     (17)

for hydrogen, and
 
$\displaystyle 4\pi \int\limits_{R_{\rm s}^{\rm He}}^{\infty}\!\!W(r)\int\limits... ...\right)\int\limits_{R_{*}}^{R_{\rm s}^{\rm He}}\!\!N_{\rm H}(r)(1 + y)~{\rm d}r$     (18)

for helium. The right-hand side of Eq. (17) splits into two integrals according to the two different regions that have to be considered: (i) the region between the stellar surface and the He ionization radius where both, H and He are singly ionized, and (ii) the region between the He and H ionization radii where only H is ionized. Obviously, the corresponding integration limits for the optical depth calculation must be adapted correctly. From Eqs. (17) and (18) the ionization radii for H, $R_{\rm s}^{\rm H}$, and He, $R_{\rm s}^{\rm He}$, can be calculated for every angle $\theta$.

These equations look quite different from the classical Strömgren sphere formula. But since they are more general, the classical Strömgren sphere, as a special solution, can be found easily as shown in Appendix A.

  
4.3 Non-spherical ionization radii in the on-the-spot approximation

The on-the-spot approximation for optically thick winds assumes that every ionizing photon generated by recombination will be absorbed very near its generation location. The diffuse field can be split into several parts and we consider diffuse photons generated by (a) recombining hydrogen atoms into the ground level; (b) recombining helium atoms into excited levels, and (c) recombining helium atoms into the ground level. In this paper we take into account neither ionization from excited levels nor collisional ionization and recombination. Both effects will strongly influence the ionization balance but we expect that they become really important only for stars with much higher radiation temperature in the Lyman continuum than the 17 000 K we are dealing with. A full solution of the level population equations together with the ionization balance equations, where these effects are included, is presently under investigation and will be published in a forthcoming paper.

While all of the diffuse photons generated by the three mentioned processes are able to ionize hydrogen, only photons resulting from the third process can ionize helium. To complete the ionization equilibrium equations for H and He in the on-the-spot approximation, we have to add the term

 
$\displaystyle N_{\rm H}(r)~\left(q_{\rm H}(r) + yq_{\rm He}(r)\right)~\left[~q_{\rm H}(r)~\alpha_{1}\left({\rm H^{0}},T\right) \right.$      
$\displaystyle \left.+ yq_{\rm He}(r)~\left(\xi ~\alpha_{1}\left({\rm He^{0}},T\right) + p~\alpha_{\rm B}\left({\rm He^{0}},T\right)\right)\right]$     (19)

that describes the additional ionizations of H due to the diffuse radiation field, to the left-hand side of Eq. (14), and the term

 \begin{displaymath} N_{\rm H}(r)~(q_{\rm H}(r) + yq_{\rm He}(r))~yq_{\rm He}(r)~(1-\xi)~\alpha_{1}\left({\rm He^{0}},T\right) \end{displaymath} (20)

for the additional ionization of He due to the diffuse radiation field, to the left-hand side of Eq. (15). With the electron density in terms of the q-values, $N_{\rm e}(r) = N_{\rm H}(r)~(q_{\rm H}(r) + yq_{\rm He}(r))$, the ionization balance equations that must now be solved can be written in the following form:
 
                                         $\displaystyle 4\pi W(r)~(1 - q_{\rm H}(r))\int\limits_{\nu_{0}}^{\infty}\frac{B... ...ht)~a_{\nu}\left({\rm H^{0}}\right)}{h\nu}~{\rm e}^{-\tau_{\nu}(r)}~{\rm d}\nu~$  
    $\displaystyle \qquad+~N_{\rm e}(r)\left[~q_{\rm H}(r)~\alpha_{1}\left({\rm H^{0... ...+ y~q_{\rm He}(r)~\left(\xi~\alpha_{1}\left({\rm He^{0}},T\right)\right.\right.$  
    $\displaystyle \qquad\left.\left.+~p~\alpha_{\rm B}\left({\rm He^{0}},T\right)\r... ...\right]~\!=~ N_{\rm e}(r)~q_{\rm H}(r)~\alpha_{\rm A}\left({\rm H^{0}},T\right)$ (21)

for hydrogen, and
 
                                             $\displaystyle 4\pi W(r)~(1 - q_{\rm He}(r))\!\!\int\limits_{\nu_{2}}^{\infty}\f... ...t({\rm He^{0}}\right)}{h\nu}~{\rm e}^{-\tau_{\nu}(r)}~{\rm d}\nu + N_{\rm e}(r)$  
    $\displaystyle ~~~\times~y~q_{\rm He}(r)~(1-\xi)~\alpha_{1}\left({\rm He^{0}},T\right) = N_{\rm e}(r) q_{\rm He}(r) \alpha_{\rm A}\left({\rm He^{0}},T\right)$ (22)

for helium. Here, $\alpha_{\rm B}$ is the recombination coefficient to all levels except of the ground level, i.e. $\alpha_{\rm B} = \alpha_{\rm A} - \alpha_{1}$, and $\xi$ is the fraction of recombining helium to the ground level which is absorbed by H atoms. The remaining fraction $1 - \xi$ is absorbed by He atoms. p is the fraction of photons generated by recombination of He to all excited levels that can ionize H. This fraction strongly depends on the electron density, because, if the electron density, $N_{\rm e}(r)$, at the location r is high enough, then collisions of electrons with the excited He atoms will depopulate the levels and no or only a few photons are produced. The critical density, $N_{\rm c}$, for collisional deexcitation is defined as the density at which collisional transitions are equally probable with radiative transitions. The values for the ratio p are either $p \simeq 0.96$ if $N_{\rm e}(r) \ll N_{\rm c}(r)$ or $p\simeq 0.66$ if $N_{\rm e}(r)\gg N_{\rm c}(r)$ (see Osterbrock 1989).

Making again the assumptions that all atoms are ionized within and neutral outside the ionization radius, ignoring the absorption by H in the He+ zone by setting $\xi = 0$, and integrating the complete ionization equilibrium equations over the radius yields again $R_{\rm s}(\theta)$ for H and He.

  
4.4 Results


  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics[clip]{H4034F3.eps}}\end{figure} Figure 3: Ionization radii in equatorial regions of H (dashed lines) and He (solid lines) for the different model calculations in the optically thin approximation. The stellar surface is shown as the dotted line.
Open with DEXTER


  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics[clip]{H4034F4.eps}}\end{figure} Figure 4: As in Fig. 3 but for the on-the-spot approximation.
Open with DEXTER

The ionization radii, $R_{\rm s}(\theta)$, calculated for the different model parameters (see Table 1), are presented in Fig. 3 for the optically thin approximation and in Fig. 4 for the on-the-spot approximation. In addition, Figs. 5 and 6 show the ionization radii of the models D and E but for a much larger distance.

The most important result is that for all of the models there is a disk-shaped neutral region around the star, and for the high-density models (A, B, C, and F) these neutral disks can even exist at or just above the surface of the hot star.

Due to the higher number of ionizing photons available in the on-the-spot approximation we would for this method expect the ionization radii to be larger compared with the optically thin results, because e.g. in the case of He the size of the ionization radius depends only on the recombination coefficient. Comparing Figs. 3 and 4 this effect is not obvious for the equatorial direction due to the choosen scaling. But the ionization radii calculated in the on-the-spot approximation are indeed larger as can be seen by comparing the results for a more polar direction or by comparing the Figs. 5 and 6. The real location of the ionization radius should lie in between the two boundaries defined by the optically thin and the optically thick approximation.

We take model A as the reference model and discuss now the effects of the change in the different free parameters on the size of the ionization radii. The higher electron temperature in model B leads to a slightly larger ionization radius because the recombination coefficient and therefore the number of recombinations decreases with increasing electron temperature (see Fig. 2). The influence of the electron temperature is, however, not very significant.


  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics[clip]{H4034F5.eps}}\end{figure} Figure 5: Optically thin approximation for the models D and E but for a much larger distance. Shown are the ionization radii for H (dashed line) and He (solid line).
Open with DEXTER


  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics[clip]{H4034F6.eps}}\end{figure} Figure 6: On-the-spot approximation for the models D and E but for a much larger distance. Shown are the ionization radii for H (dashed line) and He (solid line).
Open with DEXTER

The series of the models C, A, and D displays the behaviour of the ionization radii for a decreasing mass flux, i.e. a decreasing hydrogen density in equatorial direction. Consequently, the ionization radii of H and He increase drastically because (i) much less recombinations occur, and (ii) for a lower density, i.e. a lower optical depth in direction to the star, the ionizing photons can penetrate much deeper into the wind. While the density in model A is still high enough for effective recombination and for an effective absorption of the ionizing photons near the stellar surface, especially the H ionization radius in model D is shifted to a much larger distance (see Figs. 5 and 6).

Not only the change in mass flux leads to a change in density. Also a lower value of b, the density ratio between equator and pole, results in a lower density and leads to a shift of the ionization radius to a much larger distance (model E, see also Figs. 5 and 6).

And finally, the smaller value of s in model F, which means that the concentration of the density to equatorial directions is less strong, leads to a much broader neutral disk-like structure, as expected.

  
5 Ionization structure of H and He

In the previous section we calculated the ionization structure using the approximation that the wind is fully ionized at $r(\theta) < R_{\rm s}(\theta)$ and neutral at $r(\theta) > R_{\rm s}(\theta)$. This is a severe simplification because the region where the wind is partly ionized may be substantial. Therefore, in this section we calculate the ionization structure of the wind more exactly. As concluded from the Figs. 3 and 4, the neutral region in equatorial direction can already be reached at or near the stellar surface, as long as the wind density is high enough. For these high density models, the on-the-spot approximation is a very good tracer for the H and He ionization radii and we use this approximation further on to calculate the ionization structure in these winds in equatorial directions.

We start with the ionization balance equations in the on-the-spot approximation derived above, i.e. Eq. (21) for H and Eq. (22) for He. The optical depth is given by the Eqs. (12) and (13). From Eqs. (21) and (22) the ionization fractions for H and He can be calculated radially outwards in the wind whereby the optical depth at each point in the wind between the stellar surface and the distance r must be known. The inclusion of the optical depth along the direction to the star into the calculations leads to results for the ionization radii which are more accurate than in the approximate calculation of the previous section.

In Fig. 7 we plot the fractions of ionized and neutral helium calculated for the different models of Table 1. The plots in the three panels are thereby grouped according to the values of the equatorial hydrogen density, i.e. model C in the top panel has the highest density, while the models D and E in the bottom panel have the lowest density. Also shown, as a thick vertical line, are the locations of the approximate ionization radii extracted from Fig. 4.

At first, in the top and middle panel the distance of the approximate ionization radius is much larger than for the more accurate ionization fraction calculations. The reason for this is the optical depth which is not really zero as assumed in the approximate ionization radius calculations. Instead, there exists always a very small fraction of neutral atoms which results in a non-negligible attenuation of the stellar radiation field. For example, in the highest density model C where the He neutral region nearly coincides with the stellar radius, the approximate method results in an ionization radius that is about a factor of 8 larger. This strong discrepancy can be understood, if we look at the fraction of neutral He which turns out to be a few times 10-3 at the stellar surface. Such a large neutral fraction results in a substantial optical depth already at the stellar surface.


  \begin{figure} \par\resizebox{8.4cm}{!}{\includegraphics[clip]{H4034F7.eps}}\end{figure} Figure 7: He ionization structure in equatorial direction ( $\theta = 90\hbox {$^\circ $ }$) for the different models. The models are grouped according to their density in equatorial direction: the upper panel belongs to the highest density, the lower panel to the lowest density models. The shift of the transition radius to higher distances for lower densities is clearly visible. The solid lines represent $q_{\rm He^{+}}$ and the dashed lines $q_{\rm He^{0}} = 1 - q_{\rm He^{+}}$. The thick vertical line is the location of the ionization radius from Fig. 4.
Open with DEXTER


  \begin{figure} \par\resizebox{8.4cm}{!}{\includegraphics[clip]{H4034F8.eps}}\end{figure} Figure 8: As Fig. 7 but for the H ionization structure. Models D and E are not shown because due to their low densities no transition from ionized to neutral occurs; the ionization fraction in these winds becomes constant.
Open with DEXTER

For the models A, B, and F, i.e. the models with the intermediate density, the He neutral region starts at larger radius and the neutral fraction inside this region is much smaller (only about 10-5-10-6). The difference between the approximate and the real ionization radii is therefore much smaller, about 25%.

In the lower panel of Fig. 7 the results for the models with the lowest density, D and E, are shown. Here, the situation is different: the exact calculations lead to a larger distance of the neutral region than the ionization radius calculations. These seems not to be physically and shows us that in these two models the assumption of the validity of the on-the-spot approximation no longer holds because the density in the models D and E is already too low to guarantee that every photon produced by recombinations will be absorbed in the wind.

The main result of this comparison in Fig. 7 is that the approximate calculations, by neglecting the optical depth effects inside the ionized regions, overestimate the real locations of the ionization radii. The same behaviour can also be seen in Fig. 8 which displays the fractions of ionized and neutral hydrogen together with the locations of the approximate ionization radii.

Interestingly, when calculating the ionization fractions for the models D and E we could not find the transition from ionized to neutral H, but instead the calculations resulted in a constant ionization fraction contrary to what was found for the approximate calculations. The same result was achieved for calculations in polar directions. This discrepancy can easily be understood by inspecting the balance Eqs. (21) and (22): If we summarize on the right hand side the terms that contain the electron density, the left hand side is proportional to $W(r) N_{\rm H}(r)$ while the right hand side is proportional to $N_{\rm H}^{2}(r) \sim r^{-4}$. Since for large distances, the dilution factor becomes proportional to r-2, the left hand side also becomes proportional to r-4 which then drops out of the equations. The only r dependent term that is still in is the optical depth. But for large distances with only slowly varying q values the optical depth becomes constant. For large distances from the star, the ionization balance equations therefore become independent of r, and the ionization fractions become constant. As long as there is no change in the density distribution, e.g. when the wind reaches the shockfront where the wind material hits the interstellar medium, there will be no neutral region in the polar directions of the wind but all material stays ionized with a constant ionization fraction. In the approximate calculation of the ionization radii we make the assumption that the neutral region starts at a distance smaller than infinity, but this assumption does not hold for low density winds with a r-2 density distribution. Nevertheless, in winds with a constant density, as might be the case in planetary nebulae, the assumption is correct because in a constant density wind the ionization balance equations never become independent of r.

  
6 Discussion

The motivation for this paper was to find the location of neutral material in the equatorial regions around hot and massive stars. In our model calculations we make some assumptions that seem not to be valid for the regions of our interest, i.e. very near the stellar surface. In this section we therefore discuss these assumptions and show that they are indeed justifiable also near the stellar surface.

1.
 The constant electron temperature. In a test calculation we computed with the help of the thermal equilibrium equations for a pure H plus He wind the electron temperature distribution in equatorial direction. We found that on this short distance between stellar surface and neutral region the electron temperature varies only very slightly, so that our assumption of a constant electron temperature seems to be valid, at least for the equatorial regions.

2.
 The constant wind velocity. The wind velocity of a hot star normally increases from a value <1 km s-1 in the stellar photosphere to the terminal velocity which is reached at a distance of a few stellar radii. In polar direction, the B[e] supergiants show a typical radiation-driven CAK-type wind with a terminal velocity of about 2000 km s-1. This value was used in our calculations. Since the ionization radius in polar directions lies at distances of 105 - 107 AU, the assumption of a constant wind velocity, i.e. the terminal velocity in these directions, is valid. The only exception is model C which is the wind of highest density in our sample. Here, the polar ionization radius is reached already at a distance of 0.9 AU. For this model a proper inclusion of the radial velocity distribution is necessary when the correct value of the polar ionization radius is needed.

In the equatorial direction, in which we are mainly interested, our choice of the terminal velocity clearly overestimates the real velocity in these regions, since we found that the ionization radii here are reached already very close to the stellar surface where the wind has not yet been accelerated effectively. However, if we would include the correct, very slow wind velocity, the hydrogen density in equatorial direction which is proportional to v-1 would be much larger than in our model calculations. The overestimation of the wind velocity in our model therefore shifts the ionization radius to a larger distance.

3.
 The point source approximation for the mean stellar radiation field. For distances near the star we normally would have to take into account effects like limb darkening and the size of the stellar disk. Both effects lead to a decrease in the mean optical depth at distance r from the star. Ignoring these two effects, Eq. (11) results in an overestimation of the stellar radiation field and in a shift of the ionization radius in equatorial direction to a larger distance.

The assumption of a constant wind velocity that equals the terminal velocity and the assumption of the point source approximation for the mean stellar raditation field result both in a shift of the ionization radius to larger distances from the star. Our calculations therefore reflect the "worst case" and give an upper limit for the distance of the equatorial neutral region.

7 Comparison with observations from other hot stars

The B[e] supergiants are not the only class of stars that shows non-spherically symmetric winds and we mention here two galactic stars, the luminous blue variable (LBV) AG Carinae and the peculiar B[e] star MWC 349 A, that are also found to have emission from CO and dust coming from regions near the stellar surface.

AG Carinae is a LBV star, even one of the most luminous ones with $L = 1.7\times 10^{6}~L_{\odot}$ (Humphreys et al. 1989) and with a variable effective temperature between 9000 K and 25 000 K (Lamers 1986; Voors et al. 2000). The mass of AG Carinae is of order 35 $M_{\odot}$ (Vink & de Koter 2002). It is surrounded by a very bright, extended nebula which is composed of ionized gas and dust. Most recently, the properties of the neutral material around this star was subject to a project of Nota et al. (2002). The authors observed the lowest rotationally transitions of CO, and with their spatially resolved observations they found, most astonishingly, that the CO emission arises in regions near the star. The authors therefore suggested that the CO is located in an outflowing disk, just as it is the case for B[e] supergiants. Since LBV's have very high mass loss rates of order $10^{-5} {-} 10^{-4}~M_{\odot}$ yr-1 even at times in between individual outbursts (e.g. Leitherer et al. 1994), the wind scenario in AG Carinae might equal those of the B[e] supergiants, and a neutral disk extending nearly down to the stellar surface might surround AG Carinae. Our model calculations shown above speak in favour of such a scenario.

The other interesting star is the peculiar B[e] star MWC 349 A. Although known for nearly 100 years, its evolutionary state is still under debate because its spectra show characteristics of a pre-main sequence B[e]-type star as well as characteristics of a B[e] supergiant (Lamers et al. 1998). MWC 349 A has a luminosity of $3\times 10^{4}~L_{\odot}$, a mass loss rate of $1.2\times 10^{-5}~M_{\odot}$ yr-1 (Cohen et al. 1985), an effective temperatue of 35 000 K, and a mass of 25-30 $M_{\odot}$ (Thum et al. 1992, 1994). This star is known to possess a Keplerian rotating disk. Strong CO first-overtone band emission has been observed which must be located near the star (Kraus et al. 2000), i.e. much nearer than about 3 AU which is the dust evaporation radius (Kraus 2000).

These are only two examples that show how common the phenomenon of neutral gas nearby hot stars and located in a shielded, outflowing disk is.

In our calculations presented in this paper we took an empirical density distribution that accounts for the observed quantities like the density ratio between equator an poles, the mass loss rate and velocity in polar directions, and the density concentration towards the equator. The physical reason for such kind of density distribution is not yet fully understood. Since the B[e] supergiants are known to be fast rotators, a differential rotation of the star with a drastically increase of rotation speed towards the equator might lead to the observed angle dependent mass flux. There exist several theoretical models to describe the concentration or focussing of the material towards the equatorial region. The most promising are the rotationally induced bi-stability mechanism (see Lamers & Pauldrach 1991; Pelupessy et al. 2000) and wind compression leading either to a wind compressed disk (Bjorkman & Cassinelli 1993; Bjorkman 1998; Owocki et al. 1994, 1996, 1998) or to a wind compressed zone (e.g. Ignace et al. 1996). Unfortunately, none of them is able to explain all the observed properties of the polar and equatorial winds self-consistently. A better understanding of the physics of these outflowing disks and of the ionization structure in non-spherically symmetric winds is therefore necessary.

8 Conclusion

Our main result is that the equatorial winds of B[e] supergiants, which are formed due to a high mass flux of low velocity, can become neutral very near the stellar surface. In these neutral disk-shaped regions, which are shielded from direct stellar radiation, molecules and dust can form. The existence of molecules and dust in the disks around B[e] supergiants is already known from observations, but it is astonishing that our calculations result in neutral disks that extend down to the hot stellar surface.

These results coincide very nicely with the most recent spatially resolved observations of strong CO emission. This emission seems to originate in regions very near the hot LBV star AG Carinae. Its existence can only be understood if a neutral disk shields the material from stellar dissociation. For this star, a scenario as predicted by our model calculations, seems to be a natural way to allow CO molecules to exist very close to the hot star. The same holds also for the peculiar B[e] star MWC 349. This star also shows strong CO emission coming from the inner parts of a neutral Keplerian rotating disk.

In addition we find that in polar directions the approximate ionization radius calculation for winds with an r-2 density distribution turns out to be wrong because one uses the physically wrong assumption that there must be a turnover from ionized to neutral at a distance smaller than infinity. In fact, for large distances, the ionization balance equations become independent of r and the ionization fractions become constant so that no neutral region can be found as long as the density in the wind does not change, e.g. when reaching the shockfront where the wind hits the interstellar medium.

Although our model calculations are restricted to a simple hydrogen plus helium wind, they nevertheless mirror the general behaviour of the ionization structure in non-spherically symmetric winds of hot stars with a high mass flux in equatorial direction. Moreover, since the stellar parameters in our calculations are for a very luminous B[e] supergiant, the results are valid for the complete group of B[e] supergiants, because for less luminous stars the number of Lyman continuum photons decreases so that the wind becomes neutral even closer to the star.

Appendix A: Derivation of the classical Strömgren sphere

To show that the classical Strömgren sphere relation follows from our more general formulae we start with Eq. (14) for a pure hydrogen nebula of constant density

 \begin{displaymath}4\pi W(r) (1-q(r))\int\limits_{\nu_{0}}^{\infty}\frac{B_{\nu}... ...{h\nu}{\rm e}^{-\tau_{\nu}}{\rm d}\nu = \alpha q(r) N_{\rm H}. \end{displaymath} (A.1)

In addition we use the point source approximation, i.e. W(r) = 1/4 (R*/r)2, and multiply both sides of the equation by $4\pi r^{2}$

 \begin{displaymath}(1-q(r))\int\limits_{\nu_{0}}^{\infty}4\pi R_{*}^{2}\frac{\pi... ...e}^{-\tau_{\nu}}{\rm d}\nu = \alpha q(r) N_{\rm H} 4\pi r^{2}. \end{displaymath} (A.2)

Now, we integrate both sides over the radius and take into account the condition for q(r) which is defined by Eq. (16). The optical depth can then be calculated

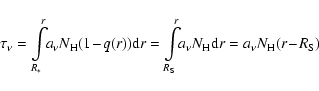\begin{displaymath}\tau_{\nu}=\int\limits_{R_{*}}^{r}\!\!a_{\nu}N_{\rm H}(1\!-\!... ...!\!a_{\nu}N_{\rm H}{\rm d}r=a_{\nu}N_{\rm H} (r\!-\!R_{\rm S}) \end{displaymath} (A.3)

and Eq. (A.2) becomes

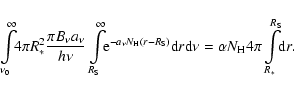\begin{displaymath}\int\limits_{\nu_{0}}^{\infty}\!\!4\pi R_{*}^{2}\frac{\pi B_{... ...a N_{\rm H} 4\pi \int\limits_{R_{*}}^{R_{\rm S}}\!\!{\rm d}r. \end{displaymath} (A.4)

The integration over the radius on the left-hand side results simply in

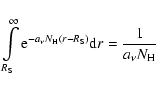\begin{displaymath}\int\limits_{R_{\rm S}}^{\infty}{\rm e}^{-a_{\nu}N_{\rm H} (r - R_{\rm S})} {\rm d}r = \frac{1}{a_{\nu}N_{\rm H}} \end{displaymath} (A.5)

so that we end up with

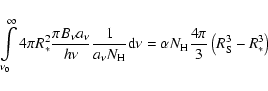\begin{displaymath}\int\limits_{\nu_{0}}^{\infty}4\pi R_{*}^{2}\frac{\pi B_{\nu}... ..._{\rm H} \frac{4\pi}{3} \left(R_{\rm S}^{3} - R_{*}^{3}\right) \end{displaymath} (A.6)

or, if we use $L_{\nu} = 4\pi R_{*}^{2} \pi B_{\nu}$ and the assumption $R_{\rm S}\gg R_{*}$,

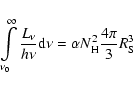\begin{displaymath}\int\limits_{\nu_{0}}^{\infty}\frac{L_{\nu}}{h\nu} {\rm d}\nu = \alpha N_{\rm H}^{2} \frac{4\pi}{3} R_{\rm S}^{3} \end{displaymath} (A.7)

which is the classical formula for the Strömgren sphere in a constant density nebula.

For a density distribution of the form $N_{\rm H}(r) = A r^{-2}$ the Strömgren sphere is

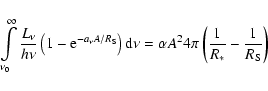\begin{displaymath}\int\limits_{\nu_{0}}^{\infty}\frac{L_{\nu}}{h\nu}\left( 1-{\... ...A^{2} 4\pi \left(\frac{1}{R_{*}} - \frac{1}{R_{\rm S}} \right) \end{displaymath} (A.8)

which can be derived from our general equations in a similar way.

Acknowledgements

We thank the unknown referee for critical comments that have led to an improvement of this paper. This work was partially supported by the German Deutsche Forschungsgemeinschaft, DFG grant number Kr 2163/2-1.

References


Copyright ESO 2003