A&A 405, 349-366 (2003)
DOI: 10.1051/0004-6361:20030467
Systematic effects in the measurement of polarization by the PLANCK telescope
G. Franco1 -
P. Fosalba1,2 -
J. A. Tauber1
1 - Research and Science Support Department of ESA, ESTEC, PO Box 299, 2200 AG Noordwijk, The Netherlands
2 - Institut d'Astrophysique de Paris, 98bis boulevard Arago, 75014 Paris, France
Received 2 October 2002 / Accepted 6 March 2003
Abstract
We present estimates of the response to polarized signals
by the PLANCK telescope. These estimates are based on a set of
simulations, using a physical optics code (GRASP8), for linearly
polarized detectors at different frequencies and located in different
positions of an early design of the PLANCK focal plane.
We show how the optical aberration introduced by the studied focal
plane configuration affects absolute and relative orientation of
the sky signals polarization planes.
In addition, we compute the spurious signal introduced by the
telescope optics into a PLANCK-type measurement of the sky polarization.
Our analysis shows that the spurious polarization expected in a
PLANCK-like experiment is typically of the order of 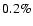 of
the unpolarized intensity.
of
the unpolarized intensity.
Key words: space vehicles: instruments -
telescopes - polarization - cosmology: cosmic microwave background - space vehicles
1 Introduction
The CMB temperature anisotropy carries an essential information on the
origin and evolution of large scale structures in the universe. Its
accurate measurement by experiments probing large (see e.g.,
Bennett et al. 1994) and small scales (see e.g., Scott et al. 2003 and
references therein) already allows us to constrain cosmological models
with good precision (see e.g., Lewis & Bridle 2002).
In addition, the quadrupole temperature anisotropy at the last
scattering surface generates a polarization signal (of order 10% of
the CMB intensity) carried by the scalar and tensor modes of the CMB
anisotropy (Rees 1968). This polarized anisotropy is a unique probe
of primordial gravitational waves (Crittenden et al. 1993a,b) and the
reionization era of the universe (see e.g., Zaldarriaga 1997;
Hu 2000). Moreover, CMB polarization helps break the
degeneracy affecting the cosmological parameter estimation from CMB
anisotropy data alone (e.g., Zaldarriaga et al. 1997).
Detecting CMB polarization is a serious experimental challenge which
requires an unprecedented experimental sensitivity, good knowledge
and clean removal of foreground contamination, and a careful analysis
of systematic effects, the latter recently attracting increasing
attention (see e.g., Carretti et al. 2001; Kaplan & Delabrouille 2001; Leahy et al. 2001;
Yurchenko 2001; Fosalba et al. 2002). Current upper limits for
CMB polarizations are at the level of 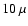 K (Hedman et al. 2001;
Keating et al. 2001; de Oliveira-Costa et al. 2003).
Despite great experimental efforts, CMB polarization
has remained undetected until very recently with the first detection of
E-mode polarization by the DASI experiment (Kovac et al. 2002).
A new generation of CMB experiments is being specifically designed
to image the polarization anisotropies in the microwave sky with
ground-based telescopes (e.g., COMPASS), interferometers (e.g., CBI),
balloons (MAXIPOL, B2K), and satellites (MAP, PLANCK).
In particular, the PLANCK experiment
K (Hedman et al. 2001;
Keating et al. 2001; de Oliveira-Costa et al. 2003).
Despite great experimental efforts, CMB polarization
has remained undetected until very recently with the first detection of
E-mode polarization by the DASI experiment (Kovac et al. 2002).
A new generation of CMB experiments is being specifically designed
to image the polarization anisotropies in the microwave sky with
ground-based telescopes (e.g., COMPASS), interferometers (e.g., CBI),
balloons (MAXIPOL, B2K), and satellites (MAP, PLANCK).
In particular, the PLANCK experiment![[*]](/icons/foot_motif.gif) will provide multi-frequency full-sky maps of the polarized sky with a
sensitivity better than
will provide multi-frequency full-sky maps of the polarized sky with a
sensitivity better than 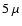 K for practically all the channels
(Tauber 2000).
Ultimately, the polarization performance of PLANCK depends on the
ability to minimize spurious instrumental effects which contaminate
the sky signal.
K for practically all the channels
(Tauber 2000).
Ultimately, the polarization performance of PLANCK depends on the
ability to minimize spurious instrumental effects which contaminate
the sky signal.
In this paper, we investigate the impact of one specific instrumental
systematic - the optical aberration in the PLANCK telescope - in the
measurement of polarized signals. The PLANCK telescope is an off-axis
aplanatic system with a very wide field of view of 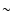
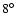 on
the sky. The focal plane is filled with individual corrugated horns
that collect radiation from the telescope and deliver it to
band-limited detectors (with bandwidth
on
the sky. The focal plane is filled with individual corrugated horns
that collect radiation from the telescope and deliver it to
band-limited detectors (with bandwidth 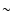 25%) within the 30-850 GHz frequency range. Detectors collect largely linearly polarized
radiation, defined either by a waveguide hybrid discriminator or by a
linear grid. This experimental scheme is common to other current CMB
polarization experiments (e.g., MAP).
25%) within the 30-850 GHz frequency range. Detectors collect largely linearly polarized
radiation, defined either by a waveguide hybrid discriminator or by a
linear grid. This experimental scheme is common to other current CMB
polarization experiments (e.g., MAP).
Although PLANCK was not originally devised as a CMB polarization
imager, its current design incorporates 7 polarized channels between
30 and 353 GHz, in the Low- and High-frequency instruments (LFI
and HFI hereafter), including a total of 88 linearly polarized
detectors. PLANCK, to be launched in 2007, is currently in its Phase
B (detailed design) during which many features, such as the
focal plane layout, are being optimised for the polarization
measurement. The scheme exploits the fact that many detectors in
the focal plane are sensitive to the same frequency band and are
spatially arranged such that their polarization planes are rotated
with respect to each other by multiples of
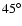 .
In this way, by combining samples from several linearly polarized
detectors, it is possible to extract all the polarization information
in terms of the Stokes parameters (see e.g., Kraus 1982;
Couchot et al. 1999).
However, an optimal measurement relies critically on the similarity
of the polarized angular responses, also called beam or
radiation patterns, of the differently oriented polarized horns.
These radiation patterns will be difficult to measure accurately on
the ground and they will have to be reconstructed in flight using
celestial sources such as planets and the Galactic plane.
.
In this way, by combining samples from several linearly polarized
detectors, it is possible to extract all the polarization information
in terms of the Stokes parameters (see e.g., Kraus 1982;
Couchot et al. 1999).
However, an optimal measurement relies critically on the similarity
of the polarized angular responses, also called beam or
radiation patterns, of the differently oriented polarized horns.
These radiation patterns will be difficult to measure accurately on
the ground and they will have to be reconstructed in flight using
celestial sources such as planets and the Galactic plane.
In this paper we shall study two basic issues regarding the ability
of PLANCK to measure polarization:
- What is the effect of the feed and telescope optics on the
properties of the measured polarized sky signal?
In particular, are the absolute and relative orientation of
polarization planes in the sky preserved by the optics?
- What is the impact of the instrumental optics
on the differential measurement of polarization?
In what follows we shall use Physical Optics (PO) modeling to
simulate the interaction of radiation with PLANCK telescope
optical system. Unlike Geometrical optics (GO), which is
characterized by the neglect of the wavelength, PO uses the
concepts of electromagnetic transverse waves and their
propagation properties to simulate the behaviour of light
in optical systems, being the most accurate method to
simulate diffraction, interference and polarization phenomena.
In this study we use GRASP8, a software package developed
by TICRA (1997), to compute the polarized radiation pattern
on the sky for different transmitting feeds located in the
focal plane![[*]](/icons/foot_motif.gif) (see Sect. A.1 for further details). In particular,
we shall simulate the feeds located at three representative (off-axis)
positions and at two different frequencies, and examine the effect of
the optical asymmetries on the measurement of the Stokes parameters.
Using such simulations we aim at answering the two basic questions
mentioned above and draw some general conclusions regarding the
impact of the PLANCK design under study in this paper, for the
measurement of CMB polarization.
(see Sect. A.1 for further details). In particular,
we shall simulate the feeds located at three representative (off-axis)
positions and at two different frequencies, and examine the effect of
the optical asymmetries on the measurement of the Stokes parameters.
Using such simulations we aim at answering the two basic questions
mentioned above and draw some general conclusions regarding the
impact of the PLANCK design under study in this paper, for the
measurement of CMB polarization.
The paper is organized as follows: in Sect. 2 we address
the problem of simulating and comparing the beam (or radiation)
patterns generated using PO modeling. Results of the simulations
are presented and discussed in Sect. 3 and our final
conclusions are given in Sect. 4. In the Appendix A we give a full description of the simulations procedures with GRASP8 code.
2 Modeling far-field radiation patterns
2.1 Introducing reference frames
Polarized radiation can be fully described by the projection of the
electric field vector, 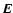 ,
in a 2-dimensional orthogonal
basis. For the far field radiation pattern,
,
in a 2-dimensional orthogonal
basis. For the far field radiation pattern,
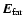 ,
we shall adopt Ludwig's 3rd definition of co- and cross-polarization (Ludwig 1973),
,
we shall adopt Ludwig's 3rd definition of co- and cross-polarization (Ludwig 1973),
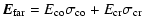 |
|
|
(1) |
where
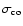 and
and
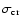 are the co- and
cross-polarization unit vectors which relate to the usual spherical
polar basis (
are the co- and
cross-polarization unit vectors which relate to the usual spherical
polar basis (
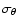 ,
,
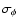 )
as follows,
)
as follows,
By projecting onto the Cartesian coordinate system,
one finds that at boresight, i.e., the north pole of the sphere
(
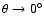 ), it holds that
), it holds that
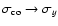 and
and
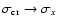 (see Eqs. (2) and (3)),
so the chosen polarization basis lies along the Cartesian one.
Away from boresight, Ludwig's polarization basis is obtained by
parallel-transporting the local Cartesian basis (
(see Eqs. (2) and (3)),
so the chosen polarization basis lies along the Cartesian one.
Away from boresight, Ludwig's polarization basis is obtained by
parallel-transporting the local Cartesian basis (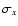 ,
, 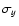 )
along great circles over the sphere.
)
along great circles over the sphere.
2.2 Defining cross-polarization for non-ideal antennas
Here we shall define a robust way of characterizing cross-polarization
in non-ideal optical systems. In particular, we discuss cross-polarization
definitions for the case of feeds with arbitrary orientations in the focal
plane.
Let us denote the orientation of a given feed (with respect to its
symmetry or rotation axis) by
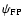 .
We define a reference
orientation, denoted by
.
We define a reference
orientation, denoted by
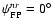 ,
with respect
to which we can define any arbitrary orientation of a given feed.
Similarly, we must introduce a corresponding far-field reference
frame with respect to which the sky beam patterns from a given feed
with an arbitrary orientation in the focal plane, will be referred to.
,
with respect
to which we can define any arbitrary orientation of a given feed.
Similarly, we must introduce a corresponding far-field reference
frame with respect to which the sky beam patterns from a given feed
with an arbitrary orientation in the focal plane, will be referred to.
For an ideal telescope![[*]](/icons/foot_motif.gif) with an on-axis feed, one can always find a
reference frame in the far field for which the cross-polarization power
(see Eq. (1)) vanishes (
with an on-axis feed, one can always find a
reference frame in the far field for which the cross-polarization power
(see Eq. (1)) vanishes (
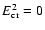 ). This constitutes
a convenient reference frame for sky beam patterns of a given feed.
However, for a real telescope, any asymmetry in the antenna system
will generally introduce a non-vanishing cross-polarization component
in the far-field radiation pattern. Moreover, non-ideal telescope
optics also introduce a differential rotation of the principal
plane of polarization in the far field with respect to that physically
applied to the feed in the focal plane.
). This constitutes
a convenient reference frame for sky beam patterns of a given feed.
However, for a real telescope, any asymmetry in the antenna system
will generally introduce a non-vanishing cross-polarization component
in the far-field radiation pattern. Moreover, non-ideal telescope
optics also introduce a differential rotation of the principal
plane of polarization in the far field with respect to that physically
applied to the feed in the focal plane.
We recall that a proper measurement of polarization in terms of
the Stokes parameters of the sky signal requires that the orientation
of the feeds in the focal plane be such that the principal planes of
polarization on the sky are spaced by
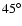 .
Therefore, it is important to choose an appropriate method for
determining this principal plane of polarization, which is here
defined as that in which the Cross Polarization Discrimination
(XPD) is maximized.
.
Therefore, it is important to choose an appropriate method for
determining this principal plane of polarization, which is here
defined as that in which the Cross Polarization Discrimination
(XPD) is maximized.
We define maximal cross-polar discrimination angle,
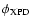 ,
as the angle by which one should rotate the reference frame in the
sky in order to maximize the Cross Polar Discrimination, XPD.
Below we introduce three different methods for the computation
of
,
as the angle by which one should rotate the reference frame in the
sky in order to maximize the Cross Polar Discrimination, XPD.
Below we introduce three different methods for the computation
of
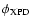 ,
each one relying on a different definition of XPD
,
each one relying on a different definition of XPD![[*]](/icons/foot_motif.gif) :
:
Note that in the equations above
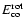 and
and
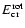 are the (complex) co- and cross-polarization components of the
radiation pattern, after having performed a rotation of the far
field coordinate system by an angle (
are the (complex) co- and cross-polarization components of the
radiation pattern, after having performed a rotation of the far
field coordinate system by an angle (
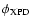 in this case)
with respect to the original reference frame (i.e., the far-field
frame defined for a non-rotated feed in the focal plane),
in this case)
with respect to the original reference frame (i.e., the far-field
frame defined for a non-rotated feed in the focal plane),
In general, the far-field radiation pattern of an asymmetric radiating
system fed by a corrugated horn has a cross-polarization pattern with
a multiple peak (rather than a simple peak) structure with
several maxima which are not spatially coincident with nor
symmetrically placed with respect to the co-polar peak
(e.g. see Fig. A.4). Such an asymmetric
cross-polarization pattern for non-ideal antennas makes the cross
polar discrimination angle defined in the 1st method potentially
ambiguous. In principle, the 3rd method should be appropriate for
measurements of diffuse polarized emission, as it is based on
integrating radiation filling the main beam (i.e., an extended
region around boresight), while the 2nd method is more appropriate
for measuring polarization from point sources as it relies on a
local measurement of power radiated.
2.3 Differential rotation of the polarization plane
Let us consider again an ideal antenna system. In this case, it is
expected that a rotation of a given feed around its own symmetry axis,
from an initial position,
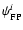 ,
to a final position,
,
to a final position,
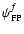 ,
would result in an equal rotation of the principal
plane of polarization of the radiation pattern in the sky
,
would result in an equal rotation of the principal
plane of polarization of the radiation pattern in the sky![[*]](/icons/foot_motif.gif) . Thus we
can write,
. Thus we
can write,
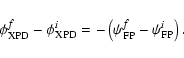 |
(8) |
Setting
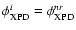 as the maximal
cross-polarization discrimination angle for the beam pattern
when the feed is in its original or non-rotated position
(
as the maximal
cross-polarization discrimination angle for the beam pattern
when the feed is in its original or non-rotated position
(
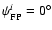 ), the previous equation becomes,
), the previous equation becomes,
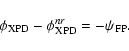 |
(9) |
This equation holds for any ideal antenna system if the polarization
properties of the radiation pattern are equally preserved for all
orientations of the feed in the focal plane.
However, for a non-ideal antenna system, such isotropy is broken and,
due to factors such as the asymmetry of the reflectors or the
off-axis positioning of the feed, Eq. (9) will
only hold to a first-order approximation, i.e.,
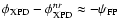 .
Consequently, in order to quantify how good this approximation is (or
on the contrary, how non-ideal is the antenna), we shall define the
residual angle,
.
Consequently, in order to quantify how good this approximation is (or
on the contrary, how non-ideal is the antenna), we shall define the
residual angle,
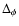 ,
as the additional angle to
which the reference frame of the beam pattern in the far-field should
be rotated, in addition to
,
as the additional angle to
which the reference frame of the beam pattern in the far-field should
be rotated, in addition to
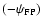 ,
so as to have the co-polar
axis of the beam pattern reference frame aligned with the principal
polarization direction. Thus we define
,
so as to have the co-polar
axis of the beam pattern reference frame aligned with the principal
polarization direction. Thus we define
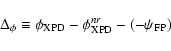 |
(10) |
where
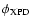 is computed using the methods described in
Sect. 2.2 and
is computed using the methods described in
Sect. 2.2 and
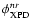 is the angle
is the angle
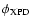 for
the non-rotated feed,
for
the non-rotated feed,
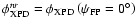 .
.
Table 1:
Maximal cross-polarization discrimination angle
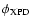 ,
,
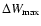 and the residual angle
and the residual angle
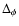 for the 30 GHz and the 100 GHz feeds
on positions 1, 4 and 27, for different orientations
for the 30 GHz and the 100 GHz feeds
on positions 1, 4 and 27, for different orientations
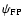 of the feeds being
of the feeds being
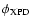 determined by the 1st Method
described in Sect. 2.2 and
determined by the 1st Method
described in Sect. 2.2 and
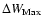 evaluated
using Eq. (4).
evaluated
using Eq. (4).
3 Simulation results
In what follows, we shall focus on determining this residual
angle, along with the associated angle
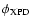 and power
difference
and power
difference
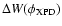 ,
making use of the PO
simulations described in Sect. A.1.
In the present study we compute the sky beam patterns for
PLANCK-LFI 30 and 100 GHz feeds at different positions in
the focal plane unit, for a range of different orientations
of the feed. The orientations studied correspond to rotations
around the symmetry axis of the feed by angles
,
making use of the PO
simulations described in Sect. A.1.
In the present study we compute the sky beam patterns for
PLANCK-LFI 30 and 100 GHz feeds at different positions in
the focal plane unit, for a range of different orientations
of the feed. The orientations studied correspond to rotations
around the symmetry axis of the feed by angles![[*]](/icons/foot_motif.gif)
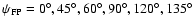 and
and
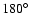 .
In particular, we carry out numerical simulations of the far-field
patterns fed by corrugated horns located at three different positions
in the focal plane ranging from very close to the optical axis, to the
edge of the field of view (see Fig. A.3).
.
In particular, we carry out numerical simulations of the far-field
patterns fed by corrugated horns located at three different positions
in the focal plane ranging from very close to the optical axis, to the
edge of the field of view (see Fig. A.3).
This will allow us to draw some general conclusions about the effect
of the feed positioning on the preservation of the polarization
properties through the antenna. We emphasize that, despite
concentrating on the PLANCK experiment, our results can be useful for
other mm/cm-wave polarimetric experiments with similar optical
systems.
3.1 Effect of feed position and orientation
Table 2:
Same as Table 1, with
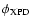 being
determined by the 2nd Method, as described in Sect. 2.2.
being
determined by the 2nd Method, as described in Sect. 2.2.
Table 3:
Same as Table 1, with
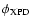 being
determined by the 3rd Method, as described in Sect. 2.2.
being
determined by the 3rd Method, as described in Sect. 2.2.
Table 4:
Misalignment angle between the y-axis of both
the feed and the far-field coordinate systems, for each position
of the feed in the focal plane. Feed positions are shown in
Fig. A.3.
Tables 1-3
display the values of the residual angle (
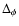 )
for all
the simulated cases. These values were computed using Eq. (10).
The corresponding values for
)
for all
the simulated cases. These values were computed using Eq. (10).
The corresponding values for
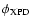 and
and
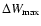 were
determined using the three different methods described in
Sect. 2.2. In each table, each
were
determined using the three different methods described in
Sect. 2.2. In each table, each
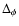 -column
shows the results for a different location of the feed in the
focal plane (see Fig. A.3).
We point out that, when using the 3rd Method, the main beam
pattern is integrated over a solid angle centered at boresight
(the north pole of the sphere) and down to a latitude
-column
shows the results for a different location of the feed in the
focal plane (see Fig. A.3).
We point out that, when using the 3rd Method, the main beam
pattern is integrated over a solid angle centered at boresight
(the north pole of the sphere) and down to a latitude
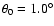 and
and
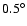 for the 30 and 100 GHz
feeds, respectively. These solid angles are chosen so as to include,
at least, all radiated power down to the FWHM (see Sect. 2.2).
for the 30 and 100 GHz
feeds, respectively. These solid angles are chosen so as to include,
at least, all radiated power down to the FWHM (see Sect. 2.2).
Our results show that the estimated differential rotation of the
polarization plane (see Sect. 2.3) in terms of the
residual angle,
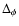 ,
depends strongly on the definition
adopted for maximum cross-polarization discrimination and the associated
angle,
,
depends strongly on the definition
adopted for maximum cross-polarization discrimination and the associated
angle,
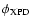 .
In practice, we see from the calculations that the 3rd Method gives what
one would intuitively expect from a robust estimate of cross-polarization:
there is no differential rotation of the polarization plane in any
of the cases studied (i.e., the residual angle,
.
In practice, we see from the calculations that the 3rd Method gives what
one would intuitively expect from a robust estimate of cross-polarization:
there is no differential rotation of the polarization plane in any
of the cases studied (i.e., the residual angle,
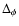 is
found to be compatible with zero in all cases, see
Table 3). In fact, the maximum value of
the differential rotation found (
is
found to be compatible with zero in all cases, see
Table 3). In fact, the maximum value of
the differential rotation found (
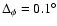 )
for
the 100 GHz feed at the off-axis positions 4 and 27 (see
Fig. A.3), is not significant given the errors,
typically of this order, coming from the accuracy in the computation
of the beam pattern itself as well as its finite sampling in
spherical cuts.
On the other hand, Methods 1 and 2 are misleading when measuring
diffuse polarization and they indicate a significant rotation of
the polarization plane, whose magnitude varies systematically
with frequency and position in the focal plane (see
Tables 1 and 2).
)
for
the 100 GHz feed at the off-axis positions 4 and 27 (see
Fig. A.3), is not significant given the errors,
typically of this order, coming from the accuracy in the computation
of the beam pattern itself as well as its finite sampling in
spherical cuts.
On the other hand, Methods 1 and 2 are misleading when measuring
diffuse polarization and they indicate a significant rotation of
the polarization plane, whose magnitude varies systematically
with frequency and position in the focal plane (see
Tables 1 and 2).
![\begin{figure}
\par\subfigure[1st Method]{\includegraphics[width=5.6cm,clip]{dif...
...d Method]{\includegraphics[width=5.6cm,clip]{dif045_1001int.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg99.gif) |
Figure 1:
Differences (in dB units) between main beam patterns in far
field reference frames rotated by
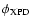 ,
for feeds at
different positions and orientations in the focal plane.
Cross-polarization definitions and ,
for feeds at
different positions and orientations in the focal plane.
Cross-polarization definitions and
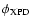 angles are
determined by Methods 1 and 3 described in Sect. 2.2
(see Tables 1 and 3).
angles are
determined by Methods 1 and 3 described in Sect. 2.2
(see Tables 1 and 3). |
| Open with DEXTER |
In summary, we see that the 3rd Method turns out to be an appropriate
definition of cross-polarization and the related cross-polar rejection
angle for measurements of diffuse polarized emission. Furthermore,
making use of this definition, we conclude that the PLANCK
telescope does not introduce any second order (i.e. detector
orientation dependent) spurious polarization.
For the absolute orientation of the polarization plane
of the sky signal there is a misalignment angle introduced by
the telescope optics. Referring to Figs. A.1 and A.2, by misalignment angle we mean the angle, as
seen from the the xy-plane of the line-of-sight Cartesian coordinate
system of the telescope![[*]](/icons/foot_motif.gif) (
(
 ),
between the y-axis of the feed coordinate system (e.g. f1) and
the y-axis of the corresponding coordinate system of the sky beam
pattern (mb1 as corresponding to f1).
),
between the y-axis of the feed coordinate system (e.g. f1) and
the y-axis of the corresponding coordinate system of the sky beam
pattern (mb1 as corresponding to f1).
Table 4 shows the results for the misalignment
angles, computed for each simulated position of the feed in the
focal plane. They take into account the values of maximal
cross-polarization rejection for the non-rotated feed,
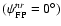 (as determined using the 3rd Method).
It can be seen that the bias or misalignment angle of the
polarization plane increases as the feed moves from
the center (on-axis) towards the edge of the focal plane
(as we would expect), yielding an upper limit of about
(as determined using the 3rd Method).
It can be seen that the bias or misalignment angle of the
polarization plane increases as the feed moves from
the center (on-axis) towards the edge of the focal plane
(as we would expect), yielding an upper limit of about 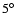 .
Note that these results are independent of feed orientation and
frequency, within the errors (see Table 3),
which means that they do not affect the differential measurement
of polarization for each position of the feed. In addition, this
bias can always be corrected by rearranging the orientation of
each detector in the focal plane.
.
Note that these results are independent of feed orientation and
frequency, within the errors (see Table 3),
which means that they do not affect the differential measurement
of polarization for each position of the feed. In addition, this
bias can always be corrected by rearranging the orientation of
each detector in the focal plane.
3.2 Predicting far-field beam patterns
PO modeling of a large telescope such as PLANCK requires
computer intensive calculations with processing time scaling
as the fourth power of frequency. Moreover, modeling the
response of a focal plane array including many detectors
at several frequencies becomes an extremely demanding task.
Therefore, we investigate to what extent it is possible to use
a known (pre-computed) model of the main beam response (i.e., the
peak of detector angular response), for a given feed and focal
plane layout, to estimate or predict the sky main beam patterns
for that detector in different focal plane configurations, i.e.,
for the feed in the same off-axis position but different
polarization sensitivity directions.
In order to do so, we must assess the similarity between the
main beam patterns for different orientations of the
radiating feed in the focal plane. At each frequency, we
compare the beam pattern generated from two different feed
orientations for which the far-field reference frame
has been rotated by
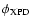 (with its co-polar component
aligned with the principal plane of polarization).
Figure 1 shows the differences (in dB units)
between the power contours of several pairs of main beam patterns.
For illustrative purposes, we display the difference contours for
the case where the definitions of maximum cross-polarization
discrimination discussed in Sect. 2.2 disagree the most
(Figs. 1a, b) and
for the cases where the feeds are closest to the center of the focal
plane (Figs. 1c, d).
(with its co-polar component
aligned with the principal plane of polarization).
Figure 1 shows the differences (in dB units)
between the power contours of several pairs of main beam patterns.
For illustrative purposes, we display the difference contours for
the case where the definitions of maximum cross-polarization
discrimination discussed in Sect. 2.2 disagree the most
(Figs. 1a, b) and
for the cases where the feeds are closest to the center of the focal
plane (Figs. 1c, d).
As can be seen from Fig. 1, co-polar power
differences are always below 3.0 dB, except for a few point-like
regions, while cross-polar power mismatches are locally found up to 15 dB. Since cross-polarization peaks are typically about 30 dB
bellow the co-polar peak (see
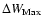 values in
Table 3), it is sufficient to concentrate
on the dominant (co-polar) component of the polarized beam
pattern to estimate how much the beam pattern changes as a
function of the feed orientation.
No significant difference is found between the co-polar patterns
in Figs. 1a and b
and therefore we conclude that these difference contours cannot
be used to determine a robust definition for cross-polarization.
values in
Table 3), it is sufficient to concentrate
on the dominant (co-polar) component of the polarized beam
pattern to estimate how much the beam pattern changes as a
function of the feed orientation.
No significant difference is found between the co-polar patterns
in Figs. 1a and b
and therefore we conclude that these difference contours cannot
be used to determine a robust definition for cross-polarization.
More interestingly, from Fig. 1,
we conclude that using a pre-computed sky main beam pattern
from a feed at a given frequency and orientation in the focal plane
(and the corresponding maximal cross-polarization rejection angle,
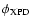 ), it is possible to predict the shape of the main
beam pattern in the sky for any other orientation of the same feed,
within
), it is possible to predict the shape of the main
beam pattern in the sky for any other orientation of the same feed,
within  3 dB (
3 dB (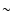 15 dB) for the the co-polar
(cross-polar) pattern.
15 dB) for the the co-polar
(cross-polar) pattern.
3.3 Spurious optical polarization
The presence of cross-polarization and the differences in the shape of
the polarized beams patterns from a given feed with different
orientations around its symmetry axis will result in an observation of
a polarized signal not present in the sky, but rather generated by the
instrument asymmetries. This is what we shall call "spurious optical
polarization''. We quantify this effect in the modeled telescope as
the response of the system to a diffuse unpolarized sky signal,
in terms of normalized Stokes parameters.
Following standard conventions (Kraus 1982), PLANCK will measure Stokes parameters
I, Q and U by combining the output of four linearly polarized
detectors; a first pair having principal planes of polarization
at right angles to each other and a second pair with principal
planes of polarization at right angles as well, but rotated by
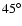 with respect to the first pair of detectors.
For this purpose we shall use the simulations results for the 30and 100 GHz feeds at different positions in the focal plane unit
and orientations
with respect to the first pair of detectors.
For this purpose we shall use the simulations results for the 30and 100 GHz feeds at different positions in the focal plane unit
and orientations
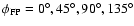 .
.
Table 5:
Normalized Stokes parameters qB and uB for
different limits of integration 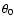 ;
at FWHM,
;
at FWHM, 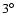 and
and
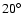 .
These parameters represent the optical spurious
polarization introduced by PLANCK telescope optics for the studied
focal plane configuration (in bold) and other study cases (see text).
.
These parameters represent the optical spurious
polarization introduced by PLANCK telescope optics for the studied
focal plane configuration (in bold) and other study cases (see text).
The power available to the detectors is proportional
to the convolution of the beam with the sky signal, i.e.
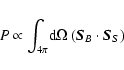 |
(11) |
where
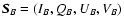 is the Stokes vector of the
beam on the sky and
is the Stokes vector of the
beam on the sky and 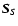 is that of the sky signal. If the sky
signal is uniform, then
is that of the sky signal. If the sky
signal is uniform, then
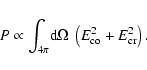 |
(12) |
We shall use normalized Stokes parameters,
qB = QB/IB, and
uB =
UB/IB, to characterize the spurious optical polarization,
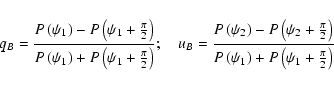 |
(13) |
where
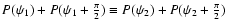 and
and 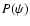 is the total power integrated over the beam
(within a co-latitude range
is the total power integrated over the beam
(within a co-latitude range
![$[ -\theta_0 ; +\theta_0 ]$](/articles/aa/full/2003/25/aa3143/img67.gif) ).
).
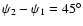 is the relative phase shift
in the polarization planes.
The calculated estimates of those parameters for the modeled feeds
are shown in Table 5 for different limits of
integration
is the relative phase shift
in the polarization planes.
The calculated estimates of those parameters for the modeled feeds
are shown in Table 5 for different limits of
integration 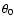 .
It can be seen that qB and uB depend
on the chosen integration limit, if it less than a few times the FWHM.
.
It can be seen that qB and uB depend
on the chosen integration limit, if it less than a few times the FWHM.
![\begin{figure}
\par\subfigure[]{\includegraphics[width=5.4cm,clip]{stu_304_3.eps...
...
\subfigure[]{\includegraphics[width=5.4cm,clip]{stq_1004_3.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg118.gif) |
Figure 2:
Contour plot of the distribution of the normalized Stokes
parameters across the main beam (with
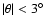 ). The plot
shows one of the parameters (uB or qB) for the two worst study
cases in Table 5; a) the 30 GHz feed on position 4
and c) the 100 GHz feed on position 27. The same parameters are also
shown for the feeds in their real positions in the studied PLANCK focal
plane layout: b) the 30 GHz feed on position 27 and d) the 100 GHz
feed on position 4. ). The plot
shows one of the parameters (uB or qB) for the two worst study
cases in Table 5; a) the 30 GHz feed on position 4
and c) the 100 GHz feed on position 27. The same parameters are also
shown for the feeds in their real positions in the studied PLANCK focal
plane layout: b) the 30 GHz feed on position 27 and d) the 100 GHz
feed on position 4. |
| Open with DEXTER |
Table 5 also shows that the spurious polarization
depends strongly on location and frequency and that a high level of
up to 5% polarized contamination of the diffuse unpolarized intensity
is found for feeds at 30 and 100 GHz. The observed large variation
of this level across the focal plane seems, at first glance, difficult
to explain. In order to illustrate the issue, we show in
Fig. 2 the dependence of qB and uB across the main beam for the two worst cases in
Table 5; the 30 GHz feed on position 4
(Fig. 2a) and the 100 GHz feed on position 27
(Fig. 2c) and for the cases where the two feeds are in their actual positions in the studied PLANCK focal plane
layout; the 30 GHz feed on position 27 (Fig. 2b)
and the 100 GHz feed on position 4 (Fig. 2d).
It can be seen that qB and uB exhibit large fluctuations across
the main beam, which may cancel out more effectively when
integrated in angular space. The final integrated values of qBand uB will therefore depend on the fine details of the modeled
patterns, which are affected by the exact location of the feed in
the focal plane. We can expect that, in a real system where the
detectors are sensitive to wide bandwidths, part of the fluctuations
will be averaged out. In addition, it is not clear to what extent the
fine details of the models will be reproduced by the real physical
systems. For these reasons we can consider that the levels of spurious
optical polarization here estimated are very conservative upper limits.
It is however emphasized that, given the expected small relative
amplitude of the polarized with respect to the unpolarized CMB signal (about 10%), this upper limit of optically-induced
polarization cannot be ignored. At these frequencies, there are
two large scale sources of unpolarized diffuse components in the sky:
the isotropic CMB emission (at
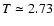 K) and the CMB dipole,
a Doppler temperature anisotropy in the sky of amplitude
K) and the CMB dipole,
a Doppler temperature anisotropy in the sky of amplitude 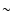
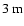 K
(see, e.g. Lineweaver et al. 1996).
As PLANCK scans the sky, spurious optical polarization will
introduce a constant bias for the former and a slowly varying
bias for the latter. The level of these biases (
K
(see, e.g. Lineweaver et al. 1996).
As PLANCK scans the sky, spurious optical polarization will
introduce a constant bias for the former and a slowly varying
bias for the latter. The level of these biases (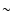
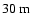 K and
K and
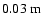 K, for each 1% of spurious polarization) is quite large
compared to the expected CMB polarized signal of
K, for each 1% of spurious polarization) is quite large
compared to the expected CMB polarized signal of 
 K.
Note however that a constant bias does not affect the measurements
of small scale anisotropies, and a slowly varying bias is likely
to be easily removable using calibration procedures.
K.
Note however that a constant bias does not affect the measurements
of small scale anisotropies, and a slowly varying bias is likely
to be easily removable using calibration procedures.
The main source of concern in the detection of polarized sky signals
for a PLANCK-like experiment will arise from the spurious signal that
leaks from the measured unpolarized intensity itself.
The percentage of spurious polarization is, in the very
worst cases, only factors of a few smaller than the percentage of
polarization signal. Potentially this spurious level will ultimately
introduce a fundamental limit on the measurement of CMB polarization
anisotropies at sub-degree scales, i.e. at angular scales
comparable to the main-beam size. It is however emphasized that
the spurious polarization estimated for the actual positions of the
PLANCK feeds is much lower than in the worst case scenario, and it is
certainly below the expected polarized CMB signal. Moreover, this
situation should be further improved if we take into account other
relevant effects such as the large detector bandwidth that tends to
suppress to a large extent the small-scale angular variations observed
on monochromatic radiation patterns.
3.4 Model uncertainties
This study has not taken into account imperfections in the optics
due to the effects of dust contamination, microcracks, asymmetry
of the focal plane, or the effects of optical misalignment, since
it is today very difficult to model such effects. However,
qualitatively it can be argued that:
- As long as dust grains are not elongated and preferentially
aligned, their effect is largely to scatter power from the main beam
into the far sidelobes. In this study we are interested in the
polarization introduced through the main beam and therefore dust
can be safely ignored.
- The effect of microcracks is qualitatively similar to that of
dust with the exception that elongation and preferential
alignment are expected. Fortunately, in the case of PLANCK, all technological
indications are that no microcracks will be present.
- Misalignment introduces additional aberration in the optics that
translates into distortion of the main beam. Distortion is always
related to depolarisation and therefore it is of potential concern.
However, the aberrations introduced by misalignment are, by design
and test, kept at a level which is a small fraction of the intrinsic
optical distortions. Therefore it is reasonable in this
initial study to assume that it will remain a second order effect.
- An asymmetric focal plane will likely introduce differential
effects in the response of a single horn to different planes of
polarization. However, the effects of mutual coupling between
PLANCK horns that are adjacent in the focal plane are kept, by
design, at a rather low level with respect to the main beam (i.e,
at least 30 dB below peak) and we assume here that they are not
affecting the main results of this study.
In PLANCK, the higher frequency detector chains include also a number
of optical elements (such as filters, detector embedding structures,
cavities, etc.) which potentially introduce polarization effects.
Such chains have been measured and found to introduce very low levels
of cross-polarization. However, since they are of the same order as
the effects listed above, they should be included in future simulations.
Finally, we emphasize that this study is based on a numerical
model, which naturally is subject to some degree of uncertainty
when compared to reality. In this respect, the software used for
our simulations (GRASP) is today considered to be the benchmark
software tool for analysis of large antenna systems. Recent
studies (Murphy et al. 2001) have been carried out to investigate the
reliability of a variety of software tools, including GRASP8, in
modelling optical systems in the submillimetre wave band. In these
studies, simulated results from different software packages were
compared to each other as well as to experimental measurements.
These studies show GRASP to be the most reliable package, agreeing
with experimental measurements down to a -40 dB level in
predicting the amplitude pattern and showing the best agreement in
phase measurements. Moreover, the same study has shown that GRASP8
is the only available package capable of handling polarization in
the case of off-axis reflectors systems.
Therefore, in terms of model uncertainties, it is considered that
this study is as close to real as can be expected, within the
assumptions made. However, it is acknowledged that the real system
performance must ultimately be measured. A comprehensive
pre-launch test campaign is planned for PLANCK; these measurements
will be later combined with in-flight characterisation to obtain
the final system performance.
4 Summary and conclusions
We have studied the systematic effects introduced by the PLANCK optical
system in the measurement of polarized signals.
For the purpose of this study we have carried out PO simulations of the
former PLANCK telescope configuration with the 30 and 100 GHz feeds at
three different feed locations (see Fig. A.3) and several
orientations. From the analysis of these simulations, our results
(see Sect. 3) yield the following main conclusions:
Further studies on the impact of PLANCK optics on the detection of
polarization should consider the following topics:
- Use of the final optical configuration of the telescope, in particular
the focal plane, has recently undergone some modifications.
- Take into account second order effects (already discussed in
Sect. 3.4) that may be important to the detection of
polarization in the main beam region.
- Extending the studied region further into the sidelobes, to
include any second order effects that may have an impact on
the detection of polarization in this regions.
Finally the results of these studies will be compared to
measurements obtained on qualification models of the PLANCK optics
during a pre-launch test campaign, planned to start in 2004.
Acknowledgements
We wish to thank F. Villa, M. Bersanelli, R. Mandolesi for
significant comments on the manuscript; the referee, J.
Delabrouille for useful comments on the manuscript;
G. Giardino, and A. Martín Polegre for substantial help with the
GRASP8 modelling. PF acknowledges a post-doctoral CMBNet
fellowship from the European Commission. GF acknowledges a
scholarship from the Fundação para a Ciência e
Tecnologia (FCT).
Appendix A: GRASP8 simulations
A.1 Simulations setup and inputs
As stated before, the telescope configuration used for the present
analysis is an early version of the current PLANCK telescope design.
It corresponds to a dual reflector optical system with an offset
aplanatic geometry. The exact telescope configuration is shown in
Table A.1.
Figures A.1 and A.2 show two different views
of the PLANCK Telescope system, with the 100 GHz feed located in three
different positions in the focal plane (positions 1, 4 and 27,
also shown with more detail in Fig. A.3).
Table A.1:
Early PLANCK Telescope configuration used for the
present study (current telescope dimensions are slightly different).
Reference frames f1, f4 and f27 are used to describe the three
different positions of the feed in the focal plane while reference
frames mb1, mb4 and mb27 are used to describe the sky beam patterns,
the latter having their z-axis (in blue) always pointing to the
center of the main beam in the sky, set to be the maximum of the
co-polar pattern.
Coordinate systems f1, f4 and f27 are defined on the basis of the
coordinate system located on the vertex of the ellipse that subtends
the primary mirror (
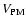 )
while mb1, mb4 and mb27, are defined on
the basis of the coordinate system located on the center of the
primary mirror (
)
while mb1, mb4 and mb27, are defined on
the basis of the coordinate system located on the center of the
primary mirror (
 )
which has the same orientation as
)
which has the same orientation as
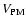 (see Figs. A.1 and A.2).
Furthermore, the orientation of
(see Figs. A.1 and A.2).
Furthermore, the orientation of
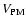 is the same as the spacecraft
coordinate system rotated by
is the same as the spacecraft
coordinate system rotated by
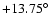 around its y-axis.
around its y-axis.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{asideview.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg126.gif) |
Figure A.1:
Cross-section of the objects that define the Alcatel version
of PLANCK telescope in the GRASP8 model of our study. Besides the
primary (PM) and secondary (SM) mirrors, this plot includes the
100 GHz feed in three different positions in the focal plane with the
corresponding coordinate systems for the feed positions (f1, f4, f27)
and the different orientations of the main beam in the sky
(mb1, mb4, mb27). It also includes the fixed coordinate systems
for the vertex (
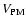 )
and the center ( )
and the center (
 )
of the primary
mirror and for the spacecraft (SC). )
of the primary
mirror and for the spacecraft (SC). |
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{anobliqueview.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg127.gif) |
Figure A.2:
Oblique view of the objects that define the Alcatel version of
PLANCK telescope in the GRASP8 input file of this study, as shown in
the previous Fig. A.1. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{LFIfocalplane.ps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg128.gif) |
Figure A.3:
Former design of PLANCK Telescope LFI focal plane
showing the detector positions used for this study: on the top
left-hand corner, positions 27 and 4 with the 30 and 100 GHz
detectors, respectively and position 1, closer to the center
of the focal plane unit, with the HFI 857 GHz detector. |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{pattern30.eps}\hspace*{2mm}
\includegraphics[width=6.8cm,clip]{pattern100.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg129.gif) |
Figure A.4:
Contour plots of the far field radiation pattern
(
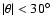 )
when the feeds radiate directly to the sky,
i.e., the input polarized signal does not go through the telescope
system. )
when the feeds radiate directly to the sky,
i.e., the input polarized signal does not go through the telescope
system. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{signal30_20.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{signal100_20.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg130.gif) |
Figure A.5:
Polar cuts, at
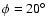 ,
of the contour plots
in Fig. A.4. ,
of the contour plots
in Fig. A.4. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{psi0_3027.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{psi0_1004.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg131.gif) |
Figure A.6:
Polar cuts at
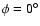 of the 30 and 100 GHz
sky radiation patterns when the input polarized signal goes through
the telescope system.
of the 30 and 100 GHz
sky radiation patterns when the input polarized signal goes through
the telescope system. |
For all simulations in this study, we used the polar coordinates
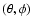 that can range to cover the whole sky
(i.e.,
that can range to cover the whole sky
(i.e.,
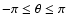 and
and
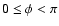 )
)![[*]](/icons/foot_motif.gif) producing ASCII data files that have
a structure such as to hold the values of the two complex amplitudes
(real and imaginary) of the two components of the beam pattern
(co- and cross-polar), for all given sets of points
producing ASCII data files that have
a structure such as to hold the values of the two complex amplitudes
(real and imaginary) of the two components of the beam pattern
(co- and cross-polar), for all given sets of points
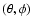 .
All simulations were done in order to determine the radiation pattern
in the sky area around the main beam. To sample this part of the sky,
coordinate
.
All simulations were done in order to determine the radiation pattern
in the sky area around the main beam. To sample this part of the sky,
coordinate 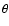 was chosen to range within the limits
was chosen to range within the limits
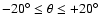 in a set of 401 points with
intervals of
in a set of 401 points with
intervals of
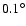 while coordinate
while coordinate 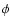 ranged within
ranged within
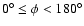 in a set of 36 polar cuts
separated by
in a set of 36 polar cuts
separated by 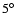 .
.
In a GRASP8 simulation, the scattered field can be calculated by using
Physical Optics (PO) combined with the Physical Theory of Diffraction
(PTD) or, alternatively, using Geometrical Optics (GO) combined with
the Geometrical Theory of Diffraction (GTD).
According to TICRA (1997), for focused reflector systems PO/PTD
is intended to be used in the far field around beam maxima, whereas
GTD can be used in the side-lobe region. For these reasons and since
we were only interested in the main beam sky area, our simulations
were done with PO/PTD calculations.
In what concerns the density of the PO integration grid, to determine
the number of points for which the PO currents are calculated in each
reflecting surface, we referred to a formula given by TICRA (1997)
where the wavelength, the reflector diameter and the maximum latitude,
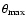 ,
are input parameters in the determination of the
minimum number of points for which the PO integration converges.
,
are input parameters in the determination of the
minimum number of points for which the PO integration converges.
To simulate the conical corrugated horns used in the PLANCK telescope,
the input radiation signal of the feeds used in our simulations
had the form of a spherical wave expansion.
Figures A.5 and A.4 show the far field
radiation pattern when the input signal radiates directly from the
feed to the sky, without going through the telescope system;
Fig. A.5 shows the plot of the polar cut
at
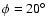 while Fig. A.4 shows the
whole contour in the (U,V) plane.
while Fig. A.4 shows the
whole contour in the (U,V) plane.
Note that to project the polar coordinate system
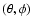 onto the (U,V) plane we have the following transformation,
onto the (U,V) plane we have the following transformation,
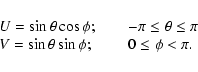 |
(A.1) |
In Figs. A.4 and A.5, note that the
beam maxima, the co-polar peaks, are not centered at
(U,V)=(0,0)nor at latitude
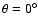 .
This off-center positioning
of the beam pattern in the coordinate system
.
This off-center positioning
of the beam pattern in the coordinate system
 when the feeds
radiate directly to the sky is due to the off-axis positioning
of the feeds in this same reference frame.
When the radiation pattern goes through the telescope system instead
of going directly from the feed to the sky, a much smaller off-center
positioning of the beam can be observed in the coordinate system
when the feeds
radiate directly to the sky is due to the off-axis positioning
of the feeds in this same reference frame.
When the radiation pattern goes through the telescope system instead
of going directly from the feed to the sky, a much smaller off-center
positioning of the beam can be observed in the coordinate system
 .
However, in order to have a centered beam maximum in all
plots and contours, for each of the three different feed positions
in the focal plane (1, 4 and 27), the coordinate system
.
However, in order to have a centered beam maximum in all
plots and contours, for each of the three different feed positions
in the focal plane (1, 4 and 27), the coordinate system
 was reoriented in order to always have the z-axis pointing to the
co-polarization power peak. This procedure originated the three
different coordinate systems (mb1, mb4 and mb27), already mentioned
before
was reoriented in order to always have the z-axis pointing to the
co-polarization power peak. This procedure originated the three
different coordinate systems (mb1, mb4 and mb27), already mentioned
before![[*]](/icons/foot_motif.gif) .
.
A.2 Simulations outputs and results
Figure A.6 shows the far field radiation patterns
when the input polarized signal goes through the telescope system.
It can be seen that, as a result of the far field reference frame
reorientation mentioned in the previous section, the co-polar peaks
are always centered at
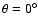 whether the feed is on
position 27 (left plot) or on position 4 (right plot).
We show the contour plots of the far field
radiation pattern around the main beam for various simulations.
In particular, Figs. A.7 and A.8 show
radiation patterns in the non-rotated far field reference frame
and in the reference frame rotated by the
whether the feed is on
position 27 (left plot) or on position 4 (right plot).
We show the contour plots of the far field
radiation pattern around the main beam for various simulations.
In particular, Figs. A.7 and A.8 show
radiation patterns in the non-rotated far field reference frame
and in the reference frame rotated by the
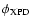 angle. This
angle is determined by each one of the three different methods described in
Sect. 2.1. Plots are shown side by side for an easier comparison.
angle. This
angle is determined by each one of the three different methods described in
Sect. 2.1. Plots are shown side by side for an easier comparison.
As expected, for simulations with a non-rotated
feed, i.e.,
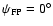 (Fig. A.8), the
highest peak is at the co-polar direction before
and after the far field reference frame is rotated by
(Fig. A.8), the
highest peak is at the co-polar direction before
and after the far field reference frame is rotated by
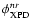 (being
(being
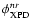 always a small angle),
while for simulations with a feed orientation of
always a small angle),
while for simulations with a feed orientation of
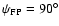 (Fig. A.7), the highest peak is at the
cross-polar direction before the far field reference
frame is rotated by
(Fig. A.7), the highest peak is at the
cross-polar direction before the far field reference
frame is rotated by
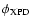 which then aligns the highest peak with the
co-polar direction.
On the other hand and also as expected, for simulations with a feed
orientation of
which then aligns the highest peak with the
co-polar direction.
On the other hand and also as expected, for simulations with a feed
orientation of
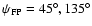 (Fig. A.9), the co- and cross-polar
patterns have similar peaks before the rotation of the far field
reference frame by
(Fig. A.9), the co- and cross-polar
patterns have similar peaks before the rotation of the far field
reference frame by
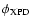 .
.
![\begin{figure}
\par\subfigure[]{\includegraphics[width=5.4cm,clip]{90nr3027.eps}...
...ubfigure[]{\includegraphics[width=5.4cm,clip]{90r3027newint.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg142.gif) |
Figure A.7:
Contour plots of the Co- and Cross-polar patterns around
the main beam (
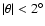 )
for the 30 GHz feed rotated
by )
for the 30 GHz feed rotated
by
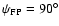 at position 27. The figure shows
a) the beam pattern in the non-rotated far field reference frame and
the same beam pattern in the far field reference frame rotated by
b)
at position 27. The figure shows
a) the beam pattern in the non-rotated far field reference frame and
the same beam pattern in the far field reference frame rotated by
b)
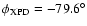 (see Table 1),
c)
(see Table 1),
c)
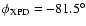 (see
Table 2) and
d)
(see
Table 2) and
d)
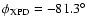 (see
Table 3).
(see
Table 3). |
![\begin{figure}
\par\subfigure[]{\includegraphics[width=5.4cm,clip]{0nr1004.eps} ...
...subfigure[]{\includegraphics[width=5.4cm,clip]{0r1004newint.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg143.gif) |
Figure A.8:
Same as Fig. A.7 (with
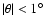 )
for the 100 GHz non-rotated feed ( )
for the 100 GHz non-rotated feed (
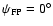 )
at position 4.
In this figure the far field reference frame is rotated by
b) )
at position 4.
In this figure the far field reference frame is rotated by
b)
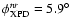 (see Table 1),
c)
(see Table 1),
c)
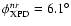 (see Table 2) and
d)
(see Table 2) and
d)
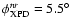 (see Table 3).
(see Table 3). |
![\begin{figure}
\par\subfigure[]{\includegraphics[width=5.4cm,clip]{45nr1001.eps}...
...ubfigure[]{\includegraphics[width=5.4cm,clip]{135r301newint.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg144.gif) |
Figure A.9:
Same as Figs. A.7 and A.8
for the 100 GHz feed rotated by
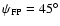 (above)
and the 30 GHz feed rotated by
(above)
and the 30 GHz feed rotated by
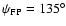 (below),
both at position 1. In this figure the far field reference
frame is rotated by b)
(below),
both at position 1. In this figure the far field reference
frame is rotated by b)
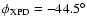 and d)
and d)
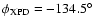 (see Table 3).
(see Table 3). |
-
Bennett, C. L., Kogut, A., Hinshaw, G., et al. 1994, ApJ, 436, 423
In the text
NASA ADS
-
Carretti, E., Tascone, R., Corbiglioni, S., et al. 2001, New Astron., 6, 173
In the text
NASA ADS
-
Couchot, F., Delabrouille, J., Kaplan, J., & Revenu, B. 1999, A&AS, 135, 579
In the text
NASA ADS
-
Crittenden, R., Bond, J. R., Davis, R. L., Efstathiou, G., & Steinhardt P. J. 1993, Phys. Rev.
Lett., 71, 324
In the text
NASA ADS
-
Crittenden, R., Davis, R. L., & Steinhardt, P. J. 1993, ApJ, 417, L13
NASA ADS
-
de Oliveira-Costa,Tegmark, M., Zaldarriaga, M., et al. 2003, Phys. Rev. D, 67, 023003
In the text
-
Fosalba, P., Doré, O., & Bouchet, F. R. 2002, Phys. Rev. D, 65, 63003
In the text
-
Hedman, M. M., Barkats, D., Gundersen, J. O., Staggs, S. T., & Winstein, B. 2001, ApJ, 548, L111
In the text
NASA ADS
-
Hu, W. 2000, ApJ, 529, 12
In the text
NASA ADS
-
Kaplan, J., & Delabrouille, J. 2001, in Astrophysical Polarized Backgrounds, ed. S. Cecchini, S. Cortiglioni, R. Sault, & C. Sbarra, AIP Conf. Proc., 609, 209
In the text
-
Keating, B. G., O'Dell, C. W., de Oliveira-Costa, A., et al. 2001, ApJ, 560, L1
In the text
NASA ADS
-
Kovac, J., Leitch, E. M., Pryke, C., & Carlstrom, J. E. 2002, Nature, 420, 772
In the text
NASA ADS
-
Kraus, J. D. 1982, Radio Astronomy (Ohio, USA)
In the text
-
Leahy, J. P., Yurchenko, V., Hastie, M. A., Bersanelli, M., & Mandolesi, N. 2002, Astrophysical Polarized Backgrounds, held 9-12 October, 2001 in Bologna Italy, ed. S. Cecchini, S. Cortiglioni, R. Sault, & C. Sbarra, AIP Conf. Proc., 609 (Melville, NY: American Institute of Physics), 215
In the text
-
Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511
In the text
-
Lineweaver, C. H., Tenorio, L., Smoot, G. F., et al. 1996, ApJ, 470, 38
In the text
NASA ADS
-
Ludwig, A. C. 1973, IEEE Trans. on Ant. and Prop., vol. AP-21, 116
In the text
-
Murphy, J. A., O'Sullivan, C., Henry, D., et al. 2000, Far IR Optics Design and Verification, Final Report of ESA TRP study contract number 13043/98/NL/NB (Phase 1). Note: the results of Phase 2 of the study, including the comparison of model to measurement, will be released in mid-2004.
In the text
-
Rees, M. J. 1968, ApJ, 153, L1
In the text
NASA ADS
-
Scott, P. F., Carreira, P., Cleary, K., et al. 2003, MNRAS, in press
In the text
-
Tauber, J. 2000, The Extragalactic Infrared Background and its Cosmological Implications, IAU Symp., 204 (England: Manchester)
In the text
-
TICRA Engineering Consultants 1997, GRASP8 Software User Manual, Version 8.0.4 (Denmark: Copenhagen)
In the text
-
Yurchenko, V. 2001, AIP Conf. Proc. Experimental Cosmology at Millimeter Wavelengths: 2K1BC Workshop (Italy: Breuil-Cervinia), 616, 234
In the text
-
Zaldarriaga, M. 1997, Phys. Rev. D, 55, 1822
In the text
-
Zaldarriaga, M., Spergel, D. N., & Seljak, U. 1997, ApJ, 488, 1
In the text
NASA ADS
Copyright ESO 2003
![$\displaystyle \Delta W_{{\rm max}}=\Delta W (\phi_{{\rm XPD}}) = 10~\log_{10}\l...
...}_{{\rm cr}}E^{{\rm rot*}}_{{\rm cr}}\right)}
\right]_{(\phi=\phi_{{\rm XPD}})}$](/articles/aa/full/2003/25/aa3143/img59.gif)
![$\displaystyle %
\Delta W_{{\rm max}}=\Delta W \left(\phi_{{\rm XPD}}\right) =
1...
...eta_0}\int_0^{\pi}
\left(E^{{\rm rot}}_{{\rm cr}}\right)^2~{\rm d}\Omega\right]$](/articles/aa/full/2003/25/aa3143/img65.gif)
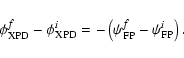
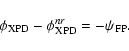
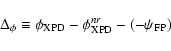
![\begin{figure}
\par\subfigure[1st Method]{\includegraphics[width=5.6cm,clip]{dif...
...d Method]{\includegraphics[width=5.6cm,clip]{dif045_1001int.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg99.gif)
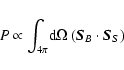
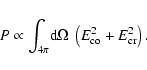
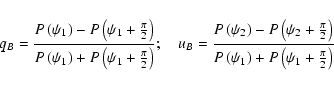
![\begin{figure}
\par\subfigure[]{\includegraphics[width=5.4cm,clip]{stu_304_3.eps...
...
\subfigure[]{\includegraphics[width=5.4cm,clip]{stq_1004_3.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg118.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{asideview.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg126.gif)
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{anobliqueview.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg127.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{LFIfocalplane.ps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg128.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{pattern30.eps}\hspace*{2mm}
\includegraphics[width=6.8cm,clip]{pattern100.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg129.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{signal30_20.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{signal100_20.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg130.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{psi0_3027.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{psi0_1004.eps}
\end{figure}](/articles/aa/full/2003/25/aa3143/Timg131.gif)
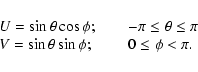
![\begin{figure}
\par\subfigure[]{\includegraphics[width=5.4cm,clip]{90nr3027.eps}...
...ubfigure[]{\includegraphics[width=5.4cm,clip]{90r3027newint.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg142.gif)
![\begin{figure}
\par\subfigure[]{\includegraphics[width=5.4cm,clip]{0nr1004.eps} ...
...subfigure[]{\includegraphics[width=5.4cm,clip]{0r1004newint.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg143.gif)
![\begin{figure}
\par\subfigure[]{\includegraphics[width=5.4cm,clip]{45nr1001.eps}...
...ubfigure[]{\includegraphics[width=5.4cm,clip]{135r301newint.eps} }\end{figure}](/articles/aa/full/2003/25/aa3143/Timg144.gif)