A&A 404, 975-990 (2003)
DOI: 10.1051/0004-6361:20030512
Stellar evolution with rotation
X. Wolf-Rayet star populations at solar metallicity
G. Meynet - A. Maeder
Geneva Observatory, 1290 Sauverny, Switzerland
Received 5 February 2003 / Accepted 6 March 2003
Abstract
We examine the properties of Wolf-Rayet (WR) stars predicted by models
of rotating stars taking account of the new mass loss rates for O-type stars
and WR stars (Vink et al. 2000, 2001; Nugis & Lamers 2000)
and of the wind anisotropies induced by rotation. We find that the rotation velocities vof WR stars are modest, i.e. about 50 km s-1, not very dependent on the initial vand masses. For the most massive stars, the evolution of v is very strongly influenced
by the values of the mass loss rates; below 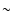 12
12  the evolution of rotation
during the MS phase and later phases is dominated by the internal coupling. Massive stars
with extreme rotation may skip the LBV phase.
the evolution of rotation
during the MS phase and later phases is dominated by the internal coupling. Massive stars
with extreme rotation may skip the LBV phase.
Models having a typical v for the O-type stars have WR lifetimes on the average two times longer
than for non-rotating models. The increase of the WR lifetimes is mainly due to that of
the H-rich eWNL phase. Rotation allows a transition WN/WC phase to be present for
initial masses lower than 60  .
The durations of the other WR subphases are
less affected by rotation. The mass threshold for forming WR stars is lowered from
37 to 22
.
The durations of the other WR subphases are
less affected by rotation. The mass threshold for forming WR stars is lowered from
37 to 22  for typical rotation. The comparisons of the predicted number ratios
WR/O, WN/WC and of the number of transition WN/WC stars show very good agreement with models with
rotation, while this is not the case for models with the present-day mass loss rates
and no rotation.
As to the chemical abundances in WR stars, rotation brings only very small changes
for WN stars, since they have equilibrium CNO values. However, WC stars with rotation
have on average lower C/He and O/He ratios. The luminosity distribution of WC stars
is also influenced by rotation.
for typical rotation. The comparisons of the predicted number ratios
WR/O, WN/WC and of the number of transition WN/WC stars show very good agreement with models with
rotation, while this is not the case for models with the present-day mass loss rates
and no rotation.
As to the chemical abundances in WR stars, rotation brings only very small changes
for WN stars, since they have equilibrium CNO values. However, WC stars with rotation
have on average lower C/He and O/He ratios. The luminosity distribution of WC stars
is also influenced by rotation.
Key words: stars: evolution - stars: rotation - stars: Wolf-Rayet
Wolf-Rayet stars play an important role in Astrophysics, as signatures
of star formation in galaxies and starbursts, as injectors of chemical elements and of the
radioactive isotope 26Al, as sources of kinetic energy into the interstellar medium and
as progenitors of supernovae and maybe as progenitors of 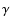 -ray bursts.
As rotation affects all outputs of stellar models (Meynet & Maeder 2000),
the main purpose of the present paper is to examine some
consequences of rotation on the properties of Wolf-Rayet (WR) stars.
-ray bursts.
As rotation affects all outputs of stellar models (Meynet & Maeder 2000),
the main purpose of the present paper is to examine some
consequences of rotation on the properties of Wolf-Rayet (WR) stars.
Let us recall
some difficulties faced by non-rotating stellar models of WR stars.
A good agreement between
the predictions of the stellar models for the WR/O number ratios and the observed
ones at different metallicities in regions of constant star formation was achieved
provided the mass loss rates were enhanced by about a factor of two during the MS
and WNL phases (Meynet et al. 1994). This solution, which at that time appeared
reasonable in view of the uncertainties pertaining to the mass loss rates, is no longer
applicable at present. Indeed, the estimates of the mass loss rates during the WR phase are
reduced by a factor of 2 to 3, when account is taken of the clumping effects
in the wind (Nugis & Lamers 2000; Hamann & Koesterke 1999).
Also, the mass loss rates for O-type stars have been substantially revised
(and in general reduced) by the new results of
Vink et al. (2000, 2001), who also account for the occurrence of bi-stability
limits which change the wind properties and mass loss rates.
In this new context, it is quite clear that with these new mass loss rates
the predicted numbers of WR stars by standard non-rotating models would be much
too low with respect to the observations.
A second difficulty of the standard models with mass loss was
the observed number of transition WN/WC stars. These stars simultaneously show some
nitrogen characteristics of WN stars and some carbon of the further WC stage.
The observed frequency of WN/WC stars among WR stars is around 4.4% (van der Hucht 2001), while
the frequency predicted by the standard models without extra mixing processes
are lower by 1-2 orders of magnitude (Maeder & Meynet 1994).
A third difficulty of the standard models as far as WR stars were concerned was that
there were relatively too many WC stars with respect to WN stars predicted (see the review
by Massey 2003). These difficulties are the signs that some process is missing
in these models.
We explore here the effects of rotation on the WR stars and their formation.
Rotation already improved
many predictions of the stellar models, bringing better agreement
with the observations. In particular, star models with rotation have at
last enabled us (Maeder & Meynet 2001)
to solve the long-standing problem of the large number of
observed red supergiants at low metallicities Z in the SMC, while current models
with any kind of reasonable mass loss usually predicted almost no red
supergiants at low Z.
Also, in addition to several
other points, the new models
also show significant He- and N-enhancements in O-type stars on the
MS (Heger & Langer 2000; Meynet & Maeder 2000), as well as in supergiants at various metallicities, as required by observations.
Section 2 summarizes the physics of these models. The evolution of the inner and surface
rotation is discussed in Sect. 3. The evolutionary tracks are shown in Sect. 4.
The effects of rotation on the WR star formation process and on the WR lifetimes
are discussed in Sect. 5. Comparisons with the observed WR populations are
performed in Sect. 6. Finally the predicted abundances in WR stars are discussed in Sect. 7.
The present grid of models at solar metallicity is based in general
on the same physical assumptions
as in the grid by Meynet & Maeder (2000, Paper V). However,
in addition we include here several improvements that have appeared since.
These are:
- As reference mass loss rates in the case of no rotation,
we use the recent data by Vink et al. (2000, 2001).
A bi-stability limit intervenes at
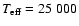 K
and produces some steep changes of the mass
loss rates during MS evolution. For the domain not covered by these authors
we use the results by de Jager et al. (1988).
Since the empirical values
for the mass loss rates
employed for non-rotating stars are based on
stars covering the whole range of rotational velocities, we must apply a reduction factor to the empirical rates to make
them correspond to the non-rotating case. The same reduction factor as
in Maeder & Meynet (2001) was used here.
K
and produces some steep changes of the mass
loss rates during MS evolution. For the domain not covered by these authors
we use the results by de Jager et al. (1988).
Since the empirical values
for the mass loss rates
employed for non-rotating stars are based on
stars covering the whole range of rotational velocities, we must apply a reduction factor to the empirical rates to make
them correspond to the non-rotating case. The same reduction factor as
in Maeder & Meynet (2001) was used here.
- During the Wolf-Rayet phase we apply
the mass loss rates proposed by Nugis & Lamers (2000). These mass loss rates,
which account for the clumping effects in the winds,
are smaller by a factor 2-3 than the mass loss rates used in our previous
non-rotating stellar grids (Meynet et al. 1994).
- The significant increases of the mass loss rates
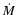 with
rotation are taken into account as explained in Maeder & Meynet (2000a). This treatment,
in contrast to the one usually used (Friend & Abbott 1986), accounts for
the non-uniform brightness of rotating stars
due to the von Zeipel theorem and for the fact that the Eddington
factor is also a function of the rotation velocity.
Due to the non-uniform brightness of a rotating star, the stellar winds
are anisotropic. The rotation-induced anisotropy of the stellar winds
is also accounted for during the Main Sequence (MS) phase according
to the prescription of Maeder (2002).
For O-type stars, the polar winds are enhanced and this means that these
stars lose a lot of mass, but a moderate amount of angular momentum.
For stars cooler than
with
rotation are taken into account as explained in Maeder & Meynet (2000a). This treatment,
in contrast to the one usually used (Friend & Abbott 1986), accounts for
the non-uniform brightness of rotating stars
due to the von Zeipel theorem and for the fact that the Eddington
factor is also a function of the rotation velocity.
Due to the non-uniform brightness of a rotating star, the stellar winds
are anisotropic. The rotation-induced anisotropy of the stellar winds
is also accounted for during the Main Sequence (MS) phase according
to the prescription of Maeder (2002).
For O-type stars, the polar winds are enhanced and this means that these
stars lose a lot of mass, but a moderate amount of angular momentum.
For stars cooler than
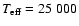 K, the equatorial ejection
becomes significant and leads to a larger ejection of angular
momentum. After the MS phase,
the ratios of the surface angular velocity to the break-up velocity
are in general much too low for the anisotropies to be important. Interestingly enough,
in cases of extreme mass loss such as in WR stars, the timescale for the transmission
of the extra torque applied at the stellar surface by the anisotropies
is longer than the timescale for the mass removal of the considered layers,
so that the effects of the anisotropies
of the stellar winds on the internal rotation are rather limited
(Maeder 2002).
K, the equatorial ejection
becomes significant and leads to a larger ejection of angular
momentum. After the MS phase,
the ratios of the surface angular velocity to the break-up velocity
are in general much too low for the anisotropies to be important. Interestingly enough,
in cases of extreme mass loss such as in WR stars, the timescale for the transmission
of the extra torque applied at the stellar surface by the anisotropies
is longer than the timescale for the mass removal of the considered layers,
so that the effects of the anisotropies
of the stellar winds on the internal rotation are rather limited
(Maeder 2002).
- In Paper V, we did not account for the effects of
horizontal turbulence on the shears (Talon & Zahn 1997). We account for it in the
present work in the same manner as we did in Paper VII (Maeder & Meynet
2001). Let us recall that the horizontal turbulence, expressed by
a diffusion coefficient
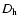 ,
tends to reduce
the shear mixing in regions of steep
,
tends to reduce
the shear mixing in regions of steep
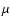 -gradients, making the diffusion coefficient
-gradients, making the diffusion coefficient
 proportional
to
proportional
to
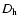 rather than to K, the thermal diffusivity.
The difference can be large and it leads to smaller
surface enhancements in the products of CNO burning. In regions of low
rather than to K, the thermal diffusivity.
The difference can be large and it leads to smaller
surface enhancements in the products of CNO burning. In regions of low
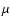 -gradients, the horizontal turbulence moderately increases the shear diffusion
coefficient, making it proportional to
-gradients, the horizontal turbulence moderately increases the shear diffusion
coefficient, making it proportional to
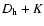 rather than to K only, with
little consequence for the surface enrichments.
rather than to K only, with
little consequence for the surface enrichments.
- A moderate overshooting is included in the present
rotating and non-rotating models. The radii of the convective cores are increased
with respect to the values obtained by the Schwarzschild criterion by a quantity
equal to 0.1
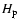 ,
where
,
where 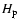 is the pressure scale height evaluated at the Schwarzschild
boundary.
is the pressure scale height evaluated at the Schwarzschild
boundary.
- As in Paper VIII (Meynet & Maeder 2002), the opacities are
from Iglesias & Rogers (1996), complemented at low
temperatures with the molecular opacities of Alexander
(http://web.physics.twsu.edu/alex/wwwdra.htm). The nuclear
reaction rates are also the same as in Paper VIII and are
based on the new NACRE data basis (Angulo et al. 1999).
- The initial composition is changed with respect to Paper V:
the mass fraction of hydrogen is X = 0.705, the mass fraction of helium Y = 0.275.
For the heavy elements,
we adopt the same mixture as the one
used to compute the opacity tables for solar composition.
The effect of rotation on the transport of the chemical species and the
angular momentum are accounted for as in our Papers VII and VIII.
All the models were computed
up to the end of the helium-burning phase.
The evolution of the rotation velocities at the stellar surface depends mainly
on 2 factors, the internal coupling and the mass loss.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{veqX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg23.gif) |
Figure 1:
Evolution of the rotational velocities for star models
of different initial masses between 120 and 9  with account taken
of anisotropic mass loss during the MS phase. The rapid decrease near the end
of the MS evolution is due to the bi-stability limit in the mass loss rates.
The location of the end of the MS phase corresponds to the vertical decrease of the velocity.
with account taken
of anisotropic mass loss during the MS phase. The rapid decrease near the end
of the MS evolution is due to the bi-stability limit in the mass loss rates.
The location of the end of the MS phase corresponds to the vertical decrease of the velocity. |
| Open with DEXTER |
1.- The coupling mechanisms transport angular momentum
in the stellar interiors. The extreme case of strong coupling is
the classical case of solid body rotation. In this case when mass loss is small, the star
reaches the critical velocity during the MS phase more or less quickly depending on the
initial rotation as shown by Sackman & Anand (1970; see also Langer 1997).
In that case, coupling ensures that
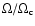 increases when the radius of the star increases.
Let us recall that for
increases when the radius of the star increases.
Let us recall that for
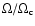 to increase when the radius of the star increases,
its suffices that
to increase when the radius of the star increases,
its suffices that 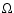 decreases less steeply with the radius than
decreases less steeply with the radius than
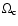 (
(
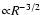 ), or
expressed in another way, if
), or
expressed in another way, if
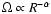 then
then
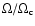 increases with the radius when
increases with the radius when
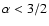 .
In the case of no coupling, i.e. of local conservation of the angular momentum,
rotation becomes more and more subcritical
(
.
In the case of no coupling, i.e. of local conservation of the angular momentum,
rotation becomes more and more subcritical
( ). In the present models, the
situation is intermediate, with a moderate coupling
due mainly to meridional circulation, which is more efficient
(Meynet & Maeder 2000) than shear transport,
as far as transport of angular momentum is concerned.
). In the present models, the
situation is intermediate, with a moderate coupling
due mainly to meridional circulation, which is more efficient
(Meynet & Maeder 2000) than shear transport,
as far as transport of angular momentum is concerned.
2.- For a given degree of coupling, the mass loss rates play a most critical role
in the evolution of the surface rotation. As shown by the comparison of the
models at Z=0.02 and Z=0.004 (Maeder & Meynet 2001), for masses greater
than 20  the models with solar composition have velocities that decrease
rather rapidly, while at Z=0.004 the velocities go up. Thus, for the most massive stars
with moderate or strong coupling, the mass loss rates are the main factor influencing
the evolution of rotation.
the models with solar composition have velocities that decrease
rather rapidly, while at Z=0.004 the velocities go up. Thus, for the most massive stars
with moderate or strong coupling, the mass loss rates are the main factor influencing
the evolution of rotation.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{omcX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg32.gif) |
Figure 2:
Evolution of the fraction
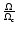 of the angular velocity to
the critical angular velocity at the surface of star models
of different initial masses between 120 and 9
of the angular velocity to
the critical angular velocity at the surface of star models
of different initial masses between 120 and 9  with account
taken of anisotropic mass loss during the MS phase.
with account
taken of anisotropic mass loss during the MS phase. |
| Open with DEXTER |
Below a mass of about 12  ,
the mass loss rates are smaller and the internal
coupling plays the main role in the evolution of the rotational velocities. This
provides an interesting possibility of tests on the internal coupling by studying
the differences in rotational velocities for stars at different distances of the
ZAMS. In particular, such a study could allow us to test the role
of magnetic coupling in radiative envelopes, which is now a major open question
in stellar rotation studies (Spruit 2002).
,
the mass loss rates are smaller and the internal
coupling plays the main role in the evolution of the rotational velocities. This
provides an interesting possibility of tests on the internal coupling by studying
the differences in rotational velocities for stars at different distances of the
ZAMS. In particular, such a study could allow us to test the role
of magnetic coupling in radiative envelopes, which is now a major open question
in stellar rotation studies (Spruit 2002).
Figures 1 and 2 show the evolution of the rotational velocities and of the fraction
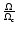 of the angular velocity to
the critical angular velocity at the surface of star models
of different initial masses between 9 and 120
of the angular velocity to
the critical angular velocity at the surface of star models
of different initial masses between 9 and 120  with account taken
of anisotropic mass loss during the MS phase. Globally these figures are
rather similar to those of previous models (Meynet & Maeder 2000), except for the fact
that the mass loss rates by Vink et al. (2000, 2001) are used here.
These rates meet a bi-stability limit at
with account taken
of anisotropic mass loss during the MS phase. Globally these figures are
rather similar to those of previous models (Meynet & Maeder 2000), except for the fact
that the mass loss rates by Vink et al. (2000, 2001) are used here.
These rates meet a bi-stability limit at
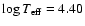 .
Below this value there is a sudden increase of the mass loss rates, which makes
the rotation velocities rapidly decrease, as for the most massive stars.
This is clearly visible for the models below 40
.
Below this value there is a sudden increase of the mass loss rates, which makes
the rotation velocities rapidly decrease, as for the most massive stars.
This is clearly visible for the models below 40  in Figs. 1 and 2.
Thus, for these models with a rapidly decreasing velocity of rotation,
we again stress that any comparison between observed and predicted rotation for these
domains of mass is really much more a test of the mass loss rates than a test on
the internal coupling and evolution of rotation. We may mention that for an initial velocity
in Figs. 1 and 2.
Thus, for these models with a rapidly decreasing velocity of rotation,
we again stress that any comparison between observed and predicted rotation for these
domains of mass is really much more a test of the mass loss rates than a test on
the internal coupling and evolution of rotation. We may mention that for an initial velocity
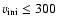 km s-1, the account taken of the anisotropic wind does not play a major
role (see Sect. 4).
km s-1, the account taken of the anisotropic wind does not play a major
role (see Sect. 4).
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{vrotwr1.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg35.gif) |
Figure 3:
Evolution as a function of the actual mass
of the rotation period, the rotational velocity
and the ratio of the angular velocity to the critical value during
the WR stage of massive stars. The continuous line corresponds
to the so-called eWNL phase (see text), the dotted and short-dashed lines show the evolution
during the eWNE and WC phases respectively. The long-dashed lines
in the panels for the velocities show the evolution of the polar radius,
(in this case the unity on the ordinates are
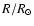 ).
Left: the WR phase of a star with an initial
mass of 85 ).
Left: the WR phase of a star with an initial
mass of 85  with
with
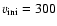 km s-1.
Right: the same for an initial mass of 25 km s-1.
Right: the same for an initial mass of 25  with
with
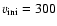 km s-1. km s-1. |
| Open with DEXTER |
Thus, the uncertainties
on the mass loss rates and bi-stability limits
prevent us from making significant tests on the internal physics and
coupling in the massive stars for models with initial masses above about
12  .
Mass loss uncertainties dominate the problem. From the rather large differences
between the values of the mass loss rates published over recent years, we know that
these uncertainties are still great. Fortunately, below 12
.
Mass loss uncertainties dominate the problem. From the rather large differences
between the values of the mass loss rates published over recent years, we know that
these uncertainties are still great. Fortunately, below 12  the comparisons may be meaningful and may reveal whether our models have the right
kind of internal coupling.
the comparisons may be meaningful and may reveal whether our models have the right
kind of internal coupling.
Figure 3 (left) shows the evolution of the rotation period P, of the
rotation velocities v and of the fraction
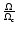 of the angular velocity to
the critical angular velocity at the surface
during the WR stages of a star model with an initial mass of
85
of the angular velocity to
the critical angular velocity at the surface
during the WR stages of a star model with an initial mass of
85  with
with
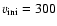 km s-1typical of a star which has both a WN and WC phase.
During the WN stage of the 85
km s-1typical of a star which has both a WN and WC phase.
During the WN stage of the 85  model,
until the actual mass of the star reaches a value near 23
model,
until the actual mass of the star reaches a value near 23  ,
the angular velocity decreases by a factor of
,
the angular velocity decreases by a factor of 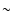 5,
correspondingly the period
5,
correspondingly the period
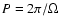 grows by the same factor and the rotation velocity
grows by the same factor and the rotation velocity
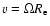 decreases much more since the equatorial radius
decreases much more since the equatorial radius
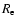 also decreases during this phase
(by a factor of
also decreases during this phase
(by a factor of 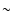 2). The fraction
2). The fraction
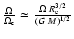 also decreases very much, because the sensitivity to the decrease of the radius is
larger than that to the mass (which decreases by a factor of
also decreases very much, because the sensitivity to the decrease of the radius is
larger than that to the mass (which decreases by a factor of 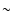 2.7).
2.7).
We adopt here the definition of the WN phases given by Foellmi et al.
(2003), putting a prefix "e'' when the class is assigned by composition properties of
the evolutionary models.
Thus, eWNE means WN stars without hydrogen, while eWNL means WN stars with hydrogen,
(see also Sect. 5 below).
When the H-content goes to zero (i.e. just before the star enters the eWNE
stage), we see a dramatic
increase of 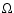 (or decrease of P), due to the strong contraction of the surface layer
because the opacity of the surface layers becomes much smaller.
This transition is fast, thus the transfer of angular momentum
by meridional circulation is limited and the evolution of the rotation at the surface
is dominated by the local conservation of angular momentum, which explains
the rapid and large increase of
(or decrease of P), due to the strong contraction of the surface layer
because the opacity of the surface layers becomes much smaller.
This transition is fast, thus the transfer of angular momentum
by meridional circulation is limited and the evolution of the rotation at the surface
is dominated by the local conservation of angular momentum, which explains
the rapid and large increase of 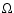 .
However, we see that
despite the strong decrease of P, the velocity v and the ratio
.
However, we see that
despite the strong decrease of P, the velocity v and the ratio
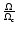 do not change
very much, since the radius is much smaller in the eWNE stage.
When the star becomes a WC star with an actual mass of
do not change
very much, since the radius is much smaller in the eWNE stage.
When the star becomes a WC star with an actual mass of  17.3
17.3  ,
there
is very little change in the velocity, since rotation is already very low
and the radius no longer decreases significantly.
,
there
is very little change in the velocity, since rotation is already very low
and the radius no longer decreases significantly.
Figure 3 (right) shows the same for a star
of 25  with
with
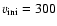 km s-1, which does not enter the
eWNE and WC stages. We see that P decreases (or
km s-1, which does not enter the
eWNE and WC stages. We see that P decreases (or  increases) during
the WN stage. This is because the star model moves from
increases) during
the WN stage. This is because the star model moves from
 4.29 to 4.70. The decrease of the radius
makes the star rotate faster, slightly overwhelming the mass loss effects
from 13.65 to 11.33
4.29 to 4.70. The decrease of the radius
makes the star rotate faster, slightly overwhelming the mass loss effects
from 13.65 to 11.33  .
The increase of
.
The increase of 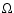 and the decrease
of R nearly compensate for each other so that v does not vary much
during most of the WN phase, except at the very end. There the increase of
and the decrease
of R nearly compensate for each other so that v does not vary much
during most of the WN phase, except at the very end. There the increase of 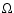 is more rapid than the decrease of the radius and an increase in the velocity
is obtained. The reason for this behaviour is that in this model the
stellar winds uncovers the layers, where the
is more rapid than the decrease of the radius and an increase in the velocity
is obtained. The reason for this behaviour is that in this model the
stellar winds uncovers the layers, where the 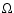 -gradient is steep, and
we start seeing layers which were deep inside and rotating rapidly.
-gradient is steep, and
we start seeing layers which were deep inside and rotating rapidly.
![\begin{figure}
\par\resizebox{8.2cm}{!}{\includegraphics[clip]{vrotwr2.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg41.gif) |
Figure 4:
Same as Fig. 3 for 60  stellar models.
Left: the WR phase of a star with an initial
mass of 60
stellar models.
Left: the WR phase of a star with an initial
mass of 60  and
and
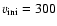 km s-1.
Right: for an initial mass of 60 km s-1.
Right: for an initial mass of 60  with
with
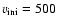 km s-1.
In the e-version, the red color corresponds to the phase where H is
present (eWNL), the black to the phase of an He-star (eWNE) and the blue to
the WC phase. km s-1.
In the e-version, the red color corresponds to the phase where H is
present (eWNL), the black to the phase of an He-star (eWNE) and the blue to
the WC phase. |
| Open with DEXTER |
Globally, we note that the rotational velocities of WR
stars are modest in the 2 cases examined above, despite the very different masses and
evolution stages.
This is firstly the result of the strong mass loss necessary to produce the WR stars
and also of the mass loss during the WR stages.
We note however that, for a given initial velocity, the velocities obtained at the end of the He-burning phase
for the WR stars decrease when the initial mass increases (see Table 1).
This results from the simple fact that the higher the initial mass, the larger the quantity
of mass (and thus of angular momentum) removed by the stellar winds.
Figure 4 shows the evolution of rotation
properties for a 60  model with
model with
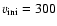 km s-1 (left)
and with
km s-1 (left)
and with
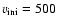 km s-1 (right). On the whole, these two cases are not
very different from the case of the 85
km s-1 (right). On the whole, these two cases are not
very different from the case of the 85  model shown above. In
Fig. 4 (left), we firstly see an increase of P and a corresponding decrease of
v and of
model shown above. In
Fig. 4 (left), we firstly see an increase of P and a corresponding decrease of
v and of
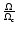 ;
this decrease of the rotation is due,
as before, to the high mass loss rates. Then,
when the actual mass is about 38
;
this decrease of the rotation is due,
as before, to the high mass loss rates. Then,
when the actual mass is about 38  ,
,
 increases again due to a decrease of the stellar radius as the star is
moving to the left in the HR diagram (Fig. 7).
The velocity v does not change very much since the stellar radius is decreasing.
When the actual mass of the star approaches 30
increases again due to a decrease of the stellar radius as the star is
moving to the left in the HR diagram (Fig. 7).
The velocity v does not change very much since the stellar radius is decreasing.
When the actual mass of the star approaches 30  ,
at an age of
,
at an age of
 yr,
yr,
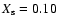 and the outer stellar layers become
more transparent, so that the star brightens rapidly above
and the outer stellar layers become
more transparent, so that the star brightens rapidly above
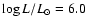 for a short time
until an age of
for a short time
until an age of
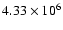 yr. The corresponding variations in radius
produce a sharp oscillation in
yr. The corresponding variations in radius
produce a sharp oscillation in  and velocity. Then at an age of
and velocity. Then at an age of
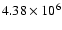 yr until
yr until
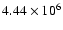 yr, the star
becomes an He-star (eWNE stage).
The angular velocity remains nearly constant (cf. the evolution of the period)
while the velocity and
yr, the star
becomes an He-star (eWNE stage).
The angular velocity remains nearly constant (cf. the evolution of the period)
while the velocity and
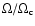 present some more variations
linked to changes in the radius.
Then, the star enters the WC stage, the mass loss rates are so large that despite
the decrease of the radius, the rotation remains small. As was the case before,
the presence of steep gradients of
present some more variations
linked to changes in the radius.
Then, the star enters the WC stage, the mass loss rates are so large that despite
the decrease of the radius, the rotation remains small. As was the case before,
the presence of steep gradients of  at the surface, may result in some cases in an
increase of
at the surface, may result in some cases in an
increase of  when the star is peeled off by the stellar winds.
when the star is peeled off by the stellar winds.
The case of 60  with
with
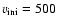 km s-1 (right) contains
features similar to the previous cases. The
beginning of the curve, with the first bump of P, behaves like the case of
km s-1 (right) contains
features similar to the previous cases. The
beginning of the curve, with the first bump of P, behaves like the case of
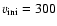 km s-1 of 60
km s-1 of 60  .
After the dip of
P at an age of
.
After the dip of
P at an age of
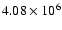 yr (actual mass of
yr (actual mass of  37
37  ), the further evolution of Pis like the case of an 85
), the further evolution of Pis like the case of an 85  star, marked by a large decrease of
the angular velocity
star, marked by a large decrease of
the angular velocity  .
Later, when the star becomes an He-star at an age
.
Later, when the star becomes an He-star at an age
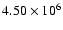 yr (actual mass
yr (actual mass 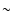 24
24  ), we
see a sharp increase
in
), we
see a sharp increase
in 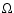 ,
in the velocity and in the ratio
,
in the velocity and in the ratio
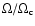 .
During the WC phase, the velocity remains between 30 and 40 km s-1,
surprisingly, this is
a factor
.
During the WC phase, the velocity remains between 30 and 40 km s-1,
surprisingly, this is
a factor  2 below the velocity reached during this phase by the 300 km s-1 stellar
model. The lower value obtained for the initially faster rotating star
results from the greater quantity of mass and thus of angular momentum lost during the
previous evolutionary stages.
2 below the velocity reached during this phase by the 300 km s-1 stellar
model. The lower value obtained for the initially faster rotating star
results from the greater quantity of mass and thus of angular momentum lost during the
previous evolutionary stages.
![\begin{figure}
\par\includegraphics[angle=-90,width=15.3cm,clip]{hrX.eps} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg50.gif) |
Figure 5:
Evolutionary tracks for non-rotating
(dotted lines) and rotating (continuous lines) models for a metallicity Z =
0.020.
The rotating models
have an initial velocity
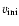 of 300 km s-1, which corresponds to an average velocity
during the MS phase of about 180 to 240 km s-1 (see Table 1).
of 300 km s-1, which corresponds to an average velocity
during the MS phase of about 180 to 240 km s-1 (see Table 1).
|
| Open with DEXTER |
The main conclusion of this section is that the predicted surface
rotation velocities of WR stars are relatively low, of the order of 50 km s-1.
Also, in the stellar interiors, rotation is modest with ratios
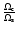 of the angular velocity
at the center to that at the surface which are only of the order of a few
unities. This is the result of the very strong mass loss
peeled off the star to make it a WR star.
It is to be examined whether
the further evolution and strong central contraction to the pre-supernova stage is
able to accelerate enough to account for the observed rotation periods
of pulsars and maybe also, for rotations fast enough,
for enabling the collapsar model to work (Woosley 2003).
A word of caution is necessary, since there are many paths leading to WR stars
and we cannot exclude that some, possibly rare paths, may lead to WR stars with
very high rotation.
of the angular velocity
at the center to that at the surface which are only of the order of a few
unities. This is the result of the very strong mass loss
peeled off the star to make it a WR star.
It is to be examined whether
the further evolution and strong central contraction to the pre-supernova stage is
able to accelerate enough to account for the observed rotation periods
of pulsars and maybe also, for rotations fast enough,
for enabling the collapsar model to work (Woosley 2003).
A word of caution is necessary, since there are many paths leading to WR stars
and we cannot exclude that some, possibly rare paths, may lead to WR stars with
very high rotation.
Figure 5 presents the tracks for non-rotating and rotating evolutionary
models for the whole mass range considered.
As a result of the change of the opacities (slightly enhanced) and of the
initial abundances (Y = 0.275, instead
of 0.30), the non-rotating tracks are shifted to lower effective temperatures
with respect to Paper V. The tracks also extend towards lower effective temperatures
during the MS phase.
This is a well known consequence of overshooting.
Overshooting and core extension by rotation are also
generally responsible for shorter
extensions of the blue loops in the He-burning phase. This is what we
observe in Fig. 5: the extension of the blue loops is further
reduced by rotation in the case of the 9  model, and the blue loops
are even suppressed in the rotating model of 12
model, and the blue loops
are even suppressed in the rotating model of 12  .
.
Table 1:
Properties of the stellar models at the end of the H-burning phase
and at the end of the He-burning phase. The masses are in solar mass, the velocities in km s-1, the lifetimes in million years and the abundances in mass fraction.
The present non-rotating
12  ,
with overshooting, pre-sents a blue loop, while the non-rotating model of Paper V,
without overshooting, shows no blue loop.
This is at first sight surprising because, as said above, more massive He-cores tend
to reduce the extension of the blue loops, if not suppressing them
(Lauterborn et al. 1971; see also the discussion in Maeder & Meynet 1989).
As explained in Paper V, this particular situation, at the limit where the loops
generally disappear, results from the higher luminosity of the
model having the more massive He-cores (either as a result of overshooting
or as a result of rotation). The higher luminosity implies that the outer
envelope is more extended, and is thus characterized by lower
temperatures and higher opacities at a given mass coordinate. As a consequence, in the model
with higher luminosity, during the first dredge-up, the outer
convective zone proceeds much more deeply in mass,
preventing the He-core to grow too much during the further evolutionary
phases and enabling the apparition of a blue loop.
,
with overshooting, pre-sents a blue loop, while the non-rotating model of Paper V,
without overshooting, shows no blue loop.
This is at first sight surprising because, as said above, more massive He-cores tend
to reduce the extension of the blue loops, if not suppressing them
(Lauterborn et al. 1971; see also the discussion in Maeder & Meynet 1989).
As explained in Paper V, this particular situation, at the limit where the loops
generally disappear, results from the higher luminosity of the
model having the more massive He-cores (either as a result of overshooting
or as a result of rotation). The higher luminosity implies that the outer
envelope is more extended, and is thus characterized by lower
temperatures and higher opacities at a given mass coordinate. As a consequence, in the model
with higher luminosity, during the first dredge-up, the outer
convective zone proceeds much more deeply in mass,
preventing the He-core to grow too much during the further evolutionary
phases and enabling the apparition of a blue loop.
The effects of rotation on the tracks have already been discussed in previous works (Heger 1998; Meynet & Maeder 2000), thus we shall be very brief here.
Let us just list the main effects:
- On and near the ZAMS, the atmospheric effects of
rotation produce a small shift of the tracks towards lower
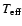 .
The effective temperature considered here is an appropriate averaged
.
The effective temperature considered here is an appropriate averaged
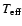 over the stellar surface (see Meynet & Maeder 1997).
over the stellar surface (see Meynet & Maeder 1997).
- Tracks with rotation become more luminous than for no rotation.
- For stars with initial masses inferior to
 30
30  ,
the MS bandwidth is enlarged by rotation. This is a consequence
of the larger He-core produced during the H-burning phase in rotating models. As a numerical example,
in the 20
,
the MS bandwidth is enlarged by rotation. This is a consequence
of the larger He-core produced during the H-burning phase in rotating models. As a numerical example,
in the 20  model with
model with
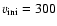 km s-1, the He-core at the end of the MS is about 38% more massive than in its
non-rotating counterpart. In the models of Paper V the enhancement
due to rotation was only 20%. Likely most of the difference
results from the inclusion here of a small overshooting.
In the present models, the core enhancement
due to rotation adds its effects to an already more extended core, having a higher central
temperature, and thus this larger core reacts more strongly to further supplies of fuel
by rotational diffusion.
km s-1, the He-core at the end of the MS is about 38% more massive than in its
non-rotating counterpart. In the models of Paper V the enhancement
due to rotation was only 20%. Likely most of the difference
results from the inclusion here of a small overshooting.
In the present models, the core enhancement
due to rotation adds its effects to an already more extended core, having a higher central
temperature, and thus this larger core reacts more strongly to further supplies of fuel
by rotational diffusion.
- For initial masses superior to about 50
 ,
the rotating tracks
show drastically reduced MS bandwidths.
This was already the case in Meynet & Maeder (2000).
For instance, the reddest point reached at the end of the MS phase by the
60
,
the rotating tracks
show drastically reduced MS bandwidths.
This was already the case in Meynet & Maeder (2000).
For instance, the reddest point reached at the end of the MS phase by the
60  non-rotating stellar model is log
non-rotating stellar model is log
 4.15, while
for the
4.15, while
for the
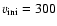 km s-1 model, it is
km s-1 model, it is  4.6, due to the fact
that the surface He-enhancement leads to a bluer track, as a consequence of the reduced opacity.
In this mass range, the rotating stellar models enter into the WR phase during
the H-burning phase (see Sect. 5). The MS phase, identified here with the
OV-type star phase, is thus considerably reduced.
Since the stars, here as in any mass range, have different initial rotational velocities,
one expects to find in the HR diagram stars corresponding to a
variety of tracks with various initial velocities. Particularly, in the upper hot
part of the HR diagram, for log
4.6, due to the fact
that the surface He-enhancement leads to a bluer track, as a consequence of the reduced opacity.
In this mass range, the rotating stellar models enter into the WR phase during
the H-burning phase (see Sect. 5). The MS phase, identified here with the
OV-type star phase, is thus considerably reduced.
Since the stars, here as in any mass range, have different initial rotational velocities,
one expects to find in the HR diagram stars corresponding to a
variety of tracks with various initial velocities. Particularly, in the upper hot
part of the HR diagram, for log 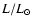 superior to about 5.8-5.9
and log
superior to about 5.8-5.9
and log
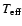 between 4.7 and 4.2, one may find in the same area of the HR
diagram stars in very different evolutionary stages, which may also correspond to
different types of massive stars: MS O-type stars, Of stars, transition stars,
blue supergiants and WR stars.
between 4.7 and 4.2, one may find in the same area of the HR
diagram stars in very different evolutionary stages, which may also correspond to
different types of massive stars: MS O-type stars, Of stars, transition stars,
blue supergiants and WR stars.
For higher rotation velocities, the actual masses at the end of both the H- and He-burning phases
become smaller (cf. Table 1). For an initial velocity of 300 km s-1 and for stars
with masses below  60
60  ,
the actual masses at the end of the core H-burning phase are decreased by less than 11% with respect
to the non-rotating models. For higher initial mass models, the decreases are much more important, because
these stars enter the WR phase already at an early stage during the H-burning phase (see Sect. 5).
,
the actual masses at the end of the core H-burning phase are decreased by less than 11% with respect
to the non-rotating models. For higher initial mass models, the decreases are much more important, because
these stars enter the WR phase already at an early stage during the H-burning phase (see Sect. 5).
The evolutionary masses of a star can be determined by searching the mass
of the evolutionary track passing through
its observed position in the HR diagram.
As can be seen from Fig. 5, the mass determined from the non-rotating evolutionary track is always
greater than the one deduced from rotating models. Thus the use of non
rotating tracks tends to overestimate the mass, and
this might be a cause of a large part of the long-standing mass discrepancy problem
(see e.g. Herrero et al. 2000).
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{finalX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg61.gif) |
Figure 6:
Relations between the final mass versus the initial mass for solar metallicity models.
The cases with and without rotation are indicated.
The line with slope one, labeled by
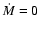 ,
would correspond to a case without mass loss.
The relation obtained from
the models of Schaller et al. (1992) is also shown. ,
would correspond to a case without mass loss.
The relation obtained from
the models of Schaller et al. (1992) is also shown.
|
| Open with DEXTER |
![\begin{figure}
\par\resizebox{8.15cm}{!}{\includegraphics[clip]{hrkiport.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg62.gif) |
Figure 7:
The two upper panels show the evolutionary tracks of a non-rotating and a rotating 60  stellar model.
The bold part of the track corresponds to the O-type star Main-Sequence phase; the dotted part shows the intermediate phase,
when present, between the O-type star phase and the WR phase; the thin continuous line is the track during
the WR phase. The two lower panels show the evolution as a function of time of the total mass and of the masses of the
convective cores during the H- and the He-burning phases.
stellar model.
The bold part of the track corresponds to the O-type star Main-Sequence phase; the dotted part shows the intermediate phase,
when present, between the O-type star phase and the WR phase; the thin continuous line is the track during
the WR phase. The two lower panels show the evolution as a function of time of the total mass and of the masses of the
convective cores during the H- and the He-burning phases.
|
| Open with DEXTER |
Figure 6 shows the final masses obtained for different initial masses and velocities.
One notes that the new mass loss rates used in the present computations
are smaller than those used
in the stellar grids of Schaller et al. (1992).
For stars with initial masses
above 40  ,
rotating models produce
final masses between 11.3 and 14.7. For comparison, non-rotating models
end with final masses between 14.1-17.3
,
rotating models produce
final masses between 11.3 and 14.7. For comparison, non-rotating models
end with final masses between 14.1-17.3  .
Interestingly, the average mass
of WC stars, estimated on the basis of the 6 WC stars
belonging to double-line spectroscopic binaries, is
.
Interestingly, the average mass
of WC stars, estimated on the basis of the 6 WC stars
belonging to double-line spectroscopic binaries, is
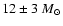 (van der Hucht 2001), nearer to the rotating model results than the non-rotating
ones. However we cannot discard the possibility that for these stars mass
transfer in a Roche lobe overflow may have occurred, in which case this
observation cannot be used to constrain single star models.
The fact that the models with and without rotation
near 50
(van der Hucht 2001), nearer to the rotating model results than the non-rotating
ones. However we cannot discard the possibility that for these stars mass
transfer in a Roche lobe overflow may have occurred, in which case this
observation cannot be used to constrain single star models.
The fact that the models with and without rotation
near 50  lead to about the same final masses, despite the
increased mass loss rates for rotating models, is due to the differences in the
evolutionary stages followed by each model (see Sect. 5).
lead to about the same final masses, despite the
increased mass loss rates for rotating models, is due to the differences in the
evolutionary stages followed by each model (see Sect. 5).
Table 1 presents some properties of the models. Columns 1 and 2 give the initial mass and the initial velocity
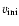 respectively.
The mean equatorial velocity
respectively.
The mean equatorial velocity
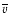 during the MS phase is indicated in Col. 3.
This quantity is defined as in Paper V.
The H-burning lifetimes
during the MS phase is indicated in Col. 3.
This quantity is defined as in Paper V.
The H-burning lifetimes 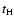 ,
the lifetimes
,
the lifetimes 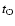 as an O-type star on the MS
(we assumed that O-type stars have an effective temperature superior to about
31 500 K as suggested by the new effective temperature scale given by Martins et al. 2002),
the masses M, the equatorial velocities v, the helium surface abundance
as an O-type star on the MS
(we assumed that O-type stars have an effective temperature superior to about
31 500 K as suggested by the new effective temperature scale given by Martins et al. 2002),
the masses M, the equatorial velocities v, the helium surface abundance 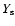 and the
surface ratios (in mass) N/C and N/O at the end of the H-burning phase are given in Cols. 4 to 10.
The Cols. 11 to 16 present some characteristics of the stellar models at the end of the He-burning phase,
and the
surface ratios (in mass) N/C and N/O at the end of the H-burning phase are given in Cols. 4 to 10.
The Cols. 11 to 16 present some characteristics of the stellar models at the end of the He-burning phase,
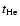 is the He-burning lifetime.
The letter I attached to the value of the initial velocity (Col. 2) indicates
that the model was calculated assuming isotropic stellar winds. These models were
calculated until the end of the MS phase, except in the case of the 60
is the He-burning lifetime.
The letter I attached to the value of the initial velocity (Col. 2) indicates
that the model was calculated assuming isotropic stellar winds. These models were
calculated until the end of the MS phase, except in the case of the 60  model for which the evolution was pursued until the end of the core He-burning
phase.
model for which the evolution was pursued until the end of the core He-burning
phase.
From Table 1 one sees that for Z=0.020 the lifetimes are
increased by about 15-25% when the initial rotational velocity
on the MS increases from 0 to 300 km s-1. Similar increases
were found in Paper V. The lifetimes of O-type stars are increased by similar amounts.
As we shall see below, the increase due to rotation of the WR lifetimes is much greater
and thus rotation predicts larger number ratios of WR to O-type stars
than non-rotating stellar models.
Except for the models with initial masses superior to 85  ,
the He-burning lifetimes are decreased by rotation. Thus the ratio of the He-burning lifetimes
to the H-burning lifetimes are in general decreased by rotation.
Typically for the 20
,
the He-burning lifetimes are decreased by rotation. Thus the ratio of the He-burning lifetimes
to the H-burning lifetimes are in general decreased by rotation.
Typically for the 20  model, this ratio
passes from 0.11 to 0.08 when the initial velocity considered increases
from 0 to 300 km s-1. The particular behaviour of the extremely massive
stars results from the lower luminosities in the WC stage, which
favour longer He-lifetimes.
model, this ratio
passes from 0.11 to 0.08 when the initial velocity considered increases
from 0 to 300 km s-1. The particular behaviour of the extremely massive
stars results from the lower luminosities in the WC stage, which
favour longer He-lifetimes.
The anisotropy of the wind induced by rotation has little impact when the initial
velocity is equal or inferior to 300 km s-1. This can be seen by comparing
the data presented in Table 1 for the two 60  models with
models with
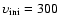 km s-1 computed with and without the account of
the anisotropy. They are indeed very similar. On the other hand, as has been shown by
Maeder (2002), for higher initial velocities, in the mass range
between 20 and 60
km s-1 computed with and without the account of
the anisotropy. They are indeed very similar. On the other hand, as has been shown by
Maeder (2002), for higher initial velocities, in the mass range
between 20 and 60  ,
the anisotropies of the mass loss
may significantly influence the evolution of the stellar velocities
and may lead many stars to break-up.
,
the anisotropies of the mass loss
may significantly influence the evolution of the stellar velocities
and may lead many stars to break-up.
Here we consider the following question:
what are the effects of rotation on the evolution of massive single
stars into the Wolf-Rayet phase? This subject has been discussed by Maeder (1987),
Fliegner & Langer (1995), Maeder & Meynet (2000b) and Meynet (2000).
We present here for the first time an extensive grid of models, accounting for the effects
of the wind anisotropy, going through the WR phase. It is important to cover the whole
mass range of star progenitors of WR stars in order to quantitatively assess the importance of rotation
in the interpretation of the WR number statistics (see Sect. 6 below).
Let us reconsider the criteria which have been chosen
to decide when a stellar model enters into the WR phase.
Ideally, of course, the physics of the models should decide
when the star is a WR star. However our poor knowledge of the atmospheric physics
involved, as well as the complexity of models
coupling stellar interiors to the winds, are such that this
approach is not yet possible.
Instead, it is necessary to adopt some empirical criteria
for deciding when a star enters the WR phase.
In this work the criteria are the following:
the star is considered to be a WR star when
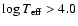 and the mass fraction of hydrogen at the surface is
and the mass fraction of hydrogen at the surface is
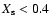 .
Reasonable changes to these values (for instance adopting
.
Reasonable changes to these values (for instance adopting
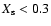 instead of 0.4) do not affect the results significantly.
instead of 0.4) do not affect the results significantly.
The correspondence between the WR-subclasses and the surface abundances is established as follows:
the stars enter the WR phase as WN stars i.e. as stars presenting strong He and N enrichments at their surface
and strong depletion in carbon and oxygen as expected from CNO processed material.
We call eWNL stars all the WN stars showing hydrogen at their surface
("e'' stands for evolutionary, as recommended by Foellmi et al. 2003).
The eWNE stars, on the other hand, are WN stars showing no hydrogen at their surface.
The transitional WN/WC phase is characterized by the simultaneous presence at the surface of both
H- and He-burning products (typically N and C or Ne). Here we suppose
that this transition phase begins when the
mass fraction of carbon at the surface becomes superior to 10%
of the mass fraction of nitrogen. The phase is supposed
to end when the mass fraction of nitrogen at the surface becomes inferior
to 10% of the mass fraction of carbon.
The WC phase corresponds to the stage where He-burning products appear at the
surface. This phase begins when the transition WN/WC phase ends.
Figure 7 shows the evolutionary tracks and the evolution
of the structure in a non-rotating and a rotating 60  model.
The rotating model has a time-averaged equatorial velocity on the Main
Sequence (MS) of about 190 km s-1,
not far from the mean equatorial velocity observed for O-type stars. Inspection of
Fig. 7 shows the following features:
model.
The rotating model has a time-averaged equatorial velocity on the Main
Sequence (MS) of about 190 km s-1,
not far from the mean equatorial velocity observed for O-type stars. Inspection of
Fig. 7 shows the following features:
- The non-rotating 60
 star goes through an intermediate Luminous Blue Variable (LBV) phase
before becoming a WR star, while the rotating model skips the
LBV phase and goes directly from the O-type star
phase into the WR phase. One also notes that during the O-type star phase,
the rotating track is bluer than its non-rotating counterpart.
This is due to the diffusion of helium into the outer radiative zone (see Heger & Langer 2000;
Meynet & Maeder 2000). This fact may slightly change the number of O-type stars deduced
from the number of ionizing photons, a technique used to estimate the number
of O-type stars from the spectral analysis of the integrated light of
distant starburst regions (e.g. Schaerer 1996).
star goes through an intermediate Luminous Blue Variable (LBV) phase
before becoming a WR star, while the rotating model skips the
LBV phase and goes directly from the O-type star
phase into the WR phase. One also notes that during the O-type star phase,
the rotating track is bluer than its non-rotating counterpart.
This is due to the diffusion of helium into the outer radiative zone (see Heger & Langer 2000;
Meynet & Maeder 2000). This fact may slightly change the number of O-type stars deduced
from the number of ionizing photons, a technique used to estimate the number
of O-type stars from the spectral analysis of the integrated light of
distant starburst regions (e.g. Schaerer 1996).
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{wr120X.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg68.gif) |
Figure 8:
Evolutionary tracks for a non-rotating (light dotted-line) and a rotating 120  stellar model
at solar metallicity. The circles along the tracks indicate the end ofthe eWNL phase, the squares
the end of the eWNE phase, and the triangles, the beginning of the WC phase. The WN/WC stars lie along
the portion of the tracks between the squares and the triangles. The crosses indicate the end of the central H-burning phase.
stellar model
at solar metallicity. The circles along the tracks indicate the end ofthe eWNL phase, the squares
the end of the eWNE phase, and the triangles, the beginning of the WC phase. The WN/WC stars lie along
the portion of the tracks between the squares and the triangles. The crosses indicate the end of the central H-burning phase.
|
| Open with DEXTER |
- There is no luminosity difference during the WC phase
between the rotating and the non-rotating models.
Since these stars follow a mass-luminosity relation (Maeder 1987; Schaerer & Maeder 1992),
this implies that the masses of these two stars at this stage are about equal (see Fig. 6).
At first sight this may be surprising. One would expect the rotating star to lose
more mass than its non-rotating counterpart.
However, in this particular case there are some compensating effects. Indeed,
the non-rotating model enters into the WR phase later, but becomes redder during the MS phase and then becomes a LBV star.
During these two last phases, the star undergoes strong mass loss (see the left panels of Fig. 7).
The rotating model, on the other hand, enters
the WR phase at an earlier stage, reaching at the end an identical mass to the non-rotating model.
In general, however, the final masses obtained from the rotating models are smaller than those obtained from the non-rotating ones
(see Fig. 6),
leading to lower luminosities during the WC phase (see Fig. 8).
- From the lower panels of Fig. 7, we see that the non-rotating star enters
the WR phase at the beginning of the core He-burning phase
with a mass of about 27
 .
Nearly the whole H-rich envelope has been removed by stellar winds during the previous phases
(more precisely at the end of the MS phase and during the LBV phase).
In this case, the main mechanism for making a WR star is
mass loss by stellar winds. For the rotating model, on the other hand,
the entry into the WR phase occurs at an earlier stage
(although not at a younger age!), while the star is still burning hydrogen in its core.
The mass of the star at this stage is about 45
.
Nearly the whole H-rich envelope has been removed by stellar winds during the previous phases
(more precisely at the end of the MS phase and during the LBV phase).
In this case, the main mechanism for making a WR star is
mass loss by stellar winds. For the rotating model, on the other hand,
the entry into the WR phase occurs at an earlier stage
(although not at a younger age!), while the star is still burning hydrogen in its core.
The mass of the star at this stage is about 45  and a large H-rich envelope is still surrounding the convective core.
The main effect making a WR star in this second case is
rotationally induced mixing (Maeder 1987; Fliegner & Langer 1995; Meynet 2000).
and a large H-rich envelope is still surrounding the convective core.
The main effect making a WR star in this second case is
rotationally induced mixing (Maeder 1987; Fliegner & Langer 1995; Meynet 2000).
In Fig. 8, the evolutionary tracks for a non-rotating and a rotating 120  stellar model
are shown. The beginning and the end of the various WR subphases are indicated
along the tracks.
The range of luminosities spanned by the rotating eWNL stars is
considerably increased. This directly results from the point underlined just above, i.e.
a rotating star enters the WR phase still with a large H-rich envelope. This considerably
increases the duration of the eWNL phase and the star will cover during this stage a greater
range of masses and luminosities. The rotating models also enter the further
WR subclasses with smaller actual masses and lower luminosities.
From Fig. 8, one sees that
the rotating eWNE, WN/WC and WC stars have luminosities decreased by about a factor of two.
stellar model
are shown. The beginning and the end of the various WR subphases are indicated
along the tracks.
The range of luminosities spanned by the rotating eWNL stars is
considerably increased. This directly results from the point underlined just above, i.e.
a rotating star enters the WR phase still with a large H-rich envelope. This considerably
increases the duration of the eWNL phase and the star will cover during this stage a greater
range of masses and luminosities. The rotating models also enter the further
WR subclasses with smaller actual masses and lower luminosities.
From Fig. 8, one sees that
the rotating eWNE, WN/WC and WC stars have luminosities decreased by about a factor of two.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{tma.eps}}\end{figure}](/articles/aa/full/2003/24/aa3569/Timg69.gif) |
Figure 9:
Lifetimes of WR stars of different initial mass for
non-rotating stellar models.
The durations of the WR sub-phases are also indicated. There is no
transition WN/WC phase. |
| Open with DEXTER |
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{tma2.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg70.gif) |
Figure 10:
Lifetimes for rotating stellar models in the WR subphases.
|
| Open with DEXTER |
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{twrviX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg71.gif) |
Figure 11:
Durations of the WR phases and of the WR sub-phases for stars of 60  with various initial velocities. with various initial velocities.
|
| Open with DEXTER |
The differences between the behaviours of the rotating and
non-rotating models have important consequences for the duration of the WR phase as a whole
and for the lifetimes spent in the different WR subtypes, as can be appreciated from Figs. 9 and
10.
- Firstly, one notes that the WR lifetimes are enhanced. Typically
for the 60
 model, the enhancement by rotation amounts to nearly a factor of 2.
model, the enhancement by rotation amounts to nearly a factor of 2.
- Second, the eWNL phase is considerably lengthened as explained just above.
The duration of this phase increases with the initial velocity as can be seen from Fig. 11.
When the initial velocity passes from 300 to 500 km s-1
(or when the time-averaged equatorial velocity during the O-type phase goes
from 190 to 330 km s-1), the eWNL phase duration is increased by a factor of about 1.7.
The durations of the eWNE and WC phases are, on the other hand, much less affected.
- Thirdly, in the rotating stellar model a new phase of modest,
but of non-negligible duration, appears: the so-called transitional WN/WC phase.
This phase is characterized by the simultaneous presence at the surface of both
H- and He-burning products. The reason for this
is the shallower chemical gradients that build up inside the rotating models.
These shallower gradients inside the stars also produce a smoother evolution of the surface abundances
as a function of time (or as a function of the remaining mass, see Figs. 16 and 18).
For a transitional WN/WC phase to occur, it is necessary to have - for a sufficiently long period - both
a He-burning core and a CNO-enriched envelope.
In the highest mass stars, mass loss removes too rapidly the CNO-enriched envelope
to allow a transitional WN/WC phase to appear.
In the low mass range, the time spent in the WR phase is
too short and the H-rich envelope too
extended to allow He-burning products to diffuse up to the surface.
Consequently, the transitional WN/WC phase only appears in the mass range between
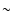 30 and 60
30 and 60  for
for
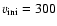 km s-1.
km s-1.
- Finally, the minimum mass for a star to become a WR star (through the single star channel)
is lowered by rotation. In the present case, the minimum mass is reduced from about
37
 for
for
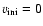 km s-1to about 22
km s-1to about 22  for
for
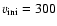 km s-1.
km s-1.
Of course, this applies to solar metallicity. At very different Z, the effects of
rotation on the various subphases may be different.
It is interesting to compare the present WR-lifetimes with those we obtained with our
previous non-rotating stellar models (Meynet et al. 1994; Maeder and Meynet 1994).
This is done in Fig. 12. We see that the present non-rotating models follow more or less
the behaviour we obtained with our normal mass loss rate models of 1994, although, due to smaller mass loss rates
in the present grid, the WR lifetimes are in general reduced and the minimum mass for WR star formation from single stars is enhanced.
Our rotating models, on the other hand, reproduce qualitatively the changes brought by an enhancement of the mass loss rates: an increase of the WR lifetimes and a decrease of
the minimum mass for a single star to go through a WR phase.
From the above considerations, one can conclude that, compared
to non-rotating models, stellar models including rotation will
predict higher values of: (a) the numbers of WR stars relative to O-type stars,
(b) the relative number of WN to WC stars, and (c) the relative number of transition WN/WC stars to WR stars. As shown in the next section, the predictions of the rotating models
are in better agreement with the observed number ratios at solar metallicity.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{twrX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg75.gif) |
Figure 12:
Lifetimes of Wolf-Rayet stars from various initial masses at solar metallicity.
The continuous line shows the results from the present rotating models. The WR lifetimes of
the non-rotating
models from the present work are shown by the dotted line. The short- and long-dashed curves
show the results obtained from the
models of Schaller et al. (1992) and
Meynet et al. (1994) with normal (
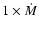 )
and enhanced mass loss rates ( )
and enhanced mass loss rates (
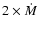 )
respectively. )
respectively. |
| Open with DEXTER |
Following Maeder (1991) and
Maeder & Meynet (1994), one can easily estimate the theoretical
number ratio of WR to O-type stars in a region of constant star formation.
This ratio is simply given by the ratios of the mean lifetime of a WR star to that
of an OV-type star. The averages are computed using an initial mass
function as the weighting factor over the respective mass intervals considered.
Assuming a Salpeter Initial Mass Function slope of 1.35, considering the O-type and WR star lifetimes
given in Tables 1 and 2, we obtain the predicted ratios given at the bottom
of this last table.
Table 2:
Lifetimes of Wolf-Rayet star from various initial masses and velocities
and predictions for different number ratios (see text). The velocities are in km s-1 and the lifetimes in Myr.
Comparisons with observed number ratios are shown in Figs. 13 and 14.
Obviously,
unless most of the WR stars at solar metallicity are formed through Roche
lobe overflow in a close binary system, which seems quite unrealistic
(see the discussion in Maeder 1996; see also Foellmi et al. 2003),
models with rotation are in much better
agreement with observations. Of course a more refined estimate of the effects
of rotation will require account of the initial distribution of the
rotational velocities.
However, since the initial velocity chosen here corresponds to a mean
rotational velocity on the Main Sequence almost equal to the observed mean,
we can hope that the present result is not too far from what one would
obtain with a more complete analysis. The conclusion is that
at solar metallicity, rotating models are in much better agreement
with the observed statistics of WR stars than the non-rotating models.
Interestingly a similar conclusion could be reached based on the results
of our Paper V, and this shows that the present results depend weakly
on overshooting or on the inclusion of the effects of horizontal turbulence
in the coefficient of shear diffusion.
![\begin{figure}
\par\resizebox{8.7cm}{!}{\includegraphics[angle=-90,clip]{wroX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg89.gif) |
Figure 13:
Variation of the number ratios of Wolf-Rayet stars to O-type stars as a function of the metallicity.
The observed points are taken as in Maeder & Meynet (1994).
The dotted and continuous lines show the predictions of the models
of Schaller et al. (1992) and Meynet et al. (1994) with normal and enhanced mass loss rates respectively.
The black square and triangle show the predictions of the present non-rotating and rotating stellar models
respectively.
|
| Open with DEXTER |
In Fig. 14, the predicted values for the WC/WN number ratios are compared
with observations. One sees that the WC/WN ratio increases with the metallicity
along a relatively well defined relation.
The observed point
for the solar neighborhood is however well above the general trend. According to Massey
(2003) this may result from an underestimate of the number of WN stars.
Comparing with the theoretical predictions at solar metallicity, one obtains that
the non-rotating models predict too few WN stars, while
the rotating models give a value in the observed trend.
This confirms the conclusion already reached above on the basis
of the WR/O number ratio: rotating models
much better account for the characteristics of the WR populations than
non-rotating models.
There are 10 WN/WC stars listed in the VIIth catalogue of galactic WR stars of van der Hucht (2001).
Compared to the total number of known galactic WR stars (226) this represents
a fraction of 4.4%. The present models predict for this fraction
a value equal to 4% in good agreement with the observed ratio.
We recall that models without mild mixing processes in radiative
zones are unable to predict correctly the number of transition WN/WC stars.
This was first shown by Langer (1991).
In future work, it has to be checked
by further computations at different metallicities that
the rotating models, with reduced mass loss rates due to clumping,
will account for the observed variation of the number ratios WR/O and WC/WN
with metallicity.
We have already presented and discussed the effects of
rotation on the surface abundance of massive stars at solar composition
(Meynet & Maeder 2000). The main point is the enhancement
of He and N during the MS phase due to the internal transport by shear mixing.
However, we note that the enhancements in He and CNO products found here
are in general smaller that those found in Meynet & Maeder (2000).
The situation is illustrated in
Fig. 15 which compares the evolution of the N/C ratios
for models with masses between 9 and 40  of the above quoted paper and of
the present work. We see that a difference in the
enhancement of N/C is created during MS evolution and that the present ratios
are smaller on average by a factor of about 1.5 for masses below 25
of the above quoted paper and of
the present work. We see that a difference in the
enhancement of N/C is created during MS evolution and that the present ratios
are smaller on average by a factor of about 1.5 for masses below 25  .
This is due to the fact that
in the present models we are accounting for the effects
of the horizontal turbulence on the shear
mixing according to the study by Talon & Zahn (1997). The horizontal
diffusion substantially reduces the effects of the shear mixing. In the higher mass range, the difference
between the two sets of models is smaller, as can be seen by comparing the two
.
This is due to the fact that
in the present models we are accounting for the effects
of the horizontal turbulence on the shear
mixing according to the study by Talon & Zahn (1997). The horizontal
diffusion substantially reduces the effects of the shear mixing. In the higher mass range, the difference
between the two sets of models is smaller, as can be seen by comparing the two
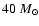 tracks in Fig. 15. In this domain of masses, the large effects of mass
loss by stellar winds are added to those of rotational mixing.
Close comparisons with
observations will be undertaken on the basis of these two sets of models to see
whether the treatment by Talon & Zahn leads to
a better agreement or not. However, the problem is intricate both
observationally, because the scatter of the observations is large,
and also theoretically because other effects may enter into the game, such as
magnetic fields (Spruit 2002) or a higher horizontal
turbulence. Let us also
recall that the enhancements in He and N are much larger at lower
metallicities Z (Maeder & Meynet 2001), because stars with lower Zhave in general steeper
tracks in Fig. 15. In this domain of masses, the large effects of mass
loss by stellar winds are added to those of rotational mixing.
Close comparisons with
observations will be undertaken on the basis of these two sets of models to see
whether the treatment by Talon & Zahn leads to
a better agreement or not. However, the problem is intricate both
observationally, because the scatter of the observations is large,
and also theoretically because other effects may enter into the game, such as
magnetic fields (Spruit 2002) or a higher horizontal
turbulence. Let us also
recall that the enhancements in He and N are much larger at lower
metallicities Z (Maeder & Meynet 2001), because stars with lower Zhave in general steeper  -gradients, which favour internal mixing.
-gradients, which favour internal mixing.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90,clip]{massey.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg91.gif) |
Figure 14:
Variation of the number ratios of WN to WC stars as a function of metallicity.
The black circles are
observed points taken from Massey & Johnson (2001 and see references therein), except
for the SMC (Massey & Duffy 2001), for NGC 300 (Schild et al. 2002)
and for IC10, for which we show the estimate from Massey & Holmes (2002).
The black square and triangle show the predictions of the present non-rotating and rotating stellar models
respectively. |
| Open with DEXTER |
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{nc.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg92.gif) |
Figure 15:
Evolution of the N/C ratios (in number) as a function of the
effective temperature at the surface of various rotating stellar models. The
N/C ratios are normalized to their initial values. The
continuous lines show the results for the present rotating models (
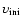 = 300 km s-1),
the dashed-lines show the evolutionary tracks for some models of Paper V. For purpose of clarity, only
a part of the 40
= 300 km s-1),
the dashed-lines show the evolutionary tracks for some models of Paper V. For purpose of clarity, only
a part of the 40  tracks are shown.
tracks are shown. |
| Open with DEXTER |
Figure 16 shows the evolution of the surface abundances in a rotating and
a non-rotating model with initial masses of 60  .
The progressive changes
of the abundances of CNO elements between the initial cosmic values
and the values of the nuclear equilibrium of the
CNO cycle are much smoother for the rotating model than for the case without
rotation. This is due to the internal mixing which makes flatter internal
chemical gradients for rotating models. The rotational mixing also makes the change
of abundances to occur much earlier in the peeling-off process.
This is also true for the changes of H and He. Another significant difference for the 60
.
The progressive changes
of the abundances of CNO elements between the initial cosmic values
and the values of the nuclear equilibrium of the
CNO cycle are much smoother for the rotating model than for the case without
rotation. This is due to the internal mixing which makes flatter internal
chemical gradients for rotating models. The rotational mixing also makes the change
of abundances to occur much earlier in the peeling-off process.
This is also true for the changes of H and He. Another significant difference for the 60  model with rotation is the absence
of an LBV phase as shown in Sect. 5. Without rotation, most of the change of CNO abundances
occurs in the LBV phase, while in the case with rotation, the transition
from cosmic to CNO equilibrium abundances occurs partly during the MS phase
and partly during the eWNL phase which immediately follows it. We note that
the nuclear equilibrium CNO values are essentially model independent as already stressed
a long time ago (Smith & Maeder 1991). This is true whether H is still
present or not.
model with rotation is the absence
of an LBV phase as shown in Sect. 5. Without rotation, most of the change of CNO abundances
occurs in the LBV phase, while in the case with rotation, the transition
from cosmic to CNO equilibrium abundances occurs partly during the MS phase
and partly during the eWNL phase which immediately follows it. We note that
the nuclear equilibrium CNO values are essentially model independent as already stressed
a long time ago (Smith & Maeder 1991). This is true whether H is still
present or not.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{xi60X.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg93.gif) |
Figure 16:
Evolution as a function of the actual mass of the abundances (in mass fraction) at the surface of a non-rotating
(upper panel) and a rotating (lower panel) 60  stellar model.
stellar model.
|
| Open with DEXTER |
We see that
at the end of the assumed eWNE phase, the transition to the WC abundances
is very sharp in the absence of rotational mixing. This is because
there is a strong chemical discontinuity in the classical models due to the fact
that the convective core is usually growing during some part of the
He-burning phase (Maeder 1983). In the rotating case, the transitions are smoother,
so that there are some stars observed with abundances in the transition regime,
with simultaneously some 12C and some 14N present.
As stated above, these correspond to the so-called WN/WC stars
(Conti & Massey 1989; Crowther et al. 1995).
These transition stars are likely to also
have some 22Ne excess. Since the attribution of spectral types
is a complex matter, it may even be that some of the stars in the
transition stage are given a spectral type eWNE or WC, thus we might well
have a situation where a WN star would have some 22Ne excess
or a WC star would still have some 14N present.
![\begin{figure}
\par\resizebox{8.75cm}{!}{\includegraphics[angle=-90,clip]{wnc.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg94.gif) |
Figure 17:
Evolution of the abundance ratio C/N at the surface of
a 40  stellar model with
stellar model with
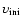 = 300 km s-1 as a function of the ratio C/He. Only the beginning of the WR phase
is shown. The equilibrium value of the C/N ratio is around 0.015.
Observations as given in the paper by Crowther et al. (1995) are
indicated.
= 300 km s-1 as a function of the ratio C/He. Only the beginning of the WR phase
is shown. The equilibrium value of the C/N ratio is around 0.015.
Observations as given in the paper by Crowther et al. (1995) are
indicated. |
| Open with DEXTER |
Figure 17 compares the predicted relation between the C/N and C/He ratios
with some recent observations by Crowther et al. (1995).
During the eWNL phase, C/He and C/N decreases, but remain around
the CNO equilibrium value equal to 0.015.
Then during the transitional WN/WC phase, there is a huge increase
of carbon, while nitrogen and helium remain constant. This is the reason
why the lower part of the curve shows that when C/N changes by a factor
103, C/He changes by the same amount.
Then, when the star evolves towards the WC stage, C/He changes only slowly, while
C/N grows very rapidly, since N quickly disappears. The comparison with the observations
by Crowther et al. (1995) shows a good agreement. However this agreement may be somewhat
misleading here, in the sense that a 60  non-rotating
model would follow a similar track in the C/N versus C/He plane.
The good correspondence here is not a real constraint on the models. What is more
constraining is the expected number of stars in the transitional WN/WC phase. As seen
in Sect. 5, the rotating models in this respect are much better than the non-rotating ones.
non-rotating
model would follow a similar track in the C/N versus C/He plane.
The good correspondence here is not a real constraint on the models. What is more
constraining is the expected number of stars in the transitional WN/WC phase. As seen
in Sect. 5, the rotating models in this respect are much better than the non-rotating ones.
In the WC stage, the abundances of chemical elements are very much model
dependent as was first shown by Smith & Maeder (1991).
This is because in the WC stars, we see the products of partial He-burning.
At the entry in the WC phase, the 12C and 16O abundances are lower,
and that of He is higher in the models with rotation, due to their smooth chemical gradients.
Also, the fraction of the WC phase spent with lower C/He and O/He ratios is longer
in models with rotation. However, rotation does not affect the high 22Ne abundance
during the WC phase. This is a consequence of the fact that most of this 22Ne results from the transformation of the 14N produced by the CNO cycle in the previous H-burning core. The value of the 14N and therefore that of the 22Ne is fixed by the
characteristics of the CNO at equilibrium, which in turn depends on the nuclear physics and not on the pecularities of the stellar models. It is interesting
to mention here that the high overabundance of 22Ne at the surface of the
WC star predicted by the models is confirmed by the observations (Willis
1999; Dessart et al. 2000). In the core, the abundance of 22Ne
will stay at this equilibrium value until eventually it is turned into 25,26Mg
with production of neutrons (through 22Ne(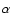 ,n)25Mg)
and of s-elements.
,n)25Mg)
and of s-elements.
Figure 18 shows the same for models of 40  with and without rotation.
The enhancements of He and N only appear in the blue and yellow supergiant stage
in the case without rotation, while they occur during the MS and blue supergiant phase
when rotation is included; also in this case the changes are more progressive.
The non-rotating model has almost no WNL phase and does not enter the WC
stage. The model with rotation is very different, it has an extended WNL phase
and then a remarkably large transition phase, where 14N is present with
a significant abundance, while 12C, 16O and 22Ne are also
there. Most of this transition phase is likely spent in the transition WN/WC phase,
but probably not the whole, so that some peculiar WN stars with products
of He-burning are possible. Also some WC stars with an unusual
occurrence of 14N are very likely. Globally, we see that the
transition phase where both characteristics of H- and He-burning phases
are present is longer for stars of lower masses (see Sect. 5).
with and without rotation.
The enhancements of He and N only appear in the blue and yellow supergiant stage
in the case without rotation, while they occur during the MS and blue supergiant phase
when rotation is included; also in this case the changes are more progressive.
The non-rotating model has almost no WNL phase and does not enter the WC
stage. The model with rotation is very different, it has an extended WNL phase
and then a remarkably large transition phase, where 14N is present with
a significant abundance, while 12C, 16O and 22Ne are also
there. Most of this transition phase is likely spent in the transition WN/WC phase,
but probably not the whole, so that some peculiar WN stars with products
of He-burning are possible. Also some WC stars with an unusual
occurrence of 14N are very likely. Globally, we see that the
transition phase where both characteristics of H- and He-burning phases
are present is longer for stars of lower masses (see Sect. 5).
Figure 19 shows an interesting diagram for the study of
so-called "slash stars'' of type Ofpe/WN, of the LBV and of the WN stars. It presents
the evolution of the surface H-content as a function of the luminosity.
The tracks go downwards in this diagram; first there is an initial
brightening due to MS evolution, then the luminosity is about constant, except
for
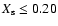 if the mass loss is very high. Thus
for stars above or equal to 25
if the mass loss is very high. Thus
for stars above or equal to 25  ,
this diagram is sensitive to both
mass loss and mixing. Since WN subtypes are sensitive to the optical
thickness of the winds, while
,
this diagram is sensitive to both
mass loss and mixing. Since WN subtypes are sensitive to the optical
thickness of the winds, while
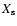 is sensitive to both mixing
and mass loss, one should try to define the domains of this
diagram where "slash stars'', LBV, WN late and WN early are each located on
average. Ideally this should also be attempted for stars in different
galaxies. For masses below 25
is sensitive to both mixing
and mass loss, one should try to define the domains of this
diagram where "slash stars'', LBV, WN late and WN early are each located on
average. Ideally this should also be attempted for stars in different
galaxies. For masses below 25  ,
this diagram indicates
up to which stage mixing is proceeding for stars of different luminosities,
which is also a useful indication.
,
this diagram indicates
up to which stage mixing is proceeding for stars of different luminosities,
which is also a useful indication.
The evolution of the (C+O)/He ratio as a function of luminosity is shown
in Fig. 20, which is the key diagram for WC stars as shown by
Smith & Maeder (1991). The evolution for a given mass is upwards,
the luminosity decreases
as the stellar masses decreases. At the same time, as a result of mass loss
and mixing, the (C+O)/He ratio goes up, since there are more and more
products of He-burning at the stellar surface.
Rotation drastically modifies the tracks of WC stars in this
diagram, as well as the lifetimes. The tracks of the models
of 85 and 120  are shifted to lower luminosities
by rotation. As there is a tight mass-luminosity relation
for He, C, O stars (Maeder 1983), this is the result of the smaller
mass at the entrance of the WC phase for models with rotation. The smaller
mass is due mainly to the much longer WN phase of rotating models.
(As a minor remark, we see that the (C+O)/He ratio goes slightly higher in models without
rotation, this is due to the fact that the He- and C-burning
proceeds a bit farther in non rotating models that have a higher mass).
For the models of 60
are shifted to lower luminosities
by rotation. As there is a tight mass-luminosity relation
for He, C, O stars (Maeder 1983), this is the result of the smaller
mass at the entrance of the WC phase for models with rotation. The smaller
mass is due mainly to the much longer WN phase of rotating models.
(As a minor remark, we see that the (C+O)/He ratio goes slightly higher in models without
rotation, this is due to the fact that the He- and C-burning
proceeds a bit farther in non rotating models that have a higher mass).
For the models of 60  ,
there is a small difference at the beginning of the WC phase
and this difference quickly disappears. The 40
,
there is a small difference at the beginning of the WC phase
and this difference quickly disappears. The 40  models enter the
WC phase only if rotation is significant.
In a previous work (Smith & Maeder 1991), we have shown that
metallicity Z strongly shifts the tracks in this diagram. Thus, we now
see that rotation is also producing great shifts. The location of WC stars
of different subtypes and composition should be attempted; it would be
particularly worth considering WC stars of galaxies of different Z.
models enter the
WC phase only if rotation is significant.
In a previous work (Smith & Maeder 1991), we have shown that
metallicity Z strongly shifts the tracks in this diagram. Thus, we now
see that rotation is also producing great shifts. The location of WC stars
of different subtypes and composition should be attempted; it would be
particularly worth considering WC stars of galaxies of different Z.
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{xsl.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg98.gif) |
Figure 19:
Evolutionary tracks in the 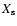 versus log
versus log 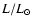 plane,
where
plane,
where 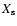 is the hydrogen mass fraction at the surface. The continuous lines
are for the rotating models, the dotted or dashed-lines are for the non-rotating models.
is the hydrogen mass fraction at the surface. The continuous lines
are for the rotating models, the dotted or dashed-lines are for the non-rotating models. |
| Open with DEXTER |
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{cohe.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg99.gif) |
Figure 20:
Evolution of the ratios (C+O)/He as a function of the luminosity at the surface of non-rotating
(dashed-lines) and rotating models (continuous lines) for various initial
mass models. The correspondence
between the (C+O)/He ratios and the different WC subtypes as given by Smith & Maeder 1991
is indicated on the right of the figure.
|
| Open with DEXTER |
The good agreement obtained here between the observed WR star populations
and the predictions of the rotating stellar models reinforces the general conclusion,
already obtained in previous works, namely that rotation is a key physical ingredient
of massive star evolution. Population synthesis for galaxies and starbursts
should also be based on stellar models with rotation. The same is true
for nucleosynthetic models.
Rotation, in addition to making the models more realistic,
opens new ways to explore very interesting questions.
Among them let we cite the possible relations between rotation and the ring nebulae observed
around some WR stars, the relation between rotation and the LBV phenomenon, the rotation
of pulsars and the link to 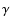 -ray bursts.
-ray bursts.
-
Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3
In the text
NASA ADS
-
Conti, P. S., & Massey, P. 1989, ApJ, 337, 251
In the text
NASA ADS
-
Crowther, P. A., Smith, L. J., & Willis, A. J. 1995, A&A, 304, 269
In the text
NASA ADS
-
Dessart, L., Crowther, P. A., Hillier, J. D., et al. 2000, MNRAS, 315, 407
In the text
NASA ADS
-
Fliegner, J., & Langer, N. 1995, IAU Symp. 163, ed. K. A van der Hucht, & P. M. Williams (Dordrecht: Kluwer), 326
In the text
-
Foellmi, C., Moffat, A. F. J., & Guerrero, M. A. 2003, MNRAS, 338, 1025
In the text
NASA ADS
-
Friend, D. B., & Abbott, D. C. 1986, A&A, 311, 701
In the text
-
Hamann, W. R., & Koesterke, L. 1999, IAU Coll. 169, ed. B. Wolf, O. Stahl, & A. W. Fullerton
(Berlin: Springer). Also Lecture Notes in Physics, 1999, 523, 239
In the text
-
Heger, A. 1998, Ph.D., Max-Planck-Institut für Astrophysik, München
In the text
-
Heger, A., & Langer, N. 2000, ApJ, 544, 1016
In the text
NASA ADS
-
Herrero, A., Puls, J., & Villamariz, M. R. 2000, A&A, 354, 193
In the text
NASA ADS
-
van der Hucht, K. A. 2001, New Astron. Rev., 45, 135
In the text
NASA ADS
-
Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 231, 384
In the text
NASA ADS
-
de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988,
A&AS, 72, 259
In the text
NASA ADS
-
Langer, N. 1991, A&A, 248, 531
In the text
NASA ADS
-
Langer, N. 1997, The Eddington Limit in Rotating Massive Stars, in ed. A. Nota, & H. Lamers, Luminous Blue Variables: Massive Stars
in Transition, ASP Conf. Ser., 120, 83
In the text
-
Lauterborn, D., Refsdal, S., & Weigert, A. 1971, A&A, 10, 97
In the text
NASA ADS
-
Maeder, A. 1983, A&A, 120, 113
In the text
NASA ADS
-
Maeder, A. 1987, A&A, 178, 159
In the text
NASA ADS
-
Maeder, A. 1991, A&A, 242, 93
In the text
NASA ADS
-
Maeder, A. 1996, in Wolf-Rayet stars in the framework
of stellar evolution, ed. J. M. Vreux, A. Detal, D. Fraipont-Caro, et al. (Université de Liège,
Institut d'Astrophysique), 39
In the text
-
Maeder, A. 2002, A&A, 392, 575
In the text
NASA ADS
-
Maeder, A., & Meynet, G. 1989, A&A, 210, 155
In the text
NASA ADS
-
Maeder, A., & Meynet, G. 1994, A&A, 287, 803
In the text
NASA ADS
-
Maeder, A., & Meynet, G. 2000a, A&A, 361, 159 (Paper VI)
In the text
NASA ADS
-
Maeder, A., & Meynet, G. 2000b, ARA&A, 38, 143
In the text
NASA ADS
-
Maeder, A., & Meynet, G. 2001, A&A, 373, 555 (Paper VII)
In the text
NASA ADS
-
Martins, F., Schaerer, D., & Hillier, D. J. 2002, A&A, 382, 999
In the text
NASA ADS
-
Massey, P. 2003, ARA&A, in press
In the text
-
Massey, P., & Johnson, O. 1998, ApJ, 505, 793
In the text
NASA ADS
-
Massey, P., & Duffy, A. S. 2001, ApJ, 550, 713
In the text
NASA ADS
-
Massey, P., & Holmes, S. 2002, ApJ, 580, L35
In the text
NASA ADS
-
Meynet, G. 2000, in Massive Stellar Clusters, ed. A. Lançon, & C. M. Boily, ASP Conf. Ser., 211, 105
In the text
-
Meynet, G., & Maeder, A. 1997, A&A, 321, 465 (Paper I)
In the text
NASA ADS
-
Meynet, G., & Maeder, A. 2000, A&A, 361, 101 (Paper V)
In the text
NASA ADS
-
Meynet, G., & Maeder, A. 2002, A&A, 390, 561 (Paper VIII)
In the text
NASA ADS
-
Meynet, G., Maeder, A., Schaller,
G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97
In the text
NASA ADS
-
Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227
In the text
NASA ADS
-
Sackman, I. J., & Anand, S. P. S. 1970, ApJ, 162, 105
In the text
NASA ADS
-
Schaerer, D. 1996, ApJ, 467, L17
In the text
NASA ADS
-
Schaerer, D., & Maeder, A. 1992, A&A, 263, 129
In the text
NASA ADS
-
Schaller, G., Schaerer, D., Meynet, G., & Maeder, A.
1992, A&AS, 96, 269
In the text
NASA ADS
-
Schild, H., Crowther, P. A., Abbott, J. B., & Schmutz, W. 2003, A&A, 397, 859
In the text
NASA ADS
-
Spruit, H. 2002, A&A, 381, 923
In the text
NASA ADS
-
Smith, L. F., & Maeder, A. 1991, A&A, 241, 77
In the text
NASA ADS
-
Talon, S., & Zahn, J. P. 1997, A&A, 317, 749
In the text
NASA ADS
-
Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295
In the text
NASA ADS
-
Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574
In the text
NASA ADS
-
Willis, A. J. 1999, IAU Symp. 193, ed. K. A. van der Hucht, G. Koenigsberger, & P. R. J. Eenens, 1
In the text
-
Woosley, S. 2003, IAU Symp. 215, ed. A. Maeder, & P. Eenens,
in press
In the text
Copyright ESO 2003
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{veqX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg23.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{omcX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg32.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{vrotwr1.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg35.gif)
![\begin{figure}
\par\resizebox{8.2cm}{!}{\includegraphics[clip]{vrotwr2.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg41.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=15.3cm,clip]{hrX.eps} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg50.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{finalX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg61.gif)
![\begin{figure}
\par\resizebox{8.15cm}{!}{\includegraphics[clip]{hrkiport.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg62.gif)
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{wr120X.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg68.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{tma.eps}}\end{figure}](/articles/aa/full/2003/24/aa3569/Timg69.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{tma2.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg70.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{twrviX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg71.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{twrX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg75.gif)
![\begin{figure}
\par\resizebox{8.7cm}{!}{\includegraphics[angle=-90,clip]{wroX.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg89.gif)
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90,clip]{massey.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg91.gif)
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{nc.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg92.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{xi60X.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg93.gif)
![\begin{figure}
\par\resizebox{8.75cm}{!}{\includegraphics[angle=-90,clip]{wnc.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg94.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{xi40X.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg96.gif)
![\begin{figure}
\par\resizebox{8.3cm}{!}{\includegraphics[clip]{xsl.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg98.gif)
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{cohe.eps}} \end{figure}](/articles/aa/full/2003/24/aa3569/Timg99.gif)