A&A 404, 1023-1032 (2003)
DOI: 10.1051/0004-6361:20030555
A puzzling paucity of double peaked X-ray pulsars
T. Bulik 1 -
D. Gondek-Rosinska 2,1 -
A. Santangelo 3 -
T. Mihara 4 -
M. Finger5 -
M. Cemeljic6
1 - Nicolaus Copernicus Astronomical Center, Bartycka 18, 00716 Warsaw, Poland
2 - LUTH, Observatoire de Paris, Place Jules Janssen, 92195 Meudon Cedex, France
3 - IFCAI-CNR, via Ugo La Malfa 153, 90146 Palermo, Italy
4 - RIKEN, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan
5 - NSSTC, 320 Sparkman Dr., Hunstville, AL 35805, USA
6 - AIP, an der Sternwarte 16, 14482 Potsdam, Germany
Received 19 November 2002 / Accepted 25 March 2003
Abstract
Accretion powered pulsars exhibit a variety of lightcurves.
In this paper we propose to classify the observed lightcurves as
single or double pulsed. We analyze the lightcurves of 89 accretion powered
pulsars and assign them to these classes. We present three datasets:
first in which the classification can be easily done, second for which
the classification is more difficult and not certain, and
third for which we were unable to classify the pulsar because of a lack
of published data. We analyze a simple model in which the angles between the magnetic
and rotation
axis 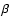 ,
and between the rotation axis and the line of sight
,
and between the rotation axis and the line of sight 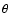 are random,
and show that it is inconsistent with the data. We also present a model in which
the angle between the magnetic axis and the rotation axis is restricted
and compare it with the data. This leads to an upper
limit on
the angle
are random,
and show that it is inconsistent with the data. We also present a model in which
the angle between the magnetic axis and the rotation axis is restricted
and compare it with the data. This leads to an upper
limit on
the angle
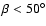 .
We conclude that there must be
a mechanism that leads to alignment of the magnetic and spin axis
in X-ray pulsars.
.
We conclude that there must be
a mechanism that leads to alignment of the magnetic and spin axis
in X-ray pulsars.
Key words: X-rays: star - stars: neutron
Accreting neutron stars were discovered
more than 30 years ago (Shklovsky 1967), with Cen X-3
beeing the first one discovered that showed pulsations
(Giacconi et al. 1971). Currently we know nearly one
hundred accreting neutron stars,
and in more than eighty of them pulsations were identified
(Liu et al. 2001,2000).
Accreting neutron stars in binaries exhibit a wide range of
X-ray light curves. They vary as a function of the photon
energy, and moreover in the transient sources the pulse shapes change
with the variation of the luminosity.
The pulse period in accreting sources is identified with the
rotation of a magnetized star. As the
matter from the companion star falls onto the neutron star
it is channeled onto the magnetic poles by the strong magnetic
field of the neutron star. Thus the polar caps
and/or accretion columns are the places where
most of the emission takes place.
Several theoretical models of radiation of magnetized accretion
powered neutron stars have been proposed and the beam shape is usually
described in terms of pencil beams, when most of the radiation is emitted
along the magnetic field, or fan beams when most of the radiation is emitted
perpendicularly to the magnetic field.
The magnetized
radiative transfer is solved using a difference scheme
(Meszaros & Nagel 1985; Bulik et al. 1992), or using Monte
Carlo scheme (Lamb et al. 1990; Isenberg et al. 1998),
for a review see Meszaros (1992).
In the pencil beam model radiation from each polar cap
produces one pulse in the light curve.
Depending on the emission cap physics and the strength
of the magnetic field each pulse may have some additional structure.
When during the rotation of
an accreting pulsar we see two polar caps the lightcurve should
exhibit two distinct pulses (peaks), and if only one cap is seen then the
lightcurve is single peaked.
In the case of dominant radiation from the accretion column
(fan beam model)
the shape of the
lightcurve will depend on the
geometry and
on the shape of the beam. Even with simple beam shapes
there can be triple or quadruple peaked lightcurves.
Each pulsar can be classified according to
the number of peaks in the lightcurve
depending on the location of the observer and
the inclination between the rotation and the magnetic axes.
We note that the observed pulsar lightcurves
can be classified into two groups:
the single
pulsed light curves and the double pulsed light curves.
At low X-ray energies this
distinction may not be clear, however in the high energy band we
clearly distinguish single or double pulses, and there are no
triple (or multiple) pulsed lightcurves, see e.g.
Bildsten et al. (1997); Nagase (1989).
By high energy band we mean at least above 10 keV, or in the pulsars where cyclotron lines were found, above the cyclotron lines.
The paper is organized as follows: in Sect. 2 we summarize the observations,
in Sect. 3 we analyze
the expected shapes and
expected fraction of single and double peaked lightcurves, in
Sect. 4 we discuss the results. We summarize the conclusions in Sect. 5.
In this section we review the existing observations of X-ray
pulsars and attempt to classify their lightcurves according to
the number of pulses in their lightcurves. We summarize our
classification in Tables 1, 2, and 3. For each pulsar we have
searched the literature for X-ray observations, and verified if
the pulsar was observed in the band above 10 keV, or above the
cyclotron line energy. The pulsars with such observations are
listed in Table 1. There are 46 entries in the Table
out of which 20 have been classified as double and 26 as single.
Additionally we have listed 31 pulsars in Table 2
for which the classification was difficult. For some of the
pulsars no lightcurve above 10 keV was available, we have
also included here three pulsars with accretion flow eclipses
(Cemeljic & Bulik 1998) that is pulsar with the light
curves exhibiting sudden dips. Such dips can be interpreted as
accretion flow eclipses, i.e. be caused by the absorption of the
X-ray flux when the accretion column passes the line of sight.
Such phenomena have been noted for at least three objects:
A0535-262 (Cemeljic & Bulik 1998), GX1+4
(Giles et al. 2000), and RX J0812.4-3114 (LS992)
(Reig & Roche 1999b). We classified them conservatively
as double, although we rather lean toward the interpretation
of single peaks with an accretion flow eclipse. There are 7
pulsars with likely double peaked light curves and 24 with
single in Table 2. We see that in each table there
are more single pulsed than double pulsed objects. For
completion we also list 13 pulsars in Table 3 for
which no information on the type of the lightcurve was
available. We define three sets of data corresponding to the
three tables: dataset
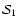 with the data of
Table 1, dataset
with the data of
Table 1, dataset
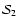 with the combined data
of Tables 1 and 2, and dataset
with the combined data
of Tables 1 and 2, and dataset
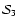 with all the data, and the entries of Table 3
are assumed to be double peaked.
with all the data, and the entries of Table 3
are assumed to be double peaked.
Table 1:
X-ray pulsars in group one, i.e. these that are easily classifiable.
Table 2:
X-ray pulsars in group two, i.e. with no pulse shape above 10 keV or were
difficult to classify.
Table 3:
X-ray pulsar in group three, for which no reliable pulse shapes were found.
Let us assume that an accreting neutron star has a pure centered
dipole field. In such a case the geometry of accretion powered
pulsars is characterized by two angles: 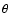 - the angle
between the rotation axis and direction to the observer, and
- the angle
between the rotation axis and direction to the observer, and
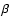 the angle between the magnetic and rotation axes.
Within the pencil beam model the
parameter space when only one cap is seen is determined by the
condition:
the angle between the magnetic and rotation axes.
Within the pencil beam model the
parameter space when only one cap is seen is determined by the
condition:
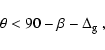 |
(1) |
where
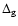 is
the gravitational light deflection of a ray emitted parallel to
the surface of the neutron star. Here we assume that the
magnetic beaming is not very strong and that there are X-ray
photons emitted parallel to the surface of the neutron star.
Ignoring the gravitational light bending effects, i.e. in the
classical Newtonian case,
is
the gravitational light deflection of a ray emitted parallel to
the surface of the neutron star. Here we assume that the
magnetic beaming is not very strong and that there are X-ray
photons emitted parallel to the surface of the neutron star.
Ignoring the gravitational light bending effects, i.e. in the
classical Newtonian case,
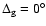 ,
the parameter space for seeing just one cap is shown as the
region above the solid line in
Fig. 1.
Thus, if the angles
,
the parameter space for seeing just one cap is shown as the
region above the solid line in
Fig. 1.
Thus, if the angles 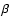 and
and 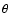 are chosen randomly the
fraction of single pulsed objects should be
are chosen randomly the
fraction of single pulsed objects should be
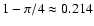 .
The region for the single peaked light curves would be
smaller if the radiation were strongly beamed. However, in this
case the double peaked light curves would exhibit narrow pulses,
contrary to what is observed - see e.g. Fig. 7 in
Bildsten et al. (1997).
.
The region for the single peaked light curves would be
smaller if the radiation were strongly beamed. However, in this
case the double peaked light curves would exhibit narrow pulses,
contrary to what is observed - see e.g. Fig. 7 in
Bildsten et al. (1997).
The angles 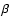 and
and 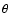 also determine the number
of pulses in the lightcurve within the fan beam model. However here the number
of pulses seen depends also on the shape of the beam.
In a simple case when there are two columns
radiating with constant specific intensity the beam will
be a function only of the angle
also determine the number
of pulses in the lightcurve within the fan beam model. However here the number
of pulses seen depends also on the shape of the beam.
In a simple case when there are two columns
radiating with constant specific intensity the beam will
be a function only of the angle 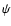 between the magnetic axis
and the direction to the observer:
between the magnetic axis
and the direction to the observer:
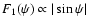 .
Interestingly, the parameter space for seeing two peaked
lightcurves is identical to the case of the pencil
beam model discussed above, the only difference being that
for the given angles
.
Interestingly, the parameter space for seeing two peaked
lightcurves is identical to the case of the pencil
beam model discussed above, the only difference being that
for the given angles 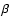 and
and 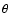 the maxima of the
lightcurve fall at different phases. Introducing
a more general beam pattern e.g.
the maxima of the
lightcurve fall at different phases. Introducing
a more general beam pattern e.g.
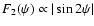 leads to dominance of multiple peaked lightcurves:
in this case we expect 4.5% single peaked, 27.8%
double peaked, 40.1% triple peaked, and 27.6% quadruple
peaked lightcurves.
leads to dominance of multiple peaked lightcurves:
in this case we expect 4.5% single peaked, 27.8%
double peaked, 40.1% triple peaked, and 27.6% quadruple
peaked lightcurves.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f1.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg21.gif) |
Figure 1:
Parameter space for viewing accreting X-ray pulsars.
The region below the solid line corresponds to
visibility of two polar caps with gravitational light bending
neglected. The region below the dashed line
corresponds to visibility of two caps with the gravitational
light deflection
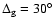 .
The shaded
region is the part of the parameter space in which
pulses would be detectable if radiation is strongly beamed.
The horizontal dotted line corresponds to the angle between
the rotation and magnetic axes .
The shaded
region is the part of the parameter space in which
pulses would be detectable if radiation is strongly beamed.
The horizontal dotted line corresponds to the angle between
the rotation and magnetic axes
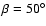 . . |
| Open with DEXTER |
For a set of data, like pulsars, with a well defined
property, i.e. either single or double pulsed, and a
given probability p that each pulsar will belong to one or other class,
the probability of observing n single peaked lightcurves and
m double peaked in an observation of randomly chosen
n+m objects is given by the binomial distribution:
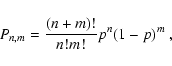 |
(2) |
and the probability of obtaining M or fewer double peaked
objects in a sample containing N sources is a sum
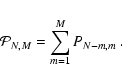 |
(3) |
We can test the consistency of the datasets defined above
with the simplest model:
random inclination of the magnetic axis to
the rotation axis 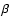 ,
random direction of the line of sight
,
random direction of the line of sight 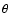 ,
and
no gravitational light deflection.
For the dataset
,
and
no gravitational light deflection.
For the dataset
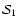 we obtain the probability
we obtain the probability
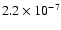 that there are 20 or fewer double pulsars in a set of 46 observed objects.
Applying this test to the dataset
that there are 20 or fewer double pulsars in a set of 46 observed objects.
Applying this test to the dataset
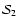 we obtained the probability
of only
we obtained the probability
of only
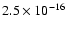 ,
and for the dataset
,
and for the dataset
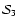 this probability is
this probability is
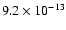 .
Thus we see
that the data are inconsistent with this simple model.
This is due to the fact that the parameter space for viewing
single pulsed objects is smaller than for the double pulsed objects.
This result holds for both the pencil beam and
fan beam F1. For the fan beam of the form F2
the results are even more significant since probability
of seeing single pulsed pulsars is even smaller:
for the set
.
Thus we see
that the data are inconsistent with this simple model.
This is due to the fact that the parameter space for viewing
single pulsed objects is smaller than for the double pulsed objects.
This result holds for both the pencil beam and
fan beam F1. For the fan beam of the form F2
the results are even more significant since probability
of seeing single pulsed pulsars is even smaller:
for the set
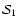 we obtain the probability
we obtain the probability
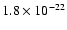 ,
for
,
for
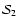 the probability is
the probability is
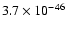 ,
and for
,
and for
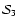 it is
it is
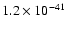 .
In this analysis we assumed that all multiple peaked model
lightcurves fall into the two peaked class.
We note, however, that the fan beam model predicts
triple and quadruple peaked lightcurves which are not observed.
.
In this analysis we assumed that all multiple peaked model
lightcurves fall into the two peaked class.
We note, however, that the fan beam model predicts
triple and quadruple peaked lightcurves which are not observed.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f2.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg30.gif) |
Figure 2:
The probability of classifying
a pulsar as single peaked
as a function of the threshold below which
the second peak is not detectable. |
| Open with DEXTER |
The real detectability of the second peak depends on the
exact shape of the beam and on the strength of the signal.
The second peak may be a small bump in the pulse shape
and when the signal to noise is low it might be undetected.
General modeling of second peak detectability is difficult
because it must include the unknown beam shape and the distribution
of signal to noise ratios. Here we present a simple model in which
we assume that we can detect the second peak if its amplitude
is at least a certain fraction of the main peak. Furthermore
we assume that the beam flux is described either
by
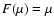 ,
or
,
or
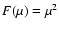 ,
where
,
where
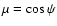 is the cosine
of the angle between the normal and the line of sight, and that the pulsar
is detectable from every direction. For these two
beam shapes we calculate the pulse shapes as a function of the
angles
is the cosine
of the angle between the normal and the line of sight, and that the pulsar
is detectable from every direction. For these two
beam shapes we calculate the pulse shapes as a function of the
angles 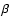 and
and 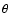 .
For each pulse shape we calculate R2 the ratio of the magnitude of the
second peak in relation to the main one.
We then define a detection threshold T for the second peak:
if R2> T a pulse shape is classified as a double and otherwise
as a single.
We calculate the probability of classifying
a pulsar as single pulsed as a function
of the detection threshold T for the two assumed beam shapes
and plot the results in
Fig. 2. The probability of classifying a pulsar as single peaked
increases with increasing the threshold T, the case
T=0 corresponds to the ideal case when even the smallest
second peaks are detectable.
When T=0.1 the value of
.
For each pulse shape we calculate R2 the ratio of the magnitude of the
second peak in relation to the main one.
We then define a detection threshold T for the second peak:
if R2> T a pulse shape is classified as a double and otherwise
as a single.
We calculate the probability of classifying
a pulsar as single pulsed as a function
of the detection threshold T for the two assumed beam shapes
and plot the results in
Fig. 2. The probability of classifying a pulsar as single peaked
increases with increasing the threshold T, the case
T=0 corresponds to the ideal case when even the smallest
second peaks are detectable.
When T=0.1 the value of
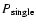 reaches
reaches
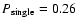 for the
for the
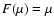 beam and
beam and
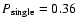 for the
for the
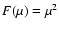 beam.
We would have classified the pulse shapes as double
peaked with the second peak as small as a few percent of the
main peak amplitude. We take the
case T=0.1, together with the
beam.
We would have classified the pulse shapes as double
peaked with the second peak as small as a few percent of the
main peak amplitude. We take the
case T=0.1, together with the
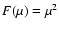 beam
i.e.
beam
i.e.
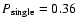 and find that
the probabilities of obtaining the observed datasets
are
and find that
the probabilities of obtaining the observed datasets
are
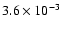 for the
for the
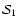 ,
,
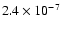 for
for
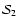 ,
and
,
and
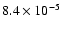 for
for
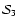 .
We note that we have assumed that a pulsar is detectable from
all directions, while for strongly beamed cases there is a
fraction of the parameter space where a
pulsar is undetectable because of small flux.
In the calculations below we consider the model
with T=0.
.
We note that we have assumed that a pulsar is detectable from
all directions, while for strongly beamed cases there is a
fraction of the parameter space where a
pulsar is undetectable because of small flux.
In the calculations below we consider the model
with T=0.
Including the effects of the gravitational light deflection
only reduces the probability of seeing one pulsed objects and makes
the values of the above probabilities smaller.
We present the probability of seeing one polar cap as a function of
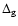 in the left panel of Fig. 3.
Another possibility to consider is that the pulsar beam is not wide
but strongly collimated, and the beam has an opening angle
of
in the left panel of Fig. 3.
Another possibility to consider is that the pulsar beam is not wide
but strongly collimated, and the beam has an opening angle
of 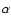 .
In this case for a given
.
In this case for a given 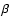 there
is only a small range of angles
there
is only a small range of angles
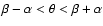 for which the pulsar is
visible at all. The restriction on the parameter space for small
for which the pulsar is
visible at all. The restriction on the parameter space for small
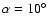 is shown in Fig. 1 as the shaded region.
The probability of seeing only one accretion cap as a function of the
angle
is shown in Fig. 1 as the shaded region.
The probability of seeing only one accretion cap as a function of the
angle 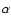 is shown in the right panel of Fig. 3.
Another possibility to consider is to allow for non
aligned dipole, i.e. to assume that the two polar caps
are not antipodal but can be placed anywhere on
the stellar surface. A straightforward calculation neglecting the
gravitational light bending effects shows
that the probability of seeing just one polar cap drops
in this case to 17%.
Thus the probabilities computed above
are conservative
and inclusion of the gravitational light bending and beaming
make the result even more significant.
is shown in the right panel of Fig. 3.
Another possibility to consider is to allow for non
aligned dipole, i.e. to assume that the two polar caps
are not antipodal but can be placed anywhere on
the stellar surface. A straightforward calculation neglecting the
gravitational light bending effects shows
that the probability of seeing just one polar cap drops
in this case to 17%.
Thus the probabilities computed above
are conservative
and inclusion of the gravitational light bending and beaming
make the result even more significant.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f3.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg42.gif) |
Figure 3:
Left panel: the probability of seeing only one polar cap
as a function of the maximal gravitational light deflection. The non-relativistic
case corresponds to
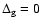 .
Right panel; the probability of seeing
only one cap as a function of the beaming angle .
Right panel; the probability of seeing
only one cap as a function of the beaming angle 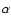 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f4.ps}\par\end{figure}](/articles/aa/full/2003/24/aa3320/Timg43.gif) |
Figure 4:
The probability of seeing only one polar cap
as a function of the maximal gravitational light deflection when the beam is described
by the from F2. The non-relativistic
case corresponds to
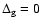 . .
|
| Open with DEXTER |
The effects of gravitational light deflection in the case
of fan beams do not alter the results.
We calculate the beam shape modified by the gravitational light bending using
the approximate formulae of Beloborodov (2002).
For the simple
fan beam F1 the probability of seeing the single or double
peaked lightcurves does not depend on
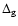 .
This is due to the fact
that gravitational light bending does not change qualitatively
the shape of the beam: it has a minimum along the magnetic axis and
a single maximum in the direction perpendicular to the magnetic axis.
We present the probability of seeing a single pulsed lightcurve
for the fan beam of the form F2 in Fig. 4.
Here the shape of the beam depends strongly on the value of
.
This is due to the fact
that gravitational light bending does not change qualitatively
the shape of the beam: it has a minimum along the magnetic axis and
a single maximum in the direction perpendicular to the magnetic axis.
We present the probability of seeing a single pulsed lightcurve
for the fan beam of the form F2 in Fig. 4.
Here the shape of the beam depends strongly on the value of
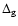 .
For small values of
.
For small values of
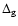 the probability
of seeing single pulsed lightcurves slightly decreases, and then it rises to
0.21 at
the probability
of seeing single pulsed lightcurves slightly decreases, and then it rises to
0.21 at
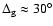 .
At this point the gravitational
light bending causes the two beams from the two
columns to merge and the beam shape is qualitatively the same
as for the case F1.
.
At this point the gravitational
light bending causes the two beams from the two
columns to merge and the beam shape is qualitatively the same
as for the case F1.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f5.ps}\par\end{figure}](/articles/aa/full/2003/24/aa3320/Timg45.gif) |
Figure 5:
The probability of observing the data
in models pencil beam parameterized by the the maximum angle
between the magnetic and rotation axis
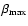 .
The solid line corresponds to the data set .
The solid line corresponds to the data set
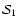 ,
and the short-dashed line corresponds to the data set ,
and the short-dashed line corresponds to the data set
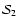 .
The long-dashed line corresponds to the data set .
The long-dashed line corresponds to the data set
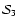 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f6.ps}\par\end{figure}](/articles/aa/full/2003/24/aa3320/Timg46.gif) |
Figure 6:
The probability of observing the data
in fan beam models parameterized by the the maximum angle
between the magnetic and rotation axis
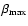 :
thin lines - fan beam F1, thick lines - fan beam F2.
The solid line corresponds to the data set :
thin lines - fan beam F1, thick lines - fan beam F2.
The solid line corresponds to the data set
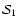 ,
and the short-dashed line corresponds to the data set ,
and the short-dashed line corresponds to the data set
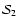 .
The long-dashed line corresponds to the data set .
The long-dashed line corresponds to the data set
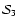 . .
|
| Open with DEXTER |
The incompatibility of the simple model with the data
prompts us to consider a more general model. We assume first that
the distribution of the inclinations of the magnetic
axes to the rotation axis is restricted, i.e. the angles
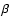 are limited to the range between 0 and
are limited to the range between 0 and
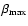 .
This corresponds to restricting the parameter space to the
region above a horizontal line at
.
This corresponds to restricting the parameter space to the
region above a horizontal line at
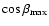 in Fig. 1.
For each value of
in Fig. 1.
For each value of
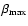 we can compute
the probability of observing the given set of data using
Eq. (3). We plot this probability
as a function of
we can compute
the probability of observing the given set of data using
Eq. (3). We plot this probability
as a function of
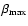 for the case of pencil beam
in Fig. 5 and for the two fan beams considered
in Fig. 6.
The standard model corresponds to the case
for the case of pencil beam
in Fig. 5 and for the two fan beams considered
in Fig. 6.
The standard model corresponds to the case
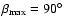 .
In Fig. 5 the probability of seeing the data
rises to nearly unity for the angles
.
In Fig. 5 the probability of seeing the data
rises to nearly unity for the angles
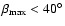 for the datasets
for the datasets
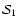 and
and
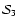 ,
and
,
and
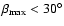 for the
dataset
for the
dataset
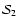 in the case of pencil beam model
of Fig. 5. The probabilities of seeing one cap
increases with decreasing
in the case of pencil beam model
of Fig. 5. The probabilities of seeing one cap
increases with decreasing
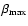 ,
and therefore
for its intermediate values the probability of seeing the data
is rising to nearly unity. For the very small values of
,
and therefore
for its intermediate values the probability of seeing the data
is rising to nearly unity. For the very small values of
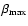 one expects to see nearly all pulsars
as single pulsed. Since each dataset contains some double
pulsed objects the probability of seeing the data drops
when
one expects to see nearly all pulsars
as single pulsed. Since each dataset contains some double
pulsed objects the probability of seeing the data drops
when
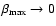 .
In the case of fan beam F2
(Fig. 6) the probability of seeing the data rises to unity
when
.
In the case of fan beam F2
(Fig. 6) the probability of seeing the data rises to unity
when
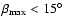 .
For this shape of the beam
there is a significant part of the parameter space where
the expected lightcurves are multiple peaked but we note that
there are no multiple peaked lightcurves
in the parameter space restricted to small angles
.
For this shape of the beam
there is a significant part of the parameter space where
the expected lightcurves are multiple peaked but we note that
there are no multiple peaked lightcurves
in the parameter space restricted to small angles
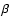 .
The triple peaked lightcurves appear when
.
The triple peaked lightcurves appear when
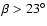 and quadruple peaked ones
when
and quadruple peaked ones
when
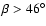 .
Thus in the framework
of the fan beam model we do not expect multiple peaked pulse shapes
if the inclination of the magnetic and rotation axes is limited
to small angles only.
.
Thus in the framework
of the fan beam model we do not expect multiple peaked pulse shapes
if the inclination of the magnetic and rotation axes is limited
to small angles only.
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{3320-f7a.ps}\hspace*{0.4cm...
...b.ps}\hspace*{0.4cm}
\includegraphics[width=5.1cm,clip]{3320-f7c.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg55.gif) |
Figure 7:
Each panel presents the region containing
the models that are consistent with the data at the level
of 60%, 90%, and 99%. The three panels correspond
to the three datasets. |
| Open with DEXTER |
A more general model taking into
account the general relativistic effects includes two parameters: the
maximal angle between the magnetic and rotation axis
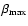 and the maximum gravitational light deflection angle
and the maximum gravitational light deflection angle
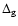 .
In the framework of the pencil beam model we compute the probability
of seeing a pulsar with only one polar cap as a function of these two angles.
In Fig. 7 we present the
regions containing the models that are consistent with
the data with the probability higher than 40%, 10%, and 1%.
The non relativistic results correspond to
the line
.
In the framework of the pencil beam model we compute the probability
of seeing a pulsar with only one polar cap as a function of these two angles.
In Fig. 7 we present the
regions containing the models that are consistent with
the data with the probability higher than 40%, 10%, and 1%.
The non relativistic results correspond to
the line
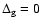 in Fig. 7.
Since the probability of seeing only one polar cap decreases
with increasing
in Fig. 7.
Since the probability of seeing only one polar cap decreases
with increasing
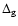 ,
we also set a limit
on its maximum value. The region corresponding to the
1% agreement limit for the dataset
,
we also set a limit
on its maximum value. The region corresponding to the
1% agreement limit for the dataset
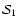 can
be expressed as
can
be expressed as
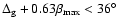 .
Thus if there were no gravitational light deflection
effects we find that the inclination angle of the magnetic
axis to the rotation axis should be smaller than
.
Thus if there were no gravitational light deflection
effects we find that the inclination angle of the magnetic
axis to the rotation axis should be smaller than
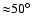 .
For the case with a moderate gravitational light bending
.
For the case with a moderate gravitational light bending
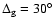 the magnetic axis inclination must
be smaller than
the magnetic axis inclination must
be smaller than
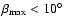 .
We also
see that the amount of gravitational light bending
cannot exceed
.
We also
see that the amount of gravitational light bending
cannot exceed 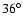 at the 99% confidence level.
The limits are even stronger when we take into account
dataset
at the 99% confidence level.
The limits are even stronger when we take into account
dataset
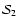 ,
however for the set
,
however for the set
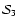 the constraints are similar to these obtained
for the dataset
the constraints are similar to these obtained
for the dataset
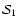 .
.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3320-f8.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg60.gif) |
Figure 8:
The value of the gravitational light bending as a
function of the emission angle, measured from the radial direction
for photons emitted at different initial radii. The
maximum gravitational light deflection is the value of deflection
for the initial angle of 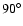 ,
i.e. parallel to the
surface. ,
i.e. parallel to the
surface. |
| Open with DEXTER |
To discuss the limit on
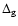 obtained above
we will consider two cases: (i) emission from a polar
cap, and (ii) emission from the accretion column. In the first
case the upper limit on the
obtained above
we will consider two cases: (i) emission from a polar
cap, and (ii) emission from the accretion column. In the first
case the upper limit on the
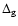 obtained above
can be interpreted as a limit on the compactness
of the star. We plot the amount of gravitational
light deflection as a function of the emission angle
for a few values of the ratio of the neutron star radius to the
gravitational radius
obtained above
can be interpreted as a limit on the compactness
of the star. We plot the amount of gravitational
light deflection as a function of the emission angle
for a few values of the ratio of the neutron star radius to the
gravitational radius
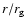 in Fig. 8.
The maximal gravitational light deflection of about
in Fig. 8.
The maximal gravitational light deflection of about
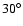 corresponds to the case with ratio
corresponds to the case with ratio
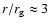 for the
photons emitted parallel to the surface.
The limit on
for the
photons emitted parallel to the surface.
The limit on
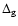 can be understood as the upper
limit on the compactness of the neutron stars.
In Fig. 9 we plot the ratio
can be understood as the upper
limit on the compactness of the neutron stars.
In Fig. 9 we plot the ratio
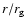 as a function of
the stellar gravitational mass for a few representative equations
of state. The ratio
as a function of
the stellar gravitational mass for a few representative equations
of state. The ratio
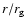 decreases with increasing mass.
The upper limit on the ratio
decreases with increasing mass.
The upper limit on the ratio
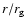 corresponds
for a given equation of state to the lower limit
on the mass of the accreting neutron stars. Masses
of neutron stars in some accreting objects have been
estimated from the observations of binary motion,
e.g. in the case of 4U1538-52
(Pakull et al. 1983; Reynolds et al. 1992) and they all seem
to be consistent with the fiducial
corresponds
for a given equation of state to the lower limit
on the mass of the accreting neutron stars. Masses
of neutron stars in some accreting objects have been
estimated from the observations of binary motion,
e.g. in the case of 4U1538-52
(Pakull et al. 1983; Reynolds et al. 1992) and they all seem
to be consistent with the fiducial
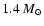 with
some uncertainty. The general consensus seems to be
that the masses of all neutron stars are consistent with
the mean value of
with
some uncertainty. The general consensus seems to be
that the masses of all neutron stars are consistent with
the mean value of 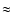 1.4
1.4 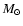 ,
and this is also
the value found for the binary pulsars
(Thorsett & Chakrabarty 1999),
however in LMXBs this range may be much wider
and reach above
,
and this is also
the value found for the binary pulsars
(Thorsett & Chakrabarty 1999),
however in LMXBs this range may be much wider
and reach above 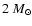 (Bulik et al. 2000).
If the neutron stars have masses around
(Bulik et al. 2000).
If the neutron stars have masses around
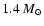 and
the beams are wide
then our results point to the
very stiff equations of state e.g. SDB (Sahu et al. 1993).
and
the beams are wide
then our results point to the
very stiff equations of state e.g. SDB (Sahu et al. 1993).
A second possibility is that we see the emission from the
accretion shock above the surface of the neutron star with the
typical properties of the fan beam and that this emission is
responsible for the observed flux at angles above 90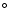 with respect to the normal. Our considerations above imply
that the emission is visible up to the angles exceeding the
perpendicular to the normal by
with respect to the normal. Our considerations above imply
that the emission is visible up to the angles exceeding the
perpendicular to the normal by
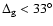 .
In the
non-relativistic case this means that such shocks can lie no
higher than
.
In the
non-relativistic case this means that such shocks can lie no
higher than
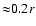 above the surface of the neutron
star. If the effects of the gravitational light bending around a
neutron star are included the maximum height allowed is even
smaller.
above the surface of the neutron
star. If the effects of the gravitational light bending around a
neutron star are included the maximum height allowed is even
smaller.
We have obtained
a limit on the possible inclination angles of the magnetic axis
with respect to the rotation axis
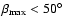 .
A hint of such a distribution was already shown by
Leahy (1991). He analyzed the lightcurves
of 20 pulsars using a simple model with the beam dependence on the
emission angle as
.
A hint of such a distribution was already shown by
Leahy (1991). He analyzed the lightcurves
of 20 pulsars using a simple model with the beam dependence on the
emission angle as
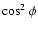 and
and
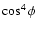 where
where
 is the direction to the normal of the surface.
For each pulsar he found the angles
is the direction to the normal of the surface.
For each pulsar he found the angles 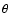 and
and 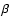 ,
however the fits were degenerate in these angles, so that
it was not clear a priori which angle is which. The resulting
distribution was inconsistent with the assumption that both
angles are random, and Leahy (1991) concluded
that the mean angle between the magnetic and rotation axis
is as small
,
however the fits were degenerate in these angles, so that
it was not clear a priori which angle is which. The resulting
distribution was inconsistent with the assumption that both
angles are random, and Leahy (1991) concluded
that the mean angle between the magnetic and rotation axis
is as small 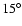 .
Inclusion of the gravitational
light bending effects (Leahy & Li 1995)
does not alter this conclusion.
Bulik et al. (1995)
modeled lightcurves of 4U 1538-52 and Vela X-1 observed by Ginga,
and obtained the inclination angles below
.
Inclusion of the gravitational
light bending effects (Leahy & Li 1995)
does not alter this conclusion.
Bulik et al. (1995)
modeled lightcurves of 4U 1538-52 and Vela X-1 observed by Ginga,
and obtained the inclination angles below 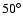 for their
fits with best significance. Kraus et al. (1996) analyzed the
pulse profiles of Cen X-3 and reconstructed the geometry and
beam pattern for this object. They found that the most likely
inclination angles of the magnetic axis to the rotation axis
are
for their
fits with best significance. Kraus et al. (1996) analyzed the
pulse profiles of Cen X-3 and reconstructed the geometry and
beam pattern for this object. They found that the most likely
inclination angles of the magnetic axis to the rotation axis
are
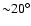 .
An analysis of
the pulse shape of Her X-1 (Blum & Kraus 2000)
also lead to a constraint on the angle between the magnetic and
rotation axis
.
An analysis of
the pulse shape of Her X-1 (Blum & Kraus 2000)
also lead to a constraint on the angle between the magnetic and
rotation axis
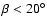 .
.
We have mentioned in Sect. 2 three special objects
A0535-262, GX1+4,and RX J0812.4-3114 for which accretion flow
eclipses have been reported (possibly this list also includes
GS1843-24, Finger et al. 1999, and XTE J1946+274, Wilson et al. 2003).
If such eclipses happen when the accretion column passes through
the line of sight then they should take place when
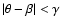 ,
where
,
where 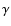 is the angular width of the
accretion column. The region corresponding to
is the angular width of the
accretion column. The region corresponding to
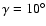 is shaded in Fig. 1. We see that such
eclipses should frequently take place in double pulsed light
curves, if the magnetic axis is randomly oriented with respect
to the rotation axis. Moreover within the single pulsed light
curves a significant fraction, - approximately 20-30%
should exhibit such dips, and this fraction increases as the
amount of gravitational light bending increases.
is shaded in Fig. 1. We see that such
eclipses should frequently take place in double pulsed light
curves, if the magnetic axis is randomly oriented with respect
to the rotation axis. Moreover within the single pulsed light
curves a significant fraction, - approximately 20-30%
should exhibit such dips, and this fraction increases as the
amount of gravitational light bending increases.
Yet the only three cases when such dips have been found are in
single pulsed light curves. The lightcurve of A0535-262 seems
to be double peaked, however Cemeljic & Bulik (1998) pointed
out that it can be interpreted as a single pulse divided by the
accretion flow eclipse. This lack of double peaked pulsars with
accretion flow eclipses (dips) may mean that the region of
parameter space for double peaked light curves with dips is
either empty or scarcely populated! Again we are drawn to the
conclusion that the magnetic axis needs to be aligned with
the rotation axis. If the magnetic axis inclination is restricted
to the region
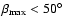 ,
then one expects that the
accretion flow eclipses to be observed only in the
one pulsed lightcurves, as is the case. While this by itself is
not a significant result, the identification of accretion flow
eclipses is consistent with the conclusion that
the range of allowed values of
,
then one expects that the
accretion flow eclipses to be observed only in the
one pulsed lightcurves, as is the case. While this by itself is
not a significant result, the identification of accretion flow
eclipses is consistent with the conclusion that
the range of allowed values of 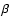 is limited.
is limited.
One should mention here that there
may possibly be a selection bias against seeing double pulsed objects.
In the case of nearly perpendicular rotators the two
pulses will be similar. It is therefore possible that
the lack of double pulsed objects is due to misidentification of the
pulse period which should be two times longer than reported.
The fraction of such misidentified objects depends on the
exact shape of the beam. For wide uncollimated beams
the two pulses look similar for a range of angles 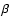 as large as the width of the beams. However, our limit
is
as large as the width of the beams. However, our limit
is
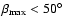 ,
so the beams would have to be very
wide. Additionally, the beam shape
would have to be very fine tuned in order to compensate for the viewing
geometry effects over such a large range of angles.
,
so the beams would have to be very
wide. Additionally, the beam shape
would have to be very fine tuned in order to compensate for the viewing
geometry effects over such a large range of angles.
Another possible selection effect against seeing double
peaked pulsars was shown by Beloborodov (2002).
Assuming that both accretion caps lie
exactly opposite one another on the surface of the neutron star
and are identical,and
that the radiation beam is well described by
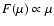 (or intensity is independent of the angle of emission),
he shows that the pulse shapes are flat in the region where both polar
caps are visible due to gravitational light bending.
This decreases the parameter space for seeing double peaked
pulsars. However detailed modeling of individual objects
tends to show that the above assumptions are not satisfied,
the data usually requires non antipodal caps, complicated beam patterns,
and sometimes differences between the two polar caps
(Kraus et al. 1996; Leahy & Li 1995; Blum & Kraus 2000; Bulik et al. 1995).
(or intensity is independent of the angle of emission),
he shows that the pulse shapes are flat in the region where both polar
caps are visible due to gravitational light bending.
This decreases the parameter space for seeing double peaked
pulsars. However detailed modeling of individual objects
tends to show that the above assumptions are not satisfied,
the data usually requires non antipodal caps, complicated beam patterns,
and sometimes differences between the two polar caps
(Kraus et al. 1996; Leahy & Li 1995; Blum & Kraus 2000; Bulik et al. 1995).
The sample of accreting pulsars presented here is dominated by transient
Be/X-ray systems. One should note that for the disk-fed persistent
sources (Her X-1, SMC X-1, SMC X-2, Cen X-3, LMC X-4, RX J0648.1-4419) there
are three double peaked objects out of six sources, still
below the expected 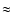 79 percent,
but this is not a significant discrepancy.
In the case of wind-fed persistent sources
(Vela X-1, 1E 1145.1-6141, 4U1907+09, 4U1583-53, GX 301-2, 2S 0114+650)
there are four double peaked out of six objects.
However, because of the small number of these sources it is
impossible to obtain any significant conclusion just from
a statistical analysis and, as we already mentioned above,
detailed modeling of two wind-fed pulsars (4U 1538-52 and Vela X-1)
and one disk-fed (Cen X-3) resulted in low values of
79 percent,
but this is not a significant discrepancy.
In the case of wind-fed persistent sources
(Vela X-1, 1E 1145.1-6141, 4U1907+09, 4U1583-53, GX 301-2, 2S 0114+650)
there are four double peaked out of six objects.
However, because of the small number of these sources it is
impossible to obtain any significant conclusion just from
a statistical analysis and, as we already mentioned above,
detailed modeling of two wind-fed pulsars (4U 1538-52 and Vela X-1)
and one disk-fed (Cen X-3) resulted in low values of 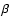 .
.
We analyzed the shapes of accretion powered pulsar light
curves, looking for the expected fraction of single and double
peaked light curves, as well as these exhibiting accretion flow
eclipses. We find that the expected number of single peaked
lightcurves is small; certainly less than about one in five
lightcurves should be single peaked
both in the framework of the pencil beam model
and a simple fan beam model. A general fan beam model
predicts predominantly triple and quadruple peaked
pulse shapes and only a small percentage of single
peaked lightcurves.
On the other hand the
observations show that quite a large fraction of
accreting pulsars have single peaked lightcurves in hard X-rays
with the rest being double peaked.
In order to explain this discrepancy between
theory and observations
we are drawn to conclude that the
magnetic axes in accretion-powered pulsars tend to be aligned
with the rotation axis. Such alignment decreases the expected
number of double peaked lightcurves, as seen in
Fig. 1. We have compared the models
parametrized by the maximal inclination of the magnetic to the
rotation axis
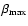 and the value of the
maximum gravitational light deflection
and the value of the
maximum gravitational light deflection
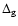 with the
data. We obtain upper limits at the
99% confidence level
with the
data. We obtain upper limits at the
99% confidence level
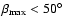 and
and
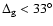 .
.
Our results are based on the classification of the neutron star lightcurves
as single or double pulsed. In order to avoid
possible misclassification we have attempted to use
the data above 10 keV, or above the cyclotron line wherever possible.
Moreover, we have attempted to classify as many pulsars
as double when we were in doubt.
In order to rid ourselves of the possible systematic effects
we have repeated the analysis for the three datasets,
and in the third dataset we included all the unclassifiable
pulsars as double peaked objects to be conservative.
The deficit of double pulsed objects is significant for
every dataset that we analyzed. Moreover we
note that the paucity of double peaked
pulsars is so strong that our results still hold even if there are still a few
misidentifications in our analysis.
We have also shown that if the pulsar beam is strongly collimated,
the deficit of double peaked objects becomes more significant.
Acknowledgements
We thank Peter Jonker, Biswajit Paul, and Silvia Zane for helpful
comments on the contents of the Tables, and the anonymous referee
for helpful comments on this paper.
This research has been supported by the KBN grants 5P03D01721
and PBZ-KBN-054/P03/2001, and
the EU Programme "Improving the Human Research Potential and the
Socio-Economic Knowledge Base'' (Research Training Network Contract
HPRN-CT-2000-00137).
TB is grateful for the hospitality of the Observatoire
de Paris in Meudon and for the support of the CNRS/PAN Jumelage programme.
-
Angelini, L., Church, M. J., Parmar, A. N., Balucinska-Church, M., &
Mineo, T. 1998, A&A, 339, L41
NASA ADS
-
Aoki, T., Dotani, T., Ebisawa, K., et al. 1992, PASJ, 44, 641
NASA ADS
-
Baldo, M., Bombaci, I., & Burgio, G. F. 1997, A&A, 328, 274
In the text
NASA ADS
-
Beloborodov, A. M. 2002, ApJ, 566, L85
In the text
NASA ADS
-
Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367
In the text
NASA ADS
-
Blum, S., & Kraus, U. 2000, ApJ, 529, 968
In the text
NASA ADS
-
Bulik, T., Kluzniak, W., & Zhang, W. 2000, A&A, 361, 153
In the text
NASA ADS
-
Bulik, T., Meszaros, P., Woo, J. W., Hagase, F., & Makishima, K.
1992, ApJ, 395, 564
In the text
NASA ADS
-
Bulik, T., Riffert, H., Meszaros, P., et al. 1995, ApJ, 444, 405
In the text
NASA ADS
-
Burderi, L., Di Salvo, T., Robba, N. R., La Barbera, A., &
Guainazzi, M. 2000, ApJ, 530, 429
NASA ADS
-
Caraveo, P. A., Bignami, G. F., & Goldwurm, A. 1989, ApJ, 338, 338
NASA ADS
-
Cemeljic, M., & Bulik, T. 1998, Acta Astronomica, 48, 65
In the text
NASA ADS
-
Chakrabarty, D., Bildsten, L., Grunsfeld, J. M., et al. 1997, ApJ,
474, 414
NASA ADS
-
Chakrabarty, D., Koh, T., Bildsten, L., et al. 1995, ApJ, 446, 826
NASA ADS
-
Coe, M. J., Roche, P., Everall, C., et al. 1994, A&A, 289, 784
NASA ADS
-
Corbet, R., Marshall, F. E., Lochner, J. C., Ozaki, M., & Ueda, Y.
1998, IAU Circ., 6803
-
Corbet, R. H. D., Finley, J. P., & Peele, A. G. 1999a,
ApJ, 511, 876
NASA ADS
-
Corbet, R. H. D., Marshall, F. E., Coe, M. J., Laycock, S., &
Handler, G. 2001, ApJ, 548, L41
NASA ADS
-
Corbet, R. H. D., Marshall, F. E., Peele, A. G., & Takeshima, T.
1999b, ApJ, 517, 956
NASA ADS
-
Corbet, R. H. D., & Peele, A. G. 1997, ApJ, 489, L83
NASA ADS
-
Cropper, M., Zane, S., Ramsay, G., Haberl, F., & Motch, C. 2001,
A&A, 365, L302
NASA ADS
-
Cusumano, G., Israel, G. L., Mannucci, F., et al. 1998, A&A, 337, 772
NASA ADS
-
Cusumano, G., Maccarone, M. C., Nicastro, L., Sacco, B., & Kaaret,
P. 2000, ApJ, 528, L25
NASA ADS
-
Dennerl, K., Haberl, F., & Pietsch, W. 1995, IAU Circ., 6184
-
Finger, M. H., Bildsten, L., Chakrabarty, D., et al. 1999, ApJ, 517,
449
In the text
NASA ADS
-
Finger, M. H., Koh, D. T., Nelson, R. W., et al. 1996, Nature, 381, 291
NASA ADS
-
Finger, M. H., Macomb, D. J., Lamb, R. C., et al. 2001, ApJ, 560, 378
NASA ADS
-
Giacconi, R., Gursky, H., Kellogg, E., Schreier, E., & Tananbaum, H.
1971, ApJ, 167, L67
In the text
NASA ADS
-
Giacconi, R., Murray, S., Gursky, H., et al. 1972, ApJ, 178, 281
NASA ADS
-
Giles, A. B., Galloway, D. K., Greenhill, J. G., Storey, M. C., &
Wilson, C. A. 2000, ApJ, 529, 447
In the text
NASA ADS
-
Grevenev, S. A., Pavlinsk, M. N., & Syunyaev, R. A. 1992, SvA Lett., 18, 228
NASA ADS
-
Haberl, F., Dennerl, K., Pietsch, W., & Reinsch, K. 1997, A&A, 318,
490
NASA ADS
-
Hall, T. A., Finley, J. P., Corbet, R. H. D., & Thomas, R. C. 2000,
ApJ, 536, 450
NASA ADS
-
Huckle, H. E., Mason, K. O., White, N. E., et al. 1977, MNRAS, 180,
21P
NASA ADS
-
Hughes, J. P. 1994, ApJ, 427, L25
NASA ADS
-
Hulleman, F., in 't Zand, J. J. M., & Heise, J. 1998, A&A, 337, L25
NASA ADS
-
Imanishi, K., Yokogawa, J., Tsujimoto, M., & Koyama, K. 1999, PASJ,
51, L15
NASA ADS
-
in 't Zand, J. J. M., Baykal, A., & Strohmayer, T. E. 1998, ApJ, 496,
386
NASA ADS
-
Isenberg, M., Lamb, D. Q., & Wang, J. C. L. 1998, ApJ, 505, 688
In the text
NASA ADS
-
Israel, G. L., Angelini, L., Campana, S., et al. 1998, MNRAS, 298, 502
NASA ADS
-
Israel, G. L., Campana, S., Covino, S., et al. 2000, ApJ, 531, L131
NASA ADS
-
Israel, G. L., Mereghetti, S., & Stella, L. 1994, ApJ, 433, L25
NASA ADS
-
Israel, G. L., Stella, L., Angelini, L., White, N. E., & Giommi, P.
1995, IAU Circ., 6277
-
Israel, G. L., Stella, L., Angelini, L., et al. 1997, ApJ, 474, L53
NASA ADS
-
Iwasawa, K., Koyama, K., & Halpern, J. P. 1992, PASJ, 44, 9
NASA ADS
-
Jonker, P. G., & van der Klis, M. 2001, ApJ, 553, L43
NASA ADS
-
Kelley, R. L., Rappaport, S., & Ayasli, S. 1983, ApJ, 274, 765
NASA ADS
-
Kinugasa, K., Torii, K., Hashimoto, Y., et al. 1998, ApJ, 495, 435
NASA ADS
-
Koh, D. T., Bildsten, L., Chakrabarty, D., et al. 1997, ApJ, 479, 933
NASA ADS
-
Koyama, K., Kawada, M., Kunieda, H., Tawara, Y., & Takeuchi, Y.
1990a, Nature, 343, 148
NASA ADS
-
Koyama, K., Kawada, M., Takeuchi, Y., et al. 1990b, ApJ,
356, L47
NASA ADS
-
Koyama, K., Kunieda, H., Takeuchi, Y., & Tawara, Y.
1990c, PASJ, 42, L59
NASA ADS
-
Koyama, K., Kawada, M., Tawara, Y., et al. 1991a, ApJ,
366, L19
NASA ADS
-
Koyama, K., Kunieda, H., Takeuchi, Y., & Tawara, Y. 1991b, ApJ, 370, L77
NASA ADS
-
Kraus, U., Blum, S., Schulte, J., Ruder, H., & Meszaros, P. 1996,
ApJ, 467, 794
In the text
NASA ADS
-
Lamb, D. Q., Wang, J. C. L., & Wasserman, I. M. 1990, ApJ, 363, 670
In the text
NASA ADS
-
Leahy, D. A. 1991, MNRAS, 251, 203
In the text
NASA ADS
-
Leahy, D. A., & Li, L. 1995, MNRAS, 277, 1177
In the text
NASA ADS
-
Levine, A., Rappaport, S., Deeter, J. E., Boynton, P. E., & Nagase,
F. 1993, ApJ, 410, 328
NASA ADS
-
Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2000, A&AS,
147, 25
NASA ADS
-
Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2001, A&A, 368, 1021
In the text
NASA ADS
-
Lochner, J. C., Marshall, F. E., Whitlock, L. A., & Brandt, N. 1998,
IAU Circ., 6814
-
Macomb, D. J., Finger, M. H., Harmon, B. A., Lamb, R. C., & Prince,
T. A. 1999, ApJ, 518, L99
NASA ADS
-
Makishima, K., Ohashi, T., Kawai, N., et al. 1990, PASJ, 42, 295
NASA ADS
-
Marsden, D., Gruber, D. E., Heindl, W. A., Pelling, M. R., &
Rothschild, R. E. 1998, ApJ, 502, L129
NASA ADS
-
McClintock, J. E., Nugent, J. J., Li, F. K., & Rappaport, S. A. 1977,
ApJ, 216, L15
NASA ADS
-
Mereghetti, S., Tiengo, A., Israel, G. L., & Stella, L. 2000, A&A,
354, 567
NASA ADS
-
Meszaros, P. 1992, High-energy radiation from magnetized neutron stars
Meszaros (Chicago: University of Chicago Press)
In the text
-
Meszaros, P., & Nagel, W. 1985, ApJ, 298, 147
In the text
NASA ADS
-
Nagase, F. 1989, PASJ, 41, 1
In the text
NASA ADS
-
Oosterbroek, T., Orlandini, M., Parmar, A. N., et al. 1999, A&A, 351,
L33
NASA ADS
-
Pakull, M., van Amerongen, S., Bakker, R., & van Paradijs, J. 1983,
A&A, 122, 79
NASA ADS
-
Paul, B., Agrawal, P. C., Mukerjee, K., et al. 2001, A&A, 370, 529
NASA ADS
-
Paul, B., & Rao, A. R. 1998, A&A, 337, 815
NASA ADS
-
Prakash, M., Bombaci, I., Prakash, M., et al. 1997, Phys. Rep., 280, 1
In the text
NASA ADS
-
Reig, P., & Coe, M. J. 1999, MNRAS, 302, 700
NASA ADS
-
Reig, P., & Roche, P. 1999a, MNRAS, 306, 100
NASA ADS
-
Reig, P., & Roche, P. 1999b, MNRAS, 306, 95
In the text
NASA ADS
-
Remillard, R., Levine, A., Takeshima, T., et al. 1998, IAU Circ., 6826
-
Reynolds, A. P., Bell, S. A., & Hilditch, R. W. 1992, MNRAS, 256, 631
In the text
NASA ADS
-
Robba, N. R., Burderi, L., Wynn, G. A., Warwick, R. S., & Murakami,
T. 1996, ApJ, 472, 341
NASA ADS
-
Robba, N. R., & Warwick, R. S. 1989, ApJ, 346, 469
NASA ADS
-
Sahu, P. K., Basu, R., & Datta, B. 1993, ApJ, 416, 267
In the text
NASA ADS
-
Santangelo, A., Cusumano, G., dal Fiume, D., et al. 1998, A&A, 338,
L59
NASA ADS
-
Santangelo, A., Segreto, A., Giarrusso, S., et al. 1999, ApJ, 523,
L85
NASA ADS
-
Saraswat, P., & Apparao, K. M. V. 1992, ApJ, 401, 678
NASA ADS
-
Saraswat, P., Mihara, T., Corbet, R., & Ebisawa, K. 1997, in All-Sky
X-Ray Observations in the Next Decade, 109
-
Schmidtke, P. C., Cowley, A. P., McGrath, T. K., & Anderson, A. L.
1995, PASP, 107, 450
NASA ADS
-
Schwentker, O. 1994, A&A, 286, L47
NASA ADS
-
Scott, D. M., Finger, M. H., Wilson, R. B., et al. 1997, ApJ, 488, 831
NASA ADS
-
Seward, F. D., Charles, P. A., & Smale, A. P. 1986, ApJ, 305, 814
NASA ADS
-
Shklovsky, I. S. 1967, ApJ, 148, L1
In the text
NASA ADS
-
Skinner, G. K., Bedford, D. K., Elsner, R. F., et al. 1982, Nature, 297,
568
NASA ADS
-
Stollberg, M. T., Finger, M. H., Wilson, R. B., et al. 1999, ApJ, 512,
313
NASA ADS
-
Sugizaki, M., Nagase, F., Torii, K., et al. 1997, PASJ, 49, L25
NASA ADS
-
Tananbaum, H., Gursky, H., Kellogg, E. M., et al. 1972, ApJ, 174,
L143
NASA ADS
-
Tawara, Y., Yamauchi, S., Awaki, H., et al. 1989, PASJ, 41, 473
NASA ADS
-
Thorsett, S. E., & Chakrabarty, D. 1999, ApJ, 512, 288
In the text
NASA ADS
-
Torii, K., Kinugasa, K., Katayama, K., et al. 1998a, ApJ,
508, 854
NASA ADS
-
Torii, K., Kinugasa, K., Katayama, K., Tsunemi, H., & Yamauchi, S.
1998b, ApJ, 503, 843
NASA ADS
-
Torii, K., Sugizaki, M., Kohmura, T., Endo, T., & Nagase, F. 1999,
ApJ, 523, L65
NASA ADS
-
Tsujimoto, M., Imanishi, K., Yokogawa, J., & Koyama, K. 1999, PASJ,
51, L21
NASA ADS
-
Ueno, M., Yokogawa, J., Imanishi, K., & Koyama, K. 2000, PASJ, 52,
L63
NASA ADS
-
Wijnands, R., & van der Klis, M. 1998, Nature, 394, 344
NASA ADS
-
Wilson, C. A., & Finger, M. H. 1998, IAU Circ., 7048
-
Wilson, C. A., Finger, M. H., Coe, M., & Negueruela, I. 2003, ApJ, 584, 996
In the text
NASA ADS
-
Wilson, C. A., Finger, M. H., Harmon, B. A., et al. 1997, ApJ, 479,
388
NASA ADS
-
Witten, E. 1984, Phys. Rev., 30, 272
In the text
-
Woo, J. W., Clark, G. W., Levine, A. M., Corbet, R. H. D., & Nagase,
F. 1996, ApJ, 467, 811
NASA ADS
-
Yokogawa, J., Imanishi, K., Tsujimoto, M., Kohno, M., & Koyama, K.
1999, PASJ, 51, 547
NASA ADS
-
Yokogawa, J., & Koyama, K. 1998, IAU Circ., 7028
-
Yokogawa, J., Imanishi, K., Ueno, M., & Koyama, K. 2000a,
PASJ, 52, L73
NASA ADS
-
Yokogawa, J., Paul, B., Ozaki, M., et al. 2000b, ApJ,
539, 191
NASA ADS
Copyright ESO 2003
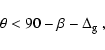
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f1.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg21.gif)
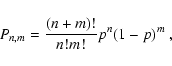
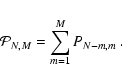
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f2.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f3.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f4.ps}\par\end{figure}](/articles/aa/full/2003/24/aa3320/Timg43.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f5.ps}\par\end{figure}](/articles/aa/full/2003/24/aa3320/Timg45.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3320-f6.ps}\par\end{figure}](/articles/aa/full/2003/24/aa3320/Timg46.gif)
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{3320-f7a.ps}\hspace*{0.4cm...
...b.ps}\hspace*{0.4cm}
\includegraphics[width=5.1cm,clip]{3320-f7c.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3320-f8.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg60.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{3320-f9.ps}\end{figure}](/articles/aa/full/2003/24/aa3320/Timg61.gif)