A&A 404, 735-742 (2003)
DOI: 10.1051/0004-6361:20030529
The lunar theory ELP revisited.
Introduction of new planetary perturbations
J. Chapront - G. Francou
Observatoire de Paris, SYRTE, UMR 8630/CNRS,
61 avenue de l'Observatoire, 75014 Paris, France
Received 19 September 2002 / Accepted 21 March 2003
Abstract
On the basis of the semi-analytical theory ELP, a new solution has been built that makes use of the planetary perturbations MPP01 constructed by P. Bidart. This new solution, called ELP/MPP02, is an analytical solution that contains all the perturbations to represent the lunar motion. The level of truncation for the series is the centimeter. This limit induces analytical developments of a reasonable dimension. ELP/MPP02 is compared to the JPL ephemerides DE405 and DE406. After fitting the constants and the reference frame to DE405, over a few centuries, numerical comparisons with DE405 show a significant improvement in precision, in particular for the radius vector. Over the long range of several millennia, comparisons with DE406 show an improvement in the long periodic perturbations due to planets.
On the time interval of one century around J2000 we added to ELP/MPP02 numerical complements
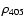 based on the differences with DE405 in such a way that ELP/MPP02+
based on the differences with DE405 in such a way that ELP/MPP02+
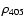 has the precision of the numerical integration. Using this new ephemeris to analyse LLR data provided since 1970, we build the solution ELP/MPP02(LLR) fitted to LLR observations.
has the precision of the numerical integration. Using this new ephemeris to analyse LLR data provided since 1970, we build the solution ELP/MPP02(LLR) fitted to LLR observations.
Various approximations have been also tested on the residuals DE406 - ELP/MPP02. We first determined corrections to the secular variations of the mean longitude, longitudes of the node and perigee under a simple polynomial form; they reduce the differences between ELP/MPP02 and DE406 to less than 3 arcsec in longitude and latitude and 2 km in distance over the whole time interval of DE406 [-3000; +3000]. Next, the differences themselves between the two solutions are approximated
over 2 millennia with Poisson series in a pseudo analytical form similar to ELP/MPP02. We reduce the residuals to less than 0.03 arcsec in longitude and latitude and 30 m in distance.
Key words: planets and satellites: general - celestial mechanics - ephemerides
This paper presents various aspects of improvements of the solution ELP.
In the first part, we recall the main features of the solution ELP, emphasizing its major
deficiency due to the computation of planetary perturbations. To improve the planetary
developments we make use of a new solution named MPP01 by Bidart (2000). In the
second part, after simplifications of the original developments of MPP01, fit of constants
and tests of precision, we derive a new solution ELP/MPP02. Several parameters and the
reference frame are fit to the JPL ephemeris DE405 (Standish 1998). The
solution ELP/MPP02(405) is then compared to DE405/DE406 over various time intervals.
In particular its validity over a long period of time is tested over the whole time interval
of DE406 [-3000; +3000]. Then, the parameters and frame are independently fitted to
LLR observations leading to the final solution ELP/MPP02(LLR). In the third part, further
numerical experiments have been tested to make ELP/MPP02 and DE406 approach over
several millennia. Two approaches are examined: first, a fit of the secular variations of the
lunar arguments to the numerical integration, second, an approximation of the
differences between the 2 solutions themselves with Poisson series.
The construction of the complete lunar theory ELP goes back to 1980. Its first version was the semi-analytical solution ELP2000-82 (Chapront-Touzé & Chapront 1983). This solution includes:
- the solution of the Main Problem (Earth, Moon and Sun with a Keplerian heliocentric orbit for the Earth-Moon barycenter) including partials with respect to various constants and parameters;
- the Earth's figure perturbations;
- the direct and indirect planetary perturbations that contain in particular the effects of the secular motions in eccentricity and perihelion of the Earth-Moon barycenter EMB and the secular motion of the ecliptic; the planetary motions come from VSOP82 (Bretagnon 1982) ;
- the relativistic effects;
- the tidal perturbations;
- the Moon's figure perturbations and coupling with libration.
This first version of ELP has not been fitted directly to observations
but via the JPL lunar ephemeris DE200-LE200. VSOP82 used the same source of comparisons and
fits. In order to increase the time domain of validity, a second version has been developed:
ELP2000-85 with a higher truncation level but introducing new expressions for the mean lunar
arguments (Chapront-Touzé & Chapront 1988). With respect to
ELP2000-82 the main improvement consists of computing secular terms proportional to
powers 3 and 4 of the time. Correlatively a comparison with the JPL lunar ephemeris LE51
(Newhall et al. 1983) over a long range has been performed to estimate the
accuracy of the secular terms. Later, the new mean lunar arguments of ELP2000-85 were
introduced in ELP2000-82, giving ELP2000-82B.
Further improvements have been brought concerning mainly the lunar and terrestrial masses,
the perturbations due to the Moon and Earth's figures including more recent
values of the gravitational parameters, the tidal perturbations with a new model separating
diurnal and semi-diurnal tides on the Earth and taking into account the tides on the Moon. As a basic JPL ephemeris for comparisons and fits of the constants we then used DE245. In parallel an improvement of the lunar librations by Moons (1982) has been done. Finally, a preliminary fit of the improved ELP2000-82B to LLR observations has been realized (Chapront & Chapront-Touzé 1997). From now on, the improved analytical solution ELP2000-82B is simply called ELP. Our last version was ELP2000-96, obtained by adding numerical complements to ELP; a complete analysis of Lunar Laser Ranging (LLR) observations from 1972 till 1998 has been performed using this solution and the completed Moons' theory of the lunar libration (Chapront et al. 1999). ELP provides the polar coordinates 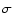 (longitude V, latitude U and distance r) under the general formulation:
(longitude V, latitude U and distance r) under the general formulation:
In the case of V one has to add to the previous formula the secular mean longitude:
w1 = w1(0)+w1(1)t+w1(2)t2+...
Ai1, i2,..., ip(n) are numerical coefficients,
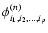 are numerical phases and
are numerical phases and 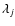 are literal arguments standing for polynomial functions of the time:
are literal arguments standing for polynomial functions of the time:
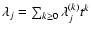 .
In the case of the Main Problem, we have also at our disposal the derivatives of the coefficients
Ai1, i2,..., ip(n) and the mean motions
.
In the case of the Main Problem, we have also at our disposal the derivatives of the coefficients
Ai1, i2,..., ip(n) and the mean motions
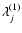 with respect to several constants (sidereal mean motions of Moon and the Sun, lunar and solar eccentricities, inclination, ratios of masses,...). The Main Problem depends on 4 arguments D, F, l and l' (see the definition of Delaunay's arguments below). For the Earth's figure perturbations we add the argument
with respect to several constants (sidereal mean motions of Moon and the Sun, lunar and solar eccentricities, inclination, ratios of masses,...). The Main Problem depends on 4 arguments D, F, l and l' (see the definition of Delaunay's arguments below). For the Earth's figure perturbations we add the argument
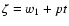 ,
where p is the precession constant for J2000. For planetary perturbations the components
,
where p is the precession constant for J2000. For planetary perturbations the components 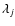 are Delaunay's arguments, and planetary secular mean longitudes known from a planetary theory like VSOP82. The reference plane of the theory is the mean dynamical ecliptic at J2000. For recent determination of the quantities related to the reference frame, see Chapront
et al. (2002).
The classical Delaunay's arguments D, F, l and l' are used in the Main Problem series and perturbation series with:
are Delaunay's arguments, and planetary secular mean longitudes known from a planetary theory like VSOP82. The reference plane of the theory is the mean dynamical ecliptic at J2000. For recent determination of the quantities related to the reference frame, see Chapront
et al. (2002).
The classical Delaunay's arguments D, F, l and l' are used in the Main Problem series and perturbation series with:
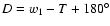 ;
F = w1 - w3 ;
l = w1 - w2 ;
;
F = w1 - w3 ;
l = w1 - w2 ;
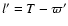 ;
w1, w2, and w3 are respectively the secular mean lunar longitude, the mean longitude of the perigee and the mean longitude of the node; T and
;
w1, w2, and w3 are respectively the secular mean lunar longitude, the mean longitude of the perigee and the mean longitude of the node; T and 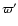 are respectively the mean longitude of EMB and its perihelion.
are respectively the mean longitude of EMB and its perihelion.
The luni-solar parameters that are used for fitting the solution to LLR observations and that are considered in Table 1 are the following:
w1(0), w2(0), w3(0): the mean longitude and the mean longitudes of perigee and node at J2000;
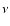 :
the sidereal mean motion of the Moon;
:
the sidereal mean motion of the Moon;
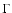 :
an inclination coefficient of the dimension of the inclination of the Moon;
:
an inclination coefficient of the dimension of the inclination of the Moon;
E: an eccentricity coefficient of the dimension of the eccentricity of the Moon;
T(0) and
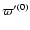 : the solar mean longitude, and the mean longitude of perihelion at J2000;
: the solar mean longitude, and the mean longitude of perihelion at J2000;
n': the sidereal mean motion of the Sun;
e': the solar eccentricity.
When comparing to observations we have to add 2 parameters fixing the reference frame (R):
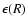 :
the inclination of the inertial mean ecliptic on the equator of (R);
:
the inclination of the inertial mean ecliptic on the equator of (R);
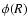 :
the separation between the origin of the right ascension in (R) and the ascending node of the inertial mean ecliptic on the equator of (R) for J2000.
:
the separation between the origin of the right ascension in (R) and the ascending node of the inertial mean ecliptic on the equator of (R) for J2000.
The half secular deceleration of the lunar mean longitude due to tidal forces is taken into account through w1(2). Finally two bias parameters in the perigee and node motions can be retained to compensate the deficiencies of the analytical solution:
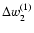 and
and
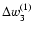 .
They are determined with a fit either to a close numerical integration or to the observations themselves.
.
They are determined with a fit either to a close numerical integration or to the observations themselves.
MPP01 is a new solution for planetary perturbations in the orbital motion of the Moon that has been elaborated by Bidart (2000, 2001a). It has been constructed within the framework of the ELP solution and the perturbation method is inspired by Brown's lunar theory whose basic concepts are discussed in Chapront-Touzé & Chapront (1980). We knew that in ELP the main limitation in precision resulted from the computation of the series for direct and indirect planetary perturbations. The aim of MPP01 was to improve the accuracy taking advantage of two recent improvements: the availability of numerical tools able to handle very large Poisson series and the appearance of a new semi-analytical planetary theory, VSOP2000 (Moisson 2000).
VSOP2000 is more precise than VSOP82 used in ELP and introduces a recent set of planetary masses (IERS92). It has a form analogous to ELP. The planetary coordinates (osculating elements) are developed as Poisson series as in (1). The numerical values of the coefficients depend on the masses but also on the values of the osculating elements for a given epoch (J2000). These elements have not been obtained directly from a fit to observations but via a comparison of the analytical solution to a JPL ephemeris DE403.
The angles are linear combinations of the planetary mean longitudes derived with a better accuracy than in VSOP82. MPP01 takes advantage of this improvement, in particular in the integration process of arguments with long periods.
Table 1:
Corrections to the nominal values of various parameters formerly fit
to DE200, resulting from the comparison of ELP/MPP02 to DE405 and LLR.
Fit to DE405: [+1950; +2060]; 40000 days; initial epoch: 1/1/1950 (0h);
number of abscissa: 2000.
Fit to LLR: [+1972; +2001]; 14500 observations; 4 observing stations.
The corrections are given in arcsecond except for 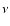 ,
n', w2(1), w3(1) in arcsecond/cy and w1(2)
in arcsecond/cy2.
,
n', w2(1), w3(1) in arcsecond/cy and w1(2)
in arcsecond/cy2.
In MPP01 the coefficients of the Poisson series have been developed up to the fifth power of the time (instead of second power in ELP) and the fourth power for the secular variations of the angular variables. Hence, this improvement increases the length of validity of the solution. The precision of computation is
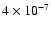 '' instead of 10-5'' in ELP. Correspondingly the number of terms in the series grows by a factor of 10. We shall see in Sect. 3 that unfortunately the gain in precision in the complete solution is not proportional to the increase in the computational precision, but is nevertheless significant.
'' instead of 10-5'' in ELP. Correspondingly the number of terms in the series grows by a factor of 10. We shall see in Sect. 3 that unfortunately the gain in precision in the complete solution is not proportional to the increase in the computational precision, but is nevertheless significant.
Concerning the method of development of the indirect perturbations (perturbations due to the deviation of the motion of the Earth-Moon Barycenter EMB from a Keplerian orbit) the approaches in ELP and MPP01 are significantly different. In ELP one computes the increments of the solar elements with respect to a moving Keplerian orbit with a perihelion motion
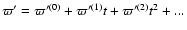 This motion is included in the Main Problem series. In MPP01 one computes the increments of the solar elements with respect to a fixed orbit. In that case, in the Main Problem series,
This motion is included in the Main Problem series. In MPP01 one computes the increments of the solar elements with respect to a fixed orbit. In that case, in the Main Problem series, 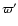 is a constant. The motion of
is a constant. The motion of 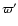 is contained in the perturbations to the Main Problem. The difference of approach renders difficult the comparison of the planetary perturbations series in ELP and MPP01. The computation of the secular variations of the lunar angular variables w1, w2, w3 has not been completely achieved in MPP01 beyond the degree 2. The coefficients of the secular parts of these variables due to planetary perturbations in t3 and t4 are borrowed from ELP2000-85 as is described in Chapront-Touzé and Chapront (1988).
is contained in the perturbations to the Main Problem. The difference of approach renders difficult the comparison of the planetary perturbations series in ELP and MPP01. The computation of the secular variations of the lunar angular variables w1, w2, w3 has not been completely achieved in MPP01 beyond the degree 2. The coefficients of the secular parts of these variables due to planetary perturbations in t3 and t4 are borrowed from ELP2000-85 as is described in Chapront-Touzé and Chapront (1988).
We recall the main steps followed by Bidart in the construction of the ephemeris based on MPP01:
First step: the complete solution MPP01 is introduced in ELP replacing the original planetary perturbation series (direct and indirect effects). No truncation is accomplished in this operation. We give in Table 2 the number of terms in each coordinate of the solution restricted to its planetary part. We call this new solution ELP/MPP01.
Second step: After having chosen a basic JPL ephemeris as a reference, a set of constants is fit to the ephemeris over an interval that covers one century. The list of parameters is the usual one given in Table 1. DE403 was chosen since it is also the reference ephemeris for the planetary theory VSOP2000. For comparison over long time spans, DE406 has been also used to produce the set of constants. Depending on the reference ephemeris (JPL) the corresponding changes in models and parameters are also introduced in ELP: tidal model, coefficients of the Earth's potential, numerical value of the Astronomical Unit in kilometers etc.
Third step: the time substitution in the solution ELP/MPP01 produces an ephemeris to which we give the same name. As noticed by Moshier (1992) in the case of ELP, a major improvement can be done when substituting time in the Poisson series that depend on the 4 literal Delaunay's arguments and on the planetary mean longitudes. Instead of considering these variables as linear functions of the time, it is preferable to consider their polynomial developments (secular variations) until t4. This procedure, which was also mentioned by Brown (1910), means conceptually that a part of the planetary perturbations of an order beyond the formal analytical developments is taken into account in the series. Practically over a long time span the differences to the numerical integration diminish noticeably. A further improvement can also be done modifying the secular part of the mean longitude. In this case, it is a fit to the reference ephemeris rather than an analytical improvement. This point will be discussed further (Sect. 4). In ELP/MPP01 a correction proposed by Moshier (1992) to the t4 secular term has been also introduced (Bidart 2001b).
Fourth step: Various comparisons with different JPL numerical ephemerides are performed (Bidart 2001b). ELP/MPP01 is compared to DE403 over one century (constants fit to DE403) and to DE406 over 6000 years (constants fit to DE406). Over the short time span covering one century a factor of 5 to 10 is improved by ELP/MPP01 compared to ELP. In particular the gain is about 10 for the distance. The comparison over a long range will be discussed in Sect. 3.
On the basis of MPP01 we have worked on a new solution, MPP02, that is simpler.
Table 2:
Number of terms in the series MPP and planetary perturbations
in ELP at different level of truncation 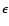 .
.
(a):
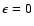 ;
the series are complete.
;
the series are complete.
(b):
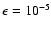 '' for the coefficients
in longitude and latitude, 1 cm in distance for periodic terms;
'' for the coefficients
in longitude and latitude, 1 cm in distance for periodic terms;
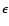 decreases from 10-5'' to 10-7''
for Poisson terms depending on the time power.
decreases from 10-5'' to 10-7''
for Poisson terms depending on the time power.
(c):
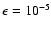 '' for the coefficients
in longitude and latitude, 2 cm in distance.
'' for the coefficients
in longitude and latitude, 2 cm in distance.
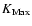 is the maximum time power of Poisson series.
The time unit is the century.
is the maximum time power of Poisson series.
The time unit is the century.
The original series in MPP01 are rather cumbersome (see Table 2). We know by experience that if we diminish the truncation level in the construction of the analytical series we correspondingly increase the number of terms and sum the terms of the whole series (several ten thousands) we degrade the final precision mainly because of the round-off errors. We have made various numerical experiments to test the precision of the complete solution when it is compared to DE405/DE406. We finally retained the solution MPP02 with the following characteristics:
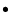 We maintain the same arguments in the Main Problem as in ELP, in particular Delaunay's arguments whose perigee is moving. The secular motion of
We maintain the same arguments in the Main Problem as in ELP, in particular Delaunay's arguments whose perigee is moving. The secular motion of  is provided by the planetary theory VSOP2000. We then avoid the expansions around a fixed value
is provided by the planetary theory VSOP2000. We then avoid the expansions around a fixed value
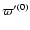 of the perigee which are rejected in the perturbations of the Main Problem in Bidart's series. This choice is governed by 2 reasons: from a theoretical point of view, the Main Problem when developed around
of the perigee which are rejected in the perturbations of the Main Problem in Bidart's series. This choice is governed by 2 reasons: from a theoretical point of view, the Main Problem when developed around
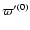 generates Poisson series with high power of the time and large coefficients; it slows down the convergence of the series. From a practical point of view, we remain closer to the original developments of the ELP series; this choice minimizes the changes in the original ELP series and facilitates the transition from ELP series to ELP/MPP02.
generates Poisson series with high power of the time and large coefficients; it slows down the convergence of the series. From a practical point of view, we remain closer to the original developments of the ELP series; this choice minimizes the changes in the original ELP series and facilitates the transition from ELP series to ELP/MPP02.
 We keep the secular arguments as they are in ELP. The reason is the same as above. As mentioned earlier, Bidart has limited the computation of the secular variations for the node and perigee to terms proportional to t and t2 (see Table 3.5 in Bidart 2000); using his values we have not observed significant improvements.
We keep the secular arguments as they are in ELP. The reason is the same as above. As mentioned earlier, Bidart has limited the computation of the secular variations for the node and perigee to terms proportional to t and t2 (see Table 3.5 in Bidart 2000); using his values we have not observed significant improvements.
 We select all the perturbations whose arguments in direct and indirect perturbations contain explicitly a planetary longitude. We then reject all the contributions induced by the secular variations of the solar perigee and eccentricity, node and inclination which have been computed very precisely in ELP until t2. This trick isolates the major part of the series that have to be improved, in particular long periodic terms (planetary small divisors, semi-resonant terms in the lunar longitude such as the well-known inequality
18Ve -16Te - l between Venus and Earth longitudes, Ve and Te, and Moon's mean anomaly, l) or short periodic terms combined with long periodic ones.
We select all the perturbations whose arguments in direct and indirect perturbations contain explicitly a planetary longitude. We then reject all the contributions induced by the secular variations of the solar perigee and eccentricity, node and inclination which have been computed very precisely in ELP until t2. This trick isolates the major part of the series that have to be improved, in particular long periodic terms (planetary small divisors, semi-resonant terms in the lunar longitude such as the well-known inequality
18Ve -16Te - l between Venus and Earth longitudes, Ve and Te, and Moon's mean anomaly, l) or short periodic terms combined with long periodic ones.
 We limit the list to terms with an amplitude less than 10-5 arcsec in longitude and latitude, 1 cm in distance for Fourier terms. This limitation in precision which is close to the truncation level in ELP (Table 2) results from numerical experiments where we gradually decreased from the ultimate precision of MPP01
(starting with 10-7 arcsec in longitude) to the present truncation level attempting to
maintain approximately the accuracy of MPP01. As a result, we drastically reduce the number
of arguments of the series in ELP/MPP02. Several comparisons with DE405/406 have been
performed and put together with Bidart's results. Numerically, the balances are comparable.
We limit the list to terms with an amplitude less than 10-5 arcsec in longitude and latitude, 1 cm in distance for Fourier terms. This limitation in precision which is close to the truncation level in ELP (Table 2) results from numerical experiments where we gradually decreased from the ultimate precision of MPP01
(starting with 10-7 arcsec in longitude) to the present truncation level attempting to
maintain approximately the accuracy of MPP01. As a result, we drastically reduce the number
of arguments of the series in ELP/MPP02. Several comparisons with DE405/406 have been
performed and put together with Bidart's results. Numerically, the balances are comparable.
In Table 2, the number of terms for the longitude in MPP02 are smaller than in ELP. It is mainly due to the fact that the truncation of computation in ELP is 10-5''. In MPP02 it is 10-7''; it is raised to 10-5'' in the final series. Hence, several terms in ELP that remained slightly above the limit of truncation were eliminated in ELP/MPP02.
Referring to Table 3, MPP02 versus ELP, we note that over the short time interval a factor 3 to 8 is improved by MPP02, the distance being the coordinate the most improved. For the long time span, see the next Section.
Two types of comparisons have been done to test the accuracy of the solutions ELP and ELP/MPP02 over a short and a long time interval. Preliminary fits of constants have been performed depending on the tested solution.
Time span: one century
Figures 1, 2 and 3 illustrate the comparisons of ELP
and ELP/MPP02 over the time span [+1950; +2060] with DE405. For all coordinates "the noise'' in ELP has
been significantly reduced in ELP/MPP02. The longitude V in ELP/MPP02
(Fig. 1) still shows an obvious signal which does not exceed 0
 006. The latitude U(Fig. 2) and radius vector
006. The latitude U(Fig. 2) and radius vector 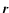 (Fig. 3) show no obvious signals. The maximum difference in distance does not exceed 2.5 m and the rms is about 50 cm. This significant improvement of the solution over the short time interval justifies by itself the choice of ELP/MPP02 as a new analytical solution.
(Fig. 3) show no obvious signals. The maximum difference in distance does not exceed 2.5 m and the rms is about 50 cm. This significant improvement of the solution over the short time interval justifies by itself the choice of ELP/MPP02 as a new analytical solution.
Time span: 55 centuries
The interval of comparison of ELP and ELP/MPP02 covers the period [-3000; +2500].
 ELP solution:
It may be noticeably improved by simply adding a few Poisson
terms with a long period to the original series for the longitude. This was first pointed
out by Moshier (1992). We add to ELP a few terms from ELP/MPP01, t2-terms and
t3-terms associated with the 5 arguments:
18Ve-16Te-l, 8Ve-13Te,
10Ve-3Te-l,
2Ju-5Sa,
4Te-8Ma+3Ju,
where Ve, Te, Ma, Ju, Sa are the mean longitudes of
Venus,
Earth, Mars, Jupiter and Saturn respectively. With these additions in the Poisson
series the new version of ELP becomes ELPa. We see in Fig. 4 the amelioration of the
differences in longitude compared to DE406. The significant oscillations in ELP due to these
long periodic terms almost vanish in ELPa.
ELP solution:
It may be noticeably improved by simply adding a few Poisson
terms with a long period to the original series for the longitude. This was first pointed
out by Moshier (1992). We add to ELP a few terms from ELP/MPP01, t2-terms and
t3-terms associated with the 5 arguments:
18Ve-16Te-l, 8Ve-13Te,
10Ve-3Te-l,
2Ju-5Sa,
4Te-8Ma+3Ju,
where Ve, Te, Ma, Ju, Sa are the mean longitudes of
Venus,
Earth, Mars, Jupiter and Saturn respectively. With these additions in the Poisson
series the new version of ELP becomes ELPa. We see in Fig. 4 the amelioration of the
differences in longitude compared to DE406. The significant oscillations in ELP due to these
long periodic terms almost vanish in ELPa.
 ELP/MPP02 solution: Figs. 5, 6
and 7 show the evolution of the differences of ELP/MPP02 with DE406. The general behaviour in longitude (Fig. 5) is similar to ELPa (Fig. 4) although slightly less precise over the long range, at the beginning of the time interval [-3000;-1000], a result that is quite surprising. Nevertheless on shorter time intervals of few centuries ELP/MPP02 has less "noise'' than ELPa and is globally more precise over [-1000; +2500].
ELP/MPP02 solution: Figs. 5, 6
and 7 show the evolution of the differences of ELP/MPP02 with DE406. The general behaviour in longitude (Fig. 5) is similar to ELPa (Fig. 4) although slightly less precise over the long range, at the beginning of the time interval [-3000;-1000], a result that is quite surprising. Nevertheless on shorter time intervals of few centuries ELP/MPP02 has less "noise'' than ELPa and is globally more precise over [-1000; +2500].
We summarize in Table 5 the maximum distance between the two solutions and DE406 over two time intervals: 55 centuries,
[-3000; +2500] and 10 centuries,
[+1500; +2500].
Table 3:
Comparisons of ELP, ELPa*, ELP/MPP02 and ELP/MPP02*
with DE405 and DE406 over a short period and a long period of time.
Maximum of the differences in absolute value.
Interval A: Differences between [+1950; +2060] with DE405
Interval B: Differences between [-3000; +2500] with DE406.
First, the solution ELP/MPP02 has been fitted to DE405 over a short time span [+1950; +2060]. The corrections of constants are listed in Table 1, Col. 2. Following the same method that we have applied earlier (Chapront et al. 1999) we build numerical complements with DE405 that we call
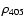 such as:
such as:
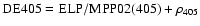 .
The notation ELP/MPP02(405) means that the constants are derived from the fit to DE405. This solution which is DE405 is now compared to LLR observations. A new set of constants is provided in Table 1, Col. 3. We substitute in our analytical solution this new set, and we obtain ELP/MPP02(LLR) which results from our fit to LLR observations. Adding the numerical complements
.
The notation ELP/MPP02(405) means that the constants are derived from the fit to DE405. This solution which is DE405 is now compared to LLR observations. A new set of constants is provided in Table 1, Col. 3. We substitute in our analytical solution this new set, and we obtain ELP/MPP02(LLR) which results from our fit to LLR observations. Adding the numerical complements
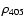 which are insensible to the change of constants at the centimeter level, the so-completed solution ELP/MPP02(LLR) +
which are insensible to the change of constants at the centimeter level, the so-completed solution ELP/MPP02(LLR) +
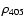 keeps the precision of a numerical integration. Figures 8, 9 and 10 show the comparison of these various solutions to DE405.
keeps the precision of a numerical integration. Figures 8, 9 and 10 show the comparison of these various solutions to DE405.
In Table 1, the discrepancies in the angles between LLR and DE405 values are
mainly due to a difference of origin in longitudes at J2000 of about
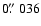 (see also Fig. 8). It is worth noticing that the "secular biases''
(see also Fig. 8). It is worth noticing that the "secular biases''
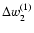 and
and
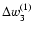 for perigee and node respectively that
exist between ELP/MPP02 and DE405 after fitting the constants to the numerical
integration have been maintained in our independent fit to LLR. In other words we correct over a short time interval (one century around J2000) the deficiency of the analytical solution with a local fit to DE405 that does not contain numerical bias over one century. Unlike our previous LLR analysis (Chapront et al. 2002) we remove from our list of parameters the quantities
for perigee and node respectively that
exist between ELP/MPP02 and DE405 after fitting the constants to the numerical
integration have been maintained in our independent fit to LLR. In other words we correct over a short time interval (one century around J2000) the deficiency of the analytical solution with a local fit to DE405 that does not contain numerical bias over one century. Unlike our previous LLR analysis (Chapront et al. 2002) we remove from our list of parameters the quantities
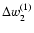 and
and
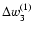 .
With respect to previous comparisons very small changes appear in the determination of the other parameters and the residuals (rms) remain very close.
.
With respect to previous comparisons very small changes appear in the determination of the other parameters and the residuals (rms) remain very close.
An attempt to improve the secular variations of the
lunar arguments w1, w2 and w3 has been done
fitting by a least square method a polynomial on the
residuals observed on these variables over the whole time
interval [-3000; +2500]. We designate by ELPa* and ELP/MPP02*
the corresponding improvements of ELPa and ELP/MPP02 respectively. This type of approximation was again suggested by Moshier who computed secular complements to ELP in w1 and w2. Bidart used the numerical values of Moshier's complements and after correction he found residuals in longitude of 13'' at maximum instead of 51'' . We have reproduced the experience with ELP/MPP02
(see Table 3.B), and confirmed the decrease of the residuals. We nevertheless obtain values different from Moshier's. The general behavior in longitude looks like ELPa* in Fig. 4.
The numerical complements are derived from a simple fit to DE406 and do not represent an analytical improvement to the secular variation of lunar longitudes for terms with large powers of the time. Numerical experiments have been done on ELPa as well as ELP/MPP02. They all show residuals of the type shown in Figs. 5 to 7 for ELP/MPP02*.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3101F04.EPS}
\end{figure}](/articles/aa/full/2003/23/aa3101/Timg54.gif) |
Figure 4:
Longitude. Various versions of ELP compared to DE406. |
| Open with DEXTER |
We give to the lunar angles wi the general form:
wi = wi(0) + wi(1)t + wi(2)t2 +...
We show 2 experiments in Table 4. In the first experiment we fit
w1(3), w1(4), w2(2), w2(3), w3(2), w3(3) ;
in the second experiment we fit
w1(4), w1(5), w2(3), w2(4), w3(3), w3(4).
In our choices of listed parameters we are governed by two requirements:
first, we do not want to degrade the quality of the solution over
short time intervals of a few centuries; second, we are willing to test the
accuracy of the secular trends in the lunar fundamental arguments for terms
with high powers of the time.
Since ELPa and ELP/MPP02 are noticeably different, in particular because of the long periodic terms, it is not surprising to have different coefficients in the two solutions. Furthermore, for a given solution, there is no overlapping of the common time powers in the two experiments. Clearly, we do not improve only the secular variations of the angular variables but make a fit of a large number of contributions, mainly terms with long periods that probably dominate the inaccuracies of the analytical secular variations themselves.
Table 5 shows the closeness in the comparisons to DE406 of ELPa* and ELP/MPP02* in the time interval [-3000; +2500] when adding such 'empirical corrections' to the lunar arguments wi.
Both bring smaller residuals which are very close. Among the tests of Table 4 our definite choice is test 1. Such an approximation can be used if we want to complete ELP/MPP02 to approach DE406 with simplicity since we have to change only few numbers in the analytical developments. Nevertheless the uncertainty of the t2-term in longitude due to tidal forces induces very much larger differences after a few centuries than the above one; hence such an improvement has no physical meaning. The numerical complements over the very long term (a few millennia) absorb also the numerical drift due to numerical integration. Newhall et al. (1983) propose in the case of the Moon in DE102 an exponential-like drift of the form:
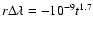 km (r is the distance,
km (r is the distance, 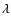 the mean longitude and t is expressed in days) which corresponds after 5000 years to a
the mean longitude and t is expressed in days) which corresponds after 5000 years to a
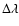 of approximately 20'' in magnitude. Note that this remark holds only if the precision of the numerical integration in DE406 is comparable to DE102.
of approximately 20'' in magnitude. Note that this remark holds only if the precision of the numerical integration in DE406 is comparable to DE102.
Taking advantage of the analytical form of the solution which is already of good precision as shown in Figs. 1-3 and 5-7, we may provide over the long range - covering several millennia - a solution which has the same form (we call it hereafter a pseudo-analytical solution) and which is closer to the numerical integration. This approximation is in the form of Poisson series as in (1) and uses the same arguments as ELP/MPP02. The main goal of this construction is to build an approximation of DE406 that is very concise, valid over two millennia and as easy to manipulate as the analytical solution ELP/MPP02 itself.
On the residuals arising from the difference between ELP/MPP02 and DE406 we have made the same type of approximation that we had performed earlier on the planetary theory VSOP82 (Chapront 2000). We compute for the 3 coordinates
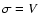 ,
U and r a residual
,
U and r a residual
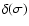 = DE406 - ELP/MPP02. We then approximate these differences by a Poisson series in a form rigorously analogous to series (1).
Here,
Ai1, i2,..., ip(n) and
= DE406 - ELP/MPP02. We then approximate these differences by a Poisson series in a form rigorously analogous to series (1).
Here,
Ai1, i2,..., ip(n) and
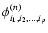 are the unknowns. The frequencies attached to the
are the unknowns. The frequencies attached to the 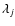 are known in the analytical developments. The unknowns are fit by the least squares method. On a given time interval, to realize this fit, we have at our disposal the basic list of arguments (the choice of the maximum number of terms N) and the maximum power of time
are known in the analytical developments. The unknowns are fit by the least squares method. On a given time interval, to realize this fit, we have at our disposal the basic list of arguments (the choice of the maximum number of terms N) and the maximum power of time
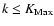 in the Poisson development tk. We have performed several adjustments. The main conclusion is that we may construct numerical complements under the same formulation, with a reasonable list of terms and a low power of the time that completes the analytical solution in a pseudo-analytical form.
An illustration of the quality of the approximation of the residuals
in the Poisson development tk. We have performed several adjustments. The main conclusion is that we may construct numerical complements under the same formulation, with a reasonable list of terms and a low power of the time that completes the analytical solution in a pseudo-analytical form.
An illustration of the quality of the approximation of the residuals
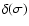 that we designate by
that we designate by
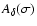 is given in Table 6 for the time interval [+500; +2500], N=500 and
is given in Table 6 for the time interval [+500; +2500], N=500 and
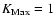 .
The differences
.
The differences
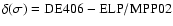 and
and
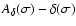 are illustrated in Fig. 11.
The pseudo-analytical sum ELP +
are illustrated in Fig. 11.
The pseudo-analytical sum ELP +
![$A_\delta = [{\rm ELP} + \delta ] + [ A_\delta - \delta ] = DE406 + [ A_\delta - \delta$](/articles/aa/full/2003/23/aa3101/img71.gif) ]
is very close to DE406 within the accuracy of the
difference: [
]
is very close to DE406 within the accuracy of the
difference: [
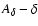 ].
].
Table 4:
Secular variations of the lunar arguments fit to DE406:
two different determinations.
Units: coefficients in arcsecond; time in century.
ELP/MPP02(LLR), whose constants are fitted to LLR data, is our new analytical version of ELP that replaces ELP2000-82B when it is used over a few tens of centuries around J2000. For very long period of time ELPa can still be used instead. Practically ELP/MPP02 is presented in the form of a Fourier series for the Main Problem and its partials plus a Poisson series for perturbations to the Main Problem. Two sets of constants are provided as well as literal expressions for the arguments (Moon, Sun and Planets):
 Constants fit to LLR data for ELP/MPP02 (LLR);
Constants fit to LLR data for ELP/MPP02 (LLR);
 Constants fit to DE405 (one century around J2000) for ELP/MPP02(405).
Constants fit to DE405 (one century around J2000) for ELP/MPP02(405).
When it is coupled to a solution for the lunar
libration and other physical models, the new ephemeris ELP/MPP02(LLR)
+
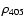 is used for the comparisons to LLR and
the determination of various parameters: lunar and solar parameters,
but also tidal acceleration, position of the dynamical reference frame,
correction to the precession constant, libration parameters, position of
the stations...
is used for the comparisons to LLR and
the determination of various parameters: lunar and solar parameters,
but also tidal acceleration, position of the dynamical reference frame,
correction to the precession constant, libration parameters, position of
the stations...
Two other sets of series are also provided:
 A solution with secular corrections to the lunar angles that "reproduces'' DE406 over the long range (6 millennia) within few arcseconds;
A solution with secular corrections to the lunar angles that "reproduces'' DE406 over the long range (6 millennia) within few arcseconds;
 A solution with a complementary approximation in a Poisson series that "reproduces'' DE406 over 2 millennia within a few hundredths of an arcsecond.
A solution with a complementary approximation in a Poisson series that "reproduces'' DE406 over 2 millennia within a few hundredths of an arcsecond.
Table 5:
Minimum (
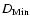 )
and maximum (
)
and maximum (
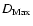 )
value of the differences
between ELP and ELP/MPP02 with DE406 for the longitude V;
maximum of the difference in absolute value
for latitude U and distance r (
)
value of the differences
between ELP and ELP/MPP02 with DE406 for the longitude V;
maximum of the difference in absolute value
for latitude U and distance r (
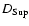 ).
).
ELP and ELP/MPP02: the original solutions; ELPa:
the original ELP solution modified with a few Poisson terms.
ELPa* and ELP/MPP02*:
solutions with secular variations of thelunar arguments fit on DE406.
Interval (B): [-3000; +2500]
Interval (C): [+1500; +2500]
Table 6:
Minimums and maximums of the differences 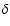 and
and
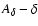 over millennia;
algebraic value for longitude (
over millennia;
algebraic value for longitude (
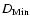 and
and
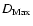 );
absolute value for latitude and distance (
);
absolute value for latitude and distance (
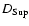 ).
).
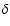 :
DE406 - ELP/MPP02;
:
DE406 - ELP/MPP02;
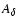 :
Approximation of the differences
:
Approximation of the differences 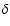 ;
Time interval: [+500; +2500].
;
Time interval: [+500; +2500].
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3101F11.EPS}
\end{figure}](/articles/aa/full/2003/23/aa3101/Timg72.gif) |
Figure 11:
Longitude of ELP/MPP02 with pseudo-analytical complements compared to DE406. |
| Open with DEXTER |
-
Bidart, P. 2000, Les perturbations planétaires dans le mouvement orbital de la Lune, Thèse de Doctorat, Observatoire de Paris
In the text
-
Bidart, P. 2001a, A&A, 366, 351
In the text
NASA ADS
-
Bidart, P. 2001b, MPP01, a new solution for Moon's planetary perturbations. Comparison to numerical integrations, in Dynamics of Natural and Artificial Celestial Bodies, Poznan
(Kluwer Academic Publishers), 205
-
Bretagnon, P. 1982, A&A, 114, 278
In the text
NASA ADS
-
Brown, E. W. 1910, Theory of the Motion of the Moon, Part V, Mem. Roy. Astron. Soc., 59, 1
In the text
-
Chapront, J. 2000, Celest. Mech., 78, 75
In the text
-
Chapront, J., & Chapront-Touzé, M. 1997, Celest. Mech., 66, 31
In the text
-
Chapront, J., Chapront-Touzé, M., & Francou, G. 1999, A&A, 343, 624
In the text
NASA ADS
-
Chapront, J., Chapront-Touzé, M., & Francou, G. 2002, A&A, 387, 700
In the text
NASA ADS
-
Chapront-Touzé, M., & Chapront, J. 1980, A&A, 91, 233
In the text
NASA ADS
-
Chapront-Touzé, M., & Chapront, J. 1983, A&A, 124, 50
In the text
NASA ADS
-
Chapront-Touzé, M., & Chapront, J. 1988, A&A, 190, 342
In the text
NASA ADS
-
Moisson, X. 2000, Intégration du mouvement des planètes dans le cadre de la relativité générale, Thèse de Doctorat, Observatoire de Paris
In the text
-
Moons, M. 1982, The Moon and Planets, 27, 257
In the text
NASA ADS
-
Moshier S. L. 1992, A&A, 262, 613
In the text
NASA ADS
-
Newhall, X. X., Standish, E. M., & Williams, J. G. 1983, A&A, 125, 150
In the text
NASA ADS
-
Standish, E. M. 1998, JPL Planetary and Lunar ephemerides, DE405/LE405, IOM, 321.F-98-048, Pasadena
In the text
Copyright ESO 2003
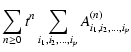
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3101F04.EPS}
\end{figure}](/articles/aa/full/2003/23/aa3101/Timg54.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3101F05.EPS}
\end{figure}](/articles/aa/full/2003/23/aa3101/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3101F06.EPS}
\end{figure}](/articles/aa/full/2003/23/aa3101/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3101F07.EPS}
\end{figure}](/articles/aa/full/2003/23/aa3101/Timg57.gif)