A&A 404, 35-46 (2003)
DOI: 10.1051/0004-6361:20030456
M. Min - J. W. Hovenier - A. de Koter
Astronomical institute Anton Pannekoek, University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
Received 4 March 2003 / Accepted 20 March 2003
Abstract
We study the effects of particle shape on the absorption and scattering cross sections of randomly oriented particles in the Rayleigh domain, i.e. particles that are very small compared to the wavelength of radiation both inside and outside the particle. In particular, we investigate the validity of the so-called statistical approach. In this approach it is assumed that the scattering and absorption properties of irregularly shaped particles can be simulated by the average properties of a distribution of simple shapes. We depart from the assumption of homogeneous spherical particles in two ways: 1) by using various distributions of elongated and flattened homogeneous ellipsoids and spheroids, 2) by using a distribution of hollow spherical particles. We derive explicit formulas for the shape averaged scattering and absorption cross sections as functions of the refractive index for various distributions of particle shapes in the Rayleigh limit. We compare the absorption cross sections as functions of the refractive index of the various distributions with each other and with those of homogeneous spheres. We also study the effects of the distributions on the shapes of absorption spectra. We find that there is a strong similarity between the absorption spectra of distributions of various non-spherical homogeneous particles and a distribution of hollow spheres. We show that the positions of features in the shape averaged mass absorption coefficient as a function of wavelength of small ellipsoidal, spheroidal or hollow spherical crystalline forsterite particles coincide with those deduced from the spectral energy distributions of various astronomical sources and with measurements of the mass absorption coefficients of small particles. This is not the case when we use homogeneous spherical particles.
Key words: scattering - stars: circumstellar matter - stars: planetary systems: protoplanetary disks
In many astrophysical environments dust is an important constituent. Radiation interacting with the dust particles can be absorbed, scattered and re-emitted. For the interpretation of infrared spectra of dusty objects it is, therefore, needed to understand the way small particles interact with light. This strongly depends on the size, structure, shape and composition of the dust grains. In this article we consider the limiting case of particles very small compared to the wavelength of radiation inside and outside the particle (the Rayleigh limit) and concentrate on how the absorption and scattering properties depend on the shape of the particles. In this paper all particles are in random orientation.
Calculations of scattering and absorption properties of homogeneous spherical particles can be done very accurately using the so called Mie theory (Mie 1908). For this reason, in most applications of light scattering the particles are considered to be spherical and homogeneous. However, if we look at, for example, pictures of interplanetary dust particles, we see that these particles are not at all spherical and in most cases are inhomogeneous in structure and composition (Warren et al. 1994). Also, when we compare the positions of features in the spectra of the mass absorption coefficients of homogeneous spherical particles with the positions of features derived from the spectral energy distributions of various astronomical dusty environments, we find that there is often no satisfactory agreement (see e.g. Bouwman et al. 2001; Hony et al. 2002). Therefore, it is important to study the absorption and scattering properties of particles that are not homogeneous and not spherical.
Because the solid particles in astrophysical environments are expected to be very irregular in shape, it is very difficult (if not impossible) to characterize the shape of the particles in an appropriate way. Therefore, we employ the idea of a statistical approach as suggested by Bohren & Huffman (1983). In this approach one simulates the scattering and absorption characteristics of irregularly shaped particles by those of a shape distribution of particles with various simple shapes, such as ellipsoids or spheroids. Important tests of this idea have been done by for example Mishchenko et al. (1997), Kahnert et al. (2002) and Kahnert & Stamnes (2002). The statistical approach has been extensively applied for ellipsoids in the Rayleigh limit (see Bohren & Huffman 1983; Fabian et al. 2001). However, it is difficult to calculate scattering by randomly oriented ellipsoids outside the Rayleigh limit. However, for ellipsoids of revolution (spheroids) with moderate aspect ratios calculations of scattering by shape distributions of randomly oriented spheroids of arbitrary size can be performed very well and with sufficient accuracy using the so-called T-matrix method in combination with appropriate approximate methods (see Min et al. 2003).
One of the main assumptions in the statistical approach is that when we average over a wide range of shapes, the typical characteristics of the separate shapes blend together into something which is independent of the choice of the separate shapes we used for the averaging. If this is true we can indeed simulate a shape distribution of irregular particles by using a distribution of simple shapes. We test this assumption by comparing the absorption characteristics of shape distributions of ellipsoids, spheroids and a distribution of hollow spheres.
Already, some studies of the effects of porosity on the absorption and extinction spectra of dust particles have been performed (see e.g. Hage & Greenberg 1990; Jones 1988; Iatì et al. 2001). As a result of the frequently employed dust model suggested by Mathis (1996), which uses composite and fluffy particles with approximately 45% vacuum, Dwek (1997) studied whether porous particles could solve the so-called "carbon crisis''. Vaidya & Gupta (1999) used the Discrete Dipole Approximation (Purcell & Pennypacker 1973) to calculate scattering by porous grains to fit the interstellar extinction curve. All these models use a fixed fraction of porosity. However, in line with the statistical approach, in this paper we study the effects of averaging over the porosity fraction, i.e. the fraction of the total volume of the sphere occupied by the vacuum inclusions.
We will first derive expressions for the scattering and absorption cross sections and the single scattering albedo of several shape distributions of randomly oriented ellipsoids and spheroids in the Rayleigh limit. All ellipsoids and spheroids in this paper are homogeneous, but we discuss homogeneous as well as hollow spheres. We will then generate formulas for a shape distribution of spheroids to be used outside the Rayleigh limit. Next we consider hollow spheres with a uniform distribution of porosity which can be used for calculations for arbitrary particle sizes using Mie theory in combination with effective medium approximations, by using hollow spherical shells or by using the exact method as discussed in Iatì et al. (2001).
We will calculate absorption cross sections as functions of the wavelength for the various shape distributions to study the similarities and differences between the spectra. Also we will compare the positions of absorption maxima in the spectrum with those derived from the spectral energy distributions of various astronomical sources.
If we want to calculate scattering by a particle that is small compared to the wavelength of the radiation inside and outside the particle, we can ignore the time variation of the incident radiation field and use the electrostatic or Rayleigh approximation. This approximation is valid when the size parameter
![]() and |mx|<<1. Here r is a typical size of the particle (we take r to be the radius of a volume equivalent sphere),
and |mx|<<1. Here r is a typical size of the particle (we take r to be the radius of a volume equivalent sphere), ![]() is the wavelength of incident radiation and m is the complex refractive index. The cross sections for scattering and absorption by an arbitrary particle in this approximation, averaged over all orientations, can be shown to be (Bohren & Huffman 1983)
is the wavelength of incident radiation and m is the complex refractive index. The cross sections for scattering and absorption by an arbitrary particle in this approximation, averaged over all orientations, can be shown to be (Bohren & Huffman 1983)
For an ellipsoid we have,
When we consider shape distributions of ellipsoidal particles with the same volume, we want to average the cross sections for absorption and scattering over the particle shapes. For
![]() this can be done by averaging the polarizabilities. However,
this can be done by averaging the polarizabilities. However,
![]() is not linearly dependent on the polarizabilities and thus, the averaging is, in general, not that easy. However, we can derive a very useful relation between the cross sections for scattering and absorption of ellipsoidal particles. For that purpose we first show the following general theorem. For every complex number z we have
is not linearly dependent on the polarizabilities and thus, the averaging is, in general, not that easy. However, we can derive a very useful relation between the cross sections for scattering and absorption of ellipsoidal particles. For that purpose we first show the following general theorem. For every complex number z we have
We now get the relation between the scattering and absorption cross sections as follows. We start by rewriting Eq. (3) in the form
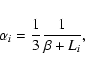 |
(7) |
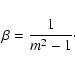 |
(8) |
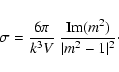 |
(13) |
It follows from Eq. (12) that in the Rayleigh approximation the single scattering albedo for a collection of randomly oriented homogeneous ellipsoids
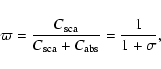 |
(14) |
The main idea behind the statistical approach is that the light scattering properties of a collection of irregularly shaped particles can be represented on average by those of a distribution of many simple shapes. The most widely used shapes for this purpose are ellipsoids. Following Bohren & Huffman (1983) we use a shape probability function,
![]() ,
resulting in an average absorption cross section for randomly oriented ellipsoids with the same volume V
,
resulting in an average absorption cross section for randomly oriented ellipsoids with the same volume V
As already mentioned in the previous section, the scattering cross section is not linearly dependent on the ![]() so the average scattering cross section,
so the average scattering cross section,
![]() ,
is in principle not as easy to calculate as
,
is in principle not as easy to calculate as
![]() .
Goncharenko et al. (1999) found an analytic solution for the averaged scattering cross section for a shape distribution quite similar to the so-called continuous distribution of ellipsoids (see next section). Although correct, the expression found by him is only applicable to his specific shape distribution. However, we can use Eq. (12) immediately to obtain for the averaged scattering cross section
.
Goncharenko et al. (1999) found an analytic solution for the averaged scattering cross section for a shape distribution quite similar to the so-called continuous distribution of ellipsoids (see next section). Although correct, the expression found by him is only applicable to his specific shape distribution. However, we can use Eq. (12) immediately to obtain for the averaged scattering cross section
As the most simple example of a distribution
![]() ,
Bohren & Huffman (1983) describe the so called Continuous Distribution of Ellipsoids (CDE) which is just
,
Bohren & Huffman (1983) describe the so called Continuous Distribution of Ellipsoids (CDE) which is just
![]() .
Using this distribution the average polarizability per unit volume is given by
.
Using this distribution the average polarizability per unit volume is given by
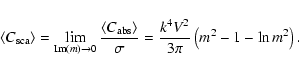 |
(20) |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H4358F1}
\end{figure}](/articles/aa/full/2003/22/aah4358/Timg59.gif) |
Figure 1:
Contour plot of the logarithm of the CDE shape distribution expressed in a/c and b/c, i.e.
|
Outside the Rayleigh limit it is more difficult to calculate light scattering properties of tri-axial ellipsoids than of spheroids. Therefore we would like to use spheroids in the statistical approach. The cross sections of shape distributions of randomly oriented spheroids with moderate aspect ratios can be calculated outside the Rayleigh limit quite well and with sufficient accuracy for most purposes (see Min et al. 2003).
Spheroids are ellipsoids with two equal semi-axes. We take L=L2 and
L1=L3=(1-L)/2 (this means a=c). For spheroids Eq. (5) gives (see van de Hulst 1957)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{H4358F2}
\end{figure}](/articles/aa/full/2003/22/aah4358/Timg61.gif) |
Figure 2: The shape distribution in a/b of the unlimited CDS as defined by Eq. (25). |
In line with the basic idea of the CDE, the CDS averages over all possible shapes by integrating
![]() and
and
![]() over L with 0<L<1 and with equal probability for all L (
over L with 0<L<1 and with equal probability for all L (
![]() ). We will refer to this distribution as the unlimited CDS, because in the next sections we will also use limited versions of the CDS where we limit the domain of aspect ratios used.
We now find for the average polarizability per unit volume of randomly oriented spheroids with the same volume in the unlimited CDS
). We will refer to this distribution as the unlimited CDS, because in the next sections we will also use limited versions of the CDS where we limit the domain of aspect ratios used.
We now find for the average polarizability per unit volume of randomly oriented spheroids with the same volume in the unlimited CDS
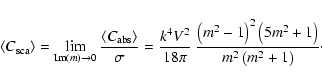 |
(24) |
Another shape distribution we can consider is the Uniform Distribution of Spheroids. This distribution actually consists of a uniform distribution of oblate spheroids with
![]() and a uniform distribution of prolate spheroids with
and a uniform distribution of prolate spheroids with
![]() ,
where all particles have the same volume,
,
where all particles have the same volume, ![]() is the maximum aspect ratio for the oblate part of the distribution and
is the maximum aspect ratio for the oblate part of the distribution and ![]() is the minimum aspect ratio of the prolate part. Thus we give equal weights to all prolate and oblate spheroidal shapes with aspect ratios between
is the minimum aspect ratio of the prolate part. Thus we give equal weights to all prolate and oblate spheroidal shapes with aspect ratios between ![]() and
and ![]() .
Because the geometrical factor L is a complicated function of the aspect ratio (Eq. (22)), it is not possible to find an analytic expression for the average polarizability per unit volume for this distribution. However, for a given
.
Because the geometrical factor L is a complicated function of the aspect ratio (Eq. (22)), it is not possible to find an analytic expression for the average polarizability per unit volume for this distribution. However, for a given ![]() it is straightforward to perform the shape averaging of the cross sections numerically.
it is straightforward to perform the shape averaging of the cross sections numerically.
In most applications of light scattering the particles are assumed to be homogeneous. This can be a good approximation in some cases but in a lot of applications the particles are inhomogeneous in composition or porous. We will study here porous particles. This means that we consider particles with a material having a refractive index m with vacuum inclusions having a refractive index equal to 1.
The simplest porous particle is a hollow spherical shell. Since for a sphere (homogeneous or hollow) the polarizability per unit material volume is isotropic we have
![]() .
The polarizability per unit material volume is (van de Hulst 1957, chap. 6)
.
The polarizability per unit material volume is (van de Hulst 1957, chap. 6)
| |
= | ||
| = | 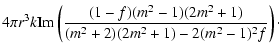 |
(27) |
A hollow spherical shell might seem quite an artificial choice for a porous particle. However, we will show that there is a strong similarity between porous spheres with multiple, randomly located vacuum inclusions and hollow spherical shells. The usual way of dealing with inhomogeneities is through an effective medium theory. The main idea behind all these theories is that, when the inclusions are isotropically distributed in the particle, the electromagnetic wave effectively encounters an average medium. We use the Maxwell-Garnett approximation (see e.g. Bohren & Huffman 1983). The main assumptions in this approximation are: 1) that the sizes of the inclusions are much smaller than the wavelength in the host material and in the inclusions and 2) that the inclusions are isolated, i.e. they scatter independently. Although these assumptions are made in the derivation of the approximation, many people found that the results can also be quite accurate when the requirements are not fulfilled (see e.g. Chýlek et al. 2000). For a study of the validity of different effective medium approximations see Kolokolova & Gustafson (2001). In our case we automatically fulfill requirement 1), since the particles containing the inclusions are in the Rayleigh limit (x<<1, |mx|<<1). In order for the inclusions to scatter independently, they must be far enough apart. However, when there is only one inclusion, both requirements are immediately fulfilled. Therefore, we can show that the polarizability per unit volume of a porous sphere, derived using the Maxwell-Garnett approximation, is exactly the same as the polarizability of a hollow spherical shell. For this purpose we first note that the effective refractive index,
![]() ,
given by the Maxwell-Garnett approximation for spherical inclusions in a material is
,
given by the Maxwell-Garnett approximation for spherical inclusions in a material is
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{H4358F3a}\hspace*{3mm}
\in...
...H4358F3c}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{H4358F3d}
\end{figure}](/articles/aa/full/2003/22/aah4358/Timg90.gif) |
Figure 3:
The imaginary part of the average polarizability per unit material volume of four distributions of particle shapes (solid contours) as functions of the real and imaginary part of the refractive index. The increment between two contours is unity. CDE stands for Continuous Distribution of Ellipsoids, CDS denotes a Continuous Distribution of Spheroids. The dashed curves represent the values of the refractive index given by the single oscillator model for various values of the wavelength in |
To analyze the wavelength dependence of the cross sections we need the wavelength dependent refractive index of the material. Fortunately, the wavelength dependence of the refractive index can be modeled in such a way that we can study the general features. We use the Lorentz oscillator model to obtain the refractive index as a function of wavelength (see e.g. Bohren & Huffman 1983). This model considers the refractive index due to harmonic lattice vibrations. The eigenfrequency of the harmonic oscillator is ![]() .
If there is only one eigenfrequency (resonance) this gives a refractive index
.
If there is only one eigenfrequency (resonance) this gives a refractive index
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{H4358F4a}\hspace*{2mm}
\in...
...H4358F4c}\hspace*{2mm}
\includegraphics[width=8.6cm,clip]{H4358F4d}
\end{figure}](/articles/aa/full/2003/22/aah4358/Timg99.gif) |
Figure 4: Similar to Fig. 3 but with the UDS, denoting a Uniform Distribution of Spheroids, and limited CDS distributions integrated between 1/5<a/b<5 (upper panels) and 1/10<a/b<10 (lower panels). |
To analyze the dependence of the shape of the absorption spectrum on the shape of the particles, we first analyze in more detail the dependence of
![]() on the refractive index. Because the refractive index is a complex number, we can represent each shape distribution uniquely by a contour plot with
on the refractive index. Because the refractive index is a complex number, we can represent each shape distribution uniquely by a contour plot with
![]() and
and
![]() on the x and y axes, respectively, and values of
on the x and y axes, respectively, and values of
![]() in the contours. The contour plots in Fig. 3 show this for the different shape distributions of Sect. 3. For homogeneous spherical particles we notice that
in the contours. The contour plots in Fig. 3 show this for the different shape distributions of Sect. 3. For homogeneous spherical particles we notice that
![]() shows a rapid increase as m approaches
shows a rapid increase as m approaches ![]() ,
as was expected from Eq. (4). For all other distributions considered in Fig. 3 we do not see this behavior. These distributions all show a somewhat similar behavior, namely, in general, increasing
,
as was expected from Eq. (4). For all other distributions considered in Fig. 3 we do not see this behavior. These distributions all show a somewhat similar behavior, namely, in general, increasing
![]() for increasing
for increasing
![]() and decreasing
and decreasing
![]() .
For the unlimited CDS
.
For the unlimited CDS
![]() is undefined at m=i since in Eq. (23)
is undefined at m=i since in Eq. (23)
![]() is undefined for
is undefined for
![]() .
In particular we can see by using Eq. (23) for
.
In particular we can see by using Eq. (23) for
![]() that we have
that we have
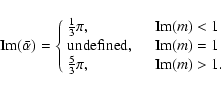 |
(35) |
Overplotted in Fig. 3 (the dashed curve) is the refractive index for various values of the wavelength for a certain choice of the parameters in Eq. (34). We see that for this choice of parameters a shift of the maximum value of
![]() from
from
![]() m for homogeneous spherical particles towards
m for homogeneous spherical particles towards
![]() m for the distribution of hollow spheres occurs.
m for the distribution of hollow spheres occurs.
We now try to find out if the shift of the maximum of
![]() when going from homogeneous spheres towards non-spherical or hollow particles is generally towards longer wavelengths.
To do this we first derive from Eq. (34) that
when going from homogeneous spheres towards non-spherical or hollow particles is generally towards longer wavelengths.
To do this we first derive from Eq. (34) that
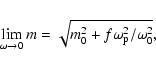 |
(36) |
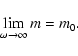 |
(37) |
Outside the Rayleigh limit numerical calculations of light scattering properties of spheroids are limited to certain ranges of sizes and aspect ratios. Therefore, it is interesting to study the effects of limiting the aspect ratios in the distributions. The UDS was already limited by the maximum and minimum aspect ratios, ![]() and
and ![]() .
For the CDS we can do something similar by using Eq. (25). When we limit the aspect ratio in the CDS this leads to
.
For the CDS we can do something similar by using Eq. (25). When we limit the aspect ratio in the CDS this leads to
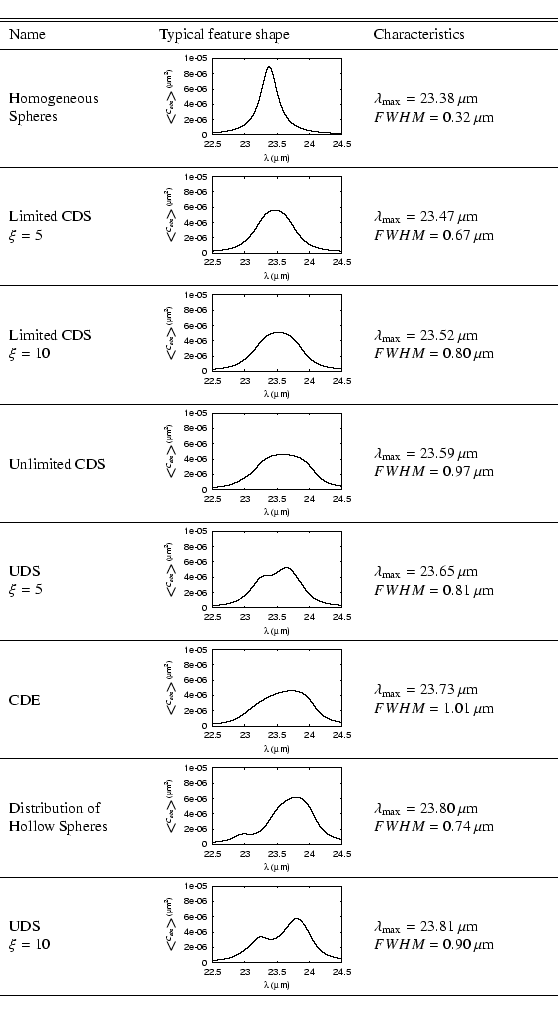
As an example of the shape of the spectral features of
![]() we used the theoretical frequency dependence of the refractive index given by Eq. (34) with the same values of the parameters as in Fig. 3. We calculated the position of the maximum of
we used the theoretical frequency dependence of the refractive index given by Eq. (34) with the same values of the parameters as in Fig. 3. We calculated the position of the maximum of
![]() and the Full Width at Half Maximum (FWHM) of
and the Full Width at Half Maximum (FWHM) of
![]() as a function of wavelength. The results are summarized in Table 1. We see that the most extreme shifts with respect to homogeneous spherical particles are produced by a UDS with
as a function of wavelength. The results are summarized in Table 1. We see that the most extreme shifts with respect to homogeneous spherical particles are produced by a UDS with ![]() and the distribution of hollow spheres. The broadest features are produced by the CDE and the unlimited CDS, because they cover the broadest range of possible shapes. The wavelength shifts and FWHM's presented in Table 1 are fairly general. Notice in Table 1 that for the UDS with
and the distribution of hollow spheres. The broadest features are produced by the CDE and the unlimited CDS, because they cover the broadest range of possible shapes. The wavelength shifts and FWHM's presented in Table 1 are fairly general. Notice in Table 1 that for the UDS with ![]() and with
and with ![]() as well as for the distribution of hollow spheres, we have two local maxima. This can be understood when we look at the contours for the distribution of hollow spheres in Fig. 3 and the contours for the UDS with
as well as for the distribution of hollow spheres, we have two local maxima. This can be understood when we look at the contours for the distribution of hollow spheres in Fig. 3 and the contours for the UDS with ![]() and with
and with ![]() in Fig. 4. We see that local maxima of the imaginary parts of the polarizabilities per unit volume as functions of the refractive index occur for these distributions, resulting in local maxima of the average absorption cross sections as functions of the wavelength.
in Fig. 4. We see that local maxima of the imaginary parts of the polarizabilities per unit volume as functions of the refractive index occur for these distributions, resulting in local maxima of the average absorption cross sections as functions of the wavelength.
For calculations of
![]() of shape distributions outside the Rayleigh limit we are restricted to the use of UDS, limited CDS or hollow spheres. However, calculations for spheroids with aspect ratios of 10 are very time consuming and not possible for all size parameters. Absorption cross sections for a shape distribution of hollow spheres can always be calculated quite fast using an effective medium approximation in combination with Mie theory or exact calculations for a shape distribution of hollow spherical shells. We should note here that the similarity of the absorption spectra in the Rayleigh domain for various shape distributions does not guarantee a similar behavior outside the Rayleigh limit.
of shape distributions outside the Rayleigh limit we are restricted to the use of UDS, limited CDS or hollow spheres. However, calculations for spheroids with aspect ratios of 10 are very time consuming and not possible for all size parameters. Absorption cross sections for a shape distribution of hollow spheres can always be calculated quite fast using an effective medium approximation in combination with Mie theory or exact calculations for a shape distribution of hollow spherical shells. We should note here that the similarity of the absorption spectra in the Rayleigh domain for various shape distributions does not guarantee a similar behavior outside the Rayleigh limit.
|
As an example we use the various shape distributions of the previous sections to calculate the wavelength dependence of the average absorption cross section of small crystalline forsterite particles in the region 20-40![]() m. The pure magnesium silicate forsterite (Mg2SiO4) is end member of the olivine family (Mg2xFe2-2xSiO4, with x between 0 and 1), and is e.g. observed in (i) the disks surrounding binary red-giant stars (Molster et al. 1999), (ii) in the circumstellar dust disks around young intermediate mass pre-main-sequence Herbig Ae/Be stars, which are believed to be sites of on-going planet formation (see e.g. Bouwman et al. 2001; Waters & Waelkens 1998), (iii) in comet Hale-Bopp (Crovisier et al. 1997; Bouwman et al. 2003), and (iv) in interplanetary dust particles (Bradley et al. 1999). The mass absorption coefficient of small forsterite particles has many narrow resonances in between about 10 and 40
m. The pure magnesium silicate forsterite (Mg2SiO4) is end member of the olivine family (Mg2xFe2-2xSiO4, with x between 0 and 1), and is e.g. observed in (i) the disks surrounding binary red-giant stars (Molster et al. 1999), (ii) in the circumstellar dust disks around young intermediate mass pre-main-sequence Herbig Ae/Be stars, which are believed to be sites of on-going planet formation (see e.g. Bouwman et al. 2001; Waters & Waelkens 1998), (iii) in comet Hale-Bopp (Crovisier et al. 1997; Bouwman et al. 2003), and (iv) in interplanetary dust particles (Bradley et al. 1999). The mass absorption coefficient of small forsterite particles has many narrow resonances in between about 10 and 40 ![]() m, due to stretching and bending modes within the SiO4 tetrahedron, but it also exhibits relatively strong features at longer wavelength. For the objects mentioned above, the characteristic dust temperatures are often such that the dust emits most effectively in the wavelength interval between
m, due to stretching and bending modes within the SiO4 tetrahedron, but it also exhibits relatively strong features at longer wavelength. For the objects mentioned above, the characteristic dust temperatures are often such that the dust emits most effectively in the wavelength interval between ![]() 20 to 40
20 to 40 ![]() m, which is why we focus our attention on this spectral range.
m, which is why we focus our attention on this spectral range.
We use the refractive index values for the three crystallographic axes as provided by Servoin & Piriou (1973). We then calculate the shape averaged mass absorption coefficient
![]() for particles with material volume V from,
for particles with material volume V from,
Also plotted in Fig. 5 (the dashed vertical lines) are positions of the features that were found in the spectral energy distributions of a large sample of stars with surrounding dust, after subtracting a continuum, and that were assigned to forsterite (Molster et al. 2002). We see that the maxima found in the average mass absorption coefficient for homogeneous spheres do not correspond to the positions of features derived from the spectral energy distributions. However for the CDE, unlimited CDS, the hollow spheres and for the UDS with ![]() ,
the positions of the maxima do match the observed positions. This means that for the interpretation of infrared spectra of these stars the use of these distributions provide a better fit than homogeneous spheres. From this we can conclude that both the forsterite particles in the measurements of Chihara et al. (2001) and the particles in circumstellar dust found by Molster et al. (2002) cannot be considered to be homogeneous spheres.
,
the positions of the maxima do match the observed positions. This means that for the interpretation of infrared spectra of these stars the use of these distributions provide a better fit than homogeneous spheres. From this we can conclude that both the forsterite particles in the measurements of Chihara et al. (2001) and the particles in circumstellar dust found by Molster et al. (2002) cannot be considered to be homogeneous spheres.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H4358F5a}\par\vs...
...space*{3mm}
\includegraphics[angle=-90,width=8.8cm,clip]{H4358F5d}
\end{figure}](/articles/aa/full/2003/22/aah4358/Timg140.gif) |
Figure 5:
The upper three panels show the average mass absorption coefficients of small crystalline forsterite particles for different shape distributions. The lower panel shows the average mass absorption coefficients of small forsterite grains as measured in the laboratory by Chihara et al. (2001). The dashed vertical lines show the positions of features attributed to forsterite as derived from spectral energy distributions of many astronomical objects. These measured peak locations are at 23.7, 27.6, 31.2, 33.6 and 36.5 |
From the strong similarity between the absorption spectra in Fig. 5 for CDE, unlimited CDS, UDS ![]() and the distribution of hollow spheres we can conclude that it can be very difficult, if not impossible, to distinguish between particles with non-spherical shapes and hollow spheres on the basis of infrared spectra. Although the first three distributions are significantly different, they all consist of ellipsoids, so the similarity of the average absorption cross sections might not be very surprising. However, the similarity for the distribution of hollow spheres is a surprising result which is a strong encouragement for the use of the statistical approach since it seems that quite different shape departures from homogeneous spheres result in most cases in more or less the same shape of the wavelength dependence of
and the distribution of hollow spheres we can conclude that it can be very difficult, if not impossible, to distinguish between particles with non-spherical shapes and hollow spheres on the basis of infrared spectra. Although the first three distributions are significantly different, they all consist of ellipsoids, so the similarity of the average absorption cross sections might not be very surprising. However, the similarity for the distribution of hollow spheres is a surprising result which is a strong encouragement for the use of the statistical approach since it seems that quite different shape departures from homogeneous spheres result in most cases in more or less the same shape of the wavelength dependence of
![]() .
This suggests that an ensemble of irregularly shaped particles will also result in this shape of the absorption spectrum. This is in agreement with the similarity of the positions of the maxima in
.
This suggests that an ensemble of irregularly shaped particles will also result in this shape of the absorption spectrum. This is in agreement with the similarity of the positions of the maxima in
![]() with the positions of features derived from observations. For calculations of scattering and absorption characteristics of small particles it is much easier to do calculations for hollow spheres than for non-spherical particles with an extreme shape distribution. Therefore we recommend to use the distribution of hollow spheres to get a quick impression of non-sphericity effects in infrared spectra. Notice that the average mass absorption coefficient of volume equivalent homogeneous non-spherical particles is roughly 50 percent higher than that of homogeneous spheres, and that the
with the positions of features derived from observations. For calculations of scattering and absorption characteristics of small particles it is much easier to do calculations for hollow spheres than for non-spherical particles with an extreme shape distribution. Therefore we recommend to use the distribution of hollow spheres to get a quick impression of non-sphericity effects in infrared spectra. Notice that the average mass absorption coefficient of volume equivalent homogeneous non-spherical particles is roughly 50 percent higher than that of homogeneous spheres, and that the
![]() of hollow spheres is even about a factor of two more than that of homogeneous spheres. The latter is essentially the result of the increase in average surface area of hollow grains relative to homogeneous spheres (see Eq. (30)). This implies that mass determinations of (in this case) forsterite material in e.g. Herbig Ae/Be objects using classical Mie calculations likely overestimate the observed mass of this material by about a factor of two.
of hollow spheres is even about a factor of two more than that of homogeneous spheres. The latter is essentially the result of the increase in average surface area of hollow grains relative to homogeneous spheres (see Eq. (30)). This implies that mass determinations of (in this case) forsterite material in e.g. Herbig Ae/Be objects using classical Mie calculations likely overestimate the observed mass of this material by about a factor of two.
In this article we have investigated shape effects in scattering and absorption by randomly oriented particles small compared to the wavelength. We first derived a relation between the average absorption cross section and the average scattering cross section of an arbitrary shape distribution of randomly oriented ellipsoidal particles with the same volume. With this relation it is possible to calculate the average scattering cross section from the average absorption cross section of this shape distribution. We have derived explicit expressions for the average polarizability per unit material volume of a continuous distribution of spheroids as well as for a distribution of hollow spheres as functions of the refractive index of the particles. With these expressions it is possible to calculate the average absorption cross sections of these distributions.
We have shown that there is a strong similarity between the polarizability per unit material volume as a function of refractive index for shape distributions with elongated and flattened ellipsoids and spheroids and a distribution of hollow spherical shells. This similarity in polarizability as a function of refractive index means that there is also a strong similarity in the average absorption cross sections as functions of the wavelength. These results are a strong encouragement for the use of the statistical approach in the interpretation of infrared spectra since it suggests that the shape of the absorption spectrum is, to a certain degree, independent of the exact shapes of the individual particles as long as we average over a wide range of shape parameters. However, this also means that it can be very difficult, if not impossible, to distinguish between different non-spherical shapes of the particles by just using infrared spectroscopy.
Using theoretical and experimental data of the wavelength dependence of the refractive index we have studied absorption spectra of homogeneous spherical particles, several shape distributions of ellipsoidal and spheroidal particles and of a distribution of hollow spheres. Using the Lorentz oscillator model for the refractive index as a function of wavelength we showed that, for all shape distributions considered, the positions of spectral features in the average absorption cross sections shift towards longer wavelengths (by about 1-2 ![]() m) when we go from homogeneous spherical particles to a shape distribution of non-spherical particles or hollow spheres. This should be kept in mind when identifying mineral species in astronomical objects. Also, the distributions of non-spherical and hollow spherical particles have a larger average mass absorption coefficient, implying that mass determinations assuming homogeneous spheres overestimate the mass of the species investigated. For the crystalline forsterite material investigated in this paper this may amount to about a factor of two.
m) when we go from homogeneous spherical particles to a shape distribution of non-spherical particles or hollow spheres. This should be kept in mind when identifying mineral species in astronomical objects. Also, the distributions of non-spherical and hollow spherical particles have a larger average mass absorption coefficient, implying that mass determinations assuming homogeneous spheres overestimate the mass of the species investigated. For the crystalline forsterite material investigated in this paper this may amount to about a factor of two.
A great advantage of the distribution of hollow spheres is that it can be used fairly easily outside the Rayleigh domain. However, we should note here that the similarity between the absorption spectra of spheroids and hollow spheres in the Rayleigh limit does not guarantee a similar behavior for particles large compared to the wavelength.
Acknowledgements
We are indebted to C. V. M. van der Mee for accurate checks and simplifications of the theory. Comments on an earlier version of this paper by M. I. Mishchenko are gratefully acknowledged.