A&A 404, 325-332 (2003)
DOI: 10.1051/0004-6361:20030433
A. Karastergiou1,2 - S. Johnston2 - M. Kramer3
1 - Max-Planck Institut für Radioastronomie, Auf dem Hügel
69, 53121 Bonn, Germany
2 - School of Physics, University of Sydney, NSW 2006, Australia
3 - Jodrell Bank Observatory, University of Manchester, Macclesfield, Chesire SK11 9DL, UK
Received 24 December 2002 / Accepted 18 March 2003
Abstract
We investigate circular polarization in pulsar radio
emission through simultaneous observations of PSR B1133+16 at two
frequencies. In particular, we investigate the association of the
handedness of circular polarization with the orthogonal polarization
mode phenomenon at two different frequencies. We find the association
to be significant across the pulse for PSR B1133+16, making a strong
case for orthogonal polarization modes determining the observed
circular polarization. The association however is not perfect and
decreases with frequency. Based on these results and assuming emission
occurs in superposed orthogonal polarization modes, we present a
technique of mode decomposition based on single pulses. Average
profiles of the polarization of each mode can then be computed by
adding the individual mode-separated single pulses. We show that
decomposing single pulses produces different average profiles for the
orthogonal polarization modes from decomposing average
profiles. Finally, we show sample single pulses and discuss the
implications of the frequency dependence of the correlation of the
circular polarization with the orthogonal polarization mode
phenomenon.
Key words: pulsars: individual: PSR B1133+16 - polarization
Perhaps one of the most elusive qualities of the highly polarized pulsar radio emission is its circular polarization. Although it is generally lower than its linearly polarized counterpart, it is amongst the highest observed in astrophysical objects. Circular polarization in pulsars has been attributed in the past to propagation effects on the radiation as it travels through the pulsar magnetosphere, geometrical effects or the emission mechanism itself.
Cordes et al. (1978) were the first to point out an
association between the position angle (PA) of the linear polarization
and the handedness of the circular polarization. More specifically,
![]() jumps in the PA were observed to occur simultaneously with
sense reversals in the circular polarization (V) in PSR B2020+28. The authors argued that this could be adequately explained
by disjoint or superposed orthogonal polarization modes (OPMs). In the
disjoint case, each of the OPMs is emitted independently and only
individual modes are observed at a time. On the other hand, the
superposed case supports the idea that the observed radiation at any
instant is a mix of both modes, which are effectively emitted at the
same time, despite each mode having its own properties. A number of
authors argued for the identification of OPMs as the natural
polarization modes in the pulsar magnetosphere (e.g. Barnard & Arons
1986; McKinnon 1997; von Hoensbroech et al. 1998; Petrova 2001). Elliptically
polarized natural modes could then provide the origin for the circular
polarization as a propagation effect.
jumps in the PA were observed to occur simultaneously with
sense reversals in the circular polarization (V) in PSR B2020+28. The authors argued that this could be adequately explained
by disjoint or superposed orthogonal polarization modes (OPMs). In the
disjoint case, each of the OPMs is emitted independently and only
individual modes are observed at a time. On the other hand, the
superposed case supports the idea that the observed radiation at any
instant is a mix of both modes, which are effectively emitted at the
same time, despite each mode having its own properties. A number of
authors argued for the identification of OPMs as the natural
polarization modes in the pulsar magnetosphere (e.g. Barnard & Arons
1986; McKinnon 1997; von Hoensbroech et al. 1998; Petrova 2001). Elliptically
polarized natural modes could then provide the origin for the circular
polarization as a propagation effect.
Stinebring et al. (1984a,b) studied the polarization behaviour of single pulses from a number of pulsars using grey-scale density plots to investigate the fluctuations of the PA, the linear polarization, L and V. They noticed that PA jumps often occur at the same pulse longitude at 430 and 1404 MHz and that the orthogonal polarization mode (OPM) phenomenon was becoming more prevalent at higher frequencies. They also noticed that at the phase bins where OPM jumps occur, the degree of linear polarization was significantly reduced, which led to the idea that, at any given instant, the radiation observed is the incoherent sum of OPMs. This has the advantage of naturally reducing the linear polarization and attributing its fluctuations to fluctuations in the polarization of the OPMs, which have a constant degree of linear polarization. In contrast, if OPMs were emitted independently, the emission mechanism would have to intrinsically produce a largely fluctuating degree of linear polarization. McKinnon & Stinebring (1998) realized that the assumption of incoherent addition of OPMs can be used to decompose an integrated pulse profile into the profiles of each OPM. By accounting for the effects of instrumental noise, this method can be used to reproduce the histograms of the distributions of the PA and L from Stinebring et al. (1984b). Mode decomposed average profiles of PSRs B0525+21 and B2020+28 were shown in McKinnon & Stinebring (2000) using their technique on the average profiles of these pulsars.
In this paper, the association of circular polarization with the orthogonal polarization modes is examined in PSR B1133+16 at 1.41 GHz and 4.85 GHz, having studied the correlation of OPMs between these two frequencies in Karastergiou et al. (2002, hereafter Paper II). We make use of contingency tables to quantify this association at each frequency, which we compare to the findings of Cordes et al. (1978). We develop a method to decompose single pulses into the individual OPMs. The method is simple and only assumes that the observed Stokes I, Q, U, V are the incoherent sum of the 100% polarized OPMs. We show the different mode-decomposed profiles of PSR B1133+16 by following our method and that of McKinnon & Stinebring (2000) and discuss the differences. Finally, we present example single-pulses from our simultaneous data set to highlight the observed effects and we discuss possible interpretations.
We use the same dataset on PSR B1133+16 as in Paper II. It consists of 4778 pulses at 4.85 and 1.41 GHz observed with the Effelsberg and
Jodrell Bank radio telescopes respectively. Full details of the
observing, calibration and data reduction can be found in Paper II. The mean signal-to-noise ratio (S/N) of V detected in the single pulses is
![]() 1. However, in a significant number of cases, the signal in Vexceeds the rms of the noise by many times at both
frequencies. At 4.85 GHz, where the flux density of this pulsar is
much less than 1.41 GHz, the sensitivity of the Effelsberg telescope
largely compensates. This is evident from the S/N of V shown in
Fig. 1 and favours our results to be intrinsic to the pulsar emission
rather than products of the instrumental noise.
1. However, in a significant number of cases, the signal in Vexceeds the rms of the noise by many times at both
frequencies. At 4.85 GHz, where the flux density of this pulsar is
much less than 1.41 GHz, the sensitivity of the Effelsberg telescope
largely compensates. This is evident from the S/N of V shown in
Fig. 1 and favours our results to be intrinsic to the pulsar emission
rather than products of the instrumental noise.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{H4198F1a.ps}\par\includegraphics[width=8.5cm,clip]{H4198F1b.ps}\end{figure}](/articles/aa/full/2003/22/aah4198/Timg5.gif) |
Figure 1:
The distribution of V and V/I in PSR B1133+16, at 4.85 GHz (top) and
1.41 GHz (bottom). Each plot has three horizontal panels. The top panel
shows the total power (I) integrated pulse profile, the middle panel
shows the distribution of flux densities of V in units of the
rms and the bottom panel shows the distribution of the fraction V/I. In the bottom panel, a threshold has been applied to exclude
the noise: only cases where the flux density of V is more than
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[angle=-90,width=8.8cm,clip]{H4198F2.ps}\end{figure}](/articles/aa/full/2003/22/aah4198/Timg6.gif) |
Figure 2: The distribution of PA, V and V/I in bin 50, near the peak of the leading component, at 4.85 GHz (top) and 1.41 GHz (bottom). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H4198F3.ps}\end{figure}](/articles/aa/full/2003/22/aah4198/Timg7.gif) |
Figure 3: The distribution of PA, V and V/I in bin 65, near the peak of the trailing component, at 4.85 GHz (top) and 1.41 GHz (bottom). |
| Open with DEXTER | |
To investigate the single-pulse behaviour of circular polarization, the value of V is plotted against the corresponding pulse phase for every single pulse. Such density plots reveal the pulse to pulse fluctuations of V. Figure 1 shows two such plots for the single-pulse data of PSR B1133+16 observed simultaneously at 4.85 GHz and 1.41 GHz. The density plots reveal that the distributions of Vat each pulse phase bin range over a few tens of rms units at both frequencies.
In the leading component, it has been shown that the OPMs are almost equally strong and dominate equally often at both frequencies (Paper II). The distribution of V in this component shows an almost equally dense population of positive and negative values. On the other hand, the trailing component is almost always dominated by one OPM and the respective V distribution favours negative values. Under incoherent addition of OPMs, the observed V is the difference between the Vof each OPM and therefore the above observation is in accordance with a particular handedness of V being associated with a certain OPM.
The seemingly bimodal distributions of V/I in the leading component in Fig. 1 are caused by the threshold applied to exclude the noise. Figure 2 shows the specific distributions of V and V/I together with the PA histogram of bin 50. The bottom row corresponds to the 1.41 GHz data and the top row to the 4.85 GHz data. The threshold on V is not applied here, in order to demonstrate how much of the distribution lies within the instrumental noise, the rms of which is represented by a small horizontal bar inside the V distribution. Only the pulses in which the S/N of the total power exceeds 2 and the fractional linear polarization exceeds 20% are considered, in order to exclude ambiguous PA values. Bin 50 exhibits a clear bimodal PA distribution at both frequencies and at the same time a mean V value very close to 0. On the other hand, Fig. 3 shows bin 65 from the trailing pulse component, that presents a slightly different picture. The PA distributions at both frequencies are dominated by one OPM (at 4.85 GHz this is not entirely clear due to the small population of points that survive the threshold) and the V distributions have a significantly non-zero negative mean. This picture is consistent with incoherently superposed OPM, each mode favouring a particular handedness of V: in bin 50 where both modes dominate equally often, V is distributed around 0, which is not the case for bin 65, where one mode essentially dominates and the handedness of V associated with this mode gives mean V its negative value.
Figures 2 and 3 show a difference between the
distributions in V and V/I. All four V/I histograms can be
adequately approximated by Gaussian distributions. In bin 50, the best
fit has a mean of -2.5% and a ![]() of 19% at 4.85 GHz and a
mean of 0.6% and a
of 19% at 4.85 GHz and a
mean of 0.6% and a ![]() of 18% at 1.41 GHz. In bin 65 on the
other hand, the best fit has a mean of -12% and a
of 18% at 1.41 GHz. In bin 65 on the
other hand, the best fit has a mean of -12% and a ![]() of
27% at 4.85 GHz and a mean of -13% and a
of
27% at 4.85 GHz and a mean of -13% and a ![]() of 24% at
1.41 GHz. These broad distributions are consistent with those seen in
other pulsars (Stinebring et al. 1984a,b) and are
largely dominated by instrumental noise (McKinnon 2002).
of 24% at
1.41 GHz. These broad distributions are consistent with those seen in
other pulsars (Stinebring et al. 1984a,b) and are
largely dominated by instrumental noise (McKinnon 2002).
In summary, the density plots of the circular polarization in Fig. 1 and the individual distributions in Figs. 2 and 3, together with the OPM analysis presented in Paper II, provide evidence that each OPM is associated with a certain handedness of V. This association, however, is obviously not perfect, and we discuss this in the following.
In Cordes et al. (1978), observations of PSR B2020+28 at 404 MHz were used to investigate a possible connection between the handedness of V and the PA value. To this goal, they plotted V versus PA in the single pulses they observed. In their paper, they give an example of a particular pulse longitude where the distribution of PAs is bimodal, in other words a phase bin where the dominant OPM alternates from pulse to pulse. The plot of V versus PA for this bin demonstrates a clear correlation between the handedness of V and the OPM.
In Paper II, a detailed study of the frequency dependence of the OPMs
in PSR B1133+16 demonstrated that, at higher frequencies, the OPMs are
seen to dominate almost equally often and the individual flux densities of the
OPMs become more equal to each other. Given this frequency evolution,
we investigate whether the V-OPM association is also frequency
dependent. Instead of V-PA plots, we follow a different route,
namely to display the tips of the polarization vectors of all the
single pulses from specific bins on the Poincar
![]() sphere. The
coordinates of a given point on the surface of the sphere are given by
two angles, the latitude (
sphere. The
coordinates of a given point on the surface of the sphere are given by
two angles, the latitude (
![]() )
and longitude (2PA). The
latitude is a measure of the ellipticity of the polarization state:
values of
)
and longitude (2PA). The
latitude is a measure of the ellipticity of the polarization state:
values of ![]() correspond to linearly polarized states whereas values
of
correspond to linearly polarized states whereas values
of ![]()
![]() correspond to purely circular states of opposite
handedness.
correspond to purely circular states of opposite
handedness.
| |
Figure 4:
Hammer-Aitoff projection of the Poincar
|
| Open with DEXTER | |
In the scheme of OPM superposition, it is very important to stress
again that the observed PA is that of the dominant mode, regardless of
the flux density difference of the two modes. Therefore, by testing
the PA vs. the sign of V association, one is effectively testing the
association of the handedness of V with OPM. For each phase bin of
the pulse and for the total number of pulses, we quantize the observed
quantities according to the following ![]() possibilities:
dominant mode 1, dominant mode 2 or not defined PA, and positive-Vor negative-V. By composing such contingency tables for each
phase bin, it is possible to quantify the association between the
handedness of V and the dominant OPM. An example for bin 50 at each
observed frequency is shown in Table 1.
possibilities:
dominant mode 1, dominant mode 2 or not defined PA, and positive-Vor negative-V. By composing such contingency tables for each
phase bin, it is possible to quantify the association between the
handedness of V and the dominant OPM. An example for bin 50 at each
observed frequency is shown in Table 1.
Table 1: Contingency tables for bin 50 of the PSR B1133+16 data, showing the frequency of occurrence of all possible combinations in the single pulses. The top table corresponds to the 4.85 GHz and the bottom table to the 1.41 GHz data.
The numbers have been obtained by applying a two step process. Where the S/N of L in the given bin is less than 2.5, we are unable to compute the PA and therefore classify these as "Undefined'' in Table 1. Then, we compare the observed PA in each single pulse to the PA of the integrated profile in this bin, to determine which mode is dominating at this particular instant. From the numbers presented in Table 1, it is possible to compare the observed cases to the null hypothesis, by using the formula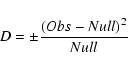 |
(1) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H4198F5.ps}\end{figure}](/articles/aa/full/2003/22/aah4198/Timg17.gif) |
Figure 5: D plotted against the pulse phase bin for the Mode 1-V- and Mode 2-V+ cases. The solid line corresponds to 1.41 GHz and the dotted line to 4.85 GHz. The negative D values signify a deficit from the null hypothesis. |
| Open with DEXTER | |
We perform this analysis across the whole profile of PSR B1133+16. What we find is that there is an excess from the null hypothesis of negative V cases across the pulse for the most common OPM (Mode 1) and a positive V excess from the null hypothesis for the other OPM (Mode 2). Figure 5 shows D as measured by Eq. (1), plotted across the pulse. The top panel of the plot shows the D values for the association between Mode 1 and negative V, whereas the bottom panel shows the same for Mode 2 and positive V, at both frequencies. From the definition of D we find that values over 5 are statistically significant. Two facts are evident from these plots. First, the values of D are generally large enough to support a strong correlation between the handedness of V and the dominant OPM. Second, the D values are consistently larger at 1.41 GHz than at 4.85 GHz, indicating that the correlation is weaker at 4.85 GHz. Also, as we have seen before, Mode 2 hardly ever dominates in the trailing pulse component and therefore the corresponding D values are all close to zero.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{H4198F6a.ps}\hsp...
...pace*{4mm}
\includegraphics[angle=-90,width=8.4cm,clip]{H4198F6d.ps}\end{figure}](/articles/aa/full/2003/22/aah4198/Timg18.gif) |
Figure 6: The top row of plots shows the average pulse profile of PSR 1133+16 at 4.85 GHz, decomposed into the profiles for Mode 1 (left) and Mode 2 (right). The bottom row is the result of the decomposition into the individual OPMs of each single pulse, which are then averaged. In each plot, the main panel shows the total power I (solid), the linear polarization L (dashed) and the circular polarization V (dashed-dotted). The secondary panel on top shows the PA. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{H4198F7a.ps}\hsp...
...ace*{4mm}
\includegraphics[angle=-90,width=8.4cm,clip]{H4198F7d.ps}
\end{figure}](/articles/aa/full/2003/22/aah4198/Timg19.gif) |
Figure 7: Same as Fig. 6 for 1.41 GHz. |
| Open with DEXTER | |
Our statistical analysis of the dual frequency PSR B1133+16 data has shown us that there is a frequency dependent correlation between the handedness of V and the dominant OPM. The contingency tables, however, show that there is a significant population of cases where the handedness of V is opposite from the expected. In other words, the V-OPM association is not perfect. This is a very important result with serious implications on the technique of decomposing pulse profiles into the individual OPMs. The significance lies in the fact that each OPM that dominates in a given single pulse may be observed instantaneously with either handedness of V. However, averaging the single pulses and decomposing the average profile is based on an assumption that is not met, namely that each OPM is clearly associated with a particular sign of V in all the single pulses. To demonstrate this, we detail the mathematics of mode-decomposition in single pulses and show the difference between the obtained profiles by decomposing and then averaging, and averaging and then decomposing the PSR B1133+16 data.
The orthogonality of the modes means that their polarization states at
a given instant are represented by antiparallel vectors on the
Poincar
![]() sphere. By definition therefore the PAs can
only take values which are exactly
sphere. By definition therefore the PAs can
only take values which are exactly ![]() apart. Incoherent
superposition allows the addition of the individual Stokes
parameters. The mathematical process is as follows:
apart. Incoherent
superposition allows the addition of the individual Stokes
parameters. The mathematical process is as follows:
The observed
Stokes parameters can be written in terms of the OPMs
| (3) | |||
| (4) |
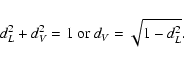 |
(5) |
| I | = | I1+I2 | |
| L | = | dL(I1-I2) | |
| V | = | (6) |
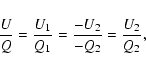 |
(10) |
| Qi = |
|
| Ui = |
(11) |
In Stinebring & McKinnon (2000), the average profiles of PSRs B0525+21
and B2020+28 are decomposed into the OPMs, using the assumption of
superposed OPM emission. We apply our method of single-pulse
decomposition and their method of average profile decomposition to PSR B1133+16 to identify and interpret the differences.
Figures 6 and 7 show the results of the two different
approaches to OPM-decomposition at 4.85 GHz and 1.41 GHz
respectively. First of all, the averaged profiles created using the
two methods are obviously different. The average circular polarization
in the case of the single-pulse decomposition has a constant
sense across the profile, which is not true for the average profile
decomposition. Also, it can be seen that the average flux density of V in each of the modes is considerably smaller in the case of
single-pulse decomposition. Another aspect of the observed differences
between the profiles is the linear polarization, which is ![]() 100%
in the decomposed average profiles and significantly less in the
decomposed single-pulse profiles. We claim that the reduced degree of
polarization is due to the spread in the PA distributions. We have
found that a
100%
in the decomposed average profiles and significantly less in the
decomposed single-pulse profiles. We claim that the reduced degree of
polarization is due to the spread in the PA distributions. We have
found that a ![]() spread in the PA distribution of a particular
phase bin, results in a
spread in the PA distribution of a particular
phase bin, results in a ![]() 20% decrease in the mean linear
polarization after averaging a few hundreds of single pulses. For this
reason, it is impossible to obtain mode-separated average profiles
constructed from decomposed single pulses that exhibit 100%
polarization unless the PA distributions are delta-functions.
20% decrease in the mean linear
polarization after averaging a few hundreds of single pulses. For this
reason, it is impossible to obtain mode-separated average profiles
constructed from decomposed single pulses that exhibit 100%
polarization unless the PA distributions are delta-functions.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{H4198F8a.ps}\vspace*{2mm}
\includegraphics[angle=-90,width=8.5cm,clip]{H4198F8b.ps}\end{figure}](/articles/aa/full/2003/22/aah4198/Timg37.gif) |
Figure 8: Single pulse number 1562 from PSR B1133+16, at 4.85 GHz (top) and 1.41 GHz (bottom). The solid line represents the total power, the dashed line the linear polarization, and the dashed-dotted line the circular polarization. The PA jumps in the same direction at both frequencies, but the circular polarization follows a swing of opposite handedness between the frequencies. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{H4198F9a.ps}\vspace*{2mm}
\includegraphics[angle=-90,width=8.5cm,clip]{H4198F9b.ps}\end{figure}](/articles/aa/full/2003/22/aah4198/Timg38.gif) |
Figure 9: Single pulse number 2438 from PSR B1133+16, at 4.85 GHz (top) and 1.41 GHz (bottom). The circular polarization disagrees in handedness between the frequencies. The V flux densities match very well, showing a peak at each phase bin of the PA jump. |
| Open with DEXTER | |
The significant correlation between V and OPM is in agreement with the initial result for PSR B2020+28 (Cordes et al. 1978) and constitutes evidence that circular polarization is closely linked to the OPM phenomenon. However, we have demonstrated that decomposing single pulses into the OPMs and averaging produces different mode-separated profiles from averaging single pulses first and then decomposing the resulting profile. This happens because the correlation of V with OPM, although significant, is not perfect, and becomes worse with frequency. Obviously, the entire mechanism that determines the polarization we observe is not well understood.
In Karastergiou et al. (2000, Paper I) and Paper II it was shown that single pulses of PSRs B1133+16 and B0329+54 observed simultaneously at two, widely spaced frequencies may often disagree in terms of the dominant OPM. Despite these frequent cases of disagreement, the cases of agreement were statistically more significant and therefore revealed a high degree of correlation in OPMs between the observed frequencies. The correlation of OPMs between frequencies is facilitated by the fact that the PAs of the OPMs are, by definition, orthogonal. Therefore, it is possible to distinguish the prevailing OPM at both frequencies and count the cases of agreement and disagreement. Unfortunately, the observed V has wide unimodal distributions around a usually very small mean. An investigation of the correlation of the handedness of V between the frequencies, is therefore dominated by the mean and the rms of the V distribution. As an example, the bins in the trailing pulse component of PSR B1133+16 as seen in Fig. 1, show broad V distributions of a clearly negative mean. A test of the association in handedness of V between the frequencies in this component obviously shows a high correlation, forced by the underlying distributions themselves. As for the leading pulse component, we have demonstrated that each mode is clearly associated to a particular handedness in Vat a given frequency. The high degree of the correlation of the OPMs between the frequencies therefore also results in a high correlation in the handedness of V. To summarize, we see a high correlation in the handedness of V between the observed frequencies, which is what we expect from our previous knowledge. This correlation, however, does not add significantly to our interpretation of the observations.
Given the simultaneity of our data, we have the opportunity to inspect single pulses as a whole observed at both frequencies. Two example single-pulses are provided in Figs. 8 and 9. Figure 8 shows pulse number 1562 from PSR B1133+16 at 4.85 GHz (top panel) and 1.41 GHz (bottom panel). The leading pulse component shows the characteristic swing and change of handedness in V usually associated with core components. The sense of the swing is opposite between the two frequencies although the PAs agree. They both show a PA jump in the same direction, although the jump happens slightly earlier at the lower frequency. In pulse 2438 in Fig. 9, an OPM jump occurs in bin 48 and the PA jumps back again in bin 52, at both frequencies. Both jumps correspond closely to the peaks in V. The shape of the V profile around these bins is also very similar between the two frequencies, but the handedness is opposite. The examples also help to extend the significance of our results to timescales comparable to the pulsar component widths.
In this paper we have demonstrated a method for decomposing single pulses into the OPMs, assuming incoherently superposed OPM emission. We support this method in light of our findings for PSR B1133+16, where the handedness of the circular polarization has been observed not to be perfectlyassociated to the dominant OPM. We have shown that the correlation of V with OPM is worse at 4.85 GHz than at 1.41 GHz, which is consistent with the conclusion of Paper II that propagation through the pulsar magnetosphere causes more severe effects at higher rather than lower frequencies. Finally, we show two examples of single pulses to demonstrate that our bin-by-bin analysis is also applicable to structures with timescales similar to pulsar components.
Acknowledgements
The authors would like to thank everybody at the Effelsberg and Lovell radio telescopes who helped in any way with the observations. AK would like to thank the Deutscher Akademischer Austausch Dienst for their financial support.