... capabilities[*]
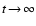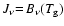We note that chemical non-equilibrium effects in the time-independent case may even lead to spurious effects since existing chemical rate networks do usually not lead to the chemical equilibrium solution for $t\!\to\!\infty$, even if $J_{\nu}\!=\!B_{\nu}(T_{\rm g})$ is assumed, which contradicts very basic thermodynamical considerations. The reason is that usually the corresponding forward and reverse processes are either not included pair-wise in all cases or that the respective rate coefficients are not properly related to each other via the Gibb's free energies of the molecules, but rather treated in an independent way. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... case[*]
Other, eventually multi-parametric descriptions of 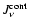$J_{\nu}^{\rm cont}$ are also conceivable, e.g. adjusted to the optically thin case. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... to H atoms[*]
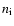In this paper, we rely on the mean molecular weight $\mu $ as indicator for the dissociative state of hydrogen, because in our dynamical calculations, the state functions enter in a tabulated form where the actual particle densities $n_{\rm i}$ are "forgotten''. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... zones[*]
Actually no single zones are split, but three new zones are carefully constructed out of two old ones, thus preventing numerical generation of mass or momentum. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... since[*]
Neglecting the difference between 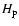$H_{\rm p}$ and $H_\rho$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
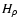... functions[*]
A detailed statistical comparison between new and classical models was not the aim of this work, but might be presented in a subsequent paper. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... parameters[*]
The choice of these parameters was guided by investigations of (Richter et al. 2002) on Fe II emission lines. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[*]
See also http://astro.physik.tu-berlin.de/~woitke/Mira.mpeg. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... work[*]
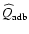Referred to as "adiabatical heating'', therefore $\widehat{Q}_{\rm adb}$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... case[*]
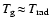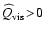The width of the complete radiative relaxation zone is smaller than the grid spacing in this case, resulting in $T_{\rm g}\!\approx\!T_{\rm rad}$ even at points where ${\widehat{Q}_{\rm vis}}\!>\!0$, e.g. at the positions of the shock waves. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... heated/cooled)[*]
The internal chemical processes responsible for the formation of H2 are assumed to be very fast in our model (assumption of chemical equilibrium, see Sect. 3.1). Thereby, the actual speed of the H2-formation is limited by the need of the gas to radiate away the liberated binding energy in our model. It remains an open question whether the three-body gas phase reactions and the surface reactions on dust grains required for the kinetical formation of H2 are actually fast enough to achieve this limiting case. A kinetic treatment of the H2-formation would be desirable, but goes beyond the scope of this paper. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... gas[*]
Strictly speaking, this is not the post-shock-cooling here. What we observe is rather a quick decrease of 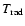$T_{\rm rad}$ due to the decreasing backwarming by the outward propagating and thereby radially diluting dust-shell. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... environment[*]
The shock wave velocity is rather controlled by 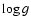$\log g$ and P than by 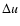$\Delta u$, compare footenote 2 in Paper II. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... numerics[*]
Neither a variation of the resolution, nor of the averaging procedure for the velocity gradient 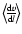$\left\langle\!\frac{{\rm d}v}{{\rm d}l}\!\right\rangle$ resulted in a qualitative change of this cooling behaviour. Of course, we cannot exclude an influence of the numerical method on these results. However, even if the initial temperature pertubations are of numerical origin, the amplification mechanism clearly has a physical nature. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Copyright ESO 2003