1 - Astronomical Observatory, Volgina 7, 11160 Belgrade 74, Serbia and Montenegro
2 - Department of Mathematics, Via Buonarroti 2, 56127 Pisa, Italy

Abstract
Using the synthetic theory, we computed proper elements for asteroids in the inner part of the main belt and in the trans-Neptunian region. We present the new results and we discuss some important implications of both their rapidly increasing number and the improved accuracy. We give complete information on the availability of asteroid proper elements through the AstDys web service, with particular emphasis on the content and update strategy of proper element catalogs. Next, we discuss the most interesting features of some important asteroid families and regions (Vesta, Phocaea, TNO). For the Vesta family we provide further evidence that the observed spread of the family members is probably due to diffusion in the proper elements caused by non-gravitational effects. We shed additional light on the long-standing question of whether Phocaea is a genuine family or an island isolated by resonances, and we show the impact of nearby secular resonances on the local dynamics. Finally, we analyzed trans-Neptunian objects by using a "dual'' of the main asteroid belt, to show that the currently known population of TNOs corresponds to the unstable outer asteroid belt beyond the 2/1 mean motion resonance with Jupiter. To discuss some of the main features of the dynamics of trans-Neptunians we use two examples, one stable over at least 100 Myr, but with proper elements slightly affected by a nonlinear secular resonance g+s-g₈-s₈, and the other chaotic, with a Lyapounov time of the order of 4000 yr, already exhibiting macroscopic instability after 6 Myr.

We have recently developed a new method for the computation of "synthetic'' proper elements of asteroids (Knezevic & Milani 2001), which consists of a set of purely numerical procedures, collectively called the synthetic theory. The procedure includes: (i) numerical integration of asteroid orbits in the framework of a realistic dynamical model; (ii) online digital filtering of the short periodic perturbations and determination of the proper semimajor axis; (iii) Fourier analysis of the output to remove the main forced terms and extract proper eccentricity, proper inclination, and the corresponding fundamental frequencies; (iv) checking of the accuracy of the results by means of running box tests.

Using this theory we produced a set of synthetic proper elements and frequencies for the asteroids in the outer main belt, between 2.5 and 4.0 AU. The accuracy of the elements has been estimated for all the asteroids included, and was found to be better by a factor of more than 3 on average, with respect to the previously available results derived by means of even the most advanced version of the analytical theory (Milani & Knezevic 1994).

In the present paper we extend our analysis to the inner part of the asteroid main belt, between 2.0 and 2.5 AU, and to the trans-Neptunian (Edgeworth-Kuiper) belt. The computation of updates of catalogs of proper elements for the Trojans and Hildas is in progress, thus we will soon achieve full coverage of the entire system.

To compute accurate synthetic proper elements for asteroids in the inner main belt, stable over long time spans, we integrate the orbits of asteroids in this region with a dynamical model including the direct perturbations by 7 major planets, from Venus to Neptune. The indirect effect of Mercury is taken into account by applying a barycentric correction to the initial conditions (as was done previously for the inner planets, Milani & Knezevic 1992). We use the ORBIT9 integrator (version 9e), which employs as a starter a symplectic single step method (implicit Runge-Kutta-Gauss), while a multi-step predictor performs most of the propagation (Milani & Nobili 1988).

To avoid problems with Mars-crossing objects and objects undergoing close approaches to Mars we exclude from our integrations the asteroids with initial osculating perihelion distance less than 1.6 AU. We then integrate orbits of all the included asteroids for 2 Myr (1 Myr forward and 1 Myr backward in time), and compute the proper values and their errors in terms of the standard deviations and maximum excursions by joining data from both runs (the only exception to this is the computation of Lyapounov Characteristic Exponents (LCE), which we determine from the forward integration only). The running box we use has a length of 1 Myr (that is, half of the total time span covered by the integrations), and a step of $\simeq$ 10⁵ yr.

We also present some new results on the trans-Neptunian objects (TNO). In this case, however, we employ the setup similar to the one we have already used for the asteroids in the outer main belt (Knezevic & Milani 2001). This means that the dynamical model includes only four outer major planets, with the barycentric correction accounting for most of the indirect effect of all the inner planets. The integrations are performed only forwards in time, but by using a much longer time step; thus we cover 100 Myr in the case of the numbered TNOs, and 10 Myr for the multi-opposition ones. For the running box tests we use a window with length one half of the total time span: 50 Myr and 5 Myr, shifting it by 5 Myr and by $5\times 10^5$ yr, respectively.

In the following we present our new results and we discuss some important implications of their rapidly increasing number and improved accuracy. What is most important is the availability of both analytic and synthetic proper elements for the entire asteroid population, with frequent updates. This allows new insights on the overall dynamics in the inner main belt: we discuss newly discovered features of some of the most prominent families and regions. For the trans-Neptunian objects, a global view of the dynamical structure was not available before, apart from the rough views which can be obtained by the use of osculating orbital elements.

2 The AstDys online information system

All the catalogs of proper elements computed by means of the analytical and synthetic theories are available from the AstDys online information service (http://hamilton.dm.unipi.it/astdys). Apart from proper elements, the AstDys system provides plenty of other information regarding all known numbered and multi-opposition objects, useful to the observers and researchers in general - osculating orbital elements, observations used to compute orbits, daily observational circumstances, statistics of the observatory performances, etc. In this respect it also represents a complement to the NEODyS system (http://newton.dm.unipi.it/neodys), which is in turn devoted specifically to the Near Earth Objects.

2.1 Proper element catalogs

The proper elements within AstDys are provided in two ways - in the form of catalogs suitable for browsing and download, and as a separate entry on the home pages of individual objects.

A total of 15 catalog files are available from within the AstDys system, 6 of them containing the data computed by means of the analytical theory, and the other 9 with the data computed by means of the synthetic theory.

The catalogs of analytically computed proper elements consist of three files each. The first file contains proper semimajor axis, eccentricity and sine of inclination, along with the fundamental frequencies (g - rate of the perihelion, and s - rate of the node), secular resonance code (RFL), quality codes for mean (QCM) and osculating (QCO) elements, and with the absolute magnitude of the asteroid. The second file lists proper longitudes of perihelion and node, and some auxiliary data. The third file contains mean elements.

Two catalogs of analytical proper elements are available, one for numbered and the other for multi-opposition main belt asteroids. The analytic proper elements are provided for all the numbered and multi-opposition asteroids for which it was possible to compute them in a reliable manner, given the intrinsic constraints of the analytic method itself (Milani & Knezevic 1994).

The catalogs of synthetic theory are again divided in three files. The main file contains the proper elements (proper semimajor axis, eccentricity and sine of inclination) and frequencies ("mean'' mean motion, perihelion and nodal rates), an estimate of the Maximum Lyapounov Characteristic Exponent and the time span of the numerical integration used to compute the data (negative if integrated backwards in time), as well as the absolute magnitude. Note that only three "action like'' proper elements are computed. The second and the third files contain the corresponding RMS and maximum excursion values, with RMS and maximum excursion of the residuals with respect to the linear fit of the "mean'' mean longitude in the penultimate column; the last column repeats the information on the integration length.

Three catalogs of synthetic proper elements are available, one for numbered main belt asteroids (MBA), one for multi-opposition MBA, one for trans-Neptunians (numbered and multi-opposition together). The synthetic proper elements are currently maintained for the main belt asteroids with 2.0<a< 4.0 AU and with initial perihelion distances > 1.6 AU for the objects with a<2.5 AU, and with q>1.75 AU for the rest. For the TNOs, synthetic proper elements are computed for 35<a<100 AU, e<0.3, $i<18^\circ$ , and q>32 AU.

As a rule, the proper elements of numbered asteroids are updated monthly. On the contrary, we are not further maintaining the files of synthetic proper elements for multi-opposition asteroids. The reason is that the orbital elements of non-numbered asteroids are still subject to changes larger than the accuracy of the proper element computation. Thus, we would have to recompute many times the synthetic proper elements for the same asteroids, but this computation is a time-consuming procedure. On the contrary, the analytic proper elements can be computed in a fraction of a second for each asteroid, thus we can update the proper elements at each update of the orbits.

The source files of the software used to produce both analytical and synthetic proper elements are available from the same AstDyS site. There are examples of the outputs from the procedures, a tar file prepared for easy download and installation (as a plug-in to the OrbFit free software system, http://newton.dm.unipi.it/orbfit/), and examples of the necessary input files, such as the ones containing the initial conditions of the major planets and the abovementioned barycentric correction. Thus, our results are completely reproducible by anyone with a computer and a Fortran 77 compiler.

On the home pages of the individual objects, both sets of elements, analytical and synthetic, are provided if available. The latter set is accompanied by the corresponding standard deviations and the Lyapounov Characteristic Exponent and time span covered by integrations, which gives an idea of the reliability of the LCE.

Note finally that the AstDys system is accompanied by a powerful search engine and a comprehensive online "help'' facility, which provides all the details on the data, their definitions, computation, retrieval, and so on.

2.2 Proper element catalogs update

We have implemented an "almost automatic'' procedure for the update of the entire AstDys database, which takes place typically once per month (the Daily Observational Circumstances are updated on a daily basis).

As a rule, the monthly update takes place at every full-moon, as soon as the observational data are made available by the Minor Planet Center. It includes the computation of orbits, corrected taking into account the new observations, for all the numbered and multi-opposition asteroids. The analytical proper elements are computed immediately after the orbital elements, and are readily available as soon as the AstDys system is back on the web. The computation of synthetic proper elements is done between two consecutive monthly updates for the newly numbered objects only. Thus, the catalogs of synthetic proper elements contain typically all the objects numbered as of the previous monthly update.

The reason for this procedure is the rapid increase of the number of asteroids in the catalogs due to the surveys that primarily search for NEA, but which observe a lot of main belt objects as well. A simple exercise shows that an asteroid of about 3 km in diameter and of an average albedo, located at 2.3 AU, would have an apparent magnitude at opposition of around 18, which is close to the limiting magnitude of most of the surveys. Thus, one would expect that most of the inner belt asteroids down to this size limit have been observed several times, and that, therefore, they are either already numbered, or perhaps waiting to be numbered in the files of multi-opposition objects. The analytical proper elements are computed in a quite efficient manner, thus we are still able, with the available computing power, to keep up with the task of recomputing proper elements for all the numbered and multi-opposition objects at each update. For the time-consuming procedure of the production of synthetic proper elements this is not possible, so we always add only the newly numbered objects.

We are continuously working to upgrade and improve the AstDys service. Thus, we plan to add the resonant proper elements for Trojans and Hildas. Possible expansions then might include also the family identifications, more advanced physical data, etc.

3 New insights on the inner asteroid belt

In Knezevic & Milani (2001) we analyzed in detail the accuracy and long-term reliability of the synthetic proper elements for the asteroids in the outer main belt. In Knezevic et al. (2003) we provided statistics for the entire main belt. Thus, we are not going to repeat the previous results, but rather we shall briefly discuss some important information which can be extracted from the new proper elements.

The increase in the numbers of proper elements available is very significant. As an example, after the November 2002 update, we had catalogs with analytic proper elements for 48 375 numbered and 69 744 multi-opposition main belt asteroids. On the same date, more accurate synthetic proper elements were available for 46 651 numbered and 3 368 multi-opposition main belt asteroids, plus 154 trans-Neptunians.

Since asteroid families are statistical entities, such an increase in number allows one to study many more of them. Moreover, the synthetic proper elements allow us to study in greater detail the internal structure of the families. The dynamical structure of the asteroid belt can be investigated more effectively. There are other applications, such as the study of the size distribution for family and non-family asteroids (A. Morbidelli, priv. comm., 2003), etc.

We shall discuss the most interesting features of some important asteroid families and regions, revealed by inspection of the newly available data. In this section we will discuss the inner main belt, in the next section the trans-Neptunian region.

3.1 The Vesta family

One of the most intriguing families in the inner part of the asteroid main belt is certainly the Vesta family. As already pointed out by Migliorini et al. (1997), since asteroid (4) Vesta appears to be the only large asteroid in that region covered with basaltic crust, the large spread found by Binzel & Xu (1993) of km-sized V-type asteroids, presumably fragments of Vesta, indicates that the family must be much larger than originally determined by Zappalà et al. (1995). Also, since family membership, apart from the parent asteroid (4) Vesta itself, consists almost entirely of small bodies (Binzel & Xu 1993), it was straightforward to assume that this family is the outcome of a cratering event. However, the attempts to fit the observed size and orbital distributions failed to provide a unique scenario of family formation and its subsequent evolution (Marzari et al. 1996). As an example, the observed spread of the family in the proper a-i plane could have been simulated only by resorting to a peculiar fragment ejection geometry. Moreover, as also shown by Migliorini et al. (1997), the dynamical behavior of essentially all known NEAs of V-type strongly suggests their injection in the Earth's vicinity through the secular $\nu_6$ resonance, and this in turn requires ejection velocities of the order of 1 km s^-1(Farinella et al. 1993).

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f1.ps}\end{figure}$	Figure 1: The Vesta region projected on the (proper a-proper e) plane (above) and on the (proper a-proper I) plane (below). On the left, all the numbered asteroids. On the right, only those larger than 7 km (assuming the same albedo as Vesta).
Open with DEXTER

Hydrocode simulations (Michel et al. 2001) indicate that, in family-forming events, a fraction of small fragments of a typical size $D\approx 1{-}3$ km can be ejected at high speeds. Thus, assuming a strong velocity-size dependence of the fragments (Cellino et al. 1999), high ejection velocities seem to be plausible for a body of the size of Vesta. Nevertheless, a comparatively small number of fragments are expected to acquire such speeds, and it appears that the extent of this family cannot be explained in terms of the ejection velocities alone.

In Fig. 1 we give a general view of the region in the inner asteroid belt that contains the Vesta family. On the left we plot all the asteroids with known synthetic proper elements in the region, while on the right we extracted only the bodies larger than 7 km in diameter. It is obvious that the entire region is fully dominated by the small bodies, and that the parent asteroid (4) Vesta is located in the very center of the region in terms of proper semimajor axis and eccentricity, somewhat closer to the edge of the family in terms of the proper inclination. The sparse distribution of larger objects implies that most of these probably belong to the background population. Such a large spread of the family is apparent even without using sophisticated classification procedures, like hierarchical clustering method or wavelet transform (Zappalà et al. 1995). Nesvorný has applied hierarchical clustering to one of our recent catalogs of proper elements: animated figures illustrating the major asteroid families are available at http://www.boulder.swri.edu/~davidn/hcluster/. The figure for the Vesta family shows the well-known phenomenon of chaining, typical of hierarchical clustering, resulting in spurious aggregation of other families when the cutoff velocity is increased to only 80 m/s. This confirms that it is not easy to define in a sharp way the family boundaries when using such a large catalog; only spectral observation can allow us to discriminate the objects orginating from Vesta. Still, Nesvorný's figures support our conclusion that the Vesta family has many thousands of known members and spreads by more than 0.1 AU in the proper semimajor axis.

Several attempts to explain the observed spread of the asteroid families in terms of an initial spread acquired at breakup, and of the subsequent long-term evolution due to the Yarkovsky non-gravitational effect, have been performed recently. These were pioneered by the demonstration of Farinella & Vokrouhlický (1999) that, due to the Yarkovsky mobility, the small asteroids can move by a substantial amount in semimajor axis over time scales significantly shorter than the collisional lifetimes. Later, Nesvorný et al. (2002) and Bottke et al. (2001) analyzed the Flora region and the Koronis family, respectively, showing that the observed spreads can, at least partly, be explained by an interplay of non-gravitational effects and chaotic diffusion.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f2.ps}\end{figure}$

Figure 2: Above: size distribution of the asteroids in the Vesta region (within the box given in the text); only the asteroids with diameter <7 km have been included, since the larger ones are mostly interlopers, as can be seen from Fig. 1. Below: for the same asteroids, distribution of the escape velocity, computed from the difference in proper elements, with respect to the family parent body, that is Vesta. Given the distribution, it is unlikely that it corresponds to the original escape velocity: it is very likely that the relative velocities have been increased by subsequent dynamical evolution.

Open with DEXTER

It is, therefore, very probable that the current extent of the Vesta family can also be explained as due mostly to Yarkovsky mobility, especially because this is a strongly size-dependent effect, shifting smaller asteroids faster and further than the larger ones. The order of magnitude of the Yarkovsky semimajor axis drift is 0.0001 AU/Myr, thus the observed dispersion could be achieved in 1 or a few Gyr by this effect alone. On the other hand, the proper elements of the asteroids in most of the Vesta region (except close to some mean motion resonances) are stable over very long time spans, so that chaotic diffusion could not play a significant role in shaping this family.

Thus, if we take the box $2.2<a<2.5~;\ 5<I<10~;\ 0.07<e<0.13$ it contains only 49 bodies with a diameter larger than 7 km and 2339 smaller than 7 km (the diameter is computed by assuming the same albedo as Vesta). This number of candidate family members may look very large, but it is not unreasonable. Even if all the small bodies in the box were members of the family (which is not likely, because there must be some background population superimposed on the family population) the total volume of the ones with diameter less than 7 km still is only $6\times 10^4$ cubic km, which is the volume of a crater with 100 km diameter and an average depth of 7 km. If the albedo feature, visible in the Hubble Space Telescope images (Thomas et al. 1997), is a crater then its volume could be even larger.

A confirmation of this analysis can be found in the histograms of Fig. 2. The size distribution (for the asteroids with diameter <7 km only) is very steep, and peaks just below 3 km, as expected from the observational selection argument given in Sect. 2.2. This is an indication that the region is dominated by family members (this does not prove that they are members of one specific family, but no other large family has been detected there). The impulsive velocity change needed to change the proper elements of Vesta into the proper elements of the small asteroids in the region is on the contrary rather flat over a broad range of velocities, which is incompatible with what would be expected from the initial breakup. If many small asteroids, all over the box we have considered, are indeed family members (this needs to be confirmed by their spectra), then diffusion in the proper elements is the only explanation and non-gravitational perturbations are the most likely cause.

3.2 The Phocaea region

The Phocaea region is a group of asteroids with a semimajor axis less than that of the 3/1 resonance, a large inclination and quite a large eccentricity; see Fig. 3. The computation of proper elements by the analytic method is not possible for such high inclinations; some results have been obtained by means of the semianalytic method (Lemaitre & Morbidelli 1994). Thus, the availability of synthetic proper elements allows some progress in understanding the dynamical structure of this region.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f3.ps}\end{figure}$	Figure 3: The Phocaea group in proper elements space. Upper left: proper a and proper e; upper right: proper a and proper $\sin I$ ; lower left: proper e and proper $\sin I$ . Lower right: histogram of accuracies of the proper elements, measured as the RMS value of changes of both proper e and $\sin I$ in the running box test.
Open with DEXTER

The Phocaea group is well isolated in the proper elements space, as is clear from Fig. 3. Note that the asteroids selected for these plots were the ones with proper elements 2.2<a<2.5 and $0.3<\sin I$ , thus the gaps around the edges of the plots are real and indicate that the group is very isolated. However, this condensation of objects should not necessarily be interpreted as a family, with a common origin from a single parent body. It might be instead a "stability island'', that is, the group might be separated from the other asteroids by gaps resulting from the destabilizing effect of some resonances. We will use the results of the proper element computations to test this hypothesis.

The boundary at low a could be caused by the 7/2 mean motion resonance. At e>0.3, chaos appears (as measured by the Lyapounov exponents computed along with the synthetic proper elements); probably this is due to shallow close approaches to Mars. Deep encounters with Mars are made impossible by the Kozai-class protection mechanism (Milani et al. 1989), thus it is likely that the dynamical lifetime is very long. This is confirmed by the good stability over time of the proper elements, although of course a test over 2 million years can only give an indication and does not prove long-term stability. We conclude that the current population may well be primordial.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f4.ps}\end{figure}$	Figure 4: Proper frequency g of the longitude of perihelion and s of the longitude of the node, in arcsec/yr. Note the alignment at the libration center due to averaging.
Open with DEXTER

The other boundaries of the Phocaea group could be understood in terms of secular resonances. To illustrate this hypothesis, we have plotted in Fig. 4 the frequencies of the critical arguments for the secular resonances g-g₆ and s-s₆. It is clear that the strip |g-g₆|<4 arcsec/yr is empty, and this is consistent with the known large strength of this resonance, which results in large-scale instabilities (including asteroids falling into the Sun, Farinella et al. (1994)). The same depletion occurs for |s-s₆|<3 and for |g-g₅|<3 (unit is arcsec/yr); the latter resonance appears in the plot around $g-g_6=g_5-g_6\simeq -24$ . This appears to confirm the "stable island'' theory, with boundaries formed by mean motion resonances, by secular resonances and by the Mars crossing region.

However, to prove that Phocaea is not a family is not so easy. If a stable island contains the parent body of a true family, and the velocity dispersion of the fragments is large enough, then the family can appear to be bound by stability boundaries, the other family members having disappeared. Also, if the original relative velocities are low, but the spread in proper elements has been increased by chaotic diffusion, the family may extend just up to the stability boundary. Given the effect of the shallow encounters with Mars, such chaotic diffusion is plausible, although not yet proven. The relative velocities among the Phocaea group asteroids, as computed from the differences in proper elements, are quite large: a histogram like the one of Fig. 2 peaks at $\simeq$ 1 km s^-1, a value consistent with chaotic diffusion. Non-gravitational perturbations should be less important, since the Phocaea we know are larger than the Vesta family members: a histogram of sizes like the one of Fig. 2 peaks at about 6 km (this is a selection effect, since the Phocaea are less frequently observed by the surveys concentrating near the ecliptic plane). Thus chaotic diffusion is the most likely explanation, if we wish to interpret the Phocaea as a single family.

Studying the internal structure of the group should help in either confirming or disproving the family hypothesis. This, however, requires proper elements with high accuracy and very long-term stability, and we have to warn the reader that this might not be the case.

A strange feature visible in Fig. 4 is the set of points almost exactly aligned, with a slope of one. This line corresponds to the secular resonance g-s-g₆+s₆. Thus the linear feature is an artifact, resulting from averaging over more than a libration period in this resonance. Indeed, when an orbit is locked in a secular resonance, the proper elements should be defined in another way, as discussed in Milani & Knezevic (1992), Sect. 4. The synthetic method, in a case with secular resonance, does not result in divergence (like the analytic method), but it does perform an averaging which destroys the information on the amplitude of the libration of the critical argument. Thus the synthetic proper elements can be used to locate the secular resonances and to detect the asteroids affected, but in a neighborhood of the resonant region the proper elements themselves lose part of their meaning, and cannot be used to study the fine structure of a group of asteroids. Ad hoc methods can be devised to describe in a better way the dynamics in this region (Morbidelli 1993), but it is difficult to adapt these special methods to the mass production of proper elements. For the moment we can only report that the g-s-g₆+s₆ resonance is important in the dynamics of the Phocaea asteroids, and that indeed a significant fraction of them is locked in this resonance.

4 Trans-Neptunian objects

The discoveries of trans-Neptunian objects have been increasing very fast. Although there are still problems in the follow-up, as of September 2002 there are 154 objects belonging to the trans-Neptunian belt and observed at two or more oppositions, for which we have computed proper elements. We have excluded objects with e>0.3because the orbit propagation would have been more demanding of computational resources; however, these orbits typically belong to the so-called scattered belt, which cannot be described by proper elements stable over millions of years.

We would like, as we have done for the main belt (Milani & Knezevic 1994), to use the proper elements catalog to investigate the dynamical structure of the trans-Neptunian belt. Notwithstanding some limitations (due to small number statistics), this is possible if we have an analytic theory providing information on the Arnold web of resonances in the region. Such an analytic theory does exist, but has an intrinsically low accuracy; for this reason, and also because it is computationally easier to generate synthetic proper elements for trans-Neptunians, we use the analytic theory only to provide qualitative information.

4.1 The two belts

To understand both the difficulty of an analytic theory and the dynamical structure, we need to compare the trans-Neptunian belt with the main belt. One way to do this is to compare the internal mean motion resonances with Jupiter, controlling the dynamical structure of the outer edge of the main belt, and the external mean motion resonances with Neptune. That is, the resonance $n/n_{\rm J}=3/2$ is compared with the resonance $n'/n_{\rm N}=2/3$ . To do this we can define a dual of the main belt by associating with each asteroid with proper semimajor axis a and proper mean motion n=k/a^3/2 a dual asteroid with proper mean motion n' such that $n/n_{\rm J}=n_{\rm N}/n'$ , that is

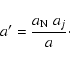
$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f5.ps}\end{figure}$

Figure 5: Trans-Neptunians (stars) and main belt asteroids brighter than absolute magnitude 8.5 (dots) plotted together on the proper a-proper e plane. For the main belt, the dual semimajor axis has been used (see formula in the text). This representation shows that the known trans-Neptunians correspond only to the outer edge of the main belt, but it is not clear whether a "main belt'' beyond the 1/2 resonance with Neptune does exist.

Open with DEXTER

Figure 5 shows the trans-Neptunian objects superimposed on the dual of the main belt numbered asteroids with absolute magnitude H<8.5 (thus comparable in size to the known trans-Neptunians). This representation suggests that the currently observable trans-Neptunians correspond to the inner part of a hypothetical belt dual to the main one. In particular, almost all the known trans-Neptunians belong to a belt corresponding to the outer edge of the main belt, the one between the n/n_j=2/1Kirkwood gap and the $n/n_{\rm J}=3/2$ Hilda group, with extension to the Thule group n/n_j=4/3. The properties of this region, for a between 3.3 and 4.3 AU, are known to be very different from the ones of most of the main belt. First, there are no known asteroid families and the size distribution is less steep, all the orbits in the region are strongly chaotic but those of the real objects are quite stable, and many orbits are affected by mean motion resonances (Milani & Nobili 1984, 1985; Milani et al. 1997). Indeed, in this region the computation of analytic proper elements is difficult, because of the second order effects of a large number of mean motion resonances.

4.2 Resonant and non resonant populations

We expected similar difficulties in the computation of analytic proper elements for the known trans-Neptunians, nevertheless we have developed an analytic theory (version 7.2) which accounts for additional second order effects due to the mean motion resonances 1/2, 2/5, 5/7 (the computations include the terms containing the square of the small divisor) in addition to all the terms included in the analytic theory we normally use for the main belt (Milani & Knezevic 1994). The results are accurate, but not accurate enough. That is, the fundamental frequencies computed in this way for semimajor axes between 36 and 52 AU have an error of only a few tens of arcsec per year, but the frequencies with which the secular resonances could arise are themselves very low, e.g., g₈=0.67 and s₈=-0.69 arcsec/yr. This implies that the location of the secular resonances can not be accurately determined. Nevertheless, some indications of the secular resonances can be obtained, and the location of the mean motion resonances is well-known.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f6.ps}\end{figure}$	Figure 6: Locations of main mean motion and secular resonances in the trans-Neptunian region in the a-e plane; the frequencies have been computed with the analytical theory for $I=3^\circ$ . The stars show the proper elements of numbered and multi-opposition trans-Neptunians.
Open with DEXTER

Thus Figs. 6 and 7 show the approximate location of the main (linear) secular resonances g-g₈ and s-s₈, of the nonlinear secular resonance g+s-g₈-s₈ and of the mean motion resonances $n/n_{\rm N}=3/4,\; 5/7,\; 2/3,\; 3/5,\; 1/2$ . The resonance with Uranus $n/n_{\rm U}=1/3$ cannot be clearly separated from the Neptune 2/3, because of the "great inequality'', that is of the near resonance $n_{\rm U}/n_{\rm N}\simeq 2/1$ ; these two mean motion resonances interact with the g-g₈ secular resonance to generate the complicated structure between 39 and 41 AU.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f7.ps}\end{figure}$	Figure 7: Locations of main mean motion and secular resonances in the trans-Neptunian region in the a-i plane; the frequencies have been computed for e=0.04.
Open with DEXTER

Figures 6 and 7 also show that the stable trans-Neptunians include two dynamically different populations, the ones in mean motion resonance with Neptune, and the ones outside the main resonances but with low eccentricity. The main resonances involved are not only the $n/n_{\rm N}=2/3$ of the so-called Plutinos, but also $n/n_{\rm N}= 3/4, \; 3/5, \; 1/2$ .

Only a few objects are neither resonant nor of low eccentricity, and most of them appear to be on less stable orbits (with comparatively large Lyapounov exponents and with less stable proper elements). As an example, we show in Fig. 8 one such unstable orbit. The plots show the time evolution of the orbital elements after filtering to remove the short periodic perturbations. In this case the computation of synthetic proper elements failed, because the eccentricity has grown, in a few million years, to the point that close approaches to Neptune become possible. Note also the strong exponential divergence of nearby orbits, indicating a Lyapounov time of $\simeq$ 4000 yrs.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f8.ps}\end{figure}$

Figure 8: For the multi-opposition trans-Neptunian 1999 CL₁₅₈ the numerical propagation of the orbit for 10 Myr resulted in macroscopic instability. The semimajor axis (upper left) shows large changes, in particular after 6 million yr, when the eccentricity (upper right) begins to increase to Neptune-crossing values. At that time the inclination (lower left) begins irregular oscillations, and the logarithm of the divergence of infinitesimally nearby orbits (lower right) grows to very large values, indicating positive Lyapounov exponents.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3507f9.ps}\end{figure}$

Figure 9: For the numbered trans-Neptunian (15 760), that is 1992 QB₁, the filtered semimajor axis (upper left) undergoes only small oscillations. The eccentricity (upper right) and inclination (lower left) show the effect of the oscillations with frequencies g-g₈, s-s₈ superimposed on a longer period oscillation, which can be attributed to the small divisor g+s-g₈-s₈: the corresponding critical argument (lower right) circulates, but it performs only 1.5 revolutions in 100 million yr.

Open with DEXTER

The example in Fig. 9 is (15760) 1992 QB₁ (the first trans-Neptunian found after Pluto). This orbit is on the contrary ostensibly stable, with a negligible divergence of nearby orbits, consistent with zero Lyapounov exponents. The synthetic proper elements as computed are accurate and stable over the very long time, thanks to the integration extended to 100 million years, with RMS of the changes among the running boxes 0.0012 for eccentricity and 0.0020 for the sine of the inclination. The very long-term oscillations in eccentricity and inclination visible in the Figure are due to the nearby secular resonance g+s-g₈-s₈. This resonance affects almost all the trans-Neptunians with low to moderate eccentricity and inclination. g₈+s₈=-0.022 arcsec/yr is small, and indeed the sum of the two fundamental frequencies is zero if the terms of order $e^2, \sin^2 I$ in the secular equations of motion are neglected; this is true even when quasi-resonant terms of the second order in perturbing mass are included. Thus for all the low e,Itrans-Neptunians g+s is also small. In the case of (15 760) $g+s=-0.002\pm 0.0015$ arcsec/yr, and the period associated with the divisor g+s-g₈-s₈ can explain the long period oscillations found in the numerical integration.

Thus the dynamical structure of the currently-observed trans-Neptunian belt is quite clear: there are three types of orbits, (1) the Neptune-resonant ones (with the Plutinos as the main group, but also other mean motion resonances populated by objects), (2) the moderate e,I orbits outside the mean motion resonances, with semimajor axes between the 5/7 and the 1/2 resonance, (3) the scattered disk of unstable orbits, containing objects we may call future comets (although the transport times to the inner solar system may be long for some of them). Some examples of scattered belt orbits are already in our proper element catalogs, e.g., the one shown in Fig. 8.

What is not clear from the existing observations and theories is apparent from Fig. 5: is the presently observed trans-Neptunian belt the "main belt'' of such objects, or is it just the inner edge, more easily observable, of a larger belt extending beyond the 1/2 resonance with Neptune? Moreover, does the 1/2 resonance correspond to a gap, like the 2/1 "Hecuba'' gap in the asteroid main belt, or rather to a group like the Plutinos and the Hildas?

The existence of the belt beyond the 1/2 Neptune resonance depends upon the original density of material in the protoplanetary nebula, and also upon the specific accretion mechanisms applicable in such a dynamically quiet region; thus an answer cannot be found by using celestial mechanics only. The existence of such an unobserved population can be constrained by estimating the observational completeness and biases, which is always difficult. Trujillo et al. (2001) and Allen et al. (2001) give plausible arguments suggesting that the population beyond the 1/2 resonance with Neptune should be either less dense or consists of smaller objects; they could not prove that this region is empty.

On the contrary, the question of the population of the 1/2 Neptune resonance can be addressed by studying the stability of the orbits in that region. If the orbits inside the resonance are unstable over the age of the solar system, or maybe stable only inside a small libration island, then the population has to be depleted, even if the primordial population was extending with a high number density to the 1/2 resonance and beyond.

The problem remains open because of two opposite arguments which could be used. The dissipative origin of the Pluto group at the 2/3 resonance (Malhotra 1995) would imply that a group should have originally formed at the 1/2 resonance. On the other hand it has been known since Message (1970) that the periodic orbit at the 1/2 resonance bifurcates into an unstable symmetric periodic orbit and a stable asymmetric one (with double period). This implies that a small amplitude of libration is impossible. Morbidelli et al. (1995) and Gallardo & Ferraz-Mello (1997) have shown that alternation can occur between small amplitude libration around the asymmetric orbit and large amplitude libration; this would suggest that the long-term stability region, if any, is very small, and that the 1/2 resonance might correspond to a gap.

A recent paper by Nesvorný & Roig (2001) confirms that there is a large unstable region inside the 1/2 resonance with Neptune. It suggests that there is also a region stable for times of the order of the age of the solar system, but this occurs for eccentricities larger than the ones stable for the Plutinos (2/3 resonant objects). From the volume of the stable region they argue that the population inside the 1/2 resonance should be smaller by a factor 3 than the one of Plutinos. This would imply that the correct answer to our question is an intermediate one, with a modest group of high eccentricity 1/2 librators (similar to the small Griqua group in the 2/1 Jupiter resonance).

This problem could be completely solved by a better understanding of the dissipative phenomena in the early solar system, by a more complete theory of chaotic diffusion in the apparently ordered regions inside the mean motion resonances, and ultimately by observations. The proper elements we have computed indicate one example of a 1/2 librator, 2000 QL₂₅₁; two other cases with larger eccentricity are discussed in Nesvorný & Roig (2001). This sample is too small to draw any conclusions.

Proper element catalogs and asteroid families

1 Introduction

2 The AstDys online information system

2.1 Proper element catalogs

2.2 Proper element catalogs update

3 New insights on the inner asteroid belt

3.1 The Vesta family

3.2 The Phocaea region

4 Trans-Neptunian objects

4.1 The two belts

4.2 Resonant and non resonant populations

References