A&A 403, 709-714 (2003)
DOI: 10.1051/0004-6361:20030412
T. Rauch1,2
1 - Dr.-Remeis-Sternwarte, Sternwartstraße 7, 96049 Bamberg, Germany
2 -
Institut für Astronomie und Astrophysik, Abteilung Astronomie, Sand 1, 72076 Tübingen, Germany
Received 18 December 2002 / Accepted 11 March 2003
Abstract
The precise analysis of properties of planetary nebulae is strongly dependent
on good models for the stellar ionizing spectrum. Observations
in the UV - X-ray wavelength range
as well as NLTE
model atmosphere calculations of spectra of their exciting stars have shown
that neither blackbody fluxes nor "standard'' NLTE atmosphere models which
are composed out of hydrogen and helium only are good approximations. Strong
differences between synthetic spectra from these compared to observed spectra
at energies higher than 54 eV (He II ground state) can be ascribed to
the neglect of metal-line blanketing.
Realistic modeling of the emergent fluxes of hot stars in the UV - X-ray wavelength range requires metal-line blanketed NLTE model atmospheres which include all elements from hydrogen up to the iron-group. For this purpose, we present a grid (solar and halo abundance ratios) of metal-line blanketed NLTE model atmosphere fluxes which covers the parameter range of central stars of planetary nebulae.
Key words: planetary nebulae: general - stars: atmospheres - stars: early-type - stars: general - ultraviolet: stars
Post-AGB stars display the hottest stage of stellar evolution just before they enter the white dwarf cooling sequence. Effective temperatures up to 180 kK have been determined (e.g. Werner et al. 1997) by means of spectral analyses based on NLTE (non local thermodynamic equilibrium) model atmosphere techniques.
A sufficient condition for the use of LTE models in spectral analyses is,
that the collisional rates between atomic states are much larger
than the corresponding radiative rates (cf. Kudritzki & Hummer 1990).
This is e.g. fulfilled in the case of "cool'' (
![]() )
DA white dwarfs (Napiwotzki 1997). However, there are always NLTE effects in any
star which are easily detectable if high-resolution high-S/N spectra, especially of
the high energy wavelength range (UV, EUV, X-ray), are evaluated (e.g. Rauch
1997 and references therein) and these effects are particularly important for
hot stars like e.g. central stars of planetary nebulae (CSPN).
)
DA white dwarfs (Napiwotzki 1997). However, there are always NLTE effects in any
star which are easily detectable if high-resolution high-S/N spectra, especially of
the high energy wavelength range (UV, EUV, X-ray), are evaluated (e.g. Rauch
1997 and references therein) and these effects are particularly important for
hot stars like e.g. central stars of planetary nebulae (CSPN).
Observations in the UV - X-ray wavelength range have shown that this region is generally dominated by metal opacities. Since the flux maxima of hot stars lie in the EUV/X-ray wavelength (Fig. 1), and the flux in this region is crucial to the ionization of ambient matter, e.g. a surrounding planetary nebulae (PN), the employment of realistic fluxes calculated from fully line-blanketed NLTE model atmospheres as ionizing spectra in photoionization models is very important. However, blackbody fluxes are still often in use.
In the early 80's of the last century, the calculation of NLTE models was rudimental and hampered by the existing insufficient numerical methods and computational capacity (cf. Rauch 1997). Following Pottasch et al. (1978), who has shown that, based on intermediate band photometry within 1500-3300 Å, some CSPN have their radiation well represented by blackbodies (and others not so well), Kaler (1983) addressed that the major problem in PN analyses is the model selection. He invoked then that a blackbody has at least the virtue of simplicity.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[clip]{h4184_01.eps}} \end{figure}](/articles/aa/full/2003/20/aah4184/Timg11.gif) |
Figure 1:
Top: comparison of NLTE model atmosphere fluxes
(
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4184_02.eps}} \end{figure}](/articles/aa/full/2003/20/aah4184/Timg14.gif) |
Figure 2:
Comparison of NLTE model atmosphere fluxes (
|
| Open with DEXTER | |
The implementation of the "accelerated lambda iteration'' (ALI) technique
in the NLTE model-atmosphere codes (Werner 1986)
provided an efficient method to calculate realistic synthetic spectra of hot stars.
However, at that time it had been impossible to calculate extensive grids of
fully line-blanketed NLTE models due to the lack of reliable atomic data
(cf. Rauch 2003). Thus,
Kwok (1994) repeated Kaler's (1983) statement, that due to the variety of CSPN parameters, the
blackbody assumption is probably not worse than any other specific set of
models. In order to demonstrate the strong deviations at energies higher than 13.6 eV and 54.4 eV
(H I and He II ground state thresholds, respectively),
we show in Fig. 1 a comparison of blackbody fluxes to NLTE model atmosphere fluxes.
The weaknesses of a blackbody are obvious. Even in a H+He model with
![]() ,
,
![]() ,
and
a solar He/H ratio, the model flux at energies higher and lower than the He II ground state
cannot be matched simultaneously with one blackbody flux. Instead, blackbody fluxes with
90 kK and 130 kK are needed, respectively. At higher energies (
,
and
a solar He/H ratio, the model flux at energies higher and lower than the He II ground state
cannot be matched simultaneously with one blackbody flux. Instead, blackbody fluxes with
90 kK and 130 kK are needed, respectively. At higher energies (
![]() ), the situation gets
even worse.
), the situation gets
even worse.
NLTE model atmosphere fluxes have been successfully used, e.g. by Rauch et al. (1994, 1996) for the construction of consistent models of PN and CSPN in the cases of the PNe K 1-27 and LoTr 4. This approach - consistent models of PN and CSPN - appears to be a promising way to improve PN analyses.
Recently, Armsdorfer et al. (2002) selected the spatially resolved, round
PN NGC 2438 as a test example to check for effects of CSPN models on
PN shell modeling. For their study they used the grid parameters
![]() and
and
![]() which are closest to the result of Rauch et al. (1999,
which are closest to the result of Rauch et al. (1999,
![]() ,
,
![]() )
from spectral analysis of the CSPN of NGC 2438.
They found that the use of a blackbody as ionizing source leads e.g. to an underestimation of the
[O III]
)
from spectral analysis of the CSPN of NGC 2438.
They found that the use of a blackbody as ionizing source leads e.g. to an underestimation of the
[O III]
![]() Å line and an overestimation of the
He II
Å line and an overestimation of the
He II
![]() Å line strength and, hence, an overestimation of the CSPN
temperature, compared to the use of a model from the H-Ca grid (Sect. 1).
Å line strength and, hence, an overestimation of the CSPN
temperature, compared to the use of a model from the H-Ca grid (Sect. 1).
Rauch (1997) has investigated in detail on the impact of light metals
(Li-Ca) on NLTE model atmospheres of compact hot stars (see this paper for a more
detailed description of advances in NLTE calculations and the consideration of
metal opacities).
He found that CNO opacities reduce the flux strongly at energies higher than
the oxygen absorption edges (Fig. 1) while the opacities of light metal reduce
the flux even more, but at higher energies.
Rauch concluded that the metal opacities have a great influence
on the structure of model atmospheres. For the calculation of realistic
emergent fluxes in the EUV and X-ray range, the consideration of metals is
indispensable. Consequently, a first grid of models which are composed out of
all elements from hydrogen to calcium had been calculated with solar
([X]![]() =
[Y] = [Z] = 0) and
halo (
[X] = [Y] = 0, [Z] = -1) abundance ratios.
This allows to interpolate or extrapolate slightly in the metal abundances [Z].
The emergent fluxes are available in tabular form at http://astro.uni-tuebingen.de/~rauch.
=
[Y] = [Z] = 0) and
halo (
[X] = [Y] = 0, [Z] = -1) abundance ratios.
This allows to interpolate or extrapolate slightly in the metal abundances [Z].
The emergent fluxes are available in tabular form at http://astro.uni-tuebingen.de/~rauch.
The influence of the iron-group elements was demonstrated e.g. by Dreizler & Werner (1993), Lanz & Hubeny (1995), and Deetjen et al. (1999). Thus, parallel to the calculation of the H-Ca grid, test calculations have been performed in order to check the impact of the iron-group opacities (Rauch 2000; Rauch & Deetjen 2001; Rauch 2002). The consideration has an influence on the atmospheric structure and thus, also on the strengths of the absorption edges of light metals. Since significant changes in the flux level in the UV - X-ray region occur (Fig. 2), the iron-group opacities should not be neglected. Thus, a second grid with all elements from hydrogen up to the iron group has been calculated. This is described in the following.
Our NLTE models (Werner 1986, 1989; Werner & Dreizler 1999; Werner et al. 2003) are plane-parallel and in hydrostatic and radiative equilibrium. Hence, our models neglect wind effect onto the spectrum, which can be significant close to the Eddington limit (Gabler et al. 1989).
All elements from hydrogen to the iron-group elements can be considered
simultaneously. More than 300 levels (limited by numerical accuracy in the
used code-version) can be treated in NLTE with more than 1000 line
transitions calculated in detail. Millions of lines of the iron-group elements
tabulated in Kurucz (1996) and data from the Opacity Project (Seaton et al.
1994) are accounted for using a statistical approach and an opacity sampling
method (Deetjen 1999, http://astro.uni-tuebingen.de/~deetjen).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4184_03.eps}} \end{figure}](/articles/aa/full/2003/20/aah4184/Timg22.gif) |
Figure 3:
Parameters of available NLTE model atmosphere fluxes.
The H-Ni models are limited to
|
| Open with DEXTER | |
For the construction of the model atoms used in our calculations, we follow Rauch (1997). H, He, C, N, O, and Ne are represented by small model atoms, the other species are modeled to fit into the capacity limit of the code. As a consequence, many of the ions of F, Na - K, (Table 1) are too small to include radiative transitions, not even the resonance lines. We performed some test calculations with larger model ions for selected atoms in order to include at least all resonance lines of these ions. We found that these lines are very weak, so they do not have any significant influence on the atmospheric structure. Since our aim is not a precise spectral analysis of a given star but the calculation of emergent fluxes as ionizing spectra, this is a good approximation.
In contrast to Rauch (1997), Ca is not treated as a single species but
combined with the iron-group elements into a generic model atom in order to
consider all Ca lines given by Kurucz (1996). Within the generic model atom,
Ca - Ni are represented with solar abundance ratios. Depending of
![]() ,
the
model atoms have individually been adjusted due to the dominant ionization
stages. The statistics of representative model atoms are summarized in
Table 1. For a more detailed description of the used atomic data and the
consideration of the iron-group elements, see Rauch & Deetjen (2003).
,
the
model atoms have individually been adjusted due to the dominant ionization
stages. The statistics of representative model atoms are summarized in
Table 1. For a more detailed description of the used atomic data and the
consideration of the iron-group elements, see Rauch & Deetjen (2003).
We calculated a grid of models within
![]() and
and
![]() (Fig. 3), with solar and halo abundances (Fig. 4). We use
(Fig. 3), with solar and halo abundances (Fig. 4). We use
![]() for the convergence criterion
(
for the convergence criterion
(
![]() is the Eddington flux). If this is closer than 2% to the
target
is the Eddington flux). If this is closer than 2% to the
target
![]() ,
the model calculation is stopped in order to stay within a
reasonable cpu time on the CRAY computers. We mention that it may take about
one day to calculate a single model.
,
the model calculation is stopped in order to stay within a
reasonable cpu time on the CRAY computers. We mention that it may take about
one day to calculate a single model.
Table 1:
Statistics of model atoms used in the calculation
of the
![]() ,
,
![]() models. NLTE is the number of levels
treated in NLTE, RBB
(radiative bound-bound)
is the number of line transitions.
495 additional levels are treated in LTE.
models. NLTE is the number of levels
treated in NLTE, RBB
(radiative bound-bound)
is the number of line transitions.
495 additional levels are treated in LTE.
Table 1: Continued. Numbers in brackets denote individual levels andlines used in the statistical NLTE line-blanketing approach for theelements Ca - Ni.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{h4184_04.eps}} \end{figure}](/articles/aa/full/2003/20/aah4184/Timg27.gif) |
Figure 4:
Comparison of NLTE model atmosphere fluxes (
|
| Open with DEXTER | |
Flux tables have subsequently been calculated within 5-2000 Å binned to
0.1 Å intervals.
![]() as well as the model's
as well as the model's
![]() and
and ![]() are given in the tables' headers (Table 2). These tables
are directly suited to be used with the photoionization code CLOUDY
(Ferland 2000,
http://www.pa.uky.edu/~gary/cloudy/, versions C96
Beta 4 and later). The complete flux tables, based on the frequency grids used
in the model calculations, are also available in case that a normalization to
a certain (e.g. V) magnitude is required.
are given in the tables' headers (Table 2). These tables
are directly suited to be used with the photoionization code CLOUDY
(Ferland 2000,
http://www.pa.uky.edu/~gary/cloudy/, versions C96
Beta 4 and later). The complete flux tables, based on the frequency grids used
in the model calculations, are also available in case that a normalization to
a certain (e.g. V) magnitude is required.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{h4184_05.eps} \end{figure}](/articles/aa/full/2003/20/aah4184/Timg31.gif) |
Figure 5:
Comparison of NLTE model atmosphere fluxes (
|
| Open with DEXTER | |
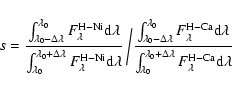 |
(1) |
A similar grid for hydrogen-deficient stars (Fig. 5) has been calculated. For this grid we selected the "typical'' abundance pattern (He:C:N:O = 33:50:2:15 by mass) of PG 1159 stars (Werner 2001). This allows to estimate abundance effects onto the emergent flux.
Table 2: Example header of a flux table.
Presently available NLTE model atmosphere codes have arrived at a very high level of sophistication (Mihalas 2003; Werner et al. 2003). The accelerated lambda iteration (ALI) method represents a powerful tool to calculate realistic metal-line blanketed atmospheres in a reasonable time, even on nowadays available PCs - these got such a tremendous number-crunching power in the last two years that they can now easily compete with CRAY and other (super)computers. The statistical approach which has been used to construct a generic model atom for all elements from Ca to Ni (Sect. 2) has been improved and can now be employed to construct model atoms for other light metals in order to consider all of their lines, provided by Kurucz (1996) and the Opacity Project (Seaton et al. 1994), in detail. Thus, there is no need to reflect on blackbodies or simple model atmospheres as ionizing sources for photoionization models.
To summarize, the use of metal-line blanketed NLTE model atmosphere fluxes, which consider at least the CNO opacities in detail, as ionizing spectra for photoionization models is highly recommended. The here presented fully metal-line blanketed NLTE model atmosphere fluxes which consider all elements from hydrogen up to the iron group are well suited for this purpose.
However, the user of these model atmosphere fluxes should be aware that they
should only be used in a PN analysis if the CSPN abundances are
in agreement with the model abundances. The use of fluxes from models
with solar abundance ratios will spoil any PN analysis if the CSPN is
hydrogen deficient because the flux shortwards of the He II ground
state edge can be different by about one dex (Fig. 5).
A preceding spectral analysis of the CSPN which yields
![]() ,
,
![]() ,
and
abundance ratios and an individually
calculated small "grid'' of NLTE model atmosphere fluxes may improve a
subsequent PN analysis - and allows to construct consistent models
of PN and CSPN (Sect. 1).
This is also a prerequisite for reliable hydrodynamical models of the PN.
,
and
abundance ratios and an individually
calculated small "grid'' of NLTE model atmosphere fluxes may improve a
subsequent PN analysis - and allows to construct consistent models
of PN and CSPN (Sect. 1).
This is also a prerequisite for reliable hydrodynamical models of the PN.
Acknowledgements
I would like to thank Klaus Werner for many helpful discussions and careful reading of the manuscript, Jochen L. Deetjen for his continuous support to calculate the iron-group opacities, the Rechenzentrum der Universität Kiel, where the model atmosphere computations were performed on CRAY computers from 1997 to 2002, for generously awarding us the necessary computational time, and my colleagues from the Institut für Theoretische Physik und Astrophysik, Abteilung Astrophysik, at Kiel University for their patience and cooperation when the hugest batch classes on the CRAYs had been blocked for a long time. This research was supported by the DLR under grants 50 OR 9705 5 and 50 OR 0201.