A&A 403, 449-462 (2003)
DOI: 10.1051/0004-6361:20030164
L. Angeletti - P. Giannone
Dipartimento di Fisica, Università "La Sapienza'', Piazzale A. Moro, 5 00185 Roma, Italy
Received 27 March 2002 / Accepted 30 January 2003
Abstract
Abundance gradients predicted by dissipative models of galaxy formation
are studied with the aid of mass models of spherical galaxies obeying the
Sersic R1/n law in projection. The link between metallicity and stellar binding
energies and angular momenta is derived from the "concentration model'' by
Lynden-Bell (1975) with the addition of a terminal wind and an age spread among the
stellar populations of individual ellipticals.
By using the calibration of the Mg2 index as a function of metallicity
and age from Single-burst Stellar Populations models, the radial profiles of Mg2
are computed for a variety of
models to illustrate the general predictions of the present approach.
We also matched the observed radial profiles of Mg2 in a sample of 11
ellipticals.
We find that observations are reproduced reasonably well in our adopted
approximation and require a considerable degree of dissipation and a metal
yield above the solar value. A terminal wind or an age spread make it easier to fit the Mg2 profiles of
the ellipticals with shallow Mg2 profiles in the innermost regions. However,
model results (with or without an age spread) show that the exact determination of the
free parameters suffers from degeneracy of their effects. Moreover,
model results also suffer from the poorly known effects of non-solar
abundance ratios on index Mg2. Other spectral indices, besides Mg2, and broad-band
colours observed in elliptical galaxies can be examined in the same way with the present
scheme; their study is postponed to a further investigation.
Key words: galaxies: elliptical and lenticular
Colour and line-strength gradients observed across elliptical galaxies (Es) are consistent with the hypothesis that such gradients stem from abundance gradients that developed when Es formed (Franx et al. 1989; Peletier et al. 1990; Davies et al. 1993; Carollo et al. 1993).
Two basic scenarios have been proposed so far for the formation of elliptical galaxies. According to the conventional view, all luminous ellipticals are coeval and old systems (Visvanathan & Sandage 1977; Bower et al. 1992) that formed through a monolithic dissipative collapse (Eggen et al. 1962; Larson 1974; Arimoto & Yoshii 1987), occurred early in the evolution of the Universe and completed at an epoch much smaller than the Hubble time. The alternative scenario proposes that the ellipticals formed through a lengthy hierarchical clustering of small objects into larger ones with an extended star formation over time (Cole et al. 1994; Baugh et al. 1996; Kauffmann 1996; Kauffmann & Charlot 1998).
Metallicity gradients in Es are predicted generally by dissipative models of galaxy formation (Larson 1976; Carlberg 1984; Theis et al. 1992). An alternative explanation (Franx & Illingworth 1990) suggests that, across an E galaxy, the star formation proceeds near the centre for a time longer than farther out, according to the local escape velocity (see also Martinelli 1998). However, the behaviour of observed indices varies so widely from one galaxy to another that it is not clear whether the explanations mentioned above can account for all individual differences (Pagel 1997).
In this paper we follow the conventional view by adopting the dissipative model of galaxy formation in the simplified analytical version by Lynden-Bell (1975, hereafter LB). The "Concentration Model'' (hereafter CM) by LB provides an analytical formula for the star-metallicity distribution, related explicitly to the degree of dissipation and to the metal yield, thus making it easier to explore the corresponding two-parameter space.
In adopting the conventional view, we have to consider the evidence found
by various authors (González 1993; Tantalo et al. 1998;
Jørgensen 1999;
Kuntschner 2000; Trager et al. 2000a,b;
Vazdekis et al. 2001; Terlevich &
Forbes 2002) of an age spread among the ellipticals. In particular, the
central regions of most Fornax and Virgo ellipticals seem old with an
age spread of a few Gyr (Kuntschner 2000; see also Trager et al. 2000a,b,
hereafter TFWG1 and TFWG2, respectively),
whereas the innermost regions of the field
or
ellipticals in small groups show a wide age spread (from 1.5 to 18 Gyr),
suggesting an environmental effect (TFWG1-2). Furthermore, age gradients
are also found within individual ellipticals (TFWG1), with ages getting
older by 25% on the average, when going from the regions within
![]() (
(![]() being the effective radius) to the outer regions within
being the effective radius) to the outer regions within
![]() .
.
We follow TFWG2, who favour a variant of the conventional view by suggesting a minor contamination of the base old population in ellipticals by younger stars (see also Kodama & Arimoto 1997, 1998) that formed from well-mixed pre-enriched gas rather than unmixed low-metallicity gas from an accreting object. The CM, as formulated by LB, is compatible with an age spread among ellipticals, but it does not take into account the age spread among the stellar populations, that formed within each elliptical galaxy successively. We shall show that such an age dependence, together with the suggestion by TFWG2, can be added easily to the analytical formulation of the CM.
The CM is used here together with the spherical R1/4-mass model of elliptical galaxies derived, by deprojection (Young 1976), from the surface-brightness profile obeying the R1/4 law (de Vaucouleurs 1948). However, we shall also consider some cases of the R1/n-mass models (n=2 to 8) obtained by deprojecting (Ciotti 1991) the generalized R1/n law (Sersic 1968). Minor modifications to CM, as formulated by LB, are introduced to include a terminal wind and an age spread, and to adapt CM to the R1/n model. In this paper we describe our approach and, as a first application to elliptical galaxies, we present the computation of the integrated absorption-line index Mg2 and a comparison of the model results with the observed radial profiles of Mg2 in 11 elliptical galaxies.
The paper is arranged as follows: Sect. 2, after reviewing the basic assumptions of CM, describes its adjustment to the R1/n model and the inclusion of a terminal wind and an age spread; Sect. 3 presents the data for Single-burst Stellar Populations used in the paper, and the model predictions concerning the Mg2 index; Sect. 4 compares the model results to the Mg2 radial profiles in a sample of 11 elliptical galaxies; Sect. 5 gives a final discussion with our conclusions. The derivation of the metallicity-distribution function is given in Appendix A for the general case and in Appendix B for some specific cases of CM with a terminal wind. Technical details on how the CM is adjusted to the R1/n model are assembled in Appendix C.
In this section we first review the basic assumptions of CM, succinctly referred to in LB, and then present some minor adjustments required by the R1/n model, the introduction of a terminal wind, and the consideration of an age spread among the stellar populations.
We limit ourselves to a spherical galaxy of total mass M0 at the
initial time t0, and consisting of gas with uniform metallicity Z0. We denote by ![]() the final epoch when the star formation ceases, and
by G(t) the gas mass at the epoch t intermediate between t0 and
the final epoch when the star formation ceases, and
by G(t) the gas mass at the epoch t intermediate between t0 and ![]() .
Setting
.
Setting
![]() ,
the final total mass of the stellar component
(long-living stars and compact stellar remnants) is
,
the final total mass of the stellar component
(long-living stars and compact stellar remnants) is
![]() .
.
The mass distribution of the stellar component, in a gas-free and
steady-state galaxy after ![]() ,
is referred to a Lagrangian mass coordinate
m, in units of
,
is referred to a Lagrangian mass coordinate
m, in units of ![]() and varying from 0 at the centre to 1 in the
outermost zones. Metallicities of stars, in e.g. the mass shell m to
and varying from 0 at the centre to 1 in the
outermost zones. Metallicities of stars, in e.g. the mass shell m to
![]() ,
are inferred by going back to the time, before
,
are inferred by going back to the time, before ![]() ,
when those stars
formed. Therefore, the CM describes the mass distribution of the stellar
component at an epoch before
,
when those stars
formed. Therefore, the CM describes the mass distribution of the stellar
component at an epoch before ![]() by using the same mass coordinate m as adopted after
by using the same mass coordinate m as adopted after ![]() .
It is assumed that spherical surfaces
(onion-wise about one another) corresponding to
constant values of m were associated with
the first-generation stars that formed on them and were slowly moving with
the long-term average motions of such stars. Here we consider the case
.
It is assumed that spherical surfaces
(onion-wise about one another) corresponding to
constant values of m were associated with
the first-generation stars that formed on them and were slowly moving with
the long-term average motions of such stars. Here we consider the case
![]() so that
so that
![]() (as in LB), deferring the case
(as in LB), deferring the case
![]() to Appendix A.
to Appendix A.
The gas is assumed to be well-mixed and its uniform metallicity Z
is evaluated according to the Simple Model (Pagel & Patchett 1975) as
| (1) |
| (2) |
For the stars formed inside ![]() ,
the CM makes the plausible assumptions that:
i) the star formation is distributed radially like the stars born before
,
the CM makes the plausible assumptions that:
i) the star formation is distributed radially like the stars born before ![]() (Appendix A), ii) the stars that form at
(Appendix A), ii) the stars that form at ![]() ,
from inelastic
collisions between clouds confined within
,
from inelastic
collisions between clouds confined within ![]() ,
have the orbital apocentres
within
,
have the orbital apocentres
within ![]() .
From item ii) one gets that the mass of the stars within
m, having metallicities not larger than
.
From item ii) one gets that the mass of the stars within
m, having metallicities not larger than ![]() ,
and born until
,
and born until ![]() ,
is
,
is
| (3) |
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{h3573f1.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg56.gif) |
Figure 1:
a) Functions s1(m) and s2(m), of the isotropic R1/4
model, versus the
mass coordinate m, and function m-m1/c (for the case c=0.7,
dashed curve), see text. b) As in panel a) but for the anisotropic
R1/4 model with anisotropy radius
|
| Open with DEXTER | |
Let us now consider the final distribution of the stellar component. The stars with
apocentres inside ![]() (partially formed at the time
(partially formed at the time ![]() )
are all confined
within the sphere
)
are all confined
within the sphere ![]() and their cumulative mass will be denoted by
and their cumulative mass will be denoted by
![]() .
The stars with apocentres outside
.
The stars with apocentres outside ![]() (completely formed at the
time
(completely formed at the
time ![]() )
are found within
)
are found within ![]() and outside
and outside ![]() and their cumulative
masses will be indicated by
and their cumulative
masses will be indicated by
![]() and
and
![]() ,
respectively.
,
respectively.
Since
![]() contains mass
contains mass
![]() ,
from Eq. (3) one should have
,
from Eq. (3) one should have
![]() :
an inequality not unconditionally true,
e.g. for the R1/n model (see Fig. 1 for the case n=4). To satisfy the condition
:
an inequality not unconditionally true,
e.g. for the R1/n model (see Fig. 1 for the case n=4). To satisfy the condition
![]() ,
one can define
,
one can define ![]() implicitly by the ansatz
implicitly by the ansatz
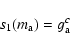 |
(4) |
In order to include a terminal wind, which removes the gas mass
![]() from
the sphere
from
the sphere
![]() ,
we expand Eq. (4) into the ansatz
,
we expand Eq. (4) into the ansatz
![\begin{displaymath}%
s_1(m_{\rm a}) = s_1(m_{\rm w}) + \left[1 - s_1(m_{\rm w})\right]\left({{g_{\rm a}-g_{\rm w}}\over {1-g_{\rm w}}}\right)^c
\end{displaymath}](/articles/aa/full/2003/20/aah3573/img69.gif) |
(5) |
The cumulative mass
![]() and the inferred metallicity-distribution function MDF,
both ensuing from Eq. (5), are as in LB for
and the inferred metallicity-distribution function MDF,
both ensuing from Eq. (5), are as in LB for
![]() ;
their derivation
for
;
their derivation
for
![]() is given in Appendix A.
The analytical expression of
is given in Appendix A.
The analytical expression of
![]() is explicitly given in Appendix B for some cases of CM with a terminal wind as considered in Sect. 3.3. Finally, Appendix C explains how function MDF is adapted to the R1/n-mass model by transferring
the dependence of MDF on the orbital apocentre and mass coordinate m into a
dependence on the binding energy and angular momentum.
is explicitly given in Appendix B for some cases of CM with a terminal wind as considered in Sect. 3.3. Finally, Appendix C explains how function MDF is adapted to the R1/n-mass model by transferring
the dependence of MDF on the orbital apocentre and mass coordinate m into a
dependence on the binding energy and angular momentum.
The CM implies that the stellar populations within an elliptical have ages
![]() (where
(where
![]() corresponds to the present epoch)
ranging from the initial age
corresponds to the present epoch)
ranging from the initial age
![]() to the final age
to the final age
![]() .
The age dependence can be added to the CM by
combining the Simple Model with the one-zone approach of chemical evolution
(Pagel 1997) and the Schmidt's law (Schmidt 1959) for the star formation rate
(Pagel & Patchett 1975), thus obtaining
.
The age dependence can be added to the CM by
combining the Simple Model with the one-zone approach of chemical evolution
(Pagel 1997) and the Schmidt's law (Schmidt 1959) for the star formation rate
(Pagel & Patchett 1975), thus obtaining
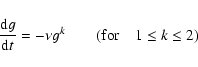 |
(6) |
| (7) |
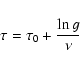 |
(8) |
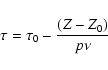 |
(9) |
An obvious improvement of our procedure would be the one-zone model developed by various authors (Arimoto & Yoshii 1987; Matteucci & Tornambé 1987; Bressan et al. 1994; Tantalo et al. 1996; Vazdekis et al. 1996) where the instantaneous recycling approximation of the Simple Model is replaced by realistic stellar lifetimes, or the hydrodynamical approach (Larson 1976; Theis et al. 1992) where the one-zone approximation is superseded by a star-formation rate that depends closely on the local gas density.
To see whether abundance gradients observed in ellipticals can be matched by the
metallicity gradients predicted by the Concentration Model, we employ
the spectral index Mg2 of the Lick/IDS system (Burstein et al. 1984;
Worthey et al. 1994; Trager et al. 1998), since it is one of the most widely
used of the Lick indices and a large body of accurate observations is
available (see Trager et al. 1998 and references therein).
In the following we describe our procedure to compute the radial profiles of
Mg2, for various choices of the concentration index c and the
metal yield p, and compare them to observations.
The initial abundance Z0=0 and the solar metallicity
![]() are adopted throughout the paper.
are adopted throughout the paper.
Mg2 is the deficit of flux, expressed in magnitudes at the Mg b + Mg H feature, compared with a nominal continuum (pseudocontinuum)
determined by interpolation from neighbouring regions. Mg2 is very sensitive
to the Mg abundance, but also depends on several other chemical species (see
Tripicco & Bell 1995). We shall refer to the index Mg2 for a Single-burst Stellar Population
(SSP) of given Z and age ![]() ,
which is derived from various sources, as
described e.g. in Worthey (1994; see also Charlot et al. 1996).
,
which is derived from various sources, as
described e.g. in Worthey (1994; see also Charlot et al. 1996).
The SSP index Mg2 is used here to compute the "integrated''
index Mg2 for the stars that are seen in projection along a line-of-sight
or within a circular aperture. Such stars span a range in metallicity
Z and age ![]() as predicted by the CM and the R1/n-mass model. Our
integrated index Mg2 is then compared to the Mg2 observed in ellipticals.
Technical details on the computation of the integrated index Mg2 from
availaible SSP data are given in Sect. 3.2
and in Appendix C.
as predicted by the CM and the R1/n-mass model. Our
integrated index Mg2 is then compared to the Mg2 observed in ellipticals.
Technical details on the computation of the integrated index Mg2 from
availaible SSP data are given in Sect. 3.2
and in Appendix C.
We need SSP libraries providing Mg2 and luminosities LB and LV in
the B and V photometric bands, respectively, at a fair grid of Z
values ranging from ![]() up to at least Z=0.05 and possibly
up to at least Z=0.05 and possibly
![]() ,
in order to make interpolations and/or extrapolations as smooth and reliable
as possible. We found three such libraries: i) Bressan et al. (1996, hereafter
BCT) and Tantalo et al. (1996), ii) Buzzoni et al. (1992, hereafter BGM) and
Buzzoni (1989 and 1995), and iii) Worthey (1994, hereafter W94). The data from
BGM include a red-horizontal-branch morphology and a mass-loss
parameter equal to 0.3. The behaviour of index Mg2 from BCT, BGM, and W94
is shown in Fig. 2.
,
in order to make interpolations and/or extrapolations as smooth and reliable
as possible. We found three such libraries: i) Bressan et al. (1996, hereafter
BCT) and Tantalo et al. (1996), ii) Buzzoni et al. (1992, hereafter BGM) and
Buzzoni (1989 and 1995), and iii) Worthey (1994, hereafter W94). The data from
BGM include a red-horizontal-branch morphology and a mass-loss
parameter equal to 0.3. The behaviour of index Mg2 from BCT, BGM, and W94
is shown in Fig. 2.
The mentioned datasets use 6 or 7 SSP metallicities from
![]() up
to Z=0.0534 (W94) or 0.1(BCT and BGM), and adopt a power-law initial mass
function (IMF) with the mass exponent x=2.35 (Salpeter's value).
Furthermore, the data we derive from them refer to the "luminous mass'' only,
i.e. long-living stars with initial masses m (in units of
up
to Z=0.0534 (W94) or 0.1(BCT and BGM), and adopt a power-law initial mass
function (IMF) with the mass exponent x=2.35 (Salpeter's value).
Furthermore, the data we derive from them refer to the "luminous mass'' only,
i.e. long-living stars with initial masses m (in units of ![]() )
in
the range
)
in
the range
![]() ,
where
,
where
![]() (BGM and W94) or 0.15
(BCT) and
(BGM and W94) or 0.15
(BCT) and
![]() is the initial mass of a star at the red giant tip.
is the initial mass of a star at the red giant tip.
![]() was taken from Bertelli et al. (1994) for the BCT data, and was
approximated by the turn-off mass
was taken from Bertelli et al. (1994) for the BCT data, and was
approximated by the turn-off mass
![]() ,
as given in Buzzoni (1989 and 1995),
for the BGM data.
,
as given in Buzzoni (1989 and 1995),
for the BGM data.
To obtain the SSP data per unit mass, we assumed m in the range
![]() and evaluated the remnant masses
and evaluated the remnant masses
![]() (in
(in ![]() )
according to the rule:
)
according to the rule:
![]() for
for
![]() and
and
![]() for
for
![]() (Renzini & Ciotti 1993).
The mass lost by stars during the first ascent along the red-giant
branch was neglected in evaluating the mass of the luminous component.
(Renzini & Ciotti 1993).
The mass lost by stars during the first ascent along the red-giant
branch was neglected in evaluating the mass of the luminous component.
BGM include metallicities up to Z=0.1 at the age of 15 Gyr, and BCT
at the ages 1 to 13 Gyr; we shall use the BGM and BCT libraries at the
ages just mentioned. W94 considers the ages 1.5 to 17 Gyr
for
![]() ,
and 8 to 17 Gyr for Z<0.01, as we shall do in the present
paper when using the W94 library. It should be noted (see Fig. 2) that the
time behaviour of Mg2, as provided by W94, is monotonic at all Z, whereas
Mg2 at Z=0.1, as given by BCT, has two minima at 1 and 7 Gyr, and two
equal maxima at 5 and 13 Gyr.
,
and 8 to 17 Gyr for Z<0.01, as we shall do in the present
paper when using the W94 library. It should be noted (see Fig. 2) that the
time behaviour of Mg2, as provided by W94, is monotonic at all Z, whereas
Mg2 at Z=0.1, as given by BCT, has two minima at 1 and 7 Gyr, and two
equal maxima at 5 and 13 Gyr.
The BCT, BGM, and W94 libraries adopt solar abundance ratios, whereas
various authors found
![]() in giant ellipticals (Worthey et al.
1992; González 1993; Kuntschner 2000, TFWG1). As emphasized by TFWG1 (see
also Weiss et al. 1995; Tantalo et al. 1998), that finding
indicates an underabundance of iron (and related
elements), rather than an overabundance of magnesium (and related elements),
with respect to the solar values. Furthermore, TFWG1 apply previous results
by Tripicco & Bell (1995) to show that, for
fixed Z and with magnesium at the solar ratio,
the underabundance of the iron-peak elements
enhances the SSP index Mg2 with respect to the case with
in giant ellipticals (Worthey et al.
1992; González 1993; Kuntschner 2000, TFWG1). As emphasized by TFWG1 (see
also Weiss et al. 1995; Tantalo et al. 1998), that finding
indicates an underabundance of iron (and related
elements), rather than an overabundance of magnesium (and related elements),
with respect to the solar values. Furthermore, TFWG1 apply previous results
by Tripicco & Bell (1995) to show that, for
fixed Z and with magnesium at the solar ratio,
the underabundance of the iron-peak elements
enhances the SSP index Mg2 with respect to the case with
![]() ,
e.g.
by about 9% for
,
e.g.
by about 9% for
![]() ,
,
![]() ,
and an age of 12 Gyr (see TFWG1,
their Table 5).
,
and an age of 12 Gyr (see TFWG1,
their Table 5).
A suitable set of SSP indices for non-solar abundance ratios, to be derived from new stellar evolutionary isocrones and new prescriptions like those by Tripicco & Bell (1995), is as yet unavailable. Therefore, we were forced to use the index Mg2 as provided by the adopted SSP libraries. However, in the following Sect. 3.3 we shall discuss briefly the possible impact on our results by non-solar abundance ratios.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f2.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg110.gif) |
Figure 2: SSP index Mg2 versus metal abundance Z, for the Salpeter's mass exponent x=2.35: i) from Bressan et al. (1996) (solid curves) for the ages of 5, 9, and 13 Gyr (from bottom to top); ii) from Buzzoni et al. (1992) for the age of 15 Gyr (dashed curve); iii) from Worthey (1994, dotted-dashed curves) for the ages of 8, 12, and 17 Gyr (from bottom to top); iv) from Vazdekis et al. (1996, filled circles) and Vazdekis (1999, filled squares), for the age of 13 Gyr, for the sake of comparison. The thick mark on the abscissae indicates the solar metallicity. |
| Open with DEXTER | |
The radial profile of index Mg2 depends on the age of stellar
populations and model parameters, such as the concentration index c,
the metal yield p, the exponent n of the R1/n law, and the
anisotropy radius ![]() .
Indeed, the R1/n models can have an isotropic, or
anisotropic, velocity dispersion, as explained in Appendix C.
The anisotropic models used in this paper
(the Osipkov-Merritt models) are specified by the anisotropy radius
.
Indeed, the R1/n models can have an isotropic, or
anisotropic, velocity dispersion, as explained in Appendix C.
The anisotropic models used in this paper
(the Osipkov-Merritt models) are specified by the anisotropy radius ![]() (
(
![]() ); for them we adopt
); for them we adopt
![]() ,
since those with
,
since those with
![]() are precluded by stability considerations (Ciotti & Lanzoni 1997) and
the models with
are precluded by stability considerations (Ciotti & Lanzoni 1997) and
the models with
![]() are superseded by those with
are superseded by those with
![]() (i.e. by isotropic
models).
(i.e. by isotropic
models).
The effect of an age spread among the stellar populations is shown
in Figs. 3 and 4 for c=0.75 and
![]() ,
and with reference to the
isotropic R1/4 model and the W94 library. The radial distance R is
given in units of the effective radius
,
and with reference to the
isotropic R1/4 model and the W94 library. The radial distance R is
given in units of the effective radius
![]() ,
the radius of a centered
circular aperture containing half of the total B light. The initial age
,
the radius of a centered
circular aperture containing half of the total B light. The initial age
![]() is 13 Gyr for all the profiles. In Fig. 3a the final age
is 13 Gyr for all the profiles. In Fig. 3a the final age
![]() ,
corresponding to the final
,
corresponding to the final
![]() ,
ranges from 11 to 2 Gyr, and the age
spread between
,
ranges from 11 to 2 Gyr, and the age
spread between ![]() and
and
![]() is that predicted by the Schmidt's law
with k=1 (see Eqs. (6) to (9)). The Mg2 profile with no age spread
(
is that predicted by the Schmidt's law
with k=1 (see Eqs. (6) to (9)). The Mg2 profile with no age spread
(
![]() Gyr) is also plotted for the sake of comparison.
Gyr) is also plotted for the sake of comparison.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f3.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg117.gif) |
Figure 3:
The Mg2 profile from the Worthey (1994) library and for the isotropic
R1/4 model with an age spread among the stellar populations (see text).
The projected radial distance R is in units of the effective radius
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f4.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg118.gif) |
Figure 4:
Mean ages |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{h3573f5.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg122.gif) |
Figure 5:
Mg2 profiles, for the isotropic R1/4 model, versus the
projected radial distance R in units of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{h3573f6.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg123.gif) |
Figure 6:
a) Radial profiles of Mg2 versus log
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f7.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg124.gif) |
Figure 7:
Mg2 profiles for the isotropic R1/4 model and with the
consideration of a terminal wind removing the gas mass
|
| Open with DEXTER | |
Figure 3a shows that the radial profile of Mg2 is influenced appreciably
by our adopted age spread only within
![]() ,
where the observations of
Mg2 in real ellipticals are usually disturbed by the seeing. In the region
outside
,
where the observations of
Mg2 in real ellipticals are usually disturbed by the seeing. In the region
outside
![]() ,
the age spread as formulated here has a negligible
effect on the observed Mg2. Furthermore, the mean luminosity-weighted age
within
,
the age spread as formulated here has a negligible
effect on the observed Mg2. Furthermore, the mean luminosity-weighted age
within
![]() is older than the age within
is older than the age within
![]() by 3%, 6%, 14%,
and 27%, when
by 3%, 6%, 14%,
and 27%, when
![]() ,
and 2 Gyr, respectively. Therefore, an age
increase by 25% from
,
and 2 Gyr, respectively. Therefore, an age
increase by 25% from
![]() out to the aperture radius
out to the aperture radius
![]() ,
according to TFWG1, is verified only when
,
according to TFWG1, is verified only when
![]() Gyr.
However, further options, like those suggested by TFWG2 and Kodama &
Arimoto (1997 and 1998), are conceivable: they imply (see Sect. 2.3) a main
episode of star formation, from
Gyr.
However, further options, like those suggested by TFWG2 and Kodama &
Arimoto (1997 and 1998), are conceivable: they imply (see Sect. 2.3) a main
episode of star formation, from
![]() Gyr to
Gyr to ![]() and involving the gas mass
1-g1, followed by a delayed minor episode occurring from
and involving the gas mass
1-g1, followed by a delayed minor episode occurring from ![]() to
to
![]() and involving the gas mass
and involving the gas mass
![]() .
.
Two of such alternatives are shown in Fig. 3b: they refer to ![]() Gyr,
Gyr, ![]() Gyr,
Gyr,
![]() Gyr, and g1=0.05 or 0.1. The
mean luminosity-weighted age within
Gyr, and g1=0.05 or 0.1. The
mean luminosity-weighted age within
![]() is older than the age within
is older than the age within
![]() by 27% and 38% when g1=0.05 and 0.1, respectively. Figure 3b
also displays the Mg2 profile at the age
by 27% and 38% when g1=0.05 and 0.1, respectively. Figure 3b
also displays the Mg2 profile at the age
![]() Gyr with no age
spread:
the comparison between the two kinds of options reveals that Mg2 is affected appreciably
only within
Gyr with no age
spread:
the comparison between the two kinds of options reveals that Mg2 is affected appreciably
only within
![]() ,
as for the profiles in Fig. 3a. The mean ages
,
as for the profiles in Fig. 3a. The mean ages
![]() of the stars,
weighted by the V luminosity and as a function of the aperture radius R,
are displayed in Fig. 4 for a model with
of the stars,
weighted by the V luminosity and as a function of the aperture radius R,
are displayed in Fig. 4 for a model with
![]() Gyr and a model with
Gyr and a model with ![]() Gyr,
Gyr, ![]() Gyr,
Gyr,
![]() Gyr, and g1=0.05.
Gyr, and g1=0.05.
In the following Figs. 5 to 7 we focus on the Mg2 profile at
![]() and, according to previous findings, we disregard any age
spread by assuming
and, according to previous findings, we disregard any age
spread by assuming
![]() .
Figure 5 refers to the Mg2 profile for
c=0.75 and the isotropic R1/4 model; panel a shows the
age-metallicity degeneracy of index Mg2 by using the W94 library: the
profile with
.
Figure 5 refers to the Mg2 profile for
c=0.75 and the isotropic R1/4 model; panel a shows the
age-metallicity degeneracy of index Mg2 by using the W94 library: the
profile with
![]() Gyr and
Gyr and
![]() is matched by the profile with
is matched by the profile with
![]() Gyr and
Gyr and
![]() ,
and similarly the profile with
,
and similarly the profile with
![]() Gyr and
Gyr and
![]() is matched by
the profile with
is matched by
the profile with
![]() Gyr and
Gyr and
![]() .
According to Eqs. (1) and (4), all the profiles in
Fig. 5 correspond to the same gradient of Z/p. By fitting an observed Mg2profile we can infer the underlying gradient of Z/p, but we cannot
determine p if the age is unknown.
.
According to Eqs. (1) and (4), all the profiles in
Fig. 5 correspond to the same gradient of Z/p. By fitting an observed Mg2profile we can infer the underlying gradient of Z/p, but we cannot
determine p if the age is unknown.
The profiles in Fig. 5a should change for
![]() ,
since Mg2 enhances
when iron is below the solar value (Sect. 2.3). On the other hand,
[Mg/Fe] appears to be constant within each elliptical, although it varies from
elliptical to elliptical (Worthey et al. 1992; Davies et al. 1993, TFWG1).
However, for a fixed
,
since Mg2 enhances
when iron is below the solar value (Sect. 2.3). On the other hand,
[Mg/Fe] appears to be constant within each elliptical, although it varies from
elliptical to elliptical (Worthey et al. 1992; Davies et al. 1993, TFWG1).
However, for a fixed
![]() the enhancement of the SSP index Mg2
depends on Z and age. TFWG1 only report a 9% increase for
the enhancement of the SSP index Mg2
depends on Z and age. TFWG1 only report a 9% increase for
![]() and the age of 12 Gyr. If the fractional enhancement of Mg2 varied mildly
with Z and age, then the profiles in Fig. 5a would be shifted upwards with
a minor change of their radial gradients.
and the age of 12 Gyr. If the fractional enhancement of Mg2 varied mildly
with Z and age, then the profiles in Fig. 5a would be shifted upwards with
a minor change of their radial gradients.
Our adopted SSP libraries are compared in Figs. 5b-c by using the
isotropic R1/4 model with c=0.75 and
![]() .
Figure 5b shows the
comparison between BGM and W94 at the age of 15 Gyr, and Fig. 5c presents the
comparison between BCT and W94 at the age of 13 Gyr. The largest central
values of Mg2 are those from the W94 library, owing to the extrapolation
of the SSP data for Z>0.053 (see Fig. 2). The flattest profile is that from
BGM, whereas the profiles from BCT and W94 have a comparable slope; such a
behaviour is related to the slope
.
Figure 5b shows the
comparison between BGM and W94 at the age of 15 Gyr, and Fig. 5c presents the
comparison between BCT and W94 at the age of 13 Gyr. The largest central
values of Mg2 are those from the W94 library, owing to the extrapolation
of the SSP data for Z>0.053 (see Fig. 2). The flattest profile is that from
BGM, whereas the profiles from BCT and W94 have a comparable slope; such a
behaviour is related to the slope
![]() of the SSP index
Mg2
versus Z (see Fig. 2).
of the SSP index
Mg2
versus Z (see Fig. 2).
We now use the BCT library, for the age of 13 Gyr, to show in Fig. 6 how
the Mg2 profile depends on parameters
![]() ,
and n. Figure 6a refers
to fixed
,
and n. Figure 6a refers
to fixed
![]() or
or
![]() ,
and a variable p; Fig. 6b
to fixed
,
and a variable p; Fig. 6b
to fixed
![]() or
or
![]() ,
and a variable c; and Fig. 6c
to a variable n with fixed
,
and a variable c; and Fig. 6c
to a variable n with fixed
![]() ,
and
,
and
![]() .
It is worth noting in panels a and b that the anisotropic models have Mg2
profiles flatter than those of the isotropic models.
.
It is worth noting in panels a and b that the anisotropic models have Mg2
profiles flatter than those of the isotropic models.
Finally, Fig. 7 displays some profiles obtained with the consideration
of a terminal wind removing the gas mass
![]() from the sphere
with
from the sphere
with
![]() (see Sect. 2.2). Here we use the isotropic R1/4 model,
the BCT library for the age of 13 Gyr, and the same metal yield
(see Sect. 2.2). Here we use the isotropic R1/4 model,
the BCT library for the age of 13 Gyr, and the same metal yield
![]() for all the profiles. One can now see that index Mg2
is weaker and its profile is flatter, especially in the central regions, than
in the absence of a terminal wind. However, such an effect is appreciable
only for
for all the profiles. One can now see that index Mg2
is weaker and its profile is flatter, especially in the central regions, than
in the absence of a terminal wind. However, such an effect is appreciable
only for ![]() ,
and is due mostly to
,
and is due mostly to
![]() rather than to
rather than to
![]() .
Indeed, the profiles with
.
Indeed, the profiles with
![]() and
and ![]() in the range 0 to 0.1 are almost identical with those in Fig. 7.
in the range 0 to 0.1 are almost identical with those in Fig. 7.
Table 1:
Parameters of Concentration Models matching the Mg2 profiles in
11 elliptical galaxies (from Davies et al. 1993) as displayed in Figs. 8 to 12. In the order,
the columns list: the galaxy name, the B-band effective radius in arcsec
(from Burstein et al. 1987), the concentration index, the metal yield, the
cumulative mass (in units of the total stellar
mass) of the stars with apocentres within the sphere with mass ![]() ,
the
index of the R1/n-mass model, the anisotropy radius (
,
the
index of the R1/n-mass model, the anisotropy radius (![]() for
the isotropic models) in units of the effective radius
for
the isotropic models) in units of the effective radius
![]() of the
R1/n-mass model, the B-band effective radius of the best fitting
model (in units of
of the
R1/n-mass model, the B-band effective radius of the best fitting
model (in units of
![]() ).
).
The model predictions of Sect. 3.3 are here compared to the observations
in a sample of 11 ellipticals. We shall use the BCT library for the
age of 13 Gyr with complementary considerations of the BGM and W94 libraries
and of an age spread among the stellar populations. Figures 8 to 12 display
our best fitting profiles (after eye inspection) for the Mg2 profiles
as measured by Davies et al. (1993, hereafter DSP) and tabulated by
them along the intermediate galaxy axis.
The effective radii from RC2 (de Vaucouleurs et al. 1976), adopted by DSP, are replaced here by the B-band radii ![]() from
Burstein et al. (1987).
The crosses along the model curves correspond to the radius (3'') of
the seeing disk: observed points within two seeing disks are probably
affected by seeing and should be excluded from the comparison. For each
elliptical of the DSP sample, Table 1 lists the galaxy name, the observed
from
Burstein et al. (1987).
The crosses along the model curves correspond to the radius (3'') of
the seeing disk: observed points within two seeing disks are probably
affected by seeing and should be excluded from the comparison. For each
elliptical of the DSP sample, Table 1 lists the galaxy name, the observed
![]() (in arcsec), and parameters
(in arcsec), and parameters
![]() ,
and
,
and
![]() of our best
model. If the inner points, affected by seeing, are included in the
comparison, then some model profiles require the values of
of our best
model. If the inner points, affected by seeing, are included in the
comparison, then some model profiles require the values of
![]() listed
in Table 1.
listed
in Table 1.
In fitting the Mg2 profile for NGC 741, we excluded the observed points at
![]() and -0.80 (see Fig. 10), which are about 0.03 mag below the
average values of the neighbouring points and cannot be matched by our models.
Furthermore, the observed Mg2 profile for NGC 4486 (see Fig. 12) drops from
0.358 mag at
and -0.80 (see Fig. 10), which are about 0.03 mag below the
average values of the neighbouring points and cannot be matched by our models.
Furthermore, the observed Mg2 profile for NGC 4486 (see Fig. 12) drops from
0.358 mag at
![]() to 0.349 at
to 0.349 at
![]() and to 0.277 mag at
and to 0.277 mag at
![]() ,
possibly denoting lower metallicities or younger ages near
the centre. We did not try composite models to match such a behaviour
and therefore we excluded the innermost two points.
,
possibly denoting lower metallicities or younger ages near
the centre. We did not try composite models to match such a behaviour
and therefore we excluded the innermost two points.
Six Es, out of eleven, have shallow profiles within about
![]() followed by steep profiles up to
followed by steep profiles up to
![]() :
they
cannot be fitted by isotropic or anisotropic CMs with
:
they
cannot be fitted by isotropic or anisotropic CMs with
![]() .
The flat profiles within
.
The flat profiles within
![]() are affected by seeing and can
be discarded; however, one can try to reproduce such profiles by CMs
with
are affected by seeing and can
be discarded; however, one can try to reproduce such profiles by CMs
with
![]() .
For the ease of presentation, we adopted
.
For the ease of presentation, we adopted
![]() and
and
![]() (see Sect. 3.3); however,
the observed profiles can be fitted equally well by CMs with values of
(see Sect. 3.3); however,
the observed profiles can be fitted equally well by CMs with values of
![]() similar to those in Table 1 but with
similar to those in Table 1 but with
![]() and a small upward
adjustment of p. The shallow profiles can also be reproduced by
CMs with an age spread among the stellar populations, as discussed in
Sect. 3.3 and shown in Fig. 8 for the Mg2 profile of NGC 3379.
and a small upward
adjustment of p. The shallow profiles can also be reproduced by
CMs with an age spread among the stellar populations, as discussed in
Sect. 3.3 and shown in Fig. 8 for the Mg2 profile of NGC 3379.
The difference between the isotropic and anisotropic CMs, shown in Figs. 6a-b,
is also illustrated in Figs. 8 and 11. NGC 3379 and NGC 4278 have Mg2 profiles
almost overlapping each other up to about
![]() and diverging farther out: they
are fitted by two CMs that differ only in the anisotropic radius
and diverging farther out: they
are fitted by two CMs that differ only in the anisotropic radius ![]() .
Moreover, we choose NGC 3379 to show in Fig. 8 the effect of
.
Moreover, we choose NGC 3379 to show in Fig. 8 the effect of
![]() :
if one sets
:
if one sets
![]() ,
the remaining parameters in Table 1 being unaltered,
the model profile coincides with that in Fig. 8 in the radial range from
,
the remaining parameters in Table 1 being unaltered,
the model profile coincides with that in Fig. 8 in the radial range from
![]() to
to
![]() while diverging upwards within
while diverging upwards within
![]() .
If the inner
profiles, observed in the afore-mentioned six Es, are flattened by
seeing, then a fair fit to the true inner profiles could be provided by CMs
with the same parameters listed in Table 1, except
.
If the inner
profiles, observed in the afore-mentioned six Es, are flattened by
seeing, then a fair fit to the true inner profiles could be provided by CMs
with the same parameters listed in Table 1, except
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f8.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg165.gif) |
Figure 8:
Radial profiles of Mg2 versus log
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f9.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg166.gif) |
Figure 9:
As in Fig. 8 but with the solid curve for NGC 4636 and the dashed curve
for NGC 7626, and with both curves from the Bressan et al. (1996) library for
the age of 13 Gyr (see Table 1). An additional profile (dotted curve) for
NGC 7626 was derived from the Worthey (1994) library for the age of 13
Gyr and with parameters as listed in Table 1, except
|
| Open with DEXTER | |
The Mg2 profiles in five Es are fairly well matched, outside two
seeing disks, by CMs with
![]() ;
however, within two seeing disks,
model values are below the observed values for NGC 4486 and NGC 7626,
or barely reach them for NGC 4261,
NGC 4472, and NGC 4636. The model fitting would worsen
if inner profiles were depressed by seeing and/or by an age effect (see
Sect. 3.3). We also note that NGC 4261, with
Mg2=0.353 near the centre
and a steep Mg2 gradient
between
;
however, within two seeing disks,
model values are below the observed values for NGC 4486 and NGC 7626,
or barely reach them for NGC 4261,
NGC 4472, and NGC 4636. The model fitting would worsen
if inner profiles were depressed by seeing and/or by an age effect (see
Sect. 3.3). We also note that NGC 4261, with
Mg2=0.353 near the centre
and a steep Mg2 gradient
between
![]() to
to
![]() ,
requires c= 0.95. Such a large concentration
implies a very peaked metallicity
distribution: about 98% of the mass is contained, according to Eq. (A.6), in
the range
,
requires c= 0.95. Such a large concentration
implies a very peaked metallicity
distribution: about 98% of the mass is contained, according to Eq. (A.6), in
the range
![]() to
to ![]() (see Appendix A). The same remark applies
to NGC 4486. Furthermore, NGC 4486 (Fig. 12) and NGC 7626 (Fig. 9) have
(see Appendix A). The same remark applies
to NGC 4486. Furthermore, NGC 4486 (Fig. 12) and NGC 7626 (Fig. 9) have
![]() near the centre. Such a large Mg2 value is obtainable hardly from the SSP
data in the BCT library, which reaches
the largest value
Mg2=0.359 at Z=0.1 (see Fig. 2). To a lesser extent, the
same problem also holds for NGC 4261 (Fig. 8).
near the centre. Such a large Mg2 value is obtainable hardly from the SSP
data in the BCT library, which reaches
the largest value
Mg2=0.359 at Z=0.1 (see Fig. 2). To a lesser extent, the
same problem also holds for NGC 4261 (Fig. 8).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f10.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg170.gif) |
Figure 10: As in Fig. 8 but with the solid curve for NGC 315, the short-dashed curve for NGC 741, and the long-dashed curve for NGC 4472. All curves are from the Bressan et al. (1996) library for the age of 13 Gyr (see Table 1). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f11.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg171.gif) |
Figure 11: As in Fig. 8 but with the solid curve for NGC 1600, the short-dashed curve for NGC 4278, and the long-dashed curve for NGC 4374. All curves are from the Bressan et al. (1996) library for the age of 13 Gyr (see Table 1). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3573f12.ps}\end{figure}](/articles/aa/full/2003/20/aah3573/Timg172.gif) |
Figure 12:
As in Fig. 8 but for NGC 4486 with
model profiles from: i) the Bressan et al. (1996) library for the age of 13 Gyr and parameters as in Table 1 (solid curve), ii) from the Worthey (1994) library for the age of
13 Gyr and parameters as in Table 1, except
|
| Open with DEXTER | |
For NGC 4636 and NGC 4472 we could not find profiles better than
those shown in Figs. 9 and 10, respectively, by using the W94 library; on
the contrary, alternative profiles from the W94 library are possible for
NGC 4261, NGC 7626, and NGC 4486, as shown in Figs. 8, 9, and 12,
respectively.
The model profiles from W94 correspond to the age of 13 Gyr,
all other parameters being those listed in Table 1
for BCT,
except
p and
![]() ,
which are given in the
figure's captions.
The ability of the W94 library
to reach, or exceed, the Mg2 values observed
within two seeing disks is due to the extrapolation of the SSP index Mg2beyond Z=0.053, as already mentioned in Sect. 3.3 and shown in Figs. 5b-c.
However, the central profiles of the afore-mentioned five Es could not be
fitted by the W94 library, if they were further depressed by an age effect,
unless the metallicity gradient is steeper than that predicted by the CM.
,
which are given in the
figure's captions.
The ability of the W94 library
to reach, or exceed, the Mg2 values observed
within two seeing disks is due to the extrapolation of the SSP index Mg2beyond Z=0.053, as already mentioned in Sect. 3.3 and shown in Figs. 5b-c.
However, the central profiles of the afore-mentioned five Es could not be
fitted by the W94 library, if they were further depressed by an age effect,
unless the metallicity gradient is steeper than that predicted by the CM.
The farthest points observed by DSP correspond to radial distances ![]()
![]() in five Es (NGC 3379, NGC 4261, NGC 4278, NGC 4374, and NGC 7626) and are in the range
in five Es (NGC 3379, NGC 4261, NGC 4278, NGC 4374, and NGC 7626) and are in the range
![]()
![]() to
to ![]()
![]() in the remaining six Es. Taking
into account ratios
in the remaining six Es. Taking
into account ratios
![]() in Table 1, one concludes that the fittings shown in Figs. 8 to 12
refer to regions enclosing in projection about 63% to 72% of the
masses of the five afore-mentioned Es, and about 48% to 62% for the
remaining Es, except NGC 315 for which the mass fraction is 42% only.
in Table 1, one concludes that the fittings shown in Figs. 8 to 12
refer to regions enclosing in projection about 63% to 72% of the
masses of the five afore-mentioned Es, and about 48% to 62% for the
remaining Es, except NGC 315 for which the mass fraction is 42% only.
The R1/n-mass model, with n>4, fits the Mg2 profiles of five Es
of the DSP sample better than the R1/4-mass model. Parameter n in Table 1
refers to the BCT library for the age of 13 Gyr, and was found by varying
parameters n, c, and p, in an attempt at matching the observed points
outside
![]() .
However, n also depends on the adopted library: indeed,
by using the R1/4-mass model with the W94 library, and disregarding the
observed points within two seeing disks, a fair fit can be found for
all the Es with n>4 as listed in Table 1, except for NGC 4472.
.
However, n also depends on the adopted library: indeed,
by using the R1/4-mass model with the W94 library, and disregarding the
observed points within two seeing disks, a fair fit can be found for
all the Es with n>4 as listed in Table 1, except for NGC 4472.
Parameter n of the R1/n-mass model, as obtained here from the Mg2 profile,
can be compared with the shape parameter n of the Sersic's law, as derived
by some authors from the luminosity profile (for the Sersic's profiles,
see Trujillo et al. 2001). Four Es in Table 1 (NGC 4374, NGC 4472, NGC 4486,
and NGC 4636) are in common with the samples studied by Caon et al. (1993)
in the B band and by Graham & Colless (1997) in the V band: their
Sersic parameters are significantly different in the quoted references and
they also differ from the values of n given in Table 1. Caon et al. (1993) also
report n=7.68 for NGC 4261, against our n=4. It is unknown to what extent
the disagreement between the quoted authors can be ascribed to their adopted
photometric bands. The CM, when used in conjunction with the R1/n-mass
model, gives B-band-luminosity profiles that agree within 0.1 mag with the
Sersic's profiles, from about
![]() up to
up to
![]() (at least). On the other hand,
some decoupling between the Mg2 and the luminosity profiles could be
expected on the ground that the SSP photometric properties, unlike the SSP
index Mg2, are affected only slightly (at fixed Z) by the non-solar ratio
(at least). On the other hand,
some decoupling between the Mg2 and the luminosity profiles could be
expected on the ground that the SSP photometric properties, unlike the SSP
index Mg2, are affected only slightly (at fixed Z) by the non-solar ratio
![]() (TFWG1; Tantalo et al. 1998).
(TFWG1; Tantalo et al. 1998).
We conclude this section by noting that the Mg2 profiles, in some Es of the DSP
sample, can be fitted with model
profiles from the BGM library with practically the same values of p, c, and n as given in
Table 1, but with a different value of ![]() .
The observed profiles
matched by the anisotropic models when using the BCT library are also fitted
by the isotropic models when using the BGM library.
.
The observed profiles
matched by the anisotropic models when using the BCT library are also fitted
by the isotropic models when using the BGM library.
The Concentration Model is admittedly an oversimplified version of more elaborate dissipative models of galaxy formation. However, Sects. 3 and 4 show that the Concentration Model, when used in conjunction with the R1/n model and the Single-burst Stellar Populations index Mg2 from available libraries, leads to non-generic predictions that compare fairly well, outside the inner two seeing disks, with detailed observations in a sample of 11 ellipticals. Such a specific comparison was the main goal of the present paper, although it has to be considered as a preliminary test to further investigations.
Our results depend obviously on the mass distribution of the R1/n model, which is only a rough approximation to real elliptical galaxies, since it is a spherical model derived from the luminosity profile by assuming a constant mass-to-light ratio. Moreover, our results also depend on the dynamical structure, as shown by the Mg2profiles obtained with isotropic and anisotropic Osipkov-Merritt models. Further computations are needed to assess to what extent the integrated Mg2 is affected by the mass and dynamical structure of alternative models of elliptical galaxies.
The age spread, among the stellar populations of individual ellipticals,
was considered in a very simple way, following the suggestion by TFWG1 and
Kodama & Arimoto (1997 and 1998). A qualitative agreement can be found with
the age gradients inferred by TFWG1 in a sample of 39 ellipticals, but the
issue would require a more suitable index and more detailed comparisons than
the few experiments we have done with index Mg2. Moreover, our
age spread produces Mg2 profiles that are flat in the innermost regions. The Concentration Model with a terminal wind offers an alternative
possibility of obtaining such profiles, at the cost of introducing the
additional parameters ![]() and
and ![]() .
.
The free parameters ![]() and
and ![]() are related, presumably, to the depth of the potential
well, the degree of dissipation, and the star-formation and supernovae rates
(see Pagel 1997). Hydrodynamical computations, like those performed by various
authors (Larson 1976; Carlberg 1984; Theis et al. 1992), are required to
obtain an acceptable relation between
are related, presumably, to the depth of the potential
well, the degree of dissipation, and the star-formation and supernovae rates
(see Pagel 1997). Hydrodynamical computations, like those performed by various
authors (Larson 1976; Carlberg 1984; Theis et al. 1992), are required to
obtain an acceptable relation between ![]() and
and
![]() .
The specific values for
.
The specific values for ![]() and
and
![]() ,
as adopted in Sect. 3, were chosen arbitrarily for illustrative purpose only.
,
as adopted in Sect. 3, were chosen arbitrarily for illustrative purpose only.
The comparison with observations, as discussed in Sect. 4, suffers from
the seeing effects: the observed Mg2 profiles, within two seeing disks,
are uncertain, so we cannot say what kind of Concentration Model (with or
without an age spread and with or without a terminal wind) is the more
appropriate one for each individual elliptical galaxy. A further uncertainty
comes from the poorly known effects of non-solar abundance ratios on index
Mg2. If the enhancement of the SSP index Mg2, for a variable Z with
a fixed
![]() ,
is like that induced by a fixed age increase for a
variable Z, then our model profiles could be considered as fair approximations
to the observed profiles. In such a case, as in the case of the
age/metallicity degeneracy considered in Sect. 3.3, we could infer the
underlying gradient of Z without determining Z in absolute units. Obviously,
this issue could only be assessed when an adequate SSP library, covering a
reasonable range of non-solar
,
is like that induced by a fixed age increase for a
variable Z, then our model profiles could be considered as fair approximations
to the observed profiles. In such a case, as in the case of the
age/metallicity degeneracy considered in Sect. 3.3, we could infer the
underlying gradient of Z without determining Z in absolute units. Obviously,
this issue could only be assessed when an adequate SSP library, covering a
reasonable range of non-solar
![]() ratios, were available.
ratios, were available.
Besides the above uncertainties, there are some degeneracies, illustrated
in Sect. 3.3, among some parameters that are needed in our approach. We
find that the slope of steep profiles, outside (say)
![]() ,
is determined chiefly by the concentration index c, and that the specific
values of index Mg2 along the profiles are controlled mainly by the metal
yield p (for a fixed age). However, a heavy degeneracy among model
parameters persists when dealing with shallow Mg2 profiles within
,
is determined chiefly by the concentration index c, and that the specific
values of index Mg2 along the profiles are controlled mainly by the metal
yield p (for a fixed age). However, a heavy degeneracy among model
parameters persists when dealing with shallow Mg2 profiles within
![]() .
.
We reiterate that the comparison with observations, discussed in Sects. 3.3 and 4, is only a preliminary test of our approach and is by no means conclusive, since it does not include colour indices and spectral indices other than Mg2. Moreover, the comparison is affected by a major uncertainty stemming from the SSP libraries we have used, which are admittedly unsatisfactory to study the spectro-photometric properties of giant ellipticals.
We summarize the main results of the paper as follows:
Acknowledgements
We would like to thank an anonimous referee for her/his valuable suggestions that helped to improve the content and presentation of this paper.
Therefore, Eq. (5) can now be rewritten as
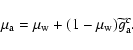 |
(A.1) |
We refer to a "fixed'' m in a galaxy after ![]() ,
and first consider
the alternative
,
and first consider
the alternative
![]() .
The stars with apocentres inside m have
metallicities from Z0 to
.
The stars with apocentres inside m have
metallicities from Z0 to ![]() :
those with
:
those with
![]() to
to ![]() formed
before
formed
before ![]() when
when
![]() ,
and those with
,
and those with
![]() to
to ![]() formed
when
formed
when
![]() .
We
discuss the cases
.
We
discuss the cases
![]() and
and
![]() in the following items I) and II), respectively,
and defer the alternative
in the following items I) and II), respectively,
and defer the alternative
![]() to item III).
to item III).
I) Case
![]()
Mass
![]() follows from the obvious condition
follows from the obvious condition
![]() ,
that is
,
that is
| (A.2) |
II) Case
![]()
Mass
![]() is solution of equation
is solution of equation
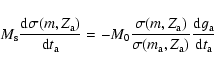 |
(A.3) |
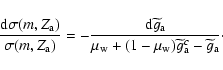 |
(A.4) |
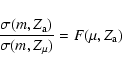 |
(A.5) |
![\begin{displaymath}%
F(\mu,Z_{\rm a}) = {\rm exp}\left[- \int_{\widetilde{g}(\mu...
...{\rm d}x}\over{\mu_{\rm w} + (1 - \mu_{\rm w})x^c - x}}\right]
\end{displaymath}](/articles/aa/full/2003/20/aah3573/img216.gif) |
(A.6) |
III) Case
![]()
The stars with
![]() to
to ![]() all formed when
all formed when
![]() varied from 1 to
varied from 1 to ![]() :
for them
:
for them
![]() coincides with mass
coincides with mass
![]() of the final distribution. By integrating Eq. (A.4) from the fixed
point
of the final distribution. By integrating Eq. (A.4) from the fixed
point
![]() to
to
![]() one gets
one gets
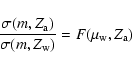 |
(A.7) |
The stars with apocentres on the surface corresponding to
![]() completed their formation
when
completed their formation
when
![]() .
Their fractional mass distribution, in the
metallicity range
.
Their fractional mass distribution, in the
metallicity range ![]() to
to
![]() d
d![]() ,
follows from Eq. (A.5) as
,
follows from Eq. (A.5) as
![]() d
d![]() ,
where
,
where
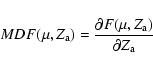 |
(A.8) |
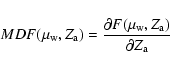 |
(A.9) |
Solutions (A.6) for c= 1/3, 1/2, 2/3, 3/4, and
![]() can be written
as
can be written
as
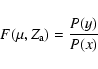 |
(B.1) |
I) Case c=1/3
One has
![]() ,
,
![]() ,
and P(q)
depending on
,
and P(q)
depending on ![]() as detailed in the following items i) to iii):
as detailed in the following items i) to iii):
i)
![\begin{eqnarray*}P(q) = (1 - q)^{\alpha}(q^2 + q + \mu_{\rm w})^{\beta}
{\rm exp}\left[- \gamma {\rm atan}\left({{2q + 1}\over {k}}\right)\right]
\end{eqnarray*}](/articles/aa/full/2003/20/aah3573/img244.gif)
ii) ![]()
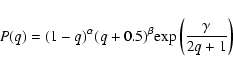
iii) ![]()
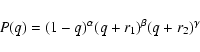
II) Case c=1/2
One has
![]() ,
,
![]() ,
and
,
and
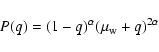
III) Case c=2/3
By setting
![]() and
and
![]() one obtains
one obtains
![\begin{displaymath}P(q) = (1 - q)^{\alpha}\left(q^2 + \mu_{\rm w} q + \mu_{\rm w...
...mma {\rm atan}\left({{2q +\mu_{\rm w}}\over {k}}\right)\right]
\end{displaymath}](/articles/aa/full/2003/20/aah3573/img262.gif)
IV) Case c=3/4
By setting
![]() and
and
![]() one has
one has
![\begin{displaymath}P(q) = (1 - q)^{\alpha}(q - r)^{\beta}(q + bq + d)^{\delta}{\...
... \left[-\gamma {\rm atan}\left({{2q + b}\over k}\right)\right]
\end{displaymath}](/articles/aa/full/2003/20/aah3573/img268.gif)
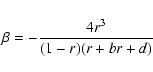
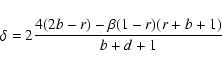
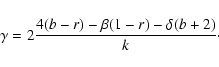
In this appendix the CM is adapted to the Sersic's R1/n model of
a spherical galaxy. Mass ![]() and effective radius
and effective radius
![]() (of the R1/n-mass
model) are adopted as units of mass and length, respectively. The
spatial radial distance will be indicated by r and the projected radial
distance by R.
(of the R1/n-mass
model) are adopted as units of mass and length, respectively. The
spatial radial distance will be indicated by r and the projected radial
distance by R.
The R1/n model can be isotropic or anisotropic according to whether,
at any location r, one has
![]() ,
or
,
or
![]() ,
respectively, where
,
respectively, where
![]() and
and
![]() are the
dispersions of the squared radial
are the
dispersions of the squared radial
![]() and transverse
and transverse ![]() velocities, respectively. Besides the isotropic
models, we shall only consider a particular kind of anisotropic models (the
so-called Osipkov-Merritt models) that have the same mass structure of the
isotropic models with the same n,
velocities, respectively. Besides the isotropic
models, we shall only consider a particular kind of anisotropic models (the
so-called Osipkov-Merritt models) that have the same mass structure of the
isotropic models with the same n, ![]() ,
and
,
and
![]() but a different dynamical
structure, i.e. a different velocity distribution. The Osipkov-Merritt models
(see below) are specified by the anisotropy radius
but a different dynamical
structure, i.e. a different velocity distribution. The Osipkov-Merritt models
(see below) are specified by the anisotropy radius ![]() (
(
![]() )
and
reduce to the corresponding isotropic models in the limit
)
and
reduce to the corresponding isotropic models in the limit
![]() .
.
Gravitational potential ![]() and binding energy
and binding energy ![]() ,
both in physical
units, will be replaced by the positive dimensionless potential
,
both in physical
units, will be replaced by the positive dimensionless potential
![]() ,
where
,
where
![]() ,
and by the dimensionless energy
,
and by the dimensionless energy
![]() ,
respectively. One
has
,
respectively. One
has
![]() (v being the modulus of the spatial velocity)
with
(v being the modulus of the spatial velocity)
with
![]() and
and
![]() .
.
The distribution function
![]() for the isotropic models, and f(Q) for
the anisotropic ones, are computed as described in the literature
(Osipkov 1979; Binney 1982; Merritt 1985; Binney & Tremaine 1987 for n=4; Ciotti 1991;
Ciotti & Lanzoni 1997 for the general case). In the anisotropic models (the
so-called Osipkov-Merritt models), the distribution function f(Q) depends on the
dimensionless (i.e. in units of
for the isotropic models, and f(Q) for
the anisotropic ones, are computed as described in the literature
(Osipkov 1979; Binney 1982; Merritt 1985; Binney & Tremaine 1987 for n=4; Ciotti 1991;
Ciotti & Lanzoni 1997 for the general case). In the anisotropic models (the
so-called Osipkov-Merritt models), the distribution function f(Q) depends on the
dimensionless (i.e. in units of ![]() )
variable
)
variable
![]() ,
where J is the angular momentum and
,
where J is the angular momentum and ![]() the anisotropy radius,
with f(Q)=0 for Q<0.
the anisotropy radius,
with f(Q)=0 for Q<0.
The mass coordinate m in Sect. 2 is replaced by M(r), the total
mass inside the sphere of radius r. Therefore, we define rm by
M(rm)=m and likewise ![]() and
and ![]() when
when
![]() and
and ![]() ,
respectively. We also write
,
respectively. We also write
![]() and likewise
and likewise
![]() and
and
![]() .
.
At location r,
![]() varies from 0 to
varies from 0 to ![]() and
and
![]() (
(![]() being the angle between vectors
being the angle between vectors
![]() and
and ![]() )
from 0 to
)
from 0 to
![]() ,
where
,
where
![]() .
The apocentric distance
.
The apocentric distance
![]() ,
solution
of equation
,
solution
of equation
![]() ,
may be smaller, or larger, than
,
may be smaller, or larger, than ![]() .
If
.
If
![]() ,
the differential distribution of metallicities, for fixed
,
the differential distribution of metallicities, for fixed
![]() and J, is then
given by
and J, is then
given by
![]() of
Eq. (A.8), where
of
Eq. (A.8), where
![]() and
and ![]() varies
from Z0 to
varies
from Z0 to
![]() with
with
![]() and
and
![]() .
If
.
If
![]() ,
then
,
then
![]() is given by
Eq. (A.9) with
is given by
Eq. (A.9) with ![]() ranging from Z0 to
ranging from Z0 to ![]() .
.
We now consider a Z-dependent function I(Z) and define
![]() as the value (per unit mass) of I(Z)
integrated over all stars with fixed
as the value (per unit mass) of I(Z)
integrated over all stars with fixed
![]() and J. If
and J. If
![]() ,
one has
,
one has
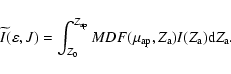 |
(C.1) |
We denote by
![]() the integrated value of I(Z) due to all
stars at location r. The contribution to
the integrated value of I(Z) due to all
stars at location r. The contribution to
![]() from the stars with
energies
from the stars with
energies
![]() to
to
![]() d
d
![]() and momenta J to J+dJ is
and momenta J to J+dJ is
![\begin{displaymath}2\pi \widetilde{I}(\epsilon,J){{f(\varepsilon)J}\over
{r\le...
...^2(\varepsilon) - J^2\right]^{1/2}}}{\rm d}\varepsilon{\rm d}J
\end{displaymath}](/articles/aa/full/2003/20/aah3573/img326.gif)
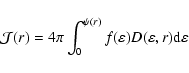 |
(C.2) |
![\begin{displaymath}%
D(\varepsilon ,r) = {1\over r} \int_0^{J_r(\varepsilon)}
...
...over {\left[J_r^2(\varepsilon) - J^2\right]^{1/2}}}
{\rm d}J.
\end{displaymath}](/articles/aa/full/2003/20/aah3573/img328.gif) |
(C.3) |
![$\displaystyle %
{\cal J}_{{\rm pr}}(R) = 8\pi \int_0^{\psi(R)} f(\varepsilon )
...
...lon,r){r\over {\left[r^2 - R^2\right]^{1/2}}} {\rm d}r\right]{\rm d}\varepsilon$](/articles/aa/full/2003/20/aah3573/img331.gif) |
(C.4) |
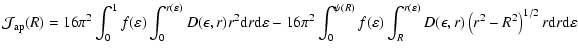 |
(C.5) |
The integrated indices
![]() (along the line-of-sight at R) and
(along the line-of-sight at R) and
![]() (within the centered aperture of radius R) are computed from
published values of the synthetic SSP index
(within the centered aperture of radius R) are computed from
published values of the synthetic SSP index
![]() (in mag), where Z is the SSP
metallicity. We write
(in mag), where Z is the SSP
metallicity. We write
![]() ,
where F1(Z) is the SSP flux
in the index passband and F2(Z) is the SSP-pseudocontinuum flux in the
same passband. Both F1(Z) and F2(Z) refer to the unit mass. We make the approximation
F2(Z)=aLV(Z) (see Greggio 1997), where LV(Z) is the SSP luminosity in
the V band (and per unit mass) and factor a is independent of Z. We then obtain
,
where F1(Z) is the SSP flux
in the index passband and F2(Z) is the SSP-pseudocontinuum flux in the
same passband. Both F1(Z) and F2(Z) refer to the unit mass. We make the approximation
F2(Z)=aLV(Z) (see Greggio 1997), where LV(Z) is the SSP luminosity in
the V band (and per unit mass) and factor a is independent of Z. We then obtain
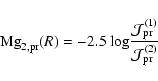 |
(C.6) |
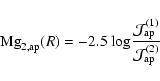 |
(C.7) |
At location r one has
![]() ,
where Q varies from 0 to
,
where Q varies from 0 to
![]() .
Therefore,
.
Therefore,
![]() varies from 0 to
varies from 0 to
![]() .
The apocentric distance
.
The apocentric distance
![]() is
solution of equation
is
solution of equation
![]() and
and
![]() in Eq. (C.1) now becomes
in Eq. (C.1) now becomes
![]() .
Quantities
.
Quantities
![]() ,
and
,
and
![]() are given
by Eqs. (C.2) and (C.4) to (C.7), respectively, when
are given
by Eqs. (C.2) and (C.4) to (C.7), respectively, when
![]() is replaced by Q,
is replaced by Q,
![]() by r(Q) {where r(Q) is solution of
by r(Q) {where r(Q) is solution of
![]() },
and
},
and
![]() by
by
![$\displaystyle %
D(Q,r) = {1\over {r\left(1 + r^2/r_{\rm a}^2\right)^{1/2}}}
\in...
...J_r(Q)}\widetilde{I}(Q,J){J\over {\left[J_r^2(Q) - J^2\right]^{1/2}}}
{\rm d}J.$](/articles/aa/full/2003/20/aah3573/img357.gif) |
(C.8) |