A&A 403, 443-448 (2003)
DOI: 10.1051/0004-6361:20030328

Anisotropy in the angular distribution of the long gamma-ray bursts?

A. Mészáros - J. Stocek

Astronomical Institute of the Charles University, V Holesovickách 2, 180 00 Prague 8, Czech Republic

Received 15 March 2002 / Accepted 28 February 2003

Abstract
The gamma-ray bursts detected by the BATSE instrument may be separated into "short", "intermediate" and "long" subgroups. Previous statistical tests found an anisotropic sky-distribution on large angular scales for the intermediate subgroup, and probably also for the short subgroup. In this article the description and the results of a further statistical test - namely the nearest neighbour analysis - are given. Surprisingly, this test gives an anisotropy for the long subgroup on small angular scales. The discussion of this result suggests that this anisotropy may be real.

Key words: gamma-rays: bursts - cosmology: miscellaneous

1 Introduction

The separation of the gamma-ray bursts (hereafter GRBs) - detected by the BATSE instrument (Meegan et al. 2000) - into subgroups is done (Kouveliotou et al. 1993; Horváth 1998; Mukherjee et al. 1998) with respect to T90, the duration during which 90% of the radiation of a burst is measured. Bursts are either short ( $T_{90} \leq 2$ s), or intermediate ( $ 2~{\rm s} < T_{90} \leq 10~{\rm s}$), or long ( T90 > 10 s). Nowadays it is practically sure that the long and short subgroups are different phenomena (Norris et al. 2001; Horváth et al. 2001). The situation concerning the intermediate subgroup is unclear; some authors query even the reality of this subgroup itself (Hakkila et al. 2000). From the afterglow data the cosmological origin is directly confirmed for the long bursts only. They are usually at high redshifts. For the short and intermediate GRBs there is only indirect evidence for a cosmological origin, and concrete redshifts are unknown (for a survey of these questions see Mészáros P. 2001).

During the last years one of the authors together with various collaborators provided several statistical tests verifying the isotropy in the angular distribution of GRBs. These tests were based on the binomial distribution (Mészáros A. 1997; Balázs et al. 1998; Balázs et al. 1999), on spherical harmonics (Mészáros A. et al. 2000a), on the counts-in-cells method (Mészáros A. et al. 2000b), on the two-point angular correlation function (Mészáros A. et al. 2000c), and on multifractal methods (Vavrek et al. 2001). These tests (for a summary see Mészáros A. et al. 2001) give an anisotropy for the intermediate subgroup. The short subgroup also seems to be distributed anisotropically; nevertheless, there are only a few tests that reject isotropy at a high enough confidence level. The long subgroup seems to be distributed isotropically; here only the test based on the two-point angular correlation function rejects the null hypothesis of isotropy (Mészáros A. et al. 2000c). Recently and fully independently these results were confirmed by Litvin et al. (2001).

In this paper we present the results of a new test; namely of the nearest neighbour analysis (hereafter NNA). This test (Scott & Tout 1989) is a standard statistical test, and - as far as known - has not been used yet for GRBs.

The paper is organized as follows. In Sect. 2 the method is described. Section 3 compares this method with other methods. Section 4 presents the results of the test. Section 5 discusses and summarizes the conclusions of the paper.

2 The method

NNA is a standard statistical test, which compares the actual angular distances among the objects on the surface of a sphere having unit radius with the theoretical angular distances in a randomly and isotropically distributed sample.

The theory of NNA was formulated by Scott & Tout (1989). Here this theory is only recapitulated and specified for the sky distribution of GRBs.

Let there be N objects on the sky, which are distributed randomly. N should be $\geq$2; for our purpose we may assume $N \gg 1$. We arbitrarily choose one object ("first object"). At an angular distance $\beta$ ( $0 \leq \beta \leq \pi$) from the first object we define an infinitesimal belt with thickness d$\beta$. This belt is defined by the distance interval $[\beta, (\beta + {\rm d}\beta)]$. The probability of having (L-1) objects at the distance $\leq$$\beta$, and one object in the infinitesimal belt is given by

                                              $\displaystyle p_{L}(\beta) {\rm d} \beta =\frac{(N-1)!}{2^{N-1}(N-L-1)!(L-1)!}$  
                        $\displaystyle \times\sin\beta (1-\cos\beta)^{L-1} (1+\cos\beta)^{N-L-1} {\rm d} \beta .$ (1)

L can be =1, 2, $\ldots, \; (N-1)$. For L=1 the nearest (or: the first nearest) object lies in the belt, for L=2 the second nearest object lies in the belt, etc.

The integral probability $\int_{0}^{\beta} p_L(\beta') {\rm d}\beta' = P_L (\beta)$ defines the probability that there are L and exactly L objects in the neighbourhood of the first object; the neighbourhood is defined by the distances  $\leq \beta$. $P_L(\pi) = 1$, as it should be. For L=1 and L=2 one obtains

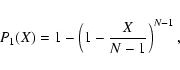\begin{displaymath}P_{1}(X) = 1-\left(1-\frac{X}{N-1}\right)^{N-1}, \end{displaymath} (2)

and
$\displaystyle P_{2}(X_2) = 1-\left(1-\frac{X_2}{(N-1)(N-2)}\right)^{N-1}$$\displaystyle -\frac{X_2}{N-2}\left(1-\frac{X_2}{(N-1)(N-2)}\right)^{N-2},$
  (3)

respectively, where $X = (N-1) \sin^2 (\beta/2)$, and $X_2=(N-1)(N-2)\sin^2\frac{\beta}{2}$. The introduction of X and X2 - instead of $\beta$ - simplifies the formulas (Slechta & Mészáros A. 1997).

If the integral probabilities for different L are given by these analytical formulas, we can use them as theoretical cumulative probability distributions. The standard Kolmogorov-Smirnov test can be used to compare them with the measured empirical cumulative distributions (Press et al. 1992; Chap. 14.3).

The test for L=1 should be done as follows. The theoretical function P1(X) is defined for $0 \leq X \leq (N-1)$ and is monotonously increasing from 0 to 1. The measured (N-1)first nearest neighbour distances are sorted into increasing sequence. Then, for any distance in this sequence, one obtains a value X, and at this value the empirical cumulative distribution function is increased by the value (N-1)-1. Hence the empirical cumulative function also runs from 0 to 1 for the same range of X. The maximal absolute value D between the two different cumulative distribution functions defines the significance level for given (N-1) (Press et al. 1992, Chap. 14.3).

One can do (N-1) tests, because the test may be done for any allowed L. For any L the theoretical cumulative function can be calculated and is an analytical function. The (N-1) Lth nearest neighbour measured angular distances can also be obtained from the positions of objects.

However, one does not need to provide all possible (N-1) tests for one sample. Let us assume that the test is made for L=1, then for L=2, ..., then for L = (N-1). If one assumes that the null hypothesis is true, viz. that the objects are distributed randomly on the surface of the sphere, then no test should reject this hypothesis. Nevertheless, it is unlikely that going to bigger and bigger L will give any new result. This may be seen as follows.

There are N(N-1)/2 distances among the observed N objects. But only (2N-3) distances are independent. (N objects on the sphere are defined by 2N coordinates (any object is defined by two spherical angles, e.g. by $\vartheta$ and $\varphi$). Nevertheless, one object may be taken - without loss of generality - at the pole (i.e. one may have $\vartheta = 0$ for this "first object"). A second arbitrary object may still be at $\varphi = 0$. There are (N-1) independent distances known immediately: they are the $\vartheta$ coordinates of (N-1) objects giving the distances from the first object. There are a further (N-2)independent distances from the second object. They can be calculated if the $\varphi$ coordinates are known. Then any further distances can be calculated from these (2N-3) independent distances.)

This means that, if one uses only L=1 and L=2, then one uses 2N distances in these two tests, which is practically identical to the number of independent distances. (For $N \gg 1$ the difference between 2N and (2N-3) is negligible.) Therefore, we will only use the L=1 and L=2 tests, but not higher L. Once the null hypothesis is rejected by either the L=1 or L=2 test at a given significance level, then this rejection is correct. Only the significance level obtained provides a lower limit for this rejection, because it is still possible that some further tests with higher L will reject the null hypothesis at a higher significance level.

There are two problems with the application of this test. One problem is general and the second is a special problem occurring for the BATSE data of GRBs.

The first problem is the following. To compare the theoretical curve with the empirical curve one needs N measured independent Lth nearest distances. We have only one single sample: the actual distribution of N objects on the sky. In it one has N Lth nearest neighbour distances; for any object one calculates the Lth nearest neighbour. But these N distances need not be independent, because some distances may occur twice. (If the Lth nearest neighbour for kth object is the mth object, then it may well happen that the Lth nearest neighbour for mth object is the kth object.) Fortunately, this is not an essential defect excluding its use (Scott & Tout 1989).

The second problem concerns the case of GRBs alone. It follows from the fact that the sky is not covered uniformly by the BATSE instrument. There is a sky-exposure function $g(\delta)$ that depends on the declination $\delta$ (Meegan et al. 2000). Therefore, the theoretical curve from Eqs. (2) and (3) is not usable at once. Fortunately it is easy to take this into account. (In the previous papers cited in Sect. 1 the effect of a non-uniform sky-exposure function could also be corrected for. Hence, if we discuss anisotropy, we always mean intrinsic anisotropy in the distribution of GRB not caused by the BATSE instrument.)

This correction may be made as follows. Let there be a burst at declination $\delta$. Then one can always introduce a new declination  $\tilde{\delta}$ unambiguously by the relation

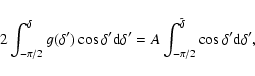\begin{displaymath}2 \int_{-\pi/2}^{\delta} g(\delta') \cos \delta' {\rm d}\delt... ... A \int_{-\pi/2}^{\tilde{\delta}} \cos \delta' {\rm d}\delta', \end{displaymath} (4)

where

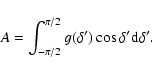\begin{displaymath}A = \int_{-\pi/2}^{\pi/2} g(\delta') \cos \delta' {\rm d}\delta'. \end{displaymath} (5)

This means that - formally - the declination is "shifted" to a new value. If there is an intrinsic isotropy in the distribution of GRBs, the GRBs should also be distributed isotropically in the new "shifted" coordinates. Note that this shift is a standard method in Statistics (Trumpler & Weaver 1953, Chap. 1.13). Note also that this elimination of the non-uniform sky-exposure function is new.

Because one should obtain isotropy in these "shifted" coordinates - if there is intrinsic isotropy - any statistical test that assumes uniform sky exposure can be used. Therefore NNA is also usable. We will provide the NNA test for L=1 and L=2 in these "shifted" coordinates for the short, intermediate and long GRBs, respectively.

3 Comparison of the method with other tests

In this section the advantages and disadvantages of NNA are summarized and compared with other tests mentioned in Sect. 1.

First of all, we want to remark that NNA is highly similar to the two-point angular correlation function method. In both cases the key idea is the same: There are N(N-1)/2 angular distances among N objects, and these measured angular distances are compared with the theoretically expected distances following from the random angular distribution of N objects.

Both methods have the great advantage that they are independent on the choice of coordinate systems and also of other artificial choices. (For example, in the counts-in-cells method the boundaries of the cells must be chosen ad hoc (Mészáros A. et al. 2000b). No such ad hoc choice is needed here.) A further advantage of these methods lies in the fact that they are also able to detect eventual anisotropies on small angular scales. (If there are N($N \gg 1$) objects on the sky, then the angular scales - measured in radians - are large, if these scales are much bigger than  $\simeq\!\!\!\!\sqrt{4\pi/N}$; small angular scales in radians correspond with distances  $\simeq\!\!\!\sqrt{4\pi/N}$; for further details see Scout & Tout 1989.) This is a great advantage of NNA compared, e.g., with the counts-in-cells method, which is insensitive to angular scales much smaller than the cell size (inside a cell eventual anisotropies may be "smoothed"; for more details see Mészáros et al. 2000b). In principle, the method based on spherical harmonics, and multifractal methods, are sensitive to small scales, too. Nevertheless, on scales  $\simeq\!\!\!\!\sqrt{4\pi/N}$radians these methods begin to have several technical problems (see, e.g., Mészáros et al. 2000a for further details). All this means that NNA and the method based on the two-point angular correlation function may well detect anisotropies on scales  $\simeq\!\!\!\sqrt{4\pi/N}$ radians, which were not detected yet by other methods.

There are two essential differences between NNA and the method based on the two-point angular correlation function. The first concerns the number of distances used: NNA uses only 2N angular distances, but the second method uses N(N-1)/2 distances. The second concerns the procedure of the calculation of significance levels: the method based on the two-point angular correlation function needs Monte-Carlo simulations (Mészáros A. et al. 2000c); NNA does not need them. It is well known that one has to be careful using pseudo-random generators and Monte-Carlo simulations (see, e.g., Chap. 7.0 of Press et al. 1992). Therefore it is essential to use a method that does not need these pseudo-random simulations. On the other hand, this advantage of NNA is lessened by the fact that it uses only 2N distances. This means that NNA may miss anisotropies detected by the correlation function method. On the other hand, any anisotropy detected by NNA method should also be detected by the correlation function method. In other words, NNA is not as powerful as the correlation function method. Its advantage is given mainly by its simplicity and by the fact that it does not need pseudo-random generations. In any case, its use in the case of GRBs is certainly justified.

Add to this that, as it is well-known in Statistics (Trumpler & Weaver 1953), it is quite usual for different tests to give different conclusions. (Different tests give different "trials".) Some tests may reject the hypothesis of isotropy while further tests do not reject it. In addition, if two different tests reject it, then this rejection may occur at different significance levels, too. Trivially, if there is an isotropic distribution, then no test should reject the hypothesis of this isotropy. This means that, at least in principle, one single test rejecting the isotropy is enough to proclaim the existence of anisotropy. On the other hand, using several tests is clearly better, because if only one single test rejects the isotropy one can never exclude with certainty that there may not have been some unknown technical problems (pseudo-random simulations, unknown instrumental effects, unknown systematic errors in measurements, etc.).

In fact this is the situation also for long GRBs (see Sect. 1): isotropy of both the short and intermediate subgroups of GRBs is rejected by several tests, and hence it may be stated that these subgroups are distributed anisotropically on the sky. On the other hand, the isotropic distribution of the long-GRB subgroup is rejected by one single test only; hence its anisotropy is questionable still.

4 The results


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{meszsto1.ps} \end{figure} Figure 1: Kolmogorov-Smirnov test for the second nearest neighbour for the long subgroup containing N= 1239 GRBs. The theoretical curve is the "smooth" curve; the empirical curve is a step function increasing in steps of 1/1239. The biggest difference D between the two curves is at around $X_2 \simeq 1500$, where the theoretical curve is at the bottom.
Open with DEXTER

There are 2702 GRBs in the BATSE Catalog (Meegan et al. 2000), and from them 2037 GRBs have measured T90. They are separated into three subgroups: 497 GRBs having $T_{90} \leq 2$ s comprise the "short" subgroup; 301 GRBs having 2 s  $< T_{90} \leq 10$ s comprise the "intermediate" subgroup; and 1239 GRBs having T90 > 10 s comprise the "long" subgroup. Because the existence of the third intermediate subgroup is not sure yet (see Sect. 1), for safety we also test the "non-short" subgroup contaning 1239 + 301 = 1540 GRBs having T90 > 2 s (i.e. the "intermediate" and "long" subgroups are taken together). For the sake of completeness we also tested the sample of "all" GRBs, containing 2702 GRBs. For any sample we provide the nearest neighbour and second nearest neighbour analysis using the standard Kolmogorov-Smirnov test. For any sample we take the bigger D from the L=1 and L=2 tests.

Table 1 shows the results.

Table 1: The results of the Kolmogorov-Smirnov tests for the three subclasses. The first column denotes the subclass; the second the number of GRBs of this subclass; the third column gives the difference D between the theoretical and empirical cumulative function; the fourth column gives the significance (in percentage) of the rejection of the null-hypothesis of isotropy (Eq. (14.3.9) of Press et al. 1992).

Table 1 gives the remarkable result: for the long subclass, and only for this subclass, is the null-hypothesis of isotropy rejected at the usual >95% significance level (viz. 99%). This result follows from the L=2 test.

Both the theoretical and empirical cumulative distribution functions for L=2 are shown in Fig. 1. From this it follows that around $X_2 \simeq 1500$, i.e. around $\beta \simeq 0.6$ radians  $ \simeq (3-4)$ degrees, the empirical curve lies significantly above the theoretical one. This means that on this angular scale the actual angular distribution of GRBs shows an overdensity compared with the random isotropic case.

5 Discussion and conclusion

If one compares the previous tests surveyed in Sect. 1 with Table 1, it seems that the occurrence of anisotropy for the long subgroup, and for this subgroup only, is a surprising result.

Nevertheless, nothing unexpected is occurring here. First, NNA is sensitive on small angular scales (for the long subgroup on  $\simeq\!\!\!\sqrt{4\pi/N} = 0.2$ radians). Previous tests were sensitive on large angular scales, so it is not strange to detect anisotropy on angular scales of a few degrees. Second, the two-point angular correlation function shows anisotropy for this subgroup, too (see the survey in Sect. 1). (As is noted in Sect. 3, it is to be expected that anisotropy detected by NNA should be detected by the method based on the correlation function, too; the opposite does not hold.) Third, from Eq. (14.3.9) of Press et al. (1992) it follows that the significance level increases with $D\sqrt{N}$. From Table 1 one sees that D is more or less the same for the first three subclasses; hence, the long subclass is anisotropic due to high N. It is therefore quite possible that the anisotropies for short and intermediate subclasses respectively are not detected by NNA due to the small N. Fourth, visual inspection of the distribution of long GRBs on the sky (Fig. 2) also shows some grouping on small angular scales. Fifth, in fact some anisotropy on degree scales is expected from Cosmology: at $z \ll 1$ (z is the redshift) the distribution of galaxies and other objects is inhomogeneous on scales $\simeq$ (10-100) Mpc (see Mészáros A. 1997 and references therein). At high z, where the long GRBs dominantly are, these scales correspond to angular scales of some degrees. (Direct measurements from GRB afterglows give z = 4.5 for the maximal redshift (Mészáros P. 2001); indirect observational data also allow $z \simeq 20$(Mészáros A. & Mészáros P. 1996).) Hence, if the present-day inhomogeneities exist also at the high redshifts and if the distribution of long GRBs reflects the distribution of matter at these high redshifts, then anisotropy of long GRBs on degree scales is quite possible.

All this means that the occurrence of anisotropy for the long subgroup and the simultaneous non-occurrence of anisotropy for the intermediate and short subgroup is not strange. On the other hand, the isotropy of the non-short sample is remarkable. It seems that GRBs from intermediate and long subgroups separately are anisotropically distributed; but differently and that their anisotropies "cancel". It is urgent to clarify the status of the intermediate subgroup - namely whether is it a real different subgroup or not (see Sect. 1). Our result, together with Horváth's recent results (Horváth 2002), suggest that the intermediate subclass may be a real subgroup.

The result concerning the sample denoted by "all" has no real meaning, because the short and long subclasses may be different phenomena (see Sect. 1).


  \begin{figure} \par\includegraphics[angle=-90,width=18cm]{meszsto2.eps} \end{figure} Figure 2: Distribution of 1239 long GRBs on the sky in equatorial coordinates and Aitof projection.
Open with DEXTER

As was already noted, theoretically (see Sect. 3), it is sufficient to have one single rejection of the null hypothesis from one single statistical test. In practice, the result is more reliable if several tests reject the null hypthesis. Concerning the long subgroup this is what we get here, because both NNA and the correlation function method reject the isotropy. Hence this paper may lead to the conclusion that the long bursts are also distributed anisotropically.

Nevertheless, the positive result of this paper, together with a similar result from the angular correlation function is encouraging, but not yet definite; we still have to be very cautious, for a number of reasons:

Keeping all this in mind, we conclude that the anisotropy of the long subclass at a $\geq$99% significance level may be real. However, to reach a more definite conclusion several further independent tests are still needed.

We are aiming to provide such tests on BATSE data in future. We also hope that the results of this paper - together with those of the earlier papers - will encourage others to provide independent statistical tests on the angular distribution of GRBs.

Acknowledgements
Useful discussions with Drs. Z. Bagoly, L. G. Balázs, I. Horváth, P. Mészáros, R. Vavrek and the valuable remarks of the referee, Dr. V. Connaughton, are kindly acknowledged. This research was supported by Czech Research Grant J13/98: 113200004.

References


Copyright ESO 2003