A&A 403, 749-756 (2003)
DOI: 10.1051/0004-6361:20030373
D. Hestroffer
IMCCE, UMR CNRS 8028, Paris Observatory, 77 Av. Denfert Rochereau 75014 Paris, France
Received 20 December 2002 / Accepted 19 February 2003
Abstract
The Hipparcos satellite successfully gathered astrometric and photometric
information for a few solar system objects including natural satellites.
In contrast to the case for asteroids, the Hipparcos main-mission does
not provide the photometry - in the conventional sense - of planetary satellites.
Nevertheless, valuable
photometric results can be obtained, such as a modelling of the centre-to-limb
darkening of the bodies. We present in this paper results obtained for the photometry
with a periodic grid of the satellites J2 Europa and S6 Titan from the Hipparcos
main mission and within the FAST data-reduction Consortium. The Minnaert
parameter of S6 Titan is found to be
![]() ,
and for J2 Europa,
,
and for J2 Europa,
![]() .
Brightness variations with orbital phase are also given for Europa.
.
Brightness variations with orbital phase are also given for Europa.
Key words: planets and satellites: general - planets and satellites: individual: J2 Europa, S6 Titan
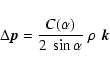
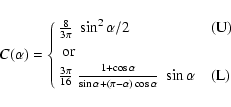
With the increasing accuracies of astrometric observations (ground-based, Hipparcos, GAIA, ...), much effort has been devoted to better knowledge or modelling of the brightness distribution of solar system objects (e.g. Morando & Lindegren 1989; Descamps 1994; Hestroffer 1998). This provides a better evaluation of the photocentre displacement (the shift of the photocentre relative to the geometric or gravity centre). Results on the brightness distribution have been obtained from speckle interferometry (McCarthy et al. 1994), analysis of the magnitude-phase curves for atmosphereless bodies (Lumme & Bowell 1981b; Domingue & Hapke 1989) or from analysis of lightcurves (Kaasalainen & Torppa 2001); in particular for natural satellites from Voyager or Pioneer observations (Buratti & Veverka 1983; Buratti 1984; Tomasko & Smith 1982), or from mutual events (Descamps et al. 1992).
It has been shown in a previous paper (Hestroffer & Mignard 1997b) that observation with a periodic grid provides the parameters of a simple centre-to-limb darkening model. The present paper gives the results obtained with this method from Hipparcos observations of natural satellites. First a general presentation of Hipparcos observations is made, next the reduction and model are developed. The application to the observations of J2 Europa and S6 Titan is given in the last sections.
The
![]() field of view of the telescope scans the sky at a velocity
of
field of view of the telescope scans the sky at a velocity
of
![]() .
During a transit of a star, the incoming light is modulated
by a periodic grid of period
.
During a transit of a star, the incoming light is modulated
by a periodic grid of period
![]() .
The fundamental periodic signal can
usefully be expanded in a second order Fourier series as:
.
The fundamental periodic signal can
usefully be expanded in a second order Fourier series as:
Once the sky background has been removed, the apparent magnitude is naturally given
in the Hipparcos photometric system Hp by:
| (2) |
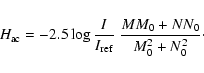 |
(3) |
While the
![]() quantity is not perturbed by stray or parasitic light of
a very extended source (because the background mainly is increased by a constant
amount), the observed magnitude
quantity is not perturbed by stray or parasitic light of
a very extended source (because the background mainly is increased by a constant
amount), the observed magnitude
![]() for the planetary satellites is significantly
corrupted. Figure 1 shows the residuals on
the absolute magnitudes, i.e. the measured
for the planetary satellites is significantly
corrupted. Figure 1 shows the residuals on
the absolute magnitudes, i.e. the measured
![]() magnitude corrected to one
astronomical unit and zero phase angle.
Stray light from Jupiter or Saturn, although strongly attenuated at large separation,
still corrupts the
magnitude corrected to one
astronomical unit and zero phase angle.
Stray light from Jupiter or Saturn, although strongly attenuated at large separation,
still corrupts the
![]() magnitudes that were measured by Hipparcos by about
0.1 mag. For this reason, no conventional
magnitude could be determined for the Hipparcos mission planetary satellites, and
the
magnitudes that were measured by Hipparcos by about
0.1 mag. For this reason, no conventional
magnitude could be determined for the Hipparcos mission planetary satellites, and
the
![]() magnitudes used in Fig. 1 were hence not published in the
Hipparcos catalogue solar system objects annex.
We will thus evaluate the magnitude bias from the observed quantity
magnitudes used in Fig. 1 were hence not published in the
Hipparcos catalogue solar system objects annex.
We will thus evaluate the magnitude bias from the observed quantity
![]() and calculated value of
and calculated value of
![]() .
The
.
The
![]() estimator is of lower accuracy than
estimator is of lower accuracy than
![]() ,
its precision also
decreases with the object's brightness. The average precision on
,
its precision also
decreases with the object's brightness. The average precision on
![]() is 0.04 for Titan and 0.015 for Europa.
is 0.04 for Titan and 0.015 for Europa.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3432f1.eps} \end{figure}](/articles/aa/full/2003/20/aa3432/Timg38.gif) |
Figure 1:
Influence of the major planet disturbing stray light versus separation.
It is given for the measures of the magnitude
|
| Open with DEXTER | |
Table 1: Values used in the reduction of S6 Titan and J2 Europa.
The attenuation of the harmonic amplitude depends on the object's size, but also on
the brightness distribution across its surface.
Taking the empirical law of Minnaert (1961), this distribution can be written:
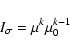
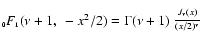 is
the hypergeometric function,
is
the hypergeometric function,
Fitting the observed magnitude bias with this model yields - for a given
diameter and photometric parameters - Minnaert's parameter k. The accuracy
of the limb-darkening parameter depends on the number of available observations and
the associated error, and we have the conservative values
![]() for
Europa, and
for
Europa, and
![]() for Titan.
for Titan.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3432f2.eps} \end{figure}](/articles/aa/full/2003/20/aa3432/Timg58.gif) |
Figure 2: Difference between the two magnitude estimators as a function of apparent diameter, for two particular cases of Minnaert's law and a spherical object seen at opposition. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3432f3.eps} \end{figure}](/articles/aa/full/2003/20/aa3432/Timg59.gif) |
Figure 3:
Magnitude bias |
| Open with DEXTER | |
The Galilean satellite Europa is known to have two significantly different
hemispheres. The leading one, visible at eastern elongation (EE), is bright and
covered with ice. In contrast, the trailing hemisphere visible at western
elongation (WE) is dark and the ice is still covered by dust. Also the brightness
distributions across the surface are different. In general, dark dusty surfaces appear
uniform and flat, while bright icy surfaces have a more pronounced centre-to-limb
darkening.
Although variation of magnitude with orbital phase is a well-known phenomenon for
the Galilean satellites (e.g. Morrison et al. 1974; Millis & Thompson 1975), it depends on
the solar phase angle, the sub-Solar point and sub-Earth point coordinates, the photometric
passband used, and at least for Europa, is far from being a simple function. Its
modelling in the
Hipparcos photometric band would be less accurate than the other transformations entering
in the reduction, thus the observations are not corrected for this effect.
Hence the bias ![]() depends not only on the apparent diameter and the limb-darkening
parameter, but also on this periodic variation.
depends not only on the apparent diameter and the limb-darkening
parameter, but also on this periodic variation.
Figure 3 shows the bias as a function of the apparent diameter
and the residuals obtained with a Minnaert parameter of k=0.58.
To compare, the residuals are given as a function of the orbital
phase angle ![]() (projected in the plane of the mean equator J2000) together with
a fit to ground-based observations in the V band (Morrison & Morrison 1977). The empirical
curve
represents the magnitude corrected for dependence on phase
(projected in the plane of the mean equator J2000) together with
a fit to ground-based observations in the V band (Morrison & Morrison 1977). The empirical
curve
represents the magnitude corrected for dependence on phase
![]() ,
and
corrected for an offset between the value
V(1,0)=-1.41 used here and the equivalent
value
V'(1,0)=-1.46 of Morrison & Morrison (1977). Interestingly, shifting this empirical curve
by about
,
and
corrected for an offset between the value
V(1,0)=-1.41 used here and the equivalent
value
V'(1,0)=-1.46 of Morrison & Morrison (1977). Interestingly, shifting this empirical curve
by about ![]() for the orbital phase would provide a better fit to the Eastern
data. No satisfactory explanation for this possible shift can be given here;
we note however that the range in solar phase angle is slightly different between
the Hipparcos (
for the orbital phase would provide a better fit to the Eastern
data. No satisfactory explanation for this possible shift can be given here;
we note however that the range in solar phase angle is slightly different between
the Hipparcos (
![]() )
and the ground-based observations (
)
and the ground-based observations (
![]() ). Moreover,
the latitude of the sub-Earth point is different between the two data sets. Last, it
is not obvious if the empirical lightcurve is corrected for light-time or plane
projection.
Nevertheless, referring to Table 2, the values for the observed
maximum (
). Moreover,
the latitude of the sub-Earth point is different between the two data sets. Last, it
is not obvious if the empirical lightcurve is corrected for light-time or plane
projection.
Nevertheless, referring to Table 2, the values for the observed
maximum (
![]() )
and minimum (
)
and minimum (
![]() )
magnitude
of Europa are larger than the results of Morrison et al. (1974), Blanco & Catalano (1974),
but in better agreement with Johnson (1971), Millis & Thompson (1975) and Domingue et al. (1991) who
consider observations from 1976 to 1989.
)
magnitude
of Europa are larger than the results of Morrison et al. (1974), Blanco & Catalano (1974),
but in better agreement with Johnson (1971), Millis & Thompson (1975) and Domingue et al. (1991) who
consider observations from 1976 to 1989.
Table 2:
Longitudes in degrees of ![]() and
and
![]() for Europa.
for Europa.
Any discrepancy in the orbital longitudes of maximal and minimal brightness has
however no consequence for the general trend of the magnitude bias and hence
the determination of the Minnaert parameter. One finds a good agreement for the
amplitude with the results of Morrison et al. (1974), Morrison & Morrison (1977), Millis & Thompson (1975) and
Domingue et al. (1991).
In particular, the amplitude in B-V, b-y and v-y are small enough so that no
further correction is required, hence the amplitude and asymmetry of the light curves
between the two different photometric systems are almost similar.
The mean value of the parameter k is acceptable for the majority of the data.
The significant scatter at western elongation is also present in the results of
Morrison & Morrison (1977).
A more pronounced centre-to-limb darkening (k=0.64) for part of the dark trailing
hemisphere (with solar elongation around
![]() )
would reduce this scatter,
but is in contradiction to the fact that dark surfaces are more likely to be less
limb-darkened. On the other hand, a less pronounced centre-to-limb darkening (k=0.5)
for the trailing hemisphere would also reduce this
scatter, but it would also yield a smaller brightness amplitude (0.28), in agreement with
Domingue et al. (1991).
Due to the complexity of the reduction and the various cross-correlations between the
corrective terms and parameters such as solar phase angle, separation or orbital phase,
no satisfactory explanation can be given here. The availability of the observed
(non-corrupted) magnitudes - and hence the actual lightcurve - would have helped to
put into evidence any variation of the limb-darkening parameter with the orbital phase.
)
would reduce this scatter,
but is in contradiction to the fact that dark surfaces are more likely to be less
limb-darkened. On the other hand, a less pronounced centre-to-limb darkening (k=0.5)
for the trailing hemisphere would also reduce this
scatter, but it would also yield a smaller brightness amplitude (0.28), in agreement with
Domingue et al. (1991).
Due to the complexity of the reduction and the various cross-correlations between the
corrective terms and parameters such as solar phase angle, separation or orbital phase,
no satisfactory explanation can be given here. The availability of the observed
(non-corrupted) magnitudes - and hence the actual lightcurve - would have helped to
put into evidence any variation of the limb-darkening parameter with the orbital phase.
Figure 4 shows the bias as a function of the apparent diameter,
and the residuals obtained with a model k=0.9 close to the value obtained from
Pioneer data by Smith (1980).
Observations around epoch
JD=2 448 936 show a strong variation in
![]() (
(![]() )
with the field of view, typical of parasitic light in the complementary
field; two suspicious data points were thus rejected.
The observations around epochs
JD=2 447 968 and
JD=2 447 989 show larger
residuals. Although Titan was close to S7 Hyperion or S5 Rhea (with a predicted
separation of less than 30 or 40 arcsec) at those epochs, the attenuation of the FOV should
have been sufficient to prevent such stray light.
)
with the field of view, typical of parasitic light in the complementary
field; two suspicious data points were thus rejected.
The observations around epochs
JD=2 447 968 and
JD=2 447 989 show larger
residuals. Although Titan was close to S7 Hyperion or S5 Rhea (with a predicted
separation of less than 30 or 40 arcsec) at those epochs, the attenuation of the FOV should
have been sufficient to prevent such stray light.
We adopt the absolute magnitude
V(1,0)=-1.28 from the Astronomical Almanac,
in accordance with the more recent observations made in July 1993 by Karkoschka (1994).
The observations are not spread over a large range of apparent diameter,
thus a small change in the value of the diameter can be balanced by a small
change in the Minnaert parameter k leaving the residuals almost unchanged; we have
roughly the linear relation
![]() .
The situation is
similar to the one encountered in lunar occultation and speckle interferometry
techniques. Since the radius of Titan (with its atmosphere) cannot be considered
as being a well-known quantity, we let it span the range from R=2800 to R=3000 km,
and find a corresponding realistic range
.
The situation is
similar to the one encountered in lunar occultation and speckle interferometry
techniques. Since the radius of Titan (with its atmosphere) cannot be considered
as being a well-known quantity, we let it span the range from R=2800 to R=3000 km,
and find a corresponding realistic range
![]() for
the Minnaert parameter by minimising the L1 norm of the residuals. A minimal value
of the residuals is however reached for R=2847 km and k=0.90.
for
the Minnaert parameter by minimising the L1 norm of the residuals. A minimal value
of the residuals is however reached for R=2847 km and k=0.90.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3432f4.eps} \end{figure}](/articles/aa/full/2003/20/aa3432/Timg73.gif) |
Figure 4:
Magnitude bias |
| Open with DEXTER | |
The Minnaert parameter k can show variation with solar phase angle and
wavelength. Moreover, since the two faces of J2 Europa have different photometric
behaviours, the derived value depends on the distribution of the observations versus
orbital phase. Descamps et al. (1992) found k=0.60 at
![]() nm and
k=0.57 at
nm and
k=0.57 at
![]() nm from analysis of ground-based observations of a mutual
event on February 10, 1991 with
nm from analysis of ground-based observations of a mutual
event on February 10, 1991 with
![]() .
Analysis of Voyager 1 and Voyager 2 observations by Buratti & Veverka (1983) yielded the average
values over the different filters
.
Analysis of Voyager 1 and Voyager 2 observations by Buratti & Veverka (1983) yielded the average
values over the different filters ![]() and 0.67 for solar phase
angles of
and 0.67 for solar phase
angles of
![]() and
and ![]() respectively. The limb-darkening
coefficients are not strongly wavelength dependent. The parameter derived
in the present study,
respectively. The limb-darkening
coefficients are not strongly wavelength dependent. The parameter derived
in the present study,
![]() ,
at larger phase angle is in global agreement
with the previous results.
The lower value may be compatible with a variation of the limb-darkening parameter
with solar phase angle. In the absence of a better knowledge of the
lightcurve of Europa in the given Hipparcos filter and at the given solar phase,
more refined values for the trailing and leading hemisphere seem difficult to
obtain. Such a limitation would not occur if the magnitude is measured
simultaneously with the modulation parameters, since the bias would be
independent of the actual brightness and its variation with solar or orbital phase
angles.
,
at larger phase angle is in global agreement
with the previous results.
The lower value may be compatible with a variation of the limb-darkening parameter
with solar phase angle. In the absence of a better knowledge of the
lightcurve of Europa in the given Hipparcos filter and at the given solar phase,
more refined values for the trailing and leading hemisphere seem difficult to
obtain. Such a limitation would not occur if the magnitude is measured
simultaneously with the modulation parameters, since the bias would be
independent of the actual brightness and its variation with solar or orbital phase
angles.
Table 3: Europa's limb-darkening parameter.
Table 4: Titan's limb-darkening parameter.
Using the composite cloud model of Tomasko (1980) for Titan, Smith (1980) derived
an average limb-darkening parameter for the small phase angle
![]() .
Using his result
.
Using his result ![]() one can derive a model-dependent value of Titan's
diameter for the different techniques of observation. The lunar occultation radius
is revised to R=2845 km, the speckle radius to R=2742 km, and the modulation
photometry radius to R=2847 km. The radius found here is in good agreement with
the results of Smith (1980),
one can derive a model-dependent value of Titan's
diameter for the different techniques of observation. The lunar occultation radius
is revised to R=2845 km, the speckle radius to R=2742 km, and the modulation
photometry radius to R=2847 km. The radius found here is in good agreement with
the results of Smith (1980),
![]() km, and Elliot et al. (1975),
though values of k "below 1 fit [their] data poorly and appear to be ruled out".
Nisenson et al. (1981) found a range
km, and Elliot et al. (1975),
though values of k "below 1 fit [their] data poorly and appear to be ruled out".
Nisenson et al. (1981) found a range
![]() for
for
![]() .
Although a systematic offset is present, where their data yield smaller values for
the diameter, there are no contradictions between our results and the speckle
data. Analysis of the best resolved observations obtained from Voyager 1 gives the
optical limb (defined here by the photometric inflection) at a radius
of
.
Although a systematic offset is present, where their data yield smaller values for
the diameter, there are no contradictions between our results and the speckle
data. Analysis of the best resolved observations obtained from Voyager 1 gives the
optical limb (defined here by the photometric inflection) at a radius
of
![]() km, with a higher optical haze layer extending up to
2845 km (Smith et al. 1981). Because Hipparcos is unable to resolve the thin
haze layer, and because we consider a brightness step function at the limb, our result
is consistent with the Voyager data.
Our result is in contradiction with the earlier determinations by Dollfus (1970),
R=2435 km, and larger than the value given by Burns (1986),
R=2775 km. Adopting the solid-surface radius R=2575 km (Lindal et al. 1983; Young et al. 2002),
we find that the atmosphere extends to about
km, with a higher optical haze layer extending up to
2845 km (Smith et al. 1981). Because Hipparcos is unable to resolve the thin
haze layer, and because we consider a brightness step function at the limb, our result
is consistent with the Voyager data.
Our result is in contradiction with the earlier determinations by Dollfus (1970),
R=2435 km, and larger than the value given by Burns (1986),
R=2775 km. Adopting the solid-surface radius R=2575 km (Lindal et al. 1983; Young et al. 2002),
we find that the atmosphere extends to about ![]() km from the surface, hence
considerably less than the value of Forrest & Nicolson (1990),
km from the surface, hence
considerably less than the value of Forrest & Nicolson (1990), ![]() km, obtained from
stellar occultation data in the R-filter band.
km, obtained from
stellar occultation data in the R-filter band.
Table 5:
Hipparcos observations of Europa, Titan and Iapetus, and corresponding aspect data. The
date of observation is given in TDT with respect to JD 2 440 000.0,
the non-conventional and biased magnitude
![]() and corresponding
precision are given in
fields 2 and 3. The distances to the Sun r and to the Hipparcos satellite
and corresponding
precision are given in
fields 2 and 3. The distances to the Sun r and to the Hipparcos satellite
![]() ,
the solar phase angle
,
the solar phase angle ![]() and the projected orbital
phase
and the projected orbital
phase ![]() are given in fields 4 to 7.
are given in fields 4 to 7.
In a normal context, those limitations encountered for Europa would not appear since the analysis of the modulated photometry with a periodic grid would be done with the measured apparent brightness. On an other hand, this modulated-photometry method is completely orthogonal to the one used, for instance, by Lumme & Bowell (1981b), Domingue & Hapke (1989) or Kaasalainen et al. (2002) to derive the scattering properties of solar system objects. The law of Minnaert is empirical and gives a rough estimation of the scattering properties of solar system bodies' surface or atmosphere. The more appropriate 2 parameter-model of Buratti & Veverka (1983) could also be used in photometric observations with a periodic grid.