M. Weiler 1 - H. Rauer 1 - J. Knollenberg 1 - L. Jorda 2 - J. Helbert 1
1 - Institute of Space Sensor Technology and Planetary
Exploration, DLR,
Rutherfordstrasse 2, 12489 Berlin, Germany
2 -
Laboratoire d'Astrophysique de Marseille, Site Pereisc,
13376 Marseille Cedex 12, France
Received 27 November 2002 / Accepted 20 February 2003
Abstract
The active comet C/1995 O1 (Hale-Bopp) was
target of an optical long-term monitoring program carried out at the European
Southern Observatory (ESO) (Rauer et al. 1997, 2003). Longslit spectra
and images were obtained at
heliocentric distances from 4.6 AU to 2.9 AU preperihelion and 2.8 AU
to 12.8 AU postperihelion. Based on these data, the dust activity of
comet Hale-Bopp is analysed. The color of the dust coma and the
Af![]() parameter are determined. A model for the dust release from
the cometary nucleus is presented and used to compute dust
production rates. The dust to gas ratio is determined.
parameter are determined. A model for the dust release from
the cometary nucleus is presented and used to compute dust
production rates. The dust to gas ratio is determined.
Key words: comets: general - comets: individual: Hale-Bopp
The dust-to-gas abundance seems to vary from comet to comet. A statistical analysis of the amount of dust in comets from different origins (e.g. Kuiper-belt comets or Oort cloud comets) could reveal inhomogenities in the preplanetary cloud. To perform such analysis, it is necessary to determine the dust to gas ratio in the comae of a large number of comets. However, deriving the dust production rates of comets is difficult because only little is known about the physical and chemical properties of the dust grains.
To estimate the dust production of a comet from the quantity of scattered sunlight, a model is needed which has to take the scattering properties of the dust particles, their physical characteristics and velocities into account.
Comet C/1995 O1 Hale-Bopp was an extraordinary bright and active comet, thus being an ideal object for long-term observations to collect data over a wide range of heliocentric distances. Observations of comet Hale-Bopp over a time of five years can be used to analyse the dust activity and its variation with changing heliocentric distances.
Table 1:
Observations of Comet Hale-Bopp. n:
number of comet spectra per night, ![]() and
and ![]() :
heliocentric and
geocentric distances,
:
heliocentric and
geocentric distances, ![]() :
phase angle,
:
phase angle,
![]() :
spatial
scale per pixel,
:
spatial
scale per pixel,
![]() :
wavelength scale per pixel, x: slit
width. Negative
:
wavelength scale per pixel, x: slit
width. Negative ![]() indicates observations before perihelion on
April 1, 1997.
indicates observations before perihelion on
April 1, 1997.
Comet C/1995 O1 Hale-Bopp was observed at optical wavelengths between
April 1996 and January 2001 at the European
Southern Observatory (ESO), Chile. Medium-resolution spectra and images were
obtained during this long-term observation campaign, covering a range
of heliocentric distances, ![]() ,
from 4.6 to 2.9 AU preperihelion
and 2.8 to 12.8 AU postperihelion (see Table 1, details of
the long-term observation program are described by Rauer et al. 2003).
,
from 4.6 to 2.9 AU preperihelion
and 2.8 to 12.8 AU postperihelion (see Table 1, details of
the long-term observation program are described by Rauer et al. 2003).
Standard data reduction routines were applied to the spectra, including bias subtraction, flatfielding, wavelengths calibration, sky background subtraction and extinction correction. At large heliocentric distances, the sky background was determined from the edges of the long-slit spectra since the coma did not fill the entire slit length. At smaller distances, separate spectra of the sky were used for background determination. They were obtained close in time to the comet observations with a spatial offset up to 30', but at the same elevation as the comet. The extinction corrections were performed using ESO standard extinction curves. Absolute flux calibration was performed using standard stars (Rauer et al. 2003). In order to separate the contributions of gaseous cometary emissions and scattered light by dust particles, a solar catalogue spectrum (Kurucz et al. 1984) was matched to the cometary spectra by convolution with a Gaussian profile and a polynomial fit. The fitted solar spectrum can be subtracted from the cometary spectrum to obtain the gaseous emissions.
In this work, the fitted solar spectra were treated as approximation
of the continuum flux
scattered by the cometary dust and used to analyse the dust activity
at
![]() AU. Beyond 6 AU, the measured spectra were used directly,
because no gas emission lines were present in the wavelengths
interval used in this study. The wavelengths interval was limited to
the range from 4100 Å to 6100 Å which is covered by most spectra
of our data set. Stellar spectra from background stars were removed
from longslit spectra by interpolation along the spatial
direction. The photometric
uncertainty of spectra is estimated to be
AU. Beyond 6 AU, the measured spectra were used directly,
because no gas emission lines were present in the wavelengths
interval used in this study. The wavelengths interval was limited to
the range from 4100 Å to 6100 Å which is covered by most spectra
of our data set. Stellar spectra from background stars were removed
from longslit spectra by interpolation along the spatial
direction. The photometric
uncertainty of spectra is estimated to be ![]() 10%. However,
additional uncertainties arise in the calibration of the cometary
spectra, e.g. due to the separation of the continuum flux and the
gas emission features. We estimate the total uncertainty to about
20-30%.
10%. However,
additional uncertainties arise in the calibration of the cometary
spectra, e.g. due to the separation of the continuum flux and the
gas emission features. We estimate the total uncertainty to about
20-30%.
Due to scattered background light on the CCD at the Danish 1.5 m telescope, wavelengths shorter than approximately 4600 Å could not be used for analysis in this work in data taken at this telescope.
To allow a test of the results obtained from longslit-spectra and to
search for spatial structures in the coma of comet Hale-Bopp, B- and
R-filter images were used. The reduction includes bias-, flatfield
and sky background correction. Images of standard stars according to
Landolt (1992) were used for photometric calibration. The calibration
was performed by using the
standard extinction and color correction terms as provided by ESO. The
accuracy of the photometric calibration could be estimated by
calibrating images of different standard star fields with the same
star used to calibrate the comet images. We estimate the uncertainty
in the comet magnitudes to be ![]() 5%. An overview on the reduced
images is given in Table 2.
5%. An overview on the reduced
images is given in Table 2.
Table 2:
Overview of B- and R-filter images used here. ![]() and
and
![]() denote heliocentric and geocentric distances. The standard
star used for calibration of the comet images is quoted. The calibrations
were performed using the standard star from each field with color
indices similar to the solar colors.
denote heliocentric and geocentric distances. The standard
star used for calibration of the comet images is quoted. The calibrations
were performed using the standard star from each field with color
indices similar to the solar colors.
As a measure of the wavelengths dependent scattering of solar light by
dust particles, the reddening ![]() is
computed. It is defined as
(Jewitt & Meech 1986):
is
computed. It is defined as
(Jewitt & Meech 1986):
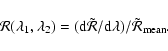 |
(1) |
![]() and d
and d
![]() is the rate of change of
is the rate of change of
![]() within the
wavelengths interval [
within the
wavelengths interval [![]() ,
,![]() ].
].
![]() is the mean value of
is the mean value of
![]() over
the wavelengths interval. The reddening is
computed for each position along the slit to obtain a reddening
profile through the cometary coma.
over
the wavelengths interval. The reddening is
computed for each position along the slit to obtain a reddening
profile through the cometary coma.
A comparison of the reddening of
spectra, given in [%/103 Å], and reddening values obtained from
image photometry using broad-band filters, B and R, is possible by
applying the relation given by Jockers (1999),
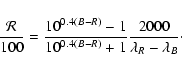 |
(2) |
As an example, the reflectivity
![]() obtained from long-slit spectra on August 28/29,
2001 is shown in Fig. 1,
normalized at 6000 Å. Two nearly linear sections
can be seen. Hence straight lines are fitted to the reflectivity
curves in the wavelengths intervalls from 4100 Å to 5400 Å (here
called "blue'') and 5400 Å to 6100 Å (here called "red'') to compute
obtained from long-slit spectra on August 28/29,
2001 is shown in Fig. 1,
normalized at 6000 Å. Two nearly linear sections
can be seen. Hence straight lines are fitted to the reflectivity
curves in the wavelengths intervalls from 4100 Å to 5400 Å (here
called "blue'') and 5400 Å to 6100 Å (here called "red'') to compute ![]() .
.
Only slight variations in the reddening along the slit have been found. Fig. 2 shows the reddening profile for one night as example.
We determined the mean reddening averaged along the slit. At large heliocentric distances, the dust coma was smaller than the projected slit length. The projected nucleocentric radius covered was then limited to a signal to noise ratio larger than five times the background noise, which could be determined at the edges of the slit. When the coma filled the whole projected slit length at small heliocentric distances, the range of nucleocentric distances used was selected based on a sufficiently high signal-to-noise ratio.
In Fig. 3 the computed mean reddening values in the cometary coma are shown. All spectra of one night with the same slit orientation were averaged. Since the blue wavelengths range was not available for observations with the Danish 1.5 m telescope due to background light on the CCD, no normalized reflectivity gradients could be derived in the wavelengths interval [4100 Å, 5400 Å] preperihelion.
The reddening obtained from B- and R-filter images, with effective wavelengths at 4400 Å and 7100 Å, are compared to the reddening obtained from spectra in Table 3 for data at large heliocentric distances. The results are in fairly good agreement. No significant spatial variations in reddening have been seen in these images, confirming the result from longslit spectra.
Figure 3 shows no significant change in reddening with heliocentric distance up to nearly 13 AU. Previous publications (Jewitt & Meech 1986, 1988) on other comets also report no systematic trends in reddening of cometary comae up to heliocentric distances of 6 AU.
The dust color depends on the grain size, the grain shape and the
optical constants of the material forming the dust particles. Since
one would not expect the shape and optical constants of cometary dust
to change dramatically with heliocentric distance, the size
distribution of the dust particles should be the major influence on
the measured reddening. Although the maximum grain radius for particles
that could be lifted from the
nucleus surface is expected to decrease below 10 ![]() m (see Sect. 5) in the range of heliocentric distances covered by our observations,
the size of dust grains dominating the optical light scattering is about 0.5
m (see Sect. 5) in the range of heliocentric distances covered by our observations,
the size of dust grains dominating the optical light scattering is about 0.5 ![]() m (Williams et al. 1997; Jones & Gehrz 2000) and thus much smaller than the maximum
grain size derived with the model described in Sect. 5. Hence, the
optical light scattering is not expected
to be affected by the variation of the dust size distribution within
the considered range of heliocentric distances. Therefore, the dust
reddening derived from optical observations is expected to be constant on
a wide range of heliocentric distances, as confirmed by our
observations.
m (Williams et al. 1997; Jones & Gehrz 2000) and thus much smaller than the maximum
grain size derived with the model described in Sect. 5. Hence, the
optical light scattering is not expected
to be affected by the variation of the dust size distribution within
the considered range of heliocentric distances. Therefore, the dust
reddening derived from optical observations is expected to be constant on
a wide range of heliocentric distances, as confirmed by our
observations.
Table 3:
Comparison of the reddening from spectra, R(spectra), on the
wavelength interval [4400 Å, 7100 Å] and from B and R filter
images, R(images). (![]() Result possibly affected by cirrus
clouds during observation of spectrophotometric standard star).
Result possibly affected by cirrus
clouds during observation of spectrophotometric standard star).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4135_F1.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg41.gif) |
Figure 1:
Reflectivity,
|
| Open with DEXTER | |
The parameter Af![]() was introduced by A'Hearn et al. (1984) as
was introduced by A'Hearn et al. (1984) as
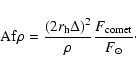 |
(3) |
Af![]() was calculated from B- and R-filter images for the nights
listed in Table 2. All values were obtained using
was calculated from B- and R-filter images for the nights
listed in Table 2. All values were obtained using
![]() km.
km. ![]() was taken from Cox (2000).
was taken from Cox (2000).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4135_F2.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg47.gif) |
Figure 2: Spatial reddening profile for August 28/29, 2000. Filled symbols show the reddening on the "blue'' interval (4100 Å to 5400 Å), open symbols on the "red'' interval (5400 Å to 6100 Å) along the slit versus projected distance from the nucleus. Negative distances denote the sunward side, positive distances the tailward side of the nucleus. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4135_F3.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg48.gif) |
Figure 3: Mean reddening in the coma of comet Hale-Bopp, for the "blue'' wavelength interval (top panel) and the "red'' interval (lower panel). Filled and open symbols mark data derived from the sunward and tailward side of the coma. |
| Open with DEXTER | |
To obtain the quantity Af![]() from long-slit spectra instead of
aperture photometry, the expected flux through a spherical diaphragm
centred on the nucleus with radius
from long-slit spectra instead of
aperture photometry, the expected flux through a spherical diaphragm
centred on the nucleus with radius ![]() is computed from the radial
intensity profile along the slit. In order to do so, it has to be
assumed that the cometary coma is rotationally symmetric. This method
is, therefore, more sensitive to coma asymmetries than large aperture
photometry. To estimate the effects of coma asymmetries, the expected
flux is calculated using radial profiles along the sunward and tailward
side of the cometary nucleus independently. The mean
values of Af
is computed from the radial
intensity profile along the slit. In order to do so, it has to be
assumed that the cometary coma is rotationally symmetric. This method
is, therefore, more sensitive to coma asymmetries than large aperture
photometry. To estimate the effects of coma asymmetries, the expected
flux is calculated using radial profiles along the sunward and tailward
side of the cometary nucleus independently. The mean
values of Af![]() are determined by averaging Af
are determined by averaging Af![]() derived from
each side of the nucleus and from all spectra of one night, obtained
with the same slit orientation. Af
derived from
each side of the nucleus and from all spectra of one night, obtained
with the same slit orientation. Af![]() from radial intensity
profiles show a weak dependency on the
from radial intensity
profiles show a weak dependency on the ![]() used. For
used. For
![]() km, the variation was found to be less then
approx. 20%.
km, the variation was found to be less then
approx. 20%.
![]() was taken from Kurucz et al. (1984).
was taken from Kurucz et al. (1984).
The computed Af![]() -parameters from R-filter images and long-slit
spectra are shown in Fig. 4. For comparison, Af
-parameters from R-filter images and long-slit
spectra are shown in Fig. 4. For comparison, Af![]() values from other publications are included. The bars connect the
individual Af
values from other publications are included. The bars connect the
individual Af![]() values computed using profiles from both sides of
the nucleus and are thus an indicator for the coma asymmetry.
values computed using profiles from both sides of
the nucleus and are thus an indicator for the coma asymmetry.
The Af![]() parameters obtained are in good agreement with previous
publications and significantly extend the observed heliocentric
distance range for comet Hale-Bopp.
parameters obtained are in good agreement with previous
publications and significantly extend the observed heliocentric
distance range for comet Hale-Bopp.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{H4135_F4.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg51.gif) |
Figure 4:
Af |
| Open with DEXTER | |
Assuming a spherical nucleus and isotropic emission of dust, the
dust number and mass production rates, QN and QM, are
related to the parameter Af![]() by (Jorda 1995):
by (Jorda 1995):
Unfortunately, only little is known about cometary dust. Therefore, a number of plausible assumptions have to be made in order to estimate the dust production rates.
In this work, the phase function ![]() from Divine (1981)
has been used:
from Divine (1981)
has been used:
| (6) |
| |
= | (7) | |
In the range of phase angles ![]() of our observations of comet
Hale-Bopp, this phase function corresponds to a correction to zero
phase angle of approximately 0.02 mag per degree. This is a low
value compared to other assumptions, e.g. 0.035 mag per degree
by Weaver et al. (1997). Corrections with 0.02 and 0.035 magnitudes per
degree result in differences of 6% up to 31% for the fluxes
corrected to zero phase angle.
of our observations of comet
Hale-Bopp, this phase function corresponds to a correction to zero
phase angle of approximately 0.02 mag per degree. This is a low
value compared to other assumptions, e.g. 0.035 mag per degree
by Weaver et al. (1997). Corrections with 0.02 and 0.035 magnitudes per
degree result in differences of 6% up to 31% for the fluxes
corrected to zero phase angle.
A Bond-albedo ![]() of 0.3 is assumed. This value is higher than the
often assumed value of
of 0.3 is assumed. This value is higher than the
often assumed value of
![]() and is based on values determined
from optical and infrared observations (Mason et al. 2001; Grün et al. 2001) of comet
Hale-Bopp. From these observations, higher albedos for comet Hale-Bopp
than for most other comets are deduced, which is assumed to be
caused by unusually small dust particles in the coma of comet Hale-Bopp
(Williams et al. 1997; Mason et al. 2001).
and is based on values determined
from optical and infrared observations (Mason et al. 2001; Grün et al. 2001) of comet
Hale-Bopp. From these observations, higher albedos for comet Hale-Bopp
than for most other comets are deduced, which is assumed to be
caused by unusually small dust particles in the coma of comet Hale-Bopp
(Williams et al. 1997; Mason et al. 2001).
The functions and parameters f(a),
![]() and
a1 = 0.1
and
a1 = 0.1 ![]() m from Newburn & Spinrad (1985) are used. The dust size
distribution function is:
m from Newburn & Spinrad (1985) are used. The dust size
distribution function is:
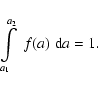 |
(9) |
The dust density is assumed by Newburn & Spinrad (1985) as
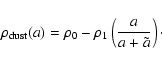 |
(10) |
In order to determine v(a) and a2, a gasdynamical model for the gas stream caused by sublimation of the comet nucleus is used. The dust particles are then treated as test particles affected by this gas stream.
The gas flow is determined by the Euler-equations. They are solved in
spherical coordinates as given by Körösmezey & Gombosi (1990), neglecting the
influence of the dust on the gas flow:
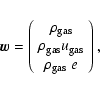 |
(12) |
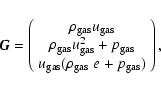 |
(13) |
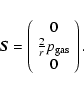 |
(14) |
We neglect the influence of the dust on the gas flow in our
model, although in case of large dust mass loading of the gas stream
this effect can be significant. However, in case of comet Hale-Bopp at the
heliocentric distances of our observations, the observed gas velocity
in the coma,
![]() ,
fitted by
,
fitted by
![]() km s-1 (Biver et al. 1999), can be well approximated by
the terminal gas velocity corresponding to isentropic expansion of a
mixture of water and carbon monoxide from a gas reservoir at the
sublimation temperature T0 (Landau & Lifschitz 1993). If the influence of
dust on the gas flow would be significant, one would expect a higher
gas velocity in the coma than derived from a reservoir outflow model
since the dust would transfer heat to the gas and thus lead to a
higher gas velocity. This is not observed and we, therefore, consider
the influence of the dust on the gas flow to be negligible at the
distance range considered here.
km s-1 (Biver et al. 1999), can be well approximated by
the terminal gas velocity corresponding to isentropic expansion of a
mixture of water and carbon monoxide from a gas reservoir at the
sublimation temperature T0 (Landau & Lifschitz 1993). If the influence of
dust on the gas flow would be significant, one would expect a higher
gas velocity in the coma than derived from a reservoir outflow model
since the dust would transfer heat to the gas and thus lead to a
higher gas velocity. This is not observed and we, therefore, consider
the influence of the dust on the gas flow to be negligible at the
distance range considered here.
We now discuss the inner boundary conditions. The inner boundary
conditions,
![]() ,
,
![]() and
and
![]() at the surface of the
comet nucleus, were determined from a reservoir outflow model in
conjunction with a fit to the observed gas production rates as
described below.
at the surface of the
comet nucleus, were determined from a reservoir outflow model in
conjunction with a fit to the observed gas production rates as
described below.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4135_F5.eps} \end{figure}](/articles/aa/full/2003/19/aah4135/Timg85.gif) |
Figure 5:
Size dependent nucleocentric terminal dust
velocities. The dust velocities calculated for grain radii |
| Open with DEXTER | |
The velocity
![]() at the surface is computed assuming the gas to
flow with Mach number M=1 from a nucleus surface with temperature T0. This leads to (Knollenberg 1994)
at the surface is computed assuming the gas to
flow with Mach number M=1 from a nucleus surface with temperature T0. This leads to (Knollenberg 1994)
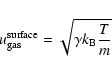 |
(15) |
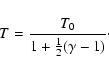 |
(16) |
For the sublimation rate
![]() an approach according to
Fanale & Salvail (1984) is used:
an approach according to
Fanale & Salvail (1984) is used:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4135_F6.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg99.gif) |
Figure 6:
Maximum dust grain radii
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4135_F7.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg100.gif) |
Figure 7: Dust production rates, determined with the model described in Sect. 5. Filled symbols show mass production rates (left scale), empty symbols production rates by number (right scale). |
| Open with DEXTER | |
In most cases, measurements of ![]() and CO production rates of
comet Hale-Bopp do not exist for the exact heliocentric distances of
our observations. They, therefore, had to be interpolated and
extrapolated to our observing dates from the various existing
production rate determinations.
Equations (17) and (18) were used to compute the water
production rates versus heliocentric distance. Then,
and CO production rates of
comet Hale-Bopp do not exist for the exact heliocentric distances of
our observations. They, therefore, had to be interpolated and
extrapolated to our observing dates from the various existing
production rate determinations.
Equations (17) and (18) were used to compute the water
production rates versus heliocentric distance. Then,
![]() was fitted to the observed water and OH production
rates given by Weaver et al. (1999), Weaver et al. (1999), Stern et al. (1999) and
DiSanti et al. (1999) by a scaling factor,
was fitted to the observed water and OH production
rates given by Weaver et al. (1999), Weaver et al. (1999), Stern et al. (1999) and
DiSanti et al. (1999) by a scaling factor, ![]() .
For this, the
nucleus radius, RN, is needed. Values of RN range from 22 km
(Altenhoff et al. 1999) to 35 km (Sekanina 1999). Here, RN is
assumed to be 30 km. The fitted solution agrees well with the observed
data and was used to obtain the water production rate at the
heliocentric distances of our observations.
The CO production rates were determined by fitting a power law to the
measured production rates as given by Biver et al. (1999).
.
For this, the
nucleus radius, RN, is needed. Values of RN range from 22 km
(Altenhoff et al. 1999) to 35 km (Sekanina 1999). Here, RN is
assumed to be 30 km. The fitted solution agrees well with the observed
data and was used to obtain the water production rate at the
heliocentric distances of our observations.
The CO production rates were determined by fitting a power law to the
measured production rates as given by Biver et al. (1999).
The gas density at the nucleus surface,
![]() ,
was
determined by distributing the gas production rate determined from
the fit to the observed values over an active nucleus surface area:
,
was
determined by distributing the gas production rate determined from
the fit to the observed values over an active nucleus surface area:
A more sophisticated model for water production of comet Hale-Bopp
(Kührt 1999) than applied in this work deduces a nuclear radius
of 13 km for a pure water ice sphere necessary to produce the observed
quantity of water released by comet Hale-Bopp. This leads, in
combination with RN, to an active surface fraction of approximately 19%, which is assumed here as our nominal value of f.
Finally,
![]() follows from the ideal gas law:
follows from the ideal gas law:
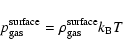 |
(20) |
The Euler-Eq. (11) were solved using a Godunov-type scheme of second order (Harten et al. 1983). The equation of motion for dust particles was solved by using a Runge-Kutta scheme of fourth order. In Eq. (4), the velocity v(a) computed at a nucleocentric distance of 103 km was used. The gas density decreases rapidly with increasing nucleocentric distance and, thus, the dust decouples within a few nuclear radii above the surface (Probstein 1969). Therefore, v(a)calculated at 103 km from the nucleus is a good aproximation of the terminal velocity of a dust particle.
The dust velocities for some dust grain radii obtained using this model
are shown in Fig. 5, together with dust velocities from other
publications. The dust velocity from Fulle et al. (1998) was derived from
coma simulations for particles of 10 ![]() m radius. The dust
velocities from Braunstein et al. (1999) and Sekanina
(1996) were
estimated from observations of moving coma structures. Projected dust
velocities as determined from observations of coma features are also
given. These values were derived from both optical and infrared
observations and do not refer to a particular dust grain size. Since the
dominant contribution to the observed light scattered by dust comes
from particles with sizes similar to the wavelength of the light, the
observational projected dust velocities are lower limits for dust
grains with radii of approximately 0.5
m radius. The dust
velocities from Braunstein et al. (1999) and Sekanina
(1996) were
estimated from observations of moving coma structures. Projected dust
velocities as determined from observations of coma features are also
given. These values were derived from both optical and infrared
observations and do not refer to a particular dust grain size. Since the
dominant contribution to the observed light scattered by dust comes
from particles with sizes similar to the wavelength of the light, the
observational projected dust velocities are lower limits for dust
grains with radii of approximately 0.5 ![]() m to a few microns.
A good agreement between our model results and observational data
over a wide range of heliocentric distances is found within the
observational and modelling uncertainties.
m to a few microns.
A good agreement between our model results and observational data
over a wide range of heliocentric distances is found within the
observational and modelling uncertainties.
The maximum radii of dust grains lifted from the
nucleus calculated with different model parameters are shown as a
function of heliocentric distance in Fig. 6. A strong
influence of the assumed nucleus radius (in Fig. 6:
25 km, 30 km, 35 km, compare B, C, D) and the assumed active
surface fraction (in Fig. 6: 5%, 19%, 50%, compare A, C, E) can be seen. An active surface fraction of 50% means the gas
production to originate from the whole sunward hemisphere of the nucleus. 5%
active fraction means a lower limit, for a nucleus with 30 km radius,
just enough to explain the observed water production rates with our
simple model using constant zenith angle.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H4135_F8.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg113.gif) |
Figure 8: Dust mass production rates for different model parameters. Upper panel: RN = 30 km and active surface fractions fof 5%, 19% and 50% of the total surface. Lower panel: active surface fraction f = 19% and RN of 25 km, 30 km and 35 km. The values for the preferred parameters (RN = 30 km, f = 19%) are shown (dots) and power law fits to the dust production rates calculated with the different parameters are plotted. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H4135_F9.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg114.gif) |
Figure 9:
Dust mass production rates for different model
parameters. Upper panel: dust size distribution parameter M = 1.8 and
N =3.3, 3.6 and 3.9. Lower panel: N = 3.6 and M = 1.8, 7.2 and 68.4 The
parameters N and M correspond to a peak in the dust size distribution
at 0.15 |
| Open with DEXTER | |
The dust production rates computed with the model described above are shown in Fig. 7.
In order to estimate the influence of the different parameters used in this model, Fig. 8 shows the variation of the dust mass production rates with changing active surface fraction f at constant nucleus radius (upper panel) and with changing nucleus radius at constant f (lower panel). A strong increase of the dust production rate with decreasing f can be seen. When reducing f, the observed gas production is concentrated on a smaller surface area, thus leading to a higher gas density at the nucleus surface. From this, a higher dust terminal velocity and a larger liftable dust size results. A higher dust velocity and larger values of a2 lead to an increase of the dust production rate.
A larger nucleus radius leads to a decrease of the dust mass
production rate due to the influence of gravitation and gas density
at the nucleus surface on the dust velocity and a2. Assuming a
minimum nucleus radius of 13 km and varing RNand f with
![]() (meaning constant active surface
area) leads to a lower a2 for a
larger RN due to gravity, but to a higher dust terminal velocity
since the gas density decreases more slightly for a larger
radius. Therefore, only a weak variation of the dust production rate
of some percent results from a combined variation of RN and f.
(meaning constant active surface
area) leads to a lower a2 for a
larger RN due to gravity, but to a higher dust terminal velocity
since the gas density decreases more slightly for a larger
radius. Therefore, only a weak variation of the dust production rate
of some percent results from a combined variation of RN and f.
The influence of the dust size distribution parameters M and N on the
dust mass production rates are shown in Fig. 9. Even
deviations from the size distribution parameters being larger than the
uncertainties derived for comet
Hale-Bopp (
![]() (Fulle et al. 1998), peak at
(Fulle et al. 1998), peak at
![]() m,
m,
![]() at 0.3-0.5
at 0.3-0.5 ![]() m for other comets
(Williams et al. 1997) have only moderate influence on the dust production
rates, compared to the influence of the nucleus parameters (Fig. 8). A reduction of the parameter a1 by a factor of 2
leads to a mean variation of the dust mass production rates of
approximately 15%.
m for other comets
(Williams et al. 1997) have only moderate influence on the dust production
rates, compared to the influence of the nucleus parameters (Fig. 8). A reduction of the parameter a1 by a factor of 2
leads to a mean variation of the dust mass production rates of
approximately 15%.
In Fig. 10, the Af![]() to gas mass ratios and dust
to gas mass ratios are shown. The gas mass production rates are
the sum of the
to gas mass ratios and dust
to gas mass ratios are shown. The gas mass production rates are
the sum of the ![]() and CO production rates, since these two
molecules are the most abundant in the coma. For
comparison, dust to gas mass ratios from different literature sources
are also shown. The dust to gas ratios according to Weaver et al. (1999)
were computed using their dust production rates and gas production
rates determined as described in Sect. 5.
and CO production rates, since these two
molecules are the most abundant in the coma. For
comparison, dust to gas mass ratios from different literature sources
are also shown. The dust to gas ratios according to Weaver et al. (1999)
were computed using their dust production rates and gas production
rates determined as described in Sect. 5.
![\begin{figure}
\par\includegraphics[width=14.2cm,clip]{H4135F10.eps}
\end{figure}](/articles/aa/full/2003/19/aah4135/Timg118.gif) |
Figure 10:
Af |
| Open with DEXTER | |
An increase of the Af![]() to gas ratio with increasing
heliocentric distance can be seen, as reported before (Rauer et al. 1997).
This trend stops at approximately 7 AU to 8 AU from the Sun.
to gas ratio with increasing
heliocentric distance can be seen, as reported before (Rauer et al. 1997).
This trend stops at approximately 7 AU to 8 AU from the Sun.
The dust to gas mass ratios obtained in this work are nearly
constant with changing heliocentric distance. A linear least squares
fit to the postperihelion mean values of
![]() over heliocentric
distance leads to
over heliocentric
distance leads to
![]() .
The
linear least squares fits to the dust to gas mass ratios obtained when
using QM computed
with the model parameters as shown in Figs. 8 and 9 are shown as dotted lines in Fig. 10. The
highest dust to gas mass ratio follows from an active surface fraction
of 5%, the lowest for an active surface fraction of 50%. A stronger
dependency of light scattering on the phase angle (e.g.
.
The
linear least squares fits to the dust to gas mass ratios obtained when
using QM computed
with the model parameters as shown in Figs. 8 and 9 are shown as dotted lines in Fig. 10. The
highest dust to gas mass ratio follows from an active surface fraction
of 5%, the lowest for an active surface fraction of 50%. A stronger
dependency of light scattering on the phase angle (e.g.
![]() per degree) would lead to slightly higher dust to gas
mass ratios and a steeper decrease with increasing heliocentric
distance. Although
the absolute values of the dust to gas mass ratios vary with changing
model parameters, the slight decrease in the dust to gas mass ratio
with increasing heliocentric distance can be seen for all parameters.
per degree) would lead to slightly higher dust to gas
mass ratios and a steeper decrease with increasing heliocentric
distance. Although
the absolute values of the dust to gas mass ratios vary with changing
model parameters, the slight decrease in the dust to gas mass ratio
with increasing heliocentric distance can be seen for all parameters.
The trend in the dust to gas mass ratio differs from results
published previously (e.g. Weaver et al. 1999; Rauer et al. 1997). This is caused by two
effects. Firstly, the dust velocity is not assumed to follow a law of
the form
![]() ,
as done in the publications
mentioned. Instead, the dust velocities used here are calculated by a
reasonable physical model. A
second influence is the increase of the maximum grain radius that can
be lifted from the nucleus surface with decreasing heliocentric
distance, thus allowing a larger mass of dust to be set free.
,
as done in the publications
mentioned. Instead, the dust velocities used here are calculated by a
reasonable physical model. A
second influence is the increase of the maximum grain radius that can
be lifted from the nucleus surface with decreasing heliocentric
distance, thus allowing a larger mass of dust to be set free.
The presented approach to compute dust production rates leads to an
approximately constant dust to gas mass ratio as a function of heliocentric
distance. The increasing Af![]() to gas ratio with increasing
heliocentric distance up to
to gas ratio with increasing
heliocentric distance up to ![]() 8 AU can be explained with the
variation of dust velocity with changing heliocentric distance.
Mechanisms proposed before, like albedo variations with varying
heliocentric distance due to icy grains (A'Hearn et al. 1995; Rauer et al. 1997), are
not necessary.
8 AU can be explained with the
variation of dust velocity with changing heliocentric distance.
Mechanisms proposed before, like albedo variations with varying
heliocentric distance due to icy grains (A'Hearn et al. 1995; Rauer et al. 1997), are
not necessary.
A rough estimate of the total dust production and the surface
erosion during one perihelion passage can be made by integration of
the dust production along the comets orbit. Assuming a dust to gas
mass ratio of
![]() ,
calculating
the water and CO production rates as described above and
integrating from 20 AU pre-perihelion to 20 AU post-perihelion gives a
total dust mass loss of about
,
calculating
the water and CO production rates as described above and
integrating from 20 AU pre-perihelion to 20 AU post-perihelion gives a
total dust mass loss of about
![]() kg. For a
nucleus of 30 km radius and a density of
kg. For a
nucleus of 30 km radius and a density of
![]() ,
one obtains a mean surface erosion of nearly 1 m of dust and gas.
,
one obtains a mean surface erosion of nearly 1 m of dust and gas.
The continuum flux of scattered sunlight as measured by longslit spectroscopy was used to analyse the dust activity of comet C/1995 O1 Hale-Bopp at heliocentric distances between 2.9 AU and 12.8 AU.
The reddening of the dust was determined and no significant variation in dust reddening with changing heliocentric distance was found.
The Af![]() parameters were derived from the spatial profiles of the
longslit spectra and used to compute the dust production rates.
parameters were derived from the spatial profiles of the
longslit spectra and used to compute the dust production rates.
To compute the dust production rates, a spherical symmetric dust emission was assumed. The gas flow by sublimation of ices from the surface of the nucleus was computed using a gasdynamical model. The dust particles were treated as spherical test particles within the gas flow. A size-dependent density and a size distribution of the dust particles were taken into account.
A dust to gas mass ratio of
![]()
![]() for the preferred model parameters in this work was found, thus showing
a very slight decrease with increasing heliocentric
distance. This is a low value compared to other publications of
dust-to-gas mass ratios for comet Hale-Bopp. However, due to the large
influence of the nucleus size and the active surface fraction on the
dust production rates, it is difficult to compare cometary dust production
rates computed with simple models.
for the preferred model parameters in this work was found, thus showing
a very slight decrease with increasing heliocentric
distance. This is a low value compared to other publications of
dust-to-gas mass ratios for comet Hale-Bopp. However, due to the large
influence of the nucleus size and the active surface fraction on the
dust production rates, it is difficult to compare cometary dust production
rates computed with simple models.
For example, if a Bond-albedo similar to other comets would be assumed for comet Hale-Bopp (e.g. 0.2), the dust to gas mass ratio would increase by a factor of 3/2. In most publications (Williams et al. 1997; Grün et al. 2001), the high value for the albedo is attributed to a large amount of small particles in comet Hale-Bopp's coma. This is consistend with a relatively low dust to gas mass ratio, nevertheless the comet appeared as one of the brightest comets for many years.
This work has shown that when deriving the coma dust flow from gasdynamical calculations, the variation of the dust to gas mass ratio with heliocentric distance is only weak. In particular, proper treatment of the gas and dust velocities with heliocentric distance is important to differentiate gas-dust dynamical effects from other influences on the observed parameters, such as icy grains or other sources of albedo variations.