...M

Geometric units G=c=1 are used throughout this text.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... infinity

Lightlike geodesics with two ends inside the black hole are of no consequence for the present discussion.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...

The normal is always oriented so that 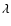$\lambda$ increases from P_fto P_i.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... observer

This strong 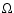$\Omega$ dependence is observed quite generally. On the basis of our numerical experience we propose a simple rule of thumb to account for some distinctions between flat and warped disk line profiles: the warp changes the flat disk line profile by the way in which infinitesimal circular disks, that the disk is made of, are seen. Two components of this aspect are: a) rings are seen at different inclinations due to the way the warp is bent and b) rings are illuminated unevenly due to shading of the light source and due to the varying direction of their normal with respect to the line of sight. Since the most characteristic feature of any ring contribution is the position of the sharp blue edge, the first effect is considerably more important for the success of flat disk fit than the second as long as the blue edge of the ring contribution has not been obliterated by shadowing. Considering a warp that bends perpendicular to the line of sight, we note that all infinitesimal disks have the same inclination with respect to the observer, therefore, their line profiles generally appear most similar to line profiles of flat disks.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.