A&A 403, 205-215 (2003)
DOI: 10.1051/0004-6361:20030308

Starspots and active regions on the chromospherically active binary MS Ser

I. Yu. Alekseev - O. V. Kozlova

Crimean Astrophysical Observatory, P/O Nauchny, 98409 Crimea, Ukraine; and Isaac Newton Institute of Chile, Crimean Branch, Ukraine

Received 27 November 2002 / Accepted 28 February 2003

Abstract
The quasisimultaneous electrophotometric, polarimetric and spectroscopic observations of the chromospherically active binary MS Ser are presented. The photometric variability of the star can be described completely by a zonal spottedness model. Spotted regions occupy up to 21% of the total stellar surface. The temperature difference between the unspotted photosphere and starspots is about 1300 K. Starspots are localized at the middle latitudes. We detected the broad-band linear polarization of the stellar light and its rotational modulation connected with the local magnetic region on the stellar surface. We suspect that there is a space connection between plages, magnetic regions and the mostly spotted stellar longitudes.

Key words: stars: activity - stars: chromospheres - stars: magnetic fields - stars: starspots

1 Introduction

The starspots is a very widespread phenomenon among cool stars. Axial rotation of a spotted star and slow variations of the starspot geometry cause so-called the BY Dra-type photometric variability, which is expressed in brightness rotational modulation and slow variations of mean stellar brightness. The magnetic field of starspots causes the Zeeman polarization effect. It can be detected in broadband linear polarimetric observations (Piirola 1977; Huovelin et al. 1985, 1988, 1989; Alekseev 2000, 2003). All spotted stars are chromospherically active and show emission lines in their spectra. One of the most typical lines for such stars is a hydrogen emission H$_{\alpha }$.

In our previous papers we obtained complex information about active regions on surfaces of some chromospherically active variables: V775 Her (Alekseev & Kozlova 2000), VY Ari (Alekseev & Kozlova 2001), and LQ Hya (Alekseev & Kozlova 2002). In these papers we carried out the uniform constructions of spottedness models for program stars on the basis of the total set of published and original photometric observations. We also considered the connection between starspots, chromospheric activity and magnetic regions. In present paper we extend our investigation on the chromospherically active binary system MS Ser.

MS Ser ( $\rm HD~143313$ = $\rm BD+25^\circ3003$ = $\rm GJ~3930$) is a SB2 chromospherically active star. Griffin (1978) first calculated the orbital elements for this system and proposed K2V/K6V as spectral types of the components. Later, Osten & Saar (1998) revised the stellar parameters for MS Ser and suggested K2IV/G8V as a better classification. Sanz-Forcada et al. (1999) have also found that the primary component may have a luminosity class IV or higher. The earliest photometric data for MS Ser were published by Eggen (1964). The photometric variability was found by Rucinski (1981) and Bopp et al. (1981). Bopp et al. (1981) also observed a variable filled-in H$_{\alpha }$ line and calculated a photometric period of 9.60 days, slightly different from the orbital one. Later the photometric observations were continued by Bopp et al. (1983); Miller & Osborn (1996); Alekseev & Shakhovskaya (1995); and Alekseev (2000, 2003). Alekseev (2000, 2003) obtained first linear polarimetric observations of MS Ser. Strassmeier et al. (1993) observed strong emission in the Ca II H & K composite spectrum. Dempsey et al. (1993) noted some filling-in in the Ca II IRT lines, but not reverse emission. Montes et al. (2000) observed nearly total filled-in H$_{\alpha }$ and H$_{\beta}$ lines, a clear emission in Ca II HK and Ca II IRT lines and a very small absorption in the He I D3 line on the base of three spectra obtained in 1995 and 1998.

2 Observations and results

2.1 Photometry

The photometric observations were carried out with the 1.25 m telescope AZT-11 of the Crimean Astrophysical Observatory equipped with the UBVRI double image chopping photometer-polarimeter of Piirola (Piirola 1984, 1988; Kalmin 1995; Kalmin & Shakhovskoy 1995). All MS Ser measures were obtained with respect to $\rm BD+26^\circ 2762$ ( $V = 8\hbox{$.\!\!^{\rm m}$ }08$, $U-B = 0\hbox{$.\!\!^{\rm m}$ }73$, $B-V = 1\hbox{$.\!\!^{\rm m}$ }08$, $V-R = 0\hbox{$.\!\!^{\rm m}$ }65$, $V-I = 1\hbox{$.\!\!^{\rm m}$ }28$), hereafter c1; and $BD+26^\circ 2623$ ( $V = 10\hbox{$.\!\!^{\rm m}$ }71$, $U-B = 1\hbox{$.\!\!^{\rm m}$ }30$, $B-V = 1\hbox{$.\!\!^{\rm m}$ }29$, $V-R = 1\hbox{$.\!\!^{\rm m}$ }02$, $V-I = 1\hbox{$.\!\!^{\rm m}$ }86$, (Rosselló et al. 1985)) was used as a check star c2. All observations utilized Johnson UBVRI filters. The measurement of each star consists of four 10-s integrations averaged in each filter. A complete observation sequence consists of three c1 - var - c2 - c1 sets averaged to obtain one data point. The observations were corrected for atmospheric extinction and transformed into the standard Johnson UBVRI system. The typical accuracy of the photometry of program stars is $0\hbox{$.\!\!^{\rm m}$ }01$. The previous results of our MS Ser photometric observations were published in (Alekseev 2000, 2003; Alekseev & Shakhovskaya 1995).


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F1.EPS}}\end{figure} Figure 1: Light curves of MS Ser in the V band. Our data are denoted as filled circles, Miller & Osborn (1996) data denoted as open circles. The continuous lines are the 2nd order weighted Fourier fits. The beginning and the end of non-duplicated data marked by dashed lines.
Open with DEXTER

MS Ser was observed regularly during 1991, 1994-1997, 2000-2002. During 1998 there were a few measurements only. Light curves of MS Ser in the Vband are shown in Fig. 1. The data were phased with a photometric period computed by Bopp et al. (1981):

\begin{displaymath}{\rm JD} = 2~444~311.96 + 9.60 E. \end{displaymath} (1)

We can see that the light curves in all seasons can be fitted by the 2nd order Fourier fits. In 1991 and 1994 there was a wide scatter in the data probably due to rapid changes in the light curve (Bopp et al. 1981). In all seasons except 1996 the light curves had a single-peaked shape. The rotational modulation amplitude $\Delta V$ varied from $0\hbox{$.\!\!^{\rm m}$ }05$ to $0\hbox{$.\!\!^{\rm m}$ }20$ with the mean brightness variations was about $0\hbox{$.\!\!^{\rm m}$ }14$. The color variations agreed with the V band modulation, showing the star is redder at light minimum. The results of our MS Ser photometric observations are given in Table 1.

Table 1: UBVRI photometric observations of MS Ser.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F2.EPS}}\end{figure} Figure 2: Long-term light curve of MS Ser in the V band. The vertical bars indicate the peak-to-peak amplitudes of the light curves. The filled circles indicate the isolated measurements.
Open with DEXTER

The long-term light curve of MS Ser was built first by Alekseev (2000, 2003). Now we extended the total time coverage to the year 2002 (Fig. 2). From Fig. 2, we can see that the rotational modulation amplitude $\Delta V$ varies from $0\hbox{$.\!\!^{\rm m}$ }05$ in 1996 to $0\hbox{$.\!\!^{\rm m}$ }20$ in 1995. The mean brightness of the star changed significantly: the amplitude of its variations is equal to about  $0\hbox{$.\!\!^{\rm m}$ }19$. The star was in the brightest state in 1980 with $V_{\max} = 8\hbox{$.\!\!^{\rm m}$ }11 \pm 0\hbox{$.\!\!^{\rm m}$ }01$, which we assumed to be an unspotted magnitude. Taking in account the Hipparchos distance r = 87.7 pc (Perryman et al. 1997) we see that the absolute brightness is $M_V = 3\hbox{$.\!\!^{\rm m}$ }39$ for the MS Ser system and $3\hbox{$.\!\!^{\rm m}$ }69$ for its primary component.

We compared values of the stellar brightness in UBRI Johnson bands with the V band ones. From this comparison we can see that the brightnesses in the UBRI bands depend linearly on V band magnitude. Such dependences are typical for all spotted variables. The corresponding linear regression coefficients are: ${\rm d}U/{\rm d}V = 1.08~ \pm~ 0.03$, ${\rm d}B/{\rm d}V = 1.08~ \pm~ 0.01$, ${\rm d}R/{\rm d}V = 0.84 \pm 0.03$and ${\rm d}I/{\rm d}V = 0.67 \pm 0.02$. Taking into account these values and the maximum brightness value $V_{\max} = 8\hbox{$.\!\!^{\rm m}$ }11 \pm 0\hbox{$.\!\!^{\rm m}$ }01$ we can obtain the color indices of the MS Ser unspotted photosphere: $U-B = 0\hbox{$.\!\!^{\rm m}$ }61 \pm 0\hbox{$.\!\!^{\rm m}$ }01$, $B-V = 0\hbox{$.\!\!^{\rm m}$ }97 \pm 0\hbox{$.\!\!^{\rm m}$ }01$, $V-R = 0\hbox{$.\!\!^{\rm m}$ }69 \pm 0\hbox{$.\!\!^{\rm m}$ }01$, $V-I = 1\hbox{$.\!\!^{\rm m}$ }19 \pm 0\hbox{$.\!\!^{\rm m}$ }01$ for the primary component. These color indices and absolute magnitude correspond to a K2IV star.

2.2 Polarimetry

The simultaneous photometric and linear polarimetric UBVRI observations were carried out in 1996-2002 on the 1.25 m telescope AZT - 11. In this case the measurement of a comparison star or a check star consists of eight 10-s integrations in each filter correspoding to eight the $\lambda/2$ polarizer positions. The each measurement of MS Ser was carried out in four series. This technique allows us to obtain a typical accuracy on the Px and PyStokes parameter measurements of about 0.02% in the U band and 0.01% in other bands and to confirm our photometric accuracy.

The results of the linear polarimetric observations in 1996 and 1997 were published by Alekseev (2000). In Tables 2a-c we list an averaged results of the UBVRI linear polarimetric observations of MS Ser in 2000-2002. For each passband we give the averaged Stokes parameters Px and Py with their deviations, the results of the standard $\chi^2$ test (the reduced $\chi^2/(N-1)$values with N-1 degrees of freedom), and the probability $F_{\rm var}$ that the Stokes parameters are variable from night to night. The $F_{\rm var}$ value should then provide an estimate of the significance of the observed variations. Also we give the average of the most significant polarization degree deviations from zero in each passband. These are values $P_{\rm s}$ of average polarization degree $2 \sigma$ greater than zero. This definition of $P_{\rm s}$ correctly determines the degree of linear polarization for stars with a large net P (Huovelin et al. 1988).

We can see from the Tables 2a-c and from Alekseev (2000), that the star shows significant linear polarization ($P_{\rm s}$) and variations of the Stokes parameters ( $F_{\rm var}$) in all passbands in 2000 and 2002, and in UBV passbands in 2001. The growth of the average polarization degree from I band to U is clearly seen. The largest amplitudes of the Stokes parameter variations were obtained in the U band: 0.22% for Px and 0.33% for Py in 1996, 0.48% for Px and 0.47% for Pyin 1997, 0.74% for Px and 0.60% for Py in 2000, 0.67% for Px and 0.47% for Py in 2001, and 0.20% for Px and 0.56% for Py in 2002 respectively. In Figs. 3a-c the linear polarization degree and the position angle in Uband are presented as a function of the photometric phase. One can see for all seasons that the photometric minimum corresponds to the polarization degree maximum with some phase shift. The differences between the phase of the maximum polarization and the phase of the minimum brightness (i.e. maximum spottedness) are 0.25 of the rotation period in 1996 and 2001, 0.28 in 1997, 0.07 in 2000, and 0.05 in 2002. These differences depend on the spot size and are typical of local magnetic fields which are localized near the most spotted longitudes (Huovelin & Saar 1991).

Table 2: (a). Linear polarization of MS Ser in 2000.

Table 2: (b). Linear polarization of MS Ser in 2001.

Table 2: (c). Linear polarization of MS Ser in 2002.

We can estimate a filling factor of the magnetic region using any assumption about the broad-band linear polarization origin. In this paper we shall consider the magnetic intensification (MI) effect above all, because the contribution of the Thompson scattering is negligible, and Rayleigh scattering gives for K2IVstar an effect three - four times less than MI one (Huovelin & Saar 1991; and Fig. 4). Saar & Huovelin (1993) showed that the maximum polarization degree for the MI effect is proportional to coefficient A which depends from the spot area S as

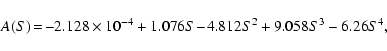\begin{displaymath}A(S) \!= \!-2.128 \times 10^{-4} + 1.076 S\! -\! 4.812 S^2 + 9.058 S^3 - 6.26 S^4,~ \end{displaymath} (2)

where S is given in percents. Saar & Huovelin (1993) computed expecting values of maximum polarization degrees in UBVRI bands for the range of $4000~{\rm K} < T_{\rm eff} < 6500$ K and $3.0 < {\rm lg}~g < 4.5$. Using these data, we can estimate from $P_{\rm s}$ the value of the magnetic region filling factor.

In Fig. 4 the comparison of observed maximum polarization values $P_{\rm s}$ with the maximum possible polarization for magnetic intensification (solid line) and Rayleigh scattering (dashed line) models in UBVRI bands are shown. One can see that in U band the maximum observed polarization degree $P_{\rm s}$ corresponds to the magnetic region filling factors varied from S = 6% in 1996 to S = 24% of the total stellar surface in 2000. These values agree with our estimations of starspot area in the same years (see below). In the B band the maximum observed polarization degree $P_{\rm s}$ corresponds to the maximum possible value. In the VRI bands the observed $P_{\rm s}$ values are greater than the theoretical polarization degrees for the adopted model.

2.3 Spectroscopy

The high resolution ( R = 20 000) spectroscopic observations of MS Ser were carried out during 4 nights in May-June 2000, 8 nights in April-June 2001, and 12 nights in February- June 2002 with the 2.6 m Shain telescope of the Crimean observatory, equipped with a Coudé spectrograph and a $1024 \times 256$ pixel CCD camera. All observations in the H$_{\alpha }$ wavelength region were made in the second order of the spectrograph with a resolution about 0.3 Å and a useful wavelength range of 60 Å. All integrations had an exposure of about 30-50 min and a typical signal-to-noise ratio of about 70-120. The images were cleaned of cosmic particles and corrected by the flat field. We used observations of a bright early-type fast rotating star for the athmospheric water correction.
  \begin{figure} \par\resizebox{15cm}{!}{\includegraphics[clip]{3340F3A.EPS}}\end{figure} Figure 3: a). Light curve of MS Ser in the V band in 1996 and 1997, polarization degree P and position angle $\theta $ in the U band as a function of photometric phase. The continuous lines are the weighted 2nd order Fourier fits. The beginning and end of non duplicated data marked by dashed lines.
Open with DEXTER


  \begin{figure} \par\resizebox{15cm}{!}{\includegraphics[clip]{3340F3B.EPS}}\end{figure} Figure 3: b). Light curve of MS Ser in the V band in 2000 and 2001, polarization degree P and position angle $\theta $ in the U band as a function of photometric phase.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F3C.EPS}}\end{figure} Figure 3: c). Light curve of MS Ser in the V band in 2002, polarization degree P and position angle $\theta $ in the U band as a function of photometric phase.
Open with DEXTER

All obtained spectra are presented in Figs. 5a-c (thin lines). In the 2000 observing run we can see in all spectra a filled-in H$_{\alpha }$line. In the spectrum taken in 04.05.00 we see a small absorption, in 06.06.00 spectrum there is a weak emission and in 08.05.00 and 09.05.00 spectra one can see both absorption and emission weak features.

In the 2001 observing run we see for two spectra (27.04.01 and 11.06.01) a filled-in H$_{\alpha }$line while in one spectrum (11.06.01) there is a weak absorption, and in other spectrum there is a small emission line. For the others six spectra we clearly see H$_{\alpha }$ emission line well above the continuum. In these spectra we see the emission core with a central reversal at the rest wavelength. This feature is typical for active red stars and formed by the optically thick chromosphere.

The same picture we see in 2002. Most spectra show a filled-in line, but in four spectra (12.03.02, 09.04.02, 10.04.02, 19.06.02) there is a clear emission core.

On the Fig. 6 we give the radial velocity curves of MS Ser. For the primary component radial velocities determination we used following lines: Fe I  $\lambda \lambda$ 6533.929, 6546.239, 6551.678, 6569.216, 6574.228, 6575.016, 6581.210, 6592.914, 6593.870 Å; Ti I $\lambda \lambda$ 6554.223, 6556.026 Å; and Ca I 6572.779 Å. The typical accuracy in the primary component radial velocity determination is about 2 km s-1. We found that most of our spectra show weak lines of the secondary component, first of all, H$_{\alpha }$ absorption line, and Fe I  $\lambda \lambda$ 6546.239, 6569.216, 6575.016, 6592.914, 6593.870 Å, and Ca I 6572.779 Å lines. On the base of these lines we constructed the radial velocity curve for the secondary component. In this case the typical accuracy in the radial velocity determination is about 4 km s-1. The results of our observations appended with Griffin (1978) data yielded the following orbital parameters: the orbital period $P_{\rm orb} = 9.01535$ days, the baricentric radial velocity $\gamma = -5.39$ km s-1, and the radial velocity amplitudes K1 = 52.04 km s-1 and K2 = 71.48 km s-1. As well as Griffin (1978) we supposed that the orbit is circular. Thus, we obtained that the mass ratio is about MA/MB = 1.37, whereas Griffin (1978) estimated it as 1.22. This mass ratio also confirm the Osten & Saar (1998) spectral classification.

The best way to obtain the chromosphere contribution to some spectral line in the chromospherically active binaries is to subtract the underlying photospheric contribution. It is espetially urgent for the H$_{\alpha }$ line which is observing frequently as a filled-in absorption line. We use the method which is based on the subtraction of a synthesized stellar spectrum constructed from corresponding Kurucz atmospheric models.

For each observed spectrum we calculated a synthetic one obtained with the help of the SYNTH and ROTATE programs of Piskunov (1992), and the VALD database of atomic spectral-line parameters (Piskunov et al. 1995, 1999). Each resulting synthetic spectrum is represented by composition of two synthetic spectra calculated for the following models: $T_{\rm eff} = 5000$ K, $\log~g = 3.5$, $V \sin i = 15$ km s-1, $V_{\rm micro} = 0.5$ km s-1, $V_{\rm macro} = 1.5$ km s-1 for the primary component and $T_{\rm eff} = 5500~{\rm K}$, $\log~g = 5.0$, $V \sin i = 7$ km s-1, $V_{\rm micro} = 0.5$ km s-1, $V_{\rm macro} = 1.5$ km s-1 for the secondary one. The synthetic spectrum of the secondary component was reduced according to the luminosity ratio of components 9.60 which is a typical for K2IV/G8V system, and moved according to the radial velocity curve. The equivalent widths of synthetic photospheric profiles show a good agreement with results of Montes et al. (2000).

Residual pure chromospheric emission spectra shown in Figs. 5a-c as dashed lines. The width of all these spectra indicate gas motion on the line of the sight with typical velocities up to $60 \div 100~\rm km~s^{-1}$. The spectra taken in 2002 observing run show blue asymmetry of the H$_{\alpha }$ pure emission profile. This asymmetry is seen as extend blue emission wing reaching the value $-100~\rm km~s^{-1}$, whereas the red wing reaching in the same spectra the value $60~\rm km~s^{-1}$. Thus, we can suspect a large-scale motions of gas (outflow) in the stellar chromosphere.

In Table 3 we give the main characteristics of the H$_{\alpha }$ line: Julian Date HJD of the spectrum and the corresponding phase; ratios $F_{\max}/F_{\rm cont}$of the peak emission flux to the continuum flux for real spectra and the same for the pure emission; the distance between the "blue" and the "red" peaks $\Delta \lambda_{\rm peak}$; the $F_{\rm red}/F_{\rm blue}$ ratio of the peak fluxes; the width of the pure emission profile FWHM and the equivalent width of the pure emission value.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F4.EPS}}\end{figure} Figure 4: Wavelength dependence of the polarization degree. Different symbols show observational estimations of the maximum polarization degree $P_{\rm s}$, the solid line shows the expected theoretical dependence in UBVRI bands for the MI model, and the dashed line shows the theoretical dependence for the Rayleigh scattering.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F5A.EPS}}\end{figure} Figure 5: a). H$_{\alpha }$ line profiles for MS Ser in 2000 May-June. The thin lines show the observed spectra, the thick line show the synthetic spectrum for the primary component, and the dashed lines show the residual pure emission spectra.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F5B.EPS}}\end{figure} Figure 5: b). H$_{\alpha }$ line profiles for MS Ser in 2001 April-June.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F5C.EPS}}\end{figure} Figure 5: c). H$_{\alpha }$ line profiles for MS Ser in 2002 February-June.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F6.EPS}}\end{figure} Figure 6: The radial velocity curves for MS Ser. The filled symbols denote data for the primary component, and the open symbols denote data for the secondary one. The circles show our data, the diamonds show Griffin (1978) data, and the squares show Osten & Saar (1998) data.
Open with DEXTER

We may roughly estimate physical parameters for the lower chromospheres of MS Ser given by the model of Cram & Mullan (1979) assumptions. It is a model of an optically thick isothermal chromosphere. The optical depth of the isothermal chromosphere is

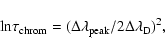\begin{displaymath}{\rm ln} \tau_{\rm chrom} = (\Delta \lambda_{\rm peak}/2 \Delta \lambda_{\rm D})^2, \end{displaymath} (3)

where $\Delta \lambda_{\rm D}$ is the Doppler width. For the typical chromospheric temperature $T_{\rm chrom} = 10~000~{\rm K}$ this value is equal to about 0.28 Å. Thus, the chromospheric optical depth may vary in active regions from 7 to 55 depending on rotational phase. The electron density may be estimated by:

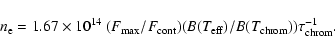\begin{displaymath}n_{\rm e} = 1.67 \times 10^{14}~(F_{\max}/F_{\rm cont}) (B(T_{\rm eff})/B(T_{\rm chrom})) \tau_{\rm chrom}^{-1}. \end{displaymath} (4)

For the Table 3 data, $n_{\rm e}$ varies from $3.7~ \times~ 10^{11}$ to $3.1~ \times~ 10^{12} ~\rm cm^{-3}$. It is important to note that if $n_{\rm e} \sim 6 \times 10^{11}~ \rm cm^{-3}$replacement of the collisional line formation mechanism by the photoionizational one must be done.

Table 3: Spectroscopic observations of MS Ser in H$_{\alpha }$ region.

3 The spottedness model simulations

Doppler Imaging is one of the most promosing methods for spottedness mapping, but it demands spectroscopic observations of rapidly rotating star with a high resolution and S/N ratio, placing strong restrictions on the observational equipment and program star choise. MS Ser have relatively small $V \sin i$velocity, and does not meet these restrictions.

An algorithm to obtaining the starspots parameters from the photometric observations is described in many papers (Dorren 1987). To find the area and temperature of the spotted region, we must know the brightness of the unspotted photosphere and the relations between the $\Delta m$ values at different wavelengths which can be estimated from the observations. In our calculations we use the $V_{\max}$ value and the coefficients ${\rm d}B/{\rm d}V$, ${\rm d}R/{\rm d}V$ and ${\rm d}I/{\rm d}V$. We must also make some initial assumptions about the spotted region configurations.

Table 4: Spottedness parameters of MS Ser.

Traditional algorithms lead to large near-pole circular spots on all stars of any spectral type. This conclusion contradicts the solar spottedness picture. On the other hand, Eaton et al. (1996) showed that the aggregate of many (5-40) low-latitude starspots can fit the photometric behaviour of any real spotted star.

Alekseev & Gershberg (1996a,b, 1997) showed that the spotted regions on cool stars can be represented by two spotted belts located symmetrically about the equator. These belts occupy regions with latitudes from $\pm \phi_0$ to $\pm (\phi_0 + \Delta \phi)$ and have a spot coverage that varies linearly with longitude from 1 at the minimum brightness phase to some value $f_{\min}$ at the maximum brightness phase, where $0 < f_{\min} < 1$. Such a zonal model can fit any light curve without the second humps. The model was applied to several spotted stars with the spectral classes from G0 to M4.5 and rotation velocities up to 25 km s-1 (Alekseev 2000, 2003; Alekseev & Kozlova 2000, 2001, 1996) and these results were in qualitative agreement with the pattern of solar spots. Later the same model was applied by Unruh et al. (2001) to the solar spottedness simulations. It should be noted that our algorithm did not impose any restriction on definable spot latitudes with the exception of a natural limit $\phi_0 + \Delta \phi < 90^\circ$, where it produces a polar spot. Thus the spot latitudes are the definable variables depending on the ${\rm d}B/{\rm d}V$, ${\rm d}R/{\rm d}V$ and ${\rm d}I/{\rm d}V$ coefficients (the value $\phi_0 + \Delta \phi/2$ increasing with the ${\rm d}B/{\rm d}V$ growth and anticorrelating with ${\rm d}R/{\rm d}V$ and ${\rm d}I/{\rm d}V$ (Alekseev & Gershberg 1996b)).

In our calculations we use two input variables. They are the brightness rotational modulation amplitude $\Delta V$, and the difference between the maximum stellar brightness in every season and the brightness of the unspotted photosphere $\Delta V_{\max}$. The five input parameters of the spot modelling are the following: the coefficients ${\rm d}B/{\rm d}V$, ${\rm d}R/{\rm d}V$ and ${\rm d}I/{\rm d}V$, the inclination of the stellar rotation axis i and the stellar photosphere temperature $T_{\rm phot}$. The limb-darkening coefficients were taken from van Hamme (1993).

To estimate the inclination angle $i = 60^\circ$, we use the values of the rotation velocity $V \sin i = 15~\rm km~s^{-1}$, the stellar radius $R = 3.50~ R_{\odot}$(Osten & Saar 1998) and the photometric period $P_{\rm rot} = 9\hbox{$.\!\!^{\rm d}$ }60$ (Bopp et al. 1981). The photospheric temperature $T_{\rm phot} = 5000~{\rm K}$ was estimated by using the calibration of Johnson (1966) from the (V-R) and (V-I) color indices of the unspotted photosphere. This value agrees with the estimations of Osten & Saar (1998) and our stellar atmosphere model choise. The starspots models for MS Ser are given in the Table 4.

According to this table, the photometric behaviour of MS Ser can be explained by a zonal model where the distance from the spotted belts to the stellar equator varies from $\phi_0 = 15^\circ$ to $\phi_0 = 41^\circ$. The spotted belt width $\Delta \phi$ varies from $11^\circ$ to $20^\circ$. The coverage parameter $f_{\min}$ varies from 0.00 to 0.68, which yields a total spot area $S_{\max} + S_{\min}$ up to 21% of the total stellar surface. The ratio of the brightnesses of the spots and the quiet photosphere $\beta_V$ is relatively small: 0.11-0.13 corresponding to a temperature difference $\Delta T$ of about $1300~{\rm K}$. The previous results of MS Ser starspot simulation were published by Alekseev (2000, 2003).

4 The starspots - active regions connection

There is an extensive bibliography devoted to the chromospheric plages and their connections with starspots. In previous papers (Alekseev & Kozlova 2000, 2001, 2002) we noted that the active regions (plages) for the chromospherically active binaries V775 Her and VY Ari, and for the active single star LQ Hya are concentrated near the most spotted longitude. We present in Figs. 7a-c the V band light curves of MS Ser in 2000-2002 compared with the H$_{\alpha }$pure emission behaviour as a function of rotational phase.

In 2000 we obtained four observational points. It is not enough to draw any conclusion about H$_{\alpha }$ variability.

In 2001 and 2002 we see a clear variability of the relative chromospheric emission intensity $F_{\max}/F_{\rm cont}$, which growth with the stellar brightness decreasing. The equivalent width EW show the similar picture in 2002, whereas in 2001 its correlation with the spottedness is more weak. The width of the pure emission profile FWHM demonstrate a possible anticorrelation with the light curve in 2002, but in 2001 the FWHM maximum do not agree with the light curve minimum. Thus we see in 2002 the presence of chromospherically active regions with higher electron density (plages) associated with the most spotted longitude, whereas in 2001 the presence of plages is more questionable.

In Fig. 8, we present the dependence of the pure H$_{\alpha }$ emission equivalent width on the stellar brightness and the dependence of the H$_{\alpha }$ luminosity on the total spot area on MS Ser constructed from 1995 to 2002 on the basis of our observations and literature data (Montes et al. 2000).


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F7A.EPS}}\end{figure} Figure 7: a). V band light curve of MS Ser in 2000 year and H$_{\alpha }$pure emission behavior as a function of rotational phase.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F7B.EPS}}\end{figure} Figure 7: b). V band light curve of MS Ser in 2001 year and H$_{\alpha }$pure emission behavior as a function of rotational phase.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F7C.EPS}}\end{figure} Figure 7: c). V band light curve of MS Ser in 2002 year and H$_{\alpha }$pure emission behavior as a function of rotational phase.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F8A.EPS}}\end{figure} Figure 8: a). The H$_{\alpha }$ pure emission equivalent width as a function of the stellar brightness. The symbols denote data by different authors: 1: Alekseev & Kozlova (1996); 2: this paper, (2000); 3: this paper, (2001); 4: this paper, (2002); 5: Montes et al. (2000).
Open with DEXTER

The V band magnitudes in Fig. 8a were measured from the unspotted photosphere brightness. The significant (about  $0\hbox{$.\!\!^{\rm m}$ }2$) photometric variability does not show clear correlation with the H$_{\alpha }$ pure emission equivalent width, which demonstrate the scattering from 0.53 to 2.32 Å (a correlation coefficient r = 0.35). Figure 8b takes into account the variations of the continuum level in the 6563 Å wavelength region. It demonstrates the comparison of the chromospheric luminosity with the stellar spottedness. The methods of the $L_{\rm chr}$ estimation from the equivalent width EW value were described by Alekseev et al. (2001). Based on the absolute magnitudes of MS Ser in the Johnson R band at the observed epoch MR, we transformed the pure H$_{\alpha }$emission equivalent width EW into absolute luminosity using the well-known calibration of the Johnson (1966) R band:

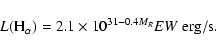\begin{displaymath}L({\rm H}_{\alpha}) = 2.1 \times 10^{31 - 0.4 M_R} EW~\rm erg/s. \end{displaymath} (5)

The total radiative losses from the stellar chromosphere $L_{\rm chr}$ can be estimated from the relation $L_{\rm chr} = L({\rm H}_{\alpha})/kl$ where k is the ratio of the H$_{\alpha }$ line flux to to the total Balmer flux and l is the ratio of the Balmer emission to the total radiation losses. According to Sundland et al. (1988), and Shakhovskaya (1974), H$_{\alpha }$ emits about 53% of the total chromospheric Balmer line emission. Further, the contribution of the Balmer lines to the total radiative losses from the chromosphere depends on the spectral type and ranges from 13% for the Sun to 77% for UV Cet (Pettersen 1987). The l value for MS Ser is about 18%.

We can see from Fig. 8b, that the spot area growth from 8 to 13% of the visible hemisphere corresponds to $L_{\rm chr}$ variations from $6.55 \times 10^{30}$ to $2.62 \times 10^{31}$ erg/s, which are not correlated with the spottedness (a correlation koefficient r = 0.14). We can see from Fig. 7, that the presence of chromospheric plages associated with the starspots can have a place in some epochs but not in others. Thus, the changes in the H$_{\alpha }$ emission can be due to the plages or to a change in the physical parameters of the chromosphere. This can be the reason of the absence of correlation between chromospheric emission and spottedness. The bolometric luminosity deficit caused by starspots varies from $1.13 \times 10^{32}$ to $1.89 \times 10^{32}$erg/s. Thus, the chromosphere of MS Ser radiates from 5 to 13% of the total stellar luminosity blocked by the starspots.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{3340F8B.EPS}}\end{figure} Figure 8: b). The chromospheric emission on MS Ser as a function of the stellar spottedness.
Open with DEXTER

5 Conclusions

In this paper we present quasi-simultaneous photometric, polarimetric and spectroscopic data of surface inhomogeneities in the photosphere and the lower chromosphere of the chromospherically active binary MS Ser. This study showed the following:

1.
The results of our photometric and spectroscopic observations confirmed the K2IV/G8V spectral classification. Thus, MS Ser is more properly classified an evolved RS CVn-type binary, rather than a BY Dra-type variable.

2.
The photometric variability of MS Ser can be described completely by the zonal spottedness model developed by Alekseev & Gershberg (1996a,b, 1997). According to this model, the spot area of MS Ser reaches up to 21% of the total stellar surface, and the temperature difference between the unspotted photosphere and the spots is about $1300~{\rm K}$.

3.
Starspots are localized on medium latitudes $23 {-} 48^\circ$. This conclusion agrees with results of our spottedness modelling for stars of the same spectral type (Alekseev & Kozlova 2000, 2001, 2002), but does not confirm an existense of near-polar starspots predicted by Doppler Imaging for some red dwarf stars. It can be noted, that Doppler Imaging is very sensitive to errors in the projected rotation velocity $V \sin i$. In particular, in the case of underestimated $V \sin i$ we shall see a polar spot (Unruh 1996). On the other hand, the flat-bottomed cores of spectral lines that are interpretated as due to polar spots, might also be caused by chromospheric activity (Bruls et al. 1999).

4.
The location of starspot pattern by our calculations is in agrement with the calculations of the flux tube rising ( $30 {-} 70^\circ$, Schüssler et al. 1996; Granzer et al. 2000). At the same time, there is no any agreement with the fact that Doppler Imaging shows near-pole spots for all K stars.

5.
The broad-band linear polarization on MS Ser was detected in all UBVRI bands. Its variability is caused by rotational modulation due to local magnetic fields on the stellar surface which are localized near the most spotted longitudes. The filling factor of these magnetic regions varies from 6% to 24% of the total stellar surface. These values are comparable with the photospheric starspot area values obtained for the same years. This result contradicts the solar picture where the magnetic regions filling factor few times greater than the spot area. On the other hand, magnetic field measurements for some spotted stars (Saar 1996) give a magnetic field filling factor up to 50-70%. Thus, the magnetic field filling factor values obtained by us may be underestimated, because the real starspot configuration is quite different from one circular magnetic spot used in Saar & Huovelin (1993) modelling.

6.
The quasi-simultaneous photometric and spectroscopic observations in 2002 show a presence of chromospherically active regions with a higher electron density (plages) which are concentrated near the most spotted active longitudes. An analysis of the H$_{\alpha }$ line shapes shows a combination of moving stellar plages and large-scale motions of gas (outflow) in the chromosphere. Electron density estimations point to a "mixed" H$_{\alpha }$ line formation.

7.
The estimation of plage area in the optically thick chromosphere may be realized in the framework of a black-body radiation model. For $T_{\rm chrom} = 10~000~{\rm K}$ the H$_{\alpha }$ pure emission surface flux is about $3.4 \times 10^7~{\rm erg} \cdot c^{-1}~ \rm cm^{-2}~ \AA^{-1}$. The H$_{\alpha }$ chromospheric luminosity of MS Ser in 2000-2002 varied from $7.5 \times 10^{29}$ to $2.5 \times 10^{30}$ erg/s. Thus, supposing all H$_{\alpha }$emission come from the plages, we can obtain that the plage area of MS Ser is about $2.7 \div 3.1 \times 10^{22} ~\rm cm^2$, i.e. is about 4% of the total stellar surface.

8.
A comparison of the spottedness with the long-term H$_{\alpha }$ variations does not show any correlation. The bolometric luminosity deficit due to starspots is from $1.13 \times 10^{32}$ to $1.89 \times 10^{32}$ erg/s. The stellar chromosphere radiates about 7% of the total energy blocked by starspots. This value corresponds to dependence noted by Alekseev et al. (2001).

Acknowledgements
This work has been partially supported by Ukrainian SFFD grant No. 02.07/00300. We thank an anonymous referee for constructive comments.

References


Copyright ESO 2003