A&A 402, 827-836 (2003)
DOI: 10.1051/0004-6361:20030279
Signatures of high energy protons in pulsar winds
E. Amato1 - D. Guetta1 - P. Blasi1
INAF/Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
Received 4 July 2002 / Accepted 4 February 2003
Abstract
The resonant cyclotron absorption model (Hoshino et al. 1992;
Gallant & Arons 1994) is very successful in describing particle
acceleration in plerions. A prediction of this model is the presence
of a substantial amount of relativistic protons in pulsar winds.
Although difficult to detect, these protons may show up through their
interactions either with the photons in the plerion environment or with the
thermal gas in the supernova ejecta.
Inelastic proton-proton (p-p) collisions are expected to be very effective in
young objects, resulting in a copious production of neutral and charged pions.
Charged pions produced during the first few hundred years after the supernova
explosion may have time to decay into muons, whose subsequent decay may
provide an additional source of electrons and positrons in these nebulae,
that adds up to the pulsar input. These secondary leptons evolve just as
the pairs in the pulsar wind, and signatures of their presence could be
found, in principle, even in the synchrotron spectrum of older objects.
p-p collisions may remain fairly efficient even in moderately old objects
resulting in the production of TeV 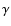 -rays and neutrinos.
We apply our calculations to the case of the Crab Nebula, the best studied
plerion thus far, and find that existing data already allow us to infer
interesting constraints on the physical properties of the Crab pulsar wind.
-rays and neutrinos.
We apply our calculations to the case of the Crab Nebula, the best studied
plerion thus far, and find that existing data already allow us to infer
interesting constraints on the physical properties of the Crab pulsar wind.
Key words: acceleration of particles - stars: pulsars: general - stars: winds, outflows
The presence in pulsar winds of a baryonic component coexisting with the
leptonic one is still an open question.
According to the most successful model so far for particle acceleration
at the pulsar wind termination shock (Hoshino et al. 1992;
Gallant & Arons 1994), baryons should not only be present
in the wind, but even carry most of its energy. This makes it mandatory
to investigate all possible ways in which signatures of their presence can
be found.
Plerions result from the interaction of a pulsar with its surrounding
medium. According to the standard picture, pulsars lose most of their
energy in the form of a magnetized relativistic wind, whose material
component is made up mostly of electron-positron pairs. The wind starts
out cold and with a highly relativistic expansion velocity. At some
distance from the pulsar the wind then needs to be slowed down in order
to match the boundary conditions imposed by the surrounding supernova
ejecta expanding at subrelativistic speed. This happens at a termination
shock where most of the outflow bulk energy is randomized. Here is
where particle
acceleration presumably occurs, giving rise to the non-thermal particle
spectrum that is the source of the plerion synchrotron and Inverse
Compton radiation.
According to both pulsar magnetospheric theories and the available data,
the termination shock is most likely a relativistic transverse shock,
meaning that the magnetic field is almost perpendicular to the flow
velocity. Standard shock acceleration mechanisms (i.e. diffusive
shock acceleration or Fermi I process, and shock drift acceleration)
are generally believed to be ineffective in this kind of shock
(e.g. Hoshino et al. 1992).
An acceleration mechanism that is able to overcome the difficulties of
the former two is based on resonant cyclotron absorption (RCA) in a
baryon-loaded plasma. Here we briefly review it in order to make clear
the assumptions we make on the proton spectrum and its relation to
the basic wind parameters.
Within the framework of the RCA model (Hoshino et al. 1992;
Gallant & Arons 1994), the ions present in the wind
have a Larmor radius
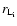 which is
which is
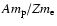 times larger than that
of the pairs, both species being cold in the wind rest frame.
When the heavier particles meet the shock in the pairs, this
appears to them as an infinitesimally thin discontinuity in the
magnetic field. The sudden enhancement of the magnetic field is expected
to cause
them to start a bunched gyration, accompanied by the collective
emission of cyclotron waves. The fundamental frequency of these waves
is the ion Larmor frequency, but also higher harmonics are excited
up to the pair gyration frequency. The latter can be resonantly absorbed
by the pairs and cause their acceleration, while the ions slowly
thermalize after crossing the shock. Efficient acceleration requires
the ions to be energetically dominant in the wind, although the pairs
are dominant by number.
times larger than that
of the pairs, both species being cold in the wind rest frame.
When the heavier particles meet the shock in the pairs, this
appears to them as an infinitesimally thin discontinuity in the
magnetic field. The sudden enhancement of the magnetic field is expected
to cause
them to start a bunched gyration, accompanied by the collective
emission of cyclotron waves. The fundamental frequency of these waves
is the ion Larmor frequency, but also higher harmonics are excited
up to the pair gyration frequency. The latter can be resonantly absorbed
by the pairs and cause their acceleration, while the ions slowly
thermalize after crossing the shock. Efficient acceleration requires
the ions to be energetically dominant in the wind, although the pairs
are dominant by number.
After crossing the shock the ions drift towards the outer parts of the
nebula with a velocity of the order of
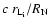 and slowly thermalize
to a temperature that is equivalent to a Lorentz factor
and slowly thermalize
to a temperature that is equivalent to a Lorentz factor 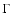 of the
order of the initial wind Lorentz factor.
The full thermalization takes several gyration periods, so, depending
on the initial wind Lorentz factor, it may never be achieved within
the nebula.
of the
order of the initial wind Lorentz factor.
The full thermalization takes several gyration periods, so, depending
on the initial wind Lorentz factor, it may never be achieved within
the nebula.
While drifting towards the edge of the nebula the ions may interact
with the plerion radiation field and with the thermal material of the
ejecta, which partly penetrates the synchrotron bubble due to
Rayleigh-Taylor instabilities. Both these interactions would lead to
pion production. The products of the subsequent pion decays could lead to
observable signatures if the interaction rate were high enough.
The most direct signature would be the instantaneous emission of
high energy photons and neutrinos.
The latter are potentially the
preferential channel to look at, since their detection would be
unequivocally associated with the presence of protons. In fact,
a few recent papers have considered the question of neutrino
production from protons accelerated in pulsar magnetospheres.
Bednarek & Protheroe (1997) computed the flux of high
energy neutrinos and 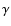 -rays that would be expected
from nuclear collisions of protons derived from the decay of neutrons
produced by the photodisintegration of accelerated nuclei in a
pulsar magnetosphere. Beall & Bednarek (2002) computed
the neutrino flux that would be produced by high energy protons
accelerated in the magnetosphere of a young fast rotating pulsar
surrounded by a supernova envelope,
and Bednarek (2001) considered the effect of this contribution
on the overall neutrino background.
-rays that would be expected
from nuclear collisions of protons derived from the decay of neutrons
produced by the photodisintegration of accelerated nuclei in a
pulsar magnetosphere. Beall & Bednarek (2002) computed
the neutrino flux that would be produced by high energy protons
accelerated in the magnetosphere of a young fast rotating pulsar
surrounded by a supernova envelope,
and Bednarek (2001) considered the effect of this contribution
on the overall neutrino background.
None of these previous investigations explicitly considered the protons that
should be part of the pulsar wind if the RCA model for shock acceleration
is actually at work in plerions. These are exactly the protons we
consider in this paper, with the aim of finding constraints from
observations on the characteristics of the pulsar wind.
In addition to computing the multi-TeV neutrinos and photon fluxes
we also worry about the secondary electrons
and positrons produced by 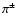 decay. If protons are present,
this process acts as an extra source of pairs in the plerion
which is expected to be especially active when the plerion is young
and compact, but could in principle leave relatively long-lasting
traces in the nebular radiation spectrum.
decay. If protons are present,
this process acts as an extra source of pairs in the plerion
which is expected to be especially active when the plerion is young
and compact, but could in principle leave relatively long-lasting
traces in the nebular radiation spectrum.
In the following we study the efficiency of the pion production
processes
as a function of time during the plerion evolution. We
approximate the plerion as spherical and expanding at a constant
velocity. For the evolution of the nebular non-thermal emission
we use the Pacini & Salvati (1973) model (PS hereafter)
for a homogeneous plerion.
2 Pion production and energy losses
Charged and neutral pions can be generated either by photo-pion production
off the photons in the nebula or by inelastic p-p scattering against the
thermal gas in the ejecta. While the decay of neutral pions results in
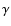 -ray production, the decay of charged particles results in neutrinos
and electron-positron pairs (we will refer to both as electrons).
-ray production, the decay of charged particles results in neutrinos
and electron-positron pairs (we will refer to both as electrons).
We describe the efficiency of both photomeson production and p-p
collisions through a parameter, 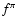 ,
defined as the probability
for a single relativistic proton to create a pion before losing energy
through other kinds of interactions:
,
defined as the probability
for a single relativistic proton to create a pion before losing energy
through other kinds of interactions:
![\begin{displaymath}
f^\pi={\rm min} \left[1, \frac{t_{\rm life}}{t^\pi} \right] \ ,
\end{displaymath}](/articles/aa/full/2003/18/aa2873/img36.gif) |
(1) |
where
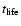 is the proton life-time against losses different
from p-
is the proton life-time against losses different
from p-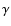 and p-p, and
and p-p, and 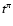 is the timescale for the process
of pion production.
The luminosity output in pions will be:
is the timescale for the process
of pion production.
The luminosity output in pions will be:
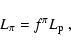 |
(2) |
with 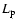 the wind luminosity in protons.
the wind luminosity in protons.
In the presence of an intense magnetic or radiation field, charged pions
may lose a considerable fraction of their energy through synchrotron or
Inverse Compton emission before decaying into muons. The same could happen
to muons before decaying into electrons and neutrinos. If any of these
effects were relevant, this would lead to a suppression
of the neutrino and electron fluxes at high energies. We shall define the
quantities 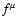 and
and 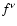 as:
as:
![\begin{displaymath}
f^\mu={\rm min} \left[1,{{t^\pi}_{\rm losses} \over
{t^\pi}...
..., {{t^\mu}_{\rm losses} \over
{t^\mu}_{\rm decay}} \right]\ ,
\end{displaymath}](/articles/aa/full/2003/18/aa2873/img41.gif) |
(3) |
where
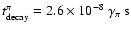 and
and
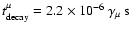 .
Since the pion energy is roughly evenly shared between the final
products of its decay, we can write
the number of neutrinos, electrons and
.
Since the pion energy is roughly evenly shared between the final
products of its decay, we can write
the number of neutrinos, electrons and 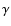 -rays injected in the
nebula per unit time and unit energy interval as:
-rays injected in the
nebula per unit time and unit energy interval as:
An important point to be noticed in the above set of equations is that in
writing Eq. (4) we take into account only muon neutrinos,
since these are the particles that neutrino telescopes are able to detect.
The possible effects of neutrino oscillations on the results of our
calculations will be discussed in Sect. 3.3.
2.1 Photo-meson production
In the case of photo-meson production the target for high energy protons
is the plerion emission.
The fractional energy loss rate of a proton with energy
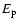 (=
(=
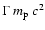 )
due to pion production results in
(Waxman & Bahcall 1997):
)
due to pion production results in
(Waxman & Bahcall 1997):
Here we have treated the plerion as homogeneous and used the fact that
the photon spectrum is a power law,
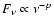 .
We have also made the approximation that the
main contribution to pion production comes from
photon energies
.
We have also made the approximation that the
main contribution to pion production comes from
photon energies
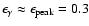 GeV,
where the p-
GeV,
where the p-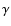 cross section peaks due to the
cross section peaks due to the 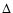 resonance.
The numerical values are obtained using:
resonance.
The numerical values are obtained using:
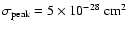 ,
,
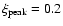 ,
,
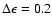 GeV,
GeV,
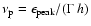 and
and
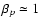 .
.
2.2 Inelastic nuclear collisions
The energy loss-rate of a relativistic proton due to inelastic nuclear
collisions can be estimated as
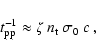 |
(8) |
where 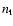 is the target density,
is the target density,
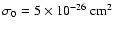 and
and
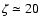 % is the average fraction of energy lost by the proton.
% is the average fraction of energy lost by the proton.
As we mentioned in the introduction, the estimate of the effective target
density, 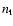 ,
is the main uncertainty in our calculation.
The distribution of the thermal material, in all cases when it is observed,
is actually far from uniform. The matter of the
ejecta penetrates the synchrotron nebulae due to Rayleigh-Taylor
instabilities,
giving rise to concentrations in the form of "filaments''. The total
amount of material contained in these filaments is not easy to estimate
with confidence. In fact the possibility that the gas detected through
thermal emission hides some colder and denser concentrations cannot be
excluded. A comparably difficult task is to estimate, from the projection
on the plane of the sky, the fraction of the nebular volume that these
filaments occupy, their so-called "filling factor''.
,
is the main uncertainty in our calculation.
The distribution of the thermal material, in all cases when it is observed,
is actually far from uniform. The matter of the
ejecta penetrates the synchrotron nebulae due to Rayleigh-Taylor
instabilities,
giving rise to concentrations in the form of "filaments''. The total
amount of material contained in these filaments is not easy to estimate
with confidence. In fact the possibility that the gas detected through
thermal emission hides some colder and denser concentrations cannot be
excluded. A comparably difficult task is to estimate, from the projection
on the plane of the sky, the fraction of the nebular volume that these
filaments occupy, their so-called "filling factor''.
Moreover the effective target density for relativistic protons, which is
our reason for worrying about the distribution of thermal matter in plerions,
is also affected by the intensity and structure of the magnetic field in and
around the "filaments'', which are not known. The magnetic field affects
in fact the physics of proton propagation and could in principle be an
obstacle to the penetration of protons in the thermal gas, leading to a
decrease of the value of 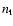 ,
or conversely be the cause of proton
trapping in the filaments, resulting in the opposite effect.
We shall summarize all these unknowns in a single parameter
,
or conversely be the cause of proton
trapping in the filaments, resulting in the opposite effect.
We shall summarize all these unknowns in a single parameter
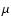 ,
which we also take to be time-constant. We define the effective
density of material in terms of the average gas density in the plerion as:
,
which we also take to be time-constant. We define the effective
density of material in terms of the average gas density in the plerion as:
 |
(9) |
where 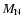 is the mass of the ejecta contained in the filaments, which
we also take to be time-constant.
Using Eq. (9) in Eq. (8) we obtain:
is the mass of the ejecta contained in the filaments, which
we also take to be time-constant.
Using Eq. (9) in Eq. (8) we obtain:
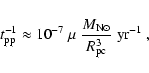 |
(10) |
which, when compared with Eq. (7), indicates nuclear collisions
as the main mechanism for pion production in plerions, if 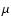 is not very
much less than 1.
is not very
much less than 1.
2.3 Energy losses
The energy distribution of particles after injection is determined, in
a plerion, mainly by the following loss-mechanisms: escape and expansion
losses, and radiative cooling through synchrotron and Inverse Compton
emission. We approximate the plerion as a homogeneous spherical bubble
filled with a uniform magnetic field and expanding at constant velocity
v, and estimate the time-scales of the different processes under these
assumptions.
The rate of adiabatic cooling is simply:
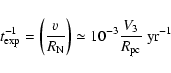 |
(11) |
where
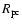 is the nebular radius in parsecs and V3is the plerion expansion velocity in units of 103 km s-1.
is the nebular radius in parsecs and V3is the plerion expansion velocity in units of 103 km s-1.
The rate of escape of a particle of mass 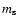 and Lorentz factor
and Lorentz factor 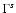 ,
whose Larmor radius in the nebular magnetic field is
,
whose Larmor radius in the nebular magnetic field is 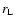 ,
can be estimated,
based on
,
can be estimated,
based on
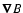 drift, as:
drift, as:
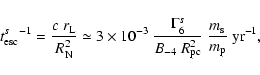 |
(12) |
where B-4 is the nebular magnetic field in units of 10-4 G and
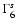 is the particle Lorentz factor in units of 106.
is the particle Lorentz factor in units of 106.
The rate of synchrotron cooling is:
Finally, the cooling rate due to Inverse Compton Scattering (ICS hereafter) is
![$\displaystyle {t^s_{\rm ICS}}^{-1}= { 4 \over 3} \sigma_T c\ \left({m_{\rm e} \...
...\nu_{\rm KN}}^{\nu_{\rm max}}
{S_\nu \over \nu^2} {\rm d}\nu \right] \Bigg\}\ ,$](/articles/aa/full/2003/18/aa2873/img83.gif) |
|
|
(14) |
where
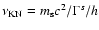 is the transition frequency between
interaction in the Thompson and Klein-Nishima regimes,
is the transition frequency between
interaction in the Thompson and Klein-Nishima regimes,
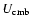 is the
energy density of the cosmic microwave-background photons, and
is the
energy density of the cosmic microwave-background photons, and 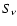 is
the volume emissivity of the plerion.
is
the volume emissivity of the plerion.
3.1 Plerion evolution
All the rates in the previous section depend on quantities that change
with time during the plerion evolution. We determine the dependency on
time of the different quantities within the framework of the PS model.
We consider the spin-down power of the pulsar to be continuously
converted into injection of fresh particles and magnetic field energy.
The spin-down luminosity of the pulsar can be parametrized as:
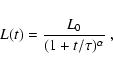 |
(15) |
where the characteristic spin-down time 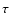 is a few hundred years,
and the index
is a few hundred years,
and the index 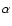 is expected to be around 2 if the breaking is
purely electromagnetic.
is expected to be around 2 if the breaking is
purely electromagnetic.
Treating the plerion as homogeneous and expanding at constant velocity,
the magnetic field evolution, resulting from the competition between the
continuous pulsar supply and adiabatic losses, can be determined analytically.
For times shorter or comparable with 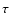 ,
one can make the approximation:
,
one can make the approximation:
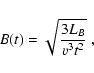 |
(16) |
where LB is the fraction of the pulsar luminosity that goes into
magnetic energy.
The other quantity we need to know as a function of time in order to
estimate ICS losses and the rate of photo-meson production is the
plerion volume emissivity 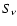 ,
due to non-thermal radiation.
To this purpose, we need to determine the time-dependences of the
spectral density N(E,t) of the emitting particles (pairs).
For the wind particles we assume that they are injected with an initial
spectrum in the form of a broken power-law:
,
due to non-thermal radiation.
To this purpose, we need to determine the time-dependences of the
spectral density N(E,t) of the emitting particles (pairs).
For the wind particles we assume that they are injected with an initial
spectrum in the form of a broken power-law:
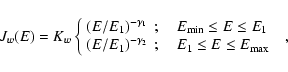 |
(17) |
where Kw is related to the fraction of pulsar luminosity that is converted
into pairs,
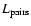 through:
through:
![$\displaystyle K_w(t)={L_{\rm pairs}(t) \over E_1^2} \left\{
{1 \over 2-\gamma_1...
...[{\left(E_{\rm max} \over E_1\right)}^{2-\gamma_2}-1\right]
\right\}^{-1} \cdot$](/articles/aa/full/2003/18/aa2873/img93.gif) |
|
|
(18) |
In the following we shall assume E1 to be constant with time
and independent of the wind Lorentz factor: we take
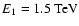 ,
roughly corresponding to the energy of the particles radiating at the
frequency at which the high energy
break of the spectrum of the Crab Nebula is observed.
As for
,
roughly corresponding to the energy of the particles radiating at the
frequency at which the high energy
break of the spectrum of the Crab Nebula is observed.
As for
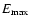 ,
this will depend on both time and the wind Lorentz
factor, due to the dependence on the latter of the proton energy and
on the dependence on the former of the nebular magnetic field strength.
In fact we assume the maximum
energy to which the pairs can be accelerated to be given by
,
this will depend on both time and the wind Lorentz
factor, due to the dependence on the latter of the proton energy and
on the dependence on the former of the nebular magnetic field strength.
In fact we assume the maximum
energy to which the pairs can be accelerated to be given by
 ,
with
,
with
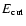 determined by the condition
determined by the condition
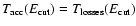 ,
i.e.
the acceleration time cannot exceed the time-scale for energy losses.
Assuming
,
i.e.
the acceleration time cannot exceed the time-scale for energy losses.
Assuming
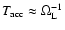 (with
(with
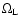 the particle
Larmor frequency) and the losses as due
to synchrotron emission in the average nebular magnetic field, one
finds
the particle
Larmor frequency) and the losses as due
to synchrotron emission in the average nebular magnetic field, one
finds
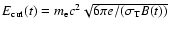 .
.
We mentioned that charged pion decay provides an additional source of
pairs in the nebula. Their evolution is completely analogous to that of
the wind particles, so that apart from the different initial spectrum,
the treatment below applies to both components.
The spectral distribution at a time t, N(E,t), is found as a function
of the injection spectrum J=Jw+Je (see Eq. (5)), as:
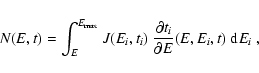 |
(19) |
where ti is the time at which the particle was born and Ei its
initial energy. N(E,t) is readily computed
once
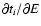 is known as a function of E and t.
is known as a function of E and t.
The needed relation between E, Ei and ti may be found from the
equation describing the
single particle energy evolution due to synchrotron and adiabatic losses:
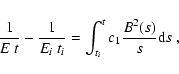 |
(20) |
where
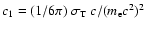 is
the constant relating the synchrotron power to magnetic field strength
and particle energy.
For
is
the constant relating the synchrotron power to magnetic field strength
and particle energy.
For
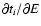 we find:
we find:
![\begin{displaymath}
{\partial t_i \over \partial E}={E_i\ t_i^2(E,t) \over E^2\ t}\
\left[ 1 + {2\ E_i \over E_b(t_i)} \right]^{-1}\ ,
\end{displaymath}](/articles/aa/full/2003/18/aa2873/img106.gif) |
(21) |
where we have used the definition of the so-called break energy:
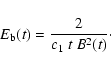 |
(22) |
For times shorter than 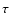 ,
when
,
when
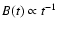 (Eq.
(16)), so that
(Eq.
(16)), so that
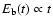 ,
one finds:
,
one finds:
![$\displaystyle t_i={t \over 2 (1 +E/E_{\rm b}(t))} {E \over E_i} \left\{ 1\!+\!
...
...E_{\rm b}(t)}
\left(1+ {E \over E_{\rm b}(t) } \right) \right]^{1/2} \right\} ,$](/articles/aa/full/2003/18/aa2873/img110.gif) |
|
|
(23) |
and the solution of Eq. (19) can be approximated as:
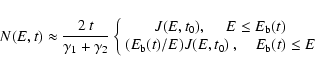 |
(24) |
with
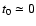 for
for 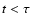 and
and
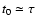 afterwards.
afterwards.
The evolution of the wind particle spectrum as a function of time is
plotted in Fig. 1 for the case
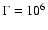 ,
,
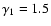 ,
,
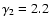 and
and
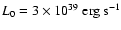 ,
with
,
with
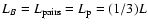 .
We plot the full solution of the problem taking into account the
real time-dependences arising from the varying pulsar input (Eq. (15) with
.
We plot the full solution of the problem taking into account the
real time-dependences arising from the varying pulsar input (Eq. (15) with 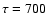 yr) together
with the approximate expression in Eq. (24).
yr) together
with the approximate expression in Eq. (24).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f1}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg123.gif) |
Figure 1:
The time evolution of the wind particle spectrum in the
case
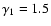 , ,
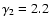 , ,
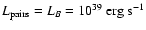 .
The different curves refer
to different epochs after the supernova explosion: .
The different curves refer
to different epochs after the supernova explosion:
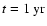 (solid),
(solid),
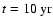 (dotted),
(dotted),
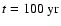 (dashed),
(dashed),
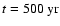 (dot-dashed). The points trace, at each time,
the approximation given in the text.
(dot-dashed). The points trace, at each time,
the approximation given in the text. |
| Open with DEXTER |
Once N(E,t) and B(t) are known, the volume emissivity 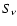 that
enters Eq. (14) is computed from synchrotron theory as:
that
enters Eq. (14) is computed from synchrotron theory as:
![\begin{displaymath}
S^{\rm sync}_\nu(\nu,t)={c_1 B \over 2 c_2} {3 \over 4\ \pi\...
...er c_2\ B}}\ N\left[\sqrt{{\nu \over c_2\ B} }\ , t \right]\ ,
\end{displaymath}](/articles/aa/full/2003/18/aa2873/img124.gif) |
(25) |
where
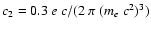 .
Knowing
.
Knowing
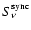 one can also compute the ICS emissivity of the plerion,
one can also compute the ICS emissivity of the plerion,
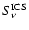 ,
following,
for instance, Blumenthal & Gould (1970).
From the total emissivity
,
following,
for instance, Blumenthal & Gould (1970).
From the total emissivity
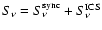 we also obtain
the flux
we also obtain
the flux 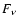 that appears in Eq. (7):
that appears in Eq. (7):
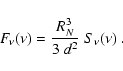 |
(26) |
3.2 Pion production efficiency
The time-evolution of the magnetic and radiation fields in the nebula
as derived in the previous section was used to compute the time-history
of pion production efficiency.
In the plots below we show the behaviour of 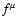 ,
,
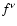 ,
,
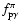 and
and
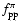 as a function of time after the
supernova explosion for various values of the pulsar luminosity L, of the
wind Lorentz factor
as a function of time after the
supernova explosion for various values of the pulsar luminosity L, of the
wind Lorentz factor 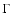 and of the remnant expansion velocity v.
In all the plots in this section we assumed the pulsar energy input
to be evenly shared between magnetic field, protons and pairs:
and of the remnant expansion velocity v.
In all the plots in this section we assumed the pulsar energy input
to be evenly shared between magnetic field, protons and pairs:
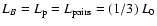 .
To compute the radiation field, we assumed the injection spectrum of the
pairs as in Eq. (17) with
.
To compute the radiation field, we assumed the injection spectrum of the
pairs as in Eq. (17) with
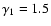 and
and
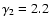 .
We consider a monoenergetic distribution of protons corresponding to the
Lorentz factor of the wind.
.
We consider a monoenergetic distribution of protons corresponding to the
Lorentz factor of the wind.
In Fig. 2 we plot
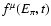 for the value of
for the value of
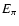 corresponding to the highest energy pions produced for each of the
values of
corresponding to the highest energy pions produced for each of the
values of 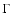 considered.
considered.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f2}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg140.gif) |
Figure 2:
The time evolution of 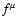 for different values of
the pulsar luminosity, of the remnant expansion velocity and of the wind
Lorentz factor. The curves plotted in different panels are computed for
different values of the wind Lorentz factor.
The different curves in each panel are marked as explained below.
Empty triangles:
for different values of
the pulsar luminosity, of the remnant expansion velocity and of the wind
Lorentz factor. The curves plotted in different panels are computed for
different values of the wind Lorentz factor.
The different curves in each panel are marked as explained below.
Empty triangles:
![$L[{\rm erg}/{\rm s}]=3 \times 10^{39}$](/articles/aa/full/2003/18/aa2873/img9.gif) , ,
![$v[\rm km~s^{-1}]=10^3$](/articles/aa/full/2003/18/aa2873/img136.gif) .
Empty squares: .
Empty squares:
![$L[{\rm erg}/{\rm s}]=3 \times 10^{39}$](/articles/aa/full/2003/18/aa2873/img9.gif) , ,
![$v[\rm km~s^{-1}]=10^4$](/articles/aa/full/2003/18/aa2873/img137.gif) .
Filled triangles: .
Filled triangles:
![$L[{\rm erg}/{\rm s}] =3 \times 10^{40}$](/articles/aa/full/2003/18/aa2873/img12.gif) , ,
![$v[\rm km~s^{-1}]=10^3$](/articles/aa/full/2003/18/aa2873/img136.gif) .
Filled squares: .
Filled squares:
![$L[{\rm erg}/{\rm s}] =3 \times 10^{40}$](/articles/aa/full/2003/18/aa2873/img12.gif) , ,
![$v[\rm km~s^{-1}]=10^4$](/articles/aa/full/2003/18/aa2873/img137.gif) .
The vertical lines represent the time at which the optical depth for neutrinos
drops below 1 in the case when .
The vertical lines represent the time at which the optical depth for neutrinos
drops below 1 in the case when
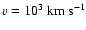 (solid) and
when
(solid) and
when
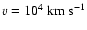 (dashed).
(dashed). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f3}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg141.gif) |
Figure 3:
The time evolution of 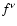 for the highest energy
pions corresponding to different values of
the pulsar luminosity, of the remnant expansion velocity and of the wind
Lorentz factor. Same notation as in Fig. 2.
for the highest energy
pions corresponding to different values of
the pulsar luminosity, of the remnant expansion velocity and of the wind
Lorentz factor. Same notation as in Fig. 2. |
| Open with DEXTER |
It is apparent from the figure that for Lorentz factors up to 105 pions never undergo any severe energy losses, not even at early times,
when the magnetic and radiation field in the plerion are most intense.
For energetic enough pions, instead, radiation losses at early times do
become important, decreasing the decay probability by a factor that can
be of the order of 102 for the lowest considered value of the
expansion velocity and highest considered pulsar luminosity
(filled triangles).
Losses at early times are found to be due mainly to synchrotron emission
and their dependence on v and L arises from the relation between the
magnetic field intensity and these two quantities (Eq. (16)).
It is interesting to note that in all the cases considered, 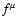 becomes 1 at very early times, and actually earlier than the time at which
the remnant stops being optically thick to neutrinos, which we mark as
a reference time in Fig. 2. This reference time is computed
considering the fact that the main source of optical depth for high energy
neutrinos are nuclear collisions that give rise to muons:
becomes 1 at very early times, and actually earlier than the time at which
the remnant stops being optically thick to neutrinos, which we mark as
a reference time in Fig. 2. This reference time is computed
considering the fact that the main source of optical depth for high energy
neutrinos are nuclear collisions that give rise to muons:
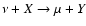 .
The cross section for this process
(e.g. Learned & Mannheim 2000) is a function of the
neutrino energy alone at the energies we consider.
Hence, the time at which
.
The cross section for this process
(e.g. Learned & Mannheim 2000) is a function of the
neutrino energy alone at the energies we consider.
Hence, the time at which
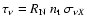 drops
below unity for the highest energy neutrinos corresponding to each
value of the Lorentz factor we consider depends only on the
Lorentz factor itself and on the density evolution of the remnant
(i.e. on its expansion velocity, once the total mass is fixed
and assumed as uniformily distributed). One has:
drops
below unity for the highest energy neutrinos corresponding to each
value of the Lorentz factor we consider depends only on the
Lorentz factor itself and on the density evolution of the remnant
(i.e. on its expansion velocity, once the total mass is fixed
and assumed as uniformily distributed). One has:
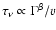 ,
with
,
with 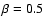 if
if
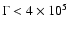 and
and 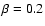 otherwise.
otherwise.
The same legenda as for Fig. 2 applies to Fig. 3, where the evolution of 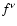 is shown (again in the case
when it is minimum, i.e. for the maximum muon energies).
is shown (again in the case
when it is minimum, i.e. for the maximum muon energies).
As we could expect, radiation losses for muons are more severe than for
pions,
and for the most energetic we are considering (lower right panel) 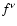 actually becomes 1 later than
actually becomes 1 later than 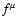 .
.
It is important to notice that as far as only the non-thermal radiation
field is taken into account, synchrotron losses are always dominant with
respect to losses due to ICS, according to our
calculation. The latter can
become important, though, if also the thermal radiation field is
taken into account, but this effect should be limited to earlier times
than that at which 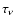 drops below 1 (Beall & Bednarek 2002).
drops below 1 (Beall & Bednarek 2002).
As far as 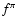 is concerned, we computed the efficiency of both
photo-meson production and p-p collisions. For the latter process
we considered
is concerned, we computed the efficiency of both
photo-meson production and p-p collisions. For the latter process
we considered
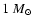 of material uniformily distributed within the
remnant and used
of material uniformily distributed within the
remnant and used 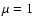 in the calculations. The results are shown
in Fig. 4.
in the calculations. The results are shown
in Fig. 4.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f4}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg150.gif) |
Figure 4:
The time evolution of 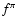 for different values of
the pulsar luminosity, of the remnant expansion velocity and of the wind
Lorentz factor. The solid curves refer to the efficiency of nuclear collisions
while the dashed ones show the efficiency of photo-meson production. Curves
referring to different values of the pulsar luminosity and remnant expansion
velocity are marked according to the same notation as for Figs. 2
and 3.
for different values of
the pulsar luminosity, of the remnant expansion velocity and of the wind
Lorentz factor. The solid curves refer to the efficiency of nuclear collisions
while the dashed ones show the efficiency of photo-meson production. Curves
referring to different values of the pulsar luminosity and remnant expansion
velocity are marked according to the same notation as for Figs. 2
and 3. |
| Open with DEXTER |
We find that radiation losses are never effective in
limiting the efficiency of p-p collisions, not even in the very intense
initial magnetic field of a bright, slowly expanding plerion.
Conversely, for high enough values of the wind Lorentz
factor 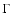 and low enough values of the wind expansion velocity,
synchrotron losses are the main limit to photo-meson production.
However, we can see from Fig. 4 that photomeson production
never reaches
efficiencies higher than about 30%, at least for the prototypical
spectrum that has been assumed here.
and low enough values of the wind expansion velocity,
synchrotron losses are the main limit to photo-meson production.
However, we can see from Fig. 4 that photomeson production
never reaches
efficiencies higher than about 30%, at least for the prototypical
spectrum that has been assumed here.
It should be noticed, finally, that
in the plots shown above for 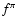 ,
,
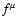 and
and 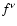 ,
when computing
both ICS losses and photo-meson production we have only
included the photon spectrum deriving from synchrotron and ICS emission of
the wind particles. In doing that, we have neglected the thermal emission
from the gas and dust in the filaments and the radiation derived from
pion decay. The consistency of the latter approximation was verified
a posteriori: after calculating the radiation flux from the
products of pion decay we checked that adding this contribution to
the target radiation for ICS losses did not change the results plotted
in Figs. 2-4.
,
when computing
both ICS losses and photo-meson production we have only
included the photon spectrum deriving from synchrotron and ICS emission of
the wind particles. In doing that, we have neglected the thermal emission
from the gas and dust in the filaments and the radiation derived from
pion decay. The consistency of the latter approximation was verified
a posteriori: after calculating the radiation flux from the
products of pion decay we checked that adding this contribution to
the target radiation for ICS losses did not change the results plotted
in Figs. 2-4.
3.3 Photon and neutrino fluxes from a "young Crab''
In this section we use the theory introduced above to compute both the
electromagnetic and neutrino emission from a young plerion with Crab-like
parameters, as a function of time after the supernova explosion.
We consider a pulsar whose initial spin-down power is
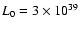 erg/s.
We assume, as in Sect. 3.2, that L0 is evenly converted
into electron, proton and magnetic field energy:
erg/s.
We assume, as in Sect. 3.2, that L0 is evenly converted
into electron, proton and magnetic field energy:
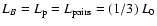 .
The distance of the pulsar and the plerion expansion velocity
are taken to be the same as for the Crab, and 1
.
The distance of the pulsar and the plerion expansion velocity
are taken to be the same as for the Crab, and 1 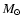 of thermal material
uniformily distributed in the plerion volume is considered as the target
for p-p collisions.
of thermal material
uniformily distributed in the plerion volume is considered as the target
for p-p collisions.
The time evolution of the pion production efficiency in such a plerion
was computed in Sect. 3.2 (curves marked with empty squares in
Figs. 2-4).
Taking the results from that section we estimate the global photon spectrum
of the plerion. The high energy part is entirely due to 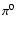 decay, while
at low energies we estimate the synchrotron emission of both wind and
secondary pairs together with the ICS emission of the former. The overall
spectrum at different times during the
plerion evolution is reported in Fig. 5.
decay, while
at low energies we estimate the synchrotron emission of both wind and
secondary pairs together with the ICS emission of the former. The overall
spectrum at different times during the
plerion evolution is reported in Fig. 5.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f5}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg153.gif) |
Figure 5:
Electromagnetic spectrum of a "young Crab''
at different times after the supernova explosion. The thick curves
correspond to the synchrotron (at low energies) and ICS (at higher energies)
emission of the wind pairs, while the lighter curves refer to
the emission of the pion decay products. The different panels correspond
to different values of the wind Lorentz factor 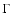 and the different
line types refer to different times.
and the different
line types refer to different times. |
| Open with DEXTER |
It is apparent from the figure that, for the set of parameters used,
the radiation due to the secondary pairs could only be detectable over the
emission due to the wind particles, at early times (up to few tens of
years after the supernova explosion) and at photon energies in the
range 100 MeV-1 TeV.
We notice that 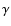 -rays from
-rays from 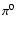 decay should be
detected even by present TeV detectors
during the first few tens of years after the supernova explosion,
if a similar plerion was born within
the galaxy. The
decay should be
detected even by present TeV detectors
during the first few tens of years after the supernova explosion,
if a similar plerion was born within
the galaxy. The 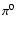 decay
decay 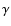 -ray flux always exceeds the ICS
emission at high enough energies for times up to several tens of years
at least.
-ray flux always exceeds the ICS
emission at high enough energies for times up to several tens of years
at least.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f6}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg154.gif) |
Figure 6:
Neutrino spectrum of a "young Crab''. The notation is
the same as for Fig. 5. The solid thick line is the detection
threshold for ICE-cube (Hill 2001), while the dot-dashed line is the
atmospheric neutrino background in a
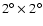 bin.
bin. |
| Open with DEXTER |
In Fig. 6 we show the expected neutrino flux from the
same plerion. We find that this is generally well above the atmospheric
background of a detector with an angular resolution of
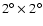 .
Moreover
a galactic object described by our set of parameters could give a flux
of neutrinos already detectable by telescopes like AMANDA II for the
first ten years. It is clear from the figure that the probability of
detecting such objects will increase considerably with the upcoming
.
Moreover
a galactic object described by our set of parameters could give a flux
of neutrinos already detectable by telescopes like AMANDA II for the
first ten years. It is clear from the figure that the probability of
detecting such objects will increase considerably with the upcoming
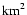 neutrino telescopes, since their lower threshold allows
neutrino detection even from older plerions, if the pulsar wind
contains a non-negligible fraction of protons.
neutrino telescopes, since their lower threshold allows
neutrino detection even from older plerions, if the pulsar wind
contains a non-negligible fraction of protons.
4 Constraining the parameters of the Crab pulsar wind
In this section, we use the Crab Nebula, the prototype
plerion, to discuss how the information coming from high
energy photon and neutrino detection could be used to constrain the
physics of plerions.
The parameters playing a role in determining the flux of high energy
photons and neutrinos are all quite well known for the Crab Nebula,
except for the parameters that enter in the determination of 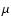 ,
the wind Lorentz factor
,
the wind Lorentz factor 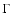 ,
and the
fraction of the pulsar spin-down power that goes into acceleration
of protons. The relevant parameters for our purposes are, from the
equations in Sect. 2:
the plerion age
,
and the
fraction of the pulsar spin-down power that goes into acceleration
of protons. The relevant parameters for our purposes are, from the
equations in Sect. 2:
the plerion age
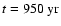 ,
its distance
,
its distance
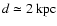 ,
its expansion velocity,
,
its expansion velocity,
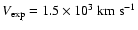 ,
the average magnetic field intensity
,
the average magnetic field intensity
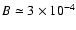 G,
and finally the amount of mass contained in the filamentary shell.
For the latter, the most recent estimates give
G,
and finally the amount of mass contained in the filamentary shell.
For the latter, the most recent estimates give
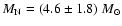 (Fesen et al. 1997). We shall consider a value
(Fesen et al. 1997). We shall consider a value
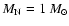 and values of
and values of 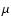 in the range
in the range 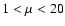 ,
according to the upper
limit on
,
according to the upper
limit on 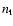 derived by Atoyan & Aharonian (1996), based
on the compatibility between the bremsstrahlung
derived by Atoyan & Aharonian (1996), based
on the compatibility between the bremsstrahlung 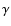 -rays and the
observed flux from the Crab Nebula above 1 GeV. We notice that if
the mass estimated by Fesen et al. (1997) was uniformally
distributed in the nebula, this would correspond to
-rays and the
observed flux from the Crab Nebula above 1 GeV. We notice that if
the mass estimated by Fesen et al. (1997) was uniformally
distributed in the nebula, this would correspond to 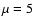 .
.
Inserting the numbers just quoted into the equations in Sect. 2 we can estimate all the relevant time-scales.
One can readily see that what is important
for computing 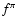 is the
comparison between
is the
comparison between
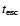 and
and
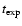 (whose relative
importance depends on
(whose relative
importance depends on 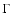 )
and
)
and
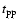 ,
since
the other three time-scales are much longer than these. From
Eqs. (1), (10)-(12),
we have:
,
since
the other three time-scales are much longer than these. From
Eqs. (1), (10)-(12),
we have:
where 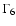 is the wind Lorentz factor in units of 106.
is the wind Lorentz factor in units of 106.
For the same values of the parameters the muon losses due to synchroton
emission or ICS (Eqs. (13) and (14)) are completely
negligible on the time-scale of their decay, even for the highest
energy we consider. The same is true for pions, whose
proper decay times are about a hundred times shorter.
In Figs. 7 and 8 we plot the
expected neutrino and photon fluxes from the Crab Nebula as a function
of energy, for different assumptions on the wind Lorentz factor and
different values of the parameter 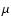 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f7}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg169.gif) |
Figure 7:
The flux of neutrinos expected from
the Crab Nebula as a function of energy, for different values of
the parameter 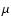 and for different values of the wind Lorentz factor
and for different values of the wind Lorentz factor
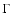 .
The different curves in each panel correspond to .
The different curves in each panel correspond to 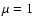 (solid),
(solid),
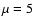 (dotted),
(dotted), 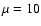 (dashed) and
(dashed) and 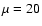 (long-dashed).
The considered
values of
(long-dashed).
The considered
values of 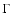 range from 104 to 107, as specified in each panel.
The solid thick line is the detection threshold for IceCube
(Hill 2001), while the dot-dashed line is the atmospheric
neutrino background in a
range from 104 to 107, as specified in each panel.
The solid thick line is the detection threshold for IceCube
(Hill 2001), while the dot-dashed line is the atmospheric
neutrino background in a
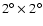 bin.
We assume 60%
of the pulsar wind energy to be carried by protons.
bin.
We assume 60%
of the pulsar wind energy to be carried by protons. |
| Open with DEXTER |
We have assumed that protons are
the main energy carriers in the wind so that we put in them about 60%
of the pulsar spin-down luminosity
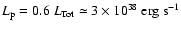 ,
being
,
being
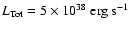 .
Our choice of the energy fraction into baryons comes from the fact that
this is the percentage of the pulsar power that is required to
be in baryons if the luminosity contrast of the Crab Nebula wisps is to
be explained through magnetic field compression due to the ion gyration
in the shocked background pair plasma (Spitkovsky & Arons 1999).
.
Our choice of the energy fraction into baryons comes from the fact that
this is the percentage of the pulsar power that is required to
be in baryons if the luminosity contrast of the Crab Nebula wisps is to
be explained through magnetic field compression due to the ion gyration
in the shocked background pair plasma (Spitkovsky & Arons 1999).
The neutrino and photon fluxes were computed from Eqs. (4) and (6) respectively,
with the pion differential spectrum per unit time
computed in the scaling approximation for the p-p scattering cross-section
(Blasi 2001). In the scaling regime a monoenergetic proton distribution
with energy 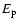 leads to the injection of pions described as:
leads to the injection of pions described as:
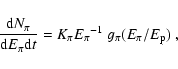 |
(28) |
where the function 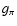 is
is
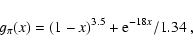 |
(29) |
and 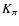 is found from the condition
is found from the condition
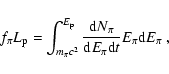 |
(30) |
leading to:
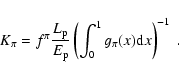 |
(31) |
It is apparent from Fig. 7 that, for the generally favoured value
of
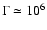 (Kennel & Coroniti 1984a
and 1984b; Gallant & Arons 1994), and for the value of
(Kennel & Coroniti 1984a
and 1984b; Gallant & Arons 1994), and for the value of
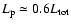 favoured by Gallant & Arons (1994)
and Spitkovsky & Arons (1999),
the flux of neutrinos from the Crab Nebula would be well above the
atmospheric neutrino background already for
favoured by Gallant & Arons (1994)
and Spitkovsky & Arons (1999),
the flux of neutrinos from the Crab Nebula would be well above the
atmospheric neutrino background already for 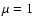 .
The chances of detecting multi-TeV neutrinos from the Crab Nebula with
IceCube look promising, based on this figure.
.
The chances of detecting multi-TeV neutrinos from the Crab Nebula with
IceCube look promising, based on this figure.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f8}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg180.gif) |
Figure 8:
The flux of high energy photons expected from the
Crab Nebula, for different values of the parameter 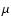 and
of the wind Lorentz factor
and
of the wind Lorentz factor 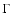 .
The notation is the same as in Fig. 7. The expected
fluxes are compared with the available data and upper limits
(de Jager et al. 1996;
Aharonian et al. 2000 and references therein). Also shown as a thick
curve in each panel is the ICS flux computed based on this model. .
The notation is the same as in Fig. 7. The expected
fluxes are compared with the available data and upper limits
(de Jager et al. 1996;
Aharonian et al. 2000 and references therein). Also shown as a thick
curve in each panel is the ICS flux computed based on this model. |
| Open with DEXTER |
However, part of the section of the parameter space that would lead to
a detectable flux of neutrinos can already be excluded based on the
available high energy 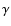 -ray data. In Fig. 8 we
plot the flux of high energy photons expected from
-ray data. In Fig. 8 we
plot the flux of high energy photons expected from 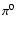 decay.
It is clear that in some cases the computed fluxes at multi-TeV energies
are above the measurements and upper limits. The latter, on the other
hand, can be comfortably explained, within the error bars, as due to
ICS (de Jager et al. 1996; Atoyan & Aharonian 1996;
Aharonian et al. 2000). Even within the framework of our crude
model, which not only treats the plerion as homogeneous but also
neglects the contribution to the target photon field of the ambient
thermal emission, the computed ICS flux is only slightly below the
TeV data points.
decay.
It is clear that in some cases the computed fluxes at multi-TeV energies
are above the measurements and upper limits. The latter, on the other
hand, can be comfortably explained, within the error bars, as due to
ICS (de Jager et al. 1996; Atoyan & Aharonian 1996;
Aharonian et al. 2000). Even within the framework of our crude
model, which not only treats the plerion as homogeneous but also
neglects the contribution to the target photon field of the ambient
thermal emission, the computed ICS flux is only slightly below the
TeV data points.
In the following, we review our expectation for the flux of neutrinos
from the Crab Nebula in the light of the constraints arising from
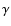 -ray observations.
-ray observations.
Before discussing these limits, however, we should also consider the
other possibility we mentioned to put constraints on the three
unknowns 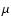 ,
,
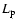 and
and 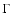 .
This is offered, at least in principle,
by the signatures that may be left by the secondary pairs in the
synchrotron radiation spectrum of the nebula.
These pairs would be injected in the Nebula according to Eq.
(5), but the injection rate (described by Eq. (28)
and depending on
.
This is offered, at least in principle,
by the signatures that may be left by the secondary pairs in the
synchrotron radiation spectrum of the nebula.
These pairs would be injected in the Nebula according to Eq.
(5), but the injection rate (described by Eq. (28)
and depending on 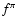 and
and 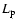 through Eq. (31))
has to be considered now as a function of time. Since we are mainly
interested in low energy pairs, with long synchrotron life-times, we
need to take into account the whole history of pion production in the
nebula. This is done as discussed in Sects. 3.1 and 3.2.
through Eq. (31))
has to be considered now as a function of time. Since we are mainly
interested in low energy pairs, with long synchrotron life-times, we
need to take into account the whole history of pion production in the
nebula. This is done as discussed in Sects. 3.1 and 3.2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f9}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg181.gif) |
Figure 9:
Consequences of pion production on the electromagnetic
spectrum of the Crab Nebula. The thick curve and the points represent the
observed emission, while the thin curves are fluxes from our model.
At low frequencies the model flux is due to
synchrotron emission associated to secondary electrons and positrons, while
the contribution at high frequencies is the same shown in Fig. 8
and comes from 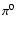 decay. The different panels refer to the emission computed
for different values of the wind Lorentz factor while the different line-types
are associated to different values of the parameter
decay. The different panels refer to the emission computed
for different values of the wind Lorentz factor while the different line-types
are associated to different values of the parameter 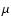 as specified in the
each panel.
as specified in the
each panel. |
| Open with DEXTER |
We show in Fig. 9 the comparison between the Crab
Nebula observed radiation
spectrum and the synchrotron flux from secondary pairs computed in the
case when
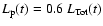 ,
with
,
with
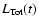 described
by Eq. (15), where
described
by Eq. (15), where
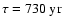 and
and
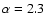 (Groth 1975). In the same figure, we also show the contribution
arising from
(Groth 1975). In the same figure, we also show the contribution
arising from 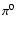 decay, in the
decay, in the 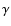 -ray part of the spectrum.
It is apparent that the emission produced by the secondary pairs,
according to our model, is a completely negligible fraction of the
present day synchrotron emission of the Crab Nebula and cannot provide
any additional constraint on the parameters we are interested in.
-ray part of the spectrum.
It is apparent that the emission produced by the secondary pairs,
according to our model, is a completely negligible fraction of the
present day synchrotron emission of the Crab Nebula and cannot provide
any additional constraint on the parameters we are interested in.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{2873.f10}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg186.gif) |
Figure 10:
The allowed parameter space for
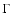 and
and
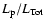 as constrained through the comparison
with observations of the photon fluxes from pion decay computed within
the framework of our model.
The allowed regions for each of the considered value of
as constrained through the comparison
with observations of the photon fluxes from pion decay computed within
the framework of our model.
The allowed regions for each of the considered value of 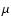 are the
ones lying under the curve of corresponding type:
are the
ones lying under the curve of corresponding type:
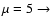 solid,
solid,
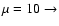 dashed,
dashed,
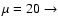 dot-dashed. No constraints
can be put on the wind parameters for
dot-dashed. No constraints
can be put on the wind parameters for 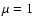 . . |
| Open with DEXTER |
In Fig. 10 we use the information that can be extracted
from high energy data (Fig. 8) to restrict the allowed
parameter space for
the values of
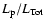 ,
,
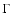 and
and 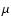 .
The allowed regions, for each choice of
.
The allowed regions, for each choice of 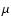 ,
are those lying below
the corresponding curve, as explained in the figure caption.
,
are those lying below
the corresponding curve, as explained in the figure caption.
It is interesting to notice that, if 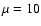 or larger, the possibility
that 60% of the pulsar wind energy might be in protons with a
Lorentz factor
or larger, the possibility
that 60% of the pulsar wind energy might be in protons with a
Lorentz factor
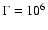 would be excluded by the data.
would be excluded by the data.
We now use the constraints in Fig. 10 to estimate the
maximum number of neutrino events that one could expect to detect from
the Crab Nebula in 1 yr of observation with a detector of area
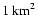 ,
such as IceCube will be.
The result of this calculation is shown in Fig. 11 where we
plot the maximum number of muons per year as a function of the wind
Lorentz factor.
,
such as IceCube will be.
The result of this calculation is shown in Fig. 11 where we
plot the maximum number of muons per year as a function of the wind
Lorentz factor. 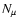 is computed taking into account the probability
for a neutrino to interact with the matter in the detector and create
a muon. For each value of
is computed taking into account the probability
for a neutrino to interact with the matter in the detector and create
a muon. For each value of 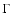 we consider the maximum allowed value
of
we consider the maximum allowed value
of
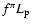 with the requirement that
with the requirement that
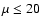 and
and
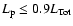 .
This determines
.
This determines
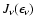 .
.
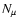 is then found as:
is then found as:
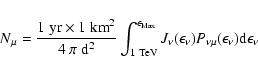 |
(32) |
where the maximum neutrino energy is
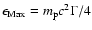 and
and
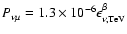 with
with 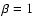 if
if
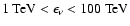 ,
and
,
and
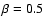 otherwise
(Gaisser et al. 1995).
otherwise
(Gaisser et al. 1995).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f11}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg198.gif) |
Figure 11:
The maximum number of muons per year that would be
produced by neutrinos coming from the Crab Nebula in a
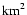 detector.
Also shown, as a dot-dashed line, are the background counts, assuming an
angular resolution of
detector.
Also shown, as a dot-dashed line, are the background counts, assuming an
angular resolution of
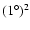 ,
such as IceCube should have. ,
such as IceCube should have. |
| Open with DEXTER |
The background counts we show in Fig. 11 are those computed
for IceCube by Alvarez-Muñiz & Halzen (2001) at the position
of the Crab Nebula. The maximum number of neutrino events allowed by the
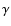 -ray data is above the background for basically the entire range
of values of
-ray data is above the background for basically the entire range
of values of 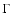 we considered. The effect of neutrino oscillations
would be to reduce these fluxes. For the case of maximal mixing, equal
abundances of neutrinos of the three flavors are obtained, so that the
flux of muon neutrinos is about half of that calculated above.
we considered. The effect of neutrino oscillations
would be to reduce these fluxes. For the case of maximal mixing, equal
abundances of neutrinos of the three flavors are obtained, so that the
flux of muon neutrinos is about half of that calculated above.
5 Conclusions
In this paper we have analysed the observational consequences that the
presence in pulsar winds of a proton component, energetically dominant,
might have.
We have found that when the plerion is very young (up to
a few tens of years after the supernova explosion) the main loss
mechanism for these protons is likely to be pion production due to
nuclear collisions. A large flux of neutrinos, 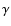 -rays and
secondary pairs can be expected during these early stages. The
synchrotron emission
from secondaries is likely to be completely negligible, while
the TeV photon and neutrino
emission from a galactic object could be detectable even by present-
day telescopes during the first few tens of years after the supernova
explosion. Detection of neutrinos from older plerions should
await the upcoming
-rays and
secondary pairs can be expected during these early stages. The
synchrotron emission
from secondaries is likely to be completely negligible, while
the TeV photon and neutrino
emission from a galactic object could be detectable even by present-
day telescopes during the first few tens of years after the supernova
explosion. Detection of neutrinos from older plerions should
await the upcoming
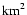 detectors.
detectors.
We have also estimated the present-day TeV photon and neutrino
emission from the Crab Nebula.
The existing TeV observations already exclude part of the parameter
space, so that not all combinations of 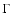 ,
,
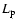 and
and 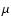 are
allowed.
are
allowed.
Finally we have computed the maximum number of neutrino events allowed by the
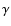 -ray data according to our modeling and found it to be larger than
the atmospheric neutrino background (as already suggested by Arons,
1998). Such a flux is likely to
be detected by a
-ray data according to our modeling and found it to be larger than
the atmospheric neutrino background (as already suggested by Arons,
1998). Such a flux is likely to
be detected by a
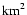 detector such as IceCube. Neutrino detection
can be therefore considered as a promising means to help answer the
question of how large a fraction of the pulsar spin-down energy goes into
relativistic baryons.
detector such as IceCube. Neutrino detection
can be therefore considered as a promising means to help answer the
question of how large a fraction of the pulsar spin-down energy goes into
relativistic baryons.
Acknowledgements
We thank F. Pacini and M. Salvati for fruitful discussions.
We are very grateful to the referee, Yves Gallant, for valuable
suggestions. This work was partly supported by MIUR under grant
Cofin 2001-02-10.
-
Aharonian, F. A., et al. 2000, ApJ, 539, 317
In the text
NASA ADS
-
Alvarez-Muñiz, J., & Halzen, F. 2001 [astro-ph/0.05408]
In the text
-
Arons, J. 1998, Mem. S.A.It., 69, 989
NASA ADS
-
Atoyan, A. M., & Aharonian, F. A. 1996, MNRAS, 278, 525
NASA ADS
-
Bednarek, W., & Protheroe, R. J. 1997, PRL, 79, 2616
In the text
-
Bednarek, W. 2001, A&A, 378, L49
In the text
NASA ADS
-
Beall, J. H., & Bednarek, W. 2002, ApJ, 569, 343
In the text
NASA ADS
-
Berezinskij, V. S., Bulanov, S. V., Dogiel, V. A., Ginzburg, V. L., & Ptuskin, V. S. 1990, Astrophysics of Cosmic Rays (Amsterdam: North-Holland)
-
Blasi, P. 2001, APh, 15, 223
In the text
NASA ADS
-
Blumenthal, G. S., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237
In the text
NASA ADS
-
Fesen, R. A., Shull, J. M., & Hurford, A. P. 1997, AJ, 113, 354
In the text
NASA ADS
-
Gaisser, T. K., Halzen, F., & Stanev, T. 1995, Phys. Rep., 258, 173
In the text
NASA ADS
-
Gallant, Y. A., & Arons, J. 1994, ApJ, 435, 230
In the text
NASA ADS
-
Groth, E. J. 1975, ApJS, 29, 431
In the text
NASA ADS
-
Halzen, F. 2001, in Intl. Symp. on High Energy Gamma Ray Astronomy, Heidelberg, June 2000 [astro-ph/0103195]
-
Hill, C. G. 2001, Proceedings of the XXXVIth Rencontres de Moriond [astro-ph/0106064]
In the text
-
Hoshino, M., et al. 1992, ApJ, 390, 454
In the text
NASA ADS
-
de Jager, O. C., et al. 1996, ApJ, 457, 253
In the text
NASA ADS
-
Kennel, C. F., & Coroniti, F. V. 1984a, ApJ, 283, 694
In the text
NASA ADS
-
Kennel, C. F., & Coroniti, F. V. 1984b, ApJ, 283, 710
In the text
NASA ADS
-
Learned, J. G., & Mannheim, K. 2000, Ann. Rev. Nucl. Part. Sci., 50, 679
In the text
NASA ADS
-
Pacini, F., & Salvati, M. 1973, ApJ, 186, 249
In the text
NASA ADS
-
Spitkovsky, A., & Arons, J. 1999, AAS, 195, 3304
In the text
NASA ADS
-
Waxman, E., & Bahcall, J. N. 1997, Phys. Rev. Lett., 78, 2292
In the text
NASA ADS
Copyright ESO 2003
![\begin{displaymath}
f^\pi={\rm min} \left[1, \frac{t_{\rm life}}{t^\pi} \right] \ ,
\end{displaymath}](/articles/aa/full/2003/18/aa2873/img36.gif)
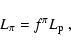
![\begin{displaymath}
f^\mu={\rm min} \left[1,{{t^\pi}_{\rm losses} \over
{t^\pi}...
..., {{t^\mu}_{\rm losses} \over
{t^\mu}_{\rm decay}} \right]\ ,
\end{displaymath}](/articles/aa/full/2003/18/aa2873/img41.gif)
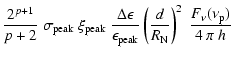
![$\displaystyle 2.5 \times 10^{-16} \frac{2^{p+1}}{p+2}
\left( \frac{d_{\rm kpc}} {R_{\rm pc}} \right)^2
F_{\nu_{\rm p}}[{\rm mJy}]\ {\rm yr}^{-1}.$](/articles/aa/full/2003/18/aa2873/img56.gif)
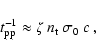

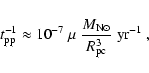
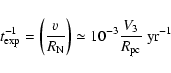
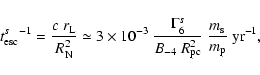
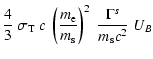
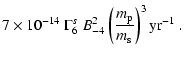
![$\displaystyle {t^s_{\rm ICS}}^{-1}= { 4 \over 3} \sigma_T c\ \left({m_{\rm e} \...
...\nu_{\rm KN}}^{\nu_{\rm max}}
{S_\nu \over \nu^2} {\rm d}\nu \right] \Bigg\}\ ,$](/articles/aa/full/2003/18/aa2873/img83.gif)
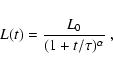
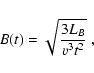
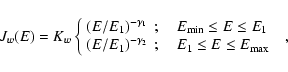
![$\displaystyle K_w(t)={L_{\rm pairs}(t) \over E_1^2} \left\{
{1 \over 2-\gamma_1...
...[{\left(E_{\rm max} \over E_1\right)}^{2-\gamma_2}-1\right]
\right\}^{-1} \cdot$](/articles/aa/full/2003/18/aa2873/img93.gif)
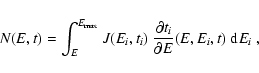
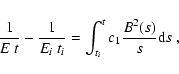
![\begin{displaymath}
{\partial t_i \over \partial E}={E_i\ t_i^2(E,t) \over E^2\ t}\
\left[ 1 + {2\ E_i \over E_b(t_i)} \right]^{-1}\ ,
\end{displaymath}](/articles/aa/full/2003/18/aa2873/img106.gif)
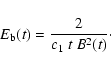
![$\displaystyle t_i={t \over 2 (1 +E/E_{\rm b}(t))} {E \over E_i} \left\{ 1\!+\!
...
...E_{\rm b}(t)}
\left(1+ {E \over E_{\rm b}(t) } \right) \right]^{1/2} \right\} ,$](/articles/aa/full/2003/18/aa2873/img110.gif)
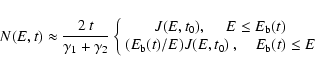
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f1}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg123.gif)
![\begin{displaymath}
S^{\rm sync}_\nu(\nu,t)={c_1 B \over 2 c_2} {3 \over 4\ \pi\...
...er c_2\ B}}\ N\left[\sqrt{{\nu \over c_2\ B} }\ , t \right]\ ,
\end{displaymath}](/articles/aa/full/2003/18/aa2873/img124.gif)
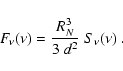
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f2}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg140.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f3}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg141.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f4}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg150.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f5}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg153.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f6}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg154.gif)
![$\displaystyle {\rm min} \left[1, {t_{\rm exp} \over t_{{\rm pp}}} {\rm min}
\left(1,{t_{\rm esc} \over t_{\rm exp}} \right) \right]$](/articles/aa/full/2003/18/aa2873/img166.gif)
![$\displaystyle {\rm min} \left[ 1, 2.8 \times 10^{-5} \mu\ {\rm min}
\left(1, {2.2 \over \Gamma_6} \right) \right],$](/articles/aa/full/2003/18/aa2873/img167.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f7}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg169.gif)
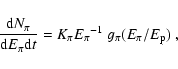
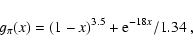
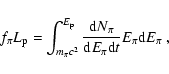
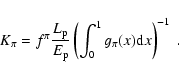
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f8}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg180.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f9}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg181.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{2873.f10}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg186.gif)
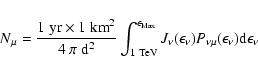
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2873.f11}\end{figure}](/articles/aa/full/2003/18/aa2873/Timg198.gif)