A&A 402, 781-789 (2003)
DOI: 10.1051/0004-6361:20030285

Fast MHD oscillations of a 3-dimensional prominence fibril

A. J. Díaz - R. Oliver - J. L. Ballester

Departament de Física, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain

Received 23 December 2002 / Accepted 20 February 2003

Abstract
High-resolution observations of quiescent filaments point out that their fine structure is made of small-scale threads or fibrils. These fibrils can be represented as thin loops having cool tops, i.e. the prominence material, while the rest of the loop displays coronal temperatures. Then, the stacking of these thin loops in the vertical and horizontal directions gives place to the fine structure of filaments. On the other hand, two-dimensional, high-resolution observations of oscillations in filaments suggest that individual fibrils or groups of fibrils may oscillate independently with their own periods (Yi et al. 1991). Díaz et al. (2001, hereafter Paper I) studied the fast magnetohydrodynamic oscillations of a single and isolated slab prominence fibril using a two-dimensional model with no dependence in the y-direction. Here, we introduce a completely different approach which allows us to build up a 3-dimensional model for the fast magnetohydrodynamic oscillations of the fibril configuration used in Paper I. As compared to the results obtained in Paper I, two relevant new features appear; first of all, the cut-off frequency varies with the longitudinal wavenumber, so more modes can be trapped within the fibril; secondly, a much better confinement of the energy of the modes within the fibril appears, diminishing the leakage of energy towards neighbouring fibrils and so difficulting their mutual excitation.

Key words: Sun: oscillations - Sun: magnetic fields - Sun: corona - Sun: prominences

1 Introduction

High-resolution observations of quiescent filaments show very fine structures within their body, suggesting that they are composed of small-scale threads or fibrils. The existence of this internal structure in prominences was already suggested by Menzel & Evans (1953), was clarified with the improvement of observational capabilities (Engvold 1976; Engvold et al. 1987), and evidence for the presence of horizontal fine structures within prominences has been provided by Schmieder & Mein (1989), Schmieder et al. (1991) and Engvold (2001).

The existence of small amplitude, periodic velocity oscillations in quiescent solar prominences is a well-known phenomenon and many theoretical investigations have been undertaken to explain them (see Engvold 2001; Oliver & Ballester 2002 for thorough reviews about observations and theoretical developments). The periods of oscillation are classified as short ( $T<10~~{\rm min}$), intermediate ( $10~~{\rm min}<T<40~~{\rm min}$) and long ( $T>40~~{\rm min}$) although this classification does not appear to reflect the origin of the prominence exciter. In addition, it appears to be well established that small amplitude, periodic changes in solar prominences are of local nature, affecting only restricted prominence areas (Tsubaki & Takeuchi 1986; Tsubaki et al. 1987; Balthasar et al. 1988a; Balthasar et al. 1988b; Balthasar et al. 1993; Thompson & Schmieder 1991; Balthasar & Wiehr 1994; Terradas et al. 2002). Two-dimensional, high-resolution observations (Yi et al. 1991; Yi & Engvold 1991) have even revealed that individual fibrils or groups of fibrils may oscillate independently with their own periods, which range between 3 and 20 min. Hence, one of the basic questions in prominence seismology that remains unanswered nowadays is whether periodic changes in prominences are always associated with their fibril structure or not.

The first theoretical investigation of periodic prominence perturbations taking into account the prominence fine structure was performed by Joarder et al. (1997). In Paper I, a more in-depth analytical and numerical study of this type of configuration was performed. Essentially, the equilibrium is similar to that in Joarder & Roberts (1992) with the difference that the plasma slab has a limited height, so the configuration is reminiscent of a thin thread with finite width and thickness. Nevertheless, the fibril is infinite in the longitudinal (y-) direction of the structure. To further simplify the problem, the influence of plasma pressure is neglected in Joarder et al. (1997) and in Paper I (zero-$\beta$limit) and consequently the slow mode is absent. Thus, one is left with the Alfvén and fast modes in a plasma threaded by a transverse magnetic field and with no longitudinal propagation (k_y=0). The most important conclusions extracted from Paper I are that prominence fibrils can only support a few modes of oscillation, those with smaller frequency, since only a few harmonics at most can be trapped inside the thin loop, and that the spatial structure of the fundamental even and odd kink modes is such that the velocity amplitude outside the fibril takes large values over long distances.

Figure 1: Sketch of the equilibrium configuration used in this study. The grey zone represents the cold part of the loop, modeling the prominence fibril. The density in the fibril, $\rho _{\rm p}$, in the evacuated (coronal) part of the loop, $\rho _{\rm e}$, and in the coronal environment, $\rho _{\rm c}$, are all uniform. Moreover, the magnetic field is uniform and parallel to the z-axis and the whole configuration is invariant in the y-direction (after Joarder et al. 1997).

Open with DEXTER

In this paper, we have considered the same equilibrium model as in Paper I, but the approach followed to study the fast MHD oscillations of the fibril is completely different. Using the total pressure as the dependent variable instead of the velocity components, a 3-dimensional wave equation is obtained and by solving it we construct a fully 3-dimensional model for the fast MHD modes of oscillation of the fibril. Here, the simplest example is considered: an equilibrium invariant in the y-direction (that leads to waves propagating with dependence in the form  ${\rm e}^{-i k_y y}$), while the investigation of the effects of adding structure in this direction is left for further work.

Our paper is organized as follows: in Sect. 2 the equilibrium model and the basic assumptions are described and also the fast wave equations obtained using our new approach are reviewed; in Sect. 3 the analytical solution suitable for this model is deduced and applied to the special case of independence on the y-coordinate to point out that this procedure leads to the same results as in Paper I; then, in Sect. 4 the results are presented and discussed, and finally in Sect. 5 our conclusions are drawn.

2 Model and basic equations

2.1 Equilibrium model

Following Paper I, we consider a single isolated fibril which is modeled as a straight slab of total length 2L, made of a cold and dense part (the prominence fibril itself) with length 2W and density $\rho _{\rm p}$, and a less dense coronal gas with density $\rho _{\rm e}$ occupying the rest of the thin loop. The width of the structure is 2b, and it is embedded in the coronal environment, with density $\rho _{\rm c}$. The loop is anchored in the photosphere, so its footpoints are subject to line-tying conditions. Finally, the plasma is permeated by a uniform magnetic field directed along the prominence fibril. Because gravity is neglected, all other physical variables ($\rho$, T and p) are also uniform in each of the three regions. We also assume invariance in the y-direction (Fig. 1).

As numerical values for the parameters defining the equilibrium model, we have considered the thickness and length of the prominence fibril $2b\simeq 100$-500 km and $2W\simeq 10~000$ km, respectively, and the total length of magnetic field lines $2L\simeq 50~000$-100 000 km, so that $b/L\simeq 0.001$-0.01and $W/L\simeq$ 0.1-0.2. Moreover, typical density values are such that $\mbox{$\rho_{{\rm c}}$ }\simeq\mbox{$\rho_{{\rm e}}$ }$ and $\mbox{$\rho_{{\rm p}}$ }\simeq 200\mbox{$\rho_{{\rm c}}$ }$.

2.2 Perturbation equations

To derive a wave equation for this model the starting point are the perturbation equations from Roberts (1991). We consider a uniform, static plasma with unperturbed density $\rho_0$ and equilibrium magnetic field ${\bf B}_0 = B_0 \hat{\bf e}_z$. Next, linear, adiabatic perturbations about this equilibrium are introduced and the magnetic field and pressure perturbations, ${\bf B}$ and p, are eliminated in favour of the velocity and the total pressure perturbations, ${\bf v}$ and $p_{{\rm T}}$, so the following equations are obtained,

$$% \frac {\partial p_{{\rm T}}} {\partial t} = \rho_0 \mbox{$c... ...rtial z} - \rho_0 \mbox{$c_{{\rm f}}^2$ }\nabla \cdot {\bf v},$$ (1)

$$% \rho_0 \left( \frac {\partial^2} {\partial t^2} - \mbox{$c_... ...+ \nabla_\perp \frac {\partial p_{{\rm T}}} {\partial t} = 0,$$ (2)

$$% \rho_0 \left( \frac {\partial^2} {\partial t^2} - \mbox{$c_... ... \left( \frac {\partial p_{{\rm T}}} {\partial t} \right) = 0,$$ (3)

where the symbol $\perp$ stands for the components of the perturbed velocity and the gradient perpendicular to ${\bf B}_0$, $c_{{\rm s}}$ is the sound speed, $c_{{\rm A}}$ the Alfvén speed and the other characteristic speeds are defined as $\mbox{$c_{{\rm f}}^2$ }=\mbox{$c_{{\rm s}}^2$ }+\mbox{$c_{{\rm A}}^2$ }$ and $c_{{\rm T}}^{-2}=c_{{\rm s}}^{-2}+c_{{\rm A}}^{-2}$.

Next, we consider the limit $\beta\rightarrow 0$, which implies $c_{{\rm s}}\rightarrow 0$, $c_{{\rm T}}\rightarrow 0$ and $c_{{\rm f}}\rightarrow c_{{\rm A}}$. Notice also that the total pressure is equal to the magnetic pressure, but we are going to use the variable  $p_{{\rm T}}$ through the paper. Under this assumption, which is quite acceptable for coronal plasmas, from Eq. (3) the component of the perturbed velocity along the magnetic field, v_z, is identically zero, showing that the slow mode is absent in this low-$\beta$ plasma approximation.

Now, if we assume dependence of the variables on the y-coordinate and select the velocity components as our dependent variables, a pair of coupled partial differential equations are obtained. However, it is still possible to write our expressions in terms of the total pressure perturbation and have only one partial differential equation to solve (see Díaz et al. 2002). For this reason, $p_{{\rm T}}$ will be our main dependent variable in the following. Using the result v_z=0 and using Eq. (2) to eliminate ${\bf v}_\perp$from Eq. (1), the resulting equations are

$$% \left( \frac {\partial^2} {\partial t^2} - \mbox{$c_{{\rm A}}^2$ } \nabla^2 \right) p_{{\rm T}}= 0,$$ (4)

$$% \rho_0 \left( \frac {\partial^2} {\partial t^2} - \mbox{$c_... ...+ \nabla_\perp \frac {\partial p_{{\rm T}}} {\partial t} = 0,$$ (5)

so the oscillatory properties of the system can be determined by solving Eq. (4) to obtain $p_{{\rm T}}$, after which all other perturbed variables can be calculated (e.g. Eq. (5) gives ${\bf v}_\perp$in terms of the total pressure perturbation). We are only interested in oscillatory perturbations, so in what follows a temporal dependence of the form ${\rm e}^{-i\omega t}$ is considered.

3 Analytical solution

The standard method for solving partial differential equations like Eq. (4) in a finite region is separation of variables. Writing $p_{{\rm T}}(x,y,z)=u(x)g(y)h(z)$ leads to the ordinary differential equations

$$% \frac {{\rm d}^2} {{\rm d}x^2} u (x) = \lambda^2 u(x),$$ (6)

$$% \frac {{\rm d}^2} {{\rm d}y^2} g (y) = - k_y^2 g(y),$$ (7)

$$% \left( \frac {{\rm d}^2} {{\rm d}z^2} + \frac {\omega^2} {\... ...}}^2$ }} \right) h(z) = - \left(\lambda^2-k_y^2\right) h(z).$$ (8)

Next, we apply the boundary conditions, namely evanescence of perturbations away from the fibril in the x-direction (but not in the y-direction), line-tying at $z=\pm L$ and the jump conditions at the boundaries $z = \pm W$ and $x = \pm b$. This issue has been extensively treated in Paper I, so we need not repeat all the details here. Nevertheless, it must be mentioned that some of the boundary conditions involve the perturbed velocity, which from Eq. (5) can be eliminated in favour of $p_{{\rm T}}$ and so one ends up with restrictions on the functions u(x) and h(z) (also see Díaz et al. 2002 for more information).

Owing to the symmetries about x=0 and z=0, the problem can be solved in the region $x\geq 0$, $0 \leq z \leq L$only. Following Joarder et al. (1997) and Paper I, solutions with v_x even/odd in x will be hereafter referred to as kink/sausage modes. Moreover, there are two regions where Eqs. (6)-(8) are to be solved, the fibril one (labelled "l'') and the coronal one (labelled "c''). The fibril in turn comprises the cool prominence material (labelled "p'') and the evacuated part with hot coronal plasma (labelled "e''). When imposing the boundary conditions at x=b it turns out that the solution of Eq. (4) must be a superposition of all the basis functions coming from Eqs. (6)-(8), see Paper I and Díaz et al. (2002). This superposition can be written in the form

$$% p_{{\rm T}}(x,y,z)= \sum_{n=1}^{\infty} {u_n(x) \; g(y) \; h_n(z)},$$ (9)

where the basis functions u_n(x), g(y) and h_n(z) can be expressed as (for even kink modes)

$$% u_n (x)= \left\{ \begin{array}{ll} A_n \exp[-\lambda_n^{{\... ...\lambda_n^{{\rm (l)}} x} , & 0 < x < b , \end{array} \right.$$ (10)

$$% g (y) = {\rm e}^{-i k_y y},$$ (11)

$$% h_n (z)= \left\{ \begin{array}{ll} L^{-1/2} \cos[\kappa_n^... ...} (L-W)} , & x \leq b, 0 \leq z \leq W, \end{array} \right.$$ (12)

where $\Lambda_n$ is a normalization constant, A_n and B_n are constant coefficients and $\kappa_n^{\rm (c)}$, $\kappa_{{\rm p}n}^{\rm (l)}$ and $\kappa_{{\rm e}n}^{\rm (l)}$ are defined as

$$% \kappa_n^2 = \lambda_n^2 - k_y^2 + \frac {\omega^2} {\mbox{$c_{{\rm A}}^2$ }},$$ (13)

with $c_{{\rm A}}$ and $\lambda_n$ substituted by the corresponding values in each of the three regions (corona, prominence fibril and evacuated part of the loop). This expression is different from that in Paper I because of the inclusion of the wavenumber in the y-direction (k_y).

In order to fulfill the line-tying conditions, the outer solution must satisfy

$$% \kappa_n^{\rm (c)} = \frac {(2n-1) \pi} {2 L},$$ (14)

for even solutions and

$$% \kappa_n^{\rm (c)} = \frac {n \pi} {L},$$ (15)

for odd solutions, while for the inner solution the line-tying requirement has already been taken into account when writing Eq. (12).

The perturbed velocity can also be calculated from Eq. (5) and turns out to be

$$% {\bf v}_\perp (x,y,z) = \frac {i \omega} {\rho_0 \mbox{$c_{... ...bla_\perp \left\{ u_n(x) {\rm e}^{-i k_y y} h_n(z) \right\},$$ (16)

or in terms of its x- and y-components,

$$% v_x (x,y,z) = \frac {i \omega} {\rho_0 \mbox{$c_{{\rm A}}^2... ...rac {1} {\lambda_n^2-k_y^2} u_n'(x) {\rm e}^{-i k_y y} h_n(z),$$ (17)

and

$$% v_y (x,y,z) = \frac {\omega k_y} {\rho_0 \mbox{$c_{{\rm A}}... ...frac {1} {\lambda_n^2-k_y^2} u_n(x) {\rm e}^{-i k_y y} h_n(z).$$ (18)

It is now clear that those boundary conditions that involve the perturbed velocity can be translated into requirements on u_n(x) and h_n(z). Notice that from our equilibrium we have $\rho_0 \mbox{$c_{{\rm A}}^2$ } \equiv \mbox{$\rho_{{\rm c}}$ }\mbox{$c_{{\rm Ac... ...}}$ }\mbox{$c_{{\rm Ap}}^2$ }= \mbox{$\rho_{{\rm e}}$ }\mbox{$c_{{\rm Ae}}^2$ }$, so the term outside the sum is only a constant for each mode. In addition, the factor i in front of the sum in Eq. (17) implies that oscillations of v_x are out of phase with respect to both $p_{{\rm T}}$ and v_y. It is also evident that kink modes, for which u_n(x) must be an odd function, are characterized by $p_{{\rm T}}$ and v_y symmetric in the x-direction (the opposite applies for sausage modes).

Moreover, to match the solutions at x=b one should use the Sturm-Liouville theorem, which states that the solutions to Eq. (8) with the line-tying boundary condition are a complete basis set, so we can expand the inner z-dependent functions in terms of the outer ones in the form

$$% h_n^{{\rm (l)}} (z) = \sum_{s=1}^\infty {H_{ns} h_s^{{\rm (c)}} (z)}.$$ (19)

The jump conditions on this boundary are (Goedbloed 1983)

$$% {\bf n} \cdot [ {\bf v} ] =0, \: \: \: {\bf n} \cdot [ {\bf B} ] =0, \: \: \: [ p_{{\rm T}}] =0,$$ (20)

since there are no flows in the equilibrium model. Then, using Eq. (19) lead to a system of equations for the coefficients B_n in Eq. (10),

 

$$% \sum_{s=1}^\infty H_{sn} \left\{ \frac {\lambda_n^{{\rm (c)}}} {{\lambda_n^{{\rm (c)}2}}-k_y^2} \cosh{\lambda_s^{{\rm (l)}} b} \right. \left. \frac {\lambda_s^{{\rm (l)}}} {{\lambda_s^{{\rm (l)}2}}-k_y^2} \sinh{\lambda_s^{{\rm (l)}} b} \right\} B_s$$ (21)

for even solutions, and a similar one for odd solutions. For these systems to have non-trivial solutions, the determinant of the coefficients must be zero, which provides us with the dispersion relation. Here it must also be noted that some of the quantities  $\lambda_s^{{\rm (l)}}$ may become complex, similar to what happened in Paper I, but now this is favoured by the new term in Eq. (13), which is always negative. The consequence is that for $k_y\neq 0$ more $\lambda_s^{{\rm (l)}}$ become complex when compared with the case k_y=0. In the case of one or more complex $\lambda_s^{{\rm (l)}}$, some of the previous mathematical expressions have to be modified in order to account for this possibility, but the overall picture remains (see Paper I for a detailed discussion of this topic).

Therefore, the main differences with the analytical solution of Paper I are that here the total pressure is used as the dependent variable, that perturbations now have y-dependence (see Eqs. (9), (11), (17) and (18)) and that $\kappa_n^{\rm (c)}$, $\kappa_{{\rm p}n}^{\rm (l)}$ and $\kappa_{{\rm e}n}^{\rm (l)}$in Eq. (13) have an extra contribution coming from the wavelength in the y-direction. Consequently, the same applies to the dispersion relation, Eq. (21). The first noticeable effect is that the cut-off frequency is no longer a fixed value, but depends on k_y. To show this point, one needs to take into account that a mode becomes leaky when $\lambda_n^{{\rm (c)} 2} < 0$ and the first basis function to satisfy this condition is the one with n=1. Hence, the cut-off appears when $\lambda_1^{{\rm (c)} 2} = 0$, so using Eqs. (13)-(15) the frequencies of trapped modes must satisfy (even modes)

$$% \frac {\pi} {2 L} + k_y^2 - \frac {\omega^2} {\mbox{$c_{{\rm Ac}}^2$ }} \geq 0,$$ (22)

and then, the cut-off frequency can be written as

$$% \frac {L} {c_{{\rm Ac}}} \omega_{{\rm cut}} = \frac {\pi} {2} \sqrt{1+ (k_y L)^2 \frac {4} {\pi^2}},$$ (23)

for even modes and

$$% \frac {L} {c_{{\rm Ac}}} \omega_{{\rm cut}} = \pi \sqrt{1+ (k_y L)^2 \frac {1} {\pi^2}},$$ (24)

for odd modes. These expressions have been written in this form to highlight that lengths are normalized against L and speeds against $c_{{\rm Ac}}$. Notice that in the limit $k_y \rightarrow 0$ the cut-off frequency reduces to $\pi/2$ and $\pi$ for even and odd modes, respectively, in accordance with Paper I, while for $k_y \gg \pi/2$ or $k_y \gg \pi$ it grows linearly with k_y in the form $\omega_{{\rm cut}} L/c_{{\rm Ac}} = k_y L$ both for even and odd modes.

	Figure 2: Frequency of the kink even modes vs. ky for the set of parameters W/L=0.1, $\mbox{$\rho_{{\rm e}}$ }/\mbox{$\rho_{{\rm c}}$ }=0.6$, $\mbox{$\rho_{{\rm p}}$ }/\mbox{$\rho_{{\rm c}}$ }=200$ and a) b/L=0.5 (only the 16 lowest frequency modes are shown), b) b/L=0.1, c) b/L=0.01 and d) b/L=0.001. The dashed line is the cut-off frequency, which can be obtained from Eq. (23).
Open with DEXTER

3.1 Special case: No dependence on y

The solution developed in the last section can be checked in the limiting case k_y=0, which was the case solved in Paper I. However, the analytical procedure here is different from that adopted in Paper I since we are now solving a partial differential equation for $p_{{\rm T}}$, while the perturbed velocity can only be obtained after the total pressure perturbation has been calculated. We now prove that both solutions agree in spite of using different dependent variables, which provides with a fine check of the present analysis.

If we assume no dependence on the y-coordinate (k_y=0), then from Eq. (16) v_y is identically zero and from Eq. (1) and in the low-beta limit we obtain

$$% \frac {\partial p_{{\rm T}}} {\partial t} = - \rho_0 c_{{\r... ... v}_\perp=-\rho_0 c_{{\rm A}}\frac {\partial v_x} {\partial x}$$ (25)

so the total pressure is directly related to the x-derivative of the only surviving component of the perturbed velocity. Also notice that when the boundary conditions in Eq. (20) are applied, the perturbed velocity must be continuous on the boundary x=b, and from Eq. (25) its derivative must be continuous too, such as was imposed in Paper I. However, even in this situation of k_y=0, the perturbed pressure has no derivative at the fibril boundary.

Going back to $p_{{\rm T}}$, the system of equations in Eq. (21) now takes the simple form

$$% \sum_{s=1}^\infty { B_s H_{sn} \left\{ \frac {1} {\lambda_s... ...^{{\rm (c)}}} \cosh{\lambda_s^{{\rm (l)}} b} \right \} } = 0.$$ (26)

For this system to have non-trivial solutions, the determinant must be identically zero. Upon multiplying the nth row by $\lambda_n^{{\rm (c)}}$and the sth column by $\lambda_s^{{\rm (l)}}$, this determinant leads exactly to the same dispersion relation deduced in Paper I.

Finally, it is straightforward to show that the x- and z-dependence of the perturbations in Paper I agree with those given by Eqs. (10) and (12). It is only necessary to take into account that here u_n(x)appears in the total pressure perturbation, while in Paper I a function with the same name appears in v_x. Nevertheless the two functions are different since we have seen, Eq. (25), that $p_{{\rm T}}$ is related to the derivative of v_x with respect to x.

4 Results

4.1 Dispersion relations

After having discussed some general properties of the modes, we turn our attention to the solutions of the dispersion relation. First of all, the variation of the frequency of the modes with respect to the longitudinal wavenumber, k_y, is studied. Figure 2 shows this behaviour for a set of fibril parameters in which the fibril thickness (b/L) is modified.

	Figure 3: Frequency of the fundamental kink even mode vs. ky L, for the set of parameters W/L=0.1, $\mbox{$\rho_{{\rm e}}$ }/\mbox{$\rho_{{\rm c}}$ }=0.6$, $\mbox{$\rho_{{\rm p}}$ }/\mbox{$\rho_{{\rm c}}$ }=200$ and b/L=0.001.
Open with DEXTER

Figure 4: Frequency of the kink even modes vs. the fibril thickness, b/L, for the set of parameters W/L=0.1, $\mbox{$\rho_{{\rm e}}$ }/\mbox{$\rho_{{\rm c}}$ }=0.6$, $\mbox{$\rho_{{\rm p}}$ }/\mbox{$\rho_{{\rm c}}$ }=200$. Circles correspond to ky L=0 (Paper I) and solid lines to ky L=3, with the horizontal dotted and dash-dotted lines representing their respective cut-off frequency. Notice that the structure of both sets of modes is very similar, except for the modification in the frequency range caused by the dependence of the cut-off frequency on ky, which results in more modes being trapped in the loop structure for a given fibril thickness.

Open with DEXTER

The first important point to remark is that the cut-off frequency depends on the y-component of the wavenumber (k_y) in the form given by Eq. (23). Therefore, the larger k_y, the more non-leaky modes can exist. Notice, however, that the frequency of the modes depends on k_y very slightly, except for some modes as they approach the cut-off frequency or for very large k_y ( $k_y L \sim 100$, say; Fig. 3). As a consequence, the introduction of propagation in the y-direction does not change drastically the frequency of non-leaky modes, but makes it possible to trap other modes that are leaky in the limit k_y=0 for the same set of parameters (Paper I).

These two effects (slight dependence of the frequency on k_y and apparition of new trapped modes) can be appreciated in Fig. 4. The overall picture does not change very much when adding propagation in the y-direction to the model, except that the cut-off frequency is raised. In fact, if a parameter set different from that used in Fig. 4 is taken, the result is again that the existing mode frequencies for k_y=0 (described in Paper I) are not noticeably affected, while the raising of the cut-off allows more modes to become trapped.

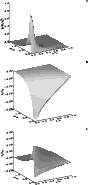Figure 5: Surface plots of the fundamental kink even mode for the set of parameters b/L=0.1, W/L=0.1, $\mbox{$\rho_{{\rm e}}$ }/\mbox{$\rho_{{\rm c}}$ }=0.6$, $\mbox{$\rho_{{\rm p}}$ }/\mbox{$\rho_{{\rm c}}$ }=200$ and ky L=3 ( $\omega L / c_{{\rm Ac}}=0.428$). Panel a) corresponds to the total pressure perturbation, b) to vx and c) to vy (which is not continuous at the boundary x=b=0.1L). The structure of these variables across the middle of the fibril is shown in Fig. 6.

Open with DEXTER

	Figure 6: Cut across the centre of the fibril (z=0) of the solutions in Fig. 5. Because of the jump conditions imposed at the interface x=b, the derivative of both $p_{{\rm T}}$ and vx is not continuous on that surface, whereas vy is not even continuous there. The fibril limit is marked with a vertical dashed line.
Open with DEXTER

4.2 Spatial structure

Following the above discussion about the dispersion relation, the spatial profiles of the different solutions are next studied. Here it should be remarked that for $k_y\neq 0$ all modes have both v_x and v_y non-zero, see Eqs. (17) and (18). The spatial structure of the fundamental kink even mode in an unrealistically thick fibril is displayed in Fig. 5. Such as was mentioned before, the symmetries in the solutions allow us to concentrate on the region $0 \leq z \leq L$, $0\leq x<\infty$, although a finite spatial range across the fibril is used in our plots since solutions decay exponentially in this direction. It can be seen in Figs. 5 and 6 that the total pressure perturbation, $p_{{\rm T}}$, and the x-component of the velocity, v_x, are not derivable at the boundary x=b and that v_y is not even continuous there. It is also worthwhile to remark that the higher k_y, the more marked the discontinuity in the derivative with respect to x of $p_{{\rm T}}$ and v_x at x=b. The normalization constant in these figures has been fixed by the condition $Max\{ p_{{\rm T}}/(\rho _{{\rm c}} c_{{\rm Ac}})\} = 1$.

Figure 7: Cut across the centre of the fibril (z=0) of a) $p_{{\rm T}}/(\rho _{\rm c} c_{{\rm Ac}}^2)$, b)  $v_x/c_{{\rm Ac}}$and c) $v_y/c_{{\rm Ac}}$ for the fundamental kink even mode. The values of the parameters used are b/L=0.001, W/L=0.1, $\mbox{$\rho_{{\rm e}}$ }/\mbox{$\rho_{{\rm c}}$ }=0.6$, $\mbox{$\rho_{{\rm p}}$ }/\mbox{$\rho_{{\rm c}}$ }=200$ and ky L=0.001 ( $\omega L / c_{{\rm Ac}}=1.567$, solid lines), ky L=1 ( $\omega L / c_{{\rm Ac}}=1.538$, dotted lines), ky L=10 ( $\omega L / c_{{\rm Ac}}=1.321$, dashed lines), ky L=100 ( $\omega L / c_{{\rm Ac}}=0.701$, dash-dotted lines) and ky L=800 ( $\omega L / c_{{\rm Ac}}=0.360$, dash-dot-dotted lines). Notice that for ky L=800 the velocity perturbations are large and the mode looks like a surface wave. The normalization constant has been chosen again from the condition $Max\{ p_{{\rm T}}/(\rho _{{\rm c}} c_{{\rm Ac}})\} = 1$.

Open with DEXTER

The number of extrema and the spatial couplings that are found now are quite similar to those in Paper I: when two modes (with different spatial structure and thus with different number of extrema) approach in frequency because of the variation of a parameter, like b/L, there is a coupling and the modes exchange their spatial structure (i.e. the number of extrema in each direction).

Figure 8: Plots of vx for the fundamental kink even mode, a) is a cut across the fibril at z=0 in logarithmic scale and b) is a cut along the fibril at x=0. The parameters used are b/L=0.001, W/L=0.1, $\mbox{$\rho_{{\rm e}}$ }/\mbox{$\rho_{{\rm c}}$ }=0.6$, $\mbox{$\rho_{{\rm p}}$ }/\mbox{$\rho_{{\rm c}}$ }=200$. The solid line corresponds to ky L=0(Paper I), the dotted line to ky L=3 and the dashed line ky L=20. The fibril boundary is marked by a vertical dashed line. To produce this figure the normalization condition now is $Max\{ v_x /c_{{\rm Ac}}\} = 1$

Open with DEXTER

At this point one may wonder which is the reasonable range of values for k_y. So far we have concentrated in dimensionless values of this parameter of order unity, but larger values of k_y have also been considered. Hence, we study how the relative amplitudes of the three relevant magnitudes ( $p_{{\rm T}}, ~ v_x, ~v_y$ from Eqs. (9), (17) and (18)) change when k_y is modified (Fig. 7). First of all, if $k_y c_{{\rm Ac}} \ll \omega$ then $v_x \sim p_{{\rm T}}$ and $v_y \sim k_y$ (in dimensionless units), so the velocity component in the x-direction dominates. On the other hand, if $k_y c_{{\rm Ac}} \gg \omega$ then $v_y \sim k_y$ and $v_x \sim k_y$, since $\lambda^{{\rm (l)}} \sim \lambda^{{\rm (c)}} \sim k_y$ from Eq. (13) so $\lambda^2-k_y^2$ is small compared with k_y or $\lambda$ in Eqs. (17) and (18), and as a consequence both velocity polarisations are of the same order and quite large in front of the total pressure perturbation. Notice also that for k_y large the modes tend to become a surface wave as those in Roberts (1981). However, for realistic values of b/L this transition is not noticeable unless k_y is rather large (about  $k_y L \approx 100$ for b/L=0.001).

Figure 9: Cut of vx a) in the z=0 direction and b) in the x=0 direction, of the first kink even harmonic. The equilibrium parameters are b/L=0.01, W/L=0.1, $\mbox{$\rho_{{\rm e}}$ }/\mbox{$\rho_{{\rm c}}$ }=0.6$ and $\mbox{$\rho_{{\rm p}}$ }/\mbox{$\rho_{{\rm c}}$ }=200$, while ky L=1.7 (solid line), ky L=2 (dashed line) and ky L=3.5 (dotted line). The boundary of the dense part is marked with a vertical dashed line and all the plots have been normalized to the same amplitude at x=z=0.

Open with DEXTER

The most relevant fact coming from the inclusion of k_y is that the cut-off is raised, so we next study the variation of the spatial structure of the modes near that frequency for $k_y\neq 0$. In Paper I, only one confined mode was present for a realistic range of parameters; this is clearly shown in Fig. 4d with k_y=0. Furthermore, for low values of k_y( $k_yL\leq 4$, say) there is still only one non-leaky mode in the system. Figure 8 gives a comparison between v_x with k_y=0 (Paper I), which from Eq. (25) is continuous and derivable at the boundary x=b, and v_x with $k_y\neq 0$, which is not derivable at x=L. The solution becomes more confined as k_y is increased, but it still has a long tail and attains non-negligible values at a distance 100 times the fibril thickness for k_yL=3.

It is also worthwhile studying the new array of confined modes that arise for $k_y\neq 0$. As an example, we concentrate on the first harmonic in Fig. 2c and plot cuts of the spatial structure of v_x (Fig. 9). This variable has three extrema in the range $-L \leq z \leq L$ (Fig. 9b), but when the frequency goes far from the cut-off as a consequence of propagation in the y-direction, some structure develops outside the fibril in the x-direction (Fig. 9a), because the second basis function, u₂(x), also has a long decaying length. Again, the larger k_y, the more confined the mode is in the x-direction (although perturbations reach large distances from the fibril axis). On the other hand, in the z-direction the amplitude in the evacuated part is larger than the amplitude in the dense part (similar to what was found for some modes in Paper I). As k_y is increased, this effect becomes more noticeable, making this kind of modes harder to detect because of their small amplitude in the prominence plasma.

5 Conclusions

In this paper we present an analytical framework which allows us to set up a 3-dimensional model for the study of fast modes in an isolated Cartesian fibril. The problem has been solved using the same analytical techniques as in Paper I, although following Díaz et al. (2002) the total pressure perturbation has now been used as the main unknown. In our discussion of the results we have emphasized the behaviour of the dispersion relations and the spatial structure of the modes. The inclusion of propagation in the y-direction ($k_y\neq 0$) in the model has two relevant effects with respect to the results of Paper I:

1.

The cut-off frequency now depends on k_y and, as a consequence, more modes become trapped within the fibril for a given set of parameters. However, the frequencies of the modes are only slightly shifted when the value of k_y is increased.

2.

The existing modes become more confined, specially the fundamental even and odd ones. Therefore, the effect of the introduction of the third dimension is to weaken the interaction between neighbouring fibrils. Then, when the separation between fibrils is increased, the probability of groups of fibrils oscillating together by mutual interaction diminishes.

The behaviour of the cut-off frequency with k_y and the possibility of more trapped modes for non-zero values of this parameter seems to be an effect of the addition of a free wave (in this work modes are not trapped in the y-direction). It should be emphasised that if the requirement of trapped modes in the x-direction is dropped, then there are leaky modes with higher frequencies than the cut-off, since the cut-off just separates two different kinds of solutions. The present work provides with the first 3-dimensional model of fast MHD oscillations in Cartesian fibrils. The next step could be to consider an orthogonal fibril, leading to trapped modes in the x- and y-directions with a fixed cut-off frequency, such as happens in a truly cylindrical prominence fibril (Díaz et al. 2002). Moreover, a comparison of Fig. 8a in the present paper and Fig. 10 in Díaz et al. (2002), which are plotted with the same scales and equilibrium parameters, shows that the inclusion of k_y in the Cartesian model has the effect of a better confinement of modes, with their spatial structure across the fibril tending to that of the cylindrical modes. Finally, the conclusions drawn here point out the importance of studying the oscillations of multifibril systems representing the actual fine structure of filaments.

Acknowledgements

A. J. Díaz, J. L. Ballester and R. Oliver acknowledge the financial support received from Spanish MCyT under grant BFM2000-1329.

References

 
• Balthasar, H., & Wiehr, E. 1994, A&A, 204, 286 In the text  
• Balthasar, H., Stellmacher, G., & Wiehr, E. 1988a, A&A, 286, 639 In the text NASA ADS  
• Balthasar, H., Wiehr, E., & Stellmacher, G. 1988b, in Dynamics and Structure of Solar Prominences, ed. J. L. Ballester, & E. R. Priest, Universitat de les Illes Balears, Spain, 63 In the text  
• Balthasar, H., Wiehr, E., Schleicher, H., & Wöhl, H. 1993, A&A, 277, 635 In the text NASA ADS  
• Díaz, A. J., Oliver, R., Erdérlyi, R., & Ballester, J. L. 2001, A&A, 379, 1083 (Paper I) In the text NASA ADS  
• Díaz, A. J., Oliver, R., & Ballester, J. L. 2002, ApJ, 580, 550 In the text NASA ADS  
• Dunn, R. B. 1960, Ph.D. Thesis, Harvard University In the text  
• Engvold, O. 1976, Sol. Phys., 49, 283 In the text NASA ADS  
• Engvold, O. 2001, in INTAS Workshop on MHD Waves in Astrophysical Plasmas, ed. J. L. Ballester, & B. Roberts, Universitat de les Illes Balears, Spain, 123 In the text  
• Engvold, O., Kjeldseth-Moe, O., Bartoe, J. D. F., & Brueckner, G. 1987, in Proceedings of the 21st ESLAB Symposium, ESA SP-275, 21 In the text  
• Goedbloed, J. P. 1983, Lecture Notes on Ideal Magnetohydrodynamics, Rijnhuizen Report In the text  
• Joarder, P. S., & Roberts, B. 1992, A&A, 261, 625 In the text NASA ADS  
• Joarder, P. S., Nakariakov, V. M., & Roberts, B. 1997, Sol. Phys., 173, 81 In the text NASA ADS  
• Menzel, D. H., & Evans, J. W. 1953, Convegno Volta, 11, 119 In the text  
• Oliver, R., & Ballester, J. L. 2002, Sol. Phys., 206, 45 In the text NASA ADS  
• Roberts, B. 1981, Sol. Phys., 69, 39 In the text NASA ADS  
• Roberts, B. 1991, in Advances in Solar System Magnetohydrodynamics, ed. E. R. Priest, & A. W. Hood (Cambridge Univ. Press), 110 In the text  
• Schmieder, B., & Mein, P. 1989, Hvar Obs. Bull., IAU Coll. 119(13), 31 In the text  
• Schmieder, B., Raadu, M., & Wiik, J. E. 1991, A&A, 252, 353 In the text NASA ADS  
• Terradas, J., Molowny-Horas, R., Wiehr, E., et al. 2002, A&A, 393, 637 In the text NASA ADS  
• Thompson, W. T., & Schmieder, B. 1991, A&A, 243, 501 In the text NASA ADS  
• Tsubaki, T., & Takeuchi, A. 1986, Sol. Phys., 104, 313 In the text NASA ADS  
• Tsubaki, T., Ohnishi, Y., & Suematsu, Y. 1987, PASJ, 40, 121 In the text  
• Yi, Z., & Engvold, O. 1991, Sol. Phys., 134, 275 In the text NASA ADS  
• Yi, Z., Engvold, O., & Keil, S. L. 1991, Sol. Phys., 132, 63 In the text NASA ADS