A&A 402, 315-319 (2003)
DOI: 10.1051/0004-6361:20030262

Infrared spectroscopy of the supersoft X-ray source MR Vel

R. E. Mennickent1,[*] - K. Matsumoto 2 - M. Diaz 3


1 - Departamento de Física, Facultad de Ciencias Físicas y Matemáticas, Universidad de Concepción, Casilla 160-C, Concepción, Chile
2 - Graduate School of Natural Science and Technology, Okayama University, Okayama 700-8530, Japan
3 - Instituto Astronômico e Geofísico, Universidade de São Paulo, Brazil

Received 5 November 2002 / Accepted 14 February 2003

Abstract
We describe the infrared spectrum of the galactic supersoft X-ray source MR Vel (RX J0925.7-4758) in the wavelength range of 1.1-2.6 $\mu$m. We find Paschen, Brackett, He I, He II and neutral and ionized oxygen lines in emission. No traces of the secondary star were found. P-Cygni profiles were observed in Paschen $\beta $ and Brackett $\gamma $, from which we conclude that these lines arise in a wind. Fitting the optical and infrared energy distribution with a supercritical disk model, incorporating white dwarf and secondary star contributions, we were able to constrain the distance to 2-5 kpc, which implies an absolute magnitude MV between -2 and 0.

Key words: accretion, accretion disks - stars: emission-line - X-rays: stars - infrared: stars - stars: individual: MR Vel


1 Introduction

The supersoft X-ray sources (SSS) are a class of luminous point sources $L_{\rm X} \sim$ 10 36-1037 ergs s-1, emitting mostly in the energy range of 20-60 eV. The most promising model for binary SSS invokes a white dwarf undergoing steady nuclear burning as a result of very rapid accretion ( $\dot{M} \sim 10^{-7}~M_{\odot}$/yr) from a Roche lobe-filling companion star (e.g. van den Heuvel et al. 1992). Whereas the bulk of the energy should be released near the white dwarf into the X-ray region, the optical and infrared spectra should be dominated by the other components of the system, namely the accretion disk and eventually the secondary star.

Most persistent SSS have been found in the Magellanic Clouds, and only few of them in the galaxy, since presumably their soft X-rays are easily absorbed by the interstellar hydrogen near the galactic plane. MR Vel (RX J0925.7-4758) is one of the few known galactic SSS and it has been relatively well studied in X-rays and optical wavelengths. The orbital period is unusually long for an SSS ( $4.0287822 \pm 0.0000026$ d, Schmidtke & Cowley 2001). During the orbital cycle, the star shows cyclic variations in the V magnitude between 17.1 and 17.3, whereas the B-V and V-R colours show no change (Schmidtke et al. 2000). The great strength of the interstellar absorption lines seen in the optical region are consistent with the position of the source behind the Vela Sheet molecular cloud. The inclination has been constrained to i= 55 $\pm$ 10$^{\circ }$(Matsumoto & Mennickent 2000). The optical emission lines show a large velocity amplitude, implying masses of 1-2 $M_{\odot}$ for the donor star, which must be a giant in order to fill its Roche lobe, and 0.5-1.7 $M_{\odot}$ for the compact star (Bearda et al. 2002). The X-ray spectrum is rather complex, and cannot be explained by the usual models of photo-ionized plasma or stellar atmospheres combined with thermal plasma in collisional ionization equilibrium (Bearda et al. 2002; Motch et al. 2002).

In spite of the recent progress made to understand the unusual properties of MR Vel, the infrared region has not yet been explored. This is also true for most SSS, which have been historically studied in X-rays and the optical region. Infrared observations of SSS could, in principle, be combined with X-rays and optical data, in order to analyse the overall spectral energy distribution, aiming to constrain models for the emitting region and get insights on stellar parameters, energetics and distances. In this paper we provide the first description of the infrared spectrum of MR Vel, and combine this information with optical data to model the optical-IR spectral energy distribution.

2 Observations and data reduction

The infrared spectroscopic observations reported in this paper were obtained at the ESO-Paranal Observatory with VLT-Antu using the ISAAC spectrograph in service mode. Spectra were taken, under photometric conditions, during the night of May 20, 2000 (UT). The exposure times were 120, 240 and 480 s for the J-band, H-band and K-band spectra, respectively. Sufficient overlapping was assured for composing a single spectrum ranging from 1.09 to 2.57 $\mu$m with a FWHM resolution of 12 (J) to 27 (K) Å. The data were reduced using IRAF[*] by first applying the combined dark and flatfield images as supplied by the ESO service mode operation group. Median sky frames were then combined for each object and spectral window. This process made use of jittered images where the object is located at different positions along the slit. Wavelength calibration was achieved by measuring the location of atmospheric OH emission lines (Rousselot et al. 2000) in the sky background. The flux calibration was performed using observations of the A0 standard HD 216009, made with the same instrumental setup (but with a wider slit) by the ESO operation team as part of the service mode program. Finally, the telluric absorption features were corrected with the aid of the absorption template constructed by dividing the spectrum of HD 216009 with a low order polynomial fit, excluding a few stellar absorption lines. The IRAF task "telluric" was used to find the best scale and shift factors which, when applied to the normalized telluric template, provided a reasonable correction of the telluric absorptions in HD 216009 and science exposures. This procedure worked well, except for the regions between 1.35-1.44 microns and 1.80-1.94 microns, characterized by heavy telluric absorption. These regions, corresponding to the ends of the J, H and K spectra, were excluded from the analysis and are not shown in this paper. Synthetic J, H, and K photometry of our calibrated standard star observations were compared to broadband photometry by Carter & Meadows (1995) showing differences below 0.08 mag.

3 Results

Synthetic magnitudes of MR Vel resulted in J = 13.05, J-H = 0.76 and H-K = 0.53, with probable uncertainties of 0.1 mag. When using a colour excess of E(B-V) = 1.94 (Matsumoto & Mennickent 2000), we find unreddened colours of J-H = 0.15and H-K = 0.17, comparable to those observed in the SSS QR And (RX J0019.8+2156, Fender & Burnell 1996). Our finding likely indicates the presence of absorbing circumstellar material or a late-type companion. To our knowledge, these are the first infrared magnitudes and colours obtained for MR Vel ever. Therefore, it would be interesting to compare these magnitudes with future data in order to search for variability.

3.1 Spectrum description

The combined spectrum reveals a steep blue continuum and weak emission lines (Fig. 1). A straight-line fit to the continuum in this region results in a slope of $-1.1 \times 10^{-15}$ ergs s-1 cm-2 Å-1/$\mu$m, which is incompatible with a power law. After a close inspection of the normalized spectrum (Fig. 2), we identified lines of neutral hydrogen (Paschen and Bracket), single ionized helium and highly ionized oxygen. These lines are listed in Table 1 along with relevant spectroscopic data. No evidence of a transient emission-line jet like those observed in H$\alpha$ by Motch (1998) was detected. No photospheric absorptions, such as CO bands, are observed in the spectra. One interesting feature is the P-Cygni profile observed in the Paschen $\beta $ and Bracket $\gamma $lines (Fig. 3). The velocities found in the corresponding blueshifted absorption wings, relative to the emission maximum, reach up to -3000 (-1500) km s-1, being the absorption minimum at -755 (-680) km s-1, for Paschen $\beta $(Brackett $\gamma $). After inspection of the data, we realized that the difference between the maximum absorption velocity of these lines are real, and they cannot be due to an error in the continuum normalization.


  \begin{figure} \par\includegraphics[width=7cm,clip]{rxj0925.eps} \end{figure} Figure 1: Flux calibrated spectrum of MR Vel. The vertical scale has been normalized to 2.03E-15 erg cm-2 s-1 Å-1.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=9cm,width=16.7cm,clip]{combined.eps} \end{figure} Figure 2: From up to down, J-band, K-band and H-band continuum normalized spectra for MR Vel. Emission lines are labeled.
Open with DEXTER

3.2 SED modeling

In the picture of the steady nuclear-burning white dwarf model, the mass accretion rate is limited in the narrow region around ${\sim}10^{-7}$  $M_{\odot}~{\rm yr^{-1}}$. Since the critical accretion rate of the white dwarf ( $\dot{M}_{\rm crit}$) is

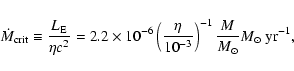\begin{displaymath}\dot{M}_{\rm crit} \equiv \frac{L_{\rm E}}{\eta c^{2}} = 2.2 ... ...10^{-3}}\right)^{-1} \frac{M}{M_\odot} M_\odot~{\rm yr}^{-1}, \end{displaymath} (1)

where $L_{\rm E}$ ( $= 1.25 \times 10^{38}~ M/M_\odot~ {\rm erg~s}^{-1}$) is the Eddington luminosity considering electron scattering and $\eta$ is the efficiency, the unstable mass transfer rate expected for semi-detached systems with q > 1 is comparable to the critical mass accretion rate $\dot{M}_{\rm crit}$.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{pcygni.eps} \end{figure} Figure 3: A zoom around the P-Cygni profiles of Paschen $\beta $ and Brackett $\gamma $.
Open with DEXTER


 
Table 1: Spectroscopic information of emission lines. The peak intensity is given in units of 10-15 erg s-1cm-2Å-1. N/A means not available.
Line Intensity EW (Å) FWHM (km s-1)
       

O II 11334-38

 2.2 -2 N/A
He II 11628-77 2.3 -2 N/A
O VI 12617 2.0 N/A N/A
O III 12692 2.2 N/A N/A
Pa$\beta $ 2.4 -5 367

Br$\iota$

 1.7 -3 555
Br$\theta$ 1.6 -2 627
Br$\eta$ 1.5 -2 560
He II 16926 1.5 -1 540
Br$\zeta$ 1.5 -4 440

O I 19463

 1.3 -9 564
He II 19548 1.2 -3 520
Br$\gamma $ 1.0 -9 473
He II 21891 0.9 -4 740
He II 23480 0.7 N/A N/A


A model of an accretion disk with a supercritical accretion rate was originally proposed by Abramowicz et al. (1988), as an optically thick and geometrically thick disk (e.g., Kato et al. 1998 for a review). Abramowicz et al. (1988) called the model a slim disk because of its medium thickness between a thin disk and a thick one. We refer it as a supercritical accretion disk, based on a physical viewpoint of the supercritical accretion rate.

The standard model for SSS indicates that we should consider a nearly critical accretion in SSS systems instead of the standard accretion disk (Shakura & Sunyaev 1973). It is also expected that a very luminous white dwarf in SSS strongly irradiates the accretion disk and eventually the companion (e.g.  Popham & Di Stefano 1996; Schandl et al. 1997; Meyer-Hofmeister et al. 1997; Matsumoto & Fukue 1998; Meyer-Hofmeister et al. 1998). These effects in SSS were investigated by Fukue & Matsumoto (2001). In this work, we have calculated the spectral energy distribution (SED) for MR Vel, including the supercritical accretion disk and the irradiation effect, and have compared it with the observed spectrum in the range of optical-IR region after dereddening with E(B-V)= 1.94 (i.e. AV $\approx$5.9, Matsumoto & Mennickent 2000). The concept and formulation of the numerical model are described in Fukue & Matsumoto (2001), and we basically conform the manner in calculations to Fukue & Matsumoto (2001) in this paper.

The inferred intrinsic X-ray luminosity highly depends on the model-atmosphere and gravity used in the fitting process, but in any case, X-ray observations and theoretical models have suggested that the white dwarf should be extremely massive (Shimura 2000; Ebisawa et al. 2001), although recent NLTE models of hot white dwarf atmospheres fail to represent the complex X-ray spectrum (Motch et al. 2002). In the following, as a working hypothesis, we assume a blackbody SED for the central source associated with a ${\sim}1.4~M_{\odot}$ white dwarf. This means that we choose the WD luminosity matching thecore-mass-luminosity relationship derived by Iben & Tutukov (1996) for cold WDs accreting hydrogen:

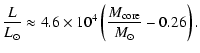$\displaystyle \frac{L}{L_{\odot}} \approx 4.6 \times {10 }^{4 } \left(\frac{M_{\rm core }}{M_{\odot}} - 0.26\right).$     (2)

This relationship is similar to those regulating the luminosity of asymptotic giant branch stars (Paczynski 1971a). Due to the Roche lobe-filling requirement, the contribution from the SED of the companion depends on the inclination angle of the binary system. The apparent variations in both of the light curve and radial velocity reject very-low inclinations, and no eclipse also indicates $i\le65^{\circ}$ (Motch et al. 1994; Matsumoto & Mennickent 2000; Schmidtke et al. 2000). Thus an inclination angle range of 45-65$^{\circ }$ seems to be plausible. Using the mass function derived by Matsumoto & Mennickent (2000) and the fixed mass of the white dwarf, the mass of the secondary star was derived for a set of allowed inclination angles. The stellar radii followed from the relationships for Roche-lobe filling secondaries in binary systems (Paczynski 1971b). The effective temperature for each mass-radius combination was calculated from the stellar evolutionary tracks by Claret & Gimenez (1989). Then we estimated the SED for these possible configurations assuming the secondary star partially shielded from the white dwarf by the disk rim. So the shielding by the disk is partial and a part of the companion is irradiated, as shown in e.g. Schandl et al. (1997). The magnitude of the irradiation was estimated considering the vertical scale height of the disk. In these calculations we neglected any possible contribution of irradiation by the hotspot.

An extremely small opening angle of the supercritical accretion disk ($\delta$) corresponds to a thin standard accretion disk. According to Hanamoto et al. (2001), $\delta$ is required to be more than 0.3$^{\circ }$ for a mass-accretion rate of ${\ge}10^{-7}~M_{\odot}~{\rm yr^{-1}}$ expected for SSS. On the other hand, larger $\delta$ brings no significant increase of the luminosity in Rayleigh-Jeans tail of the SED. This can constrain upper and lower limits for the distance.

For an inclination angle in the range from 45$^{\circ }$ to 65$^{\circ }$, we found that the calculated SED based on the supercritical model described above suggests a distance to the source between 2 and 4 kpc for a wide range of $\delta$ (0.3-5). Even in the unlikely case of $\delta= 20$, the distance is constrained to $d\sim$ 5-6 kpc. A representative fitting is shown in Fig. 4, which is calculated for a case of $i=50^{\circ }$ (corresponding to $M_{2} = 3.21~ M_{\odot}$, $R_{2} = 7.6~ R_{\odot}$, T= 7200 K) and $\delta = 0.3-5$. Besides the approximations and assumptions of our disk models, the differences between observed and theoretical spectra can be explained by a small error in the dereddening and/or the flux calibration for the optical NTT data, by photometric orbital variability or by the use of non-simultaneous optical-infrared data. From the above considerations we conclude that the distance for the source probably lies between 2 and 5 kpc.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{model.EPS} \end{figure} Figure 4: A representative SED model of MR Vel calculated for the supercritical accretion case with an inclination angle of $i=50^{\circ }$. Two solid lines denote the contributions by the white dwarf (right) and the companion (left). Total contribution from the white dwarf, companion, and supercritical accretion disk are shown by five dashed lines, which correspond to $\delta =$ 5$^{\circ }$, 3$^{\circ }$, 1$^{\circ }$, 0.5$^{\circ }$, and 0.3$^{\circ }$, from top to bottom. The de-reddened observed spectrum is over-plotted on the model SEDs by filled circles considering the best fitted case of d = 3 kpc. Optical data is from Matsumoto & Mennickent (2000) and infrared data is from this paper.
Open with DEXTER

4 Discussion

The presence of weak emission lines in the infrared (and optical) spectrum of MR Vel, the detection of highly ionized elements like He II and O VI, and the fact that the secondary star remains hidden in the IR spectrum, are consistent with a very luminous accretion disk. Are the accretion disks in longer orbital period systems more luminous? This is possible, since the thermal time scale for the secondary, regulating the mass transfer, decreases with the square of the donor mass. For instance, in QR And, whose orbital period is only 15.85 h, the He II  $\lambda \lambda$ 16926 and 21891 equivalent widths (Quaintrell & Fender 1998) are a factor 3 larger than in MR Vel, consistent with a fainter disk.

Interestingly, a P-Cygni profile has been observed in MR Vel at lines with very different excitation potential. The feature has been observed in optical H I lines (Matsumoto & Mennickent 2000; Schmidtke et al. 2000) and in the infrared (this paper). P-Cygni absorptions are also observed in X-ray lines like Fe XVII and O VIII (Bearda et al. 2002) with approaching velocities reaching a few thousands km s-1. It is not clear, at present, if the visibility of the P-Cygni profiles in the spectrum depends on the orbital phase. One may speculate that the less dense upper parts of the disk can be pushed away by the radiation pressure arising from the inner disk, producing an extended wind region where the P-Cygni absorptions arise.

It is interesting to note that the slope of the infrared continuum reported in Sect. 3 differs from the slope of an infinitely large steady state accretion disk ( $F \propto \lambda^{-7/3}$Lynden-Bell 1969). This is likely related to a non-neglectable contribution of the secondary star to the overall flux in the infrared.

Our distance estimate is consistent with the 4 kpc value given by Hartmann et al. (1999) and only marginally consistent with the range derived by Motch et al. (1994), viz.  1-2 kpc. The distance derived using the accretion disk model fitting suggests an absolute magnitude $M_{\rm V}$ between -2 and 0. Due to the nature of the assumptions considered in our modeling, this value should be taken with extreme caution. This is especially important, since in our model the secondary should contribute about 40% to the total light of the system in the infrared, however their spectral features are not visible in our spectra.

5 Conclusions

Acknowledgements
We thank the referee C. Motch, for useful comments on a first version of this paper. We also acknowledge J. Fukue who gave some advises in the calculation. This work was supported by Grant Fondecyt 1000324 and DIUC 202.01.030-1.0. MD acknowledges the CNPq support under grant # 301029.

References

 
Copyright ESO 2003