For widely adopted parameters, the stellar disk subtends an angle in the sky of less than 1 mas and the
photosphere generates a flux density at the Earth of less than 1 mJy at 1200 ![]() m. The stellar contribution
to our SEST measurements can therefore be safely ignored. Also, any line emission in this band pass is
likely to be totally negligible (Liseau & Artymowicz 1998; Liseau 1999 and references therein).
m. The stellar contribution
to our SEST measurements can therefore be safely ignored. Also, any line emission in this band pass is
likely to be totally negligible (Liseau & Artymowicz 1998; Liseau 1999 and references therein).
Assuming an opacity law of the form
![]() ,
the flux density
at long wavelenghts from an optically thin source of a certain dust population can be expressed as
,
the flux density
at long wavelenghts from an optically thin source of a certain dust population can be expressed as
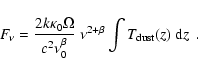 |
(1) |
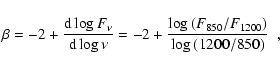 |
(2) |
| Feature | Relative |
|
Remarks |
| Offset (
|
(mJy/beam) | ||
| A | (0, 0) |
|
|
|
|
integrated over a radius of 40
|
||
| B | (-21, -26) | SW blob (Holland et al. 1998): | |
| contaminated by
|
|||
| C | (-27, -44) |
|
SW blob (this paper) |
The asymmetric flux distribution displayed in Fig. 2 may be surprising. In agreement with
our observations, Chini et al. (1991) and Dent et al. (2000)
too were unable to detect any emission in the northeast part of the disk,
where we place a ![]() -upper limit on the mass of 0.2
-upper limit on the mass of 0.2
![]() (see below; the dust temperature at 500 AU
(see below; the dust temperature at 500 AU
![]() K, when
K, when
![]() K, see Liseau & Artymowicz 1998).
K, see Liseau & Artymowicz 1998).
Given the low signal-to-noise ratio (S/N), the reality of this lopsidedness is difficult to assess, but
asymmetries in the
![]() disk have been noticed also at other wavelengths. For instance, in scattered
light, the receding NE side of the disk extends much further and is much brighter than the SW disk.
In contrast, the shorter, approaching SW disk seems much thicker (Kalas & Jewitt 1995; Larwood & Kalas 2001). The
situation is reversed in the thermal infrared (albeit on smaller spatial scales), where the SW disk
appears significantly brighter and more extended than the NE side (Lagage & Pantin 1994; Wahhaj et al. 2002;
Weinberger et al. 2002). This could be due to a "Janus-effect'', i.e. the NE being dominated
by "bright'' dust particles (high albedo, silicates), whereas in the SW, the majority of dust grains is "dark''
(high absorptivity, carbonaceous?). What would accomplish such uneven distribution in the disk
is not clear, but large differences in albedo, by more than one order of magnitude, are not uncommon,
for instance, in solar system material. Also, in order to understand the nature of feature C
(and B) velocity information would be valuable.
disk have been noticed also at other wavelengths. For instance, in scattered
light, the receding NE side of the disk extends much further and is much brighter than the SW disk.
In contrast, the shorter, approaching SW disk seems much thicker (Kalas & Jewitt 1995; Larwood & Kalas 2001). The
situation is reversed in the thermal infrared (albeit on smaller spatial scales), where the SW disk
appears significantly brighter and more extended than the NE side (Lagage & Pantin 1994; Wahhaj et al. 2002;
Weinberger et al. 2002). This could be due to a "Janus-effect'', i.e. the NE being dominated
by "bright'' dust particles (high albedo, silicates), whereas in the SW, the majority of dust grains is "dark''
(high absorptivity, carbonaceous?). What would accomplish such uneven distribution in the disk
is not clear, but large differences in albedo, by more than one order of magnitude, are not uncommon,
for instance, in solar system material. Also, in order to understand the nature of feature C
(and B) velocity information would be valuable.
Blob C would be situated in the disk midplane and on the second contour in the scattered light image of Larwood & Kalas (2001) ( 22 < R < 25 mag/arcsec2, see also Kalas & Jewitt 1995). No obvious distinct feature is seen at its position. However, to be detectable with SIMBA at the SEST, any point source at mm-wavelengths would not be point-like at visual wavelengths, and its optical surface brightness could be very low.
To gain some
quantitative insight we ran numerical models, exploiting Mie-theory, for a variety of plausible dust
mixtures regarding the chemical composition and grain size distributions (for details, see Pantin et al. 1997).
The equilibrium temperatures were found to be in the interval 16 K to 58 K
and depending on the dust albedo and scattering phase function,
the predicted integrated scattered light, to be consistent with our SEST observations, spans 8 magnitudes.
The two most extreme cases considered were (1) bright cold dust (albedo = 1 at visual wavelengths,
![]() K) which is
scattering isotropically and has albedo = 0.2 at thermal wavelengths, which results in a spatially integrated
R-magnitude of 17.3 and (2) dark warm dust (albedo = 0.02 in the visual,
K) which is
scattering isotropically and has albedo = 0.2 at thermal wavelengths, which results in a spatially integrated
R-magnitude of 17.3 and (2) dark warm dust (albedo = 0.02 in the visual,
![]() K) which
gives rise to "comet scattering'', i.e. 14% of isotropic at 90
K) which
gives rise to "comet scattering'', i.e. 14% of isotropic at 90![]() ,
and has zero albedo at thermal wavelengths,
resulting in an integrated R-magnitude of 25.6. These extreme cases are felt to be either too optimistic
or too conservative and an intermediate case might be more appropriate. Our adopted model includes
isotropically scattering dust at
,
and has zero albedo at thermal wavelengths,
resulting in an integrated R-magnitude of 25.6. These extreme cases are felt to be either too optimistic
or too conservative and an intermediate case might be more appropriate. Our adopted model includes
isotropically scattering dust at
![]() K with albedo = 0.2 at visual and zero
albedo at thermal wavelengths, yielding an integrated R-magnitude of 20. An about 10
K with albedo = 0.2 at visual and zero
albedo at thermal wavelengths, yielding an integrated R-magnitude of 20. An about 10
![]() source
(R=25 mag/arcsec2) would thus be consistent with both the optical data and our SIMBA measurement
and a deep R-band search might become successful. Similarly, the integrated 850
source
(R=25 mag/arcsec2) would thus be consistent with both the optical data and our SIMBA measurement
and a deep R-band search might become successful. Similarly, the integrated 850 ![]() m flux density is
predicted to be slightly less than 18 mJy and should become readily detectable. However, blob C is
situated outside the figure of Holland et al. 1998.
m flux density is
predicted to be slightly less than 18 mJy and should become readily detectable. However, blob C is
situated outside the figure of Holland et al. 1998.
Feature C is perfectly aligned with the optical disk plane, and its (hypothetical) mass can
be estimated from
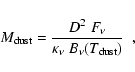 |
(3) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3878f3.ps} \end{figure}](/articles/aa/full/2003/16/aah3878/Timg59.gif) |
Figure 3:
The SED of the
|
For radiation mechanisms generating power law spectra and/or thermal dust emission from blob B,
the spectral slope is given by
![]() ,
where
,
where ![]() ,
as before, refers to A = (0
,
as before, refers to A = (0
![]() ,
0
,
0
![]() ), i.e. the
), i.e. the
![]() disk, and where
disk, and where
![]() and
and
![]()
![]() m or 1300
m or 1300 ![]() m. Because of the relatively low S/N of the SCUBA and SIMBA data, the actual flux ratios are
highly uncertain and, furthermore, calibration uncertainties and telescope beam effects could
potentially introduce large errors. The combined observations of blob B
suggest
m. Because of the relatively low S/N of the SCUBA and SIMBA data, the actual flux ratios are
highly uncertain and, furthermore, calibration uncertainties and telescope beam effects could
potentially introduce large errors. The combined observations of blob B
suggest
![]() ,
yielding
,
yielding
![]() ,
i.e. consistent
with the spectrum of A.
,
i.e. consistent
with the spectrum of A.
Copyright ESO 2003