A&A 402, 125-132 (2003)
DOI: 10.1051/0004-6361:20030154

An HST study of three very faint GRB host galaxies

A. O. Jaunsen¹ - M. I. Andersen^2,3 - J. Hjorth⁴ - J. P. U. Fynbo^5,4 - S. T. Holland⁶ - B. Thomsen⁵ - J. Gorosabel^8,9,10 - B. E. Schaefer¹¹ - G. Björnsson¹² - P. Natarajan¹³ - N. R. Tanvir¹⁴

1 - European Southern Observatory, Casilla 19001, Santiago 19, Chile
2 - Division of Astronomy, PO Box 3000, 90014 University of Oulo, Finland
3 - Astrophysikalische Institut Potsdam, An der Sterwarte 16, 14482 Potsdam, German
4 - Astronomical Observatory, University of Copenhagen, 2100 Copenhagen Ø, Denmark
5 - Department of Physics and Astronomy, University of Aarhus, 8000 Århus C, Denmark
6 - Department of Physics, University of Notre Dame, Notre Dame, IN 46556-5670, USA
7 - Danish Space Research Institute Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
8 - Instituto de Astrofísica de Andalucía (IAA-CSIC), PO Box 03004, 18080 Granada, Spain
9 - Laboratorio de Astrofísica Espacial y Física Fundamental (LAEFF-INTA), PO Box 50727, 28080, Madrid, Spain
10 - University of Texas, Department of Astronomy, C-1400, Austin, TX-78712, USA
11 - Science Institute, Dunhagi 3, University of Iceland 107 Reykjavik, Iceland
12 - Department of Astronomy, Yale University, 265 Whitney Avenue, New Haven, CT 06511, USA
13 - Department of Physical Sciences, University of Hertfordshire, College Lane, Hatfield, Hertfordshire AL10 9AB, UK

Received 16 April 2002 / Accepted 28 January 2003

Abstract
As part of the HST/STIS GRB host survey program we present the detection of three faint gamma-ray burst (GRB) host galaxies based on an accurate localisation using ground-based data of the optical afterglows (OAs). A common property of these three hosts is their extreme faintness. The location at which GRBs occur with respect to their host galaxies and surrounding environments are robust indicators of the nature of GRB progenitors. The bursts studied here are among the four most extreme outliers, in terms of relative distance from the host center, in the recent comprehensive study of Bloom et al. (2002). We obtain a revised and much higher probability that the galaxies identified as hosts indeed are related to the GRBs ( $P(n_{\rm chance})=0.69$, following Bloom et al. 2002), thereby strengthening the conclusion that GRBs are preferentially located in star-forming regions in their hosts. Apart from being faint, the three hosts consist of multiple structures, indicative of merging and active star-formation. For one of the hosts, GRB 980329, we estimate a photometric redshift of $z\sim3.5$.

Key words: gamma rays: bursts - cosmology: observations - galaxies: starburst

   
1 Introduction

There are two, possibly fundamentally different, classes of gamma-ray bursts (GRBs) - short and long duration bursts (being shorter and longer than $\sim$1 s respectively). So far every GRB with an identified optical afterglow (OA) belongs to the class of long duration bursts, with the possible exception of GRB 000301C (Jensen et al. 2001). There are two general types of models for producing GRBs, the first involves the merging of binary compact stars (Paczynski 1986), the second is related to the death of very massive stars (Woosley 1993; MacFadyen & Woosley 1999; Vietri & Stella 1998). The observations of SN bumps, Fe K-line and OA localizations close to star-forming regions favour the latter type of models for long bursts. Due to the relatively short lifetime of such massive stars, one expects them to be located in or very close to star-forming regions where they are born. Thanks to the extensive observational efforts in pursuing GRB events at various wavelengths there are now several examples where such positional correlations between the GRB OA and star forming regions in the host are seen, for instance Fynbo et al. (2000) (GRB 980425), Holland & Hjorth (1999) (GRB 990123), Hjorth et al. (2002) (GRB 980613), Fynbo et al. (2002) (GRB 000926), Bloom et al. (2001), Chary et al. (2002) and Frail et al. (2002) (GRB 010222). There are, however, a few cases in which the GRB does not seem to originate from intense star-forming regions (SFRs), e.g. GRB 990705 (Andersen et al. 2002).

In this paper we present localisations and host candidates of three OAs using ground-based data and Hubble Space Telescope (HST) STIS imaging data from the Cycle 9 program GO-8640 "A Public Survey of the Host Galaxies of Gamma-Ray Bursts'' (Holland et al. 2000) (data and further information available at http://www.ifa.au.dk/~hst/grb_hosts/index.html). These results supersede any preliminary results reported by us in GCN Circulars. In Sect. 2 we describe the image processing applied to the data, in Sect. 3 the astrometry resulting in the OA STIS-image localisations is described. In Sects. 4-6 we identify the hosts, present photometry and discuss the host environment. Finally, in Sect. 7 we discuss the implications of our localisations and host identifications. Specifically, we re-compute using our host identifications, the probability computed in Bloom et al. (2002) that none of the host identifications in that sample are random galaxies. Finally, we summarize our own results.

   
2 Data

Using the STIS-instrument onboard the HST the GRB-systems were observed using a four-point dithering pattern with shifts of 2.5 pixels ($\simeq$0 $\hbox{$.\!\!^{\prime\prime}$ }$127) between exposures. The data was pre-processed using the standard STIS pipeline and combined using the DITHER (v2.0) software (Fruchter & Hook 2002) as implemented in IRAF (v2.11.3) and STSDAS (v2.3). The STIS images were drizzled using "pixfrac  =  0.6'' and "scale  =  0.5'' (giving a pixel size of $0\hbox{$.\!\!^{\prime\prime}$ }0254$). Note that drizzling introduces correlated noise between neighbouring pixels. All GRB-systems were observed using the STIS 50CCD (hereafter CL) passband with pivotal wavelength PivW  =  5851.5 Å. GRB 980329 was also observed using the STIS F28X50LP (hereafter LP) passband, PivW  =  7228.5 Å. The HST images presented here are, as opposed to the images discussed in our previous GCN circulars, all oriented such that East is to the right and North towards the top. Whenever referring to pixel coordinates, increasing x corresponds to decreasing RA, while increasing y corresponds to increasing Dec.

The photometry was performed in circular or elliptical apertures, as appropriate, according to the morphology of the host. The size of the apertures was selected so as to measure the total flux, by first choosing a plausible shape and then increasing the size until no gain in flux could be achieved. The sky was measured in an annular aperture with a shape corresponding to that of object aperture, with inner and outer aperture size 1.5 and 4 times that of the object aperture. For the STIS zero-points, we adopted the values found by Gardner et al. (2000) for the HDF-south. The zero-points used were therefore $ZP_{\rm CL}=26.387$ and $ZP_{\rm LP}=25.291$. Foreground (Galaxy) extinction estimates were computed using the on-line NED extinction calculator based on the dust maps provided by Schlegel et al. (1998).

Signal-to-noise (S/N) estimates of the host detections were computed as the ratio between the measured counts in a circular aperture centered on the object and the sky variance as measured from circular apertures at ten (10) random positions (on the sky). The aperture diameter used was 19, 19, and 9 pixels for GRB 980329, GRB 980519 and GRB 990308, respectively. Note that the errors on the photometry is computed as in IRAF DAOPHOT/APPHOT and does not necessarily correspond to the S/N estimates.

The host pixel positions were determined by using the IRAF/APPHOT CENTER task and the "centroid'' algorithm therein. The "centroid'' algorithm computes the intensity weighted means of the marginal profiles in x and y. The results are given in Table 1.

Throughout this paper we use the following cosmological parameters; $\Omega_M=0.3$, $\Omega_\Lambda=0.7$, H₀ = 70 km s^-1 Mpc^-1.

   
3 Astrometry

The absolute astrometry presented here is based on comparison with the Guide Star Catalogue II (GSC-II) and has an average error of approximately $0\hbox{$.\!\!^{\prime\prime}$ }2$ per axis.

 

 

Table 1: GRB RA and Dec and the best fit pixel localisation (incl. 1-$\sigma$ errors) of the OA in the drizzled CL images. For each OA, the host candidate and three reference objects are given including their pixel positions and host offset from OA location

Target	RA	Dec	X		Y		$\alpha_{\rm off}$		$\delta_{\rm off}$
980329	07:02:38.02	+38:50:44.3	999.36	$\pm 1.34$	1032.33	$\pm 1.22$	0.0		0.0
host	07:02:38.07	+38:50:44.3	995.55	$\pm 0.05$	1027.35	$\pm 0.04$	0.097	$\pm 0.034$	-0.127	$\pm 0.031$
ref. 1	07:02:38.15	+38:51:03.7	941.32		1800.06
ref. 2	07:02:37.43	+38:50:34.2	1274.41		635.89
ref. 3	07:02:38.97	+38:50:33.2	564.13		598.21
980519	23:22:21.54	+77:15:43.2	1039.19	$\pm 0.68$	990.77	$\pm 0.71$	0.0		0.0
host	23:22:21.34	+77:15:43.7	1045.27	$\pm 0.07$	975.98	$\pm 0.01$	-0.154	$\pm 0.017$	-0.376	$\pm 0.018$
ref. 1	23:22:17.78	+77:15:51.3	416.04		1128.28
ref. 2	23:22:20.25	+77:15:23.8	1410.45		1673.18
ref. 3	23:22:27.36	+77:15:43.7	1514.40		462.34
990308	12:23:11.49	+06:44:04.7	813.46	$\pm 2.79$	922.50	$\pm 2.03$	0.0		0.0
OA/host1	12:23:11.49	+06:44:04.7	811.70	$\pm 0.05$	921.80	$\pm 0.07$	0.045	$\pm 0.071$	-0.018	$\pm 0.052$
host2	12:23:11.49	+06:44:04.7	815.55	$\pm 0.05$	910.90	$\pm 0.22$	-0.053	$\pm 0.071$	-0.295	$\pm 0.052$
ref. 1	12:23:10.06	+06:43:50.0	1651.27		341.10
ref. 2	12:23:12.30	+06:44:24.3	340.29		1698.05
ref. 3	12:23:10.95	+06:44:20.8	1131.42		1558.46

The procedure used for relative astrometry from ground-based images of the afterglow to the STIS data depends on the available ground-based data, but for all three objects least squares affine transformations were used. An affine transformation is the simplest possible transformation which allows for deviations from square pixels in reference and target images. It is known that some of our ground-based reference data were obtained with CCDs which have slightly non-square pixels. As we were not able to establish any clear correlation between position and astrometric residuals, it is justified to keep all transformations strictly linear, as is also preferred with a limited number of tie objects. The accuracy by which the position of a (point) source in a well sampled image can be determined is dependent on the signal-to-noise ratio (S/N) with which the source is detected, and the full width at half maximum (FWHM) of the point spread function (PSF). For low S/N the astrometric standard error per axis can be approximated with $\sigma_{\rm pos} = \sigma_{\rm PSF} / (S/N)$, where $\sigma_{\rm PSF}$ is the standard deviation of the Gaussian approximating the PSF, which formally equals FWHM/2.35. For high S/N, accuracy is limited by errors in the detector pixel geometry, usually at the level of 1/20 of a pixel or less. The level of accuracy is hence determined by how well the pixel borders are defined, which relies solely on the detector fabrication technology used. For a source detected with a S/N of 20 in $1\hbox{$^{\prime\prime}$ }$ seeing, the expected 1-$\sigma$ accuracy is $0\hbox{$.\!\!^{\prime\prime}$ }02$ per axis. If the S/N is significantly above 20 or the FWHM is sampled by less than about 3 pixels, this approximation of the astrometric error is not valid. Whenever several individual images of the afterglow is available, a transformation to the STIS reference frame is established for each image. As the error in the transformed afterglow position in the STIS image is always completely dominated by the astrometric error in the ground-based image, the errors of individually transformed afterglow positions are in practice independent. The standard deviation of the transformed positions is therefore an estimate of the actual astrometric error. To illustrate the estimation of the astrometric error, the individual transformed coordinates and the associated error budget is given in the case of GRB 990308 (Sect. 6).

   
4 GRB 980329

GRB 980329 was detected by the BeppoSAX satellite on 1998 March 29.16 UT. The radio and optical counterparts were discovered by Taylor et al. (1998) and Djorgovski et al. (1998), respectively. The latter claimed the detection of the host galaxy at an apparent magnitude of $R \sim25.7$. Palazzi et al. (1998), Gorosabel et al. (1999), Reichart et al. (1999) presented optical and near infrared detections of the OA and found it to decay at a rate typical for most detected OAs ( $\alpha_{\rm O} \sim 1.2$). This decay slope is in good agreement with that found in X-rays, where $\alpha_{\rm X} = 1.35\pm0.03$ (in 't Zand et al. 1998). A preliminary localisation of the host in the HST/STIS data was reported in Holland et al. (2000) (GCN #778). Unfortunately, the text incorrectly states the host to be southwest of the radio localisation, when it was actually to the northeast. The maximum measured (early) brightness of the OA was I = 20.8 and R= 23.6, leading to an extremely red colour $R{-}I = 2.8 \pm 0.4$(Reichart et al. 1999). Near-infrared (NIR) observations, on the other hand, showed that the NIR colours are approximately flat. These measurements led Fruchter (1999) to argue that the red colour could be caused by the Lyman forest if the redshift was $z\sim5$. This claim was subsequently challenged by the apparent non-detection of a Lyman forest in Keck II spectra (Djorgovski et al. 2001). Recently, Yost et al. (2002) presented supplementary multi-wavelength broad-band photometry of this burst and claim to rule out $z \ge5$ based on an afterglow model fit to the data. The NIR photometry shows that the HST/NICMOS October 1998 data (GO-7863, PI: A. Fruchter) contains a significant contribution from the OA and therefore it is not suited for host photometry. The GRB has also been found to be heavily extincted by dust (see Lamb et al. 1999; Bloom et al. 2002; Yost et al. 2002).

We retrieved NTT/EMMI R-band images of GRB 980329 from the ESO archive, obtained on March 29.99 and 30.99 (Palazzi et al. 1998). As the afterglow was detected at low signal-to-noise in the late-time images, the astrometry was in this case derived from the combined image. Seven tie objects, of which six are stellar and one a compact galaxy, were used for the astrometric solution. The astrometric error, as estimated from the residual of the tie object fit, is estimated to be about 1.25 drizzled STIS pixels, or $0\hbox{$.\!\!^{\prime\prime}$ }03$, which should be compared with an expected error of $0\hbox{$.\!\!^{\prime\prime}$ }02$, as estimated from the S/N of the OA image. The error in the transformation from STIS CL to the STIS LP image is a small fraction of a drizzled STIS pixel and can therefore be ignored. The best fit localisation in the CL image is given in Table 1.

An expanded section of the STIS CL and LP images, centered on the host, are shown in Fig. 1 with the OA position indicated. In the CL image several unresolved knots are seen on top of a low surface brightness area within an aperture of $0\hbox{$.\!\!^{\prime\prime}$ }5$. The measured ABMAG in the CL-band within this aperture is $27.5\pm0.2$. In the LP image an extended object is seen, but the knots seen in the CL-band are not detected. We find $26.6\pm0.2$ within the same aperture in the LP-band. Foreground extinction corrected photometry and detection significance estimates are given in Table 2. Photometry of the three brightest knots yields a total magnitude of $28.1\pm0.1$ in the CL-band and $27.7\pm0.2$ in LP. The flux in the LP measurement stems primarily from the underlying galaxy complex. Within an arcsecond of the OA position at least two fainter extended objects or structures are seen to the North and North-East in the CL-band. Their distance relative to the OA position is approximately 1 and 0.6 arcsec and photometry measurements yield $28.5\pm0.2$ and $29.5\pm0.5$, respectively.

Figure 1: Sub-section of the STIS CL and LP images centered on GRB 980329. A dashed ellipse indicates the 3-$\sigma$ OA localisation error while the solid circle gives the aperture used for photometry and a cross in the CL image marks the host center. The dash-dotted ellipse marks the 3-$\sigma$ error circle of Bloom et al. All images were smoothed by a 1.1 pixel Gaussian using IRAF/GAUSS. Axis units are in arcsec, North is up and East is to the left.

Open with DEXTER

The STIS CL and LP measurements in addition to the Keck/ESI $R =26.53\pm0.22$, $I=26.28\pm0.27$ (Bloom et al. 2002; Yost et al. 2002) and NIRC $K=23.04\pm0.42$ measurements (Yost et al. 2002) provide an excellent opportunity to estimate the photometric redshift of the host. Using the Bayesian photometric redshift (BPZ) estimation software of Benitez (2000) and restricting z >1 (due to absence of expected emission lines in spectra of the host, see Yost et al. 2002) we find $z \sim3.6$ with the best fitting SED corresponding to an Im galaxy type. Redshifts of z<1.2 and z>4.2 are excluded at the 95% confidence level (z >5 excluded at 99.99% level). These redshift estimates are consistent with the constraint z<3.9 based on the non-detection of the Lyman forest in a Keck II spectrum of the host galaxy (Djorgovski et al. 2001) and a far-ultraviolet extinction curve constraint giving 3<z<5(Lamb et al. 1999).

It is puzzling that the CL-band shows a clear multi-component nature, with at least three unresolved knots within 0.5 $^{\prime\prime}$, whereas the LP-band does not. We find an upper limit colour for the knots of CL-LP $\le$ 0.25, while for the integrated colour of the host complex, we measure CL-LP $\approx$ 0.8. The compact knots does therefore appear very blue (the wavelength cutoff is at 5500 Å in the LP-band).

Taking the measured $E_\gamma = 5.5 \times 10^{-5}$ erg cm²(in 't Zand et al. 1998) and assuming a redshift of 3.5 we find an isotropic gamma-ray energy of $E_{\rm iso} = 1.4\times10^{54}$ erg. Assuming a total average energy for GRBs of $5\times10^{50}$ erg (Frail et al. 2001) we estimate a jet opening angle of $\theta_0 = 1.5\deg$, indicating a highly collimated beam.

   
5 GRB 980519

	Figure 2: Sub-section of the STIS CL-band image centered on the OA for GRB 980519 and GRB 990308. Axis units are in arcseconds, North is up and East is to the left. Annotations as in Fig. 1 in addition to a dotted ellipse which marks the Bloom et al. (2002) host identifications.
Open with DEXTER

GRB 980519 was detected by GRO/BATSE (Muller 1998) on 1998 May 19.51 UT and subsequent BeppoSAX WFI localisation (Piro 1998) enabled the detection of the OA (Jaunsen et al. 1998). Jaunsen et al. (2001) presented a homogeneous optical data sample obtained at the Nordic Optical Telescope (NOT) and found that the light-curve breaks at around t₀ + 0.5 days, with a pre- and post-break power law of $\alpha_{\rm O1}=1.73$ and $\alpha_{\rm O2}=2.22$, respectively. The X-ray (pre-break) power law was approximately, $\alpha_{\rm X}=1.6$ though this estimate is somewhat uncertain as it is based on combining the BeppoSAX WFC and NFI measurements. The maximum measured flux of the OA was I=18.4 and R=19.8 at t₀+0.346 and t₀+0.536 days, respectively. Correcting for the decline, the approximate R-I colour was $\sim$0.6.

We used the NOT observations of the OA (Jaunsen et al. 2001) to derive an accurate position of the burst in the STIS image. As the GRB 980519 afterglow was discovered and followed up at very high airmass, differential color refraction (DCR) affects the astrometry significantly. Following Monet et al. (1992) we correct for DCR by a term which is proportional to $\sec\ ({\rm Zdist})$ and depends on the color of each individual object. Since the colors of the tie objects and the afterglow cover a narrow range, the color dependence was approximated with a linear relation. The afterglow was observed in the R and the I bands, so two different DCR corrections must be applied. To minimize the number of free parameters, we choose to derive a theoretical estimate of the relative amplitude of the DCR correction in the R and I bands. From the different refraction across the filter bandwidth it is found that DCR in R is about 2.65 times DCR in I. By using this factor, only the amplitude of DCR as function of color for the complete data set of six images has to be determined. This is done by minimizing the standard deviation of the six independent localisations. For each localisation between 7 and 10 tie objects were used. The difference between the final averaged positions with and without DCR correction is of the order of 0.7 drizzled STIS pixels, comparable to the 1-$\sigma$ astrometric error. In effect, by applying the DCR correction, the average of the three R-band positions coincide with the average of the three I-band positions. The OA localisation result is given in Table 1.

At the OA position we detect two extended objects, clearly visible in Fig. 2. The photometry yields CL ABMAGs of $27.1\pm0.1$ and $27.9\pm0.1$ for the southern and northern component, respectively. The OA is located in the very outskirts of the northern component ($S/N\sim9$), where a faint blob coinciding with the position of the OA is detected (see also Table 2). A host detection was reported by Sokolov et al. (1998) and Bloom et al. (1998) at an estimated Cousins R VEGAMAG of $26.1\pm0.3$. This detection, however, consisted of the smeared sum of both objects. By using a larger aperture of $1\hbox{$.\!\!^{\prime\prime}$ }88$ (enclosing both objects) we find $\sim$ $26.45\pm0.10$. Assuming a flat spectrum and using the STSDAS SYNPHOT/CALCPHOT we converted the CL ABMAGs to Cousins R VEGAMAG, giving $\sim$26.0, in agreement with the earlier combined detections. It is also worth noting that the combined flux of the two objects amounts to 26.7 (ABMAG) as compared to 26.45 for the large aperture. The difference in flux can be attributed to the very low surface brightness (>29 mag) regions in the vicinity of the two major components. Assuming a redshift larger than 0.5, which is reasonable given the redshift distribution of other GRB hosts and the faintness of the host, we note that the average angular scale of 1 arcsec is $\sim$$7 \pm 2$ kpc for our assumed cosmology. Given this angular scale and the disk-like morphology it is most likely that the two detected objects are galaxies which are in the process of merging. This is supported by the low (<0.003) integrated probability (Gardner et al. 2000) of having two objects of this brightness within $\sim$2 sq. arcsec. The faint neighboring patches are therefore likely to be smaller galaxy fragments belonging to the merging system.

   
6 GRB 990308

GRB 990308 was detected by GRO/BATSE on 1999 March 8.21 UT, on the RXTE All-Sky monitor and also weakly by the Ulysses GRB detector. An OA was detected using the QUEST camera on a 1.0 m Schmidt telescope in Venezuela (Schaefer et al. 1999). These optical measurements give a power law of $\alpha=2\pm2$ (Schaefer et al. 1999), and are the only data in which the OA is detected. Early non-detections by LOTIS and Super-LOTIS suggest $\alpha<1.3$, while later non-detections by the WIYN and Keck telescopes set the constraint $\alpha>1.1$. Taking all constraints into consideration, Schaefer et al. (1999) found a best fitting constant power-law, $\alpha = 1.2\pm0.1$.

 

 

Table 2: Aperture photometry of GRB hosts in AB magnitudes and corrected for foreground extinction according to Schlegel et al. (1998) using the Johnson V-band estimate for CL and Cousins I-band estimate for LP.

GRB	Obs. Date		E(B-V)	CL			LP
	absolute	days		int.	mag	S/N	int.	mag	S/N
980329	24/26 Aug. 2000	$\sim$880	0.073	8072	$27.2 \pm 0.1$	10	8156	$26.2 \pm 0.1$	9
980519	7 Jun. 2000	$\sim$750	0.240	8983	$27.0 \pm 0.2$	9	...	...	...
990308	19 Jun. 2000	$\sim$468	0.023	7842	$29.7 \pm 0.4$	5	...	...	...

We used the original QUEST data (Schaefer et al. 1999) to transform the OT position to the STIS clear image coordinate system via an intermediate transformation to a deep NOT image, due to the lack of common tie objects between the QUEST and STIS images. The QUEST camera periodically drops lines in the readout so that the CCD chips in the array keep in synchronization for objects at different declinations and this results in a small jump in right ascension at known positions on the images. No line drops occurred near the OT position on the QUEST images, so the relative astrometry does not suffer from this complication. The NOT/ALFOSC image is based on the combination of 7 R-band images with a total integration time of 6000s, obtained specifically for this purpose on 29-30 March 2001. The pixel scale in the NOT/ALFOSC image is $0\hbox{$.\!\!^{\prime\prime}$ }187$.

In Table 3 we present the individual GRB 990308 afterglow coordinates, transformed from the three QUEST images to the NOT image. Only point sources were used as tie objects. For each transformation, the standard deviation of the residuals of the fit in each axis is given, together with the number of objects included in the fit. The last column gives the expected centroid error of the afterglow coordinate, as estimated from the FWHM and the signal-to-noise ratio of the individual afterglow detections in the QUEST images. The last line gives the mean coordinate, with the error determined as the standard deviation of the individual measurements, normalized to the degrees of freedom and divided by the square root of the number of measurements. The estimated error of the mean coordinate is in good agreement with what is predicted from the signal-to-noise ratio and FWHM of the afterglow detections. In the STIS image the errors corresponds to 2.50 and 1.58 pixels in x and y respectively.

 

 

Table 3: Afterglow coordinates in the NOT image.

IMAGE	$x_{\rm {NOT}}$	$\sigma_{x}$	$y_{\rm {NOT}}$	$\sigma_{y}$	$N_{\rm {OBJ}}$	$\sigma_{\rm {centroid}}$
CCD 1	1086.46	0.31	1128.40	0.48	11	0.34
CCD 3	1085.85	0.16	1128.23	0.65	10	0.38
CCD 4	1085.29	0.20	1128.94	0.28	8	0.43
Mean	1085.87	$\pm$ 0.33	1128.53	$\pm$ 0.21		0.22

The transformation from the NOT image to the STIS image was based on 10 tie objects, all of which are relatively compact extended sources in the STIS image. The use of extended objects in the astrometric tie may potentially introduce differential colour error in the centroid determination for objects with a color gradient, as the passbands of the groundbased and STIS data are different. Such errors will appear as an increased scatter in the affine transformation. The normalized standard deviation of the residuals of the fit are 0.70 and 1.19 STIS pixels in x and y respectively. We may use these standard deviations as conservative estimates of the error imposed, when transforming the afterglow coordinate from the NOT image reference frame to the STIS image reference frame. The estimate of the error in pixels of the afterglow coordinate in the STIS image then becomes

$$\sigma_x = \sqrt{2.50^2 + 0.70^2} = 2.60 \equiv 0\hbox{$.\!\!^{\prime\prime}$ }066$$

$$\sigma_y = \sqrt{1.58^2 + 1.19^2} = 1.98 \equiv 0\hbox{$.\!\!^{\prime\prime}$ }050$$

The final STIS position and error estimate is given in Table 1.

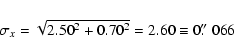
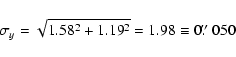
At the locus of the OA we marginally detect a very faint point-like object (see Fig. 2) which we measure to have a STIS CL magnitude of $30.1\pm0.4$ with a detection significance of $S/N \sim5$ (foreground extinction corrected photometry given in Table 2). Including the faint extended emission north of this object gives $29.9 \pm 0.4$. We also detect an extended object $0\hbox{$.\!\!^{\prime\prime}$ }3$ to the south with an estimated magnitude of $29.8\pm0.4$ ($S/N \sim3$) and $0\hbox{$.\!\!^{\prime\prime}$ }8$ to the North a much larger disk-like object with a magnitude of $27.7\pm0.1$. Using the galaxy counts of Gardner et al. (2000) we find a relatively low probability ($\sim$0.02 within a radius of 1 $^{\prime\prime}$ of the OA position) that the three objects are projected neighbors.

Could the point-like component coincident with the OA location in fact be the OA itself? Assuming a constant power-law one can deduce the decay slope by interpolating the brightness at the time of the first V-band QUEST observation and the measured brightness in the STIS observations 468 days after the burst. This gives a power-law exponent of $\alpha \sim 1.35$, consistent with the best estimate of the power-law slope, $\alpha \simeq 1.2$ (based on all available data). If correct, this would be the latest trace to date of an OA, at t₀+468 days. Another possibility is that the point-like component is caused by some re-brightening mechanism, such as e.g. dust echoing.

In summary, we identify the object coincident with the OA localisation as the possible remnant OA (point-like) or the host (extended). If the point-like object turns out to be non-variable and therefore not the OA, then the OA must have been fainter than $\sim$30 mag. This implies that the late time decay slope must have been larger than 1.35. This scenario and the constraints from the early data could be explained by introducing a break in the light-curve. Specifically, an early $\alpha\sim1.3$ slope (as supported by the early LOTIS data) followed by a steeper slope fits this scenario well. A revisit of this field with HST+ACS is required to disentangle these ambiguities.

   
7 Summary

We have localised the three OAs to high precision in the STIS images and identify the host as the nearest detected object of the OA position. The GRB 980329 host galaxy redshift is estimated to be $z \approx 3.5$. For all three candidate hosts we detect faint extended structures within a radius of $\sim$ $1\hbox{$^{\prime\prime}$ }$ ($\sim$7 proper kpc for z >0.5). This scale is similar to that seen between tidally interacting and merging galaxies (e.g. Borne et al. 2000). The hosts show signs of sub-structure (possibly star-forming and/or merging elements); 3-4 blue knots in the GRB 980329 host, a knot in the northern edge of the GRB 980519 host and a point-source within the 3-$\sigma$ localisation error of GRB 990308. The faintness of these hosts suggests that, regardless of the host luminosity, GRBs seem to be associated with star formation (SF). This correlation may allow GRBs to be used as a powerful tracer of star formation, provided the link between GRBs and SF is correct. It also implies that a significant amount of star formation is located in (optically) very faint galaxies. Their faintness may be due to dust extinction or a very steep faint-end slope of the galaxy luminosity function (see also Fynbo et al. 2002). The SF/GRB correlation may therefore be the basis of a unique and new way of finding star-forming galaxies at high redshifts (independent of the otherwise unavoidable surface-brightness bias).

Bloom et al. (2002) present a comprehensive study of 20 GRB hosts, including the three reported here, based on the same HST data and mainly Keck imaging. For GRB 980329 they found an OA position similar too ours, but with somewhat larger errors. However, their selection of the host center coincide with a small object at the center of the host complex, whereas we have chosen the galaxy most nearby the localization. From their thumbnail image (Fig. 2) it seems the northern object is much less significant than in our image and likewise the northern most blob/knot, which is practically coincident with our OA localization. For GRB 990308 Bloom et al. (2002) obtain an OA localisation with significantly larger errors than ours, and identify a large galaxy in the outskirts of their error circle (indicated in Fig. 2). Our host candidate corresponds to the object(s) seen left of the center of the error circle in their image, and which reality was noted by them as questionable. In summary, we identify different host candidates in two out of the three faint hosts investigated. These three hosts are also among the four most extreme outliers (the ones with the largest OA to host-center offset) in the Bloom et al. sample. Adopting our host identifications and OA localisations, the sample does not have obvious outliers. The relevant parameters as measured on our drizzled CL-band images are given in Table 4 including the individual $P_{\rm i}$values for direct comparison with Bloom et al. (2002). This is quantified by re-computing $P(n_{\rm chance}=0)$, defined in Bloom et al. (2002), representing the probability that none of the host identifications of the Bloom et al. sample are randomn galaxies (unrelated to the GRB). Bloom et al. (2002) found $P(n_{\rm chance}=0) = 0.483$, but by using our OA localisations and host identifications we find $P(n_{\rm chance}=0) = 0.69 (0.67)$. This means that by using our results it is unlikely that any of the 20 hosts in the Bloom et al. sample are false identifications.

 

 

Table 4: Measured properties of the host candidates used to estimate the $P_{\rm chance}$ statistic. The Rc magnitude includes the line-of-sight extinction.

Target	R0	$\sigma_{{R}_0}$	$R_{\rm {half}}$	Rc mag	$P_{\rm i}$
980329 host	0.16	0.046	0.14	27.0	0.022
980519 host	0.41	0.025	0.11	27.4	0.061
990308 host1	0.048	0.088	0.023	29.4	0.105
990308 host2	0.30	0.088	0.063	29.3	0.125

Acknowledgements

This work was supported by the Danish Natural Science Research Council (SNF). STH acknowledges support from the NASA LTSA grant NAG5-9364. JG acknowledges the receipt of a Marie Curie Grant from the European Commission. MIA acknowledges the Astrophysics group of the Department of Physical Sciences of University of Oulu for support of his work. JPUF acknowledges financial support from the Carlsberg Foundation.

References

 

• Andersen, M., Hjorth, J., Gorosabel, J., et al. 2002, A&A, submitted In the text  
• Benitez, N. 2000, ApJ, 536, 571 In the text NASA ADS  
• Bloom, J. S., Djorgovski, S. G., Gal, R. R., et al. 1998, GRB 980519 Optical Observations, GCN Circ. 87 In the text  
• Bloom, J. S., Djorgovski, S. G., Halpern, J. P., et al. 2001, GRB 010222: Keck spectroscopy., GRB Circ. 989 In the text  
• Bloom, J. S., Kulkarni, S. R., & Djorgovski, S. G. 2002, AJ, 123, 1111 In the text NASA ADS  
• Borne, K., Patton, D., Simard, L., et al. 2000, AAS Meeting, 197, #76.11 In the text  
• Chary, R., Becklin, E. E., & Armus, L. 2002, ApJ, 566, 229 In the text NASA ADS  
• Djorgovski, S. G., Kulkarni, S. R., Bloom, J., et al. 2001, in Gamma-Ray Bursts in the Afterglow Era: 2nd Workshop, ed. E. Costa, F. A. Frontera, & J. Hjorth, vol. ESO Astrophysics Symp., ESO (Springer) In the text  
• Djorgovski, S. G., Kulkarni, S. R., Sievers, J., Frail, D., & Taylor, G. 1998, GRB 980329 optical observations, GCN Circ. 41 In the text  
• Frail, D. A., Bertoldi, F., Moriarty-Schieven, G. H., et al. 2002, ApJ, 565, 829 In the text NASA ADS  
• Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2001, ApJ, 562, L55 In the text NASA ADS  
• Fruchter, A. S. 1999, ApJ, 512, L1 In the text NASA ADS  
• Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 In the text NASA ADS  
• Fynbo, J. P. U., Möller, P., Thomsen, B., et al. 2002, A&A, 388, 425 In the text NASA ADS  
• Fynbo, J. U., Holland, S., Andersen, M. I., et al. 2000, ApJ, 542, 89 In the text  
• Gardner, J. P., Baum, S. A., Brown, T. M., et al. 2000, AJ, 119, 486 In the text NASA ADS  
• Gorosabel, J., Castro-Tirado, A. J., Pedrosa, A., et al. 1999, A&A, 347, L31 In the text NASA ADS  
• Hjorth, J., Thomsen, B., Nielsen, S. R., et al. 2002, ApJ, 576, 113 In the text NASA ADS  
• Holland, S., Fynbo, J., Thomsen, B., et al. 2000, GCN Circ. 698 In the text  
• Holland, S., & Hjorth, J. 1999, A&A, 344, 67 In the text  
• in 't Zand, J. J. M., Amati, L., Antonelli, L. A., et al. 1998, ApJ, 505, L119 In the text NASA ADS  
• Jaunsen, A. O., Hjorth, J., Andersen, M. I., et al. 1998, GRB 980519, Optical observations, GCN Circ. 78 In the text  
• Jaunsen, A. O., Hjorth, J., Björnsson, G., et al. 2001, ApJ, 546, 127 In the text NASA ADS  
• Jensen, B. L., Fynbo, J. U., Gorosabel, J., et al. 2001, A&A, 370, 909 In the text NASA ADS  
• Lamb, D. Q., Castander, F. J., & Reichart, D. E. 1999, A&AS, 138, 479 In the text NASA ADS  
• MacFadyen, A. L., & Woosley, S. E. 1999, ApJ, 524, 262 In the text NASA ADS  
• Monet, D. G., Dahn, C. C., Vrba, F. J., et al. 1992, AJ, 103, 638 In the text NASA ADS  
• Muller, J. M. 1998, GRB 980519, IAU Circ. 6910 In the text  
• Paczynski, B. 1986, ApJ, 308, L43 In the text NASA ADS  
• Palazzi, E., Pian, E., Masetti, N., et al. 1998, A&A, 336, L95 In the text NASA ADS  
• Piro, L. 1998, GRB 980519, GCN Circ. 75 In the text  
• Reichart, D. E., Lamb, D. Q., Metzger, M. R., et al. 1999, ApJ, 517, 692 In the text NASA ADS  
• Schaefer, B. E., Snyder, J. A., Hernandez, J., et al. 1999, ApJ, 524, L103 In the text NASA ADS  
• Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 In the text NASA ADS  
• Sokolov, V., Zharikov, S., Palazzi, E., & Nicastro, L. 1998, GRB 980519 Optical observations, GCN Circ. 148 In the text  
• Taylor, G. B., Frail, D. A., Kulkarni, S. R., et al. 1998, ApJ, 502, L115 In the text NASA ADS  
• Vietri, M., & Stella, L. 1998, ApJ, 507, L45 In the text NASA ADS  
• Woosley, S. E. 1993, ApJ, 405, 273 In the text NASA ADS  
• Yost, S. A., Frail, D. A., Harrison, F. A., et al. 2002, ApJ, 577, 155 In the text NASA ADS