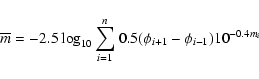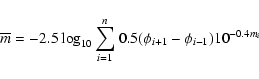Up: Identification of 13 Cepheids M 31
Subsections
We do not have all the observations in good photometric sky conditions.
Therefore we have rejected all those data points showing photometric error of
>0.2 mag. Further, for each star, the average DAOPHOT error and its standard
deviation was calculated using its observations on different nights.
Measurements with errors
exceeding to average error by more than 3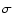 were flagged as "bad'' and
removed from further analysis. The whole procedure was iterated thrice.
Normally 1 to 10 points were removed in this process. Because two different
CCDs with different quantum efficiencies (see Table 1) and different exposure
times (see Table 2) were used, limiting magnitudes were different in different
years. Consequently some stars could not be identified in one or other years of
observations. All the stars were not present in every frame due to different
observing conditions and CCD orientations on various nights. In order to derive
useful results, we consider only those stars in our further analysis which have
more than 40 R data points. Stars which showed more than
were flagged as "bad'' and
removed from further analysis. The whole procedure was iterated thrice.
Normally 1 to 10 points were removed in this process. Because two different
CCDs with different quantum efficiencies (see Table 1) and different exposure
times (see Table 2) were used, limiting magnitudes were different in different
years. Consequently some stars could not be identified in one or other years of
observations. All the stars were not present in every frame due to different
observing conditions and CCD orientations on various nights. In order to derive
useful results, we consider only those stars in our further analysis which have
more than 40 R data points. Stars which showed more than 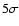 variation in 3 consecutive data points are searched for variability.
Only R band photometric data is used for this as the data sample in R
filter (133) is larger than that in I filter (116). Also photometric errors
at a given brightness are generally less in R filter (see Table 3). Finally
we analysed the variability in these stars explicitly by visual monitoring and
also using I filter data. In this way, we detected 359 variable stars in our
field.
variation in 3 consecutive data points are searched for variability.
Only R band photometric data is used for this as the data sample in R
filter (133) is larger than that in I filter (116). Also photometric errors
at a given brightness are generally less in R filter (see Table 3). Finally
we analysed the variability in these stars explicitly by visual monitoring and
also using I filter data. In this way, we detected 359 variable stars in our
field.
To find periods from unequally spaced data, we used a modified version of the
period-searching program by Press & Rybici (1989) based on the method of
Horne & Baliunas (1986). The data were initially phased
for all periods between 5 and 600 days searched in an increment step of 0.6
day. To further refine the period, an increment of 0.1 day was used around
thus derived period. In this way, we could determine period of 141 variables.
The remaining stars are either non-periodic or long-period variables.
We calculated phase weighted apparent mean
magnitude for all the Cepheid variables as suggested by Saha et al. (1994)
where n is the total number of observations, 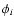 is the phase of ith observation in order of increasing phase after folding the period.
The equation requires non-existent entities
is the phase of ith observation in order of increasing phase after folding the period.
The equation requires non-existent entities 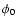 and
and
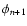 which is set identical to
which is set identical to 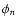 and
and 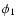 respectively. The
estimation of mean magnitude by the phase-weighted method is superior to
an ordinary mean, which minimizes the systematic biases from loss of faint
measurements in the mean magnitude (Saha & Hoessel 1990). For other variables,
mean magnitude is estimated simply by intensity averaging of all the data
points.
respectively. The
estimation of mean magnitude by the phase-weighted method is superior to
an ordinary mean, which minimizes the systematic biases from loss of faint
measurements in the mean magnitude (Saha & Hoessel 1990). For other variables,
mean magnitude is estimated simply by intensity averaging of all the data
points.
Transformation equations were derived to convert pixel
coordinates (X,Y) into celestial coordinates (
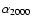 ,
,
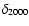 )
using 324 reference star positions from the USNO
)
using 324 reference star positions from the USNO![[*]](/icons/foot_motif.gif) catalogue. These coordinates agree within
catalogue. These coordinates agree within 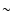 0.1 arcsec with
those given in Magnier catalogue (Magnier et al. 1992).
0.1 arcsec with
those given in Magnier catalogue (Magnier et al. 1992).


Up: Identification of 13 Cepheids M 31
Copyright ESO 2003