A&A 401, 895-901 (2003)
DOI: 10.1051/0004-6361:20030124

The nature of the absorbing torus in compact radio galaxies

G. Risaliti1,2 - L. Woltjer1,3 - M. Salvati1


1 - INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
2 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
3 - Observatoire de Haute-Provence, CNRS, 04870 Saint-Michel l'Observatoire, France

Received 7 October 2002 / Accepted 21 January 2003

Abstract
We present BeppoSAX observations of the two radio galaxies PKS 1934-63 and S5 1946+708. Strong Iron K$\alpha$ lines are detected in both objects indicating that the two sources are absorbed by column densities higher than 1024 cm-2.

Combining radio continuum, HI absorption and X-ray data we can constrain the physical state and the dimensions of the absorber. We find that the putative obscuring torus is molecular and located at a distance higher than 20 pc from the center in S5 1946+70. In PKS 1934-63 no radio nucleus has been observed. If this is due to free-free absorption a radius of only a few pc is inferred. Since the K$\alpha$ lines have been detected only at 90% confidence, we also discuss the implications if they would be not as strong as found from our data. From our results it appears that the combination of hard X-ray data and spatially resolved HI absorption measurements provides a powerful diagnostic for conditions in the absorbing "torus''.

Key words: galaxies: active - X-rays: galaxies


1 Introduction

In unified models of Seyfert galaxies Sy1/Sy2 and of quasars/radio galaxies Q/RG the Broad Line Region BLR and the optical nucleus are hidden at certain orientations by an "absorbing torus''. Direct evidence for such a torus comes from absorption at the lower energies X-rays from the nucleus. While the "torus'' needs not have a truly toroidal shape, it has to be geometrically thick. For the Seyferts the observed ratio of Sy1/Sy2 (1/3-1/6) suggests that the torus as seen from the nucleus subtends an angle of order $\pi/2$, and corresponding estimates have been made for RG.

Polarized optical broad emission lines in some Sy2 and RG have been ascribed to material above the torus, which scatters nuclear light towards us. Also X-rays may be scattered by relatively cool material with the iron K$\alpha$ line at 6.4 keV appearing in emission. When column densities in the torus approach $N_{\rm H} = 10^{24}$ cm-2, the direct X-rays are much attenuated and the equivalent width (EW) of the iron line may become 1 keV or more. If the scattering material is warm iron lines at 6.7-6.9 keV may appear.

While the X-ray data yield values or limits for $N_{\rm H}$, they do not contain information on the physical and kinematical conditions in the torus. Absorption at 21 cm by atomic hydrogen (HI) may be informative in this respect. HI absorption has been detected mainly in powerful compact radio galaxies. Line widths of up to nearly 1000 km s-1 have been observed, indicating that the HI is located rather close to the nucleus, presumably in the torus. In other cases the velocities are smaller and the location of the HI more uncertain.

The absorbing matter generally covers only a small part of the radio source. It is therefore essential to have high resolution, preferably VLBI, data to determine the optical depth in HI in front of the nucleus. Conway & Blanco (1995) obtained VLA data for CygA and found that the X-ray and HI data may be quantitatively fitted to simple models of the torus. They also concluded that the radius of the torus should exceed 15 pc if strong free-free absorption is to be avoided, which would make the radio nucleus unobservable at 1.4 GHz. This radius is larger than inferred for typical Seyferts.

To obtain further information on the tori in RG we have observed the X-ray spectra of two RG with Beppo-SAX. PKS 1934-63 is a powerful compact double with a separation of 158 pc. VLBI observation failed to locate a nucleus between these components even at 8 GHz (Tzioumis et al. 1999). It has been suggested that very strong free-free absorption might be responsible (Woltjer 2000). HI measurements (Véron-Cetty et al. 2000) also failed to find HI absorption in front of the radio source, except for a narrow weak feature, presumably due to an isolated cloud. The second source observed with BeppoSAX is S5 1946+708, a compact symmetric object (CSO[*] with a nucleus and two jets and an overall dimension of 100 pc. The HI absorption profile in front of the nucleus has a total width of 600-800 km s-1 and the absorption in front of the jets shows that the projected thickness of the "torus'' is about 30 pc with some narrower absorption further out (Peck et al. 1999). Further data on the two sources are given in Table 1. Everywhere we have taken H0= 67 km s-1 Mpc-1.

2 Observations and analysis of the BeppoSAX data

PKS 1934-63 was observed on Nov. 11/12, 2000 and again on May 03-04 2001, each time for about 50 ksec. While in May the K$\alpha$ line appeared to have a lower EW than before, the low S/N ratio was insufficient to conclusively demonstrate variability and so we combined the two data sets. The total exposure times were 38 ksec for the LECS instrument (0.1-10 keV), 95 ksec for the MECS (1.65-10 keV) and 48 ksec for the PDS (20-200 keV). The source was not detected with the PDS. The LECS and MECS images show the presence of an unknown serendipitous source 5 arcmin NW of the target, with comparable flux. To avoid contamination, the spectrum of PKS 1934-63 was extracted in a circular region with radius 2 arcmin using the XSELECT reduction package. This small radius is the one for which we obtain the highest S/N. The spectral analysis has been performed with the XSPEC code. The LECS and MECS spectra have been convolved with the response matrices provided by the BeppoSAX Science Data Center and background subtracted on the basis of a long exposure of a blank field. To check for systematic errors in this procedure we also extracted the background spectrum from a source free region in our field. After rescaling for the vignetting factor the two spectra agreed very well.


 
Table 1: Characteristics of the two radio galaxies. Subsequent lines give the redshift, the 1.4 GHz flux density from the nucleus, the radio power, the visual absorption for the Narrow Line Region and the absorption corrected [OIII]$\lambda $5007 luminosity (H0=67 km s-1 Mpc-1).
  PKS 1934-63 S5 1946+708
z 0.182 0.101
$S_{1.4 ~\rm GHz}$(Jy) 15 1.0
$\log P_{1.4 ~\rm GHz}$(W Hz-1) 27.1 25.3
AV(mag) 1.5 2.2
$\log L_{\rm [OIII]}$ (erg s-1) 43.2 42.0


Given the low S/N we can only fit simple models. A power law fit to the continuum yields a photon index $\Gamma=1.9$, but leaves a clear excess at 5.3 keV corresponding to 6.3 keV in the rest frame. This is interpreted as a Fe K$\alpha$ line with very large EW=2.0 keV. If we interpret this spectrum as reflection-dominated, we can assume a reflection efficiency, R, to estimate the intrinsic continuum and a lower limit for the absorbing column density, $N_{\rm H}$. Assuming R=5% (the maximum allowed according to reflection models as in Ghisellini et al. 1994, and therefore the one giving the lowest intrinsic continuum) we find $N_{\rm H}>2.5\times 10^{24}$ cm-2. The results are given in Table 2. This interpretation is not unique, due to the poor signal-to-noise.

An alternative possibility is suggested by the separate analysis of the two observations. The 2-10 keV continuum is higher in the second observation, while the line flux remains constant. We fitted the two spectra with the photon indexes and the line flux fixed at the values obtained in the combined fit, leaving the power law normalization free. We found that the continuum variation is significant at a confidence level of 90%. In the high-continuum observation the line is detected only at a 1.2$\sigma$ level.

Therefore, we cannot exclude that the observed spectrum is the intrinsic emission from the active nucleus, but that a variation by a factor of $\sim$2 in the continuum (not followed by a line variation, indicating that the line is produced by material far from the center) gives rise to a measured equivalent width in the combined spectrum higher than the usual values for type 1 AGNs (100-300 eV).

The spectra from the two observations are plotted in Fig. 1. The results of the separate fits are listed in Table 2.


   \begin{figure} \par {\resizebox{8.8cm}{!} {\includegraphics[clip]{h4021f1.ps}} } \end{figure} Figure 1: Spectrum and best fit model for the BeppoSAX observation of PKS 1934-63. Triangles: LECS data of the first observation; circles: MECS data of the first observation; squares: MECS data of the second observation.
Open with DEXTER


 
Table 2: Best fit models for the merged observations of PKS 1934-63 (first column) and for the two observations taken separately (second and third column). From the non-detection in the PDS we can estimate $N_{\rm H}>2.5\times 10^{24}$ cm-2, assuming a reflection efficiency of 5%. Notes: a fixed parameter, b uncorrected for absorption.
PKS 1934-63
Parameter Merged obs. First obs. Second obs.
Power law:      
Photon index $\rm 1.9^{+0.5}_{-0.6}$ $\rm 2.2_{-0.6}^{+0.5}$ $\rm 1.2_{-0.7}^{+0.7}$
Normalization (10-5 cts s-1 keV-1) $\rm 3.8^{+3.2}_{-2.0}$ $\rm 4.4^{+4.3}_{-2.4}$ $\rm 2.2_{-1.5}^{+3.0}$
Iron line:      
Peak energy (keV, rest frame) $\rm 6.26^{+0.34}_{-0.38}$ $\rm 6.31_{-0.21}^{+0.29}$ 6.4a
Equivalent width (keV) $\rm 2^{+1.2}_{-1.4}$ $\rm 3.2_{-2.6}^{+3.1}$ $\rm0.6_{-0.6}^{+0.9}$
Flux 2-10 keV (10-13 erg cm-2 s-1)b $1.5\pm 0.2$ $1.2\pm 0.2$ $2.3\pm 0.3$
$\chi^2$/d.o.f. 14.2/17 4.3/7 4.4/7


S5 1946+708 was observed by BeppoSAX for 40 ksec. Again there is another source in the field at 10 arcmin from our target. The PDS flux detected in the field could come from either source (see the discussion in the Appendix) and so we have no conclusive evidence for hard radiation from S5 1946+708. Fitting the spectrum as before we obtain from the LECS and MECS data: $\Gamma=2.6$ and a line at 6.9 keV in the rest frame with EW = 1.8 keV (Table 3 and Fig. 2). With a 90%-confidence lower limit at 6.6 keV this would suggest reflection by warm matter. However, if we were to fix the energy of the line at 6.4 keV, its statistical significance would not change much. We can also obtain a lower limit for the absorbing column density, $N_{\rm H}$, assuming that the PDS emission is entirely due our target, as we did for the best fit shown in Table 2. However, in the opposite hypothesis (i.e. PDS emission entirely due to the serendipitous source) the lower limit on $N_{\rm H}$ increases, but the other parameters do not significantly change. Finally, a low-energy cut-off is detected, indicating a second absorber along the line of sight of the reflected component.


   \begin{figure} \par {\resizebox{8.8cm}{!} {\includegraphics[clip]{h4021f2.ps}} } \end{figure} Figure 2: Spectrum and best fit model for the BeppoSAX observation of S5 1946+708.
Open with DEXTER

In conclusion both objects have rather steep spectra. Combined with the high EW of the iron lines this suggests that the sources are Compton thick (log $N_{\rm H} > 24$), with the observed X-rays resulting from scattering. Observations with higher S/N ratio are needed to confirm these results.

3 Discussion

We adopt a simple model in which a torus with radius r$_{\rm pc}$ parsec is illuminated by a point source nucleus emitting X-rays with an energy spectral index $\alpha$ = 0.7 between 1 and 100 keV with a luminosity of 1044 L44 erg s-1. The torus is taken to be isobaric with temperature 103 T3 K and particle density 106 n6 cm-3. We neglect the curvature of the torus. Our aim is to use radio and X-ray data to constrain the density and size of the circumnuclear absorber.

We shall make use of the calculations of Maloney (1996) and Neufeld et al. (1994) for single phase isobaric models at high pressure ( $p/k\sim10^{11}$ K cm-3), and of Maloney et al. (1996) at low pressure ( $p/k\sim~10^{9}$ K cm-3). Conditions in the torus depend on the effective ionization parameter $\xi_{\rm eff}$ which from Maloney et al. we write, for $\alpha =-0.7$, as

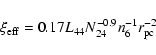\begin{displaymath}\xi_{\rm eff}=0.17 L_{44} N_{24}^{-0.9} n_6^{-1} r_{\rm pc}^{-2} \end{displaymath} (1)

with N24 the column density towards the nucleus in units of 1024 cm-2 and $r_{\rm pc}$ the distance to the center in pc. Different values of $\alpha$ should not change the results too much.

 
Table 3: Best fit model for S5 1946+708. The high column density absorber, $N_{\rm H1}$, has been estimated assuming that all the PDS emission is due to this source. b uncorrected for absorption.
S5 1946+708
Parameter Best fit value
Power law:  
Photon index $\Gamma=2.6^{+0.6}_{-0.7}$
Normalization $\rm 5.4^{+10}_{-3.7} 10^{-4}$ cts s-1 keV-1
high $N_{\rm H}$ absorber $N_{\rm H1}>2.8\times 10^{24}$ cm-2
low $N_{\rm H}$ absorber $N_{\rm H2}=2.6_{-1.9}^{+2.5}\times 10^{22}$ cm-2
Iron line:  
Peak energy (rest frame) $E=\rm 6.87^{+0.19}_{-0.24}$ keV
Equivalent width $EW=\rm 1.8^{+1.2}_{-1.1}$ keV
Flux 2-10 keV (10-13 erg cm-2 s-1)b $5.3\pm 0.6$
$\chi^2$/d.o.f. 16.5/21


All tori have an atomic zone towards the nucleus, but if the total column density through the torus $\tilde{N}_{24}$ is large enough this is followed by a mainly molecular zone. From the calculations of Neufeld et al. and of Maloney it is seen that the transition from atomic to molecular occurs in a very narrow region from log $\xi_{\rm eff}\sim -2.0$ when the gas is fully atomic to $\log \xi_{\rm eff}=-3.4$when it is fully molecular, for pressure $\tilde{p} = p/k$ in the range 10 10- 1012 K cm-3. In the high pressure range the temperature averages about 7000 K in the atomic zone and some 600 K in the molecular zone. From Maloney et al. (1996) we see that at lower pressures $\tilde{p}$ in the range 107-109 K cm-3 the transition is more gradual and temperatures as low as 100 K may be reached in the atomic zone. In a typical atomic zone the average ionized fraction is around log( $n_{\rm e}/n)\sim-1.8$ and may be lower at pressures near 107 K cm-3. In the molecular zone $n_{\rm e}$ is negligible.

The condition for a fully atomic torus, log $\xi_{\rm eff} > -2.0$, can be rewritten as a condition in the torus radius versus density plane:

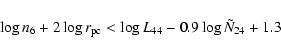\begin{displaymath}\log n_6+2 \log r_{\rm pc} < \log L_{44}-0.9 \log \tilde{N}_{24}+1.3 \end{displaymath} (2)

where $\tilde{N}$ is the total column density to the outer edge of the torus.

The ratio $n_{\rm HI}/n$ in the molecular zone depends on the destruction of H2 molecules by X-rays and on their formation on the surface of grains. Maloney et al. obtain an expression that in the molecular zone may be written as

\begin{displaymath}\log(n_{\rm HI}/n)=3.08+\log\xi_{\rm eff} \end{displaymath} (3)

where the constant involves uncertain parameters relating to the grains. It should be noted that all these calculations depend on still somewhat uncertain chemistry at low temperatures, on the degree of trapping of IR lines and on the nature of the grains. Maiolino et al. (2000) have suggested that grains in the torus may be different from those in the local interstellar medium or even perhaps largely absent.

An additional condition may be that in a steady state the pressure in the torus should be higher than or equal to the radiation pressure (Maloney 1996). This can be written as follows:

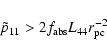\begin{displaymath}\tilde{p}_{11}>2 f_{\rm abs} L_{44} r_{\rm pc}^{-2} \end{displaymath} (4)

with $\tilde{p}=10^{11}$ $\tilde{p}_{11}$and $f_{\rm abs}$ the fraction of the X-rays absorbed in the torus. In case only gas pressure is relevant we can obtain a condition in the radius-density plane:

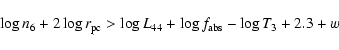\begin{displaymath}\log n_6+2 \log r_{\rm pc} > \log L_{44}+\log f_{\rm abs} - \log T_3 + 2.3 + w \end{displaymath} (5)

where w=0 if the gas is atomic and w=0.3 if molecular. We are now in a position to use our observations to test the hypothesis that the absorbing torus is atomic.

3.1 Compton-thick tori

The X-ray spectrum yields the total column density $\tilde{N}_{\rm H}$. When strong relatively narrow iron lines with EW around 1 keV or more are seen, the torus is likely to be Compton thick with $\tilde{N}_{24} > 1$(Maiolino et al. 1998). In this case the observed X-rays have been reflected or scattered and the intrinsic $L_{\rm X}$should exceed the observed value in the 2-10 keV range by a substantial factor $\zeta$. We conclude that both of our sources have $\tilde{N}_{24} > 1$ and we shall conservatively adopt $\zeta=50$. With this assumption, we have L44=5 for both sources. Taking T3=7 in an atomic torus, $\tilde{N}_{24}=1$ and for the Compton thick case $f_{\rm abs}=1$, we see that Eqs. (2) and (5) are incompatible. We note that this result is independent of $L_{\rm X}$. Thus a high pressure Compton thick torus cannot be atomic if Eq. (4) holds. $\tilde{N}_{24}=1$ is a lower limit to the actual value of $N_{\rm H}$. However, for higher values the discrepancy between Eqs. (2) and (3) increases further.

For a molecular torus $\log \xi_{\rm eff} < -3.4$ and Eq. (5) is trivially satisfied.

We can now complement the information on the total column density coming from the X-ray data with the radio data, which provide constraints on the free-free absorption, $\tau_{\rm ff}$, and the column density of atomic hydrogen $\tilde{N}_{\rm HI}$. If the torus is mainly molecular there is still an atomic zone on the inside, which is responsible for the free-free opacity. Neufeld et al. (1994) give an expression for $\tau_{\rm ff}$which at 1.4 GHz corresponds to

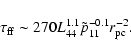\begin{displaymath}\tau_{\rm ff} \sim 270 L^{1.1}_{44} \tilde{p}_{11}^{-0.1} r_{\rm pc}^{-2}. \end{displaymath} (6)

The contribution of the molecular zone to $\tau_{\rm ff}$ is negligible.

Since the nucleus of S5 1946+708 has been observed at 1.4 GHz, the free-free opacity must satisfy $\tau_{\rm ff} \leq 3$. From Eq. (6) we then obtain:

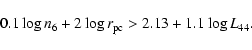\begin{displaymath}0.1 \log n_6+2 \log r_{\rm pc} > 2.13+1.1 \log L_{44}. \end{displaymath} (7)

This inequality is plotted in Fig. 3.

Peck et al. (1999) have measured the HI absorption in front of the nucleus of the source, obtaining for the HI column density log $\tilde{N}_{\rm HI} = 22.5 + \log$ $T_{\rm sp,3}$, with $T_{\rm sp}$ the spin temperature.

At high densities radiative excitation is negligible and in the molecular zone we should have $T_{\rm sp}=T\sim600$ K, or log $\tilde{N}_{\rm HI}=22.3$ which for $\tilde{N}_{24}=1$ requires log( $n_{\rm HI}/n)=-1.7$, or from Eq. (3) log $\xi_{\rm eff}=- 4.8$.

Treating the torus as a uniform layer we should evaluate $\xi_{\rm eff}$ at the mid point N24=0.5. From Eq. (1), we then obtain:

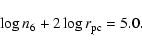\begin{displaymath}\log n_6+2\log r_{\rm pc}=5.0. \end{displaymath} (8)

This corresponds to a line in the n6- $r_{\rm pc}$ plot. Taking into account also the condition on the free-free opacity, only the part of the line with $r_{\rm pc}$larger than given by Eq. (7), corresponds to allowable configurations. So the minimum radius of the torus is about 22 pc. Since Peck et al. found evidence for free-free absorption we should expect the actual value to be not very far from the minimum, corresponding to n6 around 200. This is also suggested by the half thickness of the HI absorption of only 15 pc.

With n6=200 and $\tilde{N}_{24}=1$ the path length through the dense gas is only 0.002 pc. It is therefore likely that such a torus would be composed of small high density clouds or filaments. As stated above, the models being used here are single phase at any given radius. If the absorber is made by dense clouds, there is probably a confining medium which could be relevant in the absorption processes we are studying. We note however that a medium with temperature T> 108 K and density $n_6\sim10^{-3}$ would have the right pressure to confine our clouds, without significantly contributing either to the radio or to the X-ray absorption. A denser, colder (T< 107 K, $n_6\sim0.1)$confining gas could instead be relevant. However, this possibility can be ruled out, for it would imply a very high thermal emission in the soft X-rays, which is not observed.

All the above discussion is focused to the high pressure case. It is worth considering the possibility of a low pressure, low temperature atomic torus. Assuming $\tilde{p}\sim 10^9$ K cm3 and $T_3\sim 0.1$ we still have a relatively high density. This implies that the spin temperature is $\sim$equal to the thermal temperature. Therefore, the relation of Peck et al. (1999) rules out the possibility of a Compton thick torus. We will further discuss this scenario in the case of a Compton-thin torus (Sect. 3.2).

PKS 1934-63: Less information is available for PKS 1934-63. Since no nucleus has been observed at 8 GHz we infer $\tau_{\rm ff}>3$at that frequency, corresponding to $\tau _{\rm ff}>98$ at 1.4 GHz. However since the dynamic range in the 8 GHz observations is not very high this condition may be a bit too strict. From Eq. (7) we then obtain

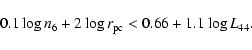\begin{displaymath}0.1 \log n_6+2 \log r_{\rm pc} < 0.66+1.1\log L_{44}. \end{displaymath} (9)

The permitted parameter space for a molecular torus in PKS 1934-63 is therefore the shaded region at the bottom-right of Fig. 3b. The distance of the absorber must be lower than $\sim$4 pc.

The case for an atomic torus in this source can be easily ruled out, using the same equations as above to show that the condition $\log \xi_{\rm eff}>-2$ and Eq. (8) are not compatible.

Some comments are in order. The adopted models are all based on the assumption that the tori in the two sources are Compton thick. We have taken $\tilde{N}_{\rm H}=1$, though the rather uncertain PDS results suggest perhaps even higher values. However as far as we are aware no detailed calculations have been made for tori with N24>1. While a thicker torus would not change $\tau_{\rm ff}$, the inferred $N_{\rm HI}$ might be affected. A second point is that the values of L44 are very uncertain if the sources are indeed Compton thick and might well be larger. And thirdly the basic assumption has been made that the same medium is responsible for the X-ray, free-free and HI absorption.


   \begin{figure} \par\includegraphics[width=7.5cm,clip]{h4021f4.ps}\end{figure} Figure 3: Radius-density diagram for the torus around our radio galaxies. a) S5 1946+708: the permitted parameters are given by the relation between total absorbing column density, HI column density and spin temperature (Peck et al. 1999). The two almost horizontal lines represent the constraints on the free-free opacity. The two points on the left represent a solution with an atomic, Compton thin torus, in the two cases of n6=0.1 and n6=0.001. The dotted lines connecting these points represent a possible solution in the low-density, low pressure regime. b) PKS 1934-63: in the molecular torus case, the allowed region is at the bottom-right of the diagram, and is delimited by the constraints on the ionization parameter $\xi _{\rm eff}<-3.4$, and on the free-free opacity $\tau _{\rm ff}>98$. In the atomic torus case, the condition on the ionization parameter becomes $\xi _{\rm eff}>-2$, while the opacity conditions gives only a constraint on the minimum density. The permitted region (the filled triangle) is however by a large factor incompatible with the requirement for the gas pressure to be equal to or greater than the radiation pressure. The small hatched triangle is obtained in the same way, but assuming a column density $N_{\rm H}=3\times 10^{22}$ cm-2.
Open with DEXTER

3.2 Compton thin tori

From our rather limited X-ray data we have concluded that the EW of K$\alpha$is large in both sources. However in several cases (e.g. 3C 120, Zdziarski & Grandi 2001) the K$\alpha$ line EW has much diminished as better observations and more sophisticated modelling of the continuum were implemented. While our present data are insufficient for the construction of more detailed models, the fact that the strong K$\alpha$ is at less than 90% confidence, indicates that it might be worthwhile to investigate what would happen if the K$\alpha$ EW would come down to values more appropriate for Compton thin sources, this the more so since also variability may have marked effects on the EW (see e.g. 3C 382, Grandi et al. 2001). In the case of S5 1946+708 we then would conclude from Table 3 that, in fact, $\log \tilde{N}_{\rm H}=22.5$. From the data of Peck et al. we have $\log \tilde{N}_{\rm HI}=22.5+\log T_{\rm sp,3}$ and thus for a high pressure atomic torus $\log N_{\rm HI}=23.4$ which is evidently impossible. So the torus should be molecular. With $T_{\rm sp,3}=0.6$ we have $\log \tilde{N}_{\rm HI}=22.3$ and $\log n_{\rm HI}/n =-0.2$, corresponding from Eq. (3) to $\log \xi_{\rm eff}=-3.3$at the mid point of the torus where $\log N_{\rm H}=-1.8$. We have $\zeta=4$ since the absorption is small and $\log L_{44}=-0.2$. From Eq. (1) we then find $\log(n_6 r_{\rm pc}^2)=3.95$ (line labelled " N24=0.03'' in Fig. 3a).

At lower pressures a cool atomic torus becomes a possibility. Since from the data of Peck et al. $\log \tilde{N}_{\rm HI}=22.5+\log T_{\rm sp,3}$ and since now $\log \tilde{N}_{\rm H}=22.5$ we should have $T_{\rm sp,3}=1$. According to the results of Maloney et al. (1996) for n6=0.1 this requires $\log \xi_{\rm eff}=-2.0$ and for n6=0.001, $\log \xi_{\rm eff}=-1.25$. Again taking a one zone model where these values refer to the midpoint $\log N_{\rm H}=22.2$ we obtain from Eq. (1) that for n6=0.1 r=67 pc and for n6=0.001, r=282 pc. From the $\log n - \log r$ plot we see that connecting the two points an extrapolation to higher densities should fit to the line for the molecular torus, which, in fact, is only marginally molecular. The pressures now are very modest: for n6=0.1 we have p11=0.001, a value more representative for the NLR. It may also be verified that $\tau_{\rm ff}$ is of the order of a few times 0.1.

We now analyze the case for Compton-thin absorption in PKS 1934-63. A low energy cut off is not required by our BeppoSAX observations. From our data we estimate $N_{\rm H}<2\times10^{22}$ cm-2. Assuming $N_{\rm H}=2\times10^{22}$ cm-2 we have log  L44=-0.09 and $f_{\rm abs}=0.1$.

With a temperature T=7000 K, the pressure condition for an atomic torus gives:

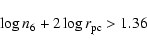\begin{displaymath}\log n_6 +2\log r_{\rm pc} > 1.36 \end{displaymath} (10)

while the condition $\xi _{\rm eff}>-2$ gives:

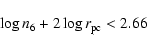\begin{displaymath}\log n_6 +2\log r_{\rm pc} < 2.66 \end{displaymath} (11)

and with the condition $\tau _{\rm ff}>98$ and Eq. (6) we have $\log n_6 >2.3$ and r<1.5 pc.

Therefore in this case an atomic torus is acceptable.

Note however that the pressure condition (Eq. (5)) is not satisfied. Therefore, this scenario is possible only if the absorbing gas is not in a steady state, or other mechanisms contribute to the internal pressure, in addition to the thermal component (for example, magnetic fields).


   \begin{figure} \par {\resizebox{8.8cm}{!} {\includegraphics[clip]{h4021f3.ps}} } \end{figure} Figure 4: Diagnostic diagram for Seyfert 2s of Bassani et al. (1999). We have superimposed the data for a sample of powerful radio galaxies for which a hard X-ray observation and [OIII] and Balmer lines measurements are available. Our two sources lie significantly above the region occupied by both Seyfert 2s and Compton-thin radio loud objects.
Open with DEXTER

The permitted region in the radius-density plane is indicated in Fig. 3b. The pressure is high, $p_{11}\sim 1$, but should be possible at such a small radius.

Some other powerful radio galaxies have data in the literature. Cyg A was discussed by Conway & Blanco (1995) who fit their HI data with an atomic torus with n6<0.2 and $r_{\rm pc}>15$. For a molecular torus Maloney (1996) finds $r_{\rm pc}>50$.

For Hya A Taylor (1996) found HI absorption corresponding to $\log N_{\rm HI}=23.1+\log T_{\rm sp,3}$, while Sambruna et al. (2000) detected an absorbed X-ray nucleus with $\log N_{\rm H}=22.5$ and $\log L(2-10 {\rm keV})=42.2$ (for H0=67 km s-1 Mpc-1). To reconcile the values of $N_{\rm H}$ and $N_{\rm HI}$ we have to take $T_{\rm sp}=250$ K which excludes a high pressure atomic torus with T=8000 K. However from the results of Maloney et al. (1996) at lower pressures we find a fit for n6=0.1 and T=250 K with $\log \xi_{\rm eff}=-2.5$ at the mid point and $r_{\rm pc}=20$. It should be noted, however, that iron K$\alpha$ line has not been measured in this source.

Bassani et al. (1999) have presented an interesting diagram for Seyfert galaxies with as coordinates the equivalent width of the iron lines near 6.5 keV and the ratio of the observed 2-10 keV X-ray flux to the absorption corrected [0III] $\lambda 5007$ flux.

In this diagram (Fig. 4) the Sy2 follow a broad sequence from high $F_{\rm X}/F_{\rm [OIII]}$ and low iron EWto low $F_{\rm X}/F_{\rm [OIII]}$ and high iron EW. The interpretation of this diagram is that as the X-ray absorption increases, the much weaker scattered component with its fluorescent iron lines becomes more conspicuous. Plotting in this diagram the powerful narrow line radio galaxies with adequate data there is perhaps a tendency for the average to be displaced towards higher $F_{\rm X}/F_{\rm [0III]}$ values, with S5 1946+708 the most extreme case. An interesting possibility is that, since our results point to a far absorber, the narrow line clouds emitting the [OIII] line are also partially covered by the X-ray absorber. In this case, using the true [OIII] flux would shift the source to the left in the plot, in the standard region for Compton-thick AGNs. If on the other hand the K$\alpha$ line is not as strong as we found, then S5 1946+708 would come down vertically and fit in with other low absorption objects.

Since in typical Seyferts the ionizing spectrum appears to have a strong "blue bump'' which is probably absent in Liners (like S5 1946+708), thereby causing an unusually low ionization, it may well be that its absence also causes $F_{\rm X}/F_{\rm [0III]}$ to be unusually high. Alternatively since these very compact radio galaxies have been shown in some cases to be very young (thousands of years, Conway 2002) it may be that the NLR has not yet had the time to fully develop. More high quality X-ray spectra are needed to further investigate these possibilities.

4 Concluding remarks

Observations with BeppoSAX seem to show that both PKS 1934-63 and S5 1946+708 are Compton thick sources. This is suggested by the high equivalent width of the iron K$\alpha$ lines (EW>1 keV) and, in the case of PKS 1934-63, by the low X-ray to [OIII] flux ratio.

Powerful radio galaxies with X-ray absorbing column densities higher than 1024 cm-2 are expected on the basis of unified models, but are still rather elusive: to our knowledge, only one such object, 3C 321 (Sambruna et al. 1999) has been observed prior to the present work.

We have used a simple modelization of the absorbing torus (under the hypothesis that the same medium is responsible for both the radio and X-ray absorption) to estimate the density and distance of the nuclear absorber. We find that in PKS 1964-93 the absorber is compact (R< 4 pc) while in S5 1946+708 the distance from the center is higher than $\sim$20 pc.

There are however some problems with the interpretation of the X-ray data as due to Compton-thick sources.

For PKS 1934-63 this does not pose particular problems and, in fact, could serve as an explanation of the absence of a radio core in this compact double. However there remains the difficulty that at 90% confidence the source is variable, which seems in contradiction to it being Compton thick on the basis of the high Fe K$\alpha$ line equivalent width, also with 90% confidence.

For S5 1946+708 there are two problems: the inferred pressure at several tens of pc from the nucleus seems to be anomalously high, while its position in the Bassani et al. diagram suggests a rather low X-ray absorption. Both problems disappear when the source is not Compton thick.

As a consequence of these ambiguities, in our Discussion we have also estimated the physical parameters of the absorbers in the scenario of Compton-thin X-ray absorption.

For most of the radio galaxies the torus appears to have a radius of several tens of pc. Another case where this was suggested on the basis of the radio data alone is PKS 1353-341 (Véron-Cetty et al. 2000). Smaller tori as in the Seyfert galaxies tend to be optically thick in free-free absorption (O'Dea et al. 2000), while those in radio galaxies must in most cases be optically thin since the radio nucleus is observable.

To make further progress higher quality X-ray spectra are needed, while also further VLBI data on HI absorption are required.

Acknowledgements
This work was partially supported by the Italian Ministry for University and Research (MURST) under grant Cofin-00-02-36.

Appendix A: Serendipitous sources

In the field of S5 1946+708 there is another source at 10' distance identified as the ROSAT source 1RXS J194639.7+704552. Wei et al. (1999) have identified this source with a star (B=16.9, R=15.2) at 7'' distance just within the 8''ROSAT error circle. It has an optical spectrum with some absorption features and H$\alpha$ and H$\beta$ in emission. They note another star at 9' (B=15.0, R=13.4) which seems to us an equally valid candidate, and state that it is a cataclysmic variable. We have been unable to locate this variable in the literature. The X-ray spectrum of this source is extremely hard ( $\Gamma=1.1_{-0.2}^{+0.1}$, with F(2-10 keV)  $=2.6\times 10^{-12}$ erg cm-2 s-1). The low energy flux is in agreement with the ROSAT measurement. This source may very well account for the flux measured with the PDS which has a field of view of 50 arcmin (Fig. 5). If so it might further increase the likelihood that S5 1946+708 is not Compton thick. It would be useful to have an optical spectrum of the ROSAT source.
   \begin{figure} \par {\resizebox{8.8cm}{!} {\includegraphics[clip]{h4021f5.ps}} } \end{figure} Figure A.1: Spectrum of the serendipitous source in the field of S5 1946+708.

In the field of PKS 1934-63 there is another source at 5' distance at $\alpha(2000)=19$ 38 56.7 and $\delta(2000)= -63$ 38 2.7. This source is not identified in the literature. With a power law fit we obtain $\Gamma=1.7_{-0.8}^{+0.7}$ and F(2-10 keV)  $=1.5\times 10^{-12}$ erg cm-2 s-1.

References

 

Copyright ESO 2003