A&A 401, 1177-1183 (2003)
DOI: 10.1051/0004-6361:20030131

Atomic data from the IRON Project

LII. Electron excitation of Ni+24[*]

M. C. Chidichimo 1 - N. R. Badnell 2 - J. A. Tully 3


1 - Department of Applied Mathematics, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada
2 - Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK
3 - Observatoire de la Côte d'Azur, Département Gian Domenico Cassini, BP 4229, 06304 Nice Cedex 4, France

Received 31 October 2002 / Accepted 28 January 2003

Abstract
This paper reports on the calculation of collision strengths for electron induced transitions in the beryllium-like ion Ni  XXV whose ground state is $\rm 1s^2~2s^2~ ^{1}S_{0}$. We make use of the R-matrix method in conjunction with the intermediate frame coupling transformation (IFCT). The target has 98 fine structure states ${\rm 1s^2}~nl~n'l'~SLJ$ corresponding to n = 2 and n' = 2, 3, 4. Our calculation extends up to 440 Ry with respect to the ground state. In order to obtain reliable rate coefficients at high temperatures (T above $2 \times 10^7$ K) we have extended our collision strengths to much higher energies by using a variety of techniques, including use of Burgess's interactive code OmeUps. The effective collision strength $\it\Upsilon$ is tabulated against ${\rm log}~T$ for the 45 transitions linking the lowest 10 levels. We also give results for 5 transitions in the X-ray region which are needed in solar studies. The temperature range $6.3 \le \log~ T \le 8.3$ is centred on ${\rm log}~T = 7.1$ which is where this ion has its maximum coronal abundance.

Key words: atomic data


1 Introduction

The raison d'être of the IRON Project (Hummer et al. 1993) was to get a small group of atomic physicists from several institutes to work with a common objective, that of calculating rate coefficients for electron induced transitions between SLJ levels in positive ions. Work has been harmonised by using the same set of computer codes, which arose out of the R-matrix ones described by Berrington et al. (1995). In its ten years existence the project members have generated an enormous amount of data which is described in more than fifty publications. Anyone wishing to have a list of these should visit the web site at http://www.usm.uni-muenchen.de/people/ip/iron-project.html

Here we present results for beryllium-like nickel, Ni+24. In 1992 there appeared a hefty publication by Zhang & Sampson devoted to collisional excitation of this ion, with earlier work by Sampson and his colleagues being reported by Goett et al. (1980). Another team in the United States also produced tables of effective collision strengths (Bhatia et al. 1986). All these earlier calculations made use of distorted wave methods that take account of electron exchange and relativistic effects.

 
Table 1: Radial function parameters for $\rm Ni^{+24}$.

nl		   cjnl Ijnl $\zeta_{jnl}$

1s		   0.98789 1 27.51310
    0.01097 1 48.93450
    -0.00004 2 12.72440
    0.00320 2 21.97850
2s   -0.33875 1 27.51310
    0.00059 1 48.93450
    1.29943 2 12.72440
    -0.30984 2 21.97850
3s   0.36943 1 17.12263
    -3.29172 2 7.29109
    3.76773 3 8.25358
4s   0.25004 1 16.24011
    -3.94079 2 5.78564
    11.62791 3 5.71076
    -8.67396 4 6.16419
2p   0.97880 2 12.84069
    0.02563 2 22.53802
3p   0.93402 2 10.80721
    -1.48168 3 8.15175
4p   0.83985 2 9.55737
    -3.84500 3 6.19587
    3.78083 4 6.20918
3d   1.00000 3 8.46223
4d   1.34954 3 7.16910
    -1.83248 4 6.13833
4f   1.00000 4 6.25668


2 Atomic orbitals for Ni+24

Clementi & Roetti (1973) is an excellent source of atomic wavefunctions and we have used their $\rm 1s, 2s$ radial orbitals while calculating $\rm 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f$ ourselves with the configuration interaction program CIV3 (Hibbert 1975; Hibbert et al. 1991). CIV3 uses analytic radial orbitals Pnl(r) which are expressed as sums of Slater type orbitals as follows :

\begin{displaymath}P_{nl}(r) = \sum_{j=1}^k c_{jnl}~ {{(2 \zeta_{jnl})^{I_{jnl}+... ..._{jnl})!]^{1\over2}}}~ r^{I_{jnl}}~ {\rm exp}(-\zeta_{jnl}~ r).\end{displaymath}

Table 1 shows the values of the coefficients and exponents used in the collision calculation.

3 Target energy levels

We used the program AUTOSTRUCTURE to calculate the energy levels of Ni  XXV and found these tallied well (eight figure agreement) with the level energies produced by the R-matrix code. The energies relative to the ground state for the lowest 98 levels are given in rydbergs (1 Ry = 109737.32 $\rm cm^{-1}$) in Table 2. AUTOSTRUCTURE gives the quantum numbers p, S, L, J of each level as well as the Label (configuration identifier) shown in Table 2.

4 The quality of the target

One way of testing the target is to calculate oscillator strengths with it and see how these compare with those of other investigators. Fawcett (1984, 1985) tabulates weighted oscillator strengths (i.e. gf values) for transitions $n=2 \to n=3$ in many beyllium-like ions, including Ni  XXV. He made use of Robert D. Cowan's code, which is widely thought to provide benchmark data. It is therefore important to compare our results with Fawcett's. Cowan's code only provides the length gauge oscillator strength, which in general is more reliable than the velocity gauge one. In Table 3 we give length gauge line and oscillator strengths for all the allowed transitions occurring amongst the lowest 10 levels. We also include some additional transitions of astrophysical importance. In Table 4 we compare our gf values with those of Fawcett.

5 Effective collision strengths

Our ultimate aim is to tabulate the temperature dependent effective collision strength $\Upsilon(i-j)$, defined by:

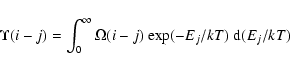
\begin{displaymath}\Upsilon(i-j) = \int_0^\infty \Omega(i-j)~ {\rm exp}(-E_j/kT)~ {\rm d}(E_j/kT) \end{displaymath}

where Ej is the energy of the colliding electron after excitation has occurred and $k = {\rm 6.3335\times 10^{-6}~Ry~deg^{-1}}$ is the Boltzmann constant. We performed the numerical integration by linearly interpolating the $\Omega(i,j)~{\rm exp}(-E_j/kT)$ data points as suggested by Burgess & Tully (1992). In order to try and delineate the resonance structure in the collision strengths we calculated each $\Omega(i-j)$ at between six and seven thousand energy points. Results are given in Table 5 for the 45 transitions between the lowest 10 levels. The temperature range is centered on $1.6 \times 10^7$ degrees which is close to the temperature at which Ni+24 has its maximum abundance under coronal equilibrium conditions (Arnaud & Rothenflug 1985). Our results for $\Upsilon (i,j)$ are given as a function of log T, which is a more convenient choice than T since the temperature in the table varies by two orders of magnitude, from $\rm 10^{6.3}~K$ to $\rm 10^{8.3}~K$.
 
Table 2: Ni  XXV level energies in rydberg units relative to the ground state. Theoretical results from AUTOSTRUCTURE.


\begin{displaymath}\begin{tabular}{lllllllllllllllllll} \hline\hline $i$ & $E(i... ...6 & $\rm 2p4s$ & $\rm ^3P_2^o$ && &&& \\ \hline \end{tabular}\end{displaymath}



 
Table 3: Ni  XXV: line strengths S, oscillator strengths f, $A({\rm s^{-1}})$ values and wavelengths $\lambda({\rm \AA})$ from AUTOSTRUCTURE ( $1.655^{-3} = 1.655 \times 10^{-3}$).

S		   f   A   $\lambda $   Transition
1.655-3   2.096-3   8.106+7   2.398+2   1-3
5.763-2   1.488-1   2.376+10   1.177+2   1-5
7.325-3   2.373-1   6.002+12   9.376+0   1-14
1.320-2   4.293-1   1.094+13   9.339+0   1-15
2.621-2   6.150-2   8.170+9   1.294+2   2-7
2.696-2   1.715-2   1.356+10   1.591+2   3-6
1.891-2   1.400-2   4.999+9   1.367+2   3-7
3.425-2   2.736-2   6.824+9   1.267+2   3-8
2.058-3   2.000-3   7.371+8   1.042+2   3-9
6.960-5   8.407-5   2.395+8   8.382+1   3-10
5.183-2   5.457-1   2.361+13   9.617+0   3-18
3.239-2   1.185-2   4.782+9   1.660+2   4-7
6.592-2   2.644-2   7.682+9   1.515+2   4-8
3.198-2   1.614-2   7.443+9   1.203+2   4-9
1.402-3   2.775-4   2.123+7   5.115+2   5-6
6.763-4   2.043-4   1.213+7   3.352+2   5-7
2.955-2   1.066-2   5.408+8   2.808+2   5-8
9.541-2   5.089-2   5.654+9   1.898+2   5-9
4.253-2   3.273-2   3.781+10   1.316+2   5-10
9.793-4   9.624-3   1.816+12   1.030+1   5-12
5.473-2   5.566-1   2.247+13   9.956+0   5-20



 
Table 4: Ni XXV: comparing the present wavelengths $\lambda $(AS) and weighted oscillator strengths gf(AS) from AUTOSTRUCTURE with those of Fawcett (1984), $\lambda ({\rm F})$ and $gf{ ({\rm F})}$. Wavelengths are in Å.
$\lambda $(AS) $\lambda $(F)   gf(AS) $gf{\rm (F)}$   Transition
9.376 9.381   0.2373 0.21   1-14
9.339 9.341   0.4293 0.45   1-15
9.892 9.917   0.0235 0.027   2-11
9.339 9.347   0.0534 0.084   2-23
9.269 9.172   0.0144 0.014   2-31
9.933 9.957   0.0703 0.077   3-11
9.623 9.632   0.5430 0.54   3-17
9.375 9.382   0.1155 0.16   3-23
9.304 9.206   0.0688 0.082   3-25
9.304 9.312   0.3809 0.51   3-26
9.294 9.302   0.1113 0.12   3-28
9.177 9.187   0.0140 0.01   3-35
10.061 10.082   0.1274 0.13   4-11
9.744 9.748   0.0366 0.036   4-17
9.738 9.743   0.5434 0.53   4-18
9.728 9.734   3.0395 2.98   4-19
9.417 9.421   0.0047 0.01   4-26
9.417 9.314   0.0764 0.096   4-31
9.296 9.300   0.5602 0.75   4-33
9.287 9.294   0.3957 0.45   4-35
10.304 10.321   0.0289 0.032   5-12
9.956 9.966   1.6698 1.82   5-20
10.231 10.233   0.0856 0.077   8-22
10.078 10.080   0.1738 0.16   8-24
9.767 9.770   2.9566 2.95   8-40
10.192 10.194   0.0536 0.048   7-21
10.171 10.174   0.0304 0.028   7-22
10.020 10.023   0.1164 0.11   7-24
10.066 10.073   0.0563 0.055   6-22
10.204 10.204   0.1380 0.13   9-27
9.846 9.853   4.6880 4.88   9-45
10.453 10.454   0.0605 0.054   10-27


We determined effective collision strengths for five additional transitions because of their special astrophysical interest. The transitions are 1-14, 1-15, 3-18, 5-12, 5-20 and results are given in Table 6.

6 A close look at the collision strengths

Figures 1 to 6 show the collision strengths for the 45 transitions between the lowest 10 levels. In each case the energy is measured relative to the final state of the transition, i.e. $\Omega (i,j)$ is plotted against Ej where the index j refers to the upper level. The range covers $0 \le E_j \le 100$ Ry. The ordinate scale is adjusted so that the highest peak touches the top of its box.

The higher a peak the narrower the resonance is likely to be. In order to avoid the possibility of getting unrealistically large contributions to $\Upsilon (i,j)$ from isolated peaks in $\Omega (i,j)$, we used a small constant step in energy of 0.0196418 rydbergs in the interval $0.0193996 \le E_2 \le 132.111$. The computing took nearly 350 hours on a Sun Ultra Enterprise 450 SunOS 5.6, with the output occupying about 15 Mb of computer space after being compressed.

One can see that we have succeeded in catching a few isolated high points, but how many more have succeeded in slipping through the net we cannot tell. One case of special interest is the transition 4-5 for which two peaks are so close to threshold (E5 = 0) that they are indistinguishable from the ordinate axis. We replot both peaks in Fig. 7 where, in order to delineate them, we have increased the number of data points in the two narrow energy intervals where the resonances occur. The inclusion of these additional data points in the collision strength file causes $\Upsilon(4,5)$ to change from 0.0626 at $\log~T = 6.3$ to 0.0382, a decrease of 40 per cent. At $\log~T = 7.1$ the decrease is 15%, which is a lot smaller but still not insignificant.

By altering the scale of the ordinate axis the dense "undergrowth'' caused by resonances can be made visible. Alternatively one can plot the logarithm of $\Omega (i,j)$, as is done in Fig. 8 for the eight transitions shown in Fig. 1. The complicated structure is very impressive but its effect on the thermally averaged collision strengths is often overshadowed by the effect of the isolated peaks which appear clearly in Figs. 1 to 6.

Since the present investigation began, one of us (NRB) has attended to the thorny problem of how best to deal with the resonances that pepper collision strengths. As a result some guidelines have been proposed by Badnell & Griffin (2001) and Badnell et al. (2001). The steplength we used is close to $4 \times 10^{-5}~ z^2 = 0.02304$ Ry, the largest steplength recommended by Badnell et al. (2001). In retrospect we see that a smaller value than this would have been preferable in certain energy intervals covered by our calculation.

7 Some minor surgery

A graphical examination of collision strengths showed that  $\Omega(1,14)$ and $\Omega(1,15)$ are negative over narrow intervals of energy. Since the cause of this is entirely numerical - a collision strength cannot be negative - we simply cut out the unphysical sections and let the collision strengths be constant across the resulting energy gaps. Before the operation the thermally averaged collision strengths are of course smaller, but only by a negligible amount. For example, at $\log~(T) = 6.5 \Upsilon(1,14)$ is 4 per cent down and 1.5 per cent at $\log~(T) = 7.1$.

8 How far to go in energy?

By choosing 22 continuum orbitals to span the spherical R-matrix box, we are able to obtain collision strengths for electrons incident on the ground state with energies not exceeding about 440 Ry. We ran the code at 5 additional points in order to span the interval 132.111 < E2 < 440 Ry in which there are no resonances. However one needs to go to even higher energies than this in order to calculate reliable effective collision strengths at temperatures which are more than about $2 \times 10^7~{\rm K}$. In order to see how far to go in energy we did a simple model calculation of $\Upsilon (i,j)$ assuming $\Omega(i,j)~=~1$ from Ej = 0 up to $E_j = E_{\rm max}$ and zero beyond. By letting $E_{\rm max}=6000~{\rm Ry}$ the error at ${\rm log}~T = 8.3$ is about 1 per cent. From this simple model we see that it is essential to calculate, or estimate, the value of $\Omega (i,j)$ for energies up to several thousand rydbergs. We did this by using the methods proposed by Burgess & Tully (1992). For optically allowed transitions oscillator stengths are needed and these we obtained from AUTOSTRUCTURE, and the results are given along with line strengths S and A values in Table 3. For optically forbidden transitions between levels with the same parity and spin we calculated the high energy Born limits in the manner described by Burgess et al. (1997), hereafter BCT. For optically forbidden intersystem transitions we make use of a comparable method developed by one of us (MCC), see Appendix. NRB has included this method in his well known AUTOSTRUCTURE code. We consider simple examples in Appendix A, showing how to perform the Racah algebra needed when just a few mixed target configurations are used to describe the target. Table 7 shows the results obtained with AUTOSTRUCTURE, in which the method described in Appendix A has been made automatic and therefore includes all the mixed target configurations present in our target. The numerical values of the collision strength given in Appendix A are not as accurate as the results presented in Table 7. Finally, by using Alan Burgess's graphical interactive program OmeUps (see Burgess & Tully 1992), it is possible to make spline fits to the last five data points of $\Omega(i-j)$ and the high energy limit point. This way we obtain values of $\Omega (i,j)$ at 8 energies ranging from 440 Ry to 109 Ry which we deem sufficient for the purpose of thermal averaging.

 
Table 5: $\rm Ni^{+24}$ effective collision strengths ${\it\Upsilon }(i-j)$ for $6.3 \le \log T \le 8.3$ $~(1.837^{-3} = ~ 1.837 \times 10^{-3})$.
i-j 6.3 6.5 6.7 6.9 7.1 7.3 7.5 7.7 7.9 8.1 8.3
1-2 1.837-3 2.018-3 2.068-3 1.942-3 1.681-3 1.360-3 1.046-3 7.747-4 5.575-4 3.929-4 2.726-4
1-3 1.631-2 1.685-2 1.731-2 1.756-2 1.761-2 1.764-2 1.776-2 1.802-2 1.843-2 1.894-2 1.954-2
1-4 1.144-2 1.162-2 1.132-2 1.031-2 8.750-3 6.985-3 5.318-3 3.910-3 2.803-3 1.976-3 1.376-3
1-5 2.801-1 2.908-1 3.048-1 3.226-1 3.444-1 3.705-1 4.006-1 4.341-1 4.699-1 5.068-1 5.450-1
1-6 1.844-4 2.110-4 2.369-4 2.477-4 2.366-4 2.102-4 1.790-4 1.499-4 1.259-4 1.074-4 9.374-5
1-7 1.943-4 2.312-4 2.591-4 2.627-4 2.375-4 1.946-4 1.481-4 1.069-4 7.451-5 5.062-5 3.380-5
1-8 6.326-4 7.018-4 7.508-4 7.585-4 7.250-4 6.703-4 6.156-4 5.721-4 5.422-4 5.239-4 5.140-4
1-9 8.529-4 9.245-4 9.668-4 9.678-4 9.335-4 8.850-4 8.410-4 8.103-4 7.932-4 7.866-4 7.867-4
1-10 6.353-4 7.062-4 7.548-4 7.569-4 7.124-4 6.415-4 5.650-4 4.948-4 4.355-4 3.880-4 3.515-4
2-3 2.749-2 2.439-2 2.172-2 1.887-2 1.569-2 1.243-2 9.458-3 6.960-3 4.991-3 3.509-3 2.432-3
2-4 1.890-2 1.770-2 1.657-2 1.509-2 1.333-2 1.159-2 1.010-2 8.969-3 8.150-3 7.590-3 7.226-3
2-5 5.371-3 6.122-3 6.401-3 6.049-3 5.198-3 4.137-3 3.112-3 2.249-3 1.579-3 1.087-3 7.388-4
2-6 1.232-3 1.245-3 1.242-3 1.174-3 1.032-3 8.483-4 6.603-4 4.932-4 3.573-4 2.531-4 1.765-4
2-7 1.316-1 1.367-1 1.434-1 1.517-1 1.619-1 1.740-1 1.878-1 2.031-1 2.191-1 2.355-1 2.522-1
2-8 3.042-3 3.413-3 3.595-3 3.477-3 3.079-3 2.529-3 1.963-3 1.461-3 1.055-3 7.454-4 5.182-4
2-9 1.454-3 1.888-3 2.034-3 1.900-3 1.587-3 1.221-3 8.875-4 6.199-4 4.218-4 2.820-4 1.864-4
2-10 2.966-4 3.674-4 3.873-4 3.585-4 2.983-4 2.288-4 1.656-4 1.151-4 7.791-5 5.177-5 3.398-5
3-4 7.408-2 6.853-2 6.331-2 5.674-2 4.891-2 4.098-2 3.400-2 2.844-2 2.430-2 2.133-2 1.927-2
3-5 2.751-2 2.582-2 2.416-2 2.160-2 1.816-2 1.446-2 1.108-2 8.326-3 6.236-3 4.725-3 3.667-3
3-6 1.353-1 1.412-1 1.492-1 1.596-1 1.722-1 1.868-1 2.031-1 2.206-1 2.386-1 2.567-1 2.751-1
3-7 9.960-2 1.037-1 1.089-1 1.150-1 1.222-1 1.306-1 1.403-1 1.510-1 1.625-1 1.744-1 1.868-1
3-8 1.799-1 1.874-1 1.963-1 2.065-1 2.183-1 2.322-1 2.486-1 2.672-1 2.877-1 3.091-1 3.316-1
3-9 1.560-2 1.726-2 1.813-2 1.824-2 1.791-2 1.755-2 1.741-2 1.758-2 1.804-2 1.871-2 1.957-2
3-10 1.441-3 1.678-3 1.764-3 1.689-3 1.500-3 1.273-3 1.066-3 9.092-4 8.037-4 7.425-4 7.156-4
4-5 3.822-2 3.679-2 3.482-2 3.120-2 2.615-2 2.063-2 1.554-2 1.135-2 8.129-3 5.771-3 4.103-3
4-6 1.297-3 1.471-3 1.578-3 1.534-3 1.345-3 1.080-3 8.136-4 5.860-4 4.097-4 2.810-4 1.904-4
4-7 1.690-1 1.766-1 1.867-1 1.992-1 2.142-1 2.315-1 2.507-1 2.714-1 2.928-1 3.143-1 3.359-1
4-8 3.425-1 3.576-1 3.769-1 4.005-1 4.286-1 4.613-1 4.982-1 5.385-1 5.806-1 6.233-1 6.669-1
4-9 1.774-1 1.851-1 1.932-1 2.015-1 2.107-1 2.217-1 2.348-1 2.497-1 2.658-1 2.823-1 2.992-1
4-10 3.018-3 3.470-3 3.595-3 3.368-3 2.882-3 2.293-3 1.728-3 1.254-3 8.850-4 6.126-4 4.184-4
5-6 7.162-3 7.917-3 8.767-3 9.685-3 1.074-2 1.195-2 1.327-2 1.461-2 1.590-2 1.712-2 1.827-2
5-7 9.157-3 9.627-3 1.001-2 1.008-2 9.838-3 9.443-3 9.076-3 8.825-3 8.707-3 8.703-3 8.793-3
5-8 1.747-1 1.844-1 1.962-1 2.096-1 2.249-1 2.423-1 2.616-1 2.822-1 3.032-1 3.241-1 3.449-1
5-9 5.264-1 5.493-1 5.781-1 6.132-1 6.553-1 7.045-1 7.598-1 8.193-1 8.803-1 9.407-1 1.000
5-10 2.145-1 2.227-1 2.335-1 2.468-1 2.625-1 2.806-1 3.006-1 3.222-1 3.445-1 3.669-1 3.898-1
6-7 1.731-2 1.959-2 2.051-2 1.955-2 1.705-2 1.384-2 1.065-2 7.886-3 5.684-3 4.023-3 2.813-3
6-8 1.584-2 1.708-2 1.764-2 1.721-2 1.594-2 1.431-2 1.273-2 1.141-2 1.040-2 9.679-3 9.174-3
6-9 4.859-3 6.210-3 6.779-3 6.432-3 5.450-3 4.248-3 3.125-3 2.213-3 1.530-3 1.045-3 7.106-4
6-10 1.615-3 2.142-3 2.415-3 2.347-3 2.013-3 1.572-3 1.148-3 8.022-4 5.436-4 3.612-4 2.370-4
7-8 4.631-2 5.113-2 5.305-2 5.096-2 4.559-2 3.871-2 3.195-2 2.618-2 2.165-2 1.828-2 1.585-2
7-9 3.054-2 3.478-2 3.642-2 3.479-2 3.064-2 2.542-2 2.037-2 1.612-2 1.282-2 1.040-2 8.683-3
7-10 6.308-3 7.518-3 7.909-3 7.410-3 6.285-3 4.932-3 3.656-3 2.604-3 1.803-3 1.224-3 8.198-4
8-9 7.110-2 8.133-2 8.555-2 8.247-2 7.390-2 6.313-2 5.284-2 4.432-2 3.784-2 3.318-2 2.993-2
8-10 1.114-2 1.281-2 1.338-2 1.278-2 1.140-2 9.779-3 8.302-3 7.134-3 6.285-3 5.701-3 5.311-3
9-10 2.010-2 2.186-2 2.282-2 2.277-2 2.200-2 2.101-2 2.017-2 1.963-2 1.936-2 1.927-2 1.928-2



 
Table 6: $\rm Ni^{+24}$ effective collision strengths for further transitions of astrophysical importance.
logT   $\Upsilon(1,14)$   $\Upsilon(1,15)$   $\Upsilon(3,18)$   $\Upsilon(5,12)$   $\Upsilon(5,20)$
6.3   4.138-3   6.108-3   5.272-2   5.685-3   6.329-2
6.5   4.102-3   6.265-3   5.443-2   4.098-3   6.511-2
6.7   4.204-3   6.626-3   5.696-2   2.979-3   6.782-2
6.9   4.502-3   7.304-3   6.083-2   2.236-3   7.208-2
7.1   5.056-3   8.419-3   6.654-2   1.785-3   7.845-2
7.3   5.922-3   1.007-2   7.450-2   1.558-3   8.736-2
7.5   7.140-3   1.234-2   8.499-2   1.504-3   9.901-2
7.7   8.734-3   1.527-2   9.814-2   1.583-3   1.134-1
7.9   1.068-2   1.883-2   1.137-1   1.765-3   1.305-1
8.1   1.296-2   2.297-2   1.315-1   2.025-3   1.497-1
8.3   1.559-2   2.774-2   1.517-1   2.353-3   1.715-1



 
Table 7: $\rm Ni^{+24}$ collision strengths for forbidden transitions in the high energy limit from AUTOSTRUCTURE.

$\Omega(1,6) = 5.901^{-5}$		 $\Omega(1,8) = 5.197^{-4}$ $\Omega(1,9) = 8.311^{-4}$ $\Omega(1,10)= 2.596^{-4}$ $\Omega(2,4) = 6.847^{-3}$ $\Omega(3,4) = 1.488^{-2}$
$\Omega(3,5) = 1.481^{-3}$ $\Omega(4,5) = 5.579^{-4}$ $\Omega(6,8) = 8.134^{-3}$ $\Omega(6,9) = 5.693^{-5}$ $\Omega(6,10)= 1.369^{-6}$ $\Omega(7,8) = 1.023^{-2}$
$\Omega(7,9) = 4.879^{-3}$ $\Omega(8,9) = 2.321^{-2}$ $\Omega(8,10)= 4.601^{-3}$ $\Omega(9,10)= 1.958^{-2}$    



 
Table 8: $\Upsilon (i,j)$ for $T {\rm = 1.2 \times 10^7}$. CBT, present results; BFS, Bhatia et al. (1986); ZS, Zhang & Sampson (1992).

i,j		 CBT BFS ZS   i,j CBT BFS ZS   i,j CBT BFS ZS
1,2 1.71-3 5.99-4 7.98-4   2,9 1.62-3 1.62-4 2.08-4   5,6 1.06-2 1.45-2 1.29-2
1,3 1.76-2 1.46-2 1.39-2   2,10 3.05-4 2.70-5 3.50-5   5,7 9.87-3 7.46-3 7.06-3
1,4 8.93-3 2.83-3 3.85-3   3,4 4.98-2 2.03-2 2.58-2   5,8 2.23-1 5.68-2 2.22-1
1,5 3.42-1 3.45-1 3.43-1   3,5 1.86-2 4.85-3 6.50-3   5,9 6.51-1 6.98-1 6.59-1
1,6 2.39-4 7.70-5 9.61-5   3,6 1.71-1 1.76-1 1.74-1   5,10 2.61-1 2.84-1 2.70-1
1,7 2.41-4 5.20-5 8.68-5   3,7 1.21-1 1.19-1 1.21-1   6,7 1.74-2 6.09-3 8.56-3
1,8 7.30-4 4.10-4 3.77-4   3,8 2.17-1 2.06-1 2.17-1   6,8 1.61-2 9.24-3 1.10-2
1,9 9.38-4 6.04-4 4.97-4   3,9 1.80-2 1.28-2 1.24-2   6,9 5.57-3 8.66-4 1.27-3
1,10 7.19-4 3.08-4 2.59-4   3,10 1.52-3 4.19-4 5.49-4   6,10 1.97-3 1.62-4 2.44-4
2,3 1.60-2 5.52-3 8.16-3   4,5 3.10-2 7.19-3 1.04-2   7,8 4.63-2 2.06-2 2.67-2
2,4 1.35-2 6.29-3 7.34-3   4,6 1.37-3 2.29-4 3.00-4   7,9 3.11-2 1.16-2 1.53-2
2,5 5.30-3 1.36-3 1.94-3   4,7 2.13-1 2.32-1 2.13-1   7,10 6.42-3 1.36-3 2.03-3
2,6 1.04-3 4.00-4 5.39-4   4,8 4.26-1 4.57-1 4.27-1   8,9 7.50-2 3.11-2 3.79-2
2,7 1.61-1 1.68-1 1.63-1   4,9 2.10-1 2.01-1 2.01-1   8,10 1.16-2 4.72-3 5.60-3
2,8 3.13-3 1.14-3 1.52-3   4,10 2.94-3 7.74-4 1.04-3   9,10 2.21-2 1.48-2 1.64-2


9 Comparing present and past

Bhatia et al. (1986), hereafter BFS, give collision strengths for transitions between the lowest 20 levels, but only at one energy, namely E1 = 110 Ry. The temperature of a thermal plasma with this mean energy is given by $110/(1.5 \times 6.3335 \times 10^{-6}) = 1.2 \times 10^7$ degrees Kelvin. This is the temperature at which BFS give level populations in their TABLE IF. Presumably they obtained these results using $\Upsilon(i,j) = \Omega(i,j)$.

Zhang & Sampson (1992), hereafter ZS, give collision strengths for Ej= 19.5075, 52.02, 130.05, 273.105, 520.20, 910.35 Ry. We used linear extrapolation to estimate the value of $\Omega (i,j)$ at Ej = 0 and then thermally averaged the data in order to obtain $\Upsilon (i,j)$ at $T = {\rm 1.2 \times 10^7~K}$. Table 8 is a comparison of the present results (CBT) with those of BFS and ZS.

From Table 8 we see that for optically allowed transitions between states with the same spin multiplicity the agreement between CBT and ZS is excellent. For optically allowed transitions between singlet and triplet states the agreement is almost perfect in the case of (5, 8) where CBT/ZS = 1.004 but otherwise varies from between CBT/ZS = 0.82 for (5, 6) up to CBT/ZS = 2.77 for (3, 10). The excellent agreement between CBT and ZS for (5, 8) is not duplicated by BFS since their result, curiously enough, is almost a factor of 4 smaller.

For the remaining transitions $\Upsilon$(CBT) always exceeds $\Upsilon$(BFS) and $\Upsilon$(ZS) by a factor not exceeding 5, except for the transitions (2, 9), (2, 10) and (6, 10). The reason for this is undoubtedly the neglect by BFS and ZS of resonances, which in our calculation occur in great profusion and have a pronounced effect on the collision strengths of optically forbidden transitions.

Acknowledgements
Dr. Helen E. Mason (Cambridge, UK) drew our attention to the transitions in Table 6 and told us that electron rate coefficients for them are likely to be needed by those studying the Sun at X-ray wavelengths. Alan Burgess (Cambridge, UK), David G. Hummer (Boulder) and Honglin Zhang (Los Alamos) provided us with suggestions for improving the content and presentation. Arati Pai, undergraduate in the Department of Electrical Engineering, University of Waterloo, undertook the running of Burgess's codes and we wish to thank her for assisting us. Finally, MCC acknowledges support by the Natural Sciences and Engineering Research Council of Canada.

References

 

Online Material


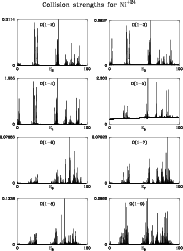 \begin{figure} {% {\psfig{figure=3249.f1.ps,height=22.0cm,width=16cm,angle=0} }}\end{figure} Figure 1: Collision strength $\Omega (i,j)$ vs. final electron energy Ej in rydbergs.
Open with DEXTER


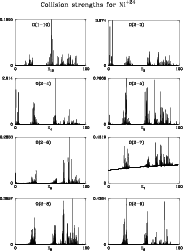 \begin{figure} {% {\psfig{figure=3249.f2.ps,height=22.0cm,width=16cm,angle=0} }}\end{figure} Figure 2: Collision strength $\Omega (i,j)$ vs. final electron energy Ej in rydbergs.
Open with DEXTER


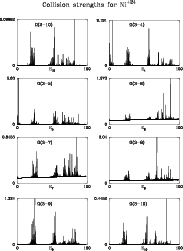 \begin{figure} {% {\psfig{figure=3249.f3.ps,height=22.0cm,width=16cm,angle=0} }}\end{figure} Figure 3: Collision strength $\Omega (i,j)$ vs. final electron energy Ej in rydbergs.
Open with DEXTER


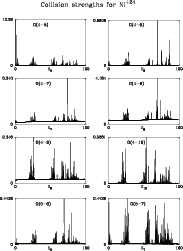 \begin{figure} {% {\psfig{figure=3249.f4.ps,height=22.0cm,width=16cm,angle=0} }}\end{figure} Figure 4: Collision strength $\Omega (i,j)$ vs. final electron energy Ej in rydbergs.
Open with DEXTER


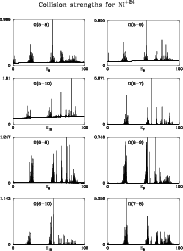 \begin{figure} {% {\psfig{figure=3249.f5.ps,height=22.0cm,width=16cm,angle=0} }}\end{figure} Figure 5: Collision strength $\Omega (i,j)$ vs. final electron energy Ej in rydbergs.
Open with DEXTER


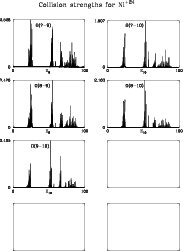 \begin{figure} {% {\psfig{figure=3249.f6.ps,height=22.0cm,width=16cm,angle=0} }}\end{figure} Figure 6: Collision strength $\Omega (i,j)$ vs. final electron energy Ej in rydbergs.
Open with DEXTER


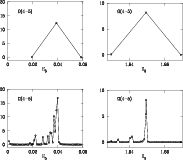 \begin{figure} {% {\psfig{figure=3249.f7.ps,height=14.0cm,width=16cm,angle=0} }}\end{figure} Figure 7: Collision strength $\Omega (4,5)$ vs. final electron energy E5 in rydbergs.
Open with DEXTER


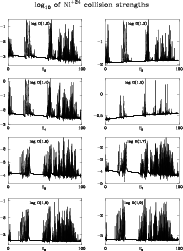 \begin{figure} {% {\psfig{figure=3249.f8.ps,height=22.0cm,width=16cm,angle=0} }}\end{figure} Figure 8: Logarithm of $\Omega (i,j)$ vs. final electron energy Ej in rydbergs.
Open with DEXTER

Appendix A: High energy Born limits: Intercombination transitions and configuration interaction (CI)

Copyright ESO 2003