A&A 401, 927-938 (2003)
DOI: 10.1051/0004-6361:20030184

The HRX-BL Lac sample - Evolution of BL Lac objects[*]

V. Beckmann1,2,3 - D. Engels 1 - N. Bade 1 - O. Wucknitz4


1 - Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
2 - INTEGRAL Science Data Centre, Chemin d'Écogia 16, 1290 Versoix, Switzerland
3 - Institut für Astronomie und Astrophysik, Universität Tübingen, Sand 1, 72076 Tübingen, Germany
4 - Universität Potsdam, Institut für Physik, Am Neuen Palais 10, 14469 Potsdam, Germany

Received 8 April 2002 / Accepted 12 February 2003

Abstract
The unification of X-ray and radio selected BL Lacs has been an outstanding problem in the blazar research in the past years. Recent investigations have shown that the gap between the two classes can be filled with intermediate objects and that apparently all differences can be explained by mutual shifts of the peak frequencies of the synchrotron and inverse Compton component of the emission. We study the consequences of this scheme using a new sample of X-ray selected BL Lac objects comprising 104 objects with z<0.9 and a mean redshift $\bar{z} = 0.34$. 77 BL Lacs, of which the redshift could be determined for 64 (83%) objects, form a complete sample. The new data could not confirm our earlier result, drawn from a subsample, that the negative evolution vanishes below a synchrotron peak frequency $\log \nu_{\rm peak} = 16.5$. The complete sample shows negative evolution at the 2$\sigma$ level ( $\langle V_{\rm e}/V_{\rm a} \rangle = 0.42 \pm 0.04$). We conclude that the observed properties of the HRX BL Lac sample show typical behaviour for X-ray selected BL Lacs. They support an evolutionary model, in which flat-spectrum radio quasars (FSRQ) with high energetic jets evolve towards low frequency peaked (mostly radio-selected) BL Lac objects and later on to high frequency peaked (mostly X-ray selected) BL Lacs.

Key words: BL Lacertae objects: general - X-rays: galaxies


1 Introduction

BL Lac objects are a rare type of Active Galactic Nuclei (AGN), which are observationally distinguished mainly by the absence of strong emission lines. They have strong X-ray and radio emission, and they often show strong variability and optical polarization. Their observational properties are usually explained by a particular line of sight toward the galaxy nucleus, which in BL Lacs is thought to be parallel to a jet emerging from this nucleus.

Two search strategies are commonly used to find BL Lacs. The first is a search for strong X-ray sources with a high ratio of X-ray to optical flux, yielding X-ray selected BL Lacs (XBL). The second is to search among flat spectrum radio sources to find radio selected ones (RBL). As the radio and X-ray surveys got more and more sensitive, the properties of both groups started to overlap, raising the question of how they are related. Padovani & Giommi (1995) noticed that the spectral energy distribution (quantified by $\log \nu L_\nu$) of radio and X-ray selected BL Lacs shows peaks at different frequencies, and suggested that this is the basic difference between the two classes of BL Lacs. They introduced the notation of high-energy cutoff BL Lacs (HBLs) and low-energy cutoff BL Lacs (LBLs). Most, but not all, XBLs are HBLs, while the group of LBLs is preferentially selected in the radio region.

In general, BL Lacs are considered as part of a larger class of objects, the blazars, which have similar properties but show emission lines in addition, and for which this scenario applies as well. Ghisellini et al. (1998) proposed that the range of peak frequencies observed is governed primarily by the efficiency of radiative cooling, and that the other physical parameters strongly depend on it. They found an inverse correlation between the energy of the Lorentz factor of particles emitting at the peaks of the SED ( $\gamma_{\rm peak}$) and the energy density of the magnetic and radiation field of $\gamma_{\rm peak} \propto U^{-0.6}$. This correlation was extended later on for low power (high peaked) BL Lacs by taking into account the finite time for the injection of particles in the jet (Ghisellini et al. 2002). Combined modelling of the time-dependent electron injection and the self consistent radiation transport in jets of high peaked blazars lead to the conclusion that differences in the appearance can be explained by either self-synchrotron or external Compton dominated processes (Böttcher & Chiang 2002). Other studies focussed on the importance of shock events in the blazar jets to explain variability on short timescales (e.g. Bicknell & Wagner 2002). Based on these models the most important factor in the appearance of blazars seems nowadays the energy density of the jet. Maraschi & Tavecchio (2002) showed that this energy density is related to the accretion rate in the AGN disk and proposed that all blazar types have similar black hole masses but that the low power blazars exhibit lower accretion rates.

Unlike all other AGNs, and different from RBLs also, the space density or the luminosity of XBLs showed an increase with time (e.g. Rector et al. 2000). This is called negative evolution. Bade et al. (1998) probed this property with a new ROSAT selected XBL sample and confirmed the negative evolution only for extreme XBLs, e.g. HBLs with very high energy cutoffs ( $\log \nu_{\rm peak} > 16.5$). The result for less extreme XBLs, called intermediate-energy cutoff BL Lacs (IBLs) by Bade et al., was compatible with no evolution. This difference in evolutionary behaviour indicated the presence of a smooth transition between HBLs and LBLs. However, these findings were based on only 39 BL Lacs, prompting us to increase the size of this sample considerably. The results of this effort, the HRX-BL Lac sample presented here, comprises now 77 BL Lacs and is the largest complete XBL sample so far.

Recent models tried to explain the different evolutionary behaviour of HBLs and LBLs by assuming that BL Lacs start as LBLs and evolve into HBLs as they grow older (Georganopoulos & Marscher 1998; Cavaliere & D'Elia 2002). As described by e.g. Padovani & Urry (1990) the spectral energy distributions (SED) of BL Lacs are characterized by two components, both consisting of beamed continuum emission from the plasma of the jets. The first component is synchrotron emission, peaking in the mm to far IR for LBLs. The second component is inverse Compton (IC) emission peaking at MeV energies. HBLs have SEDs peaking in the keV and in the GeV-TeV band respectively. A decrease of power of the jets during the BL Lac evolution would then be accompanied by an increase of the peak frequencies and accordingly a transformation of the LBLs into HBLs (Georganopoulos & Marscher 1998). This model is in fact valid for the whole blazar class: BL Lacs in general show lower power and beaming factors than the Flat Spectrum Radio Quasars (FSRQs), as revealed by e.g. Madau et al. (1987), Padovani (1992), Ghisellini et al. (1993). It naturally explains the different evolution, which is slightly negative for HBLs, slightly positive for LBLs, and clearly positive for the FSRQ/blazar class. This model explains the different types of BL Lac objects only by different global intrinsic power (Maraschi & Rovetti 1994), and not by a different viewing angle. Nevertheless different orientation is probably important as secondary effect necessary to explain the large scatter of observed quantities.

The HRX-BL Lac sample contributes to the discussion with a large and complete sample of X-ray selected BL Lac objects. Previous studies (e.g. Fossati et al. 1998) used a compilation of different BL Lac surveys, like the X-ray selected EMSS (Stocke et al. 1991; Rector et al. 2000), the radio selected 1 Jy BL Lac sample (Stickel et al. 1991; Rector & Stocke 2001), and a FSRQ sample derived from the 2 Jy radio sample of Wall & Peacock (1985) to investigate the overall picture of the blazar class, ranging from the FSRQs to the BL Lac objects. In contrast to this the HRX-BL Lac survey is concentrating on a blazar subclass, the HBLs and IBLs, and is homogeneous in having the same selection criteria for all objects, making it comparable with the REX-survey (Maccacaro et al. 1998; Caccianiga et al. 1999), the DRXBS (Perlman et al. 1998; Landt et al. 2002), and the sedentary multifrequency BL Lac sample (Giommi et al. 1999).

We will describe our selection method of BL Lac candidates in Sect. 2 and the results of the identification process using literature data and own observations in Sect. 3. The spectral energy distribution of the HRX-BL Lac sample is analyzed in Sect. 4, where we demonstrate that for the HBL class the knowledge about the X-ray and optical flux is sufficient to determine the peak frequency of the synchrotron branch. The spatial distribution of the sample is described in Sect. 5. We conclude with a discussion of the compatibility of the results from the HRX BL Lac sample with recent studies.

Throughout the article a cosmology with $H_0 = 50 \rm ~ km ~ s^{-1} ~ Mpc^{-1}$ and a deceleration parameter q0 = 0.5, assuming a Friedmann universe with $\Lambda = 0$, has been used.

 

 
Table 1: Boundaries of the selection area.
Boundaries (J2000.0) Area
$\alpha$ $\delta$ [ $~{\rm deg}^2$]
$7^{\rm h} \le \alpha < 8^{\rm h}$ $30 ^{\circ}< \delta < 85 ^{\circ}$ 426
$8^{\rm h} \le \alpha < 12^{\rm h}$ $20 ^{\circ}< \delta < 85 ^{\circ}$ 2248
$12^{\rm h} \le \alpha < 14^{\rm h}$ $20 ^{\circ}< \delta < 65 ^{\circ}$ 970
$14^{\rm h} \le \alpha \le 16^{\rm h}$ $20 ^{\circ}< \delta < 85 ^{\circ}$ 1124


  
2 BL Lac candidate selection

In the beginning the HRX-BL Lac sample originated from the Hamburg-RASS Bright X-ray AGN sample (HRX), which was created by identification of the ROSAT All-Sky Survey (RASS) with the aid of objective prism plates of the Hamburg Quasar Survey (HQS; Hagen et al. 1995). The BL Lac subsample was selected on an area of $1687 ~{\rm deg}^2$ with a count-rate limit of $hcps \ge 0.075 ~{\rm s}^{-1}$ and on additional $1150 ~{\rm deg}^2$with a limit of $hcps \ge 0.15 ~{\rm s}^{-1}$. This sample was analyzed by Bade et al. (1998) and is referred here as the HRX-BL Lac core sample. It consists of 39 BL Lacs, 34 of which are also part of the present sample.

The fraction of BL Lacs in the HRX was $\sim $10%. Therefore, an increase of the sample size based on optical identification alone is rather inefficient. This can be alleviated using radio information, as all BL Lacs from the core sample were detected as radio sources in the NRAO VLA Sky Survey (NVSS, Condon et al. 1998). Also, to the authors knowledge, all known BL Lac objects do have radio counterparts down to the $\sim $2.5 mJy level, which is similar to the detection limit of the NVSS. We concluded therefore that for the high X-ray count-rates used we can include radio detection in the NVSS as selection criterium without loosing BL Lac objects. As X-ray input we used the ROSAT Bright Source Catalog (RASS-BSC; Voges et al. 1999) with a count-rate limit ( $0.5 {-} 2.0 ~{\rm keV}$) of $hcps \ge 0.09 ~{\rm s}^{-1}$. We cross-correlated this catalogue with the NVSS adopting an error circle of 30 $^{\prime\prime}$ around the X-ray position. We extended the sky area studied to $4768 ~{\rm deg}^2$ encompassing the area of $2837 ~{\rm deg}^2$ studied by Bade et al. (1998), and we applied a unique limit of $hcps \ge 0.09 ~{\rm s}^{-1}$. The boundaries of the area are given in Table 1.

The cross-correlation yielded 223 matches between X-ray and radio sources. The complete list of these objects is given in Table 8 (this table is only availlable in electronic form). The coordinates listed are the X-ray positions (J2000.0). More than 99.9% of the sources have a positioning error $\Delta \le$ 25 $^{\prime\prime}$ (Voges et al. 1999). The column "Name'' lists alternative names to the ROSAT designation, when available. Redshifts and classification are taken from the NED or SIMBAD database or were determined on the base of own follow-up observations. All objects, for which we obtained own data are marked.

The cross correlation might be incomplete for lobe-dominated radio sources, as in those cases the radio emission will consist of more than one component offset from the X-ray position. However, for none of the X-Ray BSC sources we found multiple radio sources within the search radius, and as BL Lacs are core-dominated radio sources no selection biases are expected.

  
3 Classification of BL Lac candidates

3.1 Results from NED and SIMBAD database queries

The 223 candidates were classified in a two-step process. First we searched for known optical counterparts in the NASA/IPAC Extragalactic Database (NED)[*] and in the SIMBAD[*] database. Special care was taken to avoid confusion of BL Bac objects with normal galaxies and other types of AGNs. A database entry of an object as "galaxy'' without spectroscopic information was not accepted as an identification, because nearby BL Lac objects in elliptical galaxies might not have been recognized. For galaxies with redshift information and for objects with "AGN'' or "QSO'' identification but without additional information (e.g. redshift) the original literature was consulted before the object was dismissed as BL Lac.

In total 101 objects could be classified this way[*]. Of the remaining objects a few candidates were classifed as stars on the objective prism plates of the HQS, and another few as obvious clusters of galaxies based on direct plates and on the fact that these sources show extended X-ray emission. For all other candidates follow-up observations were obtained.


   
Table 2: Spectroscopic follow-up observation runs. The last column gives the number of objects observed. Some of the objects were observed several times.
Telescope & Instrument Date #nights Nb

3.5 m Calar Alto (MOSCA)		 March 1997 4 30
WHT / La Palma (ISIS) April 1997 2 19
3.5 m Calar Alto (MOSCA) Feb. 1998 6 89
3.5 m Calar Alto (MOSCA) Feb. 1999 ${\sim} 1^{a}$ 9
a Morning and evening hours of three nights.
b Number of objects observed in this observation run.

3.2 Observations of the remaining unclassified BL Lac candidates

Spectroscopic observations to classify the remaining BL Lac candidates and to determine their redshifts were made with the 3.5 m telescope on Calar Alto equipped with the multiobject spectrograph MOSCA and with the 4.2 m WHT on La Palma equipped with ISIS (Table 2). Most of the results from the 1997 observation runs have already been presented in Bade et al. (1998). For the classification with MOSCA, we used the G500 grism, which covers a wavelength range 4250 - 8400 Å  with a pixel-to-pixel resolution of 12 Å. If necessary, additional spectra were taken with the G1000 and R1000 grisms to determine redshifts. These spectra have a resolution of 6 Å  and cover the ranges 4400-6600 Å  and 5900-8000 Å  respectively. The spectra were reduced in a standard way: bias subtraction, flat-field correction using morning and evening skyflats, and response determination of the detector using spectrophotometric standard stars. BL Lac objects by definition have no or very weak emission lines. Integration times of ${\approx} 1000 \dots 2000~ \rm s$ were needed to detect the weak absorption lines of the host galaxy, which is often out-shined by the non-thermal continuum of the point-like central synchrotron source. Most observations were made under non-photometric conditions.

Optical photometry in the Johnson B band has been obtained for many of the optically faint BL Lacs with the Calar Alto 1.23 m telescope (Beckmann 2000a). Especially for several of the very faint objects ( $B > 20 ~{\rm mag}$) no reliable photometry was available before. For these objects we have now optical magnitudes with an error of $\Delta B \le 0.1 ~{\rm mag}$. For the other objects the acquisition frames of the spectroscopic runs have been used to determine a B magnitude, or values from the literature have been taken. For the brighter objects ( $B < 18 ~{\rm mag}$) also the HQS calibrated objective prism plates have been used, which have an error of $\Delta B \le 0.3 ~{\rm mag}$.

3.3 Results from follow-up observations

Follow-up observations were made of 117 objects, including the unidentified candidates from the BSC/NVSS correlation and additionally a number of objects, which were considered to be promising BL Lac candidates, but did not match the selection criteria described before (e.g. too low X-ray count rate). In total we discovered 53 BL Lac objects according to the classification criteria, which are discussed in Sect. 3.4. As a considerable number of the objects was discovered independently by other groups in the meantime, we are left over with 26 new BL Lacs: 11 from the BSC/NVSS correlation and 15 from the additionally observed objects.

3.3.1 The complete HRX BL Lac sample
The 11 new BL Lac objects discovered among the objects from the BSC/NVSS correlation are marked in Table 8 and their spectra are included in Fig. 8. Based on our spectra we could confirm or revise redshifts for several other BL Lac objects. Five objects from this correlation with other identifications than BL Lac and without NED or SIMBAD entry so far, are marked in Table 8 in addition.

Summarizing, the optical identification of the 223 BSC/NVSS objects leads to the following distribution of object classes within the radio/X-ray correlation (Table 3): 35% are BL Lac objects, 36% are other AGNs (QSO, Seyfert 1/2, FSRQs), 11% galaxies (including starburst galaxies and LINERs), 13% cluster of galaxies, and 4% stars (including 2 supernova remnants). Only a fraction of 1% of the 223 candidates is yet not identified.


 

 
Table 3: Summary of identifications of objects from the BSC/NVSS correlation (cf. Table 8).
object type total number fraction
BL Lac 77 34.5%
Seyfert 1 65 29.1%
Seyfert 2 8 3.6%
Quasar 6 2.7%
blazar 2 0.9%
LINER 5 2.2%
Galaxy cluster 29 13.0%
Galaxies 19 8.5%
Stars 8 3.6%
SNR 2 0.9%
Unidentified 2 0.9%
Total 223  


The 77 BL Lacs from the BSC/NVSS correlation are called the complete HRX BL Lac sample. In comparison to the EMSS BL Lac sample, this sample probes a population of objects with lower $\alpha_{\rm RO}$ and $\alpha _{\rm OX}$ values and contains therefore more radio quiet and stronger X-ray dominated objects. The HRX-BL Lac sample is the largest complete sample of X-ray selected BL Lac objects. Table 4 compares the HRX BL Lac sample with four other X-ray selected BL Lac Surveys: the EMSS based sample (Rector et al. 2000), the sample by Laurent-Muehleisen et al. (1999) based on the correlation of the RASS with the Green Bank radio survey, the REX survey using the NVSS in combination with the sources found in the ROSAT pointed observations (Caccianiga et al. 1999), and the DXRBS (Perlman et al. 1998), which uses the ROSAT data base WGACAT and PMN/NVSS radio data.


   
Table 4: Properties of the Hamburg BL Lac samples in comparison to other recent samples.
sample Reference number of X-ray radio optical
    objects limit limit limit

HRX core sample		 Bade et al. (1998) 39 $0.075/0.15 ~{\rm s}^{-1}$ a,g - -
HRX-BL Lac this work 77 $0.09 ~{\rm s}^{-1}$ a,g $2.5 ~{\rm mJy}^{b}$ -
RGB Laurent-Muehleisen 127 $0.05 ~{\rm s}^{-1}$ a,c $15 \dots 24 ~{\rm mJy}^{d}$ $18.5 ~{\rm mag}^{e}$
RGB complete et al. (1999) 33 $0.05 ~{\rm s}^{-1}$ c $15 \dots 24 ~{\rm mJy}^{d}$ $18.0 ~{\rm mag}^{e}$
EMSS Rector et al. (2000) 41 $2 \times 10^{-13}$ f - -
REX Caccianiga et al. (2002) 55 $4 \times 10^{-13}$ g $2.5 ~{\rm mJy}^{b}$ $B \le 20.5 ~{\rm mag}$
DXRBS Padovani (2001) 30 few $\times 10^{-14}$ c ${\sim} 50 ~{\rm mJy}$ -
a ROSAT All Sky Survey count rate limit.
b NVSS radio flux limit at $1.4 ~{\rm GHz}$.
c Full ( $0.1 {-} 2.4 ~{\rm keV}$) PSPC energy band.
d GB catalog flux limit at $5 ~{\rm GHz}$.
e O magnitude determined from POSS-I photographic plates.
f EINSTEIN IPC ( $0.3{ -} 3.5 ~{\rm keV}$) flux limit in $[{\rm erg} ~ {\rm cm}^{-2} ~ {\rm s}^{-1}]$.
g Hard ( $0.5 {-} 2 ~{\rm keV}$) PSPC energy band.

3.3.2 The extended HRX BL Lac sample
Among the BL Lac candidates observed additionally we could confirm another 27 BL Lac objects, from which 15 did not appear in the literature so far. Together with the 77 BL Lacs from the complete sample they form the extended HRX BL Lac sample comprising 104 objects. The spectra of the 15 new BL Lacs are presented in Fig. 8 together with the 12 new BL Lacs from the complete sample. The spectra of all other objects including those from objects not identified as BL Lacs will be accessible on the web[*].

The properties of the 104 BL Lacs of the extended sample are presented in Table 9 (this table is only availlable in electronic form). The BL Lacs discovered additionally are marked by an asterisk and the new BL Lacs are labeled by "new''. This Table lists the object names, the NVSS radio coordinates (J2000.0), redshifts, ROSAT PSPC (0.5-2.0 keV) X-ray fluxes in $10^{-12}~ {\rm erg} ~ {\rm cm}^{-2} ~ {\rm s}^{-1}$, 1.4 GHz radio fluxes in mJy from the NVSS radio catalogue, B magnitudes, K magnitudes, and the calcium break index. The radio positions have an error of less than 5 $^{\prime\prime}$ (for the faintest objects) and are therefore considerably more accurate than the X-ray positions given in Table 8.

The RASS-BSC fluxes have been computed by using the count rate and a single-power law with free fitted absorption $N_{\rm H}$. The spectral slope and $N_{\rm H}$ are determined by the hardness ratios, a method described by Schartel (1994). The hardness ratio is defined as HR = (H-S)/(H+S) with H and S being the number of counts in the hard and soft energy bands; typically two ratios are computed: HR1 with energy ranges $S = 0.1 {-} 0.4 \rm ~ keV$ and $H = 0.5 {-} 2.0 \rm ~ keV$, and HR2 with $S = 0.5 {-} 0.9 \rm ~ keV$ and $H = 1.0 {-} 2.0 \rm ~ keV$ (Voges et al. 1999). The values for the hardness ratios range by definition from +1 for extremely hard to -1 for very soft X-ray spectra. The error estimate for the $N_{\rm H}$ and $\alpha_{\rm X}$ values is based on the hardness ratios only, not on the photon spectrum itself. Therefore this method does not give $\chi^2$ values, but is able to determine  $68 \% ~ (1 \sigma)$ errors. This is done by exploring the hardness-ratio, spectral slope, and $N_{\rm H}$ parameter space, determining the $1 \sigma$region within it for a given set of parameter components.

The near infrared data are taken from the Two-Micron All-Sky Survey (2MASS, Skrutskie et al. 1995; Stiening et al. 1995). In Table 9 only the K-magnitude is listed, but for the analysis we also used J and H from the 2MASS.

The calcium break index (Ca-break) is defined as follows (Dressler & Shectman 1987):

\begin{displaymath}{\rm Ca{-}break}[\%] = 100 \cdot \frac{f_{\rm upper} - f_{\rm lower}}{f_{\rm upper}} \end{displaymath} (1)

with $f_{\rm upper}$ and $f_{\rm lower}$ being the mean fluxes measured in the 3750 Å  $< \lambda < 3950$ Å  and 4050 Å  $< \lambda < 4250$ Å  objects rest frame band respectively. The measurement of the break was possible only if the redshift was known and if the break was within the spectral range covered by the observation. Therefore break values are available for 30 of the HRX-BL Lac only. In seven cases the break value is negative. This is in most cases due to a low signal to noise of the spectra. Only for one object (1RXS J111706.3+201410) the negative calcium break index is not consistent with a value of 0% and we assume that here the underlying power law of the jet emission outshines the host galaxy, so that the measured negative "break value'' is in fact based on the synchrotron component.

Figure 1 shows the redshift distribution of the HRX-BL Lac extended and complete samples. The mean redshift for the complete and extended sample are $\bar{z} = 0.31$ and $\bar{z} = 0.34$, respectively. We note that in comparison to the core sample no new BL Lacs with z > 0.7 were found, which contribute to the complete sample.

  
3.4 BL Lac classification criteria

The characterizing feature of BL Lac spectra in the optical is the presence of a non-thermal continuum which is well described by a single power law. A second component is the emission of the host galaxy, which contributes absorption features in addition to continuum emission. If the BL Lac itself shows no emission lines at all, redshift determination is only possible by identifying these absorption features. The host galaxies are in majority giant elliptical galaxies (e.g. Urry et al. 2000), having strong absorption features caused by the stellar content.

Expected absorption features in the optical, which can be used for redshift determination, have already been discussed in detail by Bade et al. (1998). The most prominent feature in the spectra of elliptical galaxies is the so-called "calcium break'' at 4000 Å. Its strength is given by the calcium break index, as defined before.

Most of the AGN with emission lines found in the radio/ X-ray correlation are Seyfert type galaxies or LINER (see Table 3). These AGN do not show a calcium break. For the other objects the strength of the calcium break can be used to distinguish between normal elliptical galaxies and BL Lac objects. For the former, this contrast is $\ge$40% with the higher flux to the red side of the break. Our criteria to classify BL Lac objects were defined by Bade et al. (1998) for the core sample and are spectroscopically similar to those applied to the Einstein Medium-Sensitivity Survey (EMSS; Stocke et al. 1991). However, we relaxed the upper limit for the strength of the calcium break index from 25% to now 40% when other properties of the object were consistent with a BL Lac classification. This follows the findings of previous studies (Marchã et al. 1996; Laurent-Muehleisen et al. 1999; Rector et al. 2000) that there exist galaxies with strengths $25\% <$ Ca-break $< 40\%$, which fulfill all other selection criteria for BL Lac objects. Explicitly the selection criteria are now:

With respect to the first criterium no misclassifications are expected as there were no objects found within the BSC/NVSS correlation with weak emission lines and equivalent widths of several 10 Å.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2548.f1} \end{figure} Figure 1: Distribution of redshifts in the extended HRX-BL Lac sample. The hatched part refers to the complete sample.
Open with DEXTER

Borderline cases are more likely with respect to the calcium break index, because the transition between non-active elliptical galaxies and BL Lacs is smooth. This is clearly shown in Fig. 2, in which our measured break strength is plotted vs. the optical luminosity LB, as derived in Sect. 4.2. Both quantities are correlated and almost evenly distributed up to ${\rm Ca{-}break} \sim40\%$.

The observed correlation might be affected by a varying fraction of host galaxy light included in the spectra. In nearby objects the BL Lac host galaxy might not have been fully covered by the slit and therefore the calcium break strength could have been underestimated. However, as the low-redshift objects are mainly the less luminous ones, this effect cannot explain the decreasing strength of the calcium break with increasing luminosities.

This correlation is not only seen in the optical domain, but is also present if we use radio, near infrared or X-ray luminosity instead. In all wavelength regions from the optical to the X-rays the correlation between emitted luminosity and break strength is significant. Therefore we would like to stress the point that the observed correlations are not due to observational selection effects.

Misclassifications might have been occurred also due to large errors for the measured break strengths in some of our spectra with low signal to noise ratio. However for all objects except three of the HRX-BL Lac complete sample the break strengths are <25%, making a misclassification unlikely. The three objects with a calcium break strength in the range $25\% < {\rm Ca{-}break} < 40\%$ are 1ES 0927+500, 1RXS 114754.9+220548, and 1RXS 151040.8+333515 (cf. Table 9) and they were included in the sample, because they fulfill other BL Lac properties, for example strong polarization ($P >6\%$) in the NVSS.


  \begin{figure} \par\includegraphics[width=6.9cm,clip]{2548.f2} \end{figure} Figure 2: Strength of the calcium break versus monochromatic luminosity LB in the optical B-band. Circles refer to the complete sample while triangles mark additional objects found within the course of the work.
Open with DEXTER

  
4 Spectral energy distribution

To study the spectral energy distribution (SED) of the HRX-BL Lac objects, overall spectral indices were calculated to derive general correlations within the sample. Throughout this section the extended sample is analyzed. Ledden and O'Dell (1985) defined the overall spectral index between two frequencies:

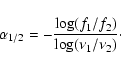\begin{displaymath}\alpha_{1/2} = - \frac{\log (f_{1} / f_{2})}{\log (\nu_{1} / \nu_{2})}\cdot \end{displaymath} (2)

Here f1 and f2 are the fluxes at two frequencies $\nu_{1}$ and $\nu_{2}$. As reference frequencies we used 1.4 GHz in the radio ( $\lambda \simeq 21$ cm), 4400 Å  in the optical ($\sim $B), and $1 ~{\rm keV}$ ( $\lambda \simeq 12.4$ Å) in the X-ray region to derive the optical-X-ray $\alpha _{\rm OX}$, the radio- X-ray $\alpha_{\rm RX}$, and the radio-optical $\alpha_{\rm RO}$ spectral index.

To compare these indices with those from the literature, shifts due to the use of different reference energies have to be taken into account. It can be shown that these shifts are small as long as the spectral shape within each band can be approximated by a single power law and the spectrum is not curved. Because the radio spectra are flat ( $\alpha_{\rm R} = 0$), the flux does not change when different reference frequencies are chosen in the radio domain. But by increasing the radio reference frequency, the $\alpha_{\rm RX}$ and $\alpha_{\rm RO}$ indices steepen. For example, if the reference frequency is changed from 1.4 to 5 GHz the radio-X-ray index changes by 6%: $\alpha_{\rm RX} (5 ~{\rm GHz},1 ~{\rm keV}) \simeq 1.06 \times \alpha_{\rm RX} (1.4 ~{\rm GHz},1 ~{\rm keV})$. If our spectral indices are compared with those using a larger X-ray reference energy, similar values for $\alpha _{\rm OX}$ and $\alpha_{\rm RX}$ are expected. Because of $f_\nu \propto \nu^{-\alpha}$, the expected flux at a higher energy is lower and the flux ratios increase. At the same time however, the frequency interval increases by about the same factor, if we assume $\alpha_{\rm E} = 1$, which is a good approximation for the mean X-ray spectral energy index of BL Lac objects The same reasoning applies for the optical region, where $\alpha_{\rm E} \mathrel{<\kern-1.0em\lower0.9ex\hbox{$\sim$ }}1$, and larger changes of the relevant indices are not expected.

\resizebox{8.3cm}{2.2mm}{The HRX-BL Lac sample shows typical values for the mean} overall spectral indices: $<\alpha_{\rm OX}>~ = 0.94 \pm 0.23$, $<\alpha_{\rm RX}> ~=$ $0.55 \pm 0.08$, $<\alpha_{\rm RO}>~ = 0.37 \pm 0.09$, if compared to Wolter et al. (1998), Laurent-Muehleisen et al. (1999), and Beckmann et al. (2002).

The region in the $\alpha _{\rm OX}- \alpha _{\rm RO}$ plane, which is covered by the HRX-BL Lac sample, is shown in Fig. 3. The center of the area covered by this sample is similar to that of the EMSS BL Lacs (see Padovani & Giommi 1995) though a larger range in $\alpha _{\rm OX}$ and $\alpha_{\rm RO}$ is covered.

4.1 Peak frequency

In order to get a more physical description of the spectral energy distribution of the BL Lac objects, we used a simple model to fit the synchrotron branch of the BL Lac. This has the advantage of describing the SED with one parameter (the peak frequency) instead of a set of three parameters ( $\alpha _{\rm OX}$, $\alpha_{\rm RO}$, and  $\alpha_{\rm RX}$). It has been shown by several authors that the synchrotron branch of the BL Lac SED is well approximated by a parabolic fit in the $\log \nu - \log \nu f_\nu$ plane (cf. Landau et al. 1986; Comastri et al. 1995; Sambruna et al. 1996; Fossati et al. 1998). In this way the peak position ( $\nu_{\rm peak}$), the total luminosity and the total flux of the synchrotron emission can be derived. We chose the parameterization using fluxes $\log \nu f_\nu = a \cdot (\log \nu)^2 + b \cdot \log \nu + c$. Using luminosities instead of fluxes would change the absolute constant c only, leaving the position of the peak frequency unaffected.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2548.f3} \end{figure} Figure 3: The $\alpha _{\rm OX}- \alpha _{\rm RO}$ plane covered by the HRX-BL Lac objects. The points refer to the complete sample, the triangles mark additional objects found within the course of the work. Objects with $\alpha _{\rm RO}< 0.2$ are called radio quiet.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2548.f4} \end{figure} Figure 4: Parabolic fit to the data of B2 0912+29.
Open with DEXTER

If only three data points were given (one in the radio, optical, and X-ray band), the parabola was definite. When more than three data points were available (i.e. the K, H, and J near infrared measurements from the 2MASS), a $\chi^2$ minimization was used to determine best fit parameters. In principle, also the spectral slope in the X-ray band could be used to constrain the fit further. Because of the large uncertainties involved deriving these slopes from hardness ratio in the RASS, they were used mostly for consistency checks. Only in cases, where the parabolic fit resulted in peak frequencies above the highest energies observed, i.e. for objects with $\log \nu_{\rm peak}$ above 2 keV and steep X-ray spectra, the slopes were taken to account. An example for a parabolic fit is shown in Fig. 4. $\nu_{\rm peak}$ is sensitive for the $f_x/f_{\rm opt}$-relation, and is therefore strongly correlated with $\alpha _{\rm OX}$. This is shown in Fig. 5.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2548.f5} \end{figure} Figure 5: Logarithm of the peak frequency vs. $\alpha _{\rm OX}$. The relation was approximated by a polynomial of third degree. The horizontal line marks the distinction between HBLs (above the line) and IBLs used in this paper.
Open with DEXTER

The relation can be approximated by a polynomial of third degree. Using an F-test, parabolic fits of higher degree gave no improvements. Thus the peak frequency can also be determined, in the case no radio data is available by applying

 \begin{displaymath}\log \nu_{\rm peak} = -3.0 \cdot \alpha_{\rm OX}^3 + 13.8 \cd... ...lpha_{\rm OX}^2 - 23.3 \cdot \alpha_{\rm OX}+ 28.5 (\pm 0.51). \end{displaymath} (3)

The standard error ( $\sigma = 0.51$) is based on the deviation of the data points from the fit in Fig. 5. This result is comparable to that found by Fossati et al. (1998) when studying the dependency of $\alpha_{\rm RO}$ and $\alpha_{\rm RX}$ on the peak frequency.

  
4.2 Correlation of luminosities with the SED

A set of physical parameters which are correlated to the peak frequency are the luminosities in the different wavelength regions. To compute luminosities for all objects, the unknown redshifts were set to z = 0.3 which is the mean value for the HRX-BL Lac sample. While the luminosities LR in the radio, LK in the near infrared, and LB in the optical region are decreasing with increasing peak frequency, the situation at X-ray energies is the other way round (as reported also by e.g. Mei et al. 2002; Beckmann 1999a).

The details about the correlation analysis are listed in Table 5, including the confidence level of the correlations.

   
Table 5: Correlation of luminosity with peak frequency in the extended HRX-BL Lac sample.
region rxy Pearson confidence level linear regressiona
  coefficient of correlation  
radio $(1.4 ~{\rm GHz})$ -0.23 >97% $\log L_R = -0.09 \cdot \log \nu_{\rm peak} + 26.4$
near IR (K-band) -0.28 ${>} 95 \%^b$ $\log L_K = -0.14 \cdot \log \nu_{\rm peak} + 25.9$
optical (B-band) -0.37 >99.9% $\log L_B = -0.13 \cdot \log \nu_{\rm peak} + 25.1$
X-ray $(1 ~{\rm keV})$ +0.51 >99.9% $\log L_{\rm X} = +0.19 \cdot \log \nu_{\rm peak} + 17.3$
total (radio - X-ray) -0.12   $\log L_{\rm sync} = -0.04 \cdot \log \nu_{\rm peak} + 22.0$
a Luminosities in $[~{\rm W/Hz}]$.
b The lower confidence level results from the lower number of objects (52) with known K-band magnitudes.
The other correlations are using the 104 BL Lacs of the extended sample.

The total luminosity $L_{\rm sync}$ within the synchrotron branch has been derived by integrating the spectral energy distribution between the radio and the X-ray band. This is a reasonable approximation as long as the peak frequency is below 1 keV ( $\log \nu = 17.4$), but systematically underestimates $L_{\rm sync}$if the peak frequency is shifted beyond $1 ~{\rm keV}$. The relation of peak frequency with the total luminosities does not show a clear correlation.

  
5 Distribution in space

5.1 Ve/Va-test

Redshifts are available for 64 (83%) of the 77 BL Lac objects which form the complete sample. Therefore it is possible to determine a luminosity function for the HRX-BL Lacs and to study the evolution by application of an $V_{\rm e}/V_{\rm a}$-test. The direct images of the BL Lacs without redshift determination show point-like structure, and most of them have optical spectra consistent with high redshifts (z>0.5). The difficulty in determining redshifts for them indicate that these objects are highly core dominated with the host galaxy outshined by the BL Lac core. This implies that the optical luminosity of these objects should be quite high.

The $V_{\rm e}/V_{\rm a}$-test is a simple method developed by Avni & Bahcall (1980) based on the $V/V_{\rm max}$ test of Schmidt (1968). $V_{\rm e}$ stands for the volume, which is enclosed by the object, and $V_{\rm a}$ is the accessible volume, in which the object could have been found (e.g. due to a flux limit of a survey). Avni & Bahcall showed that different survey areas with different flux limits in various energy bands can be combined by the $V_{\rm e}/V_{\rm a}$-test. In the case of no evolution $ \langle V_{\rm e}/V_{\rm a} \rangle = 0.5$ is expected and following Avni & Bahcall (1980) the error $\sigma_m(n)$ for a given mean value $\langle m \rangle = \langle V_{\rm e}/V_{\rm a} \rangle$ based on n objects is:

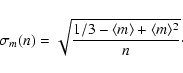\begin{displaymath}\sigma_m(n) = \sqrt{\frac{1/3 - \langle m \rangle + \langle m \rangle^2}{n}}\cdot \end{displaymath} (4)

We computed the accessible volume Va,i for each object by applying the survey limits. In most cases this volume is determined by the X-ray flux limit, only $\sim $10% of the objects have a smaller Va,i for the radio data, due to the radio flux limit of $2.5 ~{\rm mJy}$.

Applied to the complete sample the test yields $\langle V_{\rm e}/V_{\rm a} \rangle = 0.42 \pm 0.04$. This result shows that HBLs have been less numerous and/or less luminous in the past, but the significance is only $2 \sigma$. The negative evolution of X-ray selected BL Lac objects has been reported several times before. We also performed a K-S test in order to determine the probability of uniform $V_{\rm e}/V_{\rm a}$ distribution, which would mean no evolution. For the whole HRX-BL Lac sample the probability of no evolution is rather small (3.5%).

Thanks to the large number of objects with known redshifts within the HRX-BL Lac sample it is possible to examine dependencies of the evolution on other parameters, like the overall spectral indices. A division into two groups (more and less X-ray dominated objects) according to $\alpha _{\rm OX}$ was already made by Bade et al. (1998) for the core sample and resulted in a lower $\langle V_{\rm e}/V_{\rm a} \rangle=0.34\pm0.06$ for the HBLs ( $\alpha_{\rm OX}< 0.9$) than for the IBLs within the sample. The $\langle V_{\rm e}/V_{\rm a} \rangle =0.48\pm0.08$ for IBLs was even consistent with no evolution. Dividing the HRX-BL Lac sample accordingly we now get for the HBLs ( $\alpha_{\rm OX}< 0.9$) $\langle V_{\rm e}/V_{\rm a} \rangle = 0.45 \pm 0.05$(N=34) and for the IBLs $\langle V_{\rm e}/V_{\rm a} \rangle = 0.40 \pm 0.06$(N=30). The difference between the two groups has practically vanished, and we are thus not able to confirm the different types of evolution for the HBLs and the IBLs. But still there are 13 objects within the HRX-BL Lac sample without known redshift, and nearly all of them are IBLs. Including them into the $V_{\rm e}/V_{\rm a}$-test by assigning them either the mean redshift of our sample (z=0.3) or a high redshift (z=0.7) does not change the mean $V_{\rm e}/V_{\rm a}$values significantly. The results of the different $V_{\rm e}/V_{\rm a}$-tests are shown in Table 6. Assigning even higher redshifts would increase the $V_{\rm e}/V_{\rm a}$ for the IBLs, but we consider this unlikely, as the luminosities would then become exceptionally high. For example in 0716+714, PG 1246+586, or PG 1437+398 the X-ray luminosities would exceed values of $L_{\rm X} = 10^{46} \; \rm erg \; s^{-1}$ in the $0.5 {-} 2.0 \; \rm keV$ range.


   
Table 6: Results from the $V_{\rm e}/V_{\rm a}$-tests for the HRX-BL Lac complete sample.
selection unknown z Na $\langle V_{\rm e}/V_{\rm a} \rangle$ $K-S^b ~ [\%]$
  set to      
all (known z) - 64 $0.42 \pm 0.04$ 3.5
all 0.3 77 $0.44 \pm 0.03$ 5.3
all 0.7 77 $0.46 \pm 0.03$ 5.3
HBLs (known z) - 34 $0.45 \pm 0.05$ 24.0
all HBLs 0.3 36 $0.48 \pm 0.05$ 46.1
all HBLs 0.7 36 $0.48 \pm 0.05$ 46.1
IBLs (known z) - 30 $0.40 \pm 0.06$ 14.0
all IBLs 0.3 41 $0.41 \pm 0.05$ 10.7
all IBLs 0.7 41 $0.43 \pm 0.05$ 10.7
a Number of objects used for this test.
b K-S test probability that the $V_{\rm e}/V_{\rm a}$ values have a uniform distribution in the [0...1] interval (probability for no evolution).


   
Table 7: Results from the $V_{\rm e}/V_{\rm a}$-tests for comparable investigations.
survey selection unknown z Na $\langle V_{\rm e}/V_{\rm a} \rangle$
REX total 0.27 55 $0.48 \pm 0.04$
REX HBL 0.27 22 $0.49 \pm 0.06$
sedentary total 0.25 155 $0.42 \pm 0.02$
DXRBS all BL Lacs 0.40 30 $0.57 \pm 0.05$
DXRBS HBL 0.40 11 $0.65 \pm 0.09$
DXRBS LBL 0.40 19 $0.52 \pm 0.07$

a Number of objects used for this test.

We conclude therefore that the HRX sample shows no difference in evolution for HBLs and IBLs. The results presented here are in good agreement with recent other investigations on the evolutionary behaviour of BL Lac objects, as shown in Table 6. Except the sedentary survey (Giommi et al. 1999) none of the studies could confirm the highly significant negative evolution found e.g. by Bade et al. (1998) for the HRX-BL Lac core sample or by Wolter et al. (1994) for the EMSS BL Lacs. The best sample to be compared with should be the REX survey, which also uses the combination of RASS and NVSS data, although going to lower X-ray flux limits while using only the are of the PSPC pointed observation. The REX has also a mean redshift of z = 0.3 and the $\langle V_{\rm e}/V_{\rm a} \rangle$ are within one sigma when compared to the HRX-BL Lac sample.

5.2 X-ray luminosity functions

For the $V_{\rm e}/V_{\rm a}$-test the knowledge of the redshifts is of minor importance. However, the lumminosity function which defines the space density at a given object luminosity can only be derived when having a complete sample with known distances. Based on this function we wish to estimate the fraction of AGN which appear to be BL Lac objects. To determine the cumulative luminosity function (CLF), one has to count all objects within a complete sample above a given luminosity, and divide this number by the volume $V_{\rm a}$ which has been surveyed for these objects. We follow here the procedure described by Marshall (1985) to derive the space density and the corresponding errors. The survey area of the HRX-BL Lac complete sample is $4768 ~{\rm deg}^2$ (Table 1). Because the fraction of objects without known redshift is 17% the effective area which is used to compute the luminosity function is decreased by this fraction to $3959 ~{\rm deg}^2$. This implies that the redshift distribution of the missing objects is the same as for the rest. As discussed before, this assumption might be incorrect, as we expect many of them having rather high redshifts. The effect of different evolution for high and low redshift objects, described in the next paragraph, would be even stronger in this case.

The complete sample is large enough to divide it into a high redshift and a low redshift bin in order to examine possible differences in their CLF. The dividing value was set to the median of the HRX-BL Lac sample $z_{\rm median} = 0.272$. To derive high and low redshift CLFs the accessible volume Va,i for the objects with z < 0.272has been restricted to z = 0.272 whenever $z_{\max,i} > 0.272$. For the high redshift objects the accessible volume was computed from z = 0.272 up to $z_{\max,i}$. The resulting two cumulative luminosity functions are shown in Fig. 6.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2548.f6} \end{figure} Figure 6: Cumulative luminosity function of the two subsamples with z > 0.272 (circles) and z < 0.272 (open triangles).
Open with DEXTER

There seem to be differences between the high and low redshift CLF. The slope of the low redshift CLF is flatter. A linear regression gives a slope of -0.9 while for z > 0.272 the slope is -1.4. But in the overlapping regime at $L_{\rm X}(0.5 {-} 2.0 ~{\rm keV}) \sim 10^{45}$ the luminosity functions show similar slopes.

The left panel of Fig. 7 shows the comparison of the HRX-BL Lac complete sample X-ray luminosity function with the results from the EMSS BL Lac sample (Wolter et al. 1994; Padovani & Giommi 1995). The expected luminosities of the HRX-BL Lacs within the EINSTEIN IPC energy band ( $0.3{ -} 3.5 ~{\rm keV}$) were calculated assuming a spectral slope of $\alpha_{\rm X} = 1.0$. Space densities are given as number of objects per $\rm Gpc^{3}$ and X-ray luminosity bin following Padovani & Giommi (1995). The data from the EMSS are consistent with those from the HRX-BL Lac complete sample within the $1 \sigma$ error bars. The marginal differences can be due to systematic errors for the calculated luminosities in the IPC band because of differing spectral slopes, or resulting from differences in the calibration of the IPC and the PSPC detectors.

In the right panel of Fig. 7 we compare the differential luminosity function of the complete sample with the corresponding function for AGNs at z<0.5. The AGN X-ray luminosity function was taken from the ROSAC sample ("A ROSAT based Search for AGN-Clusters'', Tesch 2000). This AGN sample was constructed similarly as the HRX-BL Lac sample and both samples match closely in brightnesses and redshifts. The ROSAC-AGN sample contains 182 RASS-AGNs with z < 0.5 identified in an area of $363 ~{\rm deg}^2$in the constellation of Ursa Major. The AGN X-ray luminosities have been corrected for the different X-ray band ( $0.1 {-} 2.4 ~{\rm keV}$ instead $0.5 {-} 2.0 ~{\rm keV}$) using the same spectral slopes used for the ROSAC sample.

We find that the space density of BL Lacs in the luminosity range $44 < \log~L_{\rm X} < 46$ is about 10% of the space density of AGNs. In case that all AGNs have jets and would be classified as BL Lacs when looking into their jet, an jet opening angle of ${\sim} 50 ^{\circ}$ would follow. But as the jet emission is expected to be beamed, the BL Lacs appear to be brighter than they are. Following Urry & Shaefer (1984) the observed luminosity is $L_{\rm obs} = \delta^p ~ L_{\rm emi}$ with $L_{\rm emi}$being the emitted luminosity, and

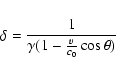\begin{displaymath}\delta = \frac{1}{\gamma ( 1- \frac{v}{c_0} \cos \theta)} \end{displaymath} (5)

where $\gamma$ is the Lorentz factor of the jet emission. p depends on the spectral slope and the jet flow model. For the simple case of a moving blob and continuous reacceleration (Lind & Blandford 1985) which applies e.g. for the model of a wide X-ray jet (Celotti et al. 1993) the exponent is $p = 3 + \alpha$, where $\alpha \simeq 1$ is the spectral index. For a conical jet this exponent is $p = 2 + \alpha$ (Urry & Shaefer 1984). Assuming an jet opening angle of $\theta \sim 30 ^{\circ}$ (Urry & Padovani 1995) and a Lorentz factor $\gamma \sim 5$ the amplification factor is $\delta^p \simeq 50$ (for the conical jet) and $\delta^p \simeq 200$ (for the wide X-ray jet). Correcting the luminosities accordingly yields a fraction of $\le $0.1% BL Lacs among all AGNs. A smaller opening angle and/or larger Lorentz factor would lead to an even lower BL Lac fraction among the AGN.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{2548.f7}\hspace*{1cm} \includegraphics[width=6.5cm,clip]{2548.f8} \end{figure} Figure 7: Left panel: The differential X-ray luminosity function of the HRX-BL Lac complete sample (circles) in comparison to EMSS BL Lacs (triangles; Padovani & Giommi 1995). The X-ray data of the HRX-BL Lac objects have been extrapolated to the EINSTEIN IPC energy band assuming a spectral slope of $\alpha _{\rm X} = 1$. Right panel: Comparison of the X-ray luminosity function of RASS selected AGNs from the ROSAC sample (triangles; Tesch 2000) with HRX-BL Lacs (circles). The density of BL Lacs is $\sim $10 times lower than for all AGNs.
Open with DEXTER

6 Discussion

The large number of objects included in the HRX-BL Lac sample enabled us to study in detail a number of BL Lac properties in different wavelength regions. In the following, we will discuss these properties with special emphasis on their compatibility with the most recent models trying to unify the HBL and LBL objects.

6.1 Strength of the calcium break and luminosities

We observed a clear anti-correlation between calcium break strength and the luminosity in the radio, near infrared, optical, and X-rays bands. We explain this with a wide range of luminosities for the non-thermal source, while the host galaxies seem to have approximately constant luminosity. The higher the luminosity of the central source, the more does the core outshine the hosting galaxy, leading to decreasing break strength with increasing luminosity.

The identification of several HRX-BL Lac with $25\% < {\rm Ca{-}break} < 40\%$ and the smooth extension of the correlation between break strength and luminosities into this range, supports previous findings that BL Lacs can have $\rm Ca{-}break > 25\%$ (Marchã et al. 1996; Laurent-Muehleisen et al. 1999; Rector et al. 2000; Landt et al. 2002) in contrast to earlier suggestions (Stocke et al. 1989).

Landt et al. (2002) studied in detail the dependency of the calcium break strength on the luminosity of the blazars inside the DXRBS sample (Padovani 2001). They found the same correlation as described here for the HRX-BL Lac sample and show that the calcium break values decrease with increasing jet power, and therefore with increasing luminosity. Based on this they conclude that the break value of BL Lac objects could be an indicator of the orientation. Nevertheless different luminosities of the core component (i.e. of the jet) will also play a major role in the effect, and it seems to be difficult to disentangle the influence from different orientation and from different jet luminosity. Thus though we find for the HRX-BL Lac sample the same correlation as described by Landt et al. (2002) we conclude here only that the break strength is an indicator of different apparent luminosity, either based on different orientation, or on different jet power, or on mixture of both effects.

6.2 HBL/LBL: Evolutionary dichotomy?

Most of the results for the HRX-BL Lac core sample (Bade et al. 1998) could be confirmed by the complete sample presented here. The most significant discrepancy are the different results of the $V_{\rm e}/V_{\rm a}$ test. We found negative evolution using the complete sample, but we did not find differences in evolution, if we divide the sample by $\alpha _{\rm OX}$ (or peak frequency).

The results of Bade et al. (1998) could have been arisen from selection effects due to the "patchy'' search area used. A Monte-Carlo simulation done on the HRX-BL Lac complete sample shows however, that this is not the case. By randomly selecting a subsample of 17 BL Lac objects (which is the number of objects for which Bade et al. found different types of evolution) out of the HBLs of the complete sample there is a chance of <1% only to find a $\langle V_{\rm e}/V_{\rm a} \rangle < 0.35$.

Another reason for the different results could be related to the different treatment of the radio properties. As radio detection was not a selection criterium in Bade et al., no radio flux limit was taken into account. Applying here the $V_{\rm e}/V_{\rm a}$-test to the complete sample (cf. Sect. 5), the accessible volume $V_{\rm a}$ was determined for $\approx$10% of the objects by the radio limit. The $V_{\rm e}/V_{\rm a}$ values are correspondingly increased compared to the case where only X-ray flux limit is taken into account, resulting in a less negative evolution. There remains the fact that no BL Lac objects were found yet, with $f_{\rm R} < 2 \; \rm mJy$ radio counterparts and the question is still open whether this is a selection effect or not. It could be that our decision to apply the radio detection as selection criterium weakens the negative evolution found in pure X-ray selected samples.

The result, that the evolution of BL Lac objects of the HBL and IBL type is consistent with no evolution is in good agreement with other recent studies. Neither REX or DXRBS, nor the HRX-BL Lac sample show a difference for the more or less X-ray dominated BL Lacs. On the contrary it seems that the evolution of the IBL might even be slightly more positive than that of the HBL class. This picture clearly differs from the EMSS BL Lac result of $\langle V_{\rm e}/V_{\rm a} \rangle = 0.36 \pm 0.05$, while the sendentary survey, presented by Giommi et al. (1999) seems not be complete enough up to now to draw a firm conclusion. Caccianiga et al. (2002) argue, that the REX might miss the negative evolution of the HBL is not visible simply because the sample is not deep enough, and this argumentation then would also apply for the HRX-BL Lac sample, which X-ray flux limit is about two times higher than that of the REX BL Lacs. Their simulation result in the conclusion that even a completion of the REX survey might not lead to a highly significant negative evolution ($2 \sigma$ for the simulated sample).

Finally, the evolution found in the course of this work is in good agreement with that of FR-I galaxies ( $\langle V_{\rm e}/V_{\rm a} \rangle = 0.40 \pm 0.06$) within the 3CR sample (Laing et al. 1984). This supports the assumption that the FR-I galaxies build the parent population of BL Lac objects (see e.g. Padovani & Urry 1990).

In contrast to HBLs, the LBLs show weak or positive evolution ( $\langle V_{\rm e}/V_{\rm a} \rangle = 0.61 \pm 0.05$) as shown for the 1 Jy sample by Rector & Stocke (2001). Following the sequence of blazars, also FSRQs exhibit significant positive evolution ( $\langle V_{\rm e}/V_{\rm a} \rangle = 0.58 \pm 0.03$ for the 119 FSRQs in the DXRBS sample; Padovani 2001). Also FR-II radio galaxies and "normal'' quasars seem to be more numerous and/or luminous at cosmological distances than in the neighborhood, leaving the question for the reasons of the HBL/LBL evolutionary dichotomy of relevance also in future.

6.3 A unifying model for LBL and HBL

The different evolutionary behaviour of HBLs and LBLs is a challenge for all theories to unify both BL Lac types into one class. However, the existence of transition objects and the numerous similar properties of LBLs and HBLs make it plausible that both classes belong to the same parent population.

As described by Böttcher & Dermer (2002) one way to unify both classes would be a transformation of LBLs into HBLs as the BL Lac objects grow older. In this model, BL Lac objects start as LBLs with jets of high energy densities. Strong cooling limits the electron energies leading to cutoff frequencies for the synchrotron component at optical wavelengths and for the IC component in the GeV energy range. As shown by Beckmann et al. (2002), this results in steep X-ray spectra with strong curvature. The core outshines the host galaxy leading to a low calcium break value (Landt et al. 2002) as seen also for the HRX-BL Lac sample (cf. Fig. 2).

When by the time the source of the jet gets less powerful the energy density within the jet decreases (Tavecchio et al. 1998). The cooling efficiency decreases as well resulting in higher cutoff frequencies for HBLs. The shift of the cutoff frequencies to higher energies is therefore accompanied by decreasing bolometric luminosities, which is evident from the decrease of the luminosities in the radio, near IR and optical bands. Due to the increasing peak frequencies of the synchrotron branch more energy is released in the X-ray band and the X-ray luminosity increases quite in contrast to the luminosities at shorter frequencies (cf. Table 5). The X-ray spectra are correspondingly flatter and less curved than in the LBL state (Beckmann & Wolter 2001).

Objects which do not fit into this scenario are doubtlessly the extremely luminous HBLs, like 1ES 1517+656 (Beckmann et al. 1999b). The scenario presented here assumes the HBLs to be on average less luminous than the LBLs. Apart from the exceptionally high X-ray luminosity, this object also shows an optical luminosity typical for a Flat Spectrum Radio Quasar (FSRQ). Padovani (2001) argues that those high state BL Lacs with high peak frequency might belong to the high energy peaked FSRQ class (HFSRQ), flat-spectrum radio quasars with synchrotron peak in the UV/X-ray band. In this case 1ES 1517+656 should show strong emission lines, e.g. strong H$_{\alpha}$ and H$_{\beta}$ which would be located in the near infrared for this high-redshift BL Lac (z = 0.7) and would have been missed by previous observations.

The HRX-BL Lac sample could be the basis to study the extreme end of the HBL population, the ultra high frequency peaked BL Lac objects (UHBL). Sambruna et al. (1996) argued that objects with cutoff frequencies higher than $10^{18} ~{\rm Hz}$ would be detected only in hard X-ray surveys but should be faint at lower frequencies, which would make their discovery difficult.

Nevertheless HBLs have already been detected at TeV energies, as e.g. 1ES 1426+428 (Aharonian et al. 2002; Horan et al. 2002) and 1ES 1959+650 (Horns & Konopelko 2002). Recently Costamante & Ghisellini (2002) showed that it is possible to select candidates for TeV BL Lacs on the basis of the knowledge of the SED, i.e. strong X-ray flux and a sufficiently strong radio-through-optical flux, which results in high peak frequencies of the synchrotron branch.

Also 13 HBLs within the HRX-BL Lac sample show peak frequencies $\nu_{\rm peak} > 10^{18} ~{\rm Hz}$from the parabolic fit to the synchrotron branch and three objects even $\nu_{\rm peak} > 10^{19} ~{\rm Hz}$. 1RXS J121158.1+224236 might even be a UHBL with a peak frequency of the synchrotron branch at $\nu_{\rm peak} \simeq 10^{22} ~{\rm Hz}$ . To confirm the high peak frequencies, for this extreme source, observations with the BeppoSAX satellite have been performed and results will be presented in a forthcoming paper. Investigations in the gamma region ( ${\sim} 1 ~ {\rm MeV}$) are needed to decide whether these energies are dominated by the synchrotron emission or if already the inverse Compton branch is rising. The SPI spectrograph on-board the INTEGRAL mission (see e.g. Winkler & Hermsen 2000), which has been successfully launched in October 2002, will allow to do spectroscopy in this energy region ( $20 ~{\rm keV}{-} 8 ~ {\rm MeV}$).

Acknowledgements
We would like to thank the anonymous referee for the valuable suggestions which helped us to improve the paper. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology under contract with the National Aeronautics and Space Administration. We acknowledge support by the Deutsche Forschungsgemeinschaft through grants Re 353/39-1 and En 176/23-1.

References

 

Online Material

Appendix: Tables to the HRX-BL Lac sample

Copyright ESO 2003