A&A 401, 733-741 (2003)
DOI: 10.1051/0004-6361:20030032
P. Tanga1,3 -
D. Hestroffer2,![]() - A. Cellino3
- M. Lattanzi3
- M. Di Martino3
- V. Zappalà3
- A. Cellino3
- M. Lattanzi3
- M. Di Martino3
- V. Zappalà3
1 - Laboratoire Cassini, Observatoire de la Côte d'Azur,
BP 4229, 06304 Nice, France
2 -
IMCCE, UMR CNRS 8028, Paris Observatory,
77 Av. Denfert Rochereau 75014 Paris, France
3 -
INAF, Osservatorio Astronomico di Torino,
Strada Osservatorio 20, 10025 Pino Torinese (TO), Italy
Received 19 August 2002 / Accepted 9 December 2002
Abstract
We present the results of the observations of
five Main Belt asteroids and one Trojan obtained using the
Fine Guidance Sensors (FGS) of the Hubble Space Telescope.
For each object, estimates of
the spin axis orientation, angular size and overall shape, as well as
possible indications of a binary structure, are derived. This enables
the computation of new physical ephemerides.
While the data concerning
(63) Ausonia are clearly compatible with a three-axis ellipsoidal
model, other
objects show more complex shapes. (15) Eunomia, (43) Ariadne and
(44) Nysa could in fact be double asteroids, or highly irregular
bodies. The data concerning (624) Hektor are not conclusive as to its
supposed binary nature, even if they agree with the signal of a single
body. The results presented here strongly support the outstanding
capabilities of the FGS for asteroid measurements, provided that the
observations are performed over a sufficient time interval.
Key words: minor planets, asteroids - methods: observational
Our observations show that there is no compelling evidence for well separated or nearly-contact binaries among the objects of our sample. The HST/FGS nevertheless provides important and accurate results on the pole orientation, size, shape, and brightness distribution of these asteroids, hence enabling the computation of a physical ephemeris. The goodness of fit obtained assuming a single triaxial ellipsoid shape varies among the different objects of our sample. While (44) Nysa and (63) Ausonia are very well modeled by prolate spheroids, the data obtained for (15) Eunomia, (43) Ariadne and (624) Hektor show slight but appreciable departures from this ideal shape. (216) Kleopatra is confirmed to have a bi-lobated dumbbell shape (see also Tanga et al. 2001) as suggested by previous observations (Ostro et al. 2000; Marchis et al. 1999).
A methodological discussion on the basic strategy was
presented in Paper I, together with the principles employed in
the data reduction. In this second paper we present the detailed
results
obtained for each of the observed bodies. In Sect. 2 the
observing circumstances are given. The results
are developed in Sect. 3, together with the physical
parameters (pole orientation, shape and size estimate) that have been
derived.
| UTC time of visit | Mag. | Sidereal | Geoc. | Solar | SEP
|
Scans | |||||
| Name | Date | first | last | V | period
|
Dist. | phase |
|
step | # | roll
|
| [h] | [h] | [h] | [AU] | [deg] | [deg] | [mas] | [deg] | ||||
|
(15) Eunomia
|
30 Sep. 98 | 23:30:03 | 00:05:10 | 8.6 | 6.0828 | 1.360 | 20.7 | 126 -8.4 | 1.5 | 4 | 42.1 |
| (43) Ariadne | 22 Aug. 98 | 17:14:45 | 17:51:47 | 10.3 | 5.7620 | 0.958 | 18.6 | 145 +44.4 | 1.0 | 4 | 273.0 |
| (44) Nysa | 05 Sep. 98 | 18:40:09 | 19:17:11 | 10.6 | 6.4214 | 1.638 | 17.2 | 221 -6.5 | 1.0 | 4 | 52.9 |
| (63) Ausonia | 02 Apr. 98 | 16:07:08 | 16:40:32 | 11.7 | 9.2976 | 1.824 | 19.7 | 304 +57.1 | 1.0 | 4 | 287.6 |
| (216) Kleopatra | 13 Jan. 00 | 13:32:59 | 14:11:17 | 10.8 | 5.3853 | 1.529 | 22.4 |
|
1.0 | 2 | 248.7 |
| (624) Hektor | 23 Oct. 98 | 12:03:52 | 12:42:43 | 15.0 | 6.9205 | 4.618 | 9.5 | 313 -32.5 | 2.4 | 6 | 55.1 |
|
(a) Coordinates of the Sub-Earth Point (SEP) with respect to the
asteroid
equator, following the pole coordinates given in
Table 2. The longitude origin is assumed to be at a semi-meridian lying on the plane that contains the major axis, and it is given for the first visit. (b) From P. Magnusson's on-line database: http://www.astro.uu.se/~per (c) Position angle of the FGS-X axis (also called "roll angle'') with respect to the North direction and counted positive toward the East. (d) Last visit on October 1st. |
Due to the limited time-allocation, only a relatively small fraction
(5-10%) of the total spin period, corresponding to the duration of
each orbit, is covered by the observations. Since the main purpose of
this
program was the detection of nearly-contact binary systems, the
asteroids were observed near their predicted light-curve maximum,
approximately corresponding to the maximal apparent separation of
possible components. The observations of each object were carried out
at an
epoch corresponding to a given value of the aspect angle ![]() .
As a
consequence, the complete three-dimensional shape of the asteroids
cannot be completely and unambiguously retrieved. In particular,
assuming for the sake of simplicity that an object is a perfect triaxial
ellipsoid
with axes a>b>c observed at the epoch of the maximum light-curve,
one should
expect that the projected area
on the sky will be an ellipse, having axes equal to a (longest
apparent
axis) and
.
As a
consequence, the complete three-dimensional shape of the asteroids
cannot be completely and unambiguously retrieved. In particular,
assuming for the sake of simplicity that an object is a perfect triaxial
ellipsoid
with axes a>b>c observed at the epoch of the maximum light-curve,
one should
expect that the projected area
on the sky will be an ellipse, having axes equal to a (longest
apparent
axis) and
![]() (shortest axis),
respectively. According to the value of the aspect angle
(shortest axis),
respectively. According to the value of the aspect angle ![]() ,
the
relative contribution of the semiaxes b and c to the corresponding
shortest axis of the projected ellipse varies significantly, although
one
could expect a priori that a pole-on view (leading to full
determination
of b and
complete indetermination of c) is rarely achievable in practice,
whereas
an aspect closer to equatorial view (corresponding to full
determination of
c and complete indetermination of b) is more likely. In principle,
having the possibility to follow an object during a significant
fraction of
its rotation period would lead to a much better determination of the
overall
shape. In our observations, we have tried to maximize the information
coming
from the slow, steady change of the apparent ellipse projected by each
object,
although it is clear that a longer available observation time would
have
allowed us to carry out a much better reconstruction of the true
three-dimensional shapes.
,
the
relative contribution of the semiaxes b and c to the corresponding
shortest axis of the projected ellipse varies significantly, although
one
could expect a priori that a pole-on view (leading to full
determination
of b and
complete indetermination of c) is rarely achievable in practice,
whereas
an aspect closer to equatorial view (corresponding to full
determination of
c and complete indetermination of b) is more likely. In principle,
having the possibility to follow an object during a significant
fraction of
its rotation period would lead to a much better determination of the
overall
shape. In our observations, we have tried to maximize the information
coming
from the slow, steady change of the apparent ellipse projected by each
object,
although it is clear that a longer available observation time would
have
allowed us to carry out a much better reconstruction of the true
three-dimensional shapes.
The recorded signal is an "S-shaped'' curve (usually called an "S-curve'') whose detailed shape depends upon the target size, shape, and surface brightness distribution. As explained in detail in Paper I, the "S-curve'' allows us to distinguish a close binary object, such as those searched for by this observing program. Many examples are shown in this paper (Figs. 7-14) and discussed in the text in the following Sections.
As explained in Paper I, the data over successive scans (corresponding
to less than 5 mn of time) are merged to obtain a higher S/N
ratio. For (624) Hektor, a smoothing of data by low-pass filtering was
performed before merging. A single S-curve is thus obtained for each
FGS axis and each visit. Because the targets were at a few
AU distance, the data were corrected for the
apparent motion of the target during the scan, produced by the
displacement of the HST platform along its orbit![]() . This
correction corresponds to a re-scaling of the FGS-axis
abscissa.
Synthetic S-curves are subsequently calculated by
convolution of a template transfer function with a shape model,
taking into account a specific brightness distribution. Different
template files acquired in 1998 and 1999 have been made available by the
STScI. They were acquired in 1998 and 1999 and correspond to
stars
Upgren 69 (B-V=0.5, file f44v0702m in the calibration
database) and HD 233877 (B-V=1.1, file f43p0501m),
whose color indexes
are close to that of a typical asteroid. No use is made of piecewise
interpolated data, but the value of T(x) for any abscissa x is
obtained by linear interpolation. Except for the asteroid
(216) Kleopatra, the calibration data obtained in 1998 for the
HD 233877 star was used for the transfer function.
. This
correction corresponds to a re-scaling of the FGS-axis
abscissa.
Synthetic S-curves are subsequently calculated by
convolution of a template transfer function with a shape model,
taking into account a specific brightness distribution. Different
template files acquired in 1998 and 1999 have been made available by the
STScI. They were acquired in 1998 and 1999 and correspond to
stars
Upgren 69 (B-V=0.5, file f44v0702m in the calibration
database) and HD 233877 (B-V=1.1, file f43p0501m),
whose color indexes
are close to that of a typical asteroid. No use is made of piecewise
interpolated data, but the value of T(x) for any abscissa x is
obtained by linear interpolation. Except for the asteroid
(216) Kleopatra, the calibration data obtained in 1998 for the
HD 233877 star was used for the transfer function.
Concerning single body shape models, only perfect triaxial ellipsoid shapes have been considered in this analysis. On one hand, this is justified by the purpose of finding basic information on the overall shapes of the objects, avoiding as a first step excessive and unnecessary complexity; on the other hand, the limited coverage of the rotational phase and the single aspect angle covered by the observations do not permit us to analyze much more complex models. As we will see, simple shapes are sufficient, in general, to reproduce the overall features of the observations, and to identify interesting discrepancies when present. Finally, for what concerns possible binarity, we assumed that the binary components are triaxial ellipsoids in synchronous rotation, with major axes mutually aligned and parallel spin axes, accordingly with the original idea of possible equilibrium models suggested by available light-curves (Cellino et al. 1985).
The values obtained for the physical ephemeris and the ellipsoid sizes
are summarized in Table 2. They were computed
assuming uniform surface brightness of the projected asteroid
shape. The error bars of each listed quantity depends critically on
the orientation of the asteroid with respect to the direction of the
two FGS axis. For this reason, details are given in the discussion
concerning each single object. However, in general the formal error
(depending upon the asteroid magnitude) is of the order of a few mas
for the best determined axis, and can be as large as 10-20% for the
less well constrained length![]() . Moreover, these formal errors refer
to the
best-fit ellipsoidal model, which may in principle
differ from the actual shape of the observed asteroid. Last, as
seen in Sect. 2.1, the modeling is based on a limited
variation
of the apparent projected ellipse during each visit as a consequence of
asteroid rotation. In this respect, faster rotations can provide in
principle a better reconstructed shape.
. Moreover, these formal errors refer
to the
best-fit ellipsoidal model, which may in principle
differ from the actual shape of the observed asteroid. Last, as
seen in Sect. 2.1, the modeling is based on a limited
variation
of the apparent projected ellipse during each visit as a consequence of
asteroid rotation. In this respect, faster rotations can provide in
principle a better reconstructed shape.
Our data analysis procedure yields the best-fit
solution for a triaxial ellipsoid assuming a uniform brightness
distribution. Introducing a limb-darkening effect of the surface leads
to
larger resulting sizes with approximately the same goodness of fit.
The
exact function describing this limb-darkening is generally not known
for the
asteroids and cannot be retrieved from our data alone. However, in
order to quantify the uncertainty in the resulting shape and size
determination due to the insufficient knowledge of limb-darkening,
we have performed a separate data reduction by assuming a normalized
brightness
distribution corresponding to a Minnaert's law (Minnaert 1941),
![]() (
(![]() and
and ![]() being the cosine of the
incidence and
reflection angles, respectively) assuming k=0.6(Hestroffer 1998; Parker et al. 2002), i.e., moderate limb-darkening. We
found
that, except for (15) Eunomia, the systematic error on size
estimate is of the order of 3%. Interestingly, we also found that
introducing a limb-darkening effect has no appreciable influence on
the resulting ellipsoid flattening. In other words, while the overall
size
increases slightly for increasing limb-darkening, the change on the
resulting
a/b and a/c ratios tends to be insignificant.
being the cosine of the
incidence and
reflection angles, respectively) assuming k=0.6(Hestroffer 1998; Parker et al. 2002), i.e., moderate limb-darkening. We
found
that, except for (15) Eunomia, the systematic error on size
estimate is of the order of 3%. Interestingly, we also found that
introducing a limb-darkening effect has no appreciable influence on
the resulting ellipsoid flattening. In other words, while the overall
size
increases slightly for increasing limb-darkening, the change on the
resulting
a/b and a/c ratios tends to be insignificant.
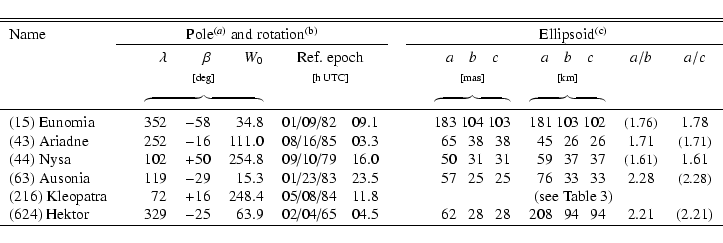
(b) The rotational phase W0 is computed for the reference epoch given on the second line. (c) The ellipsoid's flattening coefficient given in parenthesis is determined with lower precision (see text).
|

|
In the following sections we give, for each asteroid, the results for the duplicity test and the data inversion. The axial ratios of the ellipsoids are compared to the values derived by Magnusson et al. (1994) (and reference therein) on the basis of photometric analyses. The same source provides a set of pole coordinates for each object, as determined by different authors. Coordinate values are normally spread over two intervals of a few degrees, grouped around two independent pole orientations, both compatible with the available photometric data (Taylor 1979). The two orientations differ by about 180 degrees in ecliptic longitude. This is due to the fact that, for both orientations, the same fraction of the asteroid surface is visible from Earth at a given epoch; as a consequence, the integrated disk photometry is the same. However, the orientation of the projected shape of the object on the sky plane is different, therefore high-resolution observations can discriminate between the two solutions. In general, as it will be seen in the detailed discussion about each object, a single pole orientation is consistent with the HST/FGS data. Thus, we are able to eliminate the residual pole ambiguity.
On the other hand, we are not able to provide fully independent improvements of the precise value of pole coordinates, that would require observations over longer time spans, at different aspect angles. Thus, we did not include the pole coordinates in the free parameters of the fit. In fact, our observations (being restricted to a single aspect angle) are mainly sensitive to the projected position of the rotation axis on the sky plane, not its real position in space. Given the large uncertainty (several degrees) affecting the pole coordinates given in Magnusson et al. (1994), we ran several fit solutions, trying to minimize the residuals, for different values of pole coordinates. The values retained for the final fit, listed in Table 2, are always inside the uncertainty interval of the available solutions. Finally, we should note that the different photometrically-derived pole solutions available in the literature are also associated with some corresponding estimates of the axial ratios b/a and c/a, computed from the analysis of the light-curve properties under the general assumption that the objects are triaxial ellipsoids. Our HST observations are able to determine the axial ratios of the objects, given the measured (varying) axial ratios of the projected ellipses in the sky, and assuming different pole solutions. This allows us also to discriminate among different pole solutions in some cases like (43) Ariadne (see below), in which the resulting axial ratios corresponding to one of the pole solutions would be unrealistic (extreme flattening) and totally not compatible with the values derived from the photometry.
A comparison to the asteroid sizes derived by indirect methods, such
as radiometric diameters computed on the basis of IRAS-measured thermal
IR
fluxes, requires one to translate the derived shape parameters
into average radii. In the following we discuss our results by
computing the radius of a sphere equivalent in volume (![]() ).
For a three-axis ellipsoid, we thus have
).
For a three-axis ellipsoid, we thus have
![]() .
.
The data for the diameters comparison are summarized in Table 4. The graphs for the final step of our model fit process - providing the ellipsoid parameters - are given in Figs. 1 to 6. The fits of the derived model to the data ("first step'') follow (Figs. 7 to 12).
The fit with a single-body solution and the pole solution indicated
in Table 2 is acceptable
for the whole set of visits (see Fig. 1).
(15) Eunomia is an almost prolate-spheroid with sizes
![]() km.
The orientation relatively to the FGS axis is such
that the lengths of the a and c axes are well determined.
The ellipsoid flattening is larger than the one derived from the
photometry
(a/b=1.42, a/c=1.6) even if b is not well constrained.
The derived volume corresponds to an effective diameter of 248 km,
close to
the IRAS diameter (255 km).
km.
The orientation relatively to the FGS axis is such
that the lengths of the a and c axes are well determined.
The ellipsoid flattening is larger than the one derived from the
photometry
(a/b=1.42, a/c=1.6) even if b is not well constrained.
The derived volume corresponds to an effective diameter of 248 km,
close to
the IRAS diameter (255 km).
In contrast with the other asteroids of this program, the large size
of
(15) Eunomia, combined with the relatively large solar phase angle,
implies
that introducing a moderate limb-darkening (Minnaert ![]() )
provides
a slightly better goodness of fit to the data.
)
provides
a slightly better goodness of fit to the data.
A more careful analysis of fit residuals provides further insight into the the shape of this object. In fact, it can be seen that the S-curves in the X-axis are particularly asymmetric in comparison to the model. The fit residual, systematically present especially close to the S-curve maximum (Fig. 7), can reflect a shape or brightness-distribution irregularity (i.e. presence of a spot, non convex or non-symmetric shape, etc.). To test this hypothesis, a dark-spot - as was suggested by Lupishko et al. (1984) on basis of photometric data analysis - was introduced in the fitting grid with varying position, relative albedo, and diameter. The residuals - on a single-scan basis - improved considerably on the X-axis, without affecting the fit on the Y-axis. Nevertheless, the best-fit dark-spot is much too large (about 25% of the visible surface) and/or too dark to be realistic. Such model would thus be in complete disagreement with the observed photometric light-curves of this asteroid.
Such a solution being now discarded, a tentative fit with a binary structure and with diameters ratio (secondary/primary) smaller than 0.6 has been done. The residuals of each independent single visit are, again, considerably improved on the X-axis. Nevertheless, no acceptable solution fitting together all data on both X and Y axis, can be found. In conclusion, the available data show that duplicity is not convincingly suggested by the data at our disposal.
It should be stressed that this example clearly illustrates the need
to have more than two single baselines for the interferometer, and
that observations with a different scanning geometry (i.e. different
"roll'' position angle) would be valuable for the shape
reconstruction. As shown in Paper I, an egg-shaped convex profile
(Gaffey & Ostro 1987) or an octants-shape model (Cellino et al. 1989) would
provide features similar to those observed on the present S-curves
(see Fig. 13). In summary, (15) Eunomia is hardly a
binary
system nor a regular ellipsoid, but this work confirms that probably
it has an egg-like shape that could be accurately modeled with more
HST/FGS data.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Movis_EunomiaO.eps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{eunoo_x_1.eps}
\end{figure}](/articles/aa/full/2003/14/aa3023/Timg22.gif) |
Figure 13: Octants shape model for (15) Eunomia on the first visit (top), and interferogram (bottom). |
| Open with DEXTER | |
In contrast to the other asteroids of this program, two different
published
poles yield a possible solution for the triaxial ellipsoid
that adequately fit the data. Nevertheless, the shape
corresponding to one of the two solutions would be unrealistic, being
characterized by
![]() .
As we will discuss in more
detail in a future work, such a flattened body is not compatible with
photometric observations. Our results suggest that (43) Ariadne should
be a
prolate-spheroid with axial lengths
.
As we will discuss in more
detail in a future work, such a flattened body is not compatible with
photometric observations. Our results suggest that (43) Ariadne should
be a
prolate-spheroid with axial lengths
![]() km. At the epoch
of observation, however, (43) Ariadne had an intermediate aspect angle
(with SEP
latitude 44
km. At the epoch
of observation, however, (43) Ariadne had an intermediate aspect angle
(with SEP
latitude 44![]() ), so that the
length of the (c) axis is not well constrained. The
ellipsoid flattening is fairly in agreement with that derived from
photometry (a/b=1.6, a/c=1.8) taking into account the
uncertainty on c. The derived volume corresponds to an effective
diameter of 63 km, close to the IRAS diameter (66 km).
), so that the
length of the (c) axis is not well constrained. The
ellipsoid flattening is fairly in agreement with that derived from
photometry (a/b=1.6, a/c=1.8) taking into account the
uncertainty on c. The derived volume corresponds to an effective
diameter of 63 km, close to the IRAS diameter (66 km).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Movis_AriadneB.eps}\vspace*{3mm}
\includegraphics[width=8.4cm,clip]{ariab_y_9.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg25.gif) |
Figure 14: "Binary'' shape model for (43) Ariadne on the last visit (top), and interferogram (bottom). |
| Open with DEXTER | |
Although the single-ellipsoid model provides an acceptable goodness of fit, the S-curves in the Y-axis exhibit a tendency to a slight, increasing deviation from the model at the end of the observing run (see Fig. 8). In fact, a better goodness of fit is obtained with a binary model in contact where the components diameters are in the ratio 0.35 (see Fig. 14). Such a binary model, however, would not adequately reproduce the observed light-curves, and it is not clear from the available data if the components are actually separated or if (43) Ariadne could be a single object with non-ellipsoidal shape. In particular, the actual shape of the "secondary'' (a sphere here) is not well constrained. More data are certainly needed to refine the overall shape of (43) Ariadne, but for the moment we have strong indication that the asteroid is a bi-lobated or bifurcated non-convex body. In any case, our data reliably reject the tentative model of Cellino et al. (1985) (based on photometric analysis) that predicts a slightly separated binary system having nearly equal components (diameter ratio 0.93).
The fit with a single-body solution and the indicated pole solution is
good for
the whole set of visits (see Figs. 3
and 9). Any ambiguity on the pole coordinates is thus
removed. Nysa is well modeled by a prolate-spheroid of size
![]() km. At the epoch of observation this asteroid was
almost equator-on with a SEP longitude close to 220
km. At the epoch of observation this asteroid was
almost equator-on with a SEP longitude close to 220![]() ,
so that the
major
and minor axis (a and c) are well determined while the
intermediate one b) is poorly constrained. The ellipsoid
flattening is coherent with the one derived from the photometry
analysis (a/b=1.44,
a/c=1.6-2.3) taking into account the inherent
uncertainty on b. The derived volume corresponds to an effective
diameter of 83 km, larger by 16% than the IRAS diameter (71 km).
,
so that the
major
and minor axis (a and c) are well determined while the
intermediate one b) is poorly constrained. The ellipsoid
flattening is coherent with the one derived from the photometry
analysis (a/b=1.44,
a/c=1.6-2.3) taking into account the inherent
uncertainty on b. The derived volume corresponds to an effective
diameter of 83 km, larger by 16% than the IRAS diameter (71 km).
Kaasalainen et al. (2002), from analysis of photometric data, derive a
cone-like shape for (44) Nysa, that they suggest to be the signature of
a
"compound asteroid" consisting of two components of unequal size.
Although there is no strong indication of such a contact-binary
structure in the available HST/FGS data for this object, we
tested this hypothesis by fitting the data with a binary model.
The best-fit solution, given in Fig. 15, is obtained for
a
contact structure with a 0.6 diameter ratio. It is stressed that the
goodness of fit is neither considerably improved nor is it degraded in
this case, and that hence the FGS data alone cannot confirm
or rule out such a solution. A more careful analysis, combining both
photometric and interferometric data, should help to constrain a
possible non-convex model and reveal the actual shape of (44) Nysa.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Movis_NysaB.eps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{nysab_y_b.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg27.gif) |
Figure 15: "Binary'' shape model for (44) Nysa on the last visit (top), and interferogram (bottom). |
| Open with DEXTER | |
The fit of the observations by means of a single triaxial ellipsoid
model
is the best we could find in our sample. In fact, residuals
are very small for the whole set of visits (see
Figs. 4 and 10). (63) Ausonia is not a
binary
asteroid but a regular prolate spheroid with sizes
![]() km.
At the epoch of observation the SEP latitude for (63) Ausonia was
large
(57
km.
At the epoch of observation the SEP latitude for (63) Ausonia was
large
(57![]() ), so that the length
of the smallest axis (c) is poorly constrained. The ellipsoid
flattening is in good agreement with the one derived from the
photometry analysis (a/b=2.2, a/c=2.2), and in particular with
the resulting shape of Zappalà & Knezevic (1984). The derived volume
corresponds to an effective diameter of 87 km, smaller by 16% than
the IRAS diameter (103 km).
), so that the length
of the smallest axis (c) is poorly constrained. The ellipsoid
flattening is in good agreement with the one derived from the
photometry analysis (a/b=2.2, a/c=2.2), and in particular with
the resulting shape of Zappalà & Knezevic (1984). The derived volume
corresponds to an effective diameter of 87 km, smaller by 16% than
the IRAS diameter (103 km).
Unlike the other asteroids of our sample, the observed S-curves of (216) Kleopatra are not consistent with a single triaxial ellipsoid model, but are best explained by a double-lobed shape model with the pole indicated in Table 2 (Fig. 5). The fit procedure is based on assuming an ellipsoidal companion with varying size, flattening, and separation. The best-fit model is obtained by using two similarly sized elongated bodies overlapping each other. Consistently to their volume, we call them "primary'' and "secondary''. The details about this solution are given in (Tanga et al. 2001). This bi-lobated model is coherent with the radar observations of Ostro et al. (2000) and adaptive optics observations of Marchis et al. 1999.
At the epoch of observation the SEP latitude for (216) Kleopatra was
large
(-43![]() ), so that the length
of the smallest axis (c) is poorly constrained. No direct
comparison should be done with the ellipsoid flattening derived from
photometry. Nevertheless the resulting a/b ratio for
the "primary'' and the "secondary'' is of the order of 2.1, which is
still a somewhat high value for such a large asteroid. Due to the
peculiar shape, different from the simple models usually employed to
derive
sizes from thermal data, a comparison with the IRAS diameter can only
be tentative. Taking into account that the two ellipsoids of the model
are overlapping by approximately 10%, the derived volume corresponds
to an effective diameter of 95 km, smaller than the IRAS diameter
(135 km).
), so that the length
of the smallest axis (c) is poorly constrained. No direct
comparison should be done with the ellipsoid flattening derived from
photometry. Nevertheless the resulting a/b ratio for
the "primary'' and the "secondary'' is of the order of 2.1, which is
still a somewhat high value for such a large asteroid. Due to the
peculiar shape, different from the simple models usually employed to
derive
sizes from thermal data, a comparison with the IRAS diameter can only
be tentative. Taking into account that the two ellipsoids of the model
are overlapping by approximately 10%, the derived volume corresponds
to an effective diameter of 95 km, smaller than the IRAS diameter
(135 km).
The fit of the S-curves - while satisfactory - is not as good as for other asteroids in this program (see Fig. 11), and reflects non-modeled shape and/or brightness anomalies. Nevertheless, it is shown in Hestroffer et al. (2002c) that such a simple model of overlapping ellipsoids better reproduces the presently observed S-curves than would the topographic nominal model obtained by Ostro et al. (2000) from inversion of radar data.
The ellipsoid flattening is smaller than the one derived from the
photometric analysis (a/b=2.4, a/c=3.1), but it should be taken
into
account that c is not well constrained. The derived volume would
correspond
to an effective diameter of 245 km. No IRAS diameter
is available for (624) Hektor, but on the other
hand the size
![]() km found here is consistent with
the size estimate (
km found here is consistent with
the size estimate (
![]() km) given by Storrs et al. (1999)
from a deconvolution of HST/WFPC data.
km) given by Storrs et al. (1999)
from a deconvolution of HST/WFPC data.
Fit residuals indicate that there is no strong evidence of a binary structure. However, to test the binary equal-sized double as hypothesized by Hartmann & Cruikshank (1978), a fit with a binary model, with either overlapping or separated components, has also been done. The varying parameters are the diameters of the primary and of the secondary, and their separation.
This model does not improve fit residuals in comparison to the single
ellipsoid. Due to the geometry of our observations, the data on the
FGS X-axis are not very sensitive to a binary structure (see
Paper I). The best fit is obtained for a "binary'' with two
overlapping components and with a relatively large diameter ratio
(0.9), thus for a shape that, given the resolution of the instrument,
is not significantly different from that of a single ellipsoid (see
Fig. 16). Thus, our HST/FGS data do not
conclusively reject the hypothesis of a dumbbell-shape made of two
large and similarly sized bodies. The data S/N ratio together with the
limited (u,v) plane coverage are not high enough to separate those
two shape models. Nevertheless our analysis suggests that a
single-ellipsoid model better matches the data. Observations with the
recently installed astrometer FGS#1, providing higher S/N
ratio,
would be helpful for a better reconstruction of the shape of (624) Hektor.
| Name | IRAS | Ellipsoid
|
| (15) Eunomia | 255 | 248 |
| (43) Ariadne | 66 | 63 |
| (44) Nysa | 71 | 83 |
| (63) Ausonia | 103 | 87 |
| (216) Kleopatra | 135 | 95 |
| (624) Hektor | - | 245 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Movis_HektorB.eps}\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{hektb_x_9.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg32.gif) |
Figure 16: "Binary'' shape model for (624) Hektor on the last visit (top), and interferogram (bottom). |
| Open with DEXTER | |
Considering that the S/N ratio measured on the averaged S-curves is >10 for all the objects, with the exception of (624) Hektor, the technique of data reduction proves to be sufficient to extract relevant shape information from our data. As explained in Paper I, we recall here that, when fit residuals are as low as in the case of (63) Ausonia, the sensitivity of size estimates reach a level of 1-2 mas, at least on favorably projected directions.
The available data allow us to test the binary structure hypothesis, providing valuable information on the asteroid size. For instance the tentative binary models of Cellino et al. (1985), that would be in satisfactory agreement to observed light-curves, would give too large diameters ratio to be coherent with our HST/FGS data. Also, the inversion procedure applied here, which considered only ellipsoidal figures, provides good indication on the presence of unmodeled shape and/or brightness anomalies, as it can be seen in the cases of (15) Eunomia and (63) Ausonia.
None of the asteroids of this program appears to be a well separated or nearly-contact binary system, with components of similar size, as expected from a binary fission model. Except for (216) Kleopatra, which is best represented as two overlapping ellipsoids (hence resembling a nearly-contact binary structure), the observed asteroids turn out to be, on average, not very different from single triaxial ellipsoids, although some appreciable discrepancies with such a simple shape model are apparent in some cases, as quoted above. For instance, a better fit solution is obtained for (15) Eunomia when considering a single egg-like shaped convex body, while for (43) Ariadne, a contact-binary non-convex shape would provide a better fit to the data. Kaasalainen et al. (2002) give a convex conical shape-model of (44) Nysa that they suggest to be the signature of a contact structure whose components have different sizes. A more extensive test of such an hypothesis from the HST/FGS data will be done in a forthcoming work.
As for the absolute precision of the size measurements, those derived represent probably lowest boundary values, since we considered uniform brightness distributions. In fact, introducing an a priori limb-darkening would result in slightly larger sizes. Adopting a realistic Minnaert parameter of k=0.6 the size is approximately 3% larger. This would lead to an improved agreement with nominal IRAS results, but in cases, like (216) Kleopatra, in which the resulting shape is very far from a sphere. It is also clear, in any case, that a better determination of the most uncertain axis lengths would be needed to carry out a more detailed comparison with published size data.
In this respect, a whole shape reconstruction at the highest precision reachable by HST/FGS would offer a precious insight on the real shape of these asteroids. Unfortunately, our model-fitting inversion procedure is limited by the short available observing time. This was generally long enough to provide useful indications on the three-dimensional shape of the bodies, but it was nevertheless shorter than 10% of the rotation period. Moreover, our observations of each object were limited to a single value of the aspect angle. Obviously, more data covering different observing geometries could allow us to retrieve a more complete model of asteroid shapes at the available resolution. In particular, observations made at different aspect (and rotation) angles could be combined to eliminate the limited resolution that is possible in the determination of some of the principal axes. A further level of investigation will require us also to combine HST data with observations made by other techniques (e.g. radar observations Hudson & Ostro 1994 or light-curve inversion Kaasalainen & Torppa 2001). For instance, light-curve amplitudes can help to constrain the surface scattering parameters for a given ellipsoid. Furthermore, photometry can suggest asymmetric shapes that could justify the differences observed between primary and secondary extrema. This refinements represent, in fact, the next step in an analysis that should eventually lead to a reduction process that takes consistently into account, both photometry and HST/FGS interferograms at the same time.
The reduction of the residual uncertainties would allow us to compare the
obtained models to the equilibrium figures for fluid bodies (rubble
piles) as
suggested by Farinella et al. (1981). The available data seem to indicate
that the observed asteroids would resemble prolate spheroids (i.e. ![]() ), which, although not being part of the Jacobi sequence, would
suggest low bulk densities. When dealing with rubble pile structures,
which are not ideal fluid bodies,
however, one should also consider the possible role of internal
friction, as suggested by Holsapple (2001), leading to
more realistic bulk-densities and macroscopic porosities.
), which, although not being part of the Jacobi sequence, would
suggest low bulk densities. When dealing with rubble pile structures,
which are not ideal fluid bodies,
however, one should also consider the possible role of internal
friction, as suggested by Holsapple (2001), leading to
more realistic bulk-densities and macroscopic porosities.
Due to the rotation of the asteroids around their axis, not only can the sky-projected profile be measured, but it is also possible to infer information about the fully three-dimensional shape, provided that some pole solution can be found to be consistent with FGS data. Moreover, wrong pole solutions can be rejected and nearly-contact binary asteroids revealed. Results are expected to be even better using the upgraded and more sensitive FGSR#1. Depending on the geometry of the observations, the lengths of the principal axes of the bodies cannot all be determined with the same precision, but observations at different epochs would efficiently overcome such limitations.
The inversion procedures applied here have proved to be solid, being able to provide best-fit ellipsoidal figures and to test alternative, more complex models. Some evolved binary structures cannot be completely ruled out for some of the objects of our sample based on the available data, although single ellipsoidal shapes are generally a good first approximation of what we have observed. While we hope to obtain new HST/FGS data in the future, we are confident that more detailed analyses of data coming from different sources, including the data presented in this paper, will likely provide stricter constraints to the overall shapes and internal structures of large asteroids and to their past collisional evolution.
Acknowledgements
We are grateful to the FGS team at the STScI, in particular E. Nelan and D.C. Taylor. Important help concerning data reduction and modeling has been provided by D. Loreggia (OATo), F. Gugliemetti (currently at IMPRS, Munich) and J. Berthier (IMCCE). P. Descamps (IMCCE) kindly put at our disposal "MOVIS'', the shape modelling and visualization software. D. Hestroffer acknowledges funding from the OATo, and P. Tanga the support of the H. Poincaré fellowship of the Observatoire de la Côte d'Azur.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{euno_size.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg34.gif) |
Figure 1: (15) Eunomia size 2nd step fit with a single triaxial ellipsoidal model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aria_size.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg35.gif) |
Figure 2: Same as Fig. 1 for (43) Ariadne. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{nysa_size.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg36.gif) |
Figure 3: Same as Fig. 1 for (44) Nysa. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{auso_size.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg37.gif) |
Figure 4: Same as Fig. 1 for (63) Ausonia. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{kleo_size.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg38.gif) |
Figure 5: Same as Fig. 1 for (216) Kleopatra "primary''. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hekt_size.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg39.gif) |
Figure 6: Same as Fig. 1 for (624) Hektor. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{euno_fit.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg40.gif) |
Figure 7: Fit of the merged S-curve for (15) Eunomia, on both FGS axis, with a single tri-axial ellipsoidal model. Observations were carried out with the PUPIL filter on Sept. 30, 1998. Graphs are given for some selected visits. The template from observations of the star HD 233877 was used in data reduction. The graphs in the inset give the residuals (note the scale change on the ordinates). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{aria_fit.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg41.gif) |
Figure 8: Same as Fig. 7 for (43) Ariadne on Aug. 22, 1998. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{nysa_fit.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg42.gif) |
Figure 9: Same as Fig. 7 for (44) Nysa on Sept. 5, 1998. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{auso_fit.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg43.gif) |
Figure 10: Same as Fig. 7 for (63) Ausonia on Apr. 2, 1998. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{kleo_fit.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg44.gif) |
Figure 11: Same as Fig. 7 for (216) Kleopatra on Jan. 13, 2000, and with two overlapping ellipsoids. Here observations are carried out with the FGSR#1 astrometer, and the modeled S-curve is obtained with a template from the star Upgren 69. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm]{hekt_fit.eps}\end{figure}](/articles/aa/full/2003/14/aa3023/Timg45.gif) |
Figure 12: Same as Fig. 7 for (624) Hektor on Oct. 23, 1998. |
| Open with DEXTER | |