A&A 401, 631-637 (2003)
DOI: 10.1051/0004-6361:20030061
An abnormal radiant luminosity of the contact binary GZ Andromedae and
its possible explanation
Y. Yang - Q. Liu
National Astronomical Observatories/Yunnan Observatory, Chinese Academy of Sciences,
Kunming, Yunnan, China
United Laboratory of Optical Astronomy, Chinese Academy of Sciences, China
Received 24 June 2002 / Accepted 24 September 2002
Abstract
Complete BV light curves of the W UMa type binary GZ And is presented in
this paper. From the present times of minimum light and those collected from
the references, the changes in the orbital period of the system are analyzed.
The result reveals that the orbital period of GZ And continuously increased
at a period change rate of
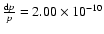 .
The
observed orbital period increase of GZ And may
be explained by a mass transfer
rate from the smaller to the larger component of
.
The
observed orbital period increase of GZ And may
be explained by a mass transfer
rate from the smaller to the larger component of
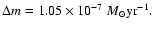 The present light curves are analyzed by means of the latest
version of the Wilson-Devinney code. The results suggest that
GZ And is a W-subtype W UMa contact binary with a mass ratio of 0.511. The
present photometric mass ratio is in agreement with that obtained
spectroscopically by Lu & Rucinski (1999). Combining the present photometric
solution with the spectroscopic orbital elements by Lu & Rucinski (1999),
we give absolute dimensions of GZ And. The determined masses and radii of the
components show that GZ And is an unevolved main-sequence binary, but the
luminosity of the primary
is abnormally low for the same mass main-sequence star. The low
luminosity of the primary may be explained by transformation between
gravitational energy and thermal energy of the system.
The present light curves are analyzed by means of the latest
version of the Wilson-Devinney code. The results suggest that
GZ And is a W-subtype W UMa contact binary with a mass ratio of 0.511. The
present photometric mass ratio is in agreement with that obtained
spectroscopically by Lu & Rucinski (1999). Combining the present photometric
solution with the spectroscopic orbital elements by Lu & Rucinski (1999),
we give absolute dimensions of GZ And. The determined masses and radii of the
components show that GZ And is an unevolved main-sequence binary, but the
luminosity of the primary
is abnormally low for the same mass main-sequence star. The low
luminosity of the primary may be explained by transformation between
gravitational energy and thermal energy of the system.
Key words: stars: binaries: close - stars: binaries: general
The variable GZ And (ADS 1693 A) is the brightest component of a multiple
star system. In 1908 Espin mentioned that either the ADS 1693 A or B
component was a variable. In 1971 and 1972 Josties and Christy obtained
multi-exposure astrometric plates of the system at the U. S. Naval Observatory
in Washington, D.C. Visual estimates from these plates by Strand showed
the A component to be variable with a brightness change of 0.6 mag in
thirty minutes (Walker 1973). The system was discovered as a W UMa-type binary
by Walker (1973). Properties of GZ And were studied by Walker (1991, 1996),
who claimed that, in addition, the W UMa binary belongs to a close triple
system with a period of about 5.3 years for the wide pair. Liu et al. (1987)
made UBV photoelectric observations of GZ And and gave times of light minima.
Both Walker (1991, 1996) and Liu et al. (1987) signaled that they obtained
photometric solutions, but their results were not available yet. The spectroscopic
observations and the radial velocity analysis of the system were published
by Lu & Ruciski (1999), who were unable to detect the third component in their
spectroscopic observations of GZ And.
No photometric solution is found in any reference, so GZ And was included
in the program of short period eclipsing binaries running at the Yunnan
Observatory using a 100-cm reflector telescope and a CCD photometric system.
The observations of GZ And in B and V bands were carried out on
November 15, 2001, with the PI1024 TKB CCD photometric system attached to the 100-cm
reflector telescope at the Yunnan Observatory in China. The effective field
of view of the photometric system is
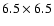 square arc minute at the
Cassegrain focus and the size of each pixel is 0.38 arcsec.
The BV color system used approximates the standard Johnson BV photometric system (Yang & Li 1999). The comparison and check stars used
are so close to the variable that they are in the same field of the observation
together with the program star. The coordinates of the variable, the comparison
star and the check star are given in Table 1.
square arc minute at the
Cassegrain focus and the size of each pixel is 0.38 arcsec.
The BV color system used approximates the standard Johnson BV photometric system (Yang & Li 1999). The comparison and check stars used
are so close to the variable that they are in the same field of the observation
together with the program star. The coordinates of the variable, the comparison
star and the check star are given in Table 1.
The integration time for each image is 100 s. A total of 101 images in Vand 99 images in B were obtained on one night in November, 2001. The aperture
photometry package of the IRAF was used to reduce the images. The reduced results
show that the difference between the magnitude of the check star and that of the
comparison star is constant within a probable error of 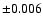 mag in Vand
mag in Vand 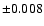 mag in B. Extinction correction is not
made as the comparison star is very close to the variable.
mag in B. Extinction correction is not
made as the comparison star is very close to the variable.
Table 1:
The coordinates of the variable, comparison star and check star.
| star |
RA(2000.0) |
Dec(2000.0) |
| variable |
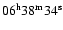 |
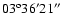 |
| comparison |
06 38 38 |
03 35 13 |
| check |
06 38 19 |
03 33 45 |
From the observations, one primary and one secondary time of minimum light
were derived by means of the parabola fitting. The new times of the minimum
light with those collected from the references are listed in Table 2,
in which the symbol "pe'' indicates the photoelectric method and "s'' shows
the visual one. The (O-C)1 values are calculated by means of
the light element formula consisting of an epoch determined in the present
study and a period given by Liu et al. (1987).
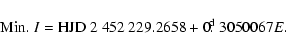 |
(1) |
From 23 times of minimum light collected from the references and
the new ones in the present article, the (O-C)1 values of the minima
computed with the above-mentioned ephemeris are plotted in Fig. 1. This
diagram shows that the orbital period of GZ And has increased continuously
since 1973. The photoelectric epochs of minimum light listed in Table 2,
except JDH 2441993.9981 (unusual large scatter), were introduced
into a least squares solution for a redetermination the ephemeris.
A quadratic ephemeris was determined as follows:
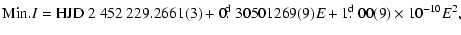 |
|
|
(2) |
which is used to compute the phases of the present observations and the
(O-C)2 values in Table 2. Using the coefficient of the square term, we
calculate a continuous period increase of
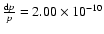 ,
i.e.
,
i.e.
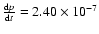 days
days
 .
.
Table 2:
The times of minimum light of GZ And.
| HJD2400000+ |
way |
E |
(O-C)1 |
(O-C)2 |
Ref. |
| 41976.8470 |
pe |
-33613.5 |
-0.0761 |
0.0007 |
[1] |
| 41977.7605 |
pe |
-33610.5 |
-0.0776 |
-0.0008 |
[1] |
| 41977.9146 |
pe |
-33610 |
-0.0760 |
0.0008 |
[1] |
| 41992.8599 |
pe |
-33561 |
-0.0760 |
0.0008 |
[1] |
| 41993.9981 |
pe |
-33557.5 |
-0.0054 |
0.0715 |
[1] |
| 45950.93175 |
pe |
-20584 |
-0.07614 |
0.00025 |
[2] |
| 45951.84676 |
pe |
-20581 |
-0.07615 |
0.00024 |
[2] |
| 45984.93999 |
pe |
-20472.5 |
-0.07614 |
0.00008 |
[2] |
| 45985.70251 |
pe |
-20470 |
-0.07614 |
0.00008 |
[2] |
| 45985.85502 |
pe |
-20469.5 |
-0.07613 |
0.00009 |
[2] |
| 45986.77004 |
pe |
-20466.5 |
-0.07613 |
0.00008 |
[2] |
| 45986.61753 |
pe |
-20467 |
-0.07614 |
0.00008 |
[2] |
| 46007.66299 |
pe |
-20398 |
-0.07614 |
-0.00003 |
[2] |
| 46008.57802 |
pe |
-20395 |
-0.07613 |
-0.00002 |
[2] |
| 46009.64554 |
pe |
-20391.5 |
-0.07614 |
-0.00003 |
[2] |
| 46012.54310 |
pe |
-20382 |
-0.07614 |
-0.00005 |
[2] |
| 46013.61063 |
pe |
-20378.5 |
-0.07613 |
-0.00005 |
[2] |
| 46015.59317 |
pe |
-20372 |
-0.07614 |
-0.00006 |
[2] |
| 49732.261 |
s |
-8186.5 |
-0.068 |
-0.046 |
[3] |
| 50390.447 |
s |
-6028.5 |
-0.046 |
-0.034 |
[4] |
| 50925.323 |
s |
-4275 |
-0.039 |
-0.016 |
[5] |
| 51384.522 |
s |
-2769.5 |
-0.028 |
-0.012 |
[6] |
| 51440.337 |
s |
-2586.5 |
-0.029 |
-0.015 |
[7] |
| 52229.1138 |
pe |
-0.5 |
0.0005 |
0.0002 |
[8] |
| 52229.2658 |
pe |
0 |
0 |
-0.0003 |
[8] |
[1] = Walker (1973); [2] = Liu et al. (1987); [3] = Locher (1995)
[4] = Locher (1997);
[5] = Locher (1998); [6] = Locher (1999)
[7] = Locher (2000); [8] = this paper.
|
101 individual observations in V band and 99 individual observations in B
band were obtained. The magnitude differences
in the sense of the variable minus the comparison star together with their
heliocentric Julian dates are listed, respectively, in Table 3 for V and
Table 4 for B. The light curves of the system are shown in Fig. 2 with full
circles.
Photometric solutions were obtained by means of the Wilson-Devinney
program which includes a new reflection treatment, the option of using
non-linear limb-darkening laws and the ability to adjust spot parameters.
All the observations are used in computing the solutions. The convergence
of the minimization procedure was obtained by means of the method of multiple
subsets (Wilson & Biermann 1976).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig1.eps}\end{figure}](/articles/aa/full/2003/14/aa2825/Timg12.gif) |
Figure 1:
The period change for GZ And. The full circles: photoelectric observations; the crosses: visual ones; the curve: fit to the observations (see text). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig2.eps}\end{figure}](/articles/aa/full/2003/14/aa2825/Timg13.gif) |
Figure 2:
The light curves for GZ And. The full circles show the observations, and the lines indicat the computed light curves with the model (see text). |
| Open with DEXTER |
The adopted parameters in the solutions are described as follows: a temperature of
5260 K for Star 1 (the star eclipsed at the Min.I), which corresponds to the
color B-V= 0.77 (Liu et al. 1987; Walker 1973; Donald & Thomas 1968),
Claret et al.'s (1990) values of the limb darkening
coefficient (x1=x2= 0.700 for V band and 0.840 for B band), Lucy's
(1967) values of the gravity darkening
coefficient (g1=g2= 0.320) and Rucinski's (1969) values of the albedo (A1=A2= 0.500). The adjustable parameters are the orbital inclination, i, the
mean temperature of Star 2, T2, the potential of the components, 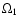 and
and 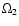 , and the monochromatic luminosity of Star 1, L1(the Planck function was used in computing the luminosity).
, and the monochromatic luminosity of Star 1, L1(the Planck function was used in computing the luminosity).
Solutions were made for a series of fixed values of the mass ratio q=m2/m1(0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 1.20, 1.40, 1.60, 1.80, 2.00, 2.40 and 3.00).
Assuming that initially it is a detached system,
the differential corrections started from the mode 2, but the converged
solutions were always obtained at the contact mode 3.
The resulting sum 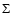 of the square deviations of the converged solutions for each value
of q shows that the fitting is best for q= 2.00.
At this point, the set of the
adjustable parameters were expanded to include q. The mass ratio converged to a
value of q= 1.95891 in the final solution. The photometric parameters are
listed in Table 5, where Star 1 indicates a more massive component and Star 2
is of lesser mass. In the final solution with the application of the WD
program, the mass ratio of q= 1.95891 suggests that the less massive component
is eclipsed at the primary eclipse. Since a mass ratio of binary systems
is often shown as less than 1, the mass ratio of GZ And was changed to
that in Table 5. The fit of the computed light curves is shown in Fig. 2 with
solid lines.
of the square deviations of the converged solutions for each value
of q shows that the fitting is best for q= 2.00.
At this point, the set of the
adjustable parameters were expanded to include q. The mass ratio converged to a
value of q= 1.95891 in the final solution. The photometric parameters are
listed in Table 5, where Star 1 indicates a more massive component and Star 2
is of lesser mass. In the final solution with the application of the WD
program, the mass ratio of q= 1.95891 suggests that the less massive component
is eclipsed at the primary eclipse. Since a mass ratio of binary systems
is often shown as less than 1, the mass ratio of GZ And was changed to
that in Table 5. The fit of the computed light curves is shown in Fig. 2 with
solid lines.
The present photometric solution indicates that GZ And is a W-subtype W UMa
contact binary with a shallow contact. The degree of geometrical contact
is only about 2.7%, which has here the expression
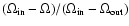 .
The photometrically derived
mass ratio is in agreement with that spectroscopically determined by Lu &
Rucinski (1999). This suggests that the solution listed in
Table 5 is satisfactory.
.
The photometrically derived
mass ratio is in agreement with that spectroscopically determined by Lu &
Rucinski (1999). This suggests that the solution listed in
Table 5 is satisfactory.
Adopting the spectroscopic orbital elements obtained by Lu & Rucinski (1999)
and combining the present photometric solution, we determined absolute dimensions
of GZ And as follows:
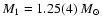 ,
,
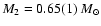 ,
,
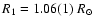 ,
,
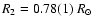 ,
,
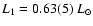 ,
,
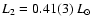 .
These physical parameters suggest
that GZ And is an
unevolved contact binary with both of the two components in the evolution
stage of main-sequence stars, but the determined luminosity of the primary
is abnormally low for the same mass main-sequence stars.
.
These physical parameters suggest
that GZ And is an
unevolved contact binary with both of the two components in the evolution
stage of main-sequence stars, but the determined luminosity of the primary
is abnormally low for the same mass main-sequence stars.
The observed abnormally low luminosity of the primary of GZ And may be explained
by transformation between gravitational energy and thermal energy of the system.
The analyses show that the orbital period of GZ And continuously increased
at a rate of
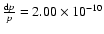 .
It may be imagined that the observed long-term orbital period increase of
GZ And could be explained by the mass transfer from the less to more massive
component.In the case of conservative mass
transfer, referring to the works of Kruszewski (1966), Plavec (1968),
Rucinski (1974), Pribulla et al. (1999)
and many other papers, the rate of mass transfer can be estimated using
the formula:
.
It may be imagined that the observed long-term orbital period increase of
GZ And could be explained by the mass transfer from the less to more massive
component.In the case of conservative mass
transfer, referring to the works of Kruszewski (1966), Plavec (1968),
Rucinski (1974), Pribulla et al. (1999)
and many other papers, the rate of mass transfer can be estimated using
the formula:
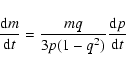 |
(3) |
where m indicates the total mass of the two components.
The observed orbital period increase of GZ And may be explained by a mass transfer
rate from the less to more massive component
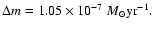 In the case of conservative mass transfer, one may have
In the case of conservative mass transfer, one may have
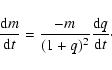 |
(4) |
Combining the Eqs. (3) and (4), one has
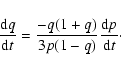 |
(5) |
The rate of change of the mass ratio of GZ And was found to be
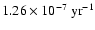 .
.
In the case of conservative mass transfer, the orbital period
increase suggests an increase in the radius of the primary. According to
Kepler's third law, one has
where A and m are the separation between the two components and the total
mass of the system, respectively, in solar units; p represents the orbital
period in days. From the definition of the relative radius of one of the two
components, one may have
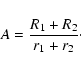 |
(7) |
According to Binnendijk (1970) and Kuiper (1941), one has
and
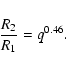 |
(9) |
Inserting Eqs. (7), (8) and (9) into Eq. (6), one may acquire
|
R13(1+q0.46)3=32.7mp2.
|
(10) |
Assuming conservation of total mass of the system, from Eq. (10), one can
obtain
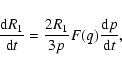 |
(11) |
where
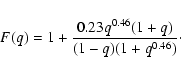 |
(12) |
Equation (11) shows a swelling rate of the primary due to an orbital period
increase and mass transfer from the less to the more massive component. For GZ And,
the swelling velocity of the primary was found to be
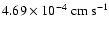 .
.
When the primary expands, the gravitational energy must be overcome by
the luminosity of the primary. In other words, part of the nuclear luminosity
of the primary could have transformed into the gravitational energy to support
the primary expansion. Here, we only care about the results of the transformation,
rather than the detailed process. Suppose the primary is spherically symmetric
with mass m1 and radius R1, then its
gravitational energy 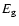 is written (Kippenhahn & Weigert 1990):
is written (Kippenhahn & Weigert 1990):
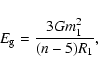 |
(13) |
where n= 3 for the main-sequence stars. Equation (13) may be rewritten as
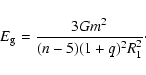 |
(14) |
From Eq. (14), the following equation can be derived
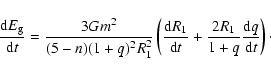 |
(15) |
Inserting Eqs. (5) and (11) into Eq. (15), one may have
![\begin{displaymath}%
\frac{{\rm d}E_{g}}{{\rm d}t}=\frac{3Gm^{2}}{(5-n)(1+q)^{2}...
...\left[F(q)-\frac{q}{1-q}\right]
\frac{{\rm d}p}{{\rm d}t}\cdot
\end{displaymath}](/articles/aa/full/2003/14/aa2825/img41.gif) |
(16) |
From Eq. (16), one can find that a gravitational luminosity of
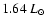 is necessary to support the swelling velocity of
is necessary to support the swelling velocity of
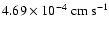 of the primary of GZ And. The primary of the
system is a main-sequence star and thus the luminosity generated from the nuclear
reactions of the primary component with a mass of
of the primary of GZ And. The primary of the
system is a main-sequence star and thus the luminosity generated from the nuclear
reactions of the primary component with a mass of
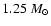 is about
is about
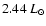 .
The observed luminosity of the primary, however, is only
.
The observed luminosity of the primary, however, is only
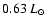 .
The luminosity generated from the nuclear reactions could
taken in three parts. The first, about
.
The luminosity generated from the nuclear reactions could
taken in three parts. The first, about
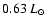 ,
may be radiated through
the surface of the primary component. The second, about
,
may be radiated through
the surface of the primary component. The second, about
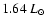 ,
may be transformed into gravitational energy of the system
to support the swell of the primary. The third, about
,
may be transformed into gravitational energy of the system
to support the swell of the primary. The third, about
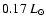 ,
may be transferred to the secondary component.
,
may be transferred to the secondary component.
The supposition of the conservation of total mass of the system may be a valid
approximation in the present study, though mass loss through L2 and
angular momentum loss could be possible because of possible magnetic activity
and/or star wind. Mass loss may result in a decrease of the orbital
period of the system, and then the observed increase of the orbital period
of GZ And may be combined from two physics processes: the mass
transfer from the secondary to the primary and the mass loss through L2.
However, the mass transfer, which can cause an increase in the orbital period, must be
dominant because the observed effect is the increase of the orbital period but
also a decrease caused by the mass loss. Furthermore, quantitative estimations
suggest that neglecting the mass loss should be allowable for the present study.
Since it is difficult to estimate the amount of mass loss of GZ And, we adopt
a mass loss rate of
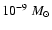 ,
which may be an average value of mass
loss rate for W UMa-type binaries. According to Pribulla et al. (1999), a decreased rate
of the orbital period can be calculated to be
,
which may be an average value of mass
loss rate for W UMa-type binaries. According to Pribulla et al. (1999), a decreased rate
of the orbital period can be calculated to be
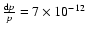 .
This is 28 times less than the observed increased rate of the orbital period.
Therefore, neglecting possible mass loss through L2, i.e., adopting the
supposition of conservation of total mass of the system, should be feasible.
.
This is 28 times less than the observed increased rate of the orbital period.
Therefore, neglecting possible mass loss through L2, i.e., adopting the
supposition of conservation of total mass of the system, should be feasible.
A long-term continuous increase or decrease in the orbital period is common
for many W UMa-type contact systems. This kind of period change
may be caused by mass exchange between the two components of a contact system and
thus a long-term change of mass ratios of many W UMa-type contact systems
may be expected. For GZ And, the mass transfer of
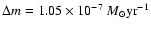 results in a mass ratio decrease of
results in a mass ratio decrease of
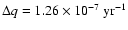 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig3.eps}\end{figure}](/articles/aa/full/2003/14/aa2825/Timg51.gif) |
Figure 3:
Mass ratios versus orbital periods for W UMa contact systems. Full circles: the systems with the spectroscopic mass ratios from
Maceroni & Veer (1996); open
circle: GZ And; line: fit to the full cirlce points. |
| Open with DEXTER |
Table 6:
W UMa type binaries with long-term continuous increase or decrease of the period.
| System |
Period |
dp/dE |
dM/dt |
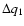 |
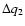 |
Ref. |
| |
[days] |
[10-10 days/cycle] |
[
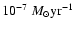 ] ] |
|
|
|
| AH Vir |
0.4075 |
2.42 |
1.09 |
-1.25 |
-1.51 |
Hobart et al. (1999) |
| 44i Boo |
0.2678 |
1.24 |
1.15 |
-1.76 |
-1.18 |
Gherega et al. (1994) |
| Dk Cyg |
0.4707 |
1.15 |
0.39 |
-0.30 |
-0.62 |
Wolf et al. (2000) |
| AD Cnc |
0.2827 |
3.40 |
1.74 |
-2.36 |
-3.06 |
Yang & Liu (2002) |
| RZ Com |
0.3385 |
0.74 |
0.61 |
-0.86 |
-0.56 |
Qian (2001) |
| RZ Tau |
0.5509 |
-1.52 |
-1.00 |
0.87 |
0.70 |
Zhai et al. (1980) |
| CN And |
0.4628 |
-1.96 |
-1.14 |
1.32 |
1.08 |
Samec et al. (1998) |
| UZ Leo |
0.6180 |
6.07 |
1.26 |
-2.76 |
-2.50 |
Hegediis & Jager (1992) |
| V839 Oph |
0.4090 |
3.46 |
3.31 |
-2.63 |
-2.15 |
Wolf et al. (1996) |
| V502 Oph |
0.4534 |
-3.40 |
-1.50 |
1.65 |
1.91 |
Herczeg (1993) |
| V1010 Oph |
0.6614 |
-7.20 |
-1.44 |
1.49 |
2.77 |
Herczeg (1993) |
| TY Boo |
0.3171 |
0.79 |
0.86 |
-1.22 |
-0.63 |
Qian (2001) |
| TX Cnc |
0.3829 |
0.59 |
0.79 |
-0.92 |
-0.39 |
Qian (2001) |
| BB Peg |
0.3615 |
0.47 |
0.34 |
-0.41 |
-0.33 |
Qian (2001) |
| AA UMa |
0.4381 |
1.16 |
0.99 |
-1.22 |
-0.63 |
Qian (2001) |
| BX Peg |
0.2804 |
-1.07 |
-1.01 |
1.58 |
0.98 |
Samac (1990) |
| YY Eri |
0.3215 |
0.20 |
0.16 |
-0.23 |
-0.16 |
Kim et al. (1997) |
| DF Hya |
0.3306 |
1.50 |
1.18 |
-1.55 |
-1.16 |
Zhang et al. (1989) |
| AB And |
0.3319 |
1.06 |
1.18 |
-1.68 |
-0.82 |
Borkovits & Hegedues (1996) |
| SW Lac |
0.3207 |
0.53 |
2.55 |
-4.53 |
-0.42 |
Pribulla et al. (1999) |
| XY Boo |
0.3706 |
6.20 |
1.80 |
-1.65 |
-4.26 |
Molik & Wolf (1998) |
| LS Del |
0.3630 |
2.24 |
2.82 |
-4.16 |
-1.57 |
Qian (2001) |
| VW Cep |
0.2783 |
-5.81 |
-4.04 |
6.67 |
5.31 |
Kaszas et al. (1998) |
| V417 Aql |
0.3701 |
-0.95 |
-0.59 |
0.68 |
0.65 |
Qian (2001) |
| EZ Hya |
0.4498 |
-8.40 |
-2.67 |
3.76 |
4.75 |
Lipari & Sistero (1989) |
| GZ And |
0.3050 |
2.00 |
3.85 |
-4.68 |
-1.87 |
present paper |
| TZ Boo |
0.2972 |
-0.96 |
-0.35 |
0.19 |
0.82 |
Qian & Liu (2000a) |
| V401 Cyg |
0.5827 |
2.20 |
1.83 |
-1.89 |
-0.96 |
Herczeg (1993) |
| CE Leo |
0.3034 |
5.98 |
7.56 |
-12.1 |
-5.02 |
Qian (2002) |
| RW Com |
0.2373 |
-0.39 |
-0.40 |
0.58 |
0.41 |
Qian (2002) |
| CT Eri |
0.6342 |
-1.02 |
-0.72 |
0.74 |
0.41 |
Lipari & Sistero (1987) |
| LT Pav |
0.3937 |
-2.71 |
-1.21 |
1.48 |
1.75 |
Cerruti (1994) |
| CK Boo |
0.355 |
4.83 |
5.77 |
-9.01 |
-3.46 |
Qian & Liu (2000b) |
As shown from GZ And, it seems to be common for many W UMa type systems that
mass transfer between the two components of a W UMa type system must cause
mass ratio changes and thus results in orbital period changes.
Adopting parameters for 38 W UMa systems with spectroscopic mass ratios listed
by Maceroni & Veer (1996), we plotted the spectroscopic mass ratios
versus the orbital periods of the systems in Fig. 3, in which the full circles
indicate the systems listed by Maceroni & Veer (1996), the line is a fit
to these systems and the open circle is GZ And. In despite of the large scatter,
from Fig. 3 one can see that mass ratios of W UMa type systems have a linear
relation with orbital period. The data of 38 systems were introduced
into a least squares solution and the following relation was obtained:
and then one can have
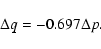 |
(18) |
These two equations suggest orbital period changes of W UMa type systems may
be accompanied by mass ratio variance, which may be
caused by mass
transfer between the two components of the system. For GZ And, adopting the
observed period change rate of
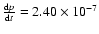 days
days
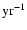 ,
from Eq. (18) we obtain
,
from Eq. (18) we obtain
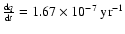 which is very
close to
which is very
close to
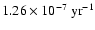 obtained from Eq. (5).
The long-term increase or decrease in the orbital periods of W UMa systems is
typical for other systems such as those listed Table 6,
in which
obtained from Eq. (5).
The long-term increase or decrease in the orbital periods of W UMa systems is
typical for other systems such as those listed Table 6,
in which
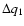 are computed from Eq. (5) and
are computed from Eq. (5) and 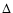 q2are computed by Eq. (18).
q2are computed by Eq. (18).
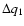 versus
versus
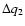 is plotted in Fig. 4. The identity
between
is plotted in Fig. 4. The identity
between
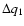 and
and
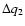 for every system in Table 6,
as shown by that of GZ And, indicates that
the linear relation between mass ratios and orbital periods of W UMa type systems,
as shown in Fig. 3 or Eqs. (17) and (18), may result from the mass
transfer between the two components of the systems because it can contribute
to both changes of the orbital period and the mass ratio of a system.
for every system in Table 6,
as shown by that of GZ And, indicates that
the linear relation between mass ratios and orbital periods of W UMa type systems,
as shown in Fig. 3 or Eqs. (17) and (18), may result from the mass
transfer between the two components of the systems because it can contribute
to both changes of the orbital period and the mass ratio of a system.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig4.eps}\end{figure}](/articles/aa/full/2003/14/aa2825/Timg58.gif) |
Figure 4:
Mass ratio chang computed from mass transfer vs. ones computed by the Eq. (18) (see text). Delta q1 show sones computed from mass transfer and Delta q2 indicates ones computed by the Eq. (18). |
| Open with DEXTER |
Both changes of the orbital period and the mass ratio of a system must cause
swell or contraction in the component radii of the system and thus gravitational
energy of the system must also change. Therefore, an abnormal luminosity of some W
UMa-type contact systems may result from transformation between gravitational
energy and thermal energy of the systems. If absolute dimensions and a long-
term continuous increase or decrease in the orbital period of a system is
determined precisely, it is possible to analyze abnormal luminosity of the
system by way of the method presented in this paper.
Acknowledgements
The authors would like to thank Mr. J. Li for his assistance
in the observations. The authors would also like to express their gratitude
for the support from the Yunnan Provincial Science & Technology Department
and the Chinese Academy of Sciences.
-
Binnendijk, L. 1970, Vistas Astron., 12, 217
In the text
-
Borkovits, T., & Hegedues, T. 1996, A&AS, 120, 63
In the text
NASA ADS
-
Cerruti, M. A. 1994, Acta Astron., 44, 291
In the text
NASA ADS
-
Claret, A., & Gimenez, A. 1990, A&A, 230, 412
In the text
NASA ADS
-
Donald, C. M., & Thomas, F. A. 1968, ApJ, 151, 611
In the text
NASA ADS
-
Eggen, O. J. 1967, MmRAS, 70, 111
NASA ADS
-
Gherega, O., Farkas, L., & Horvath, A. 1994, IBVS No. 4045
In the text
-
Herczeg, T. J. 1993, PASP, 105, 911
In the text
NASA ADS
-
Herczeg, T. J., & Jager, Z. 1992, PASP, 104, 733
NASA ADS
-
Hobart, M. A., Pena, J. H., & de La Cniz, C. 1999, Ap&SS, 260, 375
In the text
-
Kaszas, G., Vinko J., Szatmary, K., et al. 1998, A&A, 331, 231
In the text
NASA ADS
-
Kim, C. H., Jeong, J. H., Demircan, O., Muyesseroglu, Z., & Budding, E. 1997, AJ, 114, 2753
In the text
NASA ADS
-
Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution
(Berlin Springer), 184
In the text
-
Kuiper, G. P. 1941, ApJ, 93, 133
In the text
NASA ADS
-
Kruszewski, A. 1966, Adv. Astron. Astrophys., 4, 233
In the text
-
Lipari, S. L., & Sistero, R. F. 1989, AJ, 97, 207
In the text
NASA ADS
-
Lipari, S. L., & Sistero, R. F. 1987, AJ, 94, 792
In the text
NASA ADS
-
Liu, X., Yang, J., & Tan, H. 1987, IBVS No. 3080
In the text
-
Locher, K. 1995, BBSAG Bull., 108, 3
In the text
-
Locher, K. 1997, BBSAG Bull., 114, 2
In the text
-
Locher, K. 1998, BBSAG Bull., 117, 2
In the text
-
Locher, K. 1999, BBSAG Bull., 120, 2
In the text
-
Locher, K. 2000, BBSAG Bull., 121, 2
In the text
-
Lu, W., & Rucinski, S. M. 1999, AJ, 118, 515
In the text
NASA ADS
-
Lucy, L. B. 1967, Z. Astrophys., 65, 89
In the text
NASA ADS
-
Maceroni, C., & Veer, F. van't 1996, A&A, 311, 523
In the text
NASA ADS
-
Mochnacki, S. W. 1981, ApJ, 245, 650
NASA ADS
-
Molik, P., & Wolf, M. 1998, IBVS No. 4640
In the text
-
Plavec, M. 1968, Adv. Astron. Astrophys., 6, 202
In the text
-
Pribulla, T., Chochol, D., & Parimueha, S. 1999, Contrib. Astron. Obs. Skalnate Pleso, 29, 111
NASA ADS
-
Pribulla, T., Chochol, D., Rovithis-Livaniou, H., & Rovithis, P. 1999, A&A, 345, 137
In the text
NASA ADS
-
Qian, S. 2002, A&A, 384, 908
In the text
NASA ADS
-
Qian, S. 2001, MNRAS, 328, 635
In the text
NASA ADS
-
Qian, S., & Liu, Q. 2000a, A&A, 355, 171
In the text
NASA ADS
-
Qian, S., & Liu, Q. 2000b, Ap&SS, 271, 331
In the text
-
Rucinski, S. M. 1969, A&A, 19, 245
In the text
-
Rucinski, S. M. 1974, Acta Astron., 24, 119
In the text
-
Samec, R. G. 1990, AJ, 100, 808
NASA ADS
-
Samec, R. G., Laird, H., Mutzke, M., & Faulkner, D. R. 1998, IBVS No. 4616
In the text
-
Walker, R. L. 1973, IBVS No. 855
In the text
-
Walker, R. L. 1991, BAAS, 23, 881
In the text
NASA ADS
-
Walker, R. L. 1996, BAAS, 28, 921
In the text
-
Wilson, R. E., & Biermann 1976, A&A, 48, 349
In the text
NASA ADS
-
Wolf, M., & Molik, P. 1996, IBVS No. 4304
In the text
-
Wolf, M., Molik, P., Hornoch, K., & Saronovo, L. 2000, A&A, 147, 243
In the text
-
Yang, Y., & Li, L. 1999, Publication of Yunnan Observatory, 1, 32
In the text
-
Yang, Y., & Liu, Q. 2002, Chin. J. Astron. Astrophys., 2, 369
In the text
NASA ADS
-
Zhai, D., & Huang, Y. 1980, Acta Astron. Sin., 21, 158
In the text
NASA ADS
-
Zhang, Y., Liu, Q., Yang, Y., Wang, B., & Zhang, Z. 1989, IBVS No. 3349
In the text
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig1.eps}\end{figure}](/articles/aa/full/2003/14/aa2825/Timg12.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig2.eps}\end{figure}](/articles/aa/full/2003/14/aa2825/Timg13.gif)
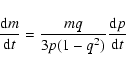
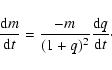
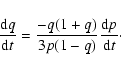
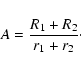
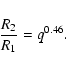
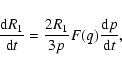
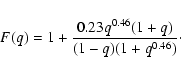
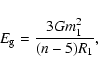
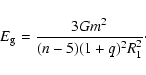
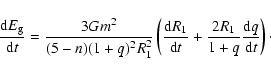
![\begin{displaymath}%
\frac{{\rm d}E_{g}}{{\rm d}t}=\frac{3Gm^{2}}{(5-n)(1+q)^{2}...
...\left[F(q)-\frac{q}{1-q}\right]
\frac{{\rm d}p}{{\rm d}t}\cdot
\end{displaymath}](/articles/aa/full/2003/14/aa2825/img41.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig3.eps}\end{figure}](/articles/aa/full/2003/14/aa2825/Timg51.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig4.eps}\end{figure}](/articles/aa/full/2003/14/aa2825/Timg58.gif)