

Up: Oscillator strengths for transitions Mn XX
In Tables 1-3 we list the energy levels arising from the (1s2) 2s22p2, 2s2p3, 2p4, 2s22p3s, 2s22p3p and 2s22p3d configurations of C-like ions,
and compare our threshold energies for K XIV, Sc XVI, Ti XVII, V XVIII, Cr XIX and Mn XX with the experimental values compiled by NIST (National Institute for Standards
and Technology: www.physics.nist.gov/PhysRefData). Since the ordering of the energy levels is not the same
for all C-like ions, the levels are listed in Tables 1-3 for each ion. The first column of each table provides an index for the corresponding level.
However, it may be noted that the
experimental values are not available for all levels, and the accuracy for some of these, especially those among the 2s22p3s, 2s22p3p and 2s22p3d configurations,
is not very high. The theoretical values available in the literature are mostly confined to the lowest 20 levels, but corresponding results involving some of the higher
excited levels have been reported by Fawcett (1987) and Zhang & Sampson (1997) in the form of transition wavelengths.
The agreement of our level energies with the experimental ones is excellent (within 3%) for all levels and for all ions.
It may be noted that the energy order of the theoretical and experimental energy levels is slightly different in a few instances; see, for example, the highest two levels
of K XIV and Sc XVI. However, the energy differences for such levels are very small (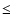 0.03 Ryd). This problem of energy order is frequently
encountered in all theoretical work, especially when the energy separation of the levels is very small. Furthermore, in the absence of definitive
experimental level energies in most of the cases, a correct energy order cannot be confirmed. In any event, it does not affect the computed values of the
oscillator strengths and collision strengths.
0.03 Ryd). This problem of energy order is frequently
encountered in all theoretical work, especially when the energy separation of the levels is very small. Furthermore, in the absence of definitive
experimental level energies in most of the cases, a correct energy order cannot be confirmed. In any event, it does not affect the computed values of the
oscillator strengths and collision strengths.
In Tables 4-9 we present our oscillator strengths and radiative rates (in length form only) for allowed transitions in K XIV, Sc XVI, Ti XVII, V XVIII, Cr XIX and Mn XX.
The indices used to represent the levels of a transition are already given in Tables 1-3. Since the indices of the various levels are not the same for all the
ions, we have included in these tables the shorter forms of the lower and upper levels of a transition. This should facilitate their identification.
The other values available in the literature for oscillator strengths (f-values) and radiative rates (A-values), apart from those of Fawcett (1987), are of Zhang & Sampson
(1996) for a few transitions among the lowest 20 levels. Their results are not only the most recent for the present ions, but are also similar and comparable to our present
calculations, as they too have adopted the GRASP code, but have restricted the inclusion of CI among the first three configurations only, i.e. 2s22p2, 2s2p3 and 2p4.
Zhang & Sampson (1997) have performed a larger calculation including the levels of the 2s22p3s, 2s22p3p and 2s22p3d configurations, but have not reported any data for
the ions under discussion here. However, a comparison between our present and their earlier results for oscillator strengths shows agreement within 20% for the available
common transitions for all ions. This is an expected result considering the limited amount of CI included by them.
Among the higher excited levels, the only results available in the literature are by Fawcett (1987), who has adopted the Hartree-Fock relativistic (HFR) code of Cowan (1981).
In Table 10 we compare our values of oscillator strengths for a few representative transitions with his HFR results. The indices used to represent a transition
correspond to those of K XIV, but a shorter form of the transitions has been included in Col. 3 in order to facilitate an easy identification of the same transition in
different ions. Generally, our GRASP and earlier HFR f-values
agree within 10%, but for a few transitions (such as 2-40 and 5-45) the differences are up to 30%, and for the 2-45 (2s22p2 3P1-2s22p3d 1P
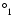 )
and 4-37 (2s22p2 1D2-2s22p3d 1D
)
and 4-37 (2s22p2 1D2-2s22p3d 1D
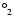 )
transitions, the two sets of results differ by a factor of two. However, the transitions for which differences between the two sets of calculations are significant are
weaker transitions, whose f-values are comparatively small. These differences arise due to different amount of CI included in the calculations.
)
transitions, the two sets of results differ by a factor of two. However, the transitions for which differences between the two sets of calculations are significant are
weaker transitions, whose f-values are comparatively small. These differences arise due to different amount of CI included in the calculations.
In general, inclusion of larger CI improves the wavefunctions, and hence leads to a more accurate determination of energy levels and radiative rates for a majority of
transitions. However, occasionally it may also result in comparatively reduced accuracy for a few transitions, as has specifically been discussed by Aggarwal (1998)
for transitions in Fe XXI. A further example of this is
provided by the 2-45 (2s22p2 3P1-2s22p3d 1P
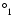 )
transition in Sc XVI, whose f-value of
)
transition in Sc XVI, whose f-value of
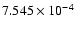 is incongrous with the corresponding f-values of other ions as shown in Table 10. Our calculations with 6, 12, 15, 16, 19 and 20 configurations yield the f-values
is incongrous with the corresponding f-values of other ions as shown in Table 10. Our calculations with 6, 12, 15, 16, 19 and 20 configurations yield the f-values
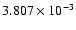 ,
,
 ,
,
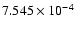 ,
,
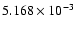 ,
,
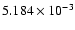 and
and
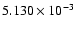 ,
respectively. Clearly, the f-value for this transition should be
,
respectively. Clearly, the f-value for this transition should be 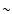 10-3, and the presently reported result of
10-3, and the presently reported result of
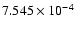 is underestimated by a factor of seven. There could be some other similar examples, but a majority of
transitions are unaffected by such inconsistencies.
is underestimated by a factor of seven. There could be some other similar examples, but a majority of
transitions are unaffected by such inconsistencies.
The accuracy of the calculated f- or A-values is generally (but not conclusively) determined by the agreement between their length and velocity forms. In any
large calculation involving a large number of transitions, as in the present work, the agreement between the two forms for all the transitions is never satisfactory.
Weak transitions (f < 0.10) being sensitive to mixing often show large variations, which can be over an order of magnitude. However, these transitions are not very
important, in general. For transitions whose f-values are significantly larger (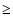 0.10), the agreement between the two forms is within 20%, and the only exception is the
33-46 (2p3p 1D2-2p3d 1F
0.10), the agreement between the two forms is within 20%, and the only exception is the
33-46 (2p3p 1D2-2p3d 1F
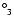 )
transition in K XIV, for which the length form is higher by a factor of two. For transitions with f-values
)
transition in K XIV, for which the length form is higher by a factor of two. For transitions with f-values 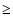 0.01, the two forms
agree within a factor of two for all transitions in all ions. In fact, for a majority of weak transitions the two forms agree to better than 40%. This is highly satisfactory.
0.01, the two forms
agree within a factor of two for all transitions in all ions. In fact, for a majority of weak transitions the two forms agree to better than 40%. This is highly satisfactory.
The measurements of A-values, in the form of lifetimes, can provide a good check on the theoretical results, and hence can help to improve the accuracy.
However, to the best of our knowledge there are no experimental values available in the literature for the ions considered here. Some experiments have reported the lifetimes
for the 2s22p2 1S0, 1D2 and 2s2p3 5S
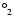 levels in other C-like ions, (see, for example, Trabert 2002 and references therein). We hope experiments
in the future will be performed for other C-like ions also, which will help us in improving upon the accuracy of the calculated atomic data.
levels in other C-like ions, (see, for example, Trabert 2002 and references therein). We hope experiments
in the future will be performed for other C-like ions also, which will help us in improving upon the accuracy of the calculated atomic data.


Up: Oscillator strengths for transitions Mn XX
Copyright ESO 2003