A&A 401, 227-242 (2003)
DOI: 10.1051/0004-6361:20030116
Anatomy of a high-mass star forming cloud:
The G24.78+0.08 (proto)stellar cluster
R. Cesaroni 1 - C. Codella 2 - R. S. Furuya 1 - L. Testi 1
1 -
Osservatorio Astrofisico di Arcetri, INAF, Largo E. Fermi 5,
50125 Firenze, Italy
2 -
Istituto di Radioastronomia, CNR, Sezione di Firenze, Largo E. Fermi 5,
50125 Firenze, Italy
Received 31 October 2002 / Accepted 21 January 2003
Abstract
We present the results of an interferometric and single-dish study of
G24.78+0.08, a region associated with high-mass star formation. Observations
have been carried out in several molecular species, which are suitable to
trace environments with different densities and temperatures. Evidence for
this region to contain a cluster of very young massive stellar objects has
been presented in a previous paper (Furuya et al. 2002). We suggest
that the embedded stars might be too young to have affected the surrounding
molecular cloud significantly on a large scale. This gives us the opportunity
to investigate the configuration of the cloud as it was prior to the star
formation episode. We assess that the (proto)stellar cluster lies at the
center of a molecular clump with diameter of  2 pc: to a good
approximation this may be described as a spherically symmetric clump with
density profile of the type
2 pc: to a good
approximation this may be described as a spherically symmetric clump with
density profile of the type
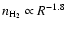 .
Inside 0.5 pc from
the center, instead, the gas is much more inhomogeneous and concentrated in a
few high-density cores surrounding the (proto)stars. Our findings indicate
that a self-regulating formation mechanism for the high-mass stars in G24.78
is plausible: in the proposed scenario star formation would occur from
inside-out collapse of the parsec-scale clump, followed by infall reversal
due to outflows powered by the newly formed massive stars. We also find that
one of the two bipolar outflows powered by the embedded YSOs is more extended
and hence older than the other, thus confirming the evolutionary sequence
proposed in our previous article.
.
Inside 0.5 pc from
the center, instead, the gas is much more inhomogeneous and concentrated in a
few high-density cores surrounding the (proto)stars. Our findings indicate
that a self-regulating formation mechanism for the high-mass stars in G24.78
is plausible: in the proposed scenario star formation would occur from
inside-out collapse of the parsec-scale clump, followed by infall reversal
due to outflows powered by the newly formed massive stars. We also find that
one of the two bipolar outflows powered by the embedded YSOs is more extended
and hence older than the other, thus confirming the evolutionary sequence
proposed in our previous article.
Key words: stars: formation - radio lines: ISM -
ISM: individual objects: G24.78+0.08 - ISM: molecules
How do stars form? Giving an answer to this question is an ambitious goal
which requires profound knowledge of both the initial conditions and
physical mechanisms involved in the process leading from a low density, cold,
large scale cloud to the formation of a kernel hot and dense enough to ignite
nuclear burning. In recent years much progress has been made in this field:
satisfactory theoretical models describing the inside-out collapse of a single
isothermal core have been elaborated and the subsequent pre-stellar evolution
of the protostar has been studied in detail. Observations have taken profit
of new powerful telescopes to investigate the interiors of molecular clouds
at radio and infrared wavelengths, thus assessing their structure and stellar
content. Although the picture is still very patchy, one may safely conclude
that we have acquired a basic understanding of the formation process of stars
with mass comparable to or less than that of the Sun. More massive stars
instead remain a mystery: according to theory, stars above 8 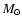 should "switch on'' during the accretion phase (Palla & Stahler 1993)
thus halting or even reversing the infall by means of their radiation
pressure. This leads to the paradox that O-B stars should not exist. Possible
ways to get round this problem are large accretion rates, accretion through
disks, or formation from merging of lower mass stars (Stahler et al.
2000). Discriminating between these possibilities is a challenging
observational task mostly for a reason: massive stars form in rich clusters
emitting copious amounts of ionising photons that profoundly alter the
surrounding environment. This makes it very difficult to find out the
primordial configuration of the molecular cloud which represents the initial
conditions for star formation.
In conclusion, observational studies of massive star forming regions must
privilege molecular clouds containing young stellar objects (YSOs) still
in a very early phase of their evolution: in this case their impact on the
surrounding material should be quite limited, thus making it possible to
compare the properties of the parental cloud with those of the newly formed
(proto)stars.
should "switch on'' during the accretion phase (Palla & Stahler 1993)
thus halting or even reversing the infall by means of their radiation
pressure. This leads to the paradox that O-B stars should not exist. Possible
ways to get round this problem are large accretion rates, accretion through
disks, or formation from merging of lower mass stars (Stahler et al.
2000). Discriminating between these possibilities is a challenging
observational task mostly for a reason: massive stars form in rich clusters
emitting copious amounts of ionising photons that profoundly alter the
surrounding environment. This makes it very difficult to find out the
primordial configuration of the molecular cloud which represents the initial
conditions for star formation.
In conclusion, observational studies of massive star forming regions must
privilege molecular clouds containing young stellar objects (YSOs) still
in a very early phase of their evolution: in this case their impact on the
surrounding material should be quite limited, thus making it possible to
compare the properties of the parental cloud with those of the newly formed
(proto)stars.
Many authors have studied high-mass star forming regions using a variety of
targets, which are believed to be signposts of newly formed O-B stars
(luminous IRAS point sources, ultracompact H II regions, etc.). Among
these, Codella et al. (1997) performed a survey towards a sample of
H2O and OH maser sources in the attempt to assess the presence of molecular
cores associated with the maser spots. The main result is that in all cases a
warm dense core is found coincident with the masers. In this article we will
consider the case of G24.78+0.08 a source located at a distance of 7.7 kpc
(Forster & Caswell 1989), which stands unique for its properties.
Two groups of maser spots are found, one with only H2O emission,
the other with both types of masers. The latter group is associated with an
unresolved ultracompact (UC) H II region and with a hot molecular core,
whereas the former seems embedded in a colder core and no free-free continuum
is detected towards it. Moreover, slightly offset from the H2O and OH
masers another UC H II region is seen, which looks more extended and
apparently not associated with any high density peak of the molecular gas.
Codella et al. (1997) conclude that they might be observing three
high-mass YSOs in different evolutionary phases. Interestingly, in all
groups the maser spots are distributed over  1
1
 ,
along parallel
directions: since H2O masers are believed to be closely associated with
outflows (see e.g. Felli et al. 1992; Moscadelli et al.
2000), Codella et al. (1997) suggest that the maser spots
might trace the axes of putative outflows from the embedded YSOs.
,
along parallel
directions: since H2O masers are believed to be closely associated with
outflows (see e.g. Felli et al. 1992; Moscadelli et al.
2000), Codella et al. (1997) suggest that the maser spots
might trace the axes of putative outflows from the embedded YSOs.
Recently, follow-up observations by Furuya et al. (2002; hereafter
Paper I) have fully confirmed the previous hypotheses. In particular, two
bipolar outflows have been found: as expected, these are centred on the
masers and aligned parallel to the distributions of the spots. Also, a new
molecular core has been detected, which brings to 4 the number of putative
high-mass YSOs in the region. In Paper I we argued that the newly detected
core might
host a massive protostar. The basic conclusion is that G24.78 consists of a
cluster of very young massive (proto)stars in different evolutionary phases,
but still deeply embedded in their parental cloud. This region represents an
ideal laboratory for studying the structure of a high-mass star-forming cloud
and the feedback between this and the embedded YSOs.
With this in mind, we have decided to carry out observations of G24.78
on a scale of a few parsecs, zooming out from the relatively small
region ( 0.3 pc) previously mapped. In this article we present
the results of single-dish observations of the molecular cloud associated
with G24.78. We also illustrate in better detail the findings of the
interferometric observations of Paper I. The combination of low and high
angular resolution observations make it possible a thorough analysis of the
gas distribution and physical parameters, and allow us to study the
interaction between the newly formed stars and their natal environment.
0.3 pc) previously mapped. In this article we present
the results of single-dish observations of the molecular cloud associated
with G24.78. We also illustrate in better detail the findings of the
interferometric observations of Paper I. The combination of low and high
angular resolution observations make it possible a thorough analysis of the
gas distribution and physical parameters, and allow us to study the
interaction between the newly formed stars and their natal environment.
2 Observations and data reduction
The 2.6 mm observations were carried out with the IRAM![[*]](/icons/foot_motif.gif) 5-antenna
interferometer in April and May 1998. The D and C1 configurations were used,
with baselines up to 147 m. The phase tracking centre was
5-antenna
interferometer in April and May 1998. The D and C1 configurations were used,
with baselines up to 147 m. The phase tracking centre was
 (J2000) = 18
(J2000) = 18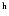 36
36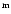 13
13
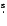 10
10
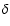 (J2000) = -07
(J2000) = -07 12
12 08
08
 0.
The 82-116 GHz SIS receiver was tuned single
side-band at the 12CO J = 1-0 frequency (115.271 GHz). The facility
correlator was configured with a bandwidth of 40 MHz centered on the
12CO line, while two bandwidths of 160 MHz each were combined to measure the
continuum. Typical system temperatures were about 150 K. The clean beam was
5
0.
The 82-116 GHz SIS receiver was tuned single
side-band at the 12CO J = 1-0 frequency (115.271 GHz). The facility
correlator was configured with a bandwidth of 40 MHz centered on the
12CO line, while two bandwidths of 160 MHz each were combined to measure the
continuum. Typical system temperatures were about 150 K. The clean beam was
5
 3
3  4
4
 1 (PA -162
1 (PA -162 ). Amplitude calibration was
achieved by observing 3C273, which was assumed to have a flux of 16.7 Jy,
while 1830-210 (1.7 Jy) and 1741-038 (3.0 Jy) were used as phase
calibrators. The typical RMS phase noise on the longest baselines was
35
). Amplitude calibration was
achieved by observing 3C273, which was assumed to have a flux of 16.7 Jy,
while 1830-210 (1.7 Jy) and 1741-038 (3.0 Jy) were used as phase
calibrators. The typical RMS phase noise on the longest baselines was
35 .
Calibration and data reduction were done using the GILDAS
software developed at IRAM and Observatoire de Grenoble. Continuum
subtraction was performed in the (u,v) plane by using the integral over the
line-free channels of the 160 MHz units. Finally, channel maps were produced
for the 12CO J = 1-0 line by averaging the observed 156 kHz channel
spacing spectra up to a final value of 625 kHz, corresponding to 1.63 km s-1 at 2.6 mm. The resulting clean beam is
.
Calibration and data reduction were done using the GILDAS
software developed at IRAM and Observatoire de Grenoble. Continuum
subtraction was performed in the (u,v) plane by using the integral over the
line-free channels of the 160 MHz units. Finally, channel maps were produced
for the 12CO J = 1-0 line by averaging the observed 156 kHz channel
spacing spectra up to a final value of 625 kHz, corresponding to 1.63 km s-1 at 2.6 mm. The resulting clean beam is
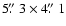 (PA -162
(PA -162 )
and the conversion factor from flux to brightness
temperature in the synthesised beam is
)
and the conversion factor from flux to brightness
temperature in the synthesised beam is  23.7 Jy K-1.
23.7 Jy K-1.
Interferometric observations of molecular lines and continuum emission at
2-mm band were carried out using the six-element Nobeyama Millimeter Array
(NMA) at Nobeyama Radio Observatory![[*]](/icons/foot_motif.gif) from December 2000 to January 2002 with three array configurations. In the
most expanded configuration, the Nobeyama 45-m telescope was added as an
element antenna of the interferometer: the telescope is located close to the
end of the North-South arm of the NMA. Resulting projected baselines ranged
from 4.1 to 198 k
from December 2000 to January 2002 with three array configurations. In the
most expanded configuration, the Nobeyama 45-m telescope was added as an
element antenna of the interferometer: the telescope is located close to the
end of the North-South arm of the NMA. Resulting projected baselines ranged
from 4.1 to 198 k and the synthesized beam size with natural
weighting 2.3
and the synthesized beam size with natural
weighting 2.3
 1.5
1.5
 .
Our observations will miss 50% of
the flux from structures
.
Our observations will miss 50% of
the flux from structures  15
15
 (see Wilner & Welch
1994), corresponding to
(see Wilner & Welch
1994), corresponding to  0.6 pc at a distance of 7.7 kpc. The
phase tracking centre was
0.6 pc at a distance of 7.7 kpc. The
phase tracking centre was 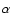 (B1950) = 18
(B1950) = 18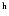 33
33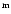 30
30
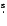 50
50
 (B1950) = -07
(B1950) = -07 14
14 42
42
 0.
Both the NMA antennas
and 45-m telescope are equipped with SIS receivers having system noise
temperatures in double-sideband of 300-500 K toward the zenith at 147 GHz.
We checked the telescope pointing of the 45-m telescope every 90-120 min
by five-point mapping of the SiO J=1-0 maser line at 43 GHz from
IRC+00363. The relative pointing offset between the 40 and 150 GHz SIS
receivers was less than 2
0.
Both the NMA antennas
and 45-m telescope are equipped with SIS receivers having system noise
temperatures in double-sideband of 300-500 K toward the zenith at 147 GHz.
We checked the telescope pointing of the 45-m telescope every 90-120 min
by five-point mapping of the SiO J=1-0 maser line at 43 GHz from
IRC+00363. The relative pointing offset between the 40 and 150 GHz SIS
receivers was less than 2
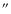 and the pointing error was within
3
and the pointing error was within
3
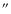 during the observations.
during the observations.
We tuned the 150 GHz SIS receiver at the frequency of C32S J=3-2 line
(146.969047 GHz) and used two types of backends: the digital
spectrocorrelator, FX, and the XF-type correlator, i.e. the Ultra Wide Band
Correlator (UWBC; Okumura et al. 2000).
The FX correlator was configured with 1024 channels per baseline and a
bandwidth of 32 MHz, giving a velocity resolution of 0.0625 km s-1 with a
velocity coverage of 64 km s-1. To cover not only the C32S line but also all Kcomponents of the CH3CN J=8-7 transition, the UWBC was configured in the
512 MHz bandwidth mode with 256 channels, providing a velocity resolution of
8.0 km s-1 after on-line smoothing. We used 3C 279 as bandpass calibrator
and 1741-038 as phase and gain calibrator for the observations. From
observations of Uranus, the flux density of 1741-038 was determined to be
2.5 Jy during the observation period. The overall flux uncertainty is about 20%. The data calibration was done using the UVPROCII software developed at
the NRO and the image construction was performed using the AIPS package of
NRAO. The typical 1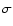 RMS noise levels were 120 mJy beam-1, after
smoothing to 0.5 km s-1 resolution, for the C32S J=3-2 line,
48 mJy beam-1 with 8.0 km s-1 resolution for the CH3CN lines, and
2.5 mJy beam-1 for the 147 GHz continuum emission which used an
effective bandwidth of
RMS noise levels were 120 mJy beam-1, after
smoothing to 0.5 km s-1 resolution, for the C32S J=3-2 line,
48 mJy beam-1 with 8.0 km s-1 resolution for the CH3CN lines, and
2.5 mJy beam-1 for the 147 GHz continuum emission which used an
effective bandwidth of  800 MHz, after merging the line free channels of
the signal band with those from the image side band at 134 GHz.
800 MHz, after merging the line free channels of
the signal band with those from the image side band at 134 GHz.
The G24.78 region was observed with the NRAO![[*]](/icons/foot_motif.gif) Very Large Array
(VLA) in its most compact (D) configuration on December 29, 2001.
The phase tracking centre was
Very Large Array
(VLA) in its most compact (D) configuration on December 29, 2001.
The phase tracking centre was
 (J2000) = 18
(J2000) = 18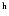 36
36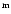 12
12
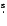 66
66
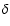 (J2000) = -07
(J2000) = -07 12
12 10
10
 146.
The source was observed in the Q-band (43.34 GHz, 0.7 cm), at the time of the
observations 25 antennas with Q-band receivers were available. We used an
observing cycle with total duration of 5 min and an efficiency of
146.
The source was observed in the Q-band (43.34 GHz, 0.7 cm), at the time of the
observations 25 antennas with Q-band receivers were available. We used an
observing cycle with total duration of 5 min and an efficiency of  60%.
Hourly pointing at X-band on the calibrators were used to correct for
pointing drifts during the Q-band observations. The flux density scale was
set by observing 3C286 and 3C48, while 1832-105 (0.7 Jy) was used as a phase
calibrator. The flux calibration is expected to be accurate within 20%. All
data editing and calibration has been performed using standard tasks within
the NRAO AIPS software package. Two self-calibration (phase only) iterations
were performed to improve the dynamic range of the final maps. All images
presented here have been produced using the AIPS IMAGR task with robust
weighting of the (u,v) datasets the resulting synthesized HPBW is
2
60%.
Hourly pointing at X-band on the calibrators were used to correct for
pointing drifts during the Q-band observations. The flux density scale was
set by observing 3C286 and 3C48, while 1832-105 (0.7 Jy) was used as a phase
calibrator. The flux calibration is expected to be accurate within 20%. All
data editing and calibration has been performed using standard tasks within
the NRAO AIPS software package. Two self-calibration (phase only) iterations
were performed to improve the dynamic range of the final maps. All images
presented here have been produced using the AIPS IMAGR task with robust
weighting of the (u,v) datasets the resulting synthesized HPBW is
2
 3
3 1
1
 7. No correction for primary beam attenuation has
been applied.
7. No correction for primary beam attenuation has
been applied.
The observations with the IRAM 30-m telescope at Pico Veleta (Granada, Spain)
were carried out in September 2001. Table 1 summarises the observed
molecular species, transitions, rest frequencies, half power beam widths
(HPBWs), and typical system temperature (
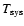 )
expressed in main-beam
brightness temperature (
)
expressed in main-beam
brightness temperature (
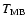 )
units. The main beam efficiency
varies from about 0.8 (at 96 GHz) to 0.5 (at 258 GHz). The pointing was
checked about every hour by observing planets and nearby continuum sources and
it was found to be accurate to within 4
)
units. The main beam efficiency
varies from about 0.8 (at 96 GHz) to 0.5 (at 258 GHz). The pointing was
checked about every hour by observing planets and nearby continuum sources and
it was found to be accurate to within 4
 .
High spectral resolution
(80 kHz) data have been obtained with an autocorrelator (AC) spectrometer
split into four parts to allow simultaneous observations of four different
transitions as well as with a 100 kHz filter bank. Moreover, lower
resolution spectra have been obtained by using a 1 MHz filter bank, split
into a suitable number of parts. The receivers were tuned according to the
following frequency setups which allowed us to observe several lines
simultaneously: (i) 12CO(1-0) and 12CO(2-1); (ii) 13CO(1-0),
C18O(1-0), C32S(3-2), and 13CO(2-1); (iii) C34S(2-1), (3-2), and
(5-4); and (iv) CH3CN(6-5), (8-7), (12-11), and (14-13). We stress that
for the 12CO lines and for the C34S(5-4) transition two receivers
have been used simultaneously in order to improve the S/N ratio.
.
High spectral resolution
(80 kHz) data have been obtained with an autocorrelator (AC) spectrometer
split into four parts to allow simultaneous observations of four different
transitions as well as with a 100 kHz filter bank. Moreover, lower
resolution spectra have been obtained by using a 1 MHz filter bank, split
into a suitable number of parts. The receivers were tuned according to the
following frequency setups which allowed us to observe several lines
simultaneously: (i) 12CO(1-0) and 12CO(2-1); (ii) 13CO(1-0),
C18O(1-0), C32S(3-2), and 13CO(2-1); (iii) C34S(2-1), (3-2), and
(5-4); and (iv) CH3CN(6-5), (8-7), (12-11), and (14-13). We stress that
for the 12CO lines and for the C34S(5-4) transition two receivers
have been used simultaneously in order to improve the S/N ratio.
![\begin{figure}
\par\includegraphics[angle=0,width=13cm,clip]{h4079f01.ps}
\end{figure}](/articles/aa/full/2003/13/aah4079/Timg28.gif) |
Figure 1:
Maps of the emission integrated under the whole line profile for
six rotational transitions observed with the 30-m telescope. Contour levels
range from 10 to 90% in steps of 10% of the peak intensity. In all cases
the lowest contour is above the 3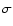 limit of the corresponding map.
The white triangles mark the positions of the H2O maser spots (Forster &
Caswell 1999). The telescope HPBW is drawn as a shaded circle in the
bottom of each map.
limit of the corresponding map.
The white triangles mark the positions of the H2O maser spots (Forster &
Caswell 1999). The telescope HPBW is drawn as a shaded circle in the
bottom of each map. |
| Open with DEXTER |
The 12CO and 13CO(1-0) data were collected with observations in
on-the-fly mode, dumping spectra every 4
 or 2 s. Off-source
spectra were observed every three on-source subscans. The off-source position
was displaced by +7071
or 2 s. Off-source
spectra were observed every three on-source subscans. The off-source position
was displaced by +7071
 in RA and -947
in RA and -947
 in Dec, and was
checked for absence of 12CO emission by means of frequency switching
observations. We observed the same region alternatively scanning along the
RA and Dec directions (B1950 coordinates were used),
in order to build up more homogeneous maps. The
CH3CN and C34S observations were performed using the wobbler
switching mode with a 240
in Dec, and was
checked for absence of 12CO emission by means of frequency switching
observations. We observed the same region alternatively scanning along the
RA and Dec directions (B1950 coordinates were used),
in order to build up more homogeneous maps. The
CH3CN and C34S observations were performed using the wobbler
switching mode with a 240
 beam-throw and a phase-duration of 2 s.
The spectra were calibrated with the standard chopper wheel method and are
reported here in
beam-throw and a phase-duration of 2 s.
The spectra were calibrated with the standard chopper wheel method and are
reported here in
 units. The data reduction were done by using
the standard GILDAS software.
units. The data reduction were done by using
the standard GILDAS software.
In order to improve the absolute positions of the C34S and C32S(3-2) maps we
realigned them to interferometric maps obtained in the same lines. For the
C34S maps we have used a map obtained with the BIMA interferometer in
the C34S(2-1) line (Beltrán, priv. communication): the 30-m maps have been
shifted by (-1
 5, -3
5, -3
 5). For C32S(3-2) instead, the NMA map
has been used as a reference: and the two single dish maps have been shifted by
(+1
5). For C32S(3-2) instead, the NMA map
has been used as a reference: and the two single dish maps have been shifted by
(+1
 7, +3
7, +3
 1) and (-1
1) and (-1
 1, -2
1, -2
 7), respectively. We
note that all the corrections applied are within the 30-m pointing error.
7), respectively. We
note that all the corrections applied are within the 30-m pointing error.
3 Results
In this section we present the maps obtained with the IRAM 30-m
telescope. We also illustrate the results of interferometric observations
performed with the PdBI and NMA, part of which has been shown in Paper I:
here, we will present additional maps and perform a comparison between
single-dish and interferometric data in the same tracers.
3.1.1 Line
We have used the IRAM 30-m telescope to map the molecular cloud associated
with the high-mass YSOs identified in Paper I. We have observed six rotational
transitions of four molecular species over a region  2
2 in size.
The maps of the integrated line emission are shown in Fig. 1: here
the locations of the two groups of H2O masers are shown to pin point the
position of the (proto) stellar cluster found in Paper I. In all tracers
the emission peaks towards the masers, but the global pattern is quite
different depending on the transition. A comparison between the CO
isotopomers is illuminating under this respect: while the central clump
associated with the masers is clearly seen in all lines, the elongated
structure traced by the 12CO transitions to the west of the main peak gets
fainter when imaged in 13CO and C18O, and is hardly visible in the
C32S map. Since the latter is a high-density tracer, these results
demonstrate that the elongated structure is characterised by relatively large
column density, but low volume density. Such a conclusion is reinforced by
the distribution of the CO lines optical depth, which we shall derive in
Sect. 4.2: here, we anticipate that the elongated structure does not
coincide with a clear peak in the optical depth map (cf. the white dotted
contour to the west in Fig. 15), but with a region where the optical
depth is slightly enhanced.
in size.
The maps of the integrated line emission are shown in Fig. 1: here
the locations of the two groups of H2O masers are shown to pin point the
position of the (proto) stellar cluster found in Paper I. In all tracers
the emission peaks towards the masers, but the global pattern is quite
different depending on the transition. A comparison between the CO
isotopomers is illuminating under this respect: while the central clump
associated with the masers is clearly seen in all lines, the elongated
structure traced by the 12CO transitions to the west of the main peak gets
fainter when imaged in 13CO and C18O, and is hardly visible in the
C32S map. Since the latter is a high-density tracer, these results
demonstrate that the elongated structure is characterised by relatively large
column density, but low volume density. Such a conclusion is reinforced by
the distribution of the CO lines optical depth, which we shall derive in
Sect. 4.2: here, we anticipate that the elongated structure does not
coincide with a clear peak in the optical depth map (cf. the white dotted
contour to the west in Fig. 15), but with a region where the optical
depth is slightly enhanced.
In conclusion, we believe that our maps demonstrate the existence of a
well defined clump, coincident with the YSOs of interest for us. Hereafter
we shall use the word "clump'' to indicate the middle-scale ( 1 pc)
cloud associated with the G24.78 cluster, not to be confused with the much
smaller (
1 pc)
cloud associated with the G24.78 cluster, not to be confused with the much
smaller ( 0.07 pc) "cores'' imaged in Paper I.
0.07 pc) "cores'' imaged in Paper I.
Smaller maps in the C34S(2-1), (3-2), and (5-4) lines have also been made.
These are shown in Fig. 2, where the positions and names of the
four YSOs identified in Paper I are reported. The C34S emission peaks towards
the position of core A and extends over a region including all YSOs. Given
the low angular resolution (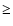 10
10
 ), it is difficult to find out the
contribution of the other YSOs to the C34S emission, but it seems clear that
the latter originates from a region of
), it is difficult to find out the
contribution of the other YSOs to the C34S emission, but it seems clear that
the latter originates from a region of  15
15
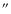 .
.
The complexity of the region under study is confirmed by the line profiles
in Fig. 3. While the optically thin lines of C34S and C18O have an almost Gaussian shape, the profiles of thicker transitions such
as those of 12CO and 13CO present multiple peaks and dips. This is
very likely due to the presence of velocity gradients in the molecular
cloud and possibly to clouds lying along the line of sight but physically
unrelated to the region of interest for us. We believe that
also self-absorption may affect the line profiles. In fact, one can
see that going from optically thin to thick tracers, the peak at
110.3 km s-1 (the systemic velocity of G24.78) is shifting towards higher
velocities: this effect can be explained by blue-shifted self-absorption.
In Sect. 4.1.2 it will be shown that this is indeed the case.
We have also observed four rotational transitions of CH3CN towards cores A
and C - in Paper I no CH3CN emission was not detected from cores B and D. The
spectra are shown in Fig. 4, where also a comparison with the
corresponding spectra obtained with the NMA is made (shaded profiles). No
noticeable difference between the profiles of the two cores can be seen,
although the intensity of the lines is stronger towards A. However, the 30-m
HPBW is greater than or comparable to the angular separation between the two
cores: this makes it very difficult to disentangle the contribution of one
core from that of the other, especially for the (6-5) and (8-7) lines. Such
an effect can be clearly seen in the (8-7) transitions by comparing the
single-dish line profiles corresponding to
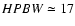
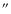 with those
obtained with the NMA, whose angular resolution is
with those
obtained with the NMA, whose angular resolution is  2
2
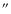 ,
i.e. much
smaller than the separation between A and C: the single-dish profile towards C is obviously strongly "contaminated'' by the emission arising from A.
,
i.e. much
smaller than the separation between A and C: the single-dish profile towards C is obviously strongly "contaminated'' by the emission arising from A.
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f02.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg31.gif) |
Figure 2:
IRAM 30-m maps of the C34S(2-1), (3-2), and (5-4) emission
integrated under the line from 105 to 116 km s-1.
The contour levels are indicated in the wedge to the right of each panel.
The thick contour corresponds to
the 50% level. Triangles mark the positions of the H2O maser spots
(Forster & Caswell 1999), while the crosses and the corresponding
labels identify the objects according to the notation used in Paper I. |
| Open with DEXTER |
It is worth pointing out that rotational diagrams of CH3CN could be used to
estimate the temperatures of the cores, as done by various authors (see e.g.
Olmi et al. 1993). In our case this method gives temperatures above
300 K for both cores. This is very likely the effect of large optical depth,
as proved by the detection of some C
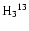 CN(8-7) transitions: for the K=0and 1 lines the intensity ratio between isotopomer and main species gives an
optical depth of
CN(8-7) transitions: for the K=0and 1 lines the intensity ratio between isotopomer and main species gives an
optical depth of  15, assuming an abundance ratio of 72 between
CH3CN and C
15, assuming an abundance ratio of 72 between
CH3CN and C
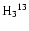 CN (Wilson & Rood 1994). In principle one could use
the optically thin lines of the 13C substituted species to get round the
optical depth problem, but in our spectra only the K=0 and 1 components of
C
CN (Wilson & Rood 1994). In principle one could use
the optically thin lines of the 13C substituted species to get round the
optical depth problem, but in our spectra only the K=0 and 1 components of
C
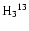 CN are clearly detected, mostly the K=0 and 1: these are obviously
insufficient to obtain an estimate of the rotational temperature.
CN are clearly detected, mostly the K=0 and 1: these are obviously
insufficient to obtain an estimate of the rotational temperature.
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f03.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg32.gif) |
Figure 3:
Spectra observed towards the position of core A
(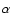 (B1950) = 18:33:30.38 (B1950) = 18:33:30.38 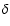 (B1950) = -07:14:42.1). The full line
corresponds to 12CO(1-0), 12CO(2-1), and C32S(3-2), the dashed line to
13CO(1-0), 13CO(2-1), and C34S(3-2) and the dotted line to C18O(1-0).
The vertical thin line marks the systemic velocity of the G24.78
region, as given in Paper I. (B1950) = -07:14:42.1). The full line
corresponds to 12CO(1-0), 12CO(2-1), and C32S(3-2), the dashed line to
13CO(1-0), 13CO(2-1), and C34S(3-2) and the dotted line to C18O(1-0).
The vertical thin line marks the systemic velocity of the G24.78
region, as given in Paper I. |
| Open with DEXTER |
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f04.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg33.gif) |
Figure 4:
Spectra of the methyl cyanide line emission towards cores A (left
panels) and C (right panels). The notation of Paper I has been adopted for the
core names. The vertical dotted lines indicate the positions of the
different K transitions of CH3CN (upper) and C
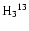 CN (lower). The shaded
profiles are the spectra obtained by integrating the CH3CN(8-7) line emission
observed with the NMA over cores A and C. CN (lower). The shaded
profiles are the spectra obtained by integrating the CH3CN(8-7) line emission
observed with the NMA over cores A and C. |
| Open with DEXTER |
In Table 2 we list the main parameters of the clump in G24.78 derived
from the lines mapped by us. For each transition we give the full width at
half maximum (
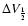 )
of the line profile, the full width at half power (FWHP)
of the clump, the corresponding angular (
)
of the line profile, the full width at half power (FWHP)
of the clump, the corresponding angular (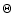 )
and linear (D) diameters
(obtained by deconvolution assuming source and beam to be Gaussian), the mass
of the clump, the corresponding H2 volume density, and the virial mass
computed from D and
)
and linear (D) diameters
(obtained by deconvolution assuming source and beam to be Gaussian), the mass
of the clump, the corresponding H2 volume density, and the virial mass
computed from D and
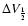 .
The value of
.
The value of
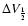 has been obtained by fitting a
Gaussian to the line with the exception of the transitions whose profile is
affected by overlap with other features and/or self-absorption: in these cases
we have read off
has been obtained by fitting a
Gaussian to the line with the exception of the transitions whose profile is
affected by overlap with other features and/or self-absorption: in these cases
we have read off
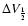 using the cursor. The masses have been calculated with
different methods. In the case of the CO isotopomers, the
emission has been integrated
under the line and over the whole clump, and we have assumed LTE at
a temperature of 30 K: the latter is equal to the maximum main beam
brightness temperature measured with the 30-m telescope in the 12CO(2-1)
line. The values thus obtained have been corrected taking into account the
line optical depth computed from the ratio between different isotopomers of
the same species. The molecular abundances relative to H2 have been
assumed equal to
using the cursor. The masses have been calculated with
different methods. In the case of the CO isotopomers, the
emission has been integrated
under the line and over the whole clump, and we have assumed LTE at
a temperature of 30 K: the latter is equal to the maximum main beam
brightness temperature measured with the 30-m telescope in the 12CO(2-1)
line. The values thus obtained have been corrected taking into account the
line optical depth computed from the ratio between different isotopomers of
the same species. The molecular abundances relative to H2 have been
assumed equal to
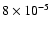 for 12CO,
for 12CO,
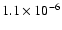 for 13CO,
for 13CO,
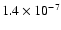 for C18O, and
for C18O, and
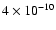 for C34S (Irvine et al. 1987; Wilson &
Rood 1994). Mean densities have been derived in a trivial way assuming
spherical symmetry. For C34S, instead, the value of the
density has been derived
directly from the line intensities, using the method described e.g.
by Cesaroni et al. (1991) and from this the mass has been computed
assuming the clump to be homogeneous and spherical. Finally, the mass
pertaining to the CH3CN region has been taken equal to the sum of the masses
of the cores detected in Paper I, because all the CH3CN emission arises from
such cores (see Sect. 3.2).
for C34S (Irvine et al. 1987; Wilson &
Rood 1994). Mean densities have been derived in a trivial way assuming
spherical symmetry. For C34S, instead, the value of the
density has been derived
directly from the line intensities, using the method described e.g.
by Cesaroni et al. (1991) and from this the mass has been computed
assuming the clump to be homogeneous and spherical. Finally, the mass
pertaining to the CH3CN region has been taken equal to the sum of the masses
of the cores detected in Paper I, because all the CH3CN emission arises from
such cores (see Sect. 3.2).
Clearly, the mass and density values listed in Table 2 differ
significantly one another. This result can be explained by the fact that
different molecules trace regions with different densities: as a
matter of fact, large gradients have been found in star forming clouds (see
e.g. Fontani et al. 2002). However, some discrepancy exists even
between mass estimates derived from lines of the same species, arising from
approximately the same region: for instance, the masses obtained from
12CO(1-0) and 12CO(2-1) differ by about a factor 3. This could be due to
a variety of effects. Very likely optical depths are large and hence
difficult to estimate. In fact, the ratio between lines of isotopomers of the
same species is prone to uncertainties related to the line profile: in our
case, multiple components and self-absorption heavily affect the spectra,
which in turn makes the line ratio quite unreliable. Furthermore, temperature
gradients are likely to exist in the gas, which is not consistent with our
assumption of isothermal clump. In conclusion, we believe that for the mass
and density values in Table 2 an uncertainty of  3 is in order.
3 is in order.
Notwithstanding this caveat, it seems that the mass estimated from the
molecular tracers is systematically greater than the corresponding virial
mass: this is consistent with the conclusions of Fontani et al. (2002),
who obtained the same result for a sample of clumps associated with high-mass
YSOs. These findings raise the question of clump stability, which will be
discussed in Sect. 5.
3.1.2 Continuum
Although no bolometric continuum observation of G24.78 has been performed by
us, we used the line-free channels of the CH3CN spectra to obtain an estimate
of the continuum level at the positions of cores A and C. This method works
reasonably well when a nutating secondary is used and if the weather
conditions are stable. We have taken 5 spectra towards A and 11 spectra
towards C: the flux estimate has been taken equal to the middle value
between the minimum and the maximum fluxes measured at each position, while
the error has been assumed equal to half the range between the minimum and
the maximum. In Fig. 5 we compare the values of the fluxes thus
obtained (big points) with the fits (curves) to the continuum
measurements obtained by other means (small points). Details on the data and
model fits have been given in Paper I. It must be noted that at 3 and 2 mm the
HPBW is much greater than the separation between A and C ( 8
8
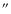 ), so
that it is impossible to disentangle the contribution of each core to the
total flux. To some extent this can be done at 1.4 and 1.2 mm where the
angular resolution is
), so
that it is impossible to disentangle the contribution of each core to the
total flux. To some extent this can be done at 1.4 and 1.2 mm where the
angular resolution is  10
10
 ,
albeit with a large uncertainty
especially on the flux of the fainter core (C). From Fig. 5 one can
see that the total flux measured at 3 and 2 mm is very similar to the values
obtained from interferometric observations, which supports the reliability of
our single-dish estimates. However, the most interesting result is the good
agreement between the two values measured at 1.4 and 1.2 mm and those
expected on the basis of the model fit from Paper I. Such an agreement is
especially evident in the top panel of Fig. 5, where the total flux
from all cores is compared to the sum of the model fits of each core. In
the bottom panel instead one can see that the 1 mm fluxes of core C lie above
the corresponding fit. However, as explained above, it is difficult to
estimate the flux of each single core: therefore, while the total flux is more
accurate, the fluxes from A and C are prone to greater uncertainties. We
conclude that our single-dish continuum measurements are consistent with the
model fit presented in Paper I.
,
albeit with a large uncertainty
especially on the flux of the fainter core (C). From Fig. 5 one can
see that the total flux measured at 3 and 2 mm is very similar to the values
obtained from interferometric observations, which supports the reliability of
our single-dish estimates. However, the most interesting result is the good
agreement between the two values measured at 1.4 and 1.2 mm and those
expected on the basis of the model fit from Paper I. Such an agreement is
especially evident in the top panel of Fig. 5, where the total flux
from all cores is compared to the sum of the model fits of each core. In
the bottom panel instead one can see that the 1 mm fluxes of core C lie above
the corresponding fit. However, as explained above, it is difficult to
estimate the flux of each single core: therefore, while the total flux is more
accurate, the fluxes from A and C are prone to greater uncertainties. We
conclude that our single-dish continuum measurements are consistent with the
model fit presented in Paper I.
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f05.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg40.gif) |
Figure 5:
Bottom panel: spectra of the continuum emission of the four objects
identified in the G24.78 region. The letters identify each spectrum
according to the notation of Paper I. The curves in the bottom panel are the
model fits (see Paper I) to the interferometric measurements represented by the
small points. The single-dish measurements toward cores A and C obtained in
this study correspond instead to the bigger points. Note that the latter are
not shown at 110 and 147 GHz because it is impossible to disentangle the
contribution of cores A and C.
Top panel: spectrum of the total continuum flux from all sources. The curve
is the sum of the model fits in the bottom panel. The bigger points indicate
our single-dish measurements. |
| Open with DEXTER |
3.2 Interferometric data
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f06.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg46.gif) |
Figure 6:
PdBI (top panel) and NMA (bottom panel) maps obtained by integrating the
emission under the 12CO(1-0) and C32S(3-2) lines, respectively. The crosses
and corresponding labels mark the four objects identified by Paper I. Contour
levels are drawn in the wedge beside each panel. |
| Open with DEXTER |
In Paper I we have already illustrated the PdBI and NMA maps of the bipolar
outflow in the 12CO(1-0) line and of the cores in the CH3CN(8-7) line and in
the millimeter continuum emission. Figure 6 shows
the maps of the
integrated emission in the 12CO(1-0) and C32S(3-2) lines: for the sake of
comparison, we also plot the positions of the four objects identified in Paper I.
We note that, while the C32S emission clearly outlines cores A and C, the main
12CO peak is not perfectly coincident with the cores. We believe that such
a disagreement is not real, but due to the complex structure of the 12CO gas
which cannot be properly mapped with the PdBI: this effect becomes dramatic
close to the line peak, where the emission is most extended and
hence difficult to image with an interferometer. This effect will be better
illustrated below (see Fig. 9). Another noticeable feature is the
absence of emission towards D. This result has already been discussed in
Paper I: here we recall that this represents evidence in favour of D
being depleted, as expected for a cold, dense protostellar core. Finally,
strong emission is detected towards B, which supports the conclusion
of Paper I that the YSO in B is more evolved - and hence no more enshrouded by
dense material.
It is also worth noting that in the NMA observations
a few lines of CH3OCH3 and C2H5CN
have been serendipitously detected.
These are seen
towards cores A and C, as illustrated in Fig. 7, which shows
the
spectra towards the peaks of these cores. Rare molecular species are indeed
commonly found in hot molecular cores, as demonstrated e.g. by the line
surveys in Orion (see e.g. Blake et al. 1996).
Figure 8 shows the spectra of the CH3CN(8-7) and C32S(3-2) lines
taken with the IRAM 30-m telescope and with the NMA. The latter has been
obtained by cleaning the NMA data with a restoring beam equal to that of the
30-m telescope. The 30-m spectrum has been resampled to the (lower) spectral
resolution of the interferometer. Within the noise, all the CH3CN emission
seen by the 30-m telescope is recovered with the NMA, which proves that the
CH3CN lines originate entirely from the A and C cores identified in Paper I.
On the contrary, a large fraction of the C32S emission is not imaged
in the core of the line. This is shown with better spectral resolution in
the right panels of Fig. 9, where we also present a comparison
between interferometric and single-dish maps obtained by integrating the
C32S(3-2) emission under the line. The left panels show the same thing for the
12CO(1-0) transition observed with the 30-m telescope and the PdBI.
As expected, the interferometric maps filter out extended structures and
are thus sensitive to the most compact, densest parts of the clump, i.e.
cores A and C. The large scale emission seen with the 30-m telescope is
instead completely resolved out by the PdBI and NMA. This effect is dramatic
close to the systemic velocity ( 110.3 km s-1), where line emission is
stronger and hence visible over more extended regions which cannot be imaged
with our interferometric observations. On the contrary,
the line wings are almost entirely recoverd.
We conclude that the morphology and kinematics of
the G24.78 cloud are very complex: that is why it is necessary to combine all
the information available to analyse the structure of the molecular gas in
this star forming region.
110.3 km s-1), where line emission is
stronger and hence visible over more extended regions which cannot be imaged
with our interferometric observations. On the contrary,
the line wings are almost entirely recoverd.
We conclude that the morphology and kinematics of
the G24.78 cloud are very complex: that is why it is necessary to combine all
the information available to analyse the structure of the molecular gas in
this star forming region.
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f07.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg47.gif) |
Figure 7:
Spectra towards the peak positions of cores A and C obtained with the NMA.
The y-axis scale is expressed in brightness temperature in the synthesised
beam of the interferometer.
The dotted vertical lines and corresponding labels indicate the position
of the CH3CN(8-7), C
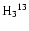 CN(8-7), and C32S(3-2) lines; also indicated are
the detected transitions of CH3OCH3(53,3-52,4),
CH3OCH3(71,7-60,6), and C2H5CN(171,17-161,16). CN(8-7), and C32S(3-2) lines; also indicated are
the detected transitions of CH3OCH3(53,3-52,4),
CH3OCH3(71,7-60,6), and C2H5CN(171,17-161,16). |
| Open with DEXTER |
In order to present an overview of the G24.78 region, we show in
Fig. 10 a composite map where the 12CO(1-0) line emission is
superimposed to the 20 cm continuum image extracted from the NRAO VLA Sky
Survey (NVSS; Condon et al. 1998). There is little doubt that we are
dealing with a high-mass star forming region: to the north, one can see an
extended H II region traced by the free-free continuum emission,
approximately coincident with a dip in a molecular ridge oriented
north-south. The water masers (triangles) pin point the position of the
cluster of massive YSOs studied in Paper I: these are located at the
south-eastern end of the ridge. It seems that we are observing a filament of
molecular gas undergoing different episodes of star formation, of which the
one associated with the masers appears to be the most recent.
In the following, we shall use all the available multi-tracer, multi-scale maps
of the G24.78 region to investigate the "anatomy'' of the molecular gas over
all scales ranging from  2 pc to
2 pc to  0.1 pc.
0.1 pc.
4.1 The clump
4.1.1 Density gradient
Massive YSOs are found embedded in dense molecular clumps a few parsecs in size.
Recently, Fontani et al. (2002) have suggested that the clumps
associated with high-mass YSOs might be on the verge of gravitational
collapse. Their hypothesis is based on the fact that the masses of such
clumps are systematically greater than the virial masses; also, they
find density gradients of the type
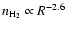 ,
with
R distance from the clump centre, similar to those characterising
singular isothermal spheres (Shu et al. 1987; Li 1999). We have
seen in Sect. 3.1.1 that also in the case of G24.78 the mass of the
clump is significantly greater than the corresponding virial mass. Now, we
want to study the density structure of the clump. For this purpose, we plot
in Fig. 11 the density estimated for each molecular tracer against
the corresponding radius (see Table 2). Although the values of the
masses derived from the CO isotopomers is quite uncertain for the reasons
discussed above, the two quantities are well correlated (corr. coeff. 0.92)
according to the relation
,
with
R distance from the clump centre, similar to those characterising
singular isothermal spheres (Shu et al. 1987; Li 1999). We have
seen in Sect. 3.1.1 that also in the case of G24.78 the mass of the
clump is significantly greater than the corresponding virial mass. Now, we
want to study the density structure of the clump. For this purpose, we plot
in Fig. 11 the density estimated for each molecular tracer against
the corresponding radius (see Table 2). Although the values of the
masses derived from the CO isotopomers is quite uncertain for the reasons
discussed above, the two quantities are well correlated (corr. coeff. 0.92)
according to the relation
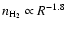 .
Although flatter
than that of Fontani et al. (2002), this curve confirms that the
density gradient is steep.
.
Although flatter
than that of Fontani et al. (2002), this curve confirms that the
density gradient is steep.
Another way to study the dependence of density upon radius in the clump is to
plot the column density,
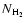 ,
obtained from an optically thin tracer
such as C18O(1-0), as a function of distance from the clump centre. In
order to obtain a mean value of
,
obtained from an optically thin tracer
such as C18O(1-0), as a function of distance from the clump centre. In
order to obtain a mean value of
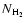 we have performed an azimuthal average
of the C18O(1-0) line brightness along equally spaced annuli centred on the
peak of the emission. Note that under the assumption of constant temperature
and optically thin emission,
we have performed an azimuthal average
of the C18O(1-0) line brightness along equally spaced annuli centred on the
peak of the emission. Note that under the assumption of constant temperature
and optically thin emission,
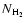 is proportional to the line brightness
temperature,
is proportional to the line brightness
temperature, 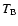 .
In Fig. 12 we plot the main beam brightness
temperature,
.
In Fig. 12 we plot the main beam brightness
temperature,
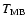 ,
normalised with respect to the peak value against the angular distance
from the centre divided by the FWHP of the clump (44
,
normalised with respect to the peak value against the angular distance
from the centre divided by the FWHP of the clump (44
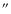 ,
according to
Table 2). This profile has been fitted with a power law after
convolution with the beam of the 30-m telescope. The best fit is obtained for
,
according to
Table 2). This profile has been fitted with a power law after
convolution with the beam of the 30-m telescope. The best fit is obtained for
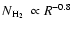 ,
which turns into a volume density
,
which turns into a volume density
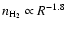 .
This is consistent with the value derived above.
.
This is consistent with the value derived above.
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f08.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg52.gif) |
Figure 8:
Comparison between the CH3CN(8-7) and C32S(3-2) spectra obtained with the
IRAM 30-m telescope (full histogram) and NMA (shaded histogram) towards the
position of core A. The two spectra have the same spectral and spatial
resolution, as explained in the text. |
| Open with DEXTER |
In conclusion, we believe that a density gradient as steep as
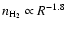 represents a good description of the internal structure of the
G24.78 clump. Theory (Shu et al. 1987) predicts an initial condition
for star formation corresponding to a singular isothermal sphere with density
represents a good description of the internal structure of the
G24.78 clump. Theory (Shu et al. 1987) predicts an initial condition
for star formation corresponding to a singular isothermal sphere with density
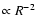 .
This sphere should rapidly undergo inside-out collapse with
the infalling gas having density
.
This sphere should rapidly undergo inside-out collapse with
the infalling gas having density
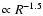 .
Note that our slope
is intermediate between these two values, which might suggest that, depending
on the tracer, we are sampling both the static outer region with slope -2and the collapsing inner region with slope -1.5. In Sect. 5 we
shall discuss this issue in better detail.
.
Note that our slope
is intermediate between these two values, which might suggest that, depending
on the tracer, we are sampling both the static outer region with slope -2and the collapsing inner region with slope -1.5. In Sect. 5 we
shall discuss this issue in better detail.
![\begin{figure}
\par {\includegraphics[angle=-90,width=13.5cm,clip]{h4079f09.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg55.gif) |
Figure 9:
Top panels: Same as Fig. 8 for the high spectral resolution
spectra of the C32S(3-2) (right panel) and 12CO(1-0) (left) lines.
Bottom panels: Overlay of the single-dish (contours) and interferometer
(grey scale) maps obtained by integrating the emission under the C32S(3-2)
(right) and 12CO(1-0) (left) lines over the
 range 105-116 km s-1.
The latter velocities are marked with vertical dotted lines in the top panels.
range 105-116 km s-1.
The latter velocities are marked with vertical dotted lines in the top panels. |
| Open with DEXTER |
4.1.2 Velocity field
Beside density gradients, also temperature variations must exist inside the
clump: in fact, Codella et al. (1997) measured temperatures as high as
90 K at  0.1 pc from the centre, whereas we have measured
0.1 pc from the centre, whereas we have measured  30 K in
a region 10 times larger. These findings indicate that also the excitation
temperature of some molecular species is likely to increase towards the
centre of the clump: in this case, self-absorption should be seen in optically
thick lines. Moreover, if the optically thick gas is undergoing expansion or
contraction, the absorption dip must be respectively blue- or red-shifted
with respect to the systemic velocity. Indeed, this expectation seems
confirmed by the profiles of the 12CO, 13CO, and C32S spectra of
Fig. 3, which present dips at the peak velocity of more optically
thin isotopomers such as C18O and C34S. In order to rule out the
possibility that such profiles are due to overlap of multiple
components, bf it is worth studying
the spatial distribution of the C32S(3-2) line
emission.
30 K in
a region 10 times larger. These findings indicate that also the excitation
temperature of some molecular species is likely to increase towards the
centre of the clump: in this case, self-absorption should be seen in optically
thick lines. Moreover, if the optically thick gas is undergoing expansion or
contraction, the absorption dip must be respectively blue- or red-shifted
with respect to the systemic velocity. Indeed, this expectation seems
confirmed by the profiles of the 12CO, 13CO, and C32S spectra of
Fig. 3, which present dips at the peak velocity of more optically
thin isotopomers such as C18O and C34S. In order to rule out the
possibility that such profiles are due to overlap of multiple
components, bf it is worth studying
the spatial distribution of the C32S(3-2) line
emission.
We computed mean profiles of the C32S(3-2) transition by averaging the
emission over circular annuli around the centre of the clump. The spectra
thus obtained towards the centre and at radial offsets in multiples of the
HPBW are shown in Fig. 13. Approaching the border of the clump, the
peak of the spectrum shifts towards the systemic velocity and the dip
disappears, consistently with self-absorption being most effective along the
line of sight through the centre, namely where the excitation temperature
gradient is maximum. Furthermore, the dip is blue-shifted with respect to the
systemic velocity, which indicates that the gas is expanding.
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f10.ps} }
\end{figure}](/articles/aa/full/2003/13/aah4079/Timg56.gif) |
Figure 10:
Comparison between the 12CO(1-0) map obtained by us with the IRAM 30-m
telescope and the 20 cm continuum image extracted from the NVSS database.
The 12CO emission has been integrated under the line: contour levels range
from 4 to 194 in steps of 10 K km s-1. The triangles mark the positions of the
H2O maser spots identified by Forster & Caswell (1999). |
| Open with DEXTER |
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f11.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg57.gif) |
Figure 11:
Plot of H2 volume density versus clump radius for all the tracers
observed by us. The values are taken from Table 2. An uncertainty
of a factor 3 has been assumed according to the discussion in Sect. 3.1.1.
The straight line is a linear fit to the data. |
| Open with DEXTER |
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f12.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg59.gif) |
Figure 12:
The histogram is a plot of the mean main beam brightness temperature
(
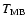 )
in the C18O(1-0) line versus the angular distance ( )
in the C18O(1-0) line versus the angular distance (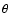 )
from the
centre of the clump. Both quantities are normalised: the former with respect
to the peak value, the latter with respect to the FWHP of the clump. The
mean has been obtained by averaging )
from the
centre of the clump. Both quantities are normalised: the former with respect
to the peak value, the latter with respect to the FWHP of the clump. The
mean has been obtained by averaging
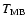 over equally spaced, concentric
annuli. The full line is the best fit to the data of a power law convolved
with the instrumental beam and corresponds to
over equally spaced, concentric
annuli. The full line is the best fit to the data of a power law convolved
with the instrumental beam and corresponds to
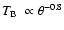 . . |
| Open with DEXTER |
Another line of evidence for the existence of blue-shifted self-absorption
can be obtained from the channel maps in the C32S(3-2) line. Without blue- or
red-shifted self-absorption the size measured in channels symmetrically
displaced with respect to the systemic velocity should be the same; if such a
self-absorption is present, instead, an asymmetry is introduced, so that the
peak emission in channels affected by self-absorption must be depressed. The
consequence of this effect is that the FWHP measured in self-absorbed
channels is larger; on the contrary, the size of the emission measured at a
3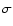 level must be unaffected because it reflects just the maximum size
of the clump at a given velocity. In order to verify these expectations, we
have measured the FWHP and the diameter at a 3
level must be unaffected because it reflects just the maximum size
of the clump at a given velocity. In order to verify these expectations, we
have measured the FWHP and the diameter at a 3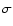 level (full width at
zero intensity; hereafter FWZI) in each channel of the C32S(3-2) line. These
are plotted in the bottom panel of Fig. 14: while the FWZI is
approximately symmetric with respect to the systemic velocity, the FWHP is by
far larger in the blue-shifted channels and reaches its maximum in
correspondence to the dip of the line profile.
level (full width at
zero intensity; hereafter FWZI) in each channel of the C32S(3-2) line. These
are plotted in the bottom panel of Fig. 14: while the FWZI is
approximately symmetric with respect to the systemic velocity, the FWHP is by
far larger in the blue-shifted channels and reaches its maximum in
correspondence to the dip of the line profile.
We conclude that we are observing blue-shifted self-absorption in the
C32S(3-2) line. The same result likely holds also for the optically thick CO
isotopomers, but in this case it is more difficult to apply the same analysis
to the data because of the presence of multiple spatial and spectral
components. Our finding has a twofold consequence: it supports the existence
of excitation temperature gradients (and hence density gradients) in the
clump; and it proves that at least part of the clump is expanding. In the
following, we shall investigate the origin of such an expansion by focusing
our analysis on the region where the compact, star-forming cores studied in
Paper I are located.
4.2 The core region
The structure and roundish appearance of the G24.78 clump indicate that on a
large scale the gas is still unaffected by the embedded YSOs. This implies
that on  1 pc one
might be observing the "primordial'' environment prior
to the current star formation episode. The same conclusion cannot hold
for the innermost regions, where the the gas has fragmented and condensed
into dense, compact cores which contain newly born massive YSOs heavily
interacting with the surrounding material.
1 pc one
might be observing the "primordial'' environment prior
to the current star formation episode. The same conclusion cannot hold
for the innermost regions, where the the gas has fragmented and condensed
into dense, compact cores which contain newly born massive YSOs heavily
interacting with the surrounding material.
In order to study the densest parts of the clump, one must use optically
thin tracers such as C34S. This is demonstrated by Fig. 15, where a
comparison is shown between the optical depth distributions of the
13CO(1-0), 13CO(2-1), C18O(1-0) and C34S(3-2) lines. The optical depth
estimates have been obtained from the ratios between 12CO and 13CO for the
13CO lines, from that between 13CO and C18O for C18O, and from that
between C32S and C34S for C34S. In all cases, such ratios have been computed
using the emission integrated under the line and the 13CO(2-1) map has been
smoothed to the same angular resolution as the C34S(3-2) map.
It is quite clear that the CO isotopomers trace the roundish, large scale
clump and are not sensitive to the small scale, densest parts of it. This
can be seen from the fact that the thickest regions in the 13CO and C18O transitions are only roughly coincident with the densest cores.
![\begin{figure}
\par {\includegraphics[angle=0,width=7.5cm,clip]{h4079f13.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg60.gif) |
Figure 13:
Mean profiles of the C34S(3-2) line at various offsets, 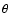 ,
from the
clump centre, as indicated in the right corner at the top of each panel. The
instrumental HPBW is 16 ,
from the
clump centre, as indicated in the right corner at the top of each panel. The
instrumental HPBW is 16
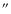 .
The vertical thin line corresponds to the
systemic velocity of 110.3 km s-1. .
The vertical thin line corresponds to the
systemic velocity of 110.3 km s-1. |
| Open with DEXTER |
![\begin{figure}
\par {\includegraphics[angle=0,width=7.5cm]{h4079f14.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg61.gif) |
Figure 14:
Top panel: profile of the C32S(3-2) line towards the centre of the clump.
Bottom panel: Comparison between the FWHP (full line) and FWZI (dashed line)
of the C32S(3-2) emission maps measured in different velocity channels.
The FWZI is the angular diameter of the contour corresponding to the
3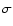 level in each channel. The vertical thin line marks the systemic
velocity of 110.3 km s-1.
level in each channel. The vertical thin line marks the systemic
velocity of 110.3 km s-1. |
| Open with DEXTER |
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f15.ps} }
\end{figure}](/articles/aa/full/2003/13/aah4079/Timg62.gif) |
Figure 15:
Top panel: maps of the mean optical depth in the C18O(1-0) (grey scale)
and 13CO(1-0) (contours) lines over the
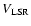 interval 105-116 km s-1.
Contour levels range from 0.15 to 0.4 in steps of 0.05 for C18O(1-0) and
from 0.35 to 0.65 in steps of 0.1 for 13CO(1-0). The white dotted contours
correspond to the 90% level of the 12CO(1-0) emission integrated under the
line.
Bottom panel: same as top panel for the C34S(3-2) (grey scale) and 13CO(2-1)
(contours) lines. Contour levels range from 0.4 to 1 in steps of 0.1 for
C34S and from 0.3 to 0.7 in steps of 0.1 for 13CO.
The triangles mark the positions of the H2O maser spots. The shaded circles
in the bottom left correspond to the instrumental HPBW. The 13CO(2-1) map
has been smoothed to the same resolution as the C34S(3-2) map.
interval 105-116 km s-1.
Contour levels range from 0.15 to 0.4 in steps of 0.05 for C18O(1-0) and
from 0.35 to 0.65 in steps of 0.1 for 13CO(1-0). The white dotted contours
correspond to the 90% level of the 12CO(1-0) emission integrated under the
line.
Bottom panel: same as top panel for the C34S(3-2) (grey scale) and 13CO(2-1)
(contours) lines. Contour levels range from 0.4 to 1 in steps of 0.1 for
C34S and from 0.3 to 0.7 in steps of 0.1 for 13CO.
The triangles mark the positions of the H2O maser spots. The shaded circles
in the bottom left correspond to the instrumental HPBW. The 13CO(2-1) map
has been smoothed to the same resolution as the C34S(3-2) map. |
| Open with DEXTER |
![\begin{figure}
\par {\includegraphics[angle=0,width=8.5cm]{h4079f16.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg63.gif) |
Figure 16:
Top: map of the C34S(3-2) line mean optical depth (grey scale) over the
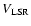 range 113-116 km s-1, superimposed to the C32S(3-2) emission integrated under
the line (contours) observed with the NMA. The triangles mark the positions
of the H2O maser spots by Forster & Caswell (1999). Contour
levels range from 0.35 to 2.15 in steps of 0.3 Jy/beam.
Bottom: map of the C34S(3-2) line mean optical depth (grey scale) over the
range 113-116 km s-1, superimposed to the C32S(3-2) emission integrated under
the line (contours) observed with the NMA. The triangles mark the positions
of the H2O maser spots by Forster & Caswell (1999). Contour
levels range from 0.35 to 2.15 in steps of 0.3 Jy/beam.
Bottom: map of the C34S(3-2) line mean optical depth (grey scale) over the
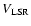 range 113-116 km s-1, superimposed to the outflow maps from Paper I. Full
and dashed contours represent respectively the blue- and red-shifted
12CO(1-0) line emission integrated under the wings from 90 to 105 km s-1 and
from 116 to 131 km s-1. Contour levels correspond to 1.1, 1.4, and 1.7 Jy/beam
(dashed contours) and 0.4, 0.6, 0.8, 1.2, and 1.6 Jy/beam (full contours).
range 113-116 km s-1, superimposed to the outflow maps from Paper I. Full
and dashed contours represent respectively the blue- and red-shifted
12CO(1-0) line emission integrated under the wings from 90 to 105 km s-1 and
from 116 to 131 km s-1. Contour levels correspond to 1.1, 1.4, and 1.7 Jy/beam
(dashed contours) and 0.4, 0.6, 0.8, 1.2, and 1.6 Jy/beam (full contours). |
| Open with DEXTER |
The situation for the C34S line is different.
This can be seen more clearly in the top panel of Fig. 16, where the
C32S(3-2) map obtained with the NMA is overlaied to the map of the optical
depth in the C34S(3-2) line. In this case, the computation of 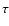 has
been performed using the integral under the red side of the line (from 113 to
116 km s-1), which is not affected by self-absorption. There is little doubt
that the largest column density in the C34S molecule corresponds
to the dense cores traced by the C32S emission. By comparing the C32S and
C34S maps one gets the impression that the cores are detached from
the surrounding gas, which forms a lower density halo around them.
We conclude that the C34S region seems to correspond to the transition
between the approximate spherical symmetry seen e.g. in the C32S line
and the clumpiness due to the formation of the compact cores.
This "symmetry break-up'' is also outlined by the presence of the bipolar
outflows detected in Paper I, which we discuss in the following.
has
been performed using the integral under the red side of the line (from 113 to
116 km s-1), which is not affected by self-absorption. There is little doubt
that the largest column density in the C34S molecule corresponds
to the dense cores traced by the C32S emission. By comparing the C32S and
C34S maps one gets the impression that the cores are detached from
the surrounding gas, which forms a lower density halo around them.
We conclude that the C34S region seems to correspond to the transition
between the approximate spherical symmetry seen e.g. in the C32S line
and the clumpiness due to the formation of the compact cores.
This "symmetry break-up'' is also outlined by the presence of the bipolar
outflows detected in Paper I, which we discuss in the following.
According to theory (Shu et al. 1987), a clump with density profiles of
the type
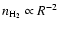 is bound to undergo inside-out collapse onto a
central protostellar core. This process should proceed until all the material
has accreted onto the protostar. However, other phenomena can modify this
simple picture: among these, outflows are believed to play a fundamental
role. In particular, they might reverse the infall and hence halt the
collapse thus setting a limit to the mass of the star. In the case of G24.78
two molecular outflows have been found in Paper I in association with cores A
and C. The bottom panel of Fig. 16 compares their morphology with
a map of the C34S optical depth,
is bound to undergo inside-out collapse onto a
central protostellar core. This process should proceed until all the material
has accreted onto the protostar. However, other phenomena can modify this
simple picture: among these, outflows are believed to play a fundamental
role. In particular, they might reverse the infall and hence halt the
collapse thus setting a limit to the mass of the star. In the case of G24.78
two molecular outflows have been found in Paper I in association with cores A
and C. The bottom panel of Fig. 16 compares their morphology with
a map of the C34S optical depth,  ,
over the velocity range 105-116 km s-1,
namely the whole line profile. Note that this differs from the map in the
top panel of the same figure where only the velocity range not affected by
self-absorption has been used for the estimate of
,
over the velocity range 105-116 km s-1,
namely the whole line profile. Note that this differs from the map in the
top panel of the same figure where only the velocity range not affected by
self-absorption has been used for the estimate of  .
Clearly, the
bottom map peaks towards the blue lobe of the flow from A: we interpret this
as the effect of self-absorption, which causes a decrease of the C32S line
intensity at blue-shifted velocities, hence increasing the ratio between
C34S and C32S and hence the corresponding estimate of
.
Clearly, the
bottom map peaks towards the blue lobe of the flow from A: we interpret this
as the effect of self-absorption, which causes a decrease of the C32S line
intensity at blue-shifted velocities, hence increasing the ratio between
C34S and C32S and hence the corresponding estimate of 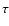 .
We conclude
that only the optical depth map in the top panel of Fig. 16
reflects the column density distribution of the gas: the one in the bottom
panel, instead, might be defined as a "pseudo-
.
We conclude
that only the optical depth map in the top panel of Fig. 16
reflects the column density distribution of the gas: the one in the bottom
panel, instead, might be defined as a "pseudo-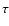 '' map, which indicates
where self-absorption is most effective. The fact that the pseudo-
'' map, which indicates
where self-absorption is most effective. The fact that the pseudo-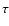 peaks towards the blue lobe of the flow from A demonstrates that the
expansion seen on a scale of
peaks towards the blue lobe of the flow from A demonstrates that the
expansion seen on a scale of  1 pc is due to the outflow from A.
1 pc is due to the outflow from A.
The prominence of the outflow from A with respect to that from C is evident
also in Fig. 17, which illustrates
a comparison between the outflows
mapped in different tracers and with different instruments. When observed
with high angular resolution (left panels) the 12CO and C32S lines trace both
outflows. At low angular resolution, instead, (right panels) the bipolar
flow is evident only towards A, which means that the outflow from A is
more extended. These characteristics are likely related to a difference in
age between the two flows, with that from A being older: such a conclusion
is important because it confirms the hypothesis made in Paper I, where we
suggested that in G24.78 one is observing a cluster of high-mass YSOs in
different evolutionary stages, with C younger than A.
5 A model for the G24.78+0.08 star forming region
Figure 18 is a sketch for the scenario we have in mind for the
G24.78 region. One is observing a molecular clump at the border of a star
forming cloud with filamentary shape. Beside the region of interest for us,
early-type stars have already ionised the surrounding gas over a few
parsecs. The YSOs observed in Paper I represent the most recent episode of
massive star formation in the cloud, as they are still deeply embedded in the
parental clump and not associated with extended H II regions, but with cores
and UC H II regions.
On a scale of  1 pc spherical symmetry is a reasonable representation
of the gas distribution, whereas inside
1 pc spherical symmetry is a reasonable representation
of the gas distribution, whereas inside  0.2 pc from the centre
the symmetry disappears and the material is concentrated in a few dense cores
with diameters of
0.2 pc from the centre
the symmetry disappears and the material is concentrated in a few dense cores
with diameters of  0.07 pc. Such a dishomogeneity is likely to be caused
by two processes: collapse and outflow. The former creates the small
cores inside which the YSOs have formed. The latter, powered by the YSOs
themselves, affects the molecular surroundings by accelerating part of
the clump gas towards the observer: this is seen in blue-shifted
self-absorption in the optically thickest transitions.
0.07 pc. Such a dishomogeneity is likely to be caused
by two processes: collapse and outflow. The former creates the small
cores inside which the YSOs have formed. The latter, powered by the YSOs
themselves, affects the molecular surroundings by accelerating part of
the clump gas towards the observer: this is seen in blue-shifted
self-absorption in the optically thickest transitions.
![\begin{figure}
\par {\includegraphics[angle=-90,width=13.5cm,clip]{h4079f17.ps} }
\end{figure}](/articles/aa/full/2003/13/aah4079/Timg66.gif) |
Figure 17:
Left panels: interferometric maps of the emission integrated under the line
wings superimposed to the corresponding continuum emission. Information
about the line and continuum observed are given in the top left of each panel.
Full contours correspond to integrals from 90 to 105 km s-1 and dashed
contours to integrals from 116 to 131 km s-1. Contour levels for 12CO(1-0) are
the same as in Fig. 16 (see also Fig. 2 of Paper I);
for C32S(3-2) they range from 0.1 to 0.6 in
steps of 0.1 Jy/beam. Triangles mark the positions of the H2O maser
spots. The crosses and corresponding labels indicate the location of the
YSOs identified in Paper I.
Right panels: same as left panels, for maps obtained with the IRAM 30-m
telescope. Contour levels range from 70 to 106 in steps of 12 K km s-1 for
12CO(2-1) and from 6 to 13.4 in steps of 1.85 K km s-1 for C32S(3-2). |
| Open with DEXTER |
In this scenario, the parsec-scale clump is only weakly affected by the embedded
YSOs and may hence be used as a template of the initial conditions prior to
the star formation episode. One possibility is that the gas density follows a
power law of the type
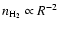 as expected for a singular
isothermal sphere. This configuration is unstable, consistently with the fact
that the clump mass is greater than the virial value. As a consequence,
inside-out collapse - and star formation - may have occurred inside a radius
as expected for a singular
isothermal sphere. This configuration is unstable, consistently with the fact
that the clump mass is greater than the virial value. As a consequence,
inside-out collapse - and star formation - may have occurred inside a radius
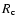 from the centre, where the theory predicts a density profile
from the centre, where the theory predicts a density profile
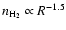 .
As already noted in Sect. 4.1.1, our findings
indicate a slope of -1.8, intermediate between that of the static region
and that of the inner collapsing layers. Indeed, in our study of the density
we have taken into account line emission from different scales, which might
mix up the contribution from different density laws and hence determine such
an "intermediate'' slope. If this is the case, one may wonder what is the
value of
.
As already noted in Sect. 4.1.1, our findings
indicate a slope of -1.8, intermediate between that of the static region
and that of the inner collapsing layers. Indeed, in our study of the density
we have taken into account line emission from different scales, which might
mix up the contribution from different density laws and hence determine such
an "intermediate'' slope. If this is the case, one may wonder what is the
value of 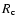 ,
i.e. the radius of the inner collapsing region.
,
i.e. the radius of the inner collapsing region.
We assume that the material collapsed inside 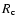 has formed the cores
observed in Paper I. The accretion rate
has formed the cores
observed in Paper I. The accretion rate
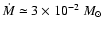 yr-1can be obtained from Eq. (23) of Shu et al. (1987), adopting a line
width
yr-1can be obtained from Eq. (23) of Shu et al. (1987), adopting a line
width
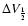 = 5 km s-1 (see Table 2). The age of the cores, i.e. the
time since the beginning of the collapse, is hence equal to
= 5 km s-1 (see Table 2). The age of the cores, i.e. the
time since the beginning of the collapse, is hence equal to
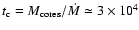 yr, where the total mass of the
cores,
yr, where the total mass of the
cores,
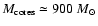 is obtained from Table 1 of Paper I.
During this period,
is obtained from Table 1 of Paper I.
During this period, 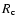 has moved outward at a speed equal to the measured
line width (Shu et al. 1987), so that at present it is equal to
has moved outward at a speed equal to the measured
line width (Shu et al. 1987), so that at present it is equal to
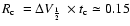 pc, corresponding to an angular diameter
of 8
pc, corresponding to an angular diameter
of 8
 .
This is in reasonable agreement with the size of the
C34S region where the spherical symmetry break-up is seen. One can
compute the infalling mass contained inside
.
This is in reasonable agreement with the size of the
C34S region where the spherical symmetry break-up is seen. One can
compute the infalling mass contained inside 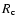 assuming that the mean
density is that
derived from C34S (see Table 2). The result is
assuming that the mean
density is that
derived from C34S (see Table 2). The result is  940
940 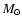 ,
indicating that
,
indicating that  50% of the mass inside
50% of the mass inside 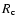 has already
accreted into the cores, while the remaining
has already
accreted into the cores, while the remaining  50% is still
in the collapsing envelope: this is
exactly what theoretical models (Shu et al. 1987) predict to happen
at any given time during the infall.
50% is still
in the collapsing envelope: this is
exactly what theoretical models (Shu et al. 1987) predict to happen
at any given time during the infall.
In the accretion scenario depicted above, one can speculate that infall does
not end onto the stellar surface, but instead creates the dense cores seen in
our interferometric maps, which in turn feed the embedded star through, e.g.
accretion from a circumstellar disk. Indeed, evidence for slightly flattened,
rotating cores has been found in objects similar to G24.78 (see e.g. Cesaroni
et al. 1994; Olmi et al. 1996; Cesaroni et al. 1999),
mostly through CH3CN line emission. Unfortunately, in our case the
spectral resolution attained with the NMA observations of the CH3CN(8-7)
transitions is insufficient to assess whether rotation exists in the cores.
However, the data are sufficient to demonstrate that such cores are
closer to virialisation than the parsec-scale clump: in fact, the ratio
between gas mass and virial mass is  8.5 for the C18O clump and only
8.5 for the C18O clump and only
 1.2 for the CH3CN cores (see Table 2). It seems that the
innermost part of the clump has reached an equilibrium configuration, as
expected for a stationary structure such as, e.g., a rotating disk.
Further, higher resolution observations are needed to unambiguously confirm
this interpretation.
1.2 for the CH3CN cores (see Table 2). It seems that the
innermost part of the clump has reached an equilibrium configuration, as
expected for a stationary structure such as, e.g., a rotating disk.
Further, higher resolution observations are needed to unambiguously confirm
this interpretation.
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f18.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg73.gif) |
Figure 18:
Sketch of the model for the G24.78 star forming region. The four objects A-D
identified in Paper I are embedded in a parsec-scale clump which is undergoing
inside-out collapse. Two bipolar molecular outflows with different size are
ejected from A and C: these have partly evacuated the infalling region.
Object B is associated with a relatively more evolved UC H II region which
according to Codella et al. (1997) is located in the foreground with
respect to the clump centre. Protostellar core D is likely to be located
behind the blue lobe of the outflow from A. |
| Open with DEXTER |
It must be pointed out that the accretion process must proceed on a free-fall
time, with the large mass accretion rate estimated above
(
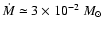 yr-1): the latter could overwhelm the
stellar radiation pressure and hence lead to the formation of the high-mass
YSOs. Moreover, this could also explain why we do not detect an UC H II region
in core C, although according to Paper I this is expected to contain high-mass
stars: in fact, such an accretion rate is sufficiently large to squelch the
ionised region even around an early O star (see e.g. Walmsley 1995).
On the basis of our results one can speculate that the stellar mass
will grow until the accretion process is stopped by the outflow powered by
the YSOs themselves. As a matter of fact, the outflow age (
yr-1): the latter could overwhelm the
stellar radiation pressure and hence lead to the formation of the high-mass
YSOs. Moreover, this could also explain why we do not detect an UC H II region
in core C, although according to Paper I this is expected to contain high-mass
stars: in fact, such an accretion rate is sufficiently large to squelch the
ionised region even around an early O star (see e.g. Walmsley 1995).
On the basis of our results one can speculate that the stellar mass
will grow until the accretion process is stopped by the outflow powered by
the YSOs themselves. As a matter of fact, the outflow age (
 yr; see
Paper I) is very similar to the age of the cores estimated above (
yr; see
Paper I) is very similar to the age of the cores estimated above (
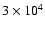 yr),
consistently with the idea that outflow and accretion are strictly related
phenomena. It is also interesting to compare the momentum in the outflow to
that in the infall: the former is derived from the parameters of the flows
given in Paper I and is equal to
yr),
consistently with the idea that outflow and accretion are strictly related
phenomena. It is also interesting to compare the momentum in the outflow to
that in the infall: the former is derived from the parameters of the flows
given in Paper I and is equal to 
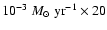 km s-1
km s-1
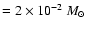 yr-1 km s-1; the latter is
yr-1 km s-1; the latter is

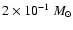 yr-1 km s-1, obtained multiplying the accretion
rate
yr-1 km s-1, obtained multiplying the accretion
rate 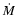 by the free-fall velocity (
by the free-fall velocity ( 6 km s-1) onto 900
6 km s-1) onto 900 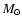 from a distance equal to
from a distance equal to
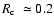 pc. The momentum in the infall is
pc. The momentum in the infall is  10 times greater than that in the outflows: however, one must take into
account that the latter is likely to be underestimated for a variety of
reasons. First of all, the interferometer may miss part of the emission from
the lobes, as demonstrated by the fact that the single-dish maps in the
12CO(2-1) line give for the outflow from A a mass
10 times greater than that in the outflows: however, one must take into
account that the latter is likely to be underestimated for a variety of
reasons. First of all, the interferometer may miss part of the emission from
the lobes, as demonstrated by the fact that the single-dish maps in the
12CO(2-1) line give for the outflow from A a mass  2 times larger than
that estimated from the PdBI maps of the 12CO(1-0) line. Moreover, one cannot
exclude that the 12CO transitions might be optically thick even in the line
wings. Finally, given the inclination of the flow with respect to the line of
sight, the real expansion velocity can be greater than the projected one.
One must also take into account the fact that we are observing just the
beginning of the star formation process in G24.78: this means that the
outflows might become more powerful as the evolution proceeds. Moreover,
additional sources might develop outflows, as it is reasonable to foresee in
the case of core D: if this contains high-mass protostars, as proposed in
Paper I, the latter are bound to contribute to the mass outflow rate in the near
future.
Therefore, one cannot exclude that outflows might contribute
significantly to stop or even reverse the infall, although such a speculation
cannot be proved on the basis of the current findings.
2 times larger than
that estimated from the PdBI maps of the 12CO(1-0) line. Moreover, one cannot
exclude that the 12CO transitions might be optically thick even in the line
wings. Finally, given the inclination of the flow with respect to the line of
sight, the real expansion velocity can be greater than the projected one.
One must also take into account the fact that we are observing just the
beginning of the star formation process in G24.78: this means that the
outflows might become more powerful as the evolution proceeds. Moreover,
additional sources might develop outflows, as it is reasonable to foresee in
the case of core D: if this contains high-mass protostars, as proposed in
Paper I, the latter are bound to contribute to the mass outflow rate in the near
future.
Therefore, one cannot exclude that outflows might contribute
significantly to stop or even reverse the infall, although such a speculation
cannot be proved on the basis of the current findings.
In conclusion, the G24.78 star forming region is an excellent
laboratory to study the formation process of high-mass stars. Our findings
suggest that such a process might occur through inside-out collapse with
large accretion rates and subsequent formation of dense molecular cores
which represent the cradle of early-type stars. Bipolar outflows are bound
to be driven by the YSOs and we speculate that they might stop the accretion
as soon as they become sufficiently powerful. This would result in a
self-regulating mechanism which allows the formation of massive stars through
accretion in a manner alike to that proposed for low-mass stars.
We have studied the molecular cloud associated with the high-mass star forming
region G24.78+0.08. Our analysis has been performed through single-dish and
interferometric observations of the continuum and molecular line emission,
thus sampling regions from a few parsecs down to 0.1 pc. The main findings
are as follows:
- The G24.78 region seems to represent the last star formation episode
in a filament of molecular gas extending approximately north-south. To the
north of such filament an extended H II region is seen, witnessing the
presence of older early-type stars.
- A roughly spherical clump is seen in various low-density tracers around
the massive YSOs identified in Paper I. Such an approximate spherical symmetry
breaks down inside
 0.2 pc from the centre, where dense, compact cores
are found.
0.2 pc from the centre, where dense, compact cores
are found.
- The density profile of the clump is well fitted by a power law with
slope -1.8, thus resembling that of a singular isothermal
sphere undergoing inside-out collapse.
- We make the hypothesis that the embedded high-mass YSOs might be formed
through inside-out collapse. This is supported by the fact that the expected
radius of the infalling region is comparable to that of the innermost,
heterogeneous region surrounding the cores; also, the mass of such a region
is very close to that of the cores, as foreseen for inside-out collapse.
- Single-dish observations in the 12CO(2-1) line demonstrate that the
bipolar outflow from core A found in Paper I is more extended, and hence
older, than that from core C: this confirms the evolutionary sequence
proposed in Paper I, where C is believed to be younger than A.
- The outflow age is comparable to the time scale required to accumulate
the mass of the cores, while the momentum in the flow could be sufficient
to stop the accretion rate of

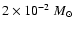 yr-1.
yr-1.
We suggest that G24.78 is an excellent laboratory to study the formation
of high-mass stars and the mechanism by which infall is reversed into
outflow thus setting the mass of the forming stars. Infall with large
accretion rates seems to represent a viable mechanism for high-mass star
formation in this region.
Acknowledgements
It is a pleasure to thank the staff of IRAM, NRAO, and NRO for carrying out
the observations and help provided during the data reduction. Special thanks
are due to Prof. Sachiko Okumura for taking care of our observations with the
Nobeyama Millimeter Array.
-
Blake, G. A., Mundy, L. G., Carlstrom, J. E., et al. 1996, ApJ, 472, L49
In the text
NASA ADS
-
Cesaroni, R., Walmsley, C. M., Kömpe, C., & Churchwell, E. 1991, A&A, 252, 278
In the text
NASA ADS
-
Cesaroni, R., Olmi, L., Walmsley, C. M., Churchwell, E., & Hofner, P. 1994,
ApJ, 435, L137
In the text
NASA ADS
-
Cesaroni, R., Felli, M., Jenness, T., et al. 1999, A&A, 345, 949
In the text
NASA ADS
-
Codella, C., Testi, L., & Cesaroni, R. 1997, A&A, 325, 282
In the text
NASA ADS
-
Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693
In the text
NASA ADS
-
Felli, M., Palagi, F., & Tofani, G. 1992, A&A, 255, 293
In the text
NASA ADS
-
Fontani, F., Cesaroni, R., Caselli, P., & Olmi, L. 2002, A&A, 389, 603
In the text
NASA ADS
-
Forster, J. R., & Caswell, J. L. 1989, A&A ,213, 339
In the text
NASA ADS
-
Forster, J. R., & Caswell, J. L. 1999, A&AS, 137, 43
In the text
NASA ADS
-
Furuya, R. S., Cesaroni, R., Codella, C., et al. 2002, A&A, 390, L1 (Paper I)
In the text
NASA ADS
-
Irvine, W. M., Goldsmith, P. F., & Hjalmarson, H. 1987, Interstellar Processes,
ed. D. J. Hollenbach, & H. A. Thronson, 561
In the text
-
Li, Z. 1999, ApJ, 526, 806
In the text
NASA ADS
-
Moscadelli, L., Cesaroni, R., & Rioja, M. J. 2000, A&A, 360, 663
In the text
NASA ADS
-
Okumura, S. K., Momose, M., Kawaguchi, N., et al. 2000, PASJ, 52, 393
In the text
NASA ADS
-
Olmi, L., Cesaroni, R., & Walmsley, C. M. 1993, A&A, 276, 489
In the text
NASA ADS
-
Olmi, L., Cesaroni, R., Neri, R., & Walmsley, C. M. 1996, A&A, 315, 565
In the text
NASA ADS
-
Palla, F., & Stahler, S. W. 1993, ApJ, 418, 414
In the text
NASA ADS
-
Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23
In the text
NASA ADS
-
Stahler, S., Palla, F., & Ho, P. T. P. 2000, in Protostars and Planets IV,
ed. V. Mannings, A. Boss, & S. Russel (Tucson: Univ. of Arizona Press), 327
In the text
-
Walmsley, C. M. 1995, Rev. Mex. Astron. Astrofis., Ser. Conf., 1,
137
In the text
-
Wilner, D. J., & Welch, W. J. 1994, ApJ, 427, 898
In the text
NASA ADS
-
Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[angle=0,width=13cm,clip]{h4079f01.ps}
\end{figure}](/articles/aa/full/2003/13/aah4079/Timg28.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f02.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg31.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f03.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg32.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f04.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg33.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f05.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg40.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f06.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg46.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f07.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg47.gif)
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f08.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg52.gif)
![\begin{figure}
\par {\includegraphics[angle=-90,width=13.5cm,clip]{h4079f09.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg55.gif)
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f10.ps} }
\end{figure}](/articles/aa/full/2003/13/aah4079/Timg56.gif)
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f11.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg57.gif)
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f12.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg59.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=7.5cm,clip]{h4079f13.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg60.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=7.5cm]{h4079f14.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg61.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=8.8cm,clip]{h4079f15.ps} }
\end{figure}](/articles/aa/full/2003/13/aah4079/Timg62.gif)
![\begin{figure}
\par {\includegraphics[angle=0,width=8.5cm]{h4079f16.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg63.gif)
![\begin{figure}
\par {\includegraphics[angle=-90,width=13.5cm,clip]{h4079f17.ps} }
\end{figure}](/articles/aa/full/2003/13/aah4079/Timg66.gif)
![\begin{figure}
\par {\includegraphics[angle=-90,width=8.8cm,clip]{h4079f18.ps} }\end{figure}](/articles/aa/full/2003/13/aah4079/Timg73.gif)