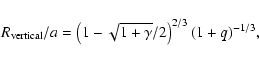A&A 401, 325-337 (2003)
DOI: 10.1051/0004-6361:20030115
Is evidence for enhanced mass transfer during dwarf-nova
outbursts well substantiated?
Y. Osaki 1 - F. Meyer 2
1 - Faculty of Education, Nagasaki University, Nagasaki
852-8521, Japan
2 -
Max-Planck-Institut für Astrophysik, Karl Schwarzschild Str. 1,
85740 Garching, Germany
Received 16 October 2002 / Accepted 21 January 2003
Abstract
Outburst mechanisms of SU UMa-type dwarf novae are discussed. Two competing
models were proposed; a pure disk instability model called the
thermal-tidal instability model (TTI model) and the enhanced mass transfer
model (EMT model). Observational evidence for enhanced mass transfer
from the secondary star during outbursts is critically examined. It is
demonstrated that most evidence for enhanced mass transfer is not well
substantiated.
Patterson et al. (2002) have recently claimed to have found
evidence for enhanced mass transfer during the 2001 outburst of WZ Sge.
We show that their evidence is probably due to a misinterpretation of their observed light
curves. Our theoretical analysis also shows that irradiation during
outburst should not affect the mass transfer rate.
A refinement of the TTI model is proposed that can explain
why superhumps appear a few days after the superoutburst maximum
in some SU UMa stars.
We present our own interpretation of the overall development of
the 2001 outburst of WZ Sge based on the TTI model that does not
require the assumption of an unproved enhanced mass transfer.
Key words: accretion, accretion disks - binaries: close -
novae, cataclysmic variables - stars: dwarf novae -
stars: individual: WZ Sge
SU UMa stars are dwarf novae of short orbital periods that show two distinct
types of outbursts, called short normal outburst and long superoutburst
(see, e.g., Warner 1995 for dwarf novae in general and SU UMa stars in
particular).
In ordinary SU UMa stars several short normal outbursts are sandwiched
between two consecutive superoutbursts. The cycle from one superoutburst
to the next is called supercycle.
During the superoutburst periodic humps called superhumps
appear that repeat with a period slightly longer than the binary
orbital period.
The superhump phenomenon in SU UMa stars is now well understood in terms of
the tidal instability (Whitehurst 1988; Hirose & Osaki 1990; Lubow 1991):
superhumps are produced by periodic tidal stressing of the eccentric
precessing accretion disk which is formed by the 3:1 resonance tidal
instability.
The short normal outburst of SU UMa stars is thought to be essentially
the same as the outburst of U Gem stars and is believed to be caused by
the thermal instability in the accretion disk. For the superoutburst
and supercycle of SU UMa stars Osaki (1989) has proposed the thermal-tidal
instability model (TTI model) in which the ordinary thermal
instability is coupled with the tidal instability.
Based on the TTI model, Osaki (1996) has presented a unification model
for outbursts of dwarf novae in which a rich variety of outburst behaviors of
non-magnetic cataclysmic variable stars is understood within the general
framework of the disk instability model.
Although the TTI model is basically successful in explaining
the superoutburst phenomenon of SU UMa stars, there still remains
some deficiency. Hellier (2001) has suggested
a minor modification to the TTI model in the case of binary
systems with extremely low mass ratio.
Moreover, objections to the TTI model were raised by
Smak (1996, 2000) and by Lasota's group (see Lasota 2001 for
a review of his group's view of this problem).
They argue that enhanced mass transfer, likely caused
by irradiation of the secondary star by the central source of radiation,
is responsible for the superoutburst of SU UMa stars (EMT model).
Historically speaking, an enhanced mass transfer model by an irradiated
secondary was proposed by Osaki (1985) to explain superoutbursts of SU UMa stars but this model was later abandoned
by its author in favor of the TTI model (Osaki 1996).
On page 486 of his (2001) review, Lasota made the following statement:
"the main deficiency of the TTI model is that it neglects a property of SU UMa stars and dwarf novae outbursts in general: the observed enhancement
of the mass-transfer rate during outbursts."
The purpose of this paper is to examine critically whether
Lasota's statement, i.e., the enhancement of the mass-transfer
during outbursts, is observationally and theoretically substantiated.
Patterson et al. (2002) recently presented extensive photometry
observations of the 2001 superoutburst of WZ Sge.
From eclipse observations during the main outburst
of WZ Sge in 2001 they claim that the mass transfer rate was enhanced
by a factor of up to 60 from its quiescent value.
We also discuss these observations and their interpretation.
In Sect. 2, we examine the various claims for enhanced mass
transfer and we show that most evidence is not well founded.
Our theoretical analysis in Sect. 3 shows severe problems for
any model that claims an effect of irradiation on the mass transfer
rate in outburst.
In response to Smak's (1996, 2001) criticism of the TTI model, we propose
in Sect. 4 a refinement of the TTI model that explains why
superhumps appear a few days after the superoutburst maximum
in some SU UMa stars.
After thus having demonstrated that enhanced
mass transfer during outburst is not well substantiated, we present
our own interpretation for the overall development of the 2001
outburst of WZ Sge in Sect. 5. In the Appendix, we critically discuss
the new interpretation of the early hump phenomenon by Kato (2002).
A conclusion of the paper is given in Sect. 6.
Periodic humps appeared during the first 10 days of the 1978 outburst of WZ Sge
that repeated with the orbital period. These humps have been called either
"outburst orbital humps" or "early superhumps". Here we call them
simply "early humps" (see the discussion in Osaki & Meyer 2002).
It is interesting to note that the early hump phenomenon was used
as evidence for enhanced mass transfer in two different ways
by Patterson et al. (1981) and by Smak (1993).
Patterson et al. (1981) interpreted the humps repeating with the orbital
period in the first 10 days of the 1978 outburst as brightening
of the hot spot caused by enhanced mass transfer.
However they had a difficulty with this interpretation
since the position of the hot spot would have had to move azimuthally
by 60 degrees from its quiescent position. The double hump nature of
early humps observed in the 2001 outburst of WZ Sge also is difficult
to explain by a hot spot brightening (Osaki & Meyer 2002).
Smak (1993) on the other hand took the early humps observed
in the 1978 WZ Sge outburst as evidence for a heated secondary. But also
he had a difficulty with the phase of maximum visibility of the
irradiated surface of
the secondary star. Nevertheless, he calculated the temperature of the
heated surface of the secondary star by assuming that radiation
of the central source intercepted by the secondary star is
thermalized in the photosphere and raises the surface temperature
of the secondary star. This point will be discussed in the next section.
However, if the early hump phenomenon is of disk origin
due to a non-axisymmetric structure produced by tidal effects
in our 2:1 resonance model (Osaki & Meyer 2002) or
in Kato's model (Kato 2002), the evidence for a brightened hot spot
or for a heated secondary star
disappears. Thus the early hump phenomenon of WZ Sge stars can not
be taken as evidence for enhanced mass transfer from the secondary star.
One piece of evidence for enhanced mass transfer referred
to by Smak (1996) was
found in the observational review of VW Hyi by Vogt
(1983). Vogt noted that significant enhancements in the hump amplitude
during short eruptions were present in only four of nine cases and
that all four cases were confined to those occurring less than 40 days
from the next superoutbursts, summarized in Fig. 4 of his paper.
In Vogt's picture, enhanced humps observed in maximum or decline
of normal short eruptions of VW Hyi were due to brightening
of the hot
spot and the enhanced amplitudes of the hot spot were evidence
for an enhanced mass transfer from the secondary star. We question
Vogt's interpretation of the enhanced orbital humps in these
four cases. Instead we suggest that the observed humps
rather are of superhump nature in an embryonic form.
By superhumps in an embryonic form we mean superhumps in the
early stage of their growth. Such embryonic
superhumps were observed in precursor outbursts in T Leo by Kato (1997) and
in V436 Cen by Semeniuk (1980).
Observations discussed below were done a quarter of a century ago and
this question can be easily settled by new observations with CCD. We
urge observers to make such observations.
In fact, the normal outburst, claimed by Vogt (1983) to have
exhibited a 15 times increase in hot spot brightness,
was the precursor outburst of the May 1977 superoutburst of VW Hyi observed
by Marino & Walker (1979). If we compare the light curve of this
superoutburst (Fig. 4 of Marino & Walker 1979) with those of the 1993
January superoutburst of T Leo observed by T. Kato (Figs. 1 and 2
of Kato 1997), we find they are very similar, exhibiting basically
the same phenomenon. Kato (1997) has found that the hump period during
decline from the precursor outburst of T Leo in January
1993 is 2.4% longer than the orbital period and thus these humps are
embryonic superhumps rather than orbital humps. In the case of the
precursor outburst in the decline stage of the May 12, 1977 outburst
observed by Marino
and Walker, only three hump maxima were seen and it would be difficult
to determine their exact period in order to decide whether they are enhanced
orbital humps or embryonic superhumps.
Marino & Walker (1979) found another hump-like feature in the decline
of the 1978 October normal outburst of VW Hyi which occurred
160 days after the previous superoutburst (the mean supercycle of VW Hyi
is 180 days), but they were puzzled because the observed hump feature
looked like a superhump with a period similar to that of superhumps
rather than that of orbital humps.
We interpret these humps as indeed embryonic superhumps
that failed to develop into fully-grown superhumps and superoutburst.
Two of the four cases claimed to exhibit an enhanced hot spot
by Vogt (1983) were the same two observations by Marino & Walker
(1979) discussed above.
The other two cases were those observed by Haefner et al. (1979).
These two are outbursts designated as No. 280 and No. 281 which occurred
around Nov. 15 and Nov. 26, 1974 while the next superoutburst
designated as No. 282 occurred around Dec. 7/8 in 1974. With respect to
the outburst
No. 281, light curves for three consecutive nights were shown in Fig. 4
of Haefner et al. (1979). The phases of the hump maxima in the first
and third night agreed with those expected from the quiescent hump
ephemeris while the phase of the biggest hump in the second night
was shifted by 0.5 from that expected. Haefner et al. (1979)
interpreted this hump maximum observed in the second night as
a secondary maximum sometimes seen in quiescent orbital humps.
However, another interpretation is possible. If we combine
the hump maxima in all three nights in one ephemeris, we would get
a hump period exceeding the orbital period by 3.8% (i.e., a beat period
of 2 days between the orbital and superhump periods). Thus these humps
in outburst No. 281 of VW Hyi could well be interpreted as embryonic
superhumps which failed to develop into fully-grown superhumps
rather than as orbital humps. No light curves for the outburst
No. 280 of VW Hyi are available in published form. However,
the enhancement of hump amplitude in this outburst claimed by Vogt
(1983) was rather small (the smallest among the four cases,
i.e., enhancement less than 5 in Vogt 1983) and we do not
discuss this outburst any further.
In conclusion, the evidence for enhanced mass transfer presented
by Vogt (1983) is not sufficient to substantiate the claim
that the mass transfer rate is enhanced in the maximum and decline stages
of normal outbursts if they occur near the next superoutburst.
Patterson et al. (2002) have presented extensive photometric
observations of the 2001 outburst of WZ Sge. During a first stage of
about 12 days early humps (outburst orbital humps or "OOH'' in
Patterson et al. 2001) were visible. This stage is discussed in Osaki & Meyer
(2002). In the following stage common superhumps were observed. Eclipses
suddenly appeared with the growth of the superhumps and were visible
all the way from the main outburst stage through the so called echo
outburst stage up to the final decline.
By synchronous summation of the superhump light curves at the orbital
period through out the beat phase between orbital and superhump period
Patterson et al. (2002) obtained "orbital lightcurves'' that looked
like those of the quiescent orbital hump (lowest right panel of their
Fig. 7 and left panel of their Fig. 16). Therefore the authors interpreted
them as hot spot light curves and the eclipses observed as eclipses of
the mass transfer hot spot. By comparing intensity amplitudes of
the hump light they concluded that the mass transfer rate during this
stage had increased by a factor up to 60 above the quiescent
level. This would strongly challenge the TTI model of SU UMa star
outbursts.
We now give evidence that the orbital hump simply results from the
orbital aspect of the superhump dissipation pattern in high
inclination systems like WZ Sge, and that the observed eclipses are
eclipses of the superhump light source itself. Thus an increased hot
spot brightness and the inferred increased mass transfer rate
are spurious, the result of a misinterpretation of observed light
curve.
We first note that the basic pattern of light curves during the common
superhump stage repeats more or less with the superhump beat period
of roughly 5 days. Eclipses were visible for only half of these beat
phases. Eclipse characteristics such as eclipse depth, eclipse width,
and time of mid-eclipse in the orbital light curve all were functions of
the beat phase (see Fig. 21 of Patterson et al. 2002).
Now the superhump light variation is an intrinsic variation produced
by time varying dissipation as the secondary orbits the eccentric
disk. But the dissipation pattern is also extremely non-axisymmetric
as can be seen e.g. in hydrodynamic simulations by Hirose & Osaki
(1990, their Fig. 7b) and Murray (1998, his Fig. 8). Figure 1 shows the
superhump dissipation pattern for the four (out of nine) phases around
superhump maximum from Murray's Fig. 8. The most conspicuous feature
in the simulations is the appearance of an arch-like tail that
extends near to the edge of the primary Roche lobe when the
dissipation is strong (near superhump maximum). Part of this arch-like
tail can be eclipsed in the case of WZ Sge. When the tidal dissipation
is weak (superhump minimum) no conspicuous feature in the tidal
dissipation is visible and as far as the dissipative light is
concerned the disk looks compact and circular.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H4045F1.ps}\end{figure}](/articles/aa/full/2003/13/aah4045/Timg2.gif) |
Figure 1:
Superhump dissipation pattern (black dots) in hydrodynamic
simulations for four different superhump phases around superhump
maximum. Axes: Cartesian coordinates in orbital plane in units of
binary separation. Contour line: primary Roche lobe; time: time
elapsed in simulation in units of orbital period /2 ;
number
within Roche contour: strength of dissipation (arbitrary unit). After
Murray (1999). ;
number
within Roche contour: strength of dissipation (arbitrary unit). After
Murray (1999). |
| Open with DEXTER |
The tidal dissipation of the superhumps occurs near the disk rim in a
region about 1/10 of the disk radius wide (see Fig. 1). This is the
same size as the estimated half thickness of the disk at its rim. Thus
about one half of the superhump light may be expected to be radiated
from the two horizontal disk surfaces and one half from a more or less
vertical disk rim. The radiation pattern of the latter part is
strongly dependent on the orbital aspect of the observer.
We have estimated how much light an observer near the orbital plane
would receive from this component due to the projection of its
radiating surface at the various orbital phases for all nine
superhumps phases displayed in Fig. 8 of Murray (1998). The resulting
orbital light curves are shown in Fig. 2. Note the strong variation of
the total dissipated light given by the numbers inside the individual
graphs. An intensity weighted superposition of these graphs yields an
"orbital light curve'', that corresponds to the synchronous
superposition of the superhump light curves at the orbital period by
Patterson et al. Figure 3
gives the resultant light curve. It shows a hump with maximum phase
around 0.75 and extending over half the orbital periods in fairly good
agreement with the observed light curve shown in Fig. 7 of Patterson
et al. (2002). The strong asymmetry of the superhump dissipation pattern thus naturally can explain the apparent orbital
hump and no increased hot spot light is needed.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H4045F2.ps}\end{figure}](/articles/aa/full/2003/13/aah4045/Timg3.gif) |
Figure 2:
Estimated orbital light curves from superhump dissipation
pattern projected for an observer at high inclination for 9 different
superhump phases from Murray's (1999) simulation. Horizontal axis:
orbital phase; vertical axis: intensity in arbitrary units; number on
top: time elapsed in simulation in units of orbital period /2 ;
number inside frame: strength of dissipation (arbitrary unit). ;
number inside frame: strength of dissipation (arbitrary unit). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{H4045F3.ps}\end{figure}](/articles/aa/full/2003/13/aah4045/Timg4.gif) |
Figure 3:
Superposition of the nine light curves of Fig. 2 weighted by
their relative dissipation strength. Horizontal axis: orbital phase;
vertical axis: intensity (arbitrary unit). This corresponds to a
synchronous summation at the orbital period of observed superhump light
curves. |
| Open with DEXTER |
There is even intrinsic evidence in Patterson's et al. (2002) data
that the observed orbital light curves and eclipses are indeed due to
the superhump light source and not due to a mass transfer hot spot. In
Fig. 18 Patterson et al. (2002) show the changes of eclipse depth and
orbital wave height as evidence for a changing mass transfer
rate. However these two variations closely follow the variation of the
superhump light amplitude itself, listed in their Table 3. This
indicates that it is the superhump light source which is eclipsed and
whose aspect varies with the orbital phase rather than a hot spot.
Why are eclipses not observed in the first 12 days of the outburst
when the early humps (or "OOH'') were seen? Osaki & Meyer (2002)
have suggested that early humps are produced by the two-armed
dissipation pattern of the 2:1 Lindblad resonance. Though at the disk
rim this spiral dissipation pattern is located azimuthally far away
from the secondary star (Fig. 3a in Lin & Papaloizou 1979). Thus it is
fairly likely that this light is not eclipsed.
We conclude that there is no evidence for enhanced mass transfer in
the common superhump stage of the 2001 outburst of WZ Sge.
Another case quoted by Smak (1996) as evidence for enhanced mass
transfer are eclipse observations during the superoutburst of Z Cha by
Warner & O'Donoghue (1988). O'Donoghue (1990) analyzed these
observations and found that, with the exception of one case, the
superhump light source was not confined to the hot spot region. In one
exceptional case called eclipse 77878 (Fig. 2a in Warner &
O'Donoghue 1988), he found that all superhump light was confined to a
region near the position of the quiescent hot spot. O'Donoghue (1992)
concluded that "as the bright spot during this eclipse is more than
twenty times as luminous as at quiescence, a brief period (due to the
rarity of this kind of eclipse) of enhanced mass transfer is the most
natural explanation''.
However, if we recall that the superhump light source is extremely
non-axisymmetric and mostly confined to an arch-like tidal tail
extending in the following lune of the accretion disk, it is most
natural to assume that the light source eclipsed in eclipse 77878 was
just the superhump light source itself rather than the hot spot.
In fact, as the light curve of eclipse 77878 in Warner & O'Donoghue
(1988) shows, the eclipse occurred at the rising phase to the superhump
maximum and the shoulder of the superhump light curve was eclipsed. We
may conclude that what was eclipsed in this case is also the superhump
light source itself and not a hot spot, and that there is no evidence
for enhanced mass transfer in this case either.
In the preceding sections we have shown that all claimed
evidence for increased mass transfer in outbursts of
cataclysmic variables is inconclusive, partially
contradictory, and in all cases can be explained otherwise, in
fact supporting the TTI model in its various features.
What is the situation from the theoretical side?
The luminosity often rises in outburst by orders of magnitude and one
might expect strong irradiation of the secondary star, raising the
surface temperature and lifting gas higher up in the gravitational
potential. Why should this not lead to a density increase in the
Lagrange point  and an increase of the mass overflow rate?
There are however well known difficulties with this simple picture,
and we show in the following that simple quantitative estimates in the
complex physical situation yield prohibitive limits on the increase of
the mass overflow. We will perform the estimates for the case of WZ
Sge. This should be a particularly sensitive system for such effects
because of the possibly very low surface temperature of its secondary
star and an extremely high luminosity increase in the outburst.
and an increase of the mass overflow rate?
There are however well known difficulties with this simple picture,
and we show in the following that simple quantitative estimates in the
complex physical situation yield prohibitive limits on the increase of
the mass overflow. We will perform the estimates for the case of WZ
Sge. This should be a particularly sensitive system for such effects
because of the possibly very low surface temperature of its secondary
star and an extremely high luminosity increase in the outburst.
The main problems with an irradiation effect on the mass transfer
are due to (1) the shadow that the accretion disk casts on the  point and (2) the high opacity in the extreme ultraviolet band which
prevents the bulk of the radiative flux from reaching the stellar
photosphere at all. In addition (3) the light that penetrates to the stellar
surface heats up the subsurface layers but this heated material cannot
effectively move towards the shadowed
point and (2) the high opacity in the extreme ultraviolet band which
prevents the bulk of the radiative flux from reaching the stellar
photosphere at all. In addition (3) the light that penetrates to the stellar
surface heats up the subsurface layers but this heated material cannot
effectively move towards the shadowed  point since strong
Coriolis forces prevent it from moving into the lower pressure region
there.
point since strong
Coriolis forces prevent it from moving into the lower pressure region
there.
Light sources are the white dwarf, the inner accretion disk and possibly a
corona above the inner disk. Important for our analysis of the effect
of irradiation is to which degree the disk casts a shadow on the
region around  .
.
Disk structure computations allow determination of the thickness of the
accretion disk in the outburst. Near the outer radius 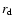 of
the disk at 1010.4 cm around a white dwarf of mass
of
the disk at 1010.4 cm around a white dwarf of mass
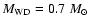 and for an estimated accretion rate for WZ Sge in the early phase of outburst of
and for an estimated accretion rate for WZ Sge in the early phase of outburst of
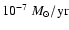 one obtains (Meyer & Meyer-Hofmeister 1982) for the height of the
disk photosphere above the midplane
one obtains (Meyer & Meyer-Hofmeister 1982) for the height of the
disk photosphere above the midplane
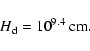 |
(1) |
The height varies weakly with the accretion rate, proportional to
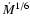 .
This height
.
This height 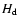 is larger than the radius of
the white dwarf
is larger than the radius of
the white dwarf
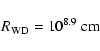 |
(2) |
(Nauenberg 1972). It is also larger than the vertical extent of the
mass transfer cross section in the  point. The latter is
obtained as the vertical scaleheight of a gas column of temperature
T0 in the Roche geometry at
point. The latter is
obtained as the vertical scaleheight of a gas column of temperature
T0 in the Roche geometry at  (e.g. Meyer &
Meyer-Hofmeister 1983; Kolb & Ritter 1990). For the assumed mass ratio q=0.1and a surface temperature
T0=103.2 K of the secondary this gives
(e.g. Meyer &
Meyer-Hofmeister 1983; Kolb & Ritter 1990). For the assumed mass ratio q=0.1and a surface temperature
T0=103.2 K of the secondary this gives
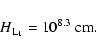 |
(3) |
The value varies proportional to T01/2. This means the region around
 is in the shadow of the disk rim.
Even light from a corona above the inner disk is shielded by the disk
rim since the height
is in the shadow of the disk rim.
Even light from a corona above the inner disk is shielded by the disk
rim since the height 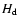 of the accretion disk rim is also larger than
the scaleheight of a corona
of the accretion disk rim is also larger than
the scaleheight of a corona 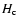 above the inner accretion
disk, for a coronal temperature of 108 K at the distance r=109 cm from
the white dwarf
above the inner accretion
disk, for a coronal temperature of 108 K at the distance r=109 cm from
the white dwarf
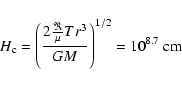 |
(4) |
with 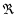 gas constant,
gas constant, 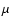 molecular weight, G gravitational constant.
molecular weight, G gravitational constant.
We conclude that the region of mass transfer at  lies deep in
the shadow band that extends 109.4 cm to both sides of the equator
of the secondary star for any light that comes from the white dwarf,
an inner disk or a corona above the inner disk.
lies deep in
the shadow band that extends 109.4 cm to both sides of the equator
of the secondary star for any light that comes from the white dwarf,
an inner disk or a corona above the inner disk.
While the mass transfer point  lies in the center of the
broad shadow of the accretion disk and receives no direct light the
possibility remains that irradiation raises the temperature
outside of this shadow zone and that by exchange of heated material
from the irradiated part with cool material in the shadow zone below
lies in the center of the
broad shadow of the accretion disk and receives no direct light the
possibility remains that irradiation raises the temperature
outside of this shadow zone and that by exchange of heated material
from the irradiated part with cool material in the shadow zone below
 the temperature also rises there. That could still result
in an increased mass transfer. We now discuss the physical aspect
of this situation in order to see whether there is an effect
on the mass transfer rate.
the temperature also rises there. That could still result
in an increased mass transfer. We now discuss the physical aspect
of this situation in order to see whether there is an effect
on the mass transfer rate.
First we derive an estimate for the temperature of the irradiated
surface of the secondary star. In quiescence the surface receives the
radiation from the hot white dwarf,
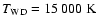 (Cheng
et al. 1997). If this radiation is fully absorbed and reradiated from
the secondary surface as black body radiation its temperature at the distance
closest to the white dwarf would be
(Cheng
et al. 1997). If this radiation is fully absorbed and reradiated from
the secondary surface as black body radiation its temperature at the distance
closest to the white dwarf would be
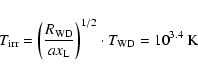 |
(5) |
where
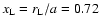 is the distance of
is the distance of  from
the primary in units of the separation a, here for the assumed
mass ratio q=0.1.
from
the primary in units of the separation a, here for the assumed
mass ratio q=0.1.
In outburst, with the accretion rate
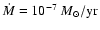 ,
the accretion luminosity of the white dwarf will rise to the value
,
the accretion luminosity of the white dwarf will rise to the value
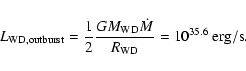 |
(6) |
The corresponding effective temperature is
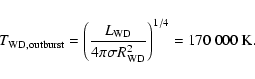 |
(7) |
Radiation of this temperature lies in the extreme ultraviolet and
supersoft X-ray range with wavelengths around 200 Å where
opacities are very large. Such radiation cannot reach the surface of
the secondary star but is absorbed and reradiated in high layers of the
secondary's atmosphere (see Suleimanov et al. 1999 for the analogous
case of supersoft X-ray sources for a detailed
discussion). Hard X-ray flux above 2 keV on the other hand could
penetrate to the photosphere. But RXTE observations between 2 and 6 keV yielded upper limits of
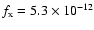 and
and
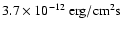 (for the flux density at earth) on the
day of discovery and 4 days into the last outburst of WZ Sge (Kuulkers
et al. 2002). With a distance to WZ Sge of about d= 50 pc (Smak 1993;
Meyer-Hofmeister et al. 1998) this corresponds to upper limits for
the X-ray luminosity
(for the flux density at earth) on the
day of discovery and 4 days into the last outburst of WZ Sge (Kuulkers
et al. 2002). With a distance to WZ Sge of about d= 50 pc (Smak 1993;
Meyer-Hofmeister et al. 1998) this corresponds to upper limits for
the X-ray luminosity
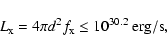 |
(8) |
an order of magnitude less than even the luminosity of
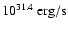 of the 15 000 K quiescent white dwarf.
Contrary to the extreme UV, near UV and optical radiation from the
accretion disk and white dwarf however can reach the photosphere of
the secondary and raise its temperature. From HST observations of WZ
Sge (Kuulkers et al. 2002) 8 days into the 2001 outburst we estimate a
flux density longward of
of the 15 000 K quiescent white dwarf.
Contrary to the extreme UV, near UV and optical radiation from the
accretion disk and white dwarf however can reach the photosphere of
the secondary and raise its temperature. From HST observations of WZ
Sge (Kuulkers et al. 2002) 8 days into the 2001 outburst we estimate a
flux density longward of 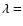 2000 Å of
2000 Å of
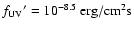 at earth. For a distance of 50 pc this corresponds to a luminosity
at earth. For a distance of 50 pc this corresponds to a luminosity
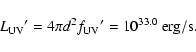 |
(9) |
If this radiation is reprocessed at the secondary's
photosphere it raises the surface temperature to
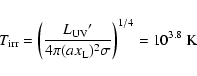 |
(10) |
at the distance
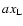 of
of  from the white dwarf.
This is a maximal
value. Surface elements farther away from the central source and inclined
to the direction of irradiation will have a lower surface temperature.
from the white dwarf.
This is a maximal
value. Surface elements farther away from the central source and inclined
to the direction of irradiation will have a lower surface temperature.
It is worth noting that this temperature estimate of
103.8 K is significantly lower than the value of 104.32 K that
Smak (1993) derived from spectral fits to IUE observations early
in the December 1978 outburst of WZ Sge. He attributed this component
to the irradiated surface of the secondary star but noted an
unexplained inconsistency between the observed and expected phases of
this component in the light curve.
Our significantly lower estimate for the surface temperature of the
secondary star in outburst provides additional support
that the source of the component determined by Smak is not the
surface of the irradiated secondary but is the 2:1 resonance
dissipation pattern at the rim of the accretion disk as suggested
in Osaki & Meyer (2002). For that dissipation pattern a temperature
around 104.3 K was estimated.
The heat deposited by irradiation at the surface of the secondary
spreads with time by radiative diffusion into the subsurface
layers. The depth down to which the temperature is raised depends on
the opacity of the gas and the duration t of the irradiation.
Using standard radiative diffusion and opacities in the temperature
range between 103.2 K and 103.8 K taken from Alexander et al. (1983)
we estimate the column density of the affected layer as
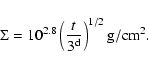 |
(11) |
This is smaller than the column density
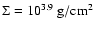 down to the level where the unirradiated star of surface temperature 103.2 K itself reaches the 103.8 K of the irradiated surface.
For this estimate we used a value of
down to the level where the unirradiated star of surface temperature 103.2 K itself reaches the 103.8 K of the irradiated surface.
For this estimate we used a value of
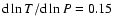 ,
a mean value near the surface of very cool low mass stars
(Buning, private communication) and a pressure at the surface
,
a mean value near the surface of very cool low mass stars
(Buning, private communication) and a pressure at the surface 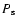 of
of
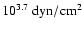 (which for WZ Sge corresponds
to a mass overflow rate of
(which for WZ Sge corresponds
to a mass overflow rate of
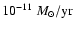 ).
).
Thus below the irradiated surface of the secondary a more or less
isothermal layer of
T=103.8 K is formed.
The heating of the subsurface material under the irradiated surface
raises the pressure and causes pressure differences on equipotential
surfaces between irradiated and unirradiated parts. They tend to drive
heated material into the shadow belt and below  which could
raise the pressure there and lead to an increase of the mass transfer
rate.
which could
raise the pressure there and lead to an increase of the mass transfer
rate.
However, the system is rotating with the binary period and due to
deformation of the stellar surface near  the rotation
frequency has a component normal to the surface. For q= 0.1 along the
meridian through
the rotation
frequency has a component normal to the surface. For q= 0.1 along the
meridian through  one obtains for this normal component
one obtains for this normal component
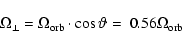 |
(12) |
where
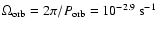 is the orbital angular frequency (
is the orbital angular frequency (
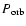 orbital period) and
orbital period) and
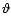 is the angle between the surface normal and the rotation axis
of the system. In the Roche geometry this angle changes gradually as
one moves away from the meridian. But along the meridian is the
shortest path out of the shadow band and the driving pressure gradient
is the largest in this direction. We will show now that rotation
practically prevents heated matter to flow into the low pressure
region below
is the angle between the surface normal and the rotation axis
of the system. In the Roche geometry this angle changes gradually as
one moves away from the meridian. But along the meridian is the
shortest path out of the shadow band and the driving pressure gradient
is the largest in this direction. We will show now that rotation
practically prevents heated matter to flow into the low pressure
region below  .
For this we simplify the curved shape of the equipotential surfaces
near
.
For this we simplify the curved shape of the equipotential surfaces
near  by adopting a locally plane geometry with Euclidian
coordinates x in the direction of constant latitude, y in the
direction of constant longitude, and z in the direction of the outward
surface normal.
by adopting a locally plane geometry with Euclidian
coordinates x in the direction of constant latitude, y in the
direction of constant longitude, and z in the direction of the outward
surface normal.
The horizontal equations of motion in this system are used by
Spruit (2002) in the context of a solar problem. There it is shown that
the equations can be simplified if the vertical extent is
small
compared to the latitudinal extent which is the case here with a few
vertical pressure scaleheights of order 108 cm, small compared to
the width of the shadow band of 109.4 cm. Since the main gradients
are perpendicular to the shadow band which spreads along the equator we
neglect gradients in the x direction and obtain (Pedlosky 1982; Spruit 2002)
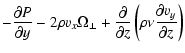 |
= |
0, |
|
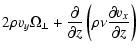 |
= |
0. |
(13) |
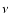 is the kinematic viscosity. Without viscosity we have the
"geostrophic'' flow along the shadow band
is the kinematic viscosity. Without viscosity we have the
"geostrophic'' flow along the shadow band
|
vx |
= |
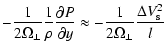 |
|
| vy |
= |
0 |
(14) |
where
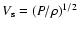 is the isothermal sound velocity and
l is the half width of the shadow band. Thus the flow velocity is at right angle to the driving pressure gradient which is balanced by the
Coriolis force, similar to flows in weather systems and oceans on the
rotating earth. Thus without friction no heat can be advected into
the shadow region below
is the isothermal sound velocity and
l is the half width of the shadow band. Thus the flow velocity is at right angle to the driving pressure gradient which is balanced by the
Coriolis force, similar to flows in weather systems and oceans on the
rotating earth. Thus without friction no heat can be advected into
the shadow region below  .
.
If a small viscosity is present the geostrophic flow is accompanied
by a small drift into the low pressure shadow band. Replacing zderivatives by division by the vertical scale height H in the
equation for vy one obtains
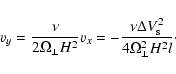 |
(15) |
What is the value of a possible viscosity? Molecular viscosity is
negligibly small. Can there be turbulent viscosity? The layer
irradiated and heated from above is stable against convection
as the temperature
is constant or even increasing upwards. This suggests that there will
be practically no viscosity in the main body of the heated
material. Only at the bottom (i.e. its densest layer) one might have
to consider that convection from the original stellar envelope below
penetrates into the heated layer above. We will now estimate the
effect that this will have on the advection of heat into the shadow
zone. For this we determine from mixing length theory
a "convective'' viscosity
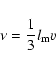 |
(16) |
where 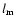 is the mixing length, e.g. the pressure
scaleheight H, and v is the convective velocity of the cool
secondary at the depth where the overlying irradiation heated zone
starts. The velocity v follows from the requirement that v transports the
convective flux, which is equal to the flux
is the mixing length, e.g. the pressure
scaleheight H, and v is the convective velocity of the cool
secondary at the depth where the overlying irradiation heated zone
starts. The velocity v follows from the requirement that v transports the
convective flux, which is equal to the flux
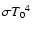 radiated
away at the surface of the unirradiated secondary. Using the value of
radiated
away at the surface of the unirradiated secondary. Using the value of
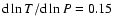 to determine the specific heat and
for a density
to determine the specific heat and
for a density
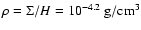 (
(
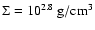 ,
Eq. (11), and
,
Eq. (11), and
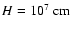 )
one
obtains (Kippenhahn & Weigert 1990, Eqs. (7.6) and (7.7))
)
one
obtains (Kippenhahn & Weigert 1990, Eqs. (7.6) and (7.7))
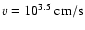 .
The value for H results from the surface gravity in Roche
geometry at the distance
l=109.4 cm of the shadow band boundary from
the Lagrange point
.
The value for H results from the surface gravity in Roche
geometry at the distance
l=109.4 cm of the shadow band boundary from
the Lagrange point  and for a temperature of 103.8 K.
Equation (16) then gives
and for a temperature of 103.8 K.
Equation (16) then gives
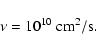 |
(17) |
The pressure ratio between surface,
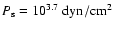 ,
and the bottom layer,
,
and the bottom layer,
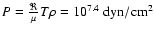 ,
determines the temperature ratio between
surface and bottom and with the surface temperature of the
unirradiated star
T0=103.2 K this gives
,
determines the temperature ratio between
surface and bottom and with the surface temperature of the
unirradiated star
T0=103.2 K this gives
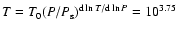 K, already very close to the temperature
of the irradiated layer of 103.8 K.
K, already very close to the temperature
of the irradiated layer of 103.8 K.
With the value for 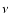 and
and
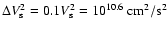 the drift velocity into the shadow zone
becomes
the drift velocity into the shadow zone
becomes
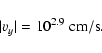 |
(18) |
This means that the time for matter to drift from irradiated parts into the
region below  becomes
becomes
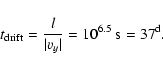 |
(19) |
This is longer than the duration of the outburst. It is also much longer
than the cooling time of three days of the column considered.
The matter therefore has cooled to temperatures in the shadow zone
long before it reaches the region below  .
.
Thus the shadowing of the mass transfer region by the accretion disk
rim and the strong Coriolis force prevent any effect of irradiation of
the secondary star on the mass transfer. This conclusion agrees with
the observational evidence that is discussed in the preceding
sections.
We discussed this here for the case of WZ Sge
in particular, but we expect the same effect to be true for other CV
systems as well.
Smak (1996, 2000) argued that "the TTI model faces a serious problem
with the sequence of events it predicts: the superhumps should appear
at an early phase of a superoutburst (certainly not later than
its maximum), while observations show that this happens only one
or two days after maximum". In the original TTI model, the last normal
outburst triggers a tidal instability, leading to an eccentric disk
which causes a major enhancement of the accretion rate. Accordingly, the superhumps should
appear in the very early phase of a superoutburst.
Therefor Smak (1996) suggested
instead a hybrid model (called EMT model) by combining the tidal
instability with the enhanced mass-transfer model.
In Smak's picture, irradiation
of the secondary star by the central white dwarf and the boundary
layer during the superoutburst causes enhanced mass transfer which
now can keep the disk in hot state for much longer time.
There is then enough time for the disk to develop the eccentric
structure, a necessary condition as claimed by Whitehurst & King (1991).
In response to Smak's criticism, we here propose a refinement
of the TTI model.
Before doing so, let us first examine the observations more carefully.
Bateson (1977) classified the superoutburst light curves of VW Hyi
into types S1 to S8 but these are basically two types; S1-S5 with simple
superoutburst light curves with one continuous rise and fall
and S6-S8 with light curves of a precursor-main outburst type.
Almost all observers note that the rising part of the superoutburst
is indistinguishable from that of the normal outburst.
As discussed by Marino & Walker (1979), in the case of the S6-S8 types the precursor normal outburst
was separated by a dip from the main part of the superoutburst
while it is already merged with
the main superoutburst in the case of S1-S5. That is, in the type S1-S5
superoutbursts, the time delay between the triggering normal outburst and
the bulk of the superoutburst is too short to be observable (Marino &
Walker 1979; van der Woerd & van Paradijs 1987).
There are several examples in which the superoutburst light curve in
optical light looked more or less as one single continuation but
it consisted of a precursor and a main outburst at shorter
wavelengths. In general, precursor
part and main part of the superoutburst are more clearly separated
as we go to shorter wavelengths. This can be seen in the Voyager
far-ultraviolet observations of the 1984 October-November superoutburst
of VW Hyi (Pringle et al. 1987), and in EUV observations of
the 1997 March superoutburst of OY Car by Mauche & Raymond (2000)
and the 1997 October superoutburst of SW UMa by Burleigh et al. (2001).
When the precursor is well separated from the main superoutburst, the main
outburst grows in amplitude with the growth of the superhump light.
The long duration of the superoutburst can not be the cause of the eccentric
disk because the superhumps grow together with the rise to the main outburst.
As far as superoutbursts of the precursor-main outburst type are concerned,
observations agree very well with the TTI model.
We now turn to the S1-S5 type superoutbursts in which
light curves look like a single continuation and the superhumps appear only
one or two days after maximum and therefore Smak's criticism seems
relevant. To deal with it, we here propose a refinement
of the original TTI model that explains why superhumps appear
a few days after the superoutburst maximum in some SU UMa stars.
We suggest that these are those outbursts in which the last normal
outburst occurs in full readiness for the superoutburst and that
the normal outburst and the superoutburst are completely merged
as explained below.
We first discuss the outburst duration
in dwarf novae. In particular, let us
address why in the TTI model the disk in normal outbursts
can not stay hot even when much mass has already been stored
in the disk for the coming superoutburst. The essential point of
the TTI model lies in the explanation of the shortness of the
normal outburst. When the normal outburst occurs, the disk jumps from the
cold state to the hot state. The surface density distribution then
changes from
 in the cold state to
in the cold state to
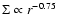 in the hot state.
On the other hand, the critical surface density
below which no hot state exists varies with the radius as
in the hot state.
On the other hand, the critical surface density
below which no hot state exists varies with the radius as
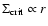 .
Thus the outer rim of a free accretion
disk (by "free" we mean not yet bound by the tidal removal
of angular momentum) will always peter out to surface densities
below the critical density below which no hot state is
possible. When the heating wave released in the outburst reaches this
critical surface density
a cooling wave is set up that moves inward and cuts off the (normal) outburst.
In the TTI model, the normal outburst is an outburst in which the
disk's outer edge does not yet reach the 3:1 resonance radius and thus we
have a rather ineffective tidal removal of angular momentum
from the disk, explaining its short duration.
.
Thus the outer rim of a free accretion
disk (by "free" we mean not yet bound by the tidal removal
of angular momentum) will always peter out to surface densities
below the critical density below which no hot state is
possible. When the heating wave released in the outburst reaches this
critical surface density
a cooling wave is set up that moves inward and cuts off the (normal) outburst.
In the TTI model, the normal outburst is an outburst in which the
disk's outer edge does not yet reach the 3:1 resonance radius and thus we
have a rather ineffective tidal removal of angular momentum
from the disk, explaining its short duration.
On the other hand, if tidal removal of angular momentum is very effective,
the expansion of the disk is stopped, i.e., the disk hits a tidal wall,
and the matter is dammed up there. If there is enough mass in the disk,
the surface density at the tidal wall is above the critical surface
density and the disk
stays in the hot state, and the long viscous depletion of mass
from the disk ensues. This explains the long duration of the outburst.
In the case of U Gem stars the tidal wall is provided at the ordinary
tidal truncation radius, in the case of SU UMa stars
at the 3:1 resonance radius, and in the case of WZ Sge at the 2:1 resonance.
Let us now come back to the problem of S1-S5 type superoutbursts.
In SU UMa stars with relatively long orbital periods, near two hours,
having binary mass ratios around 0.2 such as VW Hyi,
the tidal truncation radius lies just beyond the 3:1 resonance radius.
If the final normal outburst occurs in full readiness,
the disk will not only expand to
the 3:1 resonance radius but also pass it. The disk will then reach
the tidal truncation radius so that its expansion is stopped there
(see, the upper right-most panel of Fig. 4).
The viscous depletion of matter (i.e., the viscous plateau stage of
outburst) ensues even when the eccentric tidal instability
(i.e., superhumps) has not yet developed to observable amplitude.
One or two days after the light maximum, the tidal instability
and the superhumps have grown to large amplitude, now taking over
the role of tidal removal of angular momentum from the ordinary
tidal torques at the truncation radius.
This may be the reason why in these outbursts the superhumps grow one
or two days after the maximum.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{H4045F4.ps}\end{figure}](/articles/aa/full/2003/13/aah4045/Timg66.gif) |
Figure 4:
Various ways in which superoutbursts are triggered (see text
for details). Horizontal axis: time, vertical axis: radius. Short
dashed line: 3:1 resonance radius, long-dashed line; tidal truncation
radius, solid line: outer disk radius, asterisk: ignition of
superoutburst. In order of decreasing mass ratio (increasing
separation of tidal and 3:1 resonance radii, increasingly longer
growth time of superhumps): case A: relatively large mass ratio around
0.2 (a), (b), and (c): ordinary outbursts occurring in various stage
of readiness for a superoutburst in one and the same system. Case B:
smaller mass ratio. Case C: extremely small mass ratio. |
| Open with DEXTER |
In the original suggestion of the TTI model (Osaki 1989, 1996),
the importance of the tidal truncation radius just beyond the 3:1 resonance
radius was not appreciated and only the precursor-main outburst type
superoutburst was dealt with. With this new refinement we can now understand different aspects of superoutbursts of
various SU UMa stars.
Figure 4 illustrates how the last normal outbursts trigger the superoutburst
under different conditions. Each panel schematically
shows the time variation of the disk's outer edge. The asterisk denotes
the point where the superoutburst is triggered.
The uppermost three panels (case A) represent the longest
orbital-period SU UMa stars with periods around two hours
(typified by VW Hyi) and binary mass ratios q around 0.2
for which the 3:1 radius and the tidal truncation radius are close to
each other. The upper left panel illustrates an aborted superhump
during the last normal outburst, which fails to develop to the
superoutburst discussed in Sect. 2.2.
The upper middle panel illustrates the case in which the last normal
outburst first triggers a tidal instability and then the superoutburst
develops together with the superhumps, corresponding to the
precursor-main outburst type of S6-S8. The upper right panel illustrates
the case of full-readiness in which the disk expands to reach
the tidal truncation radius and the hot viscous plateau stage sets in.
The tidal instability and the superhumps then develop to large amplitudes,
corresponding to the S1-S5 case just discussed above.
The middle panel (case B) shows SU UMa stars with shorter orbital
periods that have lower q values.
In this case, even if the outer edge of the disk reaches the 3:1 resonance,
the growth rate of the tidal instability, proportional to q2, is so
low that there is not
enough time for the superhump to grow to large amplitude
within the normal outburst duration. Once the normal outburst ends
and the disk returns to quiescence, the outer edge of the disk
contracts due to the addition of matter with low specific angular
momentum and shrinks below the 3:1 resonance.
Observationally, the normal outburst in this case is indistinguishable
from those normal outbursts in which the disk's edge does not
reach the 3:1 resonance at all. A next normal
outburst will then push the disk edge to the tidal truncation radius.
The hot viscous plateau stage sets in. The superhumps develop
a few days after the light maximum. Most SU UMa stars correspond
to this case B.
The bottom panel (case C) illustrates the case of the shortest orbital
period SU UMa stars with the lowest mass ratio q in which normal outburst
occurs frequently. In this case the tidal truncation radius is far away from
the 3:1 resonance radius. As discussed for case B, the normal outburst,
in which the disk's outer edge reaches the 3:1 resonance, can not develop
the superhumps to large amplitude. This may repeat in the next
normal outburst as well. However, since the disk expands more and more
above the 3:1
resonance radius, it may finally not shrink below the 3:1 resonance radius
even during quiescence and the tidal instability continues to operate
in quiescence. If sufficient time elapses, the tidal instability
and the superhumps grow to large amplitude. Tidal heating at the outer edge
of the disk will then force the upward thermal transition
to the hot state, starting a new outburst. This outburst is of outside-in type
and it develops always to a superoutburst because the disk is now fully
eccentric, that is, a superoutburst triggered not by the normal outburst but
rather by the tidal instability.
An obvious prediction in this case is that the superhump should be visible
in large amplitude even during the rising branch of the outburst.
This case (case C) corresponds to ER UMa stars with the shortest
supercycle less than 50 days, and with the very short normal-outburst
cycle, as short as 4 days. (The WZ Sge stars do not belong to this
case because normal outbursts do not occur so frequently). It was a puzzle
in observations of the ER UMa stars that superhumps in large amplitude
were observed during the rising branch of the superoutburst (see observation
of ER UMa by Kato et al. 1996 and V1159 Ori by Patterson et al. 1995).
In the standard scenario of SU UMa stars, the superhumps were expected
to appear later during the superoutburst the lower the mass
ratio of the system is because of their increasingly longer growth
time. The mystery of these paradoxical
observations is now solved.
Although the 3:1 resonance and the ordinary tidal truncation both
remove angular momentum from the disk via the secondary's tidal force,
there exists an essential difference in nature between them.
In a sense the 3:1 resonance is more active but
the ordinary tidal truncation is more passive in nature:
When the eccentric disk (and the superhump) is fully developed
by the 3:1 resonance, tidal removal of angular momentum from the disk
is very strong as demonstrated by Murray (1998) with SPH hydrodynamic
simulation. This keeps the disk in the hot state longer. When the superoutburst ends,
the quiescent disk becomes quite compact and far removed from the 3:1
resonance
radius. On the other hand, the ordinary tidal truncation is passive
in that it simply inhibits the disk to expand beyond the truncation
radius but it does not cause the disk to contract far below that limit.
We conclude that the TTI model fully explains the sequence of events
of SU UMa stars and that Smak's criticism is properly dealt with
by the new refinement.
We now give a description of the overall development of the 2001
outburst of WZ Sge in terms of the TTI model, based on a very low
viscosity in quiescence and no enhanced mass transfer during the
outburst. In this latter point we differ from the observational
account by Patterson et al. (2002). As shown in Sect. 2.3 their
evidence for increased mass transfer is probably the result of a
misinterpretation of orbital light curves in the common superhump era.
(1) The main accretion event
Osaki (1995) has already
pointed out that the basic outburst energetics of WZ Sge fits to Osaki's
(1974) disk instability model in its simplest form: long quiescence of
about 30 yrs coupled with a low mass transfer rate 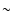 1015 gs-1
allows the disk to accumulate mass
1015 gs-1
allows the disk to accumulate mass 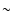 1024 g, which is
dumped onto the central white dwarf during an outburst.
Cannizzo (2001) has shown that the 2001 superoutburst
of WZ Sge can be explained by viscous depletion of matter in a disk
with an initial mass
1024 g, which is
dumped onto the central white dwarf during an outburst.
Cannizzo (2001) has shown that the 2001 superoutburst
of WZ Sge can be explained by viscous depletion of matter in a disk
with an initial mass 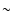 1024 g.
1024 g.
(2) Quiescence and long recurrence time
Two different models have been proposed to explain the long recurrence
time of WZ Sge of about 30 yrs. One is a model with extremely low viscosity
in quiescence (Smak 1993; Osaki 1995; Meyer-Hofmeister et al. 1998).
The other is a model of a steady
or almost steady cold disk with a standard value of viscosity
in the cold state but with its inner part truncated
(Warner et al. 1996; Hameury et al. 1997).
Such a disk is unable to store the amount of mass required for the
outburst. (See Fig. 3 of Meyer-Hofmeister et al. 1998 for a comparison
of the two models.)
The missing mass in the second model would have to be supplied during
the outburst. If 1024 g would be transferred on a time scale of
one day the enhanced mass transfer rate should be
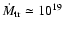 gs-1 and it may be rather unlikely to
overlook such a large increase. As discussed in
Sect. 2.3, there is no good observational evidence
for enhanced mass transfer during the outburst.
gs-1 and it may be rather unlikely to
overlook such a large increase. As discussed in
Sect. 2.3, there is no good observational evidence
for enhanced mass transfer during the outburst.
The very low quiescent viscosity in the first model can be understood
by decay of magnetic turbulence (Gammie & Menou 1998). In WZ Sge this
occurs during the final decline to quiescence (Osaki et al. 2001). The
extremely low viscosity value of WZ Sge stars may result as consequence
of a cool brown dwarf secondary that cannot support a magnetosphere
whose interaction with the accretion disk has been made responsible
for the standard quiescent viscosity of ordinary dwarf novae (Meyer &
Meyer-Hofmeister 1999).
(3) Start of outburst and early humps
Least understood in this scenario is the initial kick to start the
thermal instability in the case of extremely low quiescent viscosity.
Once the thermal instability is started and the disk goes into the hot state,
the standard high viscosity is most likely produced by the magneto-
rotational instability (Balbus and Hawley instability).
A sudden jump to high viscosity makes the accumulated mass spread
inwards and outwards and form a standard hot accretion disk.
As discussed by Osaki & Meyer (2002), the outer edge of the
disk not only reaches the 3:1 resonance
but passes it and reaches the 2:1 resonance radius where
the two armed spiral pattern of the Lindblad resonance is excited. Increased tidal torques
now stop the expansion of the disk and the tidal dissipation produces
the observed photometric double humps (early humps, or "OOH" in Patterson
et al. 2002).
(4) Late appearance of common superhumps
Within the first 12 days the large amount of mass residing
near the 2:1 resonance region is gradually cleared by tidal loss of angular
momentum. This
enhances the relative importance of mass around the 3:1 resonance
(responsible for the eccentric tidal instability).
This now allows the disk to
develop the common superhumps as discussed below.
Lubow (1991) has shown that an eccentric "corotation" resonance
(different from the familiar eccentric Lindlad resonance) occurs at the
2:1 resonance through the tidal potential component m=2, which acts to
damp eccentricity, in competition to the excitation
of eccentricity at the 3:1 resonance.
As long as a large amount of matter resides at the 2:1 resonance
the damping effect will dominate, preventing the growth of eccentricity.
As matter is cleared from the 2:1 resonance region, the
excitation effect at the 3:1 resonance will increase in relative importance
and eventually win.
The disk eccentricity will grow to large amplitude and superhumps appear.
The tidal removal of angular momentum
by the eccentric disk now takes over the role of the 2:1 resonance.
The common superhump era corresponds to this stage. Thus the 2:1 resonance not only offers an explanation for the early hump
phenomenon but it may also act as a suppressor of growth of the eccentricity
in WZ Sge stars. The rather late appearance of the common
superhumps in WZ Sge is then a natural consequence of the 2:1 resonance.
Light curves in the common superhump era were already discussed
in subsection 2.3. Orbital humps and eclipses in this stage are
due to the superhump light source itself and there is no evidence
for enhanced mass transfer.
(5) Late superhumps
The superhump light signal often stays on after the end of the main
superoutburst of SU UMa stars and the eccentric disk seems to survive for
a while. Light variations with the superhump period after the end of
the main superoutburst are called "late superhumps".
The late-superhump phenomenon is conspicuous in WZ Sge stars,
late superhumps continued to exist for one hundred days in the 2001
outburst of WZ Sge.
This phenomenon is most naturally explained by decoupling of the tidal
instability from the thermal instability proposed by Hellier (2001).
He suggested that in a binary system with extremely small mass ratio
the tidal torques on the eccentric disk are not strong enough
to keep the disk in the hot state though the tidal eccentric instability still
goes on. The premature shutdown of the thermal instability ends
the superoutburst even when the disk still has its eccentric form.
When near the transition into quiescence the superhump signal has
dwindled away and the ordinary hot spot becomes dominant but the disk
still retains a residual eccentricity a modulation in phase and
intensity of the hot spot light occurs as the impact point of the
accretion stream travels around the elliptically deformed circumference
of the disk together with the revolving mass supplying secondary. This
was documented by Rolfe et al. (2001) for the eclipsing dwarf nova IY
UMa in the very late superhump phase.
(6) Dip and Echo outbursts
The WZ Sge stars often show rebrightening or reflare after the end of the
main outburst, the most spectacular case was six consecutive rebrightenings
of EG Cnc in 1996/1997.
The 2001 outburst of WZ Sge showed the same phenomenon
but it had as many as 12 short outbursts with a mean repetition
time as short as 2 days. One of the important aspects during the echo
outburst era
is that the superhump light signal continues to exist throughout this period
even to the final decline stage and that the superhump amplitude stayed
approximately constant in intensity while the background
light intensity was highly variable.
Osaki et al. (2001) and Hellier (2001) proposed that echo outbursts of EG Cnc
are normal outbursts in the disk where tidal removal of angular
momentum from the
mass reservoir beyond the 3:1 resonance radius feeds mass into the
inner disk and repeatedly excites the thermal instability. Note that
no enhanced mass transfer is needed.
In particular, Osaki et al. (2001) demonstrated that this model can explain
the sudden cessation of echo outbursts as due to decay of magnetic
viscosity in the disk. This model can be applied to the 2001 outburst
of WZ Sge as well. The only difference being the amount of mass
in the reservoir, larger in WZ Sge than in EG Cnc.
On the other hand, Hameury et al. (2000) have proposed enhanced mass transfer
to explain echo outbursts. Patterson et al. (2002) supported this model
because they saw observational evidence for enhanced mass transfer.
However, as discussed in Sect. 2.3, their conclusion for enhanced mass
transfer is simply due to a misinterpretation of their observations. There is
no evidence for enhanced mass transfer and the supporting evidence
disappears.
Enhanced mass transfer also tends to quench an existing eccentric
structure (see Ichikawa et al. 1993; Lubow 1994) since addition of
a large amount of mass with low specific angular momentum leads to
disk shrinkage. This would contradict the observed long endurance
of late superhumps in WZ Sge and EG Cnc which may result just because
of the low mass transfer rate in these systems compared to ordinary
SU UMa stars.
(7) Final decline
As discussed by Osaki et al. (2001), the final decline
is understood in terms of decay of magnetic turbulence in the cold disk.
WZ Sge has entered into dormancy for another 20 or 30 yrs accumulating
mass in the disk for the next outburst.
We have carefully analyzed old and new claims of evidence for increased
mass overflow in outbursts of SU UMa stars. We find that all this
evidence is not well founded, inconclusive, and partially inconsistent
with the observations themselves. Our theoretical analysis supports
the conclusion of no increased mass overflow during the outbursts. In
all cases we find that a refined thermal-tidal instability model with
no increased mass overflow gives a consistent and convincing
explanation of the observational results. This appears to rule out
theoretical models for SU UMa star outbursts that postulate increased
mass overflow during outbursts, and allows a deeper insight into the
nature of these outbursts.
Acknowledgements
We would like to thank Emmi Meyer-Hofmeister for helpful discussions
and technical assistance.
Yoji Osaki acknowledges financial support from the Japanese Ministry of
Education, Culture, Sports, Science and Technology with a Grant-in Aid
for Scientific Research No. 12640237.
We thank the referee for suggesting figures and solliciting comments
on other SU UMa stars which significantly improved our presentation of
the paper.
In the context of the general outburst model for WZ Sge
we comment here on Kato's (2002) model for the early
humps of the 2001 outburst of WZ Sge, an alternative model to ours.
During the early stage of
the 2001 outburst of WZ Sge, a two-armed arch-like pattern was observed
in the Doppler maps of emission lines of He II 4686 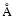 and C III/N III
on the second day of the outburst, July 24, (Baba et al. 2002) and
on July 28 (Steeghs et al. 2001a). Kato (2002) has proposed that this
and the early hump
phenomenon can be understood in terms of irradiation
of the disk by the central radiation source. In this picture, the
irradiation occurs preferably at the elevated surface of the disk,
which in turn is produced by vertical tidal deformation (Smak 2001;
Ogilvie 2002).
Thus the main energy source of early humps in Kato's model is
the irradiation of a tidally elevated disk while it is the tidal
dissipation
in our model. The elevated disk is produced in his model
by the vertical resonance discussed by Ogilvie (2002) while the 2:1
Lindblad resonance is responsible for the enhanced tidal dissipation
in our model.
and C III/N III
on the second day of the outburst, July 24, (Baba et al. 2002) and
on July 28 (Steeghs et al. 2001a). Kato (2002) has proposed that this
and the early hump
phenomenon can be understood in terms of irradiation
of the disk by the central radiation source. In this picture, the
irradiation occurs preferably at the elevated surface of the disk,
which in turn is produced by vertical tidal deformation (Smak 2001;
Ogilvie 2002).
Thus the main energy source of early humps in Kato's model is
the irradiation of a tidally elevated disk while it is the tidal
dissipation
in our model. The elevated disk is produced in his model
by the vertical resonance discussed by Ogilvie (2002) while the 2:1
Lindblad resonance is responsible for the enhanced tidal dissipation
in our model.
Here we comment on his interpretation. In our previous paper (Osaki
& Meyer 2002), we have only dealt with photometric humps of the 2001
outburst of WZ Sge and we have not discussed its Doppler maps.
Here we present our view on the two-armed arch-like pattern in Doppler
maps and its relation to the photometric humps.
In our picture, the photometric humps are thought to be produced
by the two-armed spiral pattern of the tidal dissipation due to the 2:1
Lindblad resonance. The enhanced tidal dissipation may then produce a
vertical thickening of the accretion disk in a similar azimuthal
two-armed pattern. Emission lines observed during the outburst of dwarf novae,
in particular, those of He II at 4686 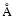 and C III/N III complex
at 4640
and C III/N III complex
at 4640  observed on July 24 and on July 28 in the 2001 outburst of
WZ Sge are most likely produced by the irradiation of the vertically elevated
disk by hard photons (EUV and soft and hard X-rays) from the central source,
in the high atmosphere of the accretion disk either by direct ionization
and recombination or by chromospheric emission due to the temperature
inversion as discussed by Smak (1991). We agree in this sense
with Kato (2002) in that emission lines of He II 4686
observed on July 24 and on July 28 in the 2001 outburst of
WZ Sge are most likely produced by the irradiation of the vertically elevated
disk by hard photons (EUV and soft and hard X-rays) from the central source,
in the high atmosphere of the accretion disk either by direct ionization
and recombination or by chromospheric emission due to the temperature
inversion as discussed by Smak (1991). We agree in this sense
with Kato (2002) in that emission lines of He II 4686  and C III/N III
are produced by irradiation of the accretion disk by hard photons
from the central radiation source. However, we do not agree
with Kato (2002) on the explanation of the early hump phenomenon.
Although two-armed arch-like pattern in the Doppler maps
and the double-humped light curve (i.e., early humps) may be somehow
related with each other, it is not so obvious that these two phenomena
are produced by the one and the same cause as suggested by Kato (2002)
because emission mechanisms are not necessarily the same for emission
lines and for the continuum radiation. It seems premature to make a
one to one correspondence between photometric humps and features
in Doppler maps.
and C III/N III
are produced by irradiation of the accretion disk by hard photons
from the central radiation source. However, we do not agree
with Kato (2002) on the explanation of the early hump phenomenon.
Although two-armed arch-like pattern in the Doppler maps
and the double-humped light curve (i.e., early humps) may be somehow
related with each other, it is not so obvious that these two phenomena
are produced by the one and the same cause as suggested by Kato (2002)
because emission mechanisms are not necessarily the same for emission
lines and for the continuum radiation. It seems premature to make a
one to one correspondence between photometric humps and features
in Doppler maps.
In fact, there is observational evidence that the light source
for photometric humps is not due to the irradiation of the disk but rather
it is due to the tidal dissipation. The observations of
the very first day of the outburst of WZ Sge (July 23, 2001) tell us
this. On the day of discovery of the 2001 outburst of WZ Sge,
Ishioka et al. (2002) had found the growing humps during the rapid
rise to maximum. On the same day, CCD spectroscopic observations
were performed by K. Ayani at Bisei observatory, as shown in Fig. 1 of
Baba et al. (2002). It showed Balmer lines in absorption but no emission lines
were found around the wavelengths of He II and the C III/N III complex.
This indicates that the irradiation of the accretion disk by hard
photons from the central part of the disk or from the central white dwarf
has not yet started on the first day. This is easily understood
in dwarf nova outbursts. On the very first day, the outer part of
the accretion disk of WZ Sge was already in the hot and high-viscosity state
and the disk was expanding both inward and outward. The outer edge of
the disk reached the 2:1 resonance radius,
thus triggering the Lindblad resonance and creating the photometric humps.
The inner edge of the hot disk had not yet reached the central white dwarf
on the first day. That is a phenomenon well known as "UV delay" in
the dwarf nova outburst. This demonstrates that the photometric humps already
observed at the very first day do not require any irradiation of the disk
at all.
Furthermore, we argue that the irradiating radiation from the
central source
most likely did not penetrate deeply into the photosphere of the accretion
disk as discussed in Sect. 3. In fact, higher Balmer lines
H and H
and H and neutral helium lines, i.e., lines of the
photospheric origin, were found in absorption even on July 24
and on July 28 when He II at 4686
and neutral helium lines, i.e., lines of the
photospheric origin, were found in absorption even on July 24
and on July 28 when He II at 4686 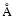 and C III/N III complex
were in emission (Baba et al. 2001) while H
and C III/N III complex
were in emission (Baba et al. 2001) while H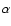 and H
and H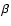 lines exhibited highly variable absorption cores together with emission wings.
This means that the heating source for continuous radiation must be
deeply seated within the accretion disk rather than coming from
the outside
(as in the case of irradiation). The continuum radiation is thus most
likely due to the tidal dissipation, an argument favoring
our tidal dissipation model against Kato's irradiation model
for the early humps.
lines exhibited highly variable absorption cores together with emission wings.
This means that the heating source for continuous radiation must be
deeply seated within the accretion disk rather than coming from
the outside
(as in the case of irradiation). The continuum radiation is thus most
likely due to the tidal dissipation, an argument favoring
our tidal dissipation model against Kato's irradiation model
for the early humps.
Let us now turn our attention to the problem of the radial range of the disk
at which the tidal pattern is produced in Kato's model and in our model.
Besides a localisation at the tidal cut-off radius, Kato (2002) considers
Ogilvie's (2002) vertical resonance as an explanation of the
two-armed arch-like pattern observed in Doppler maps. The vertical
resonance radius,
 ,
in the accretion disk is given
by (see, e.g., Lubow 1981; Stehle & Spruit 1999)
,
in the accretion disk is given
by (see, e.g., Lubow 1981; Stehle & Spruit 1999)
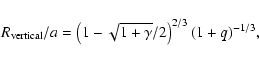 |
(A.1) |
where 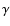 is the adiabatic exponent between pressure and density
for the disk matter, a is the binary separation, and q=M2/M1 is
the ratio of secondary star to primary star mass. It is
interesting to note that this expression has the same mass-ratio
dependence as the 3:1 resonance for the eccentric tidal mode and the 2:1
resonance for the Lindblad resonance only differing in the numerical
factor. We estimate
is the adiabatic exponent between pressure and density
for the disk matter, a is the binary separation, and q=M2/M1 is
the ratio of secondary star to primary star mass. It is
interesting to note that this expression has the same mass-ratio
dependence as the 3:1 resonance for the eccentric tidal mode and the 2:1
resonance for the Lindblad resonance only differing in the numerical
factor. We estimate
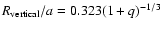 for
for
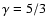 ,
and 0.441 for
,
and 0.441 for 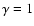 ,
while
R3:1/a= 0.481 (1+q)-1/3 for the 3:1 eccentric resonance and
R2:1/a= 0.630 (1+q)-1/3 for the 2:1 Lindblad resonance.
Thus for a reasonable value of
,
while
R3:1/a= 0.481 (1+q)-1/3 for the 3:1 eccentric resonance and
R2:1/a= 0.630 (1+q)-1/3 for the 2:1 Lindblad resonance.
Thus for a reasonable value of 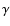 ,
the vertical resonance radius
lies well inside the 3:1 resonance radius.
,
the vertical resonance radius
lies well inside the 3:1 resonance radius.
If the two-armed arch-like pattern observed in Doppler maps of the 2001
outburst of WZ ge were produced by the vertical resonance
as suggested by Kato (2002) and if the disk in the 2001 outburst of WZ
Sge were truncated at this radius, the disk would never reach the 3:1
resonance radius and the common superhump phenomenon would not be expected.
This is another difficulty of Kato's model.
A further difference between Kato's and our model lies in the
expected absolute value of the velocity for the two-armed arch-like pattern in the Doppler map. The peak separation of double emission lines
in quiescence of WZ Sge is known to be around 700 km s-1
(e.g., Mason et al. 2001).
From phase-folded spectra or Doppler maps of He II and
H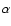 emission lines shown in Fig. 3 of Baba et al. (2002)
we find that
the velocity of the peak-intensity features during the early-hump era of the
2001 outburst of WZ Sge is around 500 km s-1. If this velocity
represents the Keplerian circular velocity, the outer edge of the disk
expanded by a factor of about two during the outburst. Since the orbital
velocity of the secondary star of WZ Sge was found to be around 500 km s-1
(Steeghs et al. 2001b) as well, the observed velocity of around 500 km s-1
for the two-armed features in Doppler maps means that they are produced
very near to the Roche lobe of the primary star, much favoring the 2:1 resonance interpretation over that of the vertical resonance.
emission lines shown in Fig. 3 of Baba et al. (2002)
we find that
the velocity of the peak-intensity features during the early-hump era of the
2001 outburst of WZ Sge is around 500 km s-1. If this velocity
represents the Keplerian circular velocity, the outer edge of the disk
expanded by a factor of about two during the outburst. Since the orbital
velocity of the secondary star of WZ Sge was found to be around 500 km s-1
(Steeghs et al. 2001b) as well, the observed velocity of around 500 km s-1
for the two-armed features in Doppler maps means that they are produced
very near to the Roche lobe of the primary star, much favoring the 2:1 resonance interpretation over that of the vertical resonance.
We note that the observational accuracy does not allow to discuss a
difference between the radii of the 2:1 resonance and the ordinary tidal
cut-off, since for very small mass ratios these two radii can lie very close
together.
-
Alexander, D. R., Johnson, H. R., & Rypma, R. L. 1983, ApJ, 272, 773
In the text
NASA ADS
-
Baba, H., Sadakane, K., Norimoto, Y., et al. 2002, PASJ, 54, L7
In the text
NASA ADS
-
Bateson, F. M. 1977, New Zealand J. Sci., 20, 73
In the text
NASA ADS
-
Burleigh, M. R., Pye, J. P., Poulton, S. W., et al. 2001, MNRAS, 325, 1458
In the text
NASA ADS
-
Cannizzo, J. K. 2001, ApJ, 561, L175
In the text
NASA ADS
-
Cheng, F. H., Sion, E. M., Szkody, P., et al. 1997, ApJ, 484, L149
In the text
NASA ADS
-
Gammie, C. F., & Menou, K. 1998, ApJL, 492, L75
In the text
NASA ADS
-
Haefner, R., Schoembs, R., & Vogt, N. 1979, A&A, 77, 7
In the text
NASA ADS
-
Hameury, J.-M., Lasota, J.-P., & Hure, J.-M. 1997, MNRAS, 287, 937
In the text
NASA ADS
-
Hameury, J.-M., Lasota, J.-P., & Warner, B. 2000, A&A, 353, 244
In the text
NASA ADS
-
Hellier, C. 2001, PASP, 113, 78
In the text
-
Hirose, M., & Osaki, Y. 1990, PASJ, 42, 135
In the text
NASA ADS
-
Ichikawa, S., Hirose, M., & Osaki, Y. 1993, PASJ, 45, 163
In the text
-
Ishioka, R., Uemura, M., Matsumoto, K., et al. 2002, A&A, 381, L41
In the text
NASA ADS
-
Kato, T., Nogami, D., & Masuda, S. 1996, PASJ, 48, L5
In the text
NASA ADS
-
Kato, T. 1997, PASJ, 49, 583
In the text
NASA ADS
-
Kato, T. 2002, PASJ, 54, L11
In the text
NASA ADS
-
Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Springer)
In the text
-
Kolb, U., & Ritter, H. 1990, A&A, 236, 385
In the text
NASA ADS
-
Kuulkers, E., Knigge, C., Steeghs, D., et al. 2002, in The Physics of Cataclysmic Variables and Related Objects, ed. T. Gaensicke, K. Beuermann, & K. Reinsch, ASP Conf. Ser., 261, 443
In the text
-
Lasota, J.-P. 2001, New Astron. Rev., 45, 449
In the text
NASA ADS
-
Lin, D. N. C., & Papaloizou, J. 1979, MNRAS, 186, 799
In the text
NASA ADS
-
Lubow, S. 1981, ApJ, 245, 274
In the text
NASA ADS
-
Lubow, S. 1991, ApJ, 381, 259
In the text
NASA ADS
-
Lubow, S. 1994, ApJ, 432, 224
In the text
NASA ADS
-
Marino, B. F., & Walker, W. S. G. 1979, in Changing Trends in Variable Star Research, ed. F. M. Bateson et al., IAU Colloq., 46, 29
In the text
-
Mason, E., Skidmore, W., Howell, S. B., et al. 2001, MNRAS, 318, 440
In the text
NASA ADS
-
Mauche, C. W., & Raymond, J. C. 2000, ApJ, 541, 924
In the text
NASA ADS
-
Meyer, F., & Meyer-Hofmeister, E. 1982, A&A, 106, 34
In the text
NASA ADS
-
Meyer, F., & Meyer-Hofmeister, E. 1983, A&A, 121, 299
In the text
-
Meyer, F., & Meyer-Hofmeister, E. 1999, A&A, 341, L23
In the text
NASA ADS
-
Meyer-Hofmeister, E., Meyer, F., & Liu, B. F. 1998, A&A, 339, 507
In the text
NASA ADS
-
Murray, J. R. 1998, MNRAS, 297, 323
In the text
NASA ADS
-
Nauenberg, M. 1972, ApJ, 175, 417
In the text
NASA ADS
-
O'Donoghue, D. 1990, MNRAS, 246, 29
In the text
NASA ADS
-
O'Donoghue, D. 1992, in Vina Del Mar Workshop on Cataclysmic Variable Stars, ed. N. Vogt, ASP Conf. Ser., 29, 136
In the text
-
Ogilvie, G. I. 2002, MNRAS, 330, 937
In the text
NASA ADS
-
Osaki, Y. 1974, PASJ, 26, 429
In the text
NASA ADS
-
Osaki, Y. 1985, A&A, 144, 369
In the text
NASA ADS
-
Osaki, Y. 1989, PASJ, 41, 1005
In the text
NASA ADS
-
Osaki, Y. 1995, PASJ, 47, 47
In the text
NASA ADS
-
Osaki, Y. 1996, PASP, 108, 39
In the text
NASA ADS
-
Osaki, Y., Meyer, F., & Meyer-Hofmeister, E. 2001, A&A, 370, 488
In the text
NASA ADS
-
Osaki, Y., & Meyer, F. 2002, A&A, 383, 574
In the text
NASA ADS
-
Patterson, J., Jablonski, F., Koen, C., et al. 1995, PASP, 107, 1183
In the text
NASA ADS
-
Patterson, J., McGraw, J. T., Coleman, et al. 1981, ApJ, 248, 1067
In the text
NASA ADS
-
Patterson, J., Masi, G., Richmond, M., et al. 2002, PASP, 114, 721
In the text
NASA ADS
-
Pedlovsky, J. 1982, Geophysical Fluid Dynamics (New York: Springer)
-
Pringle, J. E., Bateson, F. M., Hassall, B. J. M., et al. 1987, MNRAS, 225, 73
In the text
NASA ADS
-
Rolfe, D. J., Haswell, C. A., & Patterson, J. 2001, MNRAS, 324, 529
In the text
NASA ADS
-
Semeniuk, I. 1980, A&AS, 39, 29
In the text
NASA ADS
-
Smak, J. I. 1991, in Structure and Emission Properties of Accretion Disks, ed. C. Bertout, S. Collin-Souffrin, & J. P. Lasota et al. (Paris: Éditions Frontières), 247
In the text
-
Smak, J. 1993, Acta Astron. 43, 101
In the text
NASA ADS
-
Smak, J. 1996, in Cataclysmic Variables and Related Objects, ed. A. Evans, & J. H. Wood (Dordrecht: Kluwer), 45
In the text
-
Smak, J. 2000, New Astron. Rev., 44, 171
In the text
NASA ADS
-
Smak, J. I. 2001, Acta Astron., 51, 295
In the text
NASA ADS
-
Spruit, H. 2002, Sol. Phys., accepted [astro-ph/0209146]
In the text
-
Steeghs, D., Marsh, T., Kuulkers, E., & Skidmore, W. 2001a
In the text
-
Steeghs, D., Marsh, T., Knigge, C., et al. 2001b, ApJ, 562, L145
In the text
NASA ADS
-
Stehle, R., & Spruit, H. C. 1999, MNRAS, 304, 674
In the text
NASA ADS
-
Suleimanov, V., Meyer, F., & Meyer-Hofmeister, E. 1999, A&A, 350, 63
In the text
NASA ADS
-
van der Woerd, H., & van Paradijs, J. 1987, MNRAS, 224, 271
In the text
NASA ADS
-
Vogt, N. 1983, A&A, 118, 95
In the text
NASA ADS
-
Warner, B. 1995, Cataclysmic Variable Stars (Cambridge: Cambridge University Press)
In the text
-
Warner, B., & O'Donoghue, D. 1988, MNRAS, 233, 705
In the text
NASA ADS
-
Warner, B., Livio, M., & Tout, C. A. 1996, MNRAS, 282, 735
In the text
NASA ADS
-
Whitehurst, R. 1988, MNRAS, 232, 35
In the text
NASA ADS
-
Whitehurst, R., & King, A. 1991, MNRAS, 249, 25
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H4045F1.ps}\end{figure}](/articles/aa/full/2003/13/aah4045/Timg2.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H4045F2.ps}\end{figure}](/articles/aa/full/2003/13/aah4045/Timg3.gif)
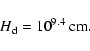
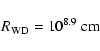
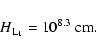
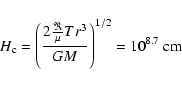
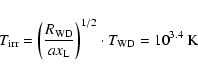
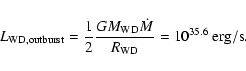
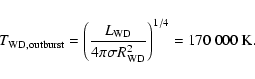
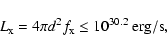
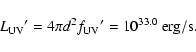
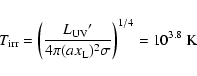
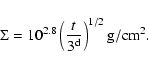
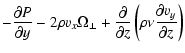
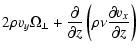
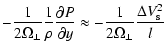
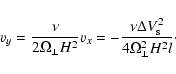
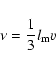
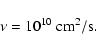
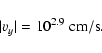
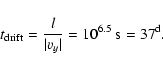
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{H4045F4.ps}\end{figure}](/articles/aa/full/2003/13/aah4045/Timg66.gif)