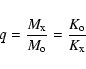 |
(1) |
Binary systems containing an X-ray pulsar are very important
astrophysically as they can offer a direct measurement of the neutron star
mass. The mass ratio of the system, q, is simply given by the ratio of the
radial velocity semi-amplitudes for each component:
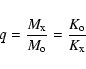 |
(1) |
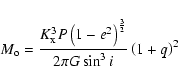 |
(2) |
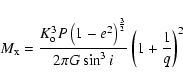 |
(3) |
We therefore have a means of calculating the mass of the neutron star if
the orbits of the two components and the inclination of the system are known.
Such a combination is possible in an eclipsing X-ray binary system, in
which the neutron star is a pulsar. X-ray pulse timing delays around the
neutron star orbit yield the value of ![]() ,
and conventional radial
velocity measurements from optical spectra yield
,
and conventional radial
velocity measurements from optical spectra yield ![]() .
.
A value for i can be obtained from the following approximations:
 |
(4) | ||
| (5) |
| A | (6) | ||
| B | (7) | ||
| C | (8) |
Only seven eclipsing X-ray binary pulsars are known (namely Her X-1, Cen X-3, Vela X-1, SMC X-1, LMC X-4, QV Nor and OAO1657-415). Orbital parameters for the first six of these are still relatively poorly known, whilst the counterpart to OAO1657-415 has only recently been identified (Chakrabarty et al. 2002) and no optical radial velocity curve has been measured. In addition, the mass of the neutron star in a seventh eclipsing X-ray binary (4U1700-37) has recently been determined by Clark et al. (2002). This system does not contain an X-ray pulsar though, and the mass determination is based on a Monte-Carlo modelling method which relies on the spectral type of the companion and is thus highly uncertain. Vela X-1 is the only one of these systems to have an eccentric orbit, and apart from OAO1657-415 is the one with the longest orbital period. For these reasons, and others discussed below, an accurate determination of the mass of the neutron star in Vela X-1 has always been difficult to obtain.
Copyright ESO 2003