A&A 400, 1043-1049 (2003)
DOI: 10.1051/0004-6361:20030014

A spectroscopic atlas of Deneb (A2 Iae) $\lambda \lambda$3826-5212

B. Albayrak¹ - A. F. Gulliver^2, - S. J. Adelman $^{3,\star\star}$ - C. Aydin¹ - D. Koçer⁴

1 - Ankara University, Science Faculty, Department of Astronomy and Space Sciences, 06100, Tandogan, Ankara, Turkey
2 - Department of Physics and Astronomy, Brandon University, Brandon, MB, R7A 6A9, Canada
3 - Department of Physics, The Citadel, 171 Moultrie Street, Charleston, SC 29409, USA
4 - Istanbul Kültür University, Science & Art Faculty, Department of Mathematics, E5 Karayolu Üzeri, 34510, Sirinevler, Istanbul, Turkey

Received 2 December 2002 / Accepted 6 January 2003

Abstract
We present a spectroscopic atlas of Deneb (A2 Iae) obtained with the long camera of the 1.22-m telescope of the Dominion Astrophysical Observatory using Reticon and CCD detectors. For $\lambda \lambda$3826-5212 the inverse dispersion is 2.4 Å  ${\rm mm}^{-1}$ with a resolution of 0.072 Å. At the continuum the mean signal-to-noise ratio is 1030. The wavelengths in the laboratory frame, the equivalent widths, and the identifications of the various spectral features are given. This atlas should provide useful guidance for studies of other stars with similar spectral types. The stellar and synthetic spectra with their corresponding line identifications can be examined at http://www.brandonu.ca/physics/gulliver/atlases.html

Key words: atlases - stars: early type - stars: individual: Deneb - stars: supergiants

1 Introduction

Deneb ($\alpha$ Cygni, 50 Cygni, HR 7924, HD 197345, BD +44$^{\circ}$ 3541, GC 28846, SAO 49941, ADS 14172, FK4 777, GCRV 12971, HIC 102098) is a relatively sharp-lined and unreddened prototype of the early A-type supergiants which are among the most luminous stars in the Milky Way and other spiral galaxies. Its spectral type is given as A2 Ia by almost all modern classifiers beginning with Morgan & Roman (1950) and Keenan & Hynek (1950). It is appropriate to add an e to the spectral type as emission line cores are seen in at least H$\alpha$. The literature concerning Deneb and similar supergiants is extensive and convoluted.

The material described here was analyzed by Albayrak (1999,2000) for his Ph.D. Thesis. It is a set of very high quality spectra obtained with modern electronic detectors on a spectrograph with a known amount of scattered light which has been removed. By making the spectrum widely available in FITS and html formats along with the line identifications, we hope this material will be useful for many other studies.

2 Observations and reductions

This atlas of Deneb's spectrum from $\lambda \lambda$3826-5212 was compiled from 2nd order exposures obtained with a Reticon and the SITe-2 CCD detector (with respective wavelength coverages of 67 and 63 Å) and the long camera of the 1.22-m telescope of the Dominion Astrophysical Observatory (DAO) with a resolution of 0.072 Å  (two pixels) and a mean signal-to-noise (S/N) ratio of 1030. The central wavelengths between $\lambda$3860 and $\lambda$5180 used 55 Å offsets. A central stop in the beam removed light in the same manner as does the secondary mirror of the telescope. The exposures were flat fielded with exposures of an incandescent lamp, which was viewed through a filter, placed in the coudé mirror train. For the observations described here, we used the IS96B image slicer.

For a continuation of this atlas, first order exposures extending further to the red using the IS96R image slicer are being obtained with a resolution of 0.144 Å. These will be posted on the URL given below and described in a future publication.

Reticon exposures were reduced to one-dimensional FITS files using the stellar and lamp exposures with the Program RET72 (Hill & Fisher 1986). For CCD exposures we also used bias exposures and the program CCDSPEC (Gulliver & Hill 2003). Bias and flat images were summed to provide mean bias and mean flat exposures. The mean bias exposures were subtracted from the mean flat and the arc and stellar exposures. Then the arc and stellar exposures were divided by the mean flat image. Cosmic rays were completely removed from the individual stellar exposures. Point spread functions perpendicular to the dispersion direction were used in an optimally weighted extraction in which the weights were proportional to the recorded intensity squared. Arc exposures were extracted using the same cross-sectional profile as the stellar images.

The arc files were measured interactively using the relevant routine in REDUCE (Hill & Fisher 1986), a spectrophotometric reduction and analysis program. An initial approximation to the dispersion characteristics of each DAO spectrograph were input and corrections, based on the agreement between the predicted and measured position of each line, were used to predict the position of each new line. When the corrections became sufficiently small, the remaining lines were measured automatically. Heliocentric radial velocity corrections were applied using the program VSUN (Hill & Fisher 1986). Wavelength-calibrated spectra were produced with REDUCE using the arc files. The wavelength scale accuracy is better than 0.005 Å. Where there were multiple spectra of the same region, we added them with program TSTACK (Hill & Fisher 1986) to increase the S/N ratio. Each spectrum was weighted appropriately by its intensity value.

The radial velocity of each spectrum was measured using the program VCROSS (Hill & Fisher 1986) that cross-correlated the stellar spectrum with a synthetic spectrum with the same atmospheric parameters as Albayrak (1999) ( $T_{\rm eff}$ = 9000 K, log g= 1.45, solar composition and a microturbulence of 8 km s^-1), produced by the program SYNTHE (Kurucz & Avrett 1981). To increase the resolution of the cross-correlation function the synthetic spectrum was broadened only by a rotational velocity of 10 km s^-1. The cross-correlation function was fitted by a Gaussian, the centroid and FWHM of which were allowed to vary. A zero background slope of the Gaussian fit was an important restriction. The mean error of the radial velocities, as shown in Table 1, is 0.3 km s^-1.

 

 

Table 1: Deneb spectrograms.

Exposure	Heliocentric	Central	Radial	S/N
Number	Julian Date	Wavelength	Velocity
		(Å)	(km s-1)
W48927687	2448847.88366	3860	-3.4 $\pm$ 0.6	540
W48922514	2448759.91626	3915	-3.8 $\pm$ 0.4	925
W48922543	2448760.91398	3970	-2.2 $\pm$ 0.4	300
W122_98_8539	2450986.73870	3970	-6.7 $\pm$ 0.5	560
W122_98_8541	2450986.75370	3970	-6.4 $\pm$ 0.5	660
W122_98_8543	2450986.76890	3970	-6.6 $\pm$ 0.4	610
W122_98_8547	2450986.83280	3970	-6.4 $\pm$ 0.4	680
Wdeneb3970		3970		1400
W48921834	2448711.05029	4025	0.1 $\pm$ 0.6	450
W122_98_7183	2450966.96830	4025	-6.4 $\pm$ 0.7	380
W122_98_7184	2450966.98000	4025	-6.7 $\pm$ 0.7	480
W122_98_7232	2450967.95800	4025	-6.6 $\pm$ 0.7	640
W122_98_7234	2450967.97670	4025	-6.8 $\pm$ 0.7	510
Wdeneb4025		4025		1020
W48892563	2447747.67640	4080	-6.0 $\pm$ 0.4	600
W122_98_11340	2451024.75820	4080	-4.9 $\pm$ 0.4	900
W122_98_11342	2451024.77030	4080	-4.8 $\pm$ 0.4	900
Wdeneb4080		4080		1100
W48904090	2448225.55567	4135	-7.5 $\pm$ 0.2	800
W48921805	2448710.01491	4190	-1.5 $\pm$ 0.2	850
W48892617	2447748.62990	4245	-5.3 $\pm$ 0.2	900
W48927667	2448846.84902	4245	-2.2 $\pm$ 0.1	850
Wdeneb4245		4245		1110
W48921775	2448708.00087	4300	-3.7 $\pm$ 0.3	590
W48904016	2448222.66580	4355	-2.8 $\pm$ 0.5	630
W48894610	2447785.56630	4410	0.5 $\pm$ 0.4	710
W48894503	2447831.57270	4465	-3.0 $\pm$ 0.5	750
W48894558	2447832.56960	4520	-3.1 $\pm$ 0.1	1100
W48901454	2448072.80101	4575	4.7 $\pm$ 0.3	525
W48901735	2448095.85210	4630	1.5 $\pm$ 0.3	400
W122_98_8741	2450992.74870	4630	-4.5 $\pm$ 0.3	250
W122_98_8743	2450992.76120	4630	-4.4 $\pm$ 0.4	550
W122_98_8745	2450992.77410	4630	-4.6 $\pm$ 0.3	620
W122_98_8747	2450992.78310	4630	-4.6 $\pm$ 0.3	500
Wdeneb4630		4630		820
W48913708	2448480.84004	4685	0.8 $\pm$ 0.2	425
W48921742	2448707.03957	4740	-4.8 $\pm$ 0.3	710
W48927812	2448851.96527	4795	-5.3 $\pm$ 0.2	650
W48927841	2448852.77771	4795	-4.6 $\pm$ 0.3	650
Wdeneb4795		4795		810
W48927851	2448852.96867	4850	-2.7 $\pm$ 0.2	1010
W122_97_9144	2450590.98785	4905	-4.7 $\pm$ 0.1	880
W48927917	2448855.98969	4960	-1.9 $\pm$ 0.8	840
W122_97_11836	2450649.98946	5015	-8.4 $\pm$ 0.1	650
W122_97_11838	2450649.98946	5015	-8.5 $\pm$ 0.2	700
Wdeneb5015		5015		1000
W48901335	2448065.78950	5070	1.0 $\pm$ 0.1	700
W122_97_9350	2450592.98665	5070	-5.8 $\pm$ 0.1	680
Wdeneb5070		5070		1300
W48901361	2446066.96520	5125	-0.6 $\pm$ 0.2	940
W48927887	2448853.96924	5180	-1.6 $\pm$ 0.2	500

Stellar intensity files were rectified with REDUCE so that the continuum was calculated from locally averaged points. The rectification was completed by interpolating between the averaged data by Hermite spline functions, which always pass through the averaged continua at the selected wavelengths. The scattered light along the spectrum was assumed to be 3.5% of the continuum (Gulliver et al. 1996). The final atlas and the published equivalent widths reflect this correction.

Rectification points were chosen by a novel technique that involves the selection of suitable intervals from the synthetic spectrum of Deneb. The parameters of this synthetic spectrum included those already mentioned as well as a macroturbulent velocity of 14 km s^-1, a v sin i of 25 km s^-1 and a digitally sampled instrumental profile with a FWHM of 0.072 Å. These rectification points need not be actual continuum points. A trial choice of suitable rectification points is based upon any wavelength interval for which the synthetic spectrum is roughly smooth and there is good agreement with the observed spectrum. Obviously, good stellar parameters are a necessity. In effect this is an iterative process in which trial points are modified or rejected if there is not good agreement between the synthetic and observed spectrum. The process is complicated by poorly known atomic data for some lines which produce discrepant line strengths and positions in the synthetic spectrum. For any suitable rectification point, an intensity level is established from the synthetic spectrum and the observed spectrum is normalized at that value.

This technique can be used for any star that has well defined stellar parameters. It is particularly useful for rectification across broad hydrogen wings, for late type stars in which true continuum may be entirely absent and, as in this case, the appending of sections of spectra to produce a single monolithic spectrum. To facilitate the seamless combination of the sections there were at least two common rectification points over each 7 to 9 Å overlap.

3 Atlas

The final monolithic spectrum is displayed at the URL http://www.brandonu.ca/physics/gulliver/deneb. The JAVA tool provided will allow the display and comparison, in any combination, of the observed and synthetic spectra and their respective line identifications. Unrectified or rectified sections of the Deneb spectrum, or the complete rectified spectrum, are also available as FITS format files from one of the authors (AFG) and the CDS. Copies of the line identifications are also available.

For the purpose of illustrating the nature of the atlas, Figs. 1 and 2 show the single section, centered at 4245 Å, of the Deneb atlas, which includes 25 such sections. The majority of the line identifications for this section are reproduced in the figures. The Java tool mentioned above would give a more accurate impression of the quality of the Deneb atlas.

	Figure 1: 4245 Å  section of the Deneb Atlas ( $\lambda \lambda$4215-4245).
Open with DEXTER

	Figure 2: 4245 Å  section of the Deneb Atlas ( $\lambda \lambda$4245-4275.)
Open with DEXTER

4 Line identifications

For each line we employed the program VLINE (Hill & Fisher 1986) to measure the equivalent width, the central wavelength, the line depth, and the full width at half maximum of the fitted profile, which was taken to be a Gaussian for most metal lines except the weak lines ($\le$20 mÅ) which were rotational profiles and some He I lines which were Lorentzian profiles. Such line profiles are satisfactory for most lines. But the extended wings of Deneb's strongest metal lines can require additional components.

Our initial rotational velocity estimate based on non-blended lines with rotational profiles near Mg II $\lambda$4481 was 27 km s^-1. Such lines with equivalent widths of 10 to 18 mÅ are sufficiently weak to be unaffected by atomic line broadening, macroturbulence, and microturbulence and are clearly on the linear part of the curve-of-growth. During the later analysis of the macroturbulence via spectral synthesis technique, $v \sin i$ was refined to 25 km s^-1 (Albayrak 1999,2000).

To begin the line identification process, we identified the cleanest lines in the spectrum which are minimally affected by noise. For Deneb this means lines with equivalent widths between 15 and 300 mÅ. These can often be found by examining stellar line identification list of stars of similar temperature, previous studies of Deneb, or working with standard references, in particular A Multiplet Table of Astrophysical Interest also known as the Revised Multiplet Table (Moore 1945). As not all atomic wavelength studies have equally well-determined wavelengths, one tries to find those which are consistent with modern determinations for Fe I and Fe II.

Stellar lines were identified with the general references A Multiplet Table of Astrophysical Interest (Moore 1945) and Wavelengths and Transition Probabilities for Atoms and Atomic Ions, Part 1 (Reader & Corliss 1980), and selected references from the bibliography of Adelman & Snijders (1974) whose most recent update is Adelman (2001). We used line identifications by Adelman and his associates for other stars which they have analyzed using DAO spectrograms, in particular $\gamma$ Gem (Adelman & Gulliver, in preparation), $\sigma$ Boo (Adelman et al. 1997), and 2 Lyn, $\omega$ UMa, and $\phi$ Aql (Caliskan & Adelman 1997). We also compared our results with previous line-identified studies of Deneb, especially that of Groth (1961).

To derive the radial velocities we compared the observed and laboratory wavelengths of clearly unblended lines. For each spectrum we derived the average radial velocity and its standard deviation. If the observed stellar wavelengths as transformed to the laboratory frame yield many head-on coincidences, i.e., these wavelengths coincide with wavelengths of atomic species known or likely to be present, then the radial velocities are considered to be good. Table 1 lists the spectrograms with the their exposure numbers, Heliocentric Julian Dates at the mid-points of their exposures, an estimate of the S/N ratio, and the derived radial velocities and their associated errors. The co-additions are labeled Wdeneb+the central wavelength in Å. The S/N ratio of each section was estimated from the root-mean-square deviation for the continuum point intervals, usually smooth regions without lines close to the continuum, as part of the rectification process. The CCD exposures generally show more consistent S/N ratios for their whole spectral region than do the Reticon spectra. The more general, overall S/N ratio of 1030:1 was determined by fitting an appropriately-filtered Fourier Transform to the entire spectrum.

Table 2 (accessible in electronic form) presents the full line identifications for $\lambda \lambda$3826-5212. The identifications are available elsewhere as noted previously. To identify as well as possible the lines in the spectrum of Deneb an established procedure was followed. After the elemental abundances of Deneb were determined, a synthetic spectrum was calculated using Program SYNTHE (Kurucz & Avrett 1981) with the adopted model atmosphere, solar abundances, the atomic data of Kurucz & Bell (1995), the instrumental profile of the long camera of the DAO coudé spectrograph, and the other parameters found for Deneb by Albayrak (1999,2000). It was a good, but not perfect match. A list of lines which contributed significantly to the spectrum was made and used to help identify unidentified features. For those lines not in other sources which are likely to be contributors, we used K as the multiplet number. The far left column contains the letters L and R are a guide to the range of lines whose wings are at least somewhat blended together. For example in Fig. 1, the features corresponding to Fe I 4219.360 and V II 4220.058 have their respective longward and shortward wings blended together and in Table 2 in the left column L and R are indicated, respectively. The columns are the measured stellar wavelength in Å, the equivalent width ( $W_{\lambda}$) in mÅ, the line depth as a fraction of the continuum height, the line width (FWHM) in Å, the laboratory wavelength in Å, which is the stellar wavelength as corrected for the stellar radial velocity of each spectrum, and the identified atomic lines which cause the observed feature. The stellar and the laboratory wavelengths should be close, but blending and errors can produce discrepancies. Possible identifications are given in parentheses and brackets indicate that an identified line may be contributing to two measured stellar features.

The following discussion indicates which atomic species were found in the observed spectral region. Usually no discussion is given for those species whose lines were found be absent. The major sources of the laboratory data which supplement A Multiplet Table of Astrophysical Interest (Moore 1945) are given after each atomic species.

1. H I: All of the Balmer lines are found.

2. He I: Most of the He I lines are found while the forbidden components are difficult to see if present. Some He I lines are blended with lines of other elements or are close to the cores of Balmer lines. Lines which are definitely present belong to multiplets 4, 5, 11, 12, 14, 16, 18, 20, 47, 48, 50, 51, 52, 53, and 55.

3. C I (Moore 1993): Lines with laboratory intensities of 5 and greater are identified. The strongest lines include $\lambda$4771.747 (multiplet 6), $\lambda$5052.167 (multiplet 8), $\lambda$4932.050 (multiplet 13), and $\lambda$4371.368 (multiplet 14) with the largest equivalent width being 4.6 mÅ.

4. C II (Moore 1993): Lines of multiplets 4 and 6 are present. Only $\lambda$4267.258 is not severely blended.

5. N I (Moore 1993): The strongest lines with intensities of 10 and greater are present, but most are blended. Lines with definitely clean identifications include: $\lambda$4223.128 (multiplet 5), $\lambda$4137.640 (multiplet 6), $\lambda$4914.937 and $\lambda$4935.121 (multiplet 9), $\lambda$4660.455 (multiplet 9.02), and $\lambda$3830.433 (multiplet 11).

6. N II (Moore 1993): Two of the strongest lines $\lambda$4630.543 (multiplet 14, intensity 15) and $\lambda$3994.998 (multiplet 12, intensity 15) are clearly present as is $\lambda$4241.784 (multiplet 48, intensity 10). A few other strong lines might be present in blends.

7. O I (Moore 1993): The lines of multiplet 3 near $\lambda$3947 appear to be blended with a Fe I line, those of multiplet 5 near $\lambda$4368 are definitely present, $\lambda$4968.7931 is possibly blended with an Fe I line, those of multiplet 16 near $\lambda$4773 are weakly present, and $\lambda$5018.7832 (multiplet 13, intensity 5) is a possible identification. Hence lines of this species are probably present.

8. Na I: Lines of multiplet 8 are possibly present in blends, but are not marked.

9. Mg I: Lines of multiplets 3, 11, and 15 are clearly present. Those in multiplets 14 and 16 are blended.

10. Mg II: Lines of multiplets 4, 5, 9, 10, 18, 19, 21, 27, and 28 are present while some other lines are probably blended.

11. Al I: The two lines of multiplet 1 are present.

12. Al II: $\lambda$4663.054 (multiplet 2) is identified with a 48 mÅ line. A few other lines might be present in blends.

13. Si I (Moore 1967): $\lambda$3905.523 (multiplet 3) is blended with a Cr II line.

14. Si II (Moore 1965): Lines of multiplets 1, 3, 3.01, 5, 7.05, 7.06, 7.07, 7.15, 7.16, 7.17, 7.18, and 23 are present.

15. S II (Pettersson 1983): Lines with intensities of 21 and greater are found often in blends. Some intensity 18 and 20 lines are found.

16. Ca I : The resonance line $\lambda$4226.728 (multiplet 2) is present. Some lines with intensities of 40 and greater are in blends.

17. Ca II: The H, the K, and the $\lambda$4799.973 lines are present.

18. Sc II: Lines with intensity 10 and greater are definitely present. Some weaker lines may be present.

19. Ti I: The strongest line $\lambda$3998.635 (multiplet 12) is probably present as well as some other nearly as intense lines in blends.

20. Ti II (Huldt et al. 1982): Most lines with intensities of 5 or greater in Huldt et al. are present as well as some weaker ones. $\lambda$4806.321 is present according to data from Kurucz & Bell (1995).

21. V II (Iglesias et al. 1988): Almost all lines with intensities $\ge$50 are present as well as some lines with intensities between 15 and 45. The intensity scale may be wavelength dependent.

22. Cr I (Kiess 1953): Lines of intensities 250 and greater are present. Weaker lines with intensities of 100 are often found in blends. A few lines with intensities as small as 50 are seen on occasion.

23. Cr II (Kiess 1951): Almost all lines with intensities 4 and greater are found. Some intensity 2 lines are found. A few predicted lines from Dworetsky (1971) and Kurucz & Bell (1995) may be present.

24. Mn I: Lines only from multiplet 1 are present.

25. Mn II (Iglesias & Velasco 1964): All lines stronger than intensity 100 are present. Some lines as weak as intensity 50 are found.

26. Fe I: Most lines with numerical intensities given are found. The wavelengths were updated using Nave et al. (1994).

27. Fe II: Most lines in Moore (1945) including predicted lines are found as are some lines from Dworetsky (1971) and Guthrie (1985). Almost all the lines in Johansson (1978) with intensities of 4 and greater are found as are most lines with intensities of 2 and 3. Shortward of $\lambda$4800, some lines with intensities of 0 and 1 found. For $\lambda$$\lambda$4800-5212 we used Johansson as the primary source.

28. Fe III (Glad 1956): $\lambda$4419.599, multiplet 4, is the only line definitely found. Kurucz & Bell (1995) indicates in addition $\lambda$4382.511.

29. Co II: We found two lines in the region studied. Lines of Co II were found by Buscombe (1951) and Groth (1961) outside our observed wavelength range and are probably correctly identified.

30. Ni I: We used the wavelengths from Litzen et al. (1993). But only a few of the strongest lines are present, often in blends.

31. Ni II: All lines observed in the laboratory were found.

32. Sr II: The two strong lines of multiplet 1 are present.

33. Y II (Nilsson et al. 1991): Most of the strong lines with intensities greater than 1050 are present.

33. Zr II: Most lines with intensities 15 and greater are found along with a few as weak as intensity 7.

34. Ba II: Both lines of multiplet 1 are found, but in blends.

35. Cd I: There are features close to the position of the two strongest lines of multiplet 2 $\lambda$5085.824 and $\lambda$4799.918. But $\lambda$4799.918 is blended with an Ca II line which has a greater residual intensity. If one ignores the blend and calculates log Cd/H, the result is an excess of 3.91 dex relative to the Sun. This strongly suggests a misidentification.

36. La II (Meggers et al. 1975): The strongest lines $\lambda$3949.10 and $\lambda$4086.72 are probably present.

37. Eu II (Meggers et al. 1975): $\lambda$3930.50, $\lambda$4129.73, and $\lambda$4205.05 suggest Eu II is weakly present.

Previously published line lists of Deneb include most of the lines which have equivalent widths $W_{\lambda} \ge$ 10 mÅ. Most differences involve the weakest lines as would be anticipated. The new species of Deneb definitely found by this study are C I, N II, Si I, Fe III, Ba II, and La II. There is no evidence for the presence of lines of A I (Taffara 1966; Zverko 1971), Si III, Ce II, Gd II, Hf II (Zverko 1971), Pr II (Groth 1961; Taffara 1966; Zverko 1971) and Cl II (Taffara 1966; Zverko 1971).

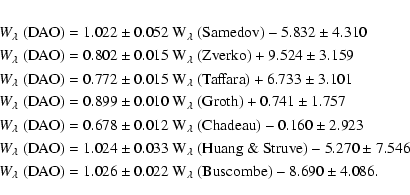
Small errors in the equivalent widths can effect the derived abundances, especially if the lines lie on the flat part of the curve-of-growth. Thus a necessary test between different analyses is a comparison of the derived equivalent widths of this analysis with the major studies of Deneb in the literature. Least squares comparisons in mÅ  of these values and those of this study (denoted by DAO) respectively for 31, 186, 302, 261, 154, 95 and 147 equivalent width values of Samedov (1993), Zverko (1971), Taffara (1966), Groth (1961), Chadeau (1955), Huang & Struve (1955), and Buscombe (1951) yield:

$$\begin{eqnarray*}&& W_{\lambda}~\rm {(DAO)} = 1.022 \pm 0.052~W_{\lambda}~\rm {(... ... 1.026 \pm 0.022~W_{\lambda}~\rm {(Buscombe)} - 8.690 \pm 4.086. \end{eqnarray*}$$

For good agreement, one would expect the coefficient of the $W_{\lambda}$ term to be close to unity while the constant term to be close to zero. The differences come from scattered light, errors in the calibration procedure especially with photographic plates and continuum placement problems. Having the linear term not unity might reflect how the line profiles were drawn or errors in the plate calibration. A non-zero constant term implies a difference in placing the continuum either higher or lower according to its sign.

Recently Aufdenberg et al. (2002) calculated a non-LTE, line-blanketed, spherical expanding model atmosphere for Deneb with the PHOENIX code (Hauschildt & Baron 1999) using a solar composition. They found $T_{\rm eff}$ = 8400 $\pm$ 100 K. A natural extension of their work and this investigation is to study the data of this atlas by adding the ability to vary the abundances in PHOENIX. We anticipate that problems with both analyses should be reduced. Such a study also provides an excellent justification to extend this atlas toward longward wavelengths.

Acknowledgements

SJA and AFG thank Dr. James E. Hesser, Director of the Dominion Astrophysical Observatory for the observing time. This research was supported in part by grants from TÜBITAK (the Scientific and Technical Research Council of Turkey), the Turkish Academy of Sciences in the framework of the Young Scientist Award Program BA/TÜBA-GEBIP/2001-2-2), the National Sciences and Engineering Research Council of Canada, and The Citadel Foundation. We also appreciate the useful comments of the referee Dr. J. Zverko.

References

 
• Adelman, S. J., Caliskan, H., Kocer, D., & Bolcal, C. 1997, MNRAS, 288, 470 In the text NASA ADS  
• Adelman, S. J., & Snijders, M. A. J. 1974, PASP, 86, 1018 In the text NASA ADS  
• Adelman, S. J. 2001, PASP, 113, 344 In the text NASA ADS  
• Albayrak, B. 1999, Ph.D. Thesis, University of Ankara In the text  
• Albayrak, B. 2000, A&A, 364, 237 In the text NASA ADS  
• Aufdenberg, J. P., Hauschildt, P. H., Baron, E., et al. 2002, ApJ, 570, 344 In the text NASA ADS  
• Buscombe, W. 1951, ApJ, 114, 73 In the text NASA ADS  
• Caliskan, H., & Adelman, S. J. 1997, MNRAS, 288, 501 In the text NASA ADS  
• Chadeau, C. 1955, Ann. Ap. 18, 100 In the text NASA ADS  
• Dworetsky, M. M. 1971, Ph.D. Thesis, University of California, Los Angeles In the text  
• Glad, S. 1956, Ark. Fys. 10, 291 In the text  
• Groth, H. G. 1961, Z. Astrophys. 51, 206 In the text  
• Gulliver, A. F., Hill, G., & Adelman, S. J. 1996, in Model Atmospheres and Spectrum Synthesis, ASP Conf. Ser., 108, 232 In the text  
• Gulliver, A. F., & Hill, G. 2003, in ASP Conf. Ser., in press In the text  
• Guthrie, B. N. G. 1985, MNRAS, 216, 1 In the text NASA ADS  
• Hauschildt, P. H., & Baron, E. 1999, J. Comp. Appl. Math., 109, 41 In the text  
• Hill, G., & Fisher, W. A. 1986, Publ. Dom. Astrophys. Obs., 16, 13 In the text  
• Huang, S.-S., & Struve, O. 1955, ApJ, 121, 84 In the text NASA ADS  
• Huldt, S., Johansson, S., Litzen, U., & Wyart, J.-F. 1982, Phys. Scripta, 25, 401 In the text NASA ADS  
• Iglesias, L., & Velasco, R. 1964, Publ. del Instituto de Optica de Madrid, 23 In the text  
• Iglesias, L., Cabeza, M. I., & de Luis, B. 1988, Publ. del Instituto de Optica de Madrid, 47 In the text  
• Johansson, S. 1978, Phys. Scr., 18, 217 In the text NASA ADS  
• Keenan, P. C., & Hynek, J. A. 1950, ApJ, 111, 1 In the text NASA ADS  
• Kiess, C. C. 1951, J. Res. NBS, 47, 385 In the text  
• Kiess, C. C. 1953, J. Res. NBS, 51, 247 In the text  
• Kurucz, R. L., & Avrett, E. H. 1981, Smithsonian Astrophys. Obs. Spec. Rep., 391 In the text  
• Kurucz, R. L., & Bell, B. 1995, Kurucz CD-Rom No. 23 In the text  
• Litzen, U., Brault, J. W., & Thorne, A. P. 1993, Phys. Scr., 47, 628 In the text NASA ADS  
• Meggers, W. F., Corliss, C. H., & Scribner, B. F. 1975, Tables of Spectral-Line Intensities Part I - Arranged by Elements, 2nd ed., (Washington, DC: Government Printing Office) In the text  
• Moore, C. E. 1945, A Multiplet Table Astrophysical Interest (Princeton University Observatory) In the text  
• Moore, C. E. 1965, NSRDS-NBS 3, Section 1 (Washington, DC: US Government Printing Office) In the text  
• Moore, C. E. 1967, NSRDS-NBS 3, Section 2 (Washington, DC: US Government Printing Office) In the text  
• Moore, C. E. 1993, Tables of Spectra of Hydrogen, Carbon, Nitrogen, and Oxygen Atoms and Ions, CRC Series in Evaluated Data in Atomic Physics, ed. J. W. Gallagher (Boca Raton, FL: CRC Press Inc.) In the text  
• Morgan, W. W., & Roman, N. G. 1950, ApJ, 112, 362 In the text NASA ADS  
• Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, ApJS, 94, 221 In the text NASA ADS  
• Nilsson, A. E., Johasson, S., & Kurucz, R. L. 1991, Phys. Scr., 44, 226 In the text NASA ADS  
• Pettersson, J. E. 1983, Phys. Scripta, 28, 421 In the text NASA ADS  
• Reader, J., & Corliss, C. H. 1980, NSRDS-NBS 68, Part 1 (Washington, DC: US Government Printing Office) In the text  
• Samedov, Z. A. 1993, Astron. Zh., 70, 82 In the text NASA ADS  
• Taffara, N. S. 1966, Mem. Soc. Astron. It., 37, 401 In the text NASA ADS  
• Zverko, J. 1971, Bull. Astron. Inst. Czech., 22, 49 In the text NASA ADS