A&A 400, 1113-1128 (2003)
DOI: 10.1051/0004-6361:20021795
P. M. Mathews 1 - P. Bretagnon2
1 - Department of Theoretical Physics, University of Madras,
Chennai 600 025, India
2 -
IMCCE, Paris Observatoire de Paris,
75014 Paris, France
Received 2 September 2002 / Accepted 20 November 2002
Abstract
The coefficients of polar motions of the rigid/nonrigid Earth in
frequency bands other than the retrograde diurnal one are
systematically computed using general expressions, derived here for
the first time, for the prograde and retrograde torques exerted on
the Earth by lunisolar potentials of arbitrary spherical harmonic
type. Taken together with the already known coefficients of low
frequency nutations and UT1 variations, they provide a complete
characterization, with high precision, of the motions of the pole of the
terrestrial reference frame in space; this is needed for high precision
studies in astronomy and space geodesy.
The inputs used for our computations are a table of tidal
amplitudes, and values of the geopotential coefficients of degrees
up to 4 and of other relevant basic Earth parameters. General
relations which connect the coefficients of high frequency nutations
to those of the equivalent polar motions are established and used
for deducing the former. The Chandler resonance plays a significant
role in low frequency polar motions. In this context, the role of
mantle anelasticity and the nature of the Earth's deformational
response to zero frequency forcing are given special consideration.
The free core nutation (FCN) resonance of low frequency nutations
is shown to affect the prograde semidiurnal nutations through the
coupling produced between the nutations in the two frequency bands
by triaxiality terms in the angular momenta of the whole Earth and
of its fluid core. It is shown in a transparent fashion that the
effect of the core triaxiality arises almost exclusively from the
huge FCN-related resonance in the wobble of the core. The magnitude
of the effect is found to be a few times smaller than reported
in a recent paper; it is also found, unlike in that paper, that the
changes in the eigenfrequencies due to trixiality are only of the
second order in the triaxiality parameter. Numerical results for the
polar motions of the nonrigid Earth in different frequency bands, as
well as for the elliptical nutations of the rigid Earth, are
tabulated and compared with available numbers from earlier works.
Key words: reference systems - Earth
High precision studies in astronomy as well as in certain areas
of geophysics and geodesy call for a sufficiently precise model of
the motions of the terrestrial reference frame (TRF) in space. The
motions of the pole of the TRF relative to that of the celestial
reference frame (CRF) are described as nutations or polar motions,
depending on the viewpoint. Recent treatments of the nutations of
the hypothetical rigid Earth, (e.g., Bretagnon et al. 1997, 1998;
Souchay & Kinoshita
1996, 1997; Souchay et al. 1999; Roosbeek &
Dehant 1998) have aimed at accuracies of 0.1 microarcseconds (![]() as) or better in the coefficients of nutation. The new
nutation series thus constructed include a considerable number of
short period or high frequency (HF) nutations, having
frequencies higher than 0.5 cycles per sidereal day (cpsd), and
with coefficients up to about 15
as) or better in the coefficients of nutation. The new
nutation series thus constructed include a considerable number of
short period or high frequency (HF) nutations, having
frequencies higher than 0.5 cycles per sidereal day (cpsd), and
with coefficients up to about 15 ![]() asmagnitude for
asmagnitude for
![]() and
and
![]() .
Low frequency nutations are
those with frequencies under 0.5 cpsd. The nutations referred to here
are motions, relative to the CRF, of the figure axis of the
Earth with time dependent deformations diregarded. The pole of the
figure axis will be taken to coincide with the pole of the TRF, the
offset between the two being too small to be of interest for the
present purposes.
.
Low frequency nutations are
those with frequencies under 0.5 cpsd. The nutations referred to here
are motions, relative to the CRF, of the figure axis of the
Earth with time dependent deformations diregarded. The pole of the
figure axis will be taken to coincide with the pole of the TRF, the
offset between the two being too small to be of interest for the
present purposes.
Conventionally, only the low frequency part (as seen from space) of the relative motion of the poles of the CRF and TRF around each other is viewed as nutation. The remaining part of the motion is pictured as "polar motion'' as seen from the terrestrial frame, with a spectrum which includes a low frequency part; in fact, the major components of polar motion are contained in this low frequency part. It is important to take note that the term "polar motion'' as employed in this context means a motion of the pole of the celestial frame as seen from the terrestrial frame. This specific meaning is implicit in the relationship of polar motion to nutation as presented by Gross (1992) (see also Brzezinski & Capitaine 1993). (Historically, the motion of the rotation axis around the figure axis - what is called "wobble'' in this work - was usually referred to as polar motion. While the two types of usage are nearly equivalent in practical terms in the case of polar motions of very low frequencies (e.g., the Chandler wobble), the two are quite different when the polar motions involved are in high frequency bands. It is necessary to keep the distinction clearly in mind to avoid confusion.)
The 1980 IAU theory of nutation (Seidelmann 1982) envisaged only polar motions of low frequencies, below 0.5 cpsd in magnitude in the TRS, besides low frequency nutations. With the restriction to long periodicities, estimation of the coefficients of spectral components of both types of motions from Very Long Baseline Interferometry (VLBI) data, which are available only at intervals of a few days, became straightforward.
The representation adopted recently by the International Astronomical Union (IAU) for the transformation between the celestial and terrestrial reference frames conforms to the convention of separating the relative motions of the poles of the CRF and the TRF into nutations and polar motions, but with a broadening of the concept of polar motions to include high frequency components too. Insofar as nutation and polar motion are visualized, in the transformation, as motions of the "Celestial Intermediate Pole'' (CIP), it needs to be recognized that for those spectral components of the relative motions of the two poles that are of low (high) frequencies in the celestial frame, the CIP is identified, in effect, with the pole of the TRF (CRF).
It is necessary, in view of the above convention, that results relating to what has been referred to in the literature hitherto as "high frequency'' or "short period'' or "diurnal and subdiurnal'' nutation be expressed now in the alternative language of polar motion (PM) with frequencies lying outside the retrograde diurnal band. The presentation of the numerical results in this paper will be done accordingly. We shall, however, use both the alternative terminologies at will, and shall indicate how one may deduce simply, from the results for polar motions, the corresponding results for HF nutations for comparison with the results of earlier authors.
Each spectral component of nutation or polar motion is associated with a corresponding wobble. Wobbles are motions of the rotation axis of the mantle or of either of the core regions relative to a terrestrial frame; where a particular region is not specifically referred to, it is to be understood that the wobble of the mantle is meant.
The frequency of a spectral component of the forced wobble motion is the same as that of the torque which excites the wobble; so is the frequency of the associated polar motion. The frequency of the corresponding nutation, being relative to a space-fixed frame, is higher by 1 cpsd (the mean rate of Earth rotation). It is important to keep this fact in mind, since we will need to refer often to the frequency of the nutation as well that of the associated wobble and polar motion.
The terms low frequency, diurnal, semidiurnal, ![]() will be used
herein for frequencies (of wobbles, nutations, or polar motions, as
the case may be) within bands of width 1 cpsd centered at
will be used
herein for frequencies (of wobbles, nutations, or polar motions, as
the case may be) within bands of width 1 cpsd centered at
![]() cpsd, as seen in the TRF for wobbles and polar motions,
and in the CRF for nutations. Positive (negative) frequencies refer
to prograde (retrograde) motions in the relevant reference frame.
cpsd, as seen in the TRF for wobbles and polar motions,
and in the CRF for nutations. Positive (negative) frequencies refer
to prograde (retrograde) motions in the relevant reference frame.
High frequency nutations result from the action of the tide
generating potential on elements of the Earth's density
distribution that give rise to geopotential coefficients
(Ck,l,Sk,l) with l > 0. Rigid Earth nutations relating
to the cases k=3,4 have been the special focus of Folgueira
et al. (1998a). A listing of diurnal and subdiurnal nutations
with coefficients down to a few hundredths of 1 ![]() asbe found
in Folgueira et al. (2001), with comparisons to values obtained by
others. Now that realistic uncertainties as low as 5
asbe found
in Folgueira et al. (2001), with comparisons to values obtained by
others. Now that realistic uncertainties as low as 5 ![]() as
become possible in the estimation of many nutation components (see,
for instance, Herring et al. 2002), high frequency nutations - at
least, those with amplitudes of several
as
become possible in the estimation of many nutation components (see,
for instance, Herring et al. 2002), high frequency nutations - at
least, those with amplitudes of several ![]() as- have to
be taken seriously from the observational point of view.
Theoretical evaluation of the amplitudes of the high frequency
nutations of the nonrigid Earth is therefore of considerable
interest. (For recent results on low frequency nutations of the
nonrigid Earth, see Mathews et al. 2002 and references cited
therein.) Bizouard et al. (2001) have presented numbers for
the coefficients of nutations of diurnal and semidiurnal frequencies.
Their results for the nonrigid Earth have been obtained by applying
(an early version of) the transfer function of Mathews
et al. (2002) to the rigid Earth numbers from the works cited
above. However, as will be seen from the theoretical development
to be presented in later sections, the use of that transfer
function, which was constructed for the low frequency nutations, is
inappropriate in principle for high frequency
nutations. Semidiurnal nutations of the nonrigid Earth have been
computed by Getino et al. (2001). Their results are
consistent with the transfer function being essentially constant
across the semidiurnal band. We shall show from very simple
physical considerations that the transfer function should be very
nearly equal to the ratio of the moment of inertia of the whole
Earth to that of the mantle; the complicated formalism used by the
above authors yields no such insights. Escapa et al. (2002)
have drawn attention to a contribution to the semidiurnal nutations
from the resonance in the retrograde diurnal wobbles related to the
free core nutation, via the Earth's triaxiality. The
approach used in the present work makes the mechanism responsible
for this contribution quite transparent.
as- have to
be taken seriously from the observational point of view.
Theoretical evaluation of the amplitudes of the high frequency
nutations of the nonrigid Earth is therefore of considerable
interest. (For recent results on low frequency nutations of the
nonrigid Earth, see Mathews et al. 2002 and references cited
therein.) Bizouard et al. (2001) have presented numbers for
the coefficients of nutations of diurnal and semidiurnal frequencies.
Their results for the nonrigid Earth have been obtained by applying
(an early version of) the transfer function of Mathews
et al. (2002) to the rigid Earth numbers from the works cited
above. However, as will be seen from the theoretical development
to be presented in later sections, the use of that transfer
function, which was constructed for the low frequency nutations, is
inappropriate in principle for high frequency
nutations. Semidiurnal nutations of the nonrigid Earth have been
computed by Getino et al. (2001). Their results are
consistent with the transfer function being essentially constant
across the semidiurnal band. We shall show from very simple
physical considerations that the transfer function should be very
nearly equal to the ratio of the moment of inertia of the whole
Earth to that of the mantle; the complicated formalism used by the
above authors yields no such insights. Escapa et al. (2002)
have drawn attention to a contribution to the semidiurnal nutations
from the resonance in the retrograde diurnal wobbles related to the
free core nutation, via the Earth's triaxiality. The
approach used in the present work makes the mechanism responsible
for this contribution quite transparent.
We begin with a systematic presentation, in Sect. 2, of the interrelations of wobbles, polar motions, and nutations induced by a spectral component of the tidal gravitational potential. General expressions for the torque exerted on the Earth by the potential of arbitrary spherical harmonic type (n,m), not found in the existing literature, are presented in Sect. 3. (The "type'' (n,m) refers to the spherical harmonic degree n and order mof the potential.) These expressions, in which separate prograde and retrograde parts appear, are fundamental to this work, and are derived in Appendix A.
Section 4 deals with the dynamical equations governing the wobble motion for a two-layer Earth composed of the mantle and the fluid core which are mutually coupled; the equations are an adaptation of those of Sasao et al. (1980) to forcing by potentials of general type (n,m). They are entirely adequate for the treatment of all except the retrograde diurnal wobbles with which the low frequency (LF) nutations are associated. The LF nutations, which are by far the most dominant, call for very detailed modeling and are specifically excluded from the ambit of this paper; see Mathews et al. (2002) for a comprehensive treatment which includes the inner core and various other effects in the modeling. Certain enhancements made in that work, like inclusion of mantle anelasticity and ocean tide effects, are retained here as they are of relevance in the case of the prograde diurnal nutations. The core-mantle electromagnetic coupling, also considered in that paper, is insignificant in the present context.
The general solution of the dynamical equations is given in Sect. 5. The LF polar motions and the prograde diurnal ones require special consideration; they are dealt with in Sects. 6 and 7, respectively. The special features in the former case are the existence of the Chandler resonance in the LF band, and the influence of mantle anelasticity on the frequency of the resonance. In the latter case, a coupling between prograde and retrograde wobbles, arising from the triaxiality terms in the angular momentum, has to be taken into account; it is of no consequence in the any other case. It is instructive (and convenient) to take advantage of this coupling for computation of the amplitudes of prograde diurnal polar motions by establishing and making use of their relation to the known amplitudes of the low frequency nutations excited by the same tidal potential; we shall do so in Sect. 7. The possible contribution from triaxiality of the fluid core is of special interest, and is investigated.
Section 8 begins with the explicit expressions for the coefficients of circular polar motions, and their interrelations. General relations connecting coefficients of circular nutations to those of the equivalent polar motions are deduced. Numerical values from computations based on our theoretical approach are presented in several tables of polar motions and/or equivalent nutations in a number of prograde and retrograde frequency bands. Comparisons of our values are made with results from earlier works, for circular motions or for elliptical ones, as available. Finally our numerical results for the contributions from possible triaxiality of the Earth's core are compared with those of Escapa et al. (2002). The concluding section summarizes the main results, highlighting some special features. In particular, we discuss the possibility of determining the trixiality of the core from observations of prograde diurnal polar motions and conclude that the prospects are dim.
The wobbles of the mantle and the fluid core are described by
![]() and
and
![]() ,
defined in terms of the
instantaneous angular velocity vectors
,
defined in terms of the
instantaneous angular velocity vectors
![]() of the
respective regions by
of the
respective regions by
![\begin{displaymath}{\vec \Omega}\!=\!\Omega_0~\left[(1+m_3)~{\vec i}_3+ {\vec m}...
...!\Omega_0~\left[m_{f3}~ {\vec i}_3+{\vec m}_{\rm f}(t)\right],
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img16.gif) |
(1) |
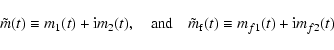 |
(2) |
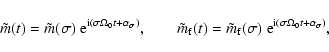 |
(3) |
The phase of a wobble due to lunisolar forcing is related, of
course, to the argument of the relevant spectral component of the
lunisolar potential. In the convention of
Cartwright & Tayler
(1971), the potential of spherical harmonic type (n,m) and
frequency ![]() at the point with colatitude
at the point with colatitude ![]() and longitude
and longitude ![]() at a geocentric distance r is expressed as
at a geocentric distance r is expressed as
![\begin{displaymath}V_{\omega}^{(n,m)}({\vec r};t) = g_{\rm e} H^{(n,m)}_\omega~(...
...a,\lambda)~
{\rm e}^{{\rm i}(\Theta_\omega(t)-\zeta_{n,m})}~],
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img26.gif) |
(4) |
| |
= | ||
| = | (5) |
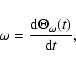 |
(6) |
| (7) |
| (8) |
| (9) |
The complex nutation variable
![]() ,
defined by
,
defined by
| (10) |
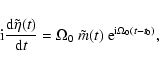 |
(11) |
| (12) |
Equation (11) is a linear approximation to the exact relation, and is
entirely adequate for the present purposes. Taken together with
Eqs. (3) and (12), it implies that a wobble
of frequency ![]() cpsd (
cpsd (
![]() or 0) has the associated
nutation of frequency
or 0) has the associated
nutation of frequency ![]() cpsd:
cpsd:
| |
= | ||
| = | (13) |
| (14) |
Now, the conventional argument ![]() of a nutation of frequency
of a nutation of frequency
![]() is related to the argument
is related to the argument
![]() of the tide which excites
the nutation through
of the tide which excites
the nutation through
| (15a) | |||
| (15b) |
| |
= | (16) | |
| = | (17) |
The special case
![]() leads to a secularly varying
leads to a secularly varying
![]() ,
representing precession:
,
representing precession:
| (18) |
Polar motion is represented by
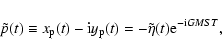 |
(19) |
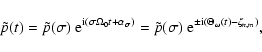 |
(20) |
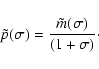 |
(21) |
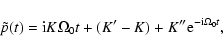 |
(22a) |
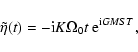 |
(22b) |
Evaluation of the torque
![]() on the Earth due to the
potential
on the Earth due to the
potential
![]() of Eq. (4) is done in Appendix A for general (n,m). Though the potential wave is strictly retrograde, the
complex combination
of Eq. (4) is done in Appendix A for general (n,m). Though the potential wave is strictly retrograde, the
complex combination
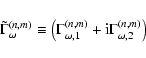 |
(23) |
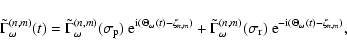 |
(24) |
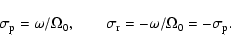 |
(25) |
It follows now from Eq. (7) that for the
torques due to nonzonal (m>0) potentials, and for the wobbles
excited by them,
![]() and
and
![]() lie in separate bands
of width 1 cpsd each, centered at m cpsd and -m cpsd,
respectively, while for m=0, the prograde and retrograde
frequencies together constitute a single band of width 1 cpsd centered at 0 cpsd. The frequency bands of the nutations
produced by
lie in separate bands
of width 1 cpsd each, centered at m cpsd and -m cpsd,
respectively, while for m=0, the prograde and retrograde
frequencies together constitute a single band of width 1 cpsd centered at 0 cpsd. The frequency bands of the nutations
produced by
![]() are shifted by +1 cpsd relative to those of
the associated wobbles, in view of (14).
are shifted by +1 cpsd relative to those of
the associated wobbles, in view of (14).
We present now explicit expressions for the amplitudes
![]() and
and
![]() (see Appendix A). The retrograde amplitude has
distinct forms for the zonal (m=0) and nonzonal cases.
(see Appendix A). The retrograde amplitude has
distinct forms for the zonal (m=0) and nonzonal cases.
| (26a) |
| (26b) |
| |
= | ||
| = | (26c) |
| Gn,m(+) | = | ||
| Gn,m | = | 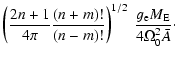 |
(27) |
In the special case of the constant term (![]() )
present in the
spectrum of any zonal potential of even order n,
)
present in the
spectrum of any zonal potential of even order n,
![]() ,
and
the expression (24) for the torque reduces to
,
and
the expression (24) for the torque reduces to
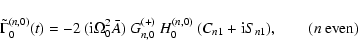 |
(28) |
It should be noted that torques due to the degree 2 sectorial (m=2) and zonal potentials are ignorable because C2,1 and S2,1 are. The origin of nutations and polar motions in the various frequency bands, as displayed in Table 1, is clear from the above considerations.
| Nutations | Frequency | due to | by potentials | Wobbles & |
| band (cpsd) | action | of type | Polar motions | |
| Long period | (-0.5,+0.5) | Cn,0 | (n,1) | Retro diurnal |
| Pro diurnal | (+0.5,+1.5) | (Cn,1,Sn,1) | (n,0) | Long period |
| Retro diurnal | (-1.5,-0.5) | (Cn,1,Sn,1) | (n,2) | Retro semidiurnal |
| Pro semidiurnal | (+1.5,+2.5) | (Cn,2,Sn,2) | (n,1) | Pro diurnal |
| Retro semidiurnal | (-2.5,-1.5) | (Cn,2,Sn,2) | (n,3) | Retro terdiurnal |
| Pro terdiurnal | (+2.5,+3.5) | (Cn,3,Sn,3) | (n,2) | Pro semidiurnal |
To compute the nutations or polar motions in a particular band of frequencies, one starts by identifying from Table 1 the types of potentials and geopotential coefficients relevant to that band, then picking out the expressions for the torques which they produce, and finally, solving the dynamical equations with these as the driving torques. For prograde semidiurnal nutations (or prograde diurnal polar motions), for instance, the relevant potentials are of type (n,1), acting on Cn,2 and Sn,2. The values of the geopotential coefficients of relevance to this work are shown in Table 2. The first set (labeled IERS92) gives the values from McCarthy (1992), used by Bretagnon et al. (1997) and other workers in computing the high frequency nutations of the rigid Earth, and the second set lists the JGM3 (Joint Gravity Model 3) values transformed to the same normalization as IERS92. We use the latter (more recent) set for our computations for the nonrigid Earth.
Since the amplitudes of the HF nutations are expected to be no
more than about 20 ![]() as, the effects of the solid inner core
are expected to be negligible at the level of 0.1
as, the effects of the solid inner core
are expected to be negligible at the level of 0.1 ![]() as, which
is the accuracy we aim for. So we treat the Earth as consisting of
only two regions - the mantle and a fluid core.
as, which
is the accuracy we aim for. So we treat the Earth as consisting of
only two regions - the mantle and a fluid core.
The coupled rotational motions of of these two regions which are
excited by potentials of any type
![]() are governed by
dynamical equations of the Sasao et al. (1980) form for the wobble
variables
are governed by
dynamical equations of the Sasao et al. (1980) form for the wobble
variables
![]() and
and
![]() .
They are, in the time domain,
.
They are, in the time domain,
![\begin{displaymath}\left ({{\rm d}\over {\rm d}t} -{\rm i}e\Omega_0\right)\tilde...
...lde m_{\rm f}(t)\right]\!=\!{\tilde\Gamma(t)\over A\Omega_0},
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img102.gif) |
(29a) |
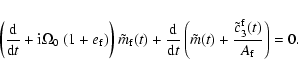 |
(29b) |
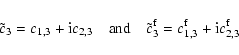 |
(30) |
The quantity
![]() in (30) represents the deformation of type (2,1) of the whole Earth due to the direct action of the tidal
potential, together with that due to incremental centrifugal
potentials associated with the wobbles
in (30) represents the deformation of type (2,1) of the whole Earth due to the direct action of the tidal
potential, together with that due to incremental centrifugal
potentials associated with the wobbles ![]() and
and
![]() .
The
origins of
.
The
origins of
![]() are similar, but the relevant deformation is
that of the core alone. For a spherically symmetric Earth, the
deformation induced by a tidal potential of type (n,m) is
strictly of the same type, and will therefore contribute nothing
to
are similar, but the relevant deformation is
that of the core alone. For a spherically symmetric Earth, the
deformation induced by a tidal potential of type (n,m) is
strictly of the same type, and will therefore contribute nothing
to
![]() or
or
![]() unless
(n,m)=(2,1). Although the
ellipticity of the Earth would result in the presence of a small
part (of the order of 1/300) of type (2,1) in the deformation due
to (n,1) potentials with
unless
(n,m)=(2,1). Although the
ellipticity of the Earth would result in the presence of a small
part (of the order of 1/300) of type (2,1) in the deformation due
to (n,1) potentials with ![]() ,
its effect on the already small nutations produced by such
potentials is entirely negligible. However, the incremental
centrifugal potentials are necessarily of type (2,1)
irrespective of the nature of the tidal potential, and so is its
contribution to deformation. Consequently, the expressions of
Sasao et al. (1980) for
,
its effect on the already small nutations produced by such
potentials is entirely negligible. However, the incremental
centrifugal potentials are necessarily of type (2,1)
irrespective of the nature of the tidal potential, and so is its
contribution to deformation. Consequently, the expressions of
Sasao et al. (1980) for
![]() and
and
![]() take the following
modified form in the general case:
take the following
modified form in the general case:
| |
= | (31a) | |
| = | (31b) |
There is a caveat to be entered in regard to the above expressions,
because the compliances have to be considered to be frequency
dependent, in general, even within a particular tidal band. The
reason is that the deformation due to ocean tides raised by the
tidal potential, and the effect of mantle anelasticity on the
deformations, are both reflected in the values of the
compliances - and one or the other of these could be strongly
frequency dependent, depending on the type (n,m)
of the potential involved (see, for instance, Mathews et al.
2002). This dependence, to the extent that it is known, can be
readily taken into account if the expressions (31) are taken in the
frequency domain, i.e., as expressions for
![]() and
and
![]() in
terms of the spectral amplitudes
in
terms of the spectral amplitudes
![]() ,
and
,
and
![]() ;
this
is what we do.
;
this
is what we do.
The frequency domain version of Eqs. (29) is now readily
obtained by replacing
![]() by
by
![]() and introducing the
expressions (31). One should keep in mind that
and introducing the
expressions (31). One should keep in mind that
![]() here stands
for
here stands
for
![]() ,
which has both prograde and retrograde parts. For any
term belonging to the prograde part,
,
which has both prograde and retrograde parts. For any
term belonging to the prograde part, ![]() is to be taken as
is to be taken as
![]() ,
and
,
and
![]() is given by (26a), while
for terms in the retrograde part,
is given by (26a), while
for terms in the retrograde part, ![]() is
is
![]() and
and
![]() is given by (26b) or (26c) according as
is given by (26b) or (26c) according as ![]() or m=0. With this understanding, we continue to use the generic
symbol
or m=0. With this understanding, we continue to use the generic
symbol ![]() in writing down the pair of frequency domain equations
for the wobbles due to a tidal perturbation of general type
in writing down the pair of frequency domain equations
for the wobbles due to a tidal perturbation of general type
![]() :
:
![\begin{displaymath}\left[(\sigma-e)+(1+\sigma)\kappa\right]~\tilde m(\sigma)+ (1...
... m_{\rm f}(\sigma)=
\tilde\Gamma(\sigma)/({\rm i}A\Omega_0^2),
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img136.gif) |
(32a) |
![\begin{displaymath}(1+\gamma)~\sigma~\tilde m(\sigma)+ \left[1+{\rm e}_{\rm f}+(1+\beta)\sigma\right]~\tilde m_{\rm f}=
0.
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img137.gif) |
(32b) |
| IERS92 | JGM3 | |||
| (k,l) | Ck,l | Sk,l | Ck,l | Sk,l |
| (2, 2) | 1.574 410 | -0.903 757 | 1.574 536 | -0.903 868 |
| (3, 1) | 2.190 181 | 0.269 185 | 2.192 799 | 0.268 012 |
| (3, 2) | 0.308 936 | -0.211 582 | 0.309 016 | -0.211 402 |
| (3, 3) | 0.100 447 | 0.197 157 | 0.100 559 | 0.197 201 |
| (4, 1) | -0.508 638 | -0.449 141 | -0.508 725 | -0.449 460 |
| (4, 2) | 0.350 670 | 0.662 571 | ||
The formal solution of the pair of linear Eqs. (32) is
nearly trivial. Denoting the secular determinant of this system
by ![]() and the coefficient
and the coefficient
![]() of
of
![]() in the second equation by
in the second equation by ![]() ,
we have
,
we have
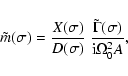 |
(33) |
| (34) |
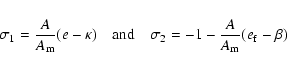 |
(35) |
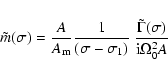 |
(36) |
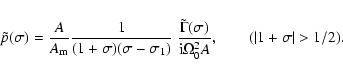 |
(37) |
If the Earth were rigid,
![]() would reduce to unity, and
would reduce to unity, and ![]() would be just e. With these substitutions, the
expression (36) reduces to the wobble amplitude
would be just e. With these substitutions, the
expression (36) reduces to the wobble amplitude
![]() of
the rigid Earth. So the transfer function from the rigid to the
nonrigid Earth becomes
of
the rigid Earth. So the transfer function from the rigid to the
nonrigid Earth becomes
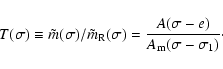 |
(38) |
When the excitation frequencies ![]() are outside the low
frequency band too, i.e., when
are outside the low
frequency band too, i.e., when
![]() (besides
(besides
![]() ),
further simplification of (36) and (38) is
possible since e and
),
further simplification of (36) and (38) is
possible since e and ![]() are then negligible relative to
are then negligible relative to ![]() which dominates by factors of the order of 300. Thus the transfer function becomes very nearly constant, equal to
which dominates by factors of the order of 300. Thus the transfer function becomes very nearly constant, equal to
![]() ;
this is the case for all nutations except
the low frequency and prograde diurnal ones.
;
this is the case for all nutations except
the low frequency and prograde diurnal ones.
Long period wobbles and polar motions (or the associated prograde diurnal nutations) have to be handled with care, because of the resonance associated with the Chandler wobble whose frequency appears in the low frequency band. These are dealt with in Sect. 6. The zero frequency term in the torque, which pertains to this band, merits special consideration, for reasons to be outlined there.
For numerical computations, which are done to an accuracy of 0.1 ![]() as and without making use of any of the approximations made
above or later, we take
as and without making use of any of the approximations made
above or later, we take
![]() ,
e=0.00328455,
and, for an elastic Earth,
,
e=0.00328455,
and, for an elastic Earth,
![]() ;
the last two are
the estimates due to Mathews et al. (2002). The other parameters
involved are
;
the last two are
the estimates due to Mathews et al. (2002). The other parameters
involved are
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
but they contribute only marginally, if at all,
to our numerical results.
,
but they contribute only marginally, if at all,
to our numerical results.
We consider now the motions excited by torques of low
frequencies (
![]() ). The potentials responsible for these
torques are of type (n,0). The nutations produced are below our
cut-off level of 0.05
). The potentials responsible for these
torques are of type (n,0). The nutations produced are below our
cut-off level of 0.05 ![]() asamplitude for all n>4.
asamplitude for all n>4.
The Chandler resonance plays a major role in the wobble response to
forcing in this band; so the value of ![]() which appears in the
Chandler frequency assumes significance. The effects of mantle
anelasticity and ocean tides on nutations can be dealt with by taking
into account the complex increments that they produce to the values
of
which appears in the
Chandler frequency assumes significance. The effects of mantle
anelasticity and ocean tides on nutations can be dealt with by taking
into account the complex increments that they produce to the values
of ![]() and other compliances, a fact that was exploited by
Mathews et al. (2002) in their treatment of low frequency nutations
and retrograde diurnal wobbles. In that context, the anelasticity
contribution was practically independent of frequency while the
ocean tide admittances were strongly frequency dependent, not only
due to the FCN resonance, but also because of other aspects of ocean
dynamics. In the low frequency tidal band that we are concerned with
now, the ocean tides are believed to be essentially equibrium tides,
with a constant admittance; but the anelasticity effect varies
strongly with frequency across the band, making the anelasticity
contribution to
and other compliances, a fact that was exploited by
Mathews et al. (2002) in their treatment of low frequency nutations
and retrograde diurnal wobbles. In that context, the anelasticity
contribution was practically independent of frequency while the
ocean tide admittances were strongly frequency dependent, not only
due to the FCN resonance, but also because of other aspects of ocean
dynamics. In the low frequency tidal band that we are concerned with
now, the ocean tides are believed to be essentially equibrium tides,
with a constant admittance; but the anelasticity effect varies
strongly with frequency across the band, making the anelasticity
contribution to ![]() strongly dependent on the forcing
frequency. So the apparent frequency of the Chandler resonance,
strongly dependent on the forcing
frequency. So the apparent frequency of the Chandler resonance,
![]() cpsd, is itself a function of the
excitation frequency
cpsd, is itself a function of the
excitation frequency ![]() .
More precisely, the polar motion
response (37) to forcing at
.
More precisely, the polar motion
response (37) to forcing at ![]() cpsd is as if there is a resonance
at
cpsd is as if there is a resonance
at
![]() .
The Chandler eigenfrequency
.
The Chandler eigenfrequency
![]() (i.e. the frequency of the free Chandler wobble mode) is not
variable, of course. It is given by the value of
(i.e. the frequency of the free Chandler wobble mode) is not
variable, of course. It is given by the value of
![]() for
the specific excitation frequency
for
the specific excitation frequency ![]() at which Re
at which Re
![]() .
Another aspect that cannot be ignored is that the imaginary part
of the anelasticity contribution to
.
Another aspect that cannot be ignored is that the imaginary part
of the anelasticity contribution to ![]() has to be taken with
a sign opposite to that of the forcing frequency: positive for
retrograde wobbles and negative for prograde ones. This is
required for ensuring that the tidal deformation lags behind the
tidal forcing; see Mathews et al. (2002), Appendix C, for
details.
has to be taken with
a sign opposite to that of the forcing frequency: positive for
retrograde wobbles and negative for prograde ones. This is
required for ensuring that the tidal deformation lags behind the
tidal forcing; see Mathews et al. (2002), Appendix C, for
details.
The anelasticity model adopted in this work is the one employed by
Mathews et al. (2002). It belongs to the class of models that
Wahr & Bergen (1986)
refer to as the ![]() model of
Sailor & Dziewonski
(1978). The essential feature of these models is that the value of a
deformational response parameter (e.g.,
model of
Sailor & Dziewonski
(1978). The essential feature of these models is that the value of a
deformational response parameter (e.g., ![]() )
of the anelastic
Earth to harmonic excitation at some frequency
)
of the anelastic
Earth to harmonic excitation at some frequency
![]() differs from the
elastic-Earth value at a reference frequency
differs from the
elastic-Earth value at a reference frequency
![]() by an amount
proportional to
by an amount
proportional to
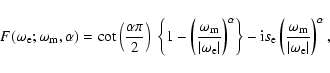 |
(39) |
It is evident, however, that the model (39) cannot remain valid
down to zero frequency: F would become infinite at ![]() ,
leading to
an infinite anelasticity contribution. The zero frequency term
present in the (4, 0) tidal potential presents, therefore, an
exception that cannot be handled by the above procedure. The
deformational responses to an incessantly acting potential
should actually be characterized by the so-called secular or
fluid Love numbers. Now, the compliance
,
leading to
an infinite anelasticity contribution. The zero frequency term
present in the (4, 0) tidal potential presents, therefore, an
exception that cannot be handled by the above procedure. The
deformational responses to an incessantly acting potential
should actually be characterized by the so-called secular or
fluid Love numbers. Now, the compliance ![]() is known to have
a simple relation to the k Love number (see, for example,
Sasao et al. 1980):
is known to have
a simple relation to the k Love number (see, for example,
Sasao et al. 1980):
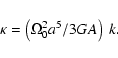 |
(40a) |
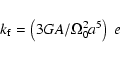 |
(40b) |
This finding has interesting consequences. One sees trivially that
with ![]() and
and
![]() ,
the frequency domain Eqs. (32) lead to the unphysical result that
,
the frequency domain Eqs. (32) lead to the unphysical result that
![]() is infinite.
One has to go back therefore to the time domain Eqs. (29),
with
is infinite.
One has to go back therefore to the time domain Eqs. (29),
with
![]() and
and
![]() replaced by the expressions (31), noting
that the
replaced by the expressions (31), noting
that the
![]() terms drop out since m=0 the present case.
One sees
immediately that the terms proportional to
terms drop out since m=0 the present case.
One sees
immediately that the terms proportional to
![]() in Eq. (29a)
cancel out as a consequence of the vanishing of
in Eq. (29a)
cancel out as a consequence of the vanishing of ![]() ,
and that
in the entirely adequate approximation wherein terms of
,
and that
in the entirely adequate approximation wherein terms of
![]() are neglected, the two equations then take the forms
are neglected, the two equations then take the forms
![]() and
and
![]() ,
with
,
with
![]() .
Subtraction of one from the other yields
.
Subtraction of one from the other yields
![]() ,
which is a constant in the present case since
,
which is a constant in the present case since
![]() is.
The solution for
is.
The solution for
![]() is then immediate:
is then immediate:
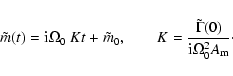 |
(41) |
The initial value
![]() of
of
![]() is arbitrary. The value of K in
the case of the (4, 0) potential may be obtained from Eqs. (28) and (27):
is arbitrary. The value of K in
the case of the (4, 0) potential may be obtained from Eqs. (28) and (27):
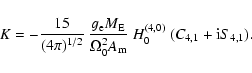 |
(42) |
The solution (41) describes a secular motion, relative to the pole of
maximum moment of inertia, of the Earth's instantaneous rotation pole.
The associated nutation
![]() ,
obtained by integrating
Eq. (11) after introducing (41), is
,
obtained by integrating
Eq. (11) after introducing (41), is
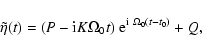 |
(43) |
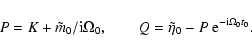 |
(44) |
| (45) |
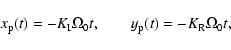 |
(46) |
The prograde semidiurnal nutations arise primarily from the direct
action of the (2,1) tidal potential on the Earth's triaxial structure.
Triaxiality, i.e., inequality of the two principal equatorial moments
of inertia A and B, is characterized by the parameter e':
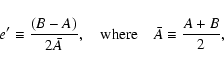 |
(47a) |
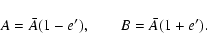 |
(47b) |
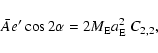 |
(48a) |
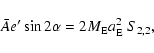 |
(48b) |
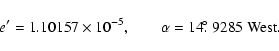 |
(49) |
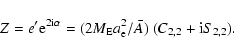 |
(50) |
Contributions to the prograde semidiurnal nutations arise
from the appearance of triaxiality through
![]() ,
and
,
and ![]() in the equatorial components of the angular momentum vectors
in the equatorial components of the angular momentum vectors ![]() and
and
![]() .
In a
coordinate system with its axes along the principal axes of the
inertia tensor, the equatorial components of
.
In a
coordinate system with its axes along the principal axes of the
inertia tensor, the equatorial components of ![]() are, for the
triaxial Earth,
are, for the
triaxial Earth,
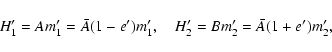 |
(51a) |
![\begin{displaymath}\tilde H'(t) = H_1'(t)+{\rm i}H_2'(t)=\bar A~[~\tilde m'(t) -e'\tilde m'^*(t)].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img245.gif) |
(51b) |
![\begin{displaymath}\tilde H(t)= \bar A~[\tilde m(t)-Z~\tilde m^*(t)~ ].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img249.gif) |
(52) |
| |
= | ||
| = | |||
| = | (53) |
The triaxiality terms appearing through the expressions (52) and (53) had not been
included in the dynamical equations in the earlier sections, as
the triaxiality contributions to the nutations considered there
were far below the 0.1 ![]() asbecause of the weakness of
the driving potentials of degree >2. With the inclusion of these
terms here, the dynamical Eqs. (29) get modified to
asbecause of the weakness of
the driving potentials of degree >2. With the inclusion of these
terms here, the dynamical Eqs. (29) get modified to
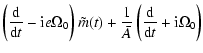 |
|||
![$\displaystyle \times\left[\tilde c_3(t)+\bar A_{\rm f}\tilde m_{\rm f}(t)-\bar ...
...
Z_{\rm f}\tilde m_{\rm f}^*(t)\right] = {\tilde\Gamma(t)\over \bar A\Omega_0},$](/articles/aa/full/2003/12/aa3056/img258.gif) |
(54a) | ||
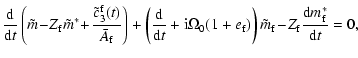 |
(54b) |
Consider now the frequency domain version of the above equations,
corresponding to a spectral component having the time
dependence
![]() .
Noting that the amplitude
of the term in
.
Noting that the amplitude
of the term in
![]() which has this time dependence is
which has this time dependence is
![]() ,
and similarly for
,
and similarly for
![]() ,
one sees that the equations
are:
,
one sees that the equations
are:
| (55a) | |||
| (55b) |
It is to be expected that the triaxiality terms in Eqs. (55) will lead to small increments to the frequencies of the free
wobbles. These increments are of the second order in triaxiality,
as may be shown very generally from the structure of these
equations. For an elementary
illustration, consider the rigid Earth, whose free wobbles are
governed by the equation
![]() ,
which is the relevant special case of (55a). On taking its complex
conjugate and making the replacement
,
which is the relevant special case of (55a). On taking its complex
conjugate and making the replacement
![]() ,
one obtains a
second equation relating
,
one obtains a
second equation relating
![]() and
and
![]() .
This pair of equations
yields the secular equation
.
This pair of equations
yields the secular equation
![]() ,
where e'=|Z|. Thus
the change in the Chandler eigenfrequency due to triaxiality is from e to
e(1-e'2/2e2), to the lowest order in the triaxiality.
Given the magnitudes of e and e', the fractional change is seen
to be of the order of 10-5, which is much too small be of
interest. For the Earth with a fluid core, a similar procedure
starting with both the Eqs. (55) and their complex conjugates
with the sign of
,
where e'=|Z|. Thus
the change in the Chandler eigenfrequency due to triaxiality is from e to
e(1-e'2/2e2), to the lowest order in the triaxiality.
Given the magnitudes of e and e', the fractional change is seen
to be of the order of 10-5, which is much too small be of
interest. For the Earth with a fluid core, a similar procedure
starting with both the Eqs. (55) and their complex conjugates
with the sign of ![]() reversed, leads to a similar result also for
the second eigenfrequency associated with the free core nutation.
reversed, leads to a similar result also for
the second eigenfrequency associated with the free core nutation.
Moving on now to forced prograde diurnal wobbles due to the (2,1) potential, it is advantageous, in view of their coupling to the
retrograde diurnals, to express the potential in the form employed
by Mathews et al. (1991) in their treatment of the retrograde
diurnal wobbles:
![\begin{displaymath}\phi^{(2,1)}({\vec r};t) =
-\Omega_0^2\left[~\phi_1(t) xz+\phi_2(t) yz~\right].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img273.gif) |
(56) |
![\begin{displaymath}\tilde\Gamma= -{\rm i}\bar A\Omega_0^2\ \left[~e\tilde\phi(t)+Z\tilde\phi^*(t)~\right].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img276.gif) |
(57) |
For a spectral component of the potential (56) with angular
frequency ![]() ,
,
![]() is proportional to
is proportional to
![]() ,
,
![]() being the longitude, according to the Cartwright-Tayler
convention. This is ensured by taking the spectral components of
being the longitude, according to the Cartwright-Tayler
convention. This is ensured by taking the spectral components of ![]() and
and ![]() to be
to be
| (58) |
| |
|||
| = | (59) |
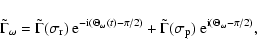 |
(60) |
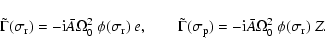 |
(61) |
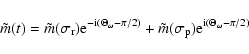 |
(62) |
We can now specialize Eqs. (55) to the case of prograde
wobbles by setting
![]() and
and
![]() and introducing from Eqs. (31) the expressions
and introducing from Eqs. (31) the expressions
| |
= | ||
| = | (63) |
| (64a) | |||
| (64b) |
In the coefficients of
![]() and
and
![]() in Eqs. (64),
in Eqs. (64),
![]() is close to 1 while all other quantities except
is close to 1 while all other quantities except
![]() are
of
are
of
![]() .
Substituting for
.
Substituting for
![]() in Eqs. (64a) from (64b), one finds, with the neglect of small quantities of
in Eqs. (64a) from (64b), one finds, with the neglect of small quantities of
![]() ,
that
,
that
| (65) |
Before proceeding futher on these lines, it is useful to get an
idea of the relative magnitudes of the various terms on the right
hand side of (65). The dominant term is the first one representing
the external torque acting on the triaxiality. Both
![]() and
and
![]() in the remaining terms are affected by the resonance at
in the remaining terms are affected by the resonance at
![]() associated with the FCN. Nevertheless,
the factor
associated with the FCN. Nevertheless,
the factor
![]() stays close to e at the frequencies of
interest here, deviating from it only by about 30% even at the
stays close to e at the frequencies of
interest here, deviating from it only by about 30% even at the ![]() frequency (
frequency (
![]() )
responsible for the
retrograde annual nutation. Therefore the contribution from the
second term on the right in (65) relative to that of the first term
is
)
responsible for the
retrograde annual nutation. Therefore the contribution from the
second term on the right in (65) relative to that of the first term
is ![]()
![]() ,
since
,
since
![]() is close to unity;
hence the contribution of this term to any of the semidiurnal
polar motion coefficients is at most about 0.1
is close to unity;
hence the contribution of this term to any of the semidiurnal
polar motion coefficients is at most about 0.1 ![]() as, the
largest of the coefficients being about 15
as, the
largest of the coefficients being about 15 ![]() as.
If the core
is triaxial (
as.
If the core
is triaxial (
![]() ), the huge resonance in
), the huge resonance in
![]() enters
the picture:
enters
the picture:
![]() is as large as 800
for the
is as large as 800
for the ![]() frequency, and about 200 at the frequency
(
frequency, and about 200 at the frequency
(![]() )
of the K1 tide (which causes the precession) and at
the nearby frequency with which the 18.6 year retrograde nutation
is associated. Thus, if the triaxiality of the core were to have
the same magnitude as that of the whole Earth (
)
of the K1 tide (which causes the precession) and at
the nearby frequency with which the 18.6 year retrograde nutation
is associated. Thus, if the triaxiality of the core were to have
the same magnitude as that of the whole Earth (
![]() ), the
magnitude of the contribution of the
), the
magnitude of the contribution of the
![]() term in (65) relative to that of the external torque would become
term in (65) relative to that of the external torque would become
![]() for
for
![]() (the 0.99727 day
polar motion driven by the K1 tide); the corresponding number
is large, about 0.39, for the PM due to the
(the 0.99727 day
polar motion driven by the K1 tide); the corresponding number
is large, about 0.39, for the PM due to the ![]() tide close to
the resonance, but only 0.0022 for that due to the O1 tide far
from the resonance. The magnitude of the actual contribution to
the larger of the PM coefficients for the 0.99727 day polar motion
turns out to be about 1
tide close to
the resonance, but only 0.0022 for that due to the O1 tide far
from the resonance. The magnitude of the actual contribution to
the larger of the PM coefficients for the 0.99727 day polar motion
turns out to be about 1 ![]() as, which is not insignificant.
Further discussion of the numerical results on the effects of core
triaxiality will be deferred to Sect. 8, where a
comparison will be made with the results of Escapa et al. (2002) who have already drawn attention to the role of the
FCN resonance in the context of semidiurnal nutations (equivalent
to the prograde diurnal polar motions).
as, which is not insignificant.
Further discussion of the numerical results on the effects of core
triaxiality will be deferred to Sect. 8, where a
comparison will be made with the results of Escapa et al. (2002) who have already drawn attention to the role of the
FCN resonance in the context of semidiurnal nutations (equivalent
to the prograde diurnal polar motions).
Returning now to the development of the theoretical
expressions, we note that no generally accepted quantitative
estimates are avaliable for the triaxiality of the
core, and so we ignore its effects hereafter. We have then, to
an approximation which neglects terms of
![]() ,
,
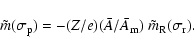 |
(66) |
Now, in view of Eq. (62), the prograde part of the wobble in
the time domain is
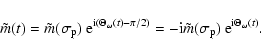 |
(67) |
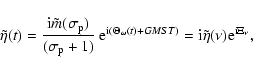 |
(68) |
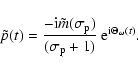 |
(69) |
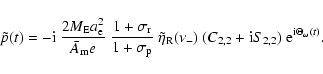 |
(70) |
According to Eq. (20),
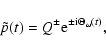 |
(71) |
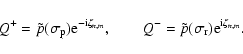 |
(72) |
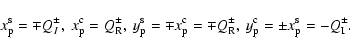 |
(73) |
| |
= | (74a) | |
| = | (74b) |
| Q- | = | (75a) | |
| Fn,0(-) | = | (75b) |
| Forcing | Coefficients in
|
Coefficients in
|
||
| potential |
|
|
|
|
| Prograde polar motions | ||||
| (2, 1) | C2,2 | S2,2 | -S2,2 | C2,2 |
| (3, 0) | -C3,1 | -S3,1 | S3,1 | -C3,1 |
| (3, 1) | -S3,2 | C3,2 | -C3,2 | -S3,2 |
| (3, 2) | -C3,3 | -S3,3 | S3,3 | -C3,3 |
| (4, 0) | S4,1 | -C4,1 | C4,1 | S4,1 |
| (4, 1) | C4,2 | S4,2 | -S4,2 | C4,2 |
| Retrograde polar motions | ||||
| (3, 0) | -C3,1 | S3,1 | S3,1 | C3,1 |
| (3, 2) | C3,1 | S3,1 | S3,1 | -C3,1 |
| (3, 3) | S3,2 | -C3,2 | -C3,2 | -S3,2 |
| (4, 0) | -S4,1 | -C4,1 | -C4,1 | S4,1 |
We have carried out the numerical evaluation of the coefficients of
polar motions due to tidal potentials of degrees up to 4,
starting from the tidal amplitudes defined according to the
conventions of
Cartwright & Tayler (1971).
Actually, we used
the RATGP series of Roosbeek (1996) and converted the amplitudes
from this series to their Cartwright-Tayler equivalents through
multiplication by the appropriate factors fn,m taken from
Table 6.5 of the IERS Conventions 1996. (The sign of the factor f3,1 given there has to be reversed; the
value
f4,0= 0.317600 not listed there was
needed to compute polar motions with coefficients down to 0.05 ![]() as,
there being a few that are excited by
(4, 0) potentials.)
For the prograde diurnal polar motions, we have also used the
alternative approach explained in Sect. 7, using the known
amplitudes of the long period nutations as inputs instead of the
tidal amplitudes. The JGM3 values listed in Table 2 were used for the
geopotential coefficients in computations for the nonrigid Earth;
the IERS92 values were used for the rigid Earth case, to
facilitate comparisons with the results of earlier workers.
as,
there being a few that are excited by
(4, 0) potentials.)
For the prograde diurnal polar motions, we have also used the
alternative approach explained in Sect. 7, using the known
amplitudes of the long period nutations as inputs instead of the
tidal amplitudes. The JGM3 values listed in Table 2 were used for the
geopotential coefficients in computations for the nonrigid Earth;
the IERS92 values were used for the rigid Earth case, to
facilitate comparisons with the results of earlier workers.
We present in Table 4 the periodic polar
motions having amplitudes exceeding 0.5 ![]() as. Only the low
frequency polar motions due to (3, 0) potentials and the prograde
diurnals excited by the (2, 1) potentials attain these
magnitudes. The secular polar motion due to the constant term in
the (4, 0) potential is also shown. The argument of the polar motion,
denoted by (arg) in the Table, is
as. Only the low
frequency polar motions due to (3, 0) potentials and the prograde
diurnals excited by the (2, 1) potentials attain these
magnitudes. The secular polar motion due to the constant term in
the (4, 0) potential is also shown. The argument of the polar motion,
denoted by (arg) in the Table, is
![]() if the motion is
prograde, and
if the motion is
prograde, and
![]() if retrograde. It is expressed here as a
linear combination,
if retrograde. It is expressed here as a
linear combination,
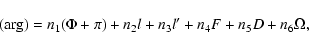 |
(76) |
The argument of the HF nutation equivalent to the polar motion of (76) is
| (77) |
| n | Multipliers of | Period |
|
|
Nutation | |||||||
| l | l' | F | D | of PM | Period | |||||||
| 3 | 0 | -1 | 0 | -1 | 0 | -1 | -13.719 | 1.39 | .17 | -.17 | 1.39 | 1.07545 |
| 3 | 0 | 0 | 0 | -1 | 0 | 0 | -27.212 | 2.48 | .30 | -.30 | 2.48 | 1.03521 |
| 3 | 0 | 0 | 0 | -1 | 0 | -1 | -27.322 | 15.75 | 1.93 | -1.93 | 15.75 | 1.03505 |
| 3 | 0 | 0 | 0 | -1 | 0 | -2 | -27.432 | -.82 | -.10 | .10 | -.82 | 1.03489 |
| 3 | 0 | -1 | 0 | -1 | 2 | -1 | -193.560 | .81 | .10 | -.10 | .81 | 1.00243 |
| 3 | 0 | 1 | 0 | -1 | 0 | 0 | -2190.35 | 1.86 | .24 | -.24 | 1.86 | .99772 |
| 3 | 0 | 1 | 0 | -1 | 0 | -1 | -3231.50 | 12.32 | 1.59 | -1.59 | 12.32 | .99758 |
| 3 | 0 | 1 | 0 | -1 | 0 | -2 | -6159.14 | -.68 | -.09 | .09 | -.68 | .99743 |
| 3 | 0 | -1 | 0 | 1 | 0 | 2 | 6159.14 | .78 | .09 | -.09 | .78 | .99711 |
| 3 | 0 | -1 | 0 | 1 | 0 | 1 | 3231.50 | -16.16 | -1.83 | 1.83 | -16.16 | .99696 |
| 3 | 0 | -1 | 0 | 1 | 0 | 0 | 2190.35 | -2.78 | -.31 | .31 | -2.78 | .99682 |
| 3 | 0 | 1 | 1 | -1 | 0 | 0 | 438.360 | -.63 | .12 | -.12 | -.63 | .99501 |
| 3 | 0 | 1 | 1 | -1 | 0 | -1 | 411.807 | 1.05 | .27 | -.27 | 1.05 | .99486 |
| 3 | 0 | 0 | 0 | 1 | -1 | 1 | 365.242 | 1.31 | .20 | -.20 | 1.31 | .99455 |
| 3 | 0 | 1 | 0 | 1 | -2 | 1 | 193.560 | 2.10 | .27 | -.27 | 2.10 | .99216 |
| 3 | 0 | 0 | 0 | 1 | 0 | 2 | 27.432 | -.87 | -.11 | .11 | -.87 | .96229 |
| 3 | 0 | 0 | 0 | 1 | 0 | 1 | 27.322 | 16.64 | 2.04 | -2.04 | 16.64 | .96215 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 27.212 | 2.62 | .32 | -.32 | 2.62 | .96201 |
| 3 | 0 | 1 | 0 | 1 | 0 | 1 | 13.719 | 1.28 | .16 | -.16 | 1.28 | .92969 |
| 2 | 1 | -1 | 0 | -2 | 0 | -1 | 1.11970 | -.44 | .25 | -.25 | -.44 | .52747 |
| 2 | 1 | -1 | 0 | -2 | 0 | -2 | 1.11951 | -2.31 | 1.32 | -1.32 | -2.31 | .52743 |
| 2 | 1 | 1 | 0 | -2 | -2 | -2 | 1.11346 | -.44 | .25 | -.25 | -.44 | .52608 |
| 2 | 1 | 0 | 0 | -2 | 0 | -1 | 1.07598 | -2.14 | 1.23 | -1.23 | -2.14 | .51756 |
| 2 | 1 | 0 | 0 | -2 | 0 | -2 | 1.07581 | -11.36 | 6.52 | -6.52 | -11.36 | .51753 |
| 2 | 1 | -1 | 0 | 0 | 0 | 0 | 1.03472 | .84 | -.48 | .48 | .84 | .50782 |
| 2 | 1 | 0 | 0 | -2 | 2 | -2 | 1.00275 | -4.76 | 2.73 | -2.73 | -4.76 | .50000 |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | .99727 | 14.27 | -8.19 | 8.19 | 14.27 | .49863 |
| 2 | 1 | 0 | 0 | 0 | 0 | -1 | .99712 | 1.93 | -1.11 | 1.11 | 1.93 | .49860 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | .96244 | .76 | -.43 | .43 | .76 | .48977 |
| Rate of secular polar motion ( |
||||||||||||
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | -3.80 | -4.31 | .99727 | |||
The coefficients of the HF nutations may be inferred from those of the equivalent polar motions from the following considerations.
Beginning with the fact that
![]() ,
which
produces an overall sign difference between the
coefficients of
,
which
produces an overall sign difference between the
coefficients of
![]() and
and
![]() in
in
![]() and
and
![]() ,
on the one hand, and those of
,
on the one hand, and those of
![]() and
and
![]() in
in
![]() and
and
![]() on the other hand, one takes note of the other sign differences
that occur: a sign (-1)m depending on the order m of the tidal
potential giving rise to the motions, which arises from the
relations (15) between
on the other hand, one takes note of the other sign differences
that occur: a sign (-1)m depending on the order m of the tidal
potential giving rise to the motions, which arises from the
relations (15) between
![]() and
and
![]() ,
and a further
minus sign that arises between the coefficients in
,
and a further
minus sign that arises between the coefficients in
![]() on the one hand and those in
on the one hand and those in
![]() on the other
because of the fact that
on the other
because of the fact that
![]() while
while
![]() .
Thus, with
superscripts s and c identifying coefficients of the sine and
cosine functions, respectively, of (arg) or
.
Thus, with
superscripts s and c identifying coefficients of the sine and
cosine functions, respectively, of (arg) or ![]() as the case
may be, we have
as the case
may be, we have
| (78a) | |||
| (78b) |
The above relations, when combined with (73), show that the coeffients
of any circular polar motion and of the corresponding nutation can all
be obtained from just two of them, say
![]() and
and
![]() .
They
supersede Eqs. (24) of Mathews & Bretagnon (2002)
which fail to be valid in general as the sign factors referred to
below Eq. (17) were overlooked.
.
They
supersede Eqs. (24) of Mathews & Bretagnon (2002)
which fail to be valid in general as the sign factors referred to
below Eq. (17) were overlooked.
Our results for a few of the leading terms in the semidiurnal
nutations due to degree 2 potentials, which are strictly prograde
and hence circular, are compared with the results from earlier
works in Table 5. The coefficients
![]() and
and
![]() are
shown both for the rigid and the nonrigid Earth;
are
shown both for the rigid and the nonrigid Earth;
![]() and
and
![]() in the
present case. The values shown against BCpc were obtained by
conversion from recent polar motion coefficients of
Brzezinski & Capitaine
(private communication, 2002).
Elliptical nutations (including semidiurnal ones) that are induced
by higher degree potentials are considered below.
in the
present case. The values shown against BCpc were obtained by
conversion from recent polar motion coefficients of
Brzezinski & Capitaine
(private communication, 2002).
Elliptical nutations (including semidiurnal ones) that are induced
by higher degree potentials are considered below.
| Period | Rigid Earth | Nonrigid Earth | ||||
| (days) | Authors |
|
|
Authors |
|
|
| 0.51753 | BRS97 | 5.79 | 10.09 | GFE01 | 6.54 | 11.39 |
| FBS01 | 5.8 | 10.0 | FBS01 | 6.5 | 11.3 | |
| BCpc | 5.83 | 10.16 | BCpc | 6.57 | 11.45 | |
| Present | 5.87 | 10.22 | Present | 6.52 | 11.36 | |
| 0.50000 | BRS97 | 2.43 | 4.23 | GFE01 | 2.74 | 4.77 |
| FBS01 | 2.37 | 4.13 | FBS01 | 2.7 | 4.7 | |
| BCpc | 2.44 | 4.25 | BCpc | 2.75 | 4.79 | |
| Present | 2.46 | 4.28 | Present | 2.73 | 4.76 | |
| 0.49863 | BRS97 | -7.27 | -12.67 | GFE01 | -8.21 | -14.30 |
| FBS01 | -7.12 | -12.40 | FBS01 | -8.0 | -14.0 | |
| BCpc | -7.32 | -12.75 | BCpc | -8.25 | -14.37 | |
| Present | -7.27 | -12.67 | Present | -8.19 | -14.27 | |
|
a BRS97: Bretagnon et al. (1997); FBS01:
Folgueira et al. (2001); GFE01: Getino et al. (2001); and BCpc: Brzezinski & Capitaine (private communication, 2002). |
| Type of | Period (days) of | Coefficients | ||||
| Tide | Wobble | Nutation |
|
|
|
|
| Diurnal nutations | ||||||
| (3,0) | -27.322 | 1.03505 | -34.201 | -4.204 | -1.672 | 13.604 |
| (3,2) | -.50790 | -1.03505 | .604 | -.074 | -.030 | -.240 |
| Total | -34.805 | -4.278 | -1.642 | 13.364 | ||
| BRS97 | -34.821 | -4.271 | -1.640 | 13.371 | ||
| FBS01 | -35.404 | -4.351 | -1.587 | 12.911 | ||
| (3,0) | -3231.5 | .99758 | -19.881 | -2.444 | -.972 | 7.908 |
| (3,2) | -.49871 | -.99758 | .031 | -.004 | -.002 | -.012 |
| Total | -19.912 | -2.448 | -.970 | 7.896 | ||
| BRS97 | -19.854 | -2.491 | -.988 | 7.873 | ||
| FBS01 | -19.940 | -2.451 | -.972 | 7.906 | ||
| (3,0) | 27.322 | .96215 | -38.080 | -4.680 | -1.862 | 15.147 |
| (3,2) | -.48970 | -.96215 | .050 | -.006 | -.002 | -.020 |
| Total | -38,130 | -4.686 | -1.860 | 15.127 | ||
| BRS97 | -38.128 | -4.695 | -1.863 | 15.127 | ||
| FBS01 | -38.231 | -4.699 | -1.857 | 15.106 | ||
| Semidiurnal nutations | ||||||
| (3,1) | .89050 | .527517 | -.074 | -.108 | -.043 | .029 |
| (3,3) | -2.89050 | -.527517 | .106 | -.154 | -.061 | -.042 |
| Total | -.180 | -.262 | .018 | -.013 | ||
| BRS97 | -.178 | -.258 | .020 | -.013 | ||
| FBS01 | -.109 | -.388 | .234 | -.092 | ||
| (3,1) | .963499 | .507904 | -.206 | -.301 | -.120 | .082 |
| (3,3) | -2.963499 | -.507904 | .013 | -.019 | -.008 | -.005 |
| Total | -.219 | -.320 | -.112 | .077 | ||
| BRS97 | -.219 | -.321 | -.113 | .077 | ||
| FBS01 | -.244 | -.356 | -.097 | .067 | ||
The combination of two circular motions differing only in the sign
of the frequency describes an elliptical motion. In Table 4,
such prograde-retrograde pairs of terms appear only among the low
frequency polar motions. The argument
![]() of the prograde part is
assigned to the elliptical polar motion. Since
of the prograde part is
assigned to the elliptical polar motion. Since
![]() for
the retrograde part, the signs of the coefficients in the sine
columns have to be reversed in the row pertaining to any retrograde
PM before adding to the coefficients in the row pertaining to the
corresponding prograde PM to obtain the coefficients for the
elliptical motion.
For the elliptical PM with the 27.322 day period, for
instance, one finds the coefficients (in the same order as in the
table) to be (
0.89, 3.99, -0.11, 32.35)
for
the retrograde part, the signs of the coefficients in the sine
columns have to be reversed in the row pertaining to any retrograde
PM before adding to the coefficients in the row pertaining to the
corresponding prograde PM to obtain the coefficients for the
elliptical motion.
For the elliptical PM with the 27.322 day period, for
instance, one finds the coefficients (in the same order as in the
table) to be (
0.89, 3.99, -0.11, 32.35) ![]() as; they are (
-28.49,
-0.24, 3.44, -3.85)
as; they are (
-28.49,
-0.24, 3.44, -3.85) ![]() as for the 3231.496 day polar motion. Note
the predominance of the cosine part of
as for the 3231.496 day polar motion. Note
the predominance of the cosine part of ![]() in the former case and
of the sine part of
in the former case and
of the sine part of ![]() in the latter. The difference in
behaviour is due to the presence of the Chandler mode in between
these periods.
in the latter. The difference in
behaviour is due to the presence of the Chandler mode in between
these periods.
For higher frequency PM, (e.g., the semidiurnals), the
prograde and retrograde parts originate in the action of the
same potential on different geopotential coefficients, e.g.,
by the action of (3, 2) potentials on C3,3 and S3,3 for
prograde semidiurnals, and on C3,1 and S3,1 for the
retrograde ones. The largest of these, with periods of +0.52752and -0.52752 have coefficients (
-0.330, -.0041, -0.041,
0.330) and (
-0.028,-0.055,0.055,-0.028) ![]() as, respectively; both
sets are below the cuf-off for inclusion in Table 4. The elliptical
motion from their combination has coefficients (
-0.358, -0.096, 0.014,
0.302)
as, respectively; both
sets are below the cuf-off for inclusion in Table 4. The elliptical
motion from their combination has coefficients (
-0.358, -0.096, 0.014,
0.302) ![]() as.
as.
In contrast to elliptical polar motions, elliptical HF nutations
result from the combination of a pair of prograde and retrograde
nutations produced by different potentials acting on the same C and S coefficients. It must be noted that the semidiurnal
nutations arising from the action of degree 2 potentials on C2,2
and S2,2 are strictly prograde and circular: there exists no (2, 3) potential to generate retrograde components. Thus the elliptical
nutations are generated only by higher degree potentials. Table 6
shows a few examples from our computations for the rigid Earth, and
comparisons with the results of Bretagnon et al. (1997) and
Folgueira et al. (2001) - both of which are for elliptical
nutations only. Since both these works have employed
the values listed under IERS92 in Table 2 for Cn,m and Sn,m, our numbers used for the comparison are based on the
same values. The ratios
![]() and
and
![]() should be equal to
(-C3,1/S3,1) for the diurnal nutations and
(S3,2/C3,2) for the semidiurnals, as may be seen from our
theory. This requirement is satisfied rather well by all the sets of
coefficients shown, except those of Folgueira et al. (2001)
for the 0.527517 day nutation which are inconsistent with the above
requirement. In fact, the fractional differences of their
numbers from ours are not really small for the other listed
semidiurnals too. Our sets of values are very close to those of
Bretagnon et al.; and for the diurnal nutations, they are
quite close to Folgueira et al. too.
should be equal to
(-C3,1/S3,1) for the diurnal nutations and
(S3,2/C3,2) for the semidiurnals, as may be seen from our
theory. This requirement is satisfied rather well by all the sets of
coefficients shown, except those of Folgueira et al. (2001)
for the 0.527517 day nutation which are inconsistent with the above
requirement. In fact, the fractional differences of their
numbers from ours are not really small for the other listed
semidiurnals too. Our sets of values are very close to those of
Bretagnon et al.; and for the diurnal nutations, they are
quite close to Folgueira et al. too.
The coefficients shown in Table 4 for the prograde diurnal polar
motions do not take account of possible triaxiality of the core.
How much of a difference could core triaxiality make? To answer
this question, we have made computations based on Eqs. (64)
with nonzero ![]() as well as with
as well as with
![]() ,
and taken the
difference. To facilitate comparison with the results of
Escapa et al. (2002), we present in Table 7 our results for the
contributions from
,
and taken the
difference. To facilitate comparison with the results of
Escapa et al. (2002), we present in Table 7 our results for the
contributions from ![]() to the equivalent semidiurnal nutations
when
to the equivalent semidiurnal nutations
when
![]() ,
together with numbers from the IT columns
of Table 1 of their paper which pertain to the same ratio for
,
together with numbers from the IT columns
of Table 1 of their paper which pertain to the same ratio for
![]() which is, in their notation,
which is, in their notation,
![]() .
Only the
coefficients of the increment
.
Only the
coefficients of the increment
![]() due to
due to ![]() are
shown. It is evident that the Escapa et al. values are 2.4 to 3 times as large as ours, except for the .51753 day nutation
for which the factor is nearly 8. We have not been able to
discern the reason for the discrepancies; and we find no scope
for modifying our expressions to bridge the gap, our derivations
being entirely transparent.
are
shown. It is evident that the Escapa et al. values are 2.4 to 3 times as large as ours, except for the .51753 day nutation
for which the factor is nearly 8. We have not been able to
discern the reason for the discrepancies; and we find no scope
for modifying our expressions to bridge the gap, our derivations
being entirely transparent.
| Nutation perioda | Present work | Escapa et al. | |||
| PSD | LF |
|
|
|
|
| .49863 | .468 | .815 | 1.211 | 2.110 | |
| .49860 | -6798.38 | .068 | .118 | .175 | .304 |
| .50000 | 182.62 | -.045 | -.079 | -.134 | -.233 |
| .49795 | -365.26 | -.021 | -.036 | -.049 | -.085 |
| .51753 | 13.66 | -.010 | -.017 | -.076 | -.132 |
|
a Periods, in solar days, of the prograde semidiurnal
(PSD) and low frequency (LF) nutations produced by the same retrograde diurnal potential are shown in each row. |
The comparisons presented in the last section show that the
coefficients of high frequency nutations or of corresponding
polar motions, as presented by different groups, do not differ
by more than a few tenths of a microarcsecond for any of the
frequencies involved. This is not surprising, considering that
the largest of the polar motion amplitudes are under 20 ![]() as.
We focus here, therefore, on a few special features referred to
in earlier sections.
as.
We focus here, therefore, on a few special features referred to
in earlier sections.
Firstly, the Chandler resonance in the low frequency polar
motions: We pointed out at the beginning of Sect. 6 that the
resonance frequency varies with the frequency of excitation. We
find that the largest effect of this variation is on the ![]() 3231 day polar motions: -0.08 and 0.16
3231 day polar motions: -0.08 and 0.16 ![]() as, respectively,
on the coefficients
as, respectively,
on the coefficients
![]() and
and
![]() of the retrograde one,
and -0.17 and 0.02 on those of the prograde one. These are
not ignorable at the 0.1
of the retrograde one,
and -0.17 and 0.02 on those of the prograde one. These are
not ignorable at the 0.1 ![]() as level. Another point concerns the
flipping of the sign of the imaginary part of the resonance
frequency which has to accompany the passage from positive to
negative excitation frequencies. If this flip were ignored,
as level. Another point concerns the
flipping of the sign of the imaginary part of the resonance
frequency which has to accompany the passage from positive to
negative excitation frequencies. If this flip were ignored,
![]() would be in error by (
-0.17, 0.02)
would be in error by (
-0.17, 0.02) ![]() as for
the -3231 day polar motion.
as for
the -3231 day polar motion.
Secondly, the presence of the secular term in the polar motion of the nonrigid Earth due to the constant part of the (4,0) potential (Sect. 6 and Table 4), which was noted already by Mathews & Bretagnon (2002) and Brzezinski & Capitaine (2002): It seems necessary to point out here that the "observed secular motion of the pole'', referred to by the latter, is a linear drift of the Earth's rotation pole in relation to the TRF while the polar motions dealt with here (and elsewhere) in the context of the transformation between the CRF and the TRF are the secular and periodic motions (with periods outside the retrograde diurnal band) of the pole of the CRF as seen from the TRF. It is unfortunate that the use of the term "polar motion'' with different meanings in different contexts lends scope for avoidable confusion.
Thirdly, the effects of possible triaxiality ![]() of the core:
We have brought out explicitly the coupling of the retrograde and
prograde diurnal wobbles that is produced by the Z and
of the core:
We have brought out explicitly the coupling of the retrograde and
prograde diurnal wobbles that is produced by the Z and ![]() terms in the angular momentum, and the role played thereby in the
prograde semidiurnal nutations by the FCN resonance (more
specifically, by the resonance in the retrograde diurnal wobble of
the core) through
this coupling. We find the increments to the wobble
eigenfrequencies due to triaxiality to be of no observational
consequence: they are of the second order in the triaxiality
parameter, proportional to
terms in the angular momentum, and the role played thereby in the
prograde semidiurnal nutations by the FCN resonance (more
specifically, by the resonance in the retrograde diurnal wobble of
the core) through
this coupling. We find the increments to the wobble
eigenfrequencies due to triaxiality to be of no observational
consequence: they are of the second order in the triaxiality
parameter, proportional to
![]() (as noted in the first
para of Sect. 7.3) or to
(as noted in the first
para of Sect. 7.3) or to
![]() ,
as the case may be, in contrast to the first order
changes found by Escapa et al. (2002). (It is hard to
comprehend how their first order changes could involve the
moduli of the triaxiality parametes rather than the complex
parameters themselves.) In regard to the forced motions, we have
confirmed that the contributions from core triaxiality
,
as the case may be, in contrast to the first order
changes found by Escapa et al. (2002). (It is hard to
comprehend how their first order changes could involve the
moduli of the triaxiality parametes rather than the complex
parameters themselves.) In regard to the forced motions, we have
confirmed that the contributions from core triaxiality ![]() could
be significant, as observed by Escapa et al. especially if
could
be significant, as observed by Escapa et al. especially if ![]() were a few times Z; but the numbers we obtain for
the these contributions are only about 40% of those reported
by these authors, or less.
Brzezinsky & Capitaine
(2002) have computed
were a few times Z; but the numbers we obtain for
the these contributions are only about 40% of those reported
by these authors, or less.
Brzezinsky & Capitaine
(2002) have computed ![]() from the mantle tomographic model of
Morelli & Dziewonski (1987)
and the mantle convection
model of Defraigne et al. (1996). But the modeling of the
core mantle boundary with the precision needed to make a useful
estimate of
from the mantle tomographic model of
Morelli & Dziewonski (1987)
and the mantle convection
model of Defraigne et al. (1996). But the modeling of the
core mantle boundary with the precision needed to make a useful
estimate of ![]() is notoriously difficult, and the general
consensus seems to be that the value of
is notoriously difficult, and the general
consensus seems to be that the value of ![]() remains highy
uncertain. One might perhaps hope that, if the core triaxiality
were large enough, its estimation from observations of diurnal
polar motions/semidiurnal nutations would become possible if and
when the precision of estimation of such motions approaches the 1
remains highy
uncertain. One might perhaps hope that, if the core triaxiality
were large enough, its estimation from observations of diurnal
polar motions/semidiurnal nutations would become possible if and
when the precision of estimation of such motions approaches the 1 ![]() as level. However, it is important to take note that the
prograde diurnal polar motions considered here, which are due
to the torques exerted on the triaxial structure by degree 2 tesseral (m=1) tidal potentials, are at least 10 times smaller
than those due to the ocean tides raised by the very same tidal
potentials; see Table 6 of Chao et al. (1996) for a
comparative listing of observational estimates and theoretical
predictions from various works. Even if the contribution from
as level. However, it is important to take note that the
prograde diurnal polar motions considered here, which are due
to the torques exerted on the triaxial structure by degree 2 tesseral (m=1) tidal potentials, are at least 10 times smaller
than those due to the ocean tides raised by the very same tidal
potentials; see Table 6 of Chao et al. (1996) for a
comparative listing of observational estimates and theoretical
predictions from various works. Even if the contribution from ![]() ,
which is largest for the nutation period of 0.49863 days
(0.99727 day polar motion), were as large as a few
,
which is largest for the nutation period of 0.49863 days
(0.99727 day polar motion), were as large as a few ![]() as, it
would still be only a few percent of the ocean tide contribution for
the same period. To estimate the core triaxiality contribution
accurately enough from observations on prograde diurnal polar
motions to permit useful bounds to be placed
on the triaxiality
as, it
would still be only a few percent of the ocean tide contribution for
the same period. To estimate the core triaxiality contribution
accurately enough from observations on prograde diurnal polar
motions to permit useful bounds to be placed
on the triaxiality ![]() ,
one needs predictions for the dominant
ocean tide contribution that are good at least at the 1
,
one needs predictions for the dominant
ocean tide contribution that are good at least at the 1 ![]() as
level. The prospects for modeling the ocean tide contribution to
this level of accuracy seem quite dim, given the uncertainties in
the modeling of ocean tides and their effects.
as
level. The prospects for modeling the ocean tide contribution to
this level of accuracy seem quite dim, given the uncertainties in
the modeling of ocean tides and their effects.
Acknowledgements
We are happy to acknowledge illuminating discussions with Aleksander Brzezinsky during the final stages of the preparation of this paper. We are also indebted to an anonymous referee for a detailed and thoughtful review of the paper, leading to improvements in presentation.
We start with the expression (4), written slightly more explicitly:
| |
= | 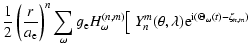 |
|
| (A.1) |
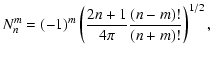 |
(A.2a) | ||
| (A.2b) |
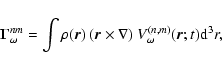 |
(A.3) |
| |
= | (A.4a) | |
| = | (A.4b) |
| cnm = [ (n-m)(n+m+1) ]1/2. | (A.5) |
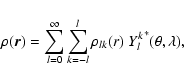 |
(A.6) |
 |
(A.7) |
| (A.8) |
![\begin{displaymath}\tilde\Gamma^{(n0)}_\omega={\rm i}{g_{\rm e}\over 2a_{\rm e}^...
...})}+
~{\rm e}^{{\rm -i}(\Theta_\omega(t)-\zeta_{n,0})}~\right]
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img422.gif) |
(A.9) |
 |
(A.10) |
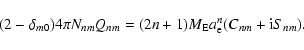 |
(A.11) |