A&A 400, 1085-1094 (2003)
DOI: 10.1051/0004-6361:20021811
Stability limits in double stars
A study of inclined planetary orbits
E. Pilat-Lohinger - B. Funk - R. Dvorak
Institute for Astronomy, University of Vienna,
Türkenschanzstrasse 17, 1180 Vienna, Austria
Received 25 July 2002 / Accepted 12 November 2002
Abstract
We treat the problem of the stability of planetary orbits in double stars with
the aid of numerical studies in the model of the elliptic restricted
three-body problem. Many investigations exist for the limits of the
stability of the S-type planetary motion (i.e. the motion around one
component of the binary). In this paper we present a numerical investigation of
the so-called P-type orbits which are defined as orbits of the planet
around both primary masses. The growing interest of such stability studies
is due to the discovery of the numerous extra-solar planets, where five
of them move in double star systems.
Two different methods are used; in a first study the stability was
investigated systematically
for different initial conditions of the planet, which is regarded to be
massless. We vary
the initial starting distance from the barycenter (always with velocities
corresponding to circular orbits at the beginning), the angle to the
connecting line of the binary and the starting position of the primaries
(peri-astron and apo-astron); the primaries' masses are considered to be
equal.
The numerical stability criterion is set to the condition that during the
whole integration time (50 000 periods of the primaries) the planet should not
suffer from a close encounter to one of the primaries.
The binary's eccentricity (e) is increased form 0 to 0.5 with
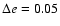 ,
and the initial distance (
,
and the initial distance ( )
to the barycenter is taken of the range from 1.8 to
)
to the barycenter is taken of the range from 1.8 to
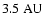 (for
(for
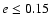 )
or to
)
or to
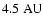 (for
(for
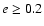 )
with
)
with
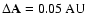 .
For the first time, we study inclined P-type orbits
(
.
For the first time, we study inclined P-type orbits
(
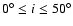 with a step of
with a step of
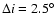 )
for which we analyse
the border line of the stable zone.
Additionally we also record the escape times for all orbits.
In the second part of our study we apply the Fast Lyapunov Indicator (FLI)
to distinguish between the differnt types of motion, taking the same
initial
conditions, only the grid for the initial distance to the barycenter was
finer (
)
for which we analyse
the border line of the stable zone.
Additionally we also record the escape times for all orbits.
In the second part of our study we apply the Fast Lyapunov Indicator (FLI)
to distinguish between the differnt types of motion, taking the same
initial
conditions, only the grid for the initial distance to the barycenter was
finer (
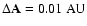 ). Since the FLI is known to be a fast chaos indicator
we reduced the integration time to 104 periods of the primaries.
A comparison of the results of the two studies show that they are in
good agreement.
It turned out that the inclination does not influence the stability
significantly. The stability limit itself varies
between
). Since the FLI is known to be a fast chaos indicator
we reduced the integration time to 104 periods of the primaries.
A comparison of the results of the two studies show that they are in
good agreement.
It turned out that the inclination does not influence the stability
significantly. The stability limit itself varies
between
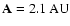 (for e=0 and
(for e=0 and
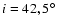 )
and
)
and
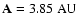 (for e=0.5and
(for e=0.5and
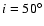 ).
).
Key words: stars: binaries: general -
stars: planetary systems
Until now more than 100 extra-solar planets![[*]](/icons/foot_motif.gif) have been discovered;
most of them are single-planetary systems.
We find (a) very massive planets (from
0.12 to 11 Jupiter-masses; note that only 1/3 of the planets have
masses
have been discovered;
most of them are single-planetary systems.
We find (a) very massive planets (from
0.12 to 11 Jupiter-masses; note that only 1/3 of the planets have
masses
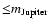 ), (b) planets which are very close to their
host-stars (more than 1/3 move in orbits closer than Mercury around the
Sun) and (c) high eccentric orbits (about half of the planets move in
orbits with eccentricities
), (b) planets which are very close to their
host-stars (more than 1/3 move in orbits closer than Mercury around the
Sun) and (c) high eccentric orbits (about half of the planets move in
orbits with eccentricities
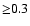 ). We did not yet discover
an extra-solar planetary system similar to our solar system,
even if some planets have been found in the so-called
habitable zone. All of them are giant planets moving in high eccentric
orbits, except HD 28185 which has an eccentricity of only 0.06 but more
than 5 Jupiter-masses. However, recently Marcy et al. (2002)
discovered the first giant planet moving at
about
). We did not yet discover
an extra-solar planetary system similar to our solar system,
even if some planets have been found in the so-called
habitable zone. All of them are giant planets moving in high eccentric
orbits, except HD 28185 which has an eccentricity of only 0.06 but more
than 5 Jupiter-masses. However, recently Marcy et al. (2002)
discovered the first giant planet moving at
about
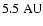 (which can be compared with Jupiter's distance from our Sun)
around its host-star 55 Cancri, which is the first extra-solar Jupiter-like
planet moving in a similar orbit to Jupiter.
(which can be compared with Jupiter's distance from our Sun)
around its host-star 55 Cancri, which is the first extra-solar Jupiter-like
planet moving in a similar orbit to Jupiter.
With the detection of more and more extra-solar planetary systems, general
stability studies of orbits in such systems have become more and more
important. On the one hand, there are many investigations - mainly
with the aid of numerical experiments - for individual exo-solar systems,
especially for those with multiple planetary companions like
Ups Andromedae (see e.g. Lissauer 1999; Laughlin &
Adams 1999;
Rivera & Lissauer 2000; Stepinski
et al. 2000; Laskar 2000;
Barnes & Quinn 2000; Jiang & Ip 2000; Laughlin &
Chambers 2001; Kiseleva-Eggleton & Bois 2001; Gozdziewski
et al. 2001),
Gliese 876 (see e.g. Laughlin & Chambers 2001;
Marcy et al. 2001; Kinoshita & Nakai 2001;
Rivera & Lissauer 2001; Rivera & Lissauer 2002;
Gozdziewski et al. 2002; Hadjidemetriou 2002; Jianghui et al. 2002) or
HD 82943 (see e.g. Gozdziewski & Maciejewski 2001;
Hadjidemetriou 2002). These three planetary systems are of great interest,
since the planets move in resonant orbits.
On the other hand there are general stability studies of P- and S-type
motions![[*]](/icons/foot_motif.gif) using the elliptic restricted three body problem
using the elliptic restricted three body problem![[*]](/icons/foot_motif.gif) like the ones by
Harrington (1977), Szebehely (1980), Szebehely & McKenzie (1981),
Dvorak (1984, 1986)
Rabl & Dvorak (1988), and Dvorak et al. (1989).
More recently these studies have been continued by Holman & Wiegert (1999),
Pilat-Lohinger (2000a,b) and Pilat-Lohinger & Dvorak (2002).
Since all these investigations are restricted to the planar motion of
the planet we have no information on the influence of the inclination
on the stable motion. This is the subject of this paper.
Stability studies in double star systems are of great interest, not only
since we know already 5 examples of
S-type motion but also because of the fact that more than half of the stars
form double or multiple systems.
like the ones by
Harrington (1977), Szebehely (1980), Szebehely & McKenzie (1981),
Dvorak (1984, 1986)
Rabl & Dvorak (1988), and Dvorak et al. (1989).
More recently these studies have been continued by Holman & Wiegert (1999),
Pilat-Lohinger (2000a,b) and Pilat-Lohinger & Dvorak (2002).
Since all these investigations are restricted to the planar motion of
the planet we have no information on the influence of the inclination
on the stable motion. This is the subject of this paper.
Stability studies in double star systems are of great interest, not only
since we know already 5 examples of
S-type motion but also because of the fact that more than half of the stars
form double or multiple systems.
In the following sections we present our stability study of P-type
motion in a binary with mass-ratio![[*]](/icons/foot_motif.gif) (
(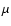 )
equal to 0.5 (i.e. the two
stars have equal masses).
For such a system there exist several studies of periodic orbits
in the circular resticted three body problem. The first investigations
for the three dimensional case date back to Goudas (1961, 1963),
followed by the work of Markellos (1977, 1978), Michalodimitrakis (1979),
Perdios & Markellos (1988) and Zagouras (1977) and more recently
Broucke (2001).
In the present study we determine numerically (a) by means of orbital
computations and (b) with the aid of the Fast Lyapunov Indicator (FLI)
(Froesché et al. 1997) the variation of the stable zone by increasing the eccentricity
of the binary from 0 to 0.5. The computations are carried
out for planar planetary orbits and inclined ones (for i up to
)
equal to 0.5 (i.e. the two
stars have equal masses).
For such a system there exist several studies of periodic orbits
in the circular resticted three body problem. The first investigations
for the three dimensional case date back to Goudas (1961, 1963),
followed by the work of Markellos (1977, 1978), Michalodimitrakis (1979),
Perdios & Markellos (1988) and Zagouras (1977) and more recently
Broucke (2001).
In the present study we determine numerically (a) by means of orbital
computations and (b) with the aid of the Fast Lyapunov Indicator (FLI)
(Froesché et al. 1997) the variation of the stable zone by increasing the eccentricity
of the binary from 0 to 0.5. The computations are carried
out for planar planetary orbits and inclined ones (for i up to 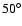 ).
).
In Sect. 2 we describe the initial conditions and their variations
for the different numerical studies and we define the stability criterion.
The results for the circular and for the elliptic problem will be discussed
in Sects. 3 and 4, respectively. Section 5 is concerned with the escape
times, which are given for all unstable orbits and finally in Sect. 6
we present our computations of the FLIs in the elliptic problem and a
comparison with the results of the orbital computations.
To establish the limiting curve for stable planetary orbits, we analyzed the
results of the
numerical integration
of the three dimensional equations of motion of the elliptic restricted
three-body problem using two integration methods (a) the
Lie-series (see e.g. Lichtenegger 1984 and Hanslmeier & Dvorak 1984)
for the orbital computations and (b) the Bulirsch-Stoer method for the
computation of the FLIs (this program was kindly provided by R. Gonczi from
the Observatory of Nice).
According to previous results - and contrary to the S-type orbits - the
stability limits for P-types are almost independent of the mass-ratio
of the primaries (see Dvorak et al. 1989).
As a consequence we studied only the case of equal massive
primary bodies.
To examine the phase space around such a binary with mass-ratio (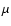 )
equal 0.5, we varied the initial conditions in the following way:
)
equal 0.5, we varied the initial conditions in the following way:
- 1.
- for the orbits of the binary:
- (a)
- the eccentricity e was increased from 0 to 0.5 with
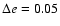 ;
;
- (b)
- for the starting positions of the primaries we used the apo-astron
and peri-astron (for e > 0);
- 2.
- for the planetary orbits:
- (a)
- the inclination i of the planetary orbit to the plane of
motion of the binary was increased from
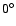 to
to 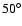 with a step size
of
with a step size
of
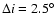 ;
;
- (b)
- the initial distance (
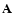 )
of the planet from the barycenter of the binary was varied from 1.8 to either
)
of the planet from the barycenter of the binary was varied from 1.8 to either
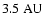 (for
(for
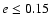 )
or
)
or
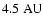 (for
(for
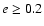 )
with
)
with
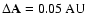 and
and
- (c)
- for each
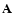 we used 4 starting positions for the planets which
are defined by the following angles of the planetary orbit to the connecting
line of the primaries:
we used 4 starting positions for the planets which
are defined by the following angles of the planetary orbit to the connecting
line of the primaries:
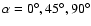 and
and 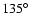 .
.
All planetary orbits were initially circular with respect to the barycenter of
the system. From the variations of the initial conditions it follows that we computed for
all distances from the barycenter 8 (if e > 0) or 4 (if e=0) planetary
orbits. The stable motion is defined by the initial distances
of the planets to the barycenter of the binary where all integrated orbits for
a certain 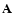 are stable within the integration time. Therefore, the
stable region depends on two parameters, namely on the eccentricity of the
binary
and on the inclination of the planet.
are stable within the integration time. Therefore, the
stable region depends on two parameters, namely on the eccentricity of the
binary
and on the inclination of the planet.
In total almost 50 000 orbits were integrated for 50 000 periods
of the primaries.
To study the dependence of the stable zone on e and i we analyzed all
computed orbits and determined:
- an upper critical orbit (UCO) (see Dvorak et al. 1989), which
forms the border of the stable zone and is therefore defined as the innermost
orbit where all 8 (or 4 if e=0) different starting positions were found to
be stable;
- a lower critical orbit (LCO) which forms the border of the
unstable zone, since it is the outermost orbit where
all 8 (or 4 if e=0) different starting positions were found to be chaotic;
- an escape time for the unstable orbits, which is given by the time
when a close encounter
with one of the primaries occurred (within the Hill's sphere).
From these studies it follows that we divided the phase space around the binary
with 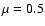 into 3 regions: a stable zone, an unstable zone and in between
a so-called mixed zone
into 3 regions: a stable zone, an unstable zone and in between
a so-called mixed zone![[*]](/icons/foot_motif.gif) ,
where both stable and unstable motion was found for
a certain distance from the barycenter.
,
where both stable and unstable motion was found for
a certain distance from the barycenter.
In the second part of our study we used a fast method, the so-called
Fast Lyapunov Indicator (Froeschlé et al. 1997), to distinguish
between regular and chaotic motion. According to the definition of this
indicator, which is simply the norm of the largest tangent vector vi:
(n denotes the dimension of the phase space) it is obvious that chaotic
orbits can be found very quickly because of the exponential growth of this
vector in the chaotic region. Therefore, we needed only a few
number of primary revolutions to determine the orbital behaviour.
In order to define the stable motion we introduced a
critical value for the FLIs, which was set to 107according to the computed FLIs.
The computation of the FLIs has been done in principal for the same initial
conditions as described above but with the following changes:
- we considered only the peri-astron positions of the binary;
- we took a finer grid in
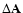 ,
namely
,
namely
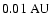 and
and
- we reduced the computation time to 10 000 periods of the binary.
For this case we used a finer grid in the initial distance 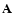 (
(
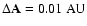 - the same as for all FLI computations)
for the orbital computations based on the Lie-series method which enables us
to see a more detailed structure of the phase space at the borders between
the different types of motion.
Figure 1 shows a summary of the results of the circular problem in the (
- the same as for all FLI computations)
for the orbital computations based on the Lie-series method which enables us
to see a more detailed structure of the phase space at the borders between
the different types of motion.
Figure 1 shows a summary of the results of the circular problem in the (
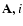 )
plane, where one can see the variation of the 3 types of motion: black
for the stable, grey for the mixed and light grey for the unstable one
with respect to the different initial inclinations
of the orbital planes of the planets. In this case we see
a nearly constant UCO (at
)
plane, where one can see the variation of the 3 types of motion: black
for the stable, grey for the mixed and light grey for the unstable one
with respect to the different initial inclinations
of the orbital planes of the planets. In this case we see
a nearly constant UCO (at
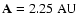 )
for inclinations up to
)
for inclinations up to
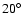 ,
and subsequently we observe
an almost linear incresase of the stable zone, which starts at
,
and subsequently we observe
an almost linear incresase of the stable zone, which starts at
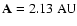 for
for
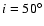 .
For the LCO we did not find a significant
change with the inclination, which can be seen by the almost straight line
at
.
For the LCO we did not find a significant
change with the inclination, which can be seen by the almost straight line
at
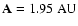 .
The region between the LCO and UCO is the so-called mixed zone
(where both motions can be found for a certain
.
The region between the LCO and UCO is the so-called mixed zone
(where both motions can be found for a certain 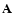 ),
whose size is
),
whose size is
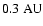 for all inclinations from
for all inclinations from 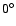 to
to 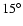 .
Thereafter, we recognize a separation of this zone due to a finger-like stable
area from
.
Thereafter, we recognize a separation of this zone due to a finger-like stable
area from
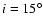 to
to
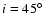 .
A second finger-like separation due to
another stable region occurs at inclinations between
.
A second finger-like separation due to
another stable region occurs at inclinations between
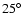 and
and 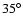 which finally results in a large
stable region close to the unstable zone from
which finally results in a large
stable region close to the unstable zone from
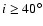 on.
Furthermore, for
on.
Furthermore, for
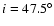 and
and
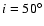 a small completely unstable region
appears at
a small completely unstable region
appears at
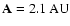 so that the mixed region disappears almost
completely for such large values of the initial inclinations.
Recently, Broucke (2001) studied periodic orbits in a binary, where
among others the family of direct orbits around both primaries with a
radius 2.1 were investigated. The stability of this L1v family (according
to Hénon's terminolgy 1973) is not in contradiction to our results,
since this distance belongs to the chaotic region (see Fig. 1), where the
stable motion depends strongly on the initial position of the massless body.
Moreover, for inclinations between
so that the mixed region disappears almost
completely for such large values of the initial inclinations.
Recently, Broucke (2001) studied periodic orbits in a binary, where
among others the family of direct orbits around both primaries with a
radius 2.1 were investigated. The stability of this L1v family (according
to Hénon's terminolgy 1973) is not in contradiction to our results,
since this distance belongs to the chaotic region (see Fig. 1), where the
stable motion depends strongly on the initial position of the massless body.
Moreover, for inclinations between 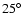 and
and 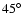 one can see a finger-like
stable region at this distance.
one can see a finger-like
stable region at this distance.
In general the result shows an increase of the stable zone for higher
inclinations. This seems to be in contrast to the study by Kozai (1962), who
found more instability for high inclined orbits in the asteroid belt, which is
caused by a resonance that pumps up the initial small eccentricities to large
ones. But already for the outer Solar System it was found that the Kozai
resonances plays only a role for orbits with high inclination and large
eccentricity (see Thomas & Morbidelli 1996). Since we study P-type orbits
started in circular motion the Kozai resonance cannot be observed in our
results.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{pfd_f1.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg45.gif) |
Figure 1:
The results of the circular problem presented in the (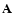 ,
i)
plane, where both axes are plotted from the highest to the lowest
value, black shows the stable zone, white the unstable one and in between
is a mixed region. ,
i)
plane, where both axes are plotted from the highest to the lowest
value, black shows the stable zone, white the unstable one and in between
is a mixed region. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg46.gif) |
Figure 2:
The escape times computed for all orbits in the circular problem are
summarized in the figure. One can see the distance of the planet from the
barycenter on the x-axis, the different inclinations on the y-axis and the
inverse of the escape time on the z-axis. |
| Open with DEXTER |
In the "escape diagram'' (Fig. 2) we plotted the inverse of the escape
time![[*]](/icons/foot_motif.gif) for all orbits in the (A, i) plane. One can see clearly the border
between the stable and the mixed zone. Also the fingerlike stable island within
the mixed area at high inclinations is visible. In contrast
thereto, it is difficult to distinguish between the mixed and unstable
regions, due to the fact that the mean escape time at this border differs
only by about 10 periods of the binary between the two types of motion.
for all orbits in the (A, i) plane. One can see clearly the border
between the stable and the mixed zone. Also the fingerlike stable island within
the mixed area at high inclinations is visible. In contrast
thereto, it is difficult to distinguish between the mixed and unstable
regions, due to the fact that the mean escape time at this border differs
only by about 10 periods of the binary between the two types of motion.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{pfd_f3.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg47.gif) |
Figure 3:
The results of the FLI computation for the different distances
to the barycenter (x-axis) and the different inclinations (y-axis).
Note that the scaling of the axes in both
directions is from the largest to the lowest value. The different
shades represent the different types of motion:
from black for small values of the FLIs (which corresponds to stable motion)
to white for very large values of the FLIs (which corresponds to unstable
region of Fig. 1). |
| Open with DEXTER |
The results of the circular problem obtained by using the
Fast Lyapunov Indicator are summarized in Fig. 3, where we show again
for each distance from the barycenter (x-axis) and for the different
inclinations (y-axis) whether an orbit belongs to the stable (black)
to the mixed (grey) or to the unstable (white) zone.
In general the result is in good agreement with that of the long-term
orbital computations (Fig. 1). We see again almost constant zones
for orbits with an inclination from 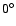 to nearly
to nearly 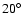 .
The finger-like
stable zone in the mixed area is similar to that of the orbital
computations. The main difference is that the number of stable orbits
in the mixed region found by means of the FLIs is smaller than that
of the orbital computations for high inclinations.
This is probably due to the
fact that the computation of the FLIs indicates chaotic motion earlier.
A new phenomenon found in this study is the appearance of a small strip of
chaotic islands inside the stable region orientated parallel to the contour
of the UCO.
This may be caused by a mean motion resonance between the primaries and the
planet, which will be studied more in detail in a further investigation.
.
The finger-like
stable zone in the mixed area is similar to that of the orbital
computations. The main difference is that the number of stable orbits
in the mixed region found by means of the FLIs is smaller than that
of the orbital computations for high inclinations.
This is probably due to the
fact that the computation of the FLIs indicates chaotic motion earlier.
A new phenomenon found in this study is the appearance of a small strip of
chaotic islands inside the stable region orientated parallel to the contour
of the UCO.
This may be caused by a mean motion resonance between the primaries and the
planet, which will be studied more in detail in a further investigation.
![\begin{figure}
\par\includegraphics[height=5.4cm,clip]{fig4a.eps}\hspace*{3cm}
\...
...s}\hspace*{3cm}
\includegraphics[height=5.4cm,clip]{pfd_f4h.eps}\par\end{figure}](/articles/aa/full/2003/12/aa2955/Timg48.gif) |
Figure 4:
The panels on the left side show the inverse of the escape time
in the ( ,
i)-plane and those on the right side show the stable zone (black), the mixed zone (grey) and the unstable zone (white) for ,
i)-plane and those on the right side show the stable zone (black), the mixed zone (grey) and the unstable zone (white) for
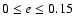 (all for the same grid of initial conditions).
(all for the same grid of initial conditions). |
| Open with DEXTER |
In the elliptic problem we studied 10 different models:
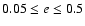 (with
(with
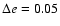 ), for which we used only a grid of
), for which we used only a grid of
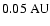 for the
distance from the barycenter. Because of the ellipticity of the binary we
have now to integrate 8 initial positions for a given
for the
distance from the barycenter. Because of the ellipticity of the binary we
have now to integrate 8 initial positions for a given 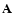 ,
since the computations have been done starting with the binary in the
peri-astron and in the apo-astron.
The results for the 10 elliptic models are given in Figs. 4-6;
where we show for each eccentricity of the binary (from e=0 to 0.5 with
,
since the computations have been done starting with the binary in the
peri-astron and in the apo-astron.
The results for the 10 elliptic models are given in Figs. 4-6;
where we show for each eccentricity of the binary (from e=0 to 0.5 with
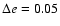 )
two figures: a 3D plot for the escape times and a contour
plot which displays the 3 zones of the different types of motion. Looking
at the border between unstable and mixed motion, which is given by the
computations of the LCO, one can recognize that it remains nearly constant
for a given eccentricity, with two exceptions: for e=0.1 at high
inclinations, where a small island of mixed motion can be found around
)
two figures: a 3D plot for the escape times and a contour
plot which displays the 3 zones of the different types of motion. Looking
at the border between unstable and mixed motion, which is given by the
computations of the LCO, one can recognize that it remains nearly constant
for a given eccentricity, with two exceptions: for e=0.1 at high
inclinations, where a small island of mixed motion can be found around
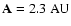 and for e=0.3 which shows a variation of this border with
the inclination. Furthermore, one can see a shift outwards (to larger
and for e=0.3 which shows a variation of this border with
the inclination. Furthermore, one can see a shift outwards (to larger
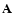 values) when we increase e. This behaviour is visible
when increasing e from 0 to 0.1 (Fig. 4: first three contour plots from
the top) and again from e=0.25 to 0.35 (Fig. 5: last three contour plots),
in the other cases this shift is much smaller.
values) when we increase e. This behaviour is visible
when increasing e from 0 to 0.1 (Fig. 4: first three contour plots from
the top) and again from e=0.25 to 0.35 (Fig. 5: last three contour plots),
in the other cases this shift is much smaller.
The border of the stable motion which is given by the UCO shows an
interesting appearance of unstable "fingers'' starting at
high inclinations (Fig. 4: second contour plot from the top), which
become larger in the direction of zero inclination (Fig. 4:
last two contour plots) when increasing the binary eccentricity.
Then they split up the stable region and finally the border of the stable
zone is shifted outward to a larger value of 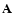 (Fig. 5: contour
plot on the top).
This development is visible from e=0.05 to e=0.2 and again from e=0.2
to e=0.5, where in the second appearance the stable island remains longer
within the mixed zone.
(Fig. 5: contour
plot on the top).
This development is visible from e=0.05 to e=0.2 and again from e=0.2
to e=0.5, where in the second appearance the stable island remains longer
within the mixed zone.
In the three dimensional graph of the LCO (Fig. 7), which is given by
the initial distance from the barycenter of the last unstable orbit in
the (e,i)-plane, one can observe an increase of the LCO for an
eccentricity up to 0.1 with a more or less constant behaviour with
respect to the inclination (from
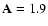 to
to
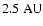 ). Between
e=0.1 and 0.3 we find a slightly inclined plateau to larger
). Between
e=0.1 and 0.3 we find a slightly inclined plateau to larger 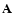 values
(from 2.5 to
values
(from 2.5 to
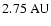 ). A further increase of e up to 0.35 yields a jump
in
). A further increase of e up to 0.35 yields a jump
in 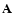 and subsequently
and subsequently 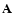 neither depends on e nor on i(
neither depends on e nor on i(
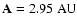 ).
).
The behaviour of the UCO (Fig. 8), which shows the dependence of the border
of the stable zone on the eccentricity of the binary and on the inclination
of the planet's orbit, is somewhat similar to the LCO. We observe
for small eccentricities (
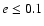 )
a weak dependence on the inclination
of the planetary orbit. Between e=0.1 and 0.3 one can see some
irregularities and three small plateaus - one for high inclinations between
)
a weak dependence on the inclination
of the planetary orbit. Between e=0.1 and 0.3 one can see some
irregularities and three small plateaus - one for high inclinations between 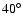 and
and 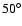 ,
the second around
,
the second around
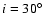 (both for e from 0.1 to 0.2) and the
third for low inclined orbits (
(both for e from 0.1 to 0.2) and the
third for low inclined orbits (
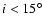 )
and e between 0.15 and 0.25.
The irregularities between e=0.15 and 0.3 cause jumps of the UCO followed
by a big plateau, where neither e nor i will change the UCO in this region
(for
)
and e between 0.15 and 0.25.
The irregularities between e=0.15 and 0.3 cause jumps of the UCO followed
by a big plateau, where neither e nor i will change the UCO in this region
(for
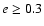 ). Furthermore, the figure shows a "hill structure'' for
high eccentricities (
). Furthermore, the figure shows a "hill structure'' for
high eccentricities (
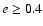 )
and high inclinations (
)
and high inclinations (
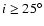 ).
).
From the orbital computations we determined the escape times, which are
defined by the moment of a close encounter of the planet with a primary.
The three dimensional plots (Figs. 4-6: left) show the inverse of the
mean value of the escape times (calculated from all 8 (or 4 if e=0) orbits
for a certain distance from the barycenter). Globally, we can say that the
border between stable and mixed motion is much more visible than that
between mixed and unstable motion - this is again due to the fact that the
escape times near the LCO of the two motions do not differ very much.
From the limit of the stable zone, one can see a steep increase in the
3D plots, which means that a closer initial distance to the binary
leads to an earlier escape of the planet. An analysis of the innermost
computed orbit (i.e.
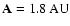 )
shows that the higher the
eccentricity and the inclination the faster an escape occurs.
)
shows that the higher the
eccentricity and the inclination the faster an escape occurs.
In this study we considered only the orbits where the
primaries were started in the peri-astron, so that the comparison of the
results shows not only differences due to the different integration methods
but also due to the fact that we ignored the apo-astron starting positions.
The computations have been carried out for 10 000 periods of the primaries.
In order to distinguish between the different types of motion we took the same
critical value for the FLIs as in the circular problem (i.e. 107) to
define the border of the stable motion.
The calculation of 4 orbits for each distance from the barycenter - due
to the variation of 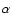 (as described in Sect. 2) - leads again to
3 types
of motion: the stable, the mixed and the unstable ones, which are represented by
different grey colors in the figures. The study of the FLIs has been carried out to confirm the
results of the orbital computations, especially the size of the stable
region. Therefore, we show two examples for the
elliptic case (Fig. 9 for e=0.1, and Fig. 10 for e=0.5), since
the differences of the two studies for the other eccentricities are similar
to those shown in Figs. 9 and 10.
In general, we can say that there is no strong influence of the inclination
on the zones of the different types of motion. The main differences between
the two studies occur due to the fact that we used a finer grid in
(as described in Sect. 2) - leads again to
3 types
of motion: the stable, the mixed and the unstable ones, which are represented by
different grey colors in the figures. The study of the FLIs has been carried out to confirm the
results of the orbital computations, especially the size of the stable
region. Therefore, we show two examples for the
elliptic case (Fig. 9 for e=0.1, and Fig. 10 for e=0.5), since
the differences of the two studies for the other eccentricities are similar
to those shown in Figs. 9 and 10.
In general, we can say that there is no strong influence of the inclination
on the zones of the different types of motion. The main differences between
the two studies occur due to the fact that we used a finer grid in 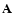 for the computations of the FLIs, which gives a more detailed structure of
the phase space.
for the computations of the FLIs, which gives a more detailed structure of
the phase space.
The results of the FLIs show also the shift of the mixed and the stable zones
outwards, i.e. to larger distances form the barycenter when we increase the
eccentricity. More precisely,
the border between unstable and mixed motion (i.e. the LCO) is shifted
from
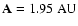 (for e=0) to
(for e=0) to
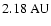 (for e=0.05) and to
distances between 2.6 and
(for e=0.05) and to
distances between 2.6 and
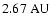 depending on the inclination for e=0.1(Fig. 9). Thereafter the limit remains at this position up to
e=0.3. For an eccentricity of e=0.35 we observe another shift to about
depending on the inclination for e=0.1(Fig. 9). Thereafter the limit remains at this position up to
e=0.3. For an eccentricity of e=0.35 we observe another shift to about
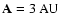 which corresponds to the position of a chaotic strip in the stable
region for e=0.1 (Fig. 9). This chaotic strip is the main difference
between the two studies, since it ends at about
which corresponds to the position of a chaotic strip in the stable
region for e=0.1 (Fig. 9). This chaotic strip is the main difference
between the two studies, since it ends at about
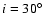 in the plot of
the orbital computations (Fig. 5 - third contour plot). Therefore,
we have the same border between stable and mixed motion for the high inclined
orbits, while for orbits with
in the plot of
the orbital computations (Fig. 5 - third contour plot). Therefore,
we have the same border between stable and mixed motion for the high inclined
orbits, while for orbits with
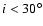 the UCO varies of about
the UCO varies of about
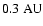 for the two studies. A further increase of the eccentricity causes that the
stable zone between the LCO and UCO gets smaller and smaller, which finally
leads to a shift of the two borders. Additionally, another chaotic island
appears at about
for the two studies. A further increase of the eccentricity causes that the
stable zone between the LCO and UCO gets smaller and smaller, which finally
leads to a shift of the two borders. Additionally, another chaotic island
appears at about
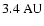 from the barycenter - a first indication can
already be seen in Fig. 9 for
from the barycenter - a first indication can
already be seen in Fig. 9 for
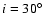 ,
while in the results of the orbital
computations it appears for the first time for e=0.2.
The second example for the elliptic case (e=0.5) shows the same border
between unstable and mixed motion, while the stable zone begins beyond
,
while in the results of the orbital
computations it appears for the first time for e=0.2.
The second example for the elliptic case (e=0.5) shows the same border
between unstable and mixed motion, while the stable zone begins beyond
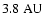 from the barycenter which is about
from the barycenter which is about
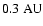 farther outside than in the
result of the orbital computations - except for high inclinations (
farther outside than in the
result of the orbital computations - except for high inclinations (
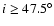 ), where the UCO is the same in both studies. The finer grid
in
), where the UCO is the same in both studies. The finer grid
in  shows again a more detailed structure of the phase space (which
seemed to be without structure in the results of the orbital computations -
Fig. 6 last contour plot).
shows again a more detailed structure of the phase space (which
seemed to be without structure in the results of the orbital computations -
Fig. 6 last contour plot).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pfd_f9.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg76.gif) |
Figure 9:
Global result of the FLI computation when the two components
of the double star move in low eccentric orbits (e=0.1).
The different distances to the barycenter are plotted on the x-axis and the
different inclinations are shown of the y-axis.
Note that the scaling of the axes in both
directions is from the largest to the lowest value. The different shades
represent the different types of motion: from black for stable motion to
white for unstable motion. |
| Open with DEXTER |
Up to now there are no known planets in binaries moving around both stars but
from the cosmogonic point of view this scenario cannot be excluded.
Certainly, for a stability study in the habitable zone (i.e. at distances
from the star where liquid water may exist)
it is more interessting to study S-type orbits.
To tackle the problem of stability of P-type motion in
a binary, we did numerical experiments in the framework of the spatial elliptic restricted three body problem.
The new results concern the stability of inclined orbits with respect to the orbit of the binary. Two different
series of numerical integrations of the equations of motion were analyzed.
For a simple analysis of the stability (stable within the integration time
without a close encounter with one of the primaries)
we integrated with the Lie-series method almost 50 000 orbits for 50 000 periods
of the binary and checked their stability or instability, so that the phase
space was divided into 3 regions (stable, mixed and unstable one) by the
determination of an Upper Critical Orbit (UCO) and a Lower Critical Orbit
(LCO). Furthermore, the escape time was computed for each orbit.
The respective diagrams were compared and were found to be in good agreement.
Additionally,
in another numerical integration using the Bulirsch-Stoer method we computed
the Fast Lyapunov Indicator (FLI) which was used as chaos indicator.
Summarizing, we can say the following:
- the stability limit varies between
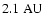 and
and
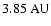 depending on the
eccentricity of the binary;
depending on the
eccentricity of the binary;
- for some eccentricities only we found a clear dependence of the
stability limits on the inclination of the planetary orbit
- the regions of stable, mixed and unstable orbits show the following
behaviour: for certain eccentricities a small finger-like unstable
island appears at high inclinations and evolves to a small strip of
instability in the (
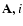 )
plots if we increase the binary's eccentricity.
This developement leads finally to a shift of the stable zone to larger
distances from the barycenter (this can be seen from e=0.05 to e=0.2and repeats for eccentricities from 0.2 to 0.5);
)
plots if we increase the binary's eccentricity.
This developement leads finally to a shift of the stable zone to larger
distances from the barycenter (this can be seen from e=0.05 to e=0.2and repeats for eccentricities from 0.2 to 0.5);
- the computations of the FLIs show in principal the same result, only
the unstable islands in the stable zone appear earlier and evolve faster
to unstable strips so that the border of the stable zone is shifted
outwards earlier. Of course the plots show a more detailed structure
due to the finer grid in the distance from the barycenter. Differences
occur also due to the reduced integration time - sometimes there are small
islands of mixed motion in the unstable zone (Fig. 9) or stable motion
was found in the mixed zone (Fig. 10);
- an interessting phenomenon was found in the result of the circular
problem obtained by the computations of the FLIs, which shows a strip
of chaotic behaviour in the stable region (for high inclinations). This is
probably due to a resonance, which has to be studied in more detail, since
it could not confirmed with long-term integrations using the Lie-series
method for 106 periods of the binary.
As a next step, we will investigate the detailed structure of the resonances
of the P-type motion in binaries,
and we will study how the three zones will be influenced by a massive planet
(in the different models), which leads to secular resonances.
Acknowledgements
We thank the referee for suggestions
to improve our paper.
This work was carried out within the framework of the FWF project
No. P14375-TPH. One of the authors (EP-L) was financed by the
Hertha-Firnberg-Project T122.
- Barnes, R., & Quinn, T. 2001, ApJ, 550, 884
NASA ADS
- Broucke, R. A. 2001, CMDA, 81, 321
In the text
- Dvorak, R. 1984, CMDA, 34, 369
In the text
- Dvorak, R. 1986, A&A, 167, 379
In the text
NASA ADS
- Dvorak, R., Froeschlé, Ch., & Froeschlé, C. 1989,
A&A, 226, 335
In the text
NASA ADS
- Froeschlé, C., Lega, E., & Gonczi, R. 1997, CMDA, 67, 41
In the text
- Gozdziewski, K., Bois, E., Maciejewski, A. J., & Kiseleva-Eggleton, L. 2001, A&A, 378, 569
In the text
NASA ADS
- Gozdziewski, K., & Maciejewski, A. J. 2001, A&A, 563, L81
- Gozdziewski, K., Bois, E., & Maciejewski, A. J. 2002, MNRAS, 332, 839
In the text
NASA ADS
- Goudas, C. L. 1963, Icarus, 2, 1
In the text
NASA ADS
- Hadjidemetriou, J. 2002, CMDA, 83, 141
In the text
- Hanslmeier, A., & Dvorak, R. 1984, A&A, 132, 203
In the text
NASA ADS
- Harrington, R. S. 1977, AJ, 82, 753
In the text
NASA ADS
- Hénon, M., A&A, 28, 415
NASA ADS
- Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621
In the text
NASA ADS
- Jiang, I., & Ip, W. 2001, A&A, 367, 943
NASA ADS
- Jianghui, J., Guangyu, L., & Lin, L. 2002, ApJ, 572, 1041
In the text
NASA ADS
- Kinoshita, H., & Nakai, H. 2001, Publications of the Astronomical Society of Japan, 53, L25
In the text
NASA ADS
- Kiseleva-Eggleton, L., & Bois, E. 2001, ApJ, 553, L73
In the text
NASA ADS
- Kozai, Y. 1962, AJ, 67, 591
In the text
NASA ADS
- Laskar, J. 2000, Phys. Rev. Lett., 84, 3240
In the text
NASA ADS
- Laughlin, G., & Adams, F. C. 1999, ApJ, 526, 881
In the text
NASA ADS
- Laughlin, G., & Chambers, J. E. 2001, ApJ, 551, L109
In the text
NASA ADS
- Lichtenegger, H. 1984, CMDA, 34, 357
In the text
- Lissauer, J. J. 1999, Nature, 398, 659
In the text
NASA ADS
- Marcy, G., Butler, R. P., Fischer, D., et al. 2001, ApJ, 556, 296
In the text
NASA ADS
- Marcy, G., Butler, R. P., Fischer, D. A., et al. 2002, ApJ, 581, 1375
In the text
NASA ADS
- Markellos, V. V. 1977, MNRAS, 180, 103
In the text
NASA ADS
- Markellos, V. V. 1978, MNRAS, 184, 273
In the text
NASA ADS
- Michalodimitrakis, M. 1979, A&A, 76, 6
In the text
NASA ADS
- Pilat-Lohinger, E. 2000a, Proc. of the 5th Alexander von Humboldt Colloq. on Celestial Mechanics, ed. R. Dvorak, & J. Henrard (Kluwer Academic Publisher), 329
In the text
- Pilat-Lohinger, E. 2000b, Proc. of the 2nd Austrian Hungarian Workshop on Trojans and related Topics, ed. F. Freistetter, R. Dvorak, & B. Erdi (Eötvös University Press), 77
- Pilat-Lohinger, E., & Dvorak, R. 2002, CMDA, 82, 143
In the text
- Perdios, E., & Markellos, V. V. 1988,
CMDA, 42, 187
In the text
- Rabl, G., & Dvorak, R. 1988, A&A, 191, 385
In the text
NASA ADS
- Rivera, E. J., & Lissauer, J. J. 2000, ApJ, 530, 454
In the text
NASA ADS
- Rivera, E. J., & Lissauer, J. J. 2001, ApJ, 558, 392
In the text
NASA ADS
- Stepinski, T., Malhotra, R., & Black, D. C. 2000, ApJ, 545, 1044
In the text
NASA ADS
- Szebehely, V. 1980, CMDA, 22, 7
In the text
- Szebehely, V., & McKenzie, R. 1981, CMDA, 23, 3
In the text
- Thomas, F., & Morbidelli, A. 1996, CMDA, 64, 209
In the text
- Zagouras, C. G., & Markellos, V. V. 1977, A&A,
59, 79
In the text
NASA ADS
Copyright ESO 2003
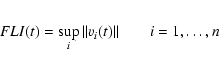
![\begin{figure}
\includegraphics[width=8.8cm,clip]{pfd_f1.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg45.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg46.gif)
![\begin{figure}
\includegraphics[width=8.8cm,clip]{pfd_f3.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg47.gif)
![\begin{figure}
\par\includegraphics[height=5.4cm,clip]{fig4a.eps}\hspace*{3cm}
\...
...s}\hspace*{3cm}
\includegraphics[height=5.4cm,clip]{pfd_f4h.eps}\par\end{figure}](/articles/aa/full/2003/12/aa2955/Timg48.gif)
![\begin{figure}
\par\includegraphics[height=5.4cm,clip]{fig5a.eps}\hspace*{3cm}
\...
...s}\hspace*{3cm}
\includegraphics[height=5.4cm,clip]{pfd_f5h.eps}\par\end{figure}](/articles/aa/full/2003/12/aa2955/Timg49.gif)
![\begin{figure}
\par\includegraphics[height=5.3cm,clip]{fig6a.eps}\hspace*{3cm}
\...
...c.eps}\hspace*{3cm}
\includegraphics[height=5.3cm,clip]{pfd_f6f.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg50.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pfd_f8.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg54.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pfd_f7.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg67.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pfd_f9.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pfd_f10.eps}\end{figure}](/articles/aa/full/2003/12/aa2955/Timg77.gif)