4 Discussion

   
4.1 The distribution of E₀ and ${\alpha }$

Figure 3 displays ${\alpha }$ as a function of the cutoff energy E₀for the 35 GRBs studied here. We have also plotted for comparison 9 GRBs/XRFs discussed in Kippen et al. 2001 and 12 GRBs described in Amati et al. (2002). This figure shows a good agreement between the values measured by BeppoSAX and FREGATE. We note two features which we will discuss more extensively in the next sections: most values of ${\alpha }$ are compatible with the predictions of the synchrotron shock model and there is a tail of GRBs with ${E_{\rm0}}$ extending well below 100 keV.

Figure 3: Spectral parameters of 31 GRBs detected by FREGATE (dark symbols). As in the following plots group A GRBs (see text) are shown with dark triangles, group B GRBs with dark squares and the two short/hard GRBs with dark circles. A typical error bar (on ${\alpha }$ and E0) is also shown. Four GRBs with ${E_{\rm0}}$ above the FREGATE energy range upper limit are not shown in this plot. For comparison we also display 9 GRBs/XRFs discussed by Kippen et al. (2001) (empty squares) and 12 GRBs discussed in Amati et al. (2002) (crosses). The dotted horizontal lines delimit the range of ${\alpha }$ predicted by the synchrotron shock model (Lloyd & Petrosian 2000).

   
4.1.1 The distribution of ${\alpha }$

Table 1 and Fig. 4 show that, with the exception of GRB 010213 ( $\alpha = -2.14$, but see discussion below), and GRB 020214 ( $\alpha = -.256$), the GRBs in our sample have ${\alpha }$ in the range -3/2 to -2/3, compatible with the values expected from radiation produced by synchrotron emission from shock accelerated electrons (Katz 1994; Cohen et al. 1997; Lloyd & Petrosian 2000).

GRB 010213 has the softest spectrum of our sample; its steep spectral index suggests a GRB having a very low ${E_{\rm p}}$, in any case below 20 keV. We consider that the spectral index which is measured by FREGATE in this case is probably NOT ${\alpha }$, but rather $\beta$. In fact a joint fit of the WXM and FREGATE data gives $\alpha = -1.37$, $\beta = -2.14$ and ${E_{\rm0}}$ = 4 keV ( ${E_{\rm p}}$ = 2.5 keV) for this burst (Kawai et al. 2003; Sakamoto et al. 2003).

GRB 020214 has a very hard spectrum, which is definitely not compatible with synchrotron radiation in its simple form (Lloyd 2002). We fit the spectrum of this GRB with the Band function, in order to check how the fit by a power law with a cutoff affected the value of ${\alpha }$. Because this GRB has many high energy photons, we were able to determine the 4 parameters of the Band function. We find $\alpha = -0.14$, ${E_{\rm0}}$ = 140 keV and $\beta = -2.11$ (with the errors [-0.42; +0.12], [104; 213], [-10; -1.75], respectively). The fit with the Band model tends to increase the value of ${\alpha }$, and therefore the difference with the canonical synchrotron values. We should keep in mind however that this GRB arrived on the detectors with a large off axis angle and that its spectral parameters can change quickly if we assume a slightly different angle of incidence (e.g. if we consider an angle of 68$^\circ$, the 90% error bar on ${\alpha }$ is [-0.72; 0], marginally consistent with the predictions of the synchrotron shock model).

Figure 4: Low energy spectral indices for 35 GRBs detected by FREGATE. The horizontal lines show the error bars on ${\alpha }$ for each of the 35 GRBs discussed in the paper. GRBs of group A (see text) have a positive ordinate. The two short/hard GRBs are indicated with dotted lines. The two vertical lines indicate the range of ${\alpha }$ expected for synchrotron radiation models (e.g. Lloyd & Petrosian 2000).

   
4.1.2 The distribution of ${E_{\rm p}}$

In this section we again exclude the two short/hard GRBs. GRBs of group A have ${E_{\rm p}}$ which vary from 27 keV to 358 keV, with 2 events having ${E_{\rm p}}$ below 50 keV.

GRBs of group B can essentially be divided into 2 subgroups: a few hard bursts which have ${E_{\rm p}}$ above the upper energy limit of FREGATE (GRB 010612, GRB 010923, GRB 011216, GRB 021004, GRB 021014) and soft bursts with ${E_{\rm p}}$ in the range 20-60 keV (GRB 010213, GRB 010225, GRB 010326B, GRB 011019, GRB 011130, GRB 011212, GRB 020201, and GRB 020317). One event (GRB 021112) has ${E_{\rm p}}$ well within the FREGATE energy range but is so faint (two times fainter than the faintest event of group A) that it can adequately be fit by a simple power law.

Overall we thus have nine GRBs with ${E_{\rm p}}$ lower than 50 keV in a sample of 33 events (we define here soft GRBs as GRBs with ${E_{\rm p}}$ $\leq$ 50 keV, this is an arbitrary boundary but our conclusions do not depend on the choice of this number).

The low ${E_{\rm p}}$ values for GRBs of group B could be questioned however because the break energies of these bursts are not well constrained. We mentioned in Sect. 3.2 that these GRBs are fainter events with less counts than the GRBs of group A. We discuss below whether this lack of statistics can bias their spectral parameters. To this aim, we decreased the intensity of GRBs in the group A by a factor 6.5 to construct a new set, A', with the same number of photons as group B GRBs, and computed the spectral parameters of this new set. We characterize the spectral hardness of events in groups A, A' and B by two parameters: an average softness ratio $S_x / S_{\gamma}$ and the fraction r of events with ${E_{\rm p}}$ lower than 50 keV (even if ${E_{\rm0}}$ is not well constrained for samples A' and B). We find that log( $S_x / S_{\gamma}$) = -0.67 $\pm$ 0.08, -0.58 $\pm$ 0.11, and -0.28 $\pm$ 0.09 and r = 2/19, 2/19 and 7/14 for GRBs of group A, A' and B respectively. These numbers show that the spectral softness of GRBs in group B is not an artifact of their smaller number of photons. We are thus led to the conclusion that group B contains many intrinsically soft GRBs. These soft GRBs have few photons above 50 keV, and for them the effective energy range of FREGATE is significantly reduced explaining why their energy spectra can be fit with a single power law.

This analysis also shows that the ratio $S_x / S_{\gamma}$ is a robust estimator of the softness of FREGATE GRBs, and in the following we define soft GRBs as having ${E_{\rm p}}$ $\leq$ 50 keV or equivalently $S_x / S_{\gamma}$ greater than 0.60.

   
4.1.3 X-ray rich GRBs

The evidence for GRBs with low values of ${E_{\rm p}}$ ( ${E_{\rm p}}$ $\le$ 50 keV) has been accumulating over recent years. In 1998, Strohmayer et al. (1998) studied the X-ray to $\gamma$-ray spectra of 22 GRBs (they performed joint fits of the data recorded by a proportional counter and a scintillator spanning energies from 2 to 400 keV). They found 7 GRBs with ${E_{\rm p}}$ lower than 10 keV and 5 more with ${E_{\rm p}}$ lower than 50 keV, providing the first evidence for a population of soft GRBs. In the 1990's several authors studied the distribution of ${E_{\rm p}}$ for BATSE GRBs (e.g. Mallozzi et al. 1995; Brainerd et al. 2001). They reached the conclusion that ${E_{\rm p}}$ peaks around 200 keV with few GRBs having ${E_{\rm p}}$ below 50 keV. Recently Heise et al. (2001) discovered short transients in the Wide Field Cameras of BeppoSAX, which had little or no emission in the GRBM, at energies above 40 keV. These events were called X-Ray Flashes (XRFs). Kippen et al. (2001) found 9 of these events in the untriggered BATSE data and performed a joint fit of the WFC+BATSE data in order to derive ${E_{\rm p}}$ for these XRFs. They find values ranging from 4 to 90 keV, much lower than the average for BATSE triggered GRBs.

Based on the criterion ${E_{\rm p}}$ $\leq$ 50 keV, we find that our sample contains 9 soft bursts from a total of 33 long GRBs. While their ${E_{\rm p}}$ are not well constrained, we consider that these 9 events certainly have ${E_{\rm p}}$ lower than 50 keV. This percentage is comparable with 12 GRBs out of 22 with ${E_{\rm p}}$ $\le$ 50 keV in the GINGA sample (Strohmayer et al. 1998) and with 17 out of 66 GRBs in the BeppoSAX/WFC sample (Heise et al. 2001). Thus, following the lead of GINGA and BeppoSAX, HETE-2 confirms the existence of soft GRBs (with ${E_{\rm p}}$ lower than 50 keV). The connection of these soft GRBs with the population of "classical'' GRBs with ${E_{\rm p}}$ of a few hundred keV is discussed in the next section.

   
4.2 X-ray rich GRBs and the hardness-intensity correlation

Since FREGATE provides, for the first time, continuous coverage from 7 to 400 keV with a single instrument, it is ideally suited to study the question of whether events observed at low energies have the same properties as the classical GRBs observed at higher energies. In a first attempt to understand the possible connection between soft GRBs and classical GRBs, we use the fluence/fluence diagram plotted in Fig. 5. It is clear from this figure that there is no gap between the classical GRBs and the soft GRBs. Despite the small number of events, Fig. 5 suggests a continuous evolution of GRB hardness with intensity. This is the well known hardness-intensity correlation (hereafter HIC), but FREGATE shows that this correlation extends over 3 orders of magnitude in fluence.

In addition to FREGATE GRBs, Fig. 5 also displays two stars indicating the position of the two most X-ray rich GRBs detected by the GRBM on BeppoSAX: GRB981226 on the left (Frontera et al. 2000b) and GRB990704 (Feroci et al. 2001). Frontera et al. 2000b say that "GRB981226 has the weakest gamma-ray peak flux detected with the BeppoSAX GRBM''. Figure 5 shows that there is room for faint X-ray rich events which are too faint for the GRBM and could only be seen by the WFC. This confirms the results of Kippen et al. (2001) and clarifies the link between the X-ray rich GRBs detected by the GRBM+WFC on BeppoSAX and the XRFs detected only by the WFC.

Another way to display the hardness-intensity correlation is given in Fig. 6 which shows the inverse of the hardness (defined as the ratio of the fluence in the range 30-400 keV to the fluence in the range 7-30 keV) as a function of the total fluence (in the range 7-400 keV).

Figure 5: Fluence in the energy range 7-30 keV as a function of the fluence in the range 30-400 keV. Dark triangles show group A GRBs (see text) and empty triangles group B bursts. The solid line indicates events of constant hardness, the spectral hardness is higher below the line. The two stars indicate the position of the two most X-ray rich GRBs detected with the GRBM on BeppoSAX (see text).

Figure 6: X-ray richness vs the total fluence. This plot shows the hardness-intensity correlation observed by FREGATE. The four lines indicate how GRB 020813, GRB 010921, GRB 020124, and GRB 021004 (from right to left) would evolve on this diagram if their redshifts were increased from the measured value (z = 1.25, 0.45, 3.2, and 2.31 respectively) to z= 10. For increasing redshifts, these GRBs move towards the upper left corner of the figure (their fluence decreases and their X-ray richness increases). Redshifts 1 and 5 are marked with crosses and redshifts 2 and 10 with empty diamonds.

In order to give a more quantitative statement on the significance of this correlation we computed the average hardness ratio for the brightest 16 GRBs and the faintest 16 GRBs in our sample (excluding the two short/hard GRBs). Taking into account only the statistical errors (which are dominant) we find log( $S_x / S_{\gamma}$) = -0.79 $\pm$ 0.07 for the bright GRBs and log( $S_x / S_{\gamma}$) = -0.25 $\pm$ 0.07 for the faint GRBs. This difference is significant at the 5.5 sigma level, and it confirms the findings of other instruments (Atteia et al. 1994; Mallozzi et al. 1995; Dezalay et al. 1997; Atteia 2000). A linear fit of the correlation between the soft fluence (7-30 keV) and the hard fluence (30-400 keV) gives the following relation:

$$\begin{eqnarray*}S_x = 3.2^{+2.7}_{-1.5} ~10^{-3} \times S_{\gamma} ^{0.643 \pm 0.046}. \end{eqnarray*}$$

This fit should not however be taken too literally because the apparent deficit of faint hard GRBs could be a selection effect caused by the small number of photons of these bursts. The lack of bright X-ray rich GRBs is real.

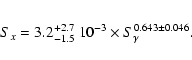
In the past the origin of the hardness-intensity correlation in GRBs has been attributed to cosmological effects or to an intrinsic hardness-luminosity correlation. We now discuss these two interpretations using the FREGATE data.

Figure 6 plots the evolution of four GRBs with known redshift (GRB 010921 Ricker et al. 2002; GRB 020124 Hjorth et al. 2003; GRB 020813 Price et al. 2002; Fiore et al. 2002; and GRB 021004 Chornok & Filippenko 2002; Savaglio et al. 2002; Castro-Tirado et al. 2002b). with the redshift (up to z=10) on a fluence/hardness diagram. The spectra of these 4 GRBs were fit with a Band function having the same alpha and ${E_{\rm0}}$ as the cutoff power law fit and $\beta = -2.3$. For this study we used a Band function because it was not appropriate to neglect the high energy spectral index which plays an important role for GRBs at high redshift. We chose $\beta = -2.3$ because it is the average value found by Preece et al. (2000). For these computations we asssumed a flat universe with $\Omega_0$ = 0.7, $\Omega_\Lambda$ = 0.3 and H₀ = 65 km s^-1 Mpc^-1.

Figure 6 shows that cosmological effects could in principle explain the observed correlation. In this case, however, we would also expect a significant time dilation of the soft GRBs. Figure 7 plots the duration T₉₀ as a function of the total fluence. It shows that there is no significant time dilation of the faint GRBs. We note here that because the widths of the peaks in the time histories of GRBs - and the durations of GRBs - are shorter at higher energies (e.g., Fenimore et al. 1995 ), this partly (but only partly) compensates for the time dilation due to the cosmological redshift. GRB durations go approximately like E^-0.4, so that this effect shortens the observed durations of GRBs at a redshift z = 10 relative to the durations of GRBs at a redshift z = 1 by a factor of about [(1+10)/(1+1)]^0.4 = 2. Time dilation would be expected to increase the duration of the bursts by [(1+10)/(1+1)] = 5.5. Thus, overall, one expects bursts at high redshifts to be longer by a factor of only about 2.7. Still, Fig. 7 does not support such a dependence.

While it is always possible to invoke GRB evolution to produce intrinsically shorter GRBs at high redhifts, we consider that our observations do not favor the interpretation of the HIC purely in terms of cosmological effects. Finally, we note that Amati et al. (2002) find a correlation between the intrinsic (redshift corrected) ${E_{\rm p}}$ of 12 GRBs with known redshifts, and E₅₂, their isotropic-equivalent energy radiated in gamma-rays, in units of 10⁵² ergs: ${E_{\rm p}}$ = 100  E₅₂^0.52 keV. This correlation, if it extends over a sufficient range of redshifts could certainly explain the hardness-intensity correlation we observe. With this interpretation, the HIC would be the reflection of a more fundamental correlation between the radiated isotropic-equivalent energy and the spectral hardness in GRBs. Our observations suggest that this correlation could include the X-ray rich GRBs. If X-ray rich GRBs are intrinsically fainter, we should also expect them to be closer on average than bright GRBs. We discuss this issue in the next section.

Figure 7: GRB duration (T90) as a function of the total fluence. This figure shows that faint GRBs are not significantly longer than bright events.

   
4.3 The distance and nature of X-ray rich GRBs

A quick survey of the literature shows that X-ray rich GRBs have no or very faint optical afterglows. The only tentative identification of an optical afterglow is reported by Fruchter et al. (2002c) for GRB 020410: a faint source is seen with the STIS on the HST at V= 25.4 on May 8 and V= 26.9 on June 14. This identification is not certain however due to the possible confusion with a field supernova unrelated to the GRB.

X-ray rich GRBs, on the other hand, seem to have X-ray afterglows (e.g. GRB 981226, GRB 990704, GRB 011030, GRB 020410 or GRB 020427) and for some of them radio afterglows (GRB 981226, GRB 011030). Thanks to the good localization capabilities of Chandra, the host galaxies of GRB 981226, GRB 011030 and GRB 020427 have been identified (Frail et al. 1999; Fruchter et al. 2002a; Castro-Tirado et al. 2002a; Fruchter et al. 2002b), but their redshifts have not yet been measured. To summarize, we still have no measure of the distance of an X-ray rich GRB.

The nature of X-ray rich GRBs can be addressed from the theoretical or from an empirical point of view. From the theoretical point of view, we note that the model of internal shocks predicts that X-ray rich GRBs could be produced by fireballs with less efficient shocks (due to lower magnetic fields or to a lower contrast of the Lorentz factors within the ejecta) or by clean fireballs (with a low baryon load) (Zhang & Mészáros 2002; Daigne et al. 2002; Mochkovitch et al. 2003). In a clean fireball the initial Lorentz factor is higher but the internal shocks take place at larger distances from the central source where the density and the magnetic fields are smaller, leading to the emission of less energetic photons. Further theoretical studies are needed to assess whether one of these conditions can also explain the correlation found by Amati et al. (2002), the lack of bright optical afterglows and the unusual properties of the X-ray afterglows of X-ray rich GRBs (Frontera et al. 2000b; Feroci et al. 2001).

From the empirical point of view, if we combine the evidence in this paper that (a) X-ray rich GRBs are not a separate class of GRBs but represent an extension of the properties of "typical'' GRBs, and (b) the HIC correlation extends over three orders of magnitude in fluence and applies to X-ray rich GRBs with the conclusion of Frail et al. (2001) that the total energy of GRBs is roughly constant, we are led to the conclusion that the jet opening angle of X-ray rich GRBs are substantially larger than the jet opening angle of "typical'' GRBs. Additional observations are clearly required to understand the role of the progenitor and/or its environment in shaping the properties of the prompt GRB emission, particularly the peak energy.