A&A 400, 1021-1030 (2003)
DOI: 10.1051/0004-6361:20030074

Spectral analysis of 35 GRBs/XRFs observed with HETE-2/FREGATE[*]

C. Barraud1 - J.-F. Olive2 - J. P. Lestrade1,[*] - J.-L. Atteia1 - K. Hurley3 - G. Ricker4 - D. Q. Lamb5 - N. Kawai6,7 - M. Boer2 - J.-P. Dezalay2 - G. Pizzichini12 - R. Vanderspek4 - G. Crew4 - J. Doty4 - G. Monnelly4 - J. Villasenor4 - N. Butler4 - A. Levine4 - A. Yoshida7,8 - Y. Shirasaki10 - T. Sakamoto6,7,11 - T. Tamagawa7 - K. Torii7 - M. Matsuoka9 - E. E. Fenimore11 - M. Galassi11 - T. Tavenner11 - T. Q. Donaghy5 - C. Graziani5 - J. G. Jernigan3


1 - Laboratoire d'Astrophysique, Observatoire Midi-Pyrénées, 31400 Toulouse, France
2 - C.E.S.R., Observatoire Midi-Pyrénées, 31028 Toulouse Cedex, France
3 - UC Berkeley Space Sciences Laboratory, Berkeley CA 94720-7450, USA
4 - Center for Space Reserach, MIT, Cambridge, MA , USA
5 - Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
6 - Department of Physics, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan
7 - RIKEN (Institute of Physical and Chemical Research), 2-1 Hirosawa, Wako, Saitama 351-0198, Japan
8 - Department of Physics, Aoyama Gakuin University, Chitosedai 6-16-1 Setagaya-ku, Tokyo 157-8572, Japan
9 - Tsukuba Space Center, National Space Development Agency of Japan, Tsukuba, Ibaraki, 305-8505, Japan
10 - National Astronomical Observatory, Osawa 2-21-1, Mitaka, Tokyo 181-8588 Japan
11 - Los Alamos National Laboratory, PO Box 1663, Los Alamos, NM, 87545, USA
12 - Consiglio Nazionale delle Ricerche (IASF), via Piero Gobetti, 101-40129 Bologna, Italy

Received 21 June 2002 / Accepted 13 January 2003

Abstract
We present a spectral analysis of 35 GRBs detected with the HETE-2 gamma-ray detectors (the FREGATE instrument) in the energy range 7-400 keV. The GRB sample analyzed is made of GRBs localized with the Wide Field X-ray Monitor onboard HETE-2 or with the GRB Interplanetary Network. We derive the spectral parameters of the time-integrated spectra, and present the distribution of the low-energy photon index, alpha, and of the peak energy, ${E_{\rm p}}$. We then discuss the existence and nature of the recently discovered X-Ray Flashes and their relationship with classical GRBs.

Key words: gamma-rays: bursts


   
1 Introduction

The radiation mechanisms at work during the prompt phase of GRBs remain poorly understood, despite the observation of hundreds of GRB spectra and extensive theoretical work (e.g. Cohen et al. 1997; Daigne & Mochkovitch 1998; Lloyd & Petrosian 2000; Mészáros & Rees 2000; Panaitescu & Meszaros 2000; Piran 2000; Zhang & Mészáros 2002). One of the reasons for this situation is the lack of broad-band coverage of this brief phase of GRB emission (contrary to the afterglows which can be observed from hours to days after the burst). Recently, however, several instruments have extended the spectral coverage of the prompt GRB emission to the X-ray range, and to optical wavelengths in the case of GRB 990123 (Akerlof et al. 1999), raising hopes for a better understanding of this crucial phase of GRB emission.

We present here the broad-band spectra of 35 GRBs observed by HETE-2/FREGATE in the energy range 7-400 keV. We analyse the time-integrated spectra in order to derive the distribution of their peak energies and of their low-energy spectral indices. We also discuss the existence of a possible new class of soft bursts, called X-ray flashes.

HETE-2's unique instrument suite provides broadband energy coverage of the prompt emission extending into the X-ray range. The three instruments include a gamma-ray spectrometer sensitive in the range 7-400 keV (FREGATE, Atteia et al. 2002), a Wide Field X-ray Monitor sensitive in the range 2-25 keV (WXM, Kawai et al. 2002) and a CCD based Soft X-ray Camera working in the range 1-14 keV (SXC, Villasenor et al. 2002). In this paper we restrict our analysis to FREGATE data because this instrument, with its larger field of view, detects about two times more GRBs than WXM (the Half Width at Zero Maximum is 70$^\circ$ for FREGATE compared to 40$^\circ$ for the WXM) and because in most cases FREGATE data are sufficient to determine the GRB spectral parameters. We finally note that FREGATE offers for the first time a continuous coverage from 7 keV to 400 hundred keV with a single instrument. This eliminates any possible problems caused by normalizing the responses of different instruments to one another. This characteristic of FREGATE appears essential when we try to understand whether events seen at low energies are of the same nature as classical GRBs seen at higher energies.

This work follows many previous studies which contributed to our understanding of the GRB spectral properties at gamma-ray energies (Band et al. 1993; Preece et al. 1998) and in hard X-rays (Strohmayer et al. 1998; Frontera et al. 2000a; Kippen et al. 2001). This paper is the first of a series devoted to the spectral analysis of the GRBs detected with HETE-2. Forthcoming papers will discuss the spectral evolution of bright GRBs and the broad-band spectral distribution from 2 keV to 400 keV by combining the data from FREGATE and the WXM for the events which are detected by both instruments.

   
2 Spectral calibration

FREGATE has been designed to provide reliable spectral data on the gamma-ray bursts and a detailed description of the instrument can be found in Atteia et al. (2002). The detectors use cleaved NaI crystals encapsulated in a beryllium housing offering a good sensitivity at low energies (the transmission of the window is greater than 65% at 6 keV). A graded shield made of lead, tantalum, tin, copper and aluminum reduces the background and eliminates many GRBs arriving at angles more than 70$^\circ$ off-axis. Two on-board sources of baryum 133 provide a continuous monitoring of the gain of the 4 detectors. The gain adjustment is done on the ground; there is no automatic gain control. The whole instrument has been carefully simulated with GEANT software from the CERN (see http://wwwinfo.cern.ch/asd/geant/index.html) and the output of the simulation program has been checked and validated against extensive calibrations done with radioactive sources (9 sources, 11 energies at 5 angles). Finally the in-flight spectral response has been checked with the Crab nebula as described in Olive et al. (2002a) and briefly explained below.

As a consequence of the antisolar orientation of HETE-2, the Earth occults the sources in the field of view of FREGATE once per orbit. We used this feature, to reconstruct the spectrum of the Crab nebula from the size of the Crab occultation steps measured at various energies. We then used the standard spectral analysis of FREGATE to derive the spectral parameters of the Crab nebula, assuming a power law spectrum. Olive et al. (2002a) find a spectral index of $2.16 \pm 0.03$ in the range 6-200 keV, and a normalization of 7.2 $\times$ 10-3 ph cm-2 s-1 keV-1 at 30 keV, fully consistent with values measured by other instruments at these energies.

   
3 Spectral analysis

Figure 1 displays the angular response of FREGATE. This figure emphasizes the importance of knowing the GRB off-axis angle to perform a reliable spectral analysis. Our spectral analysis includes the following steps:

1.
Selection of the burst sample (Sect. 3.1).
2.
Construction of gain corrected spectra and addition of the spectra from the 4 detectors.
3.
Determination of the maximum energy ${E_{{\rm max}}}$ at which there is still some signal from the burst (Sect. 3.2).
4.
Determination of the arrival angle of the burst to within 5 degrees.
5.
Spectral deconvolution with XSPEC and determination of the burst fluence and spectral parameters.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2820_effarea_ang.eps}\end{figure} Figure 1: FREGATE effective area as a function of the burst angle at 50 keV (solid line) and 300 keV (dotted line).
Open with DEXTER

   
3.1 The GRB sample

From October 2000 to mid November 2002, FREGATE detected 88 confirmed GRBs of which 61 were within the 70$^\circ$ field of view (FOV) of the detector[*]. However not all these 61 bursts were localized and since we cannot perform accurate spectral studies of GRBs with unknown off-axis angles, we concentrate here on the analysis of the spectra of 35 GRBs which have been localized with the WXM or the Interplanetary Network (IPN). The list of these 35 GRBs is given in Table 1 with their off-axis angle and their duration T90. Thirty three GRBs are within 60$^\circ$ of the detector axis. Figure 1 shows that for these bursts we have an efficiency $\geq$15% at low (E = 50 keV) energies and the instrument response remains constant for small variations in angle. Beyond 60$^\circ$, the efficiency of the detector is very low at low energies and its energy response changes quickly for small changes in angle. As a consequence, the parameters for GRB 020214 and GRB 020418 (at 66$^\circ$ and 64$^\circ$respectively) must be taken with caution.

Our sample includes two short/hard GRBs: GRB 020113 and GRB 020531 (Lamb et al. 2003). In fact only 2 out of the 61 confirmed GRBs within the FOV of HETE-2/FREGATE are short/hard GRBs (less than 5%), whereas about 20% of the BATSE bursts were short, hard GRBs (Paciesas et al. 1999). This is most likely due to two factors:

(1) BATSE was less sensitive to X-ray-rich GRBs (all of which are long GRBs). However, a substantial percentage of the GRBs in the FREGATE sample are X-ray-rich (for example, 9 of the 35 GRBs in Table 1 have $S_x / S_{\gamma}$ $\ge$ 0.6; i.e., nearly 30% of our sample are X-ray-rich). Therefore the number of GRBs in the FREGATE sample which should be compared to the BATSE sample is significantly smaller than 61.

(2) Because short, hard GRBs are generally quite hard (by definition), it is possible that we have classified a few of them as having occurred outside the FREGATE FOV when in fact they occurred within the FREGATE FOV (see footnote 1).

Factor (1) could reduce the size of the sample of GRBs that should be compared with the BATSE result by as much as 30% (0.7 $\times$ 61 = 42). This would make the statistics to $\sim$2/42, which corresponds to $\sim$5% (with large errors). If we have mis-classified 2 or 3 short, hard GRBs as having occurred outside the FREGATE FOV when in reality they occurred within the FREGATE FOV, the fraction becomes $\sim$4/42 or $\sim$5/42, which corresponds to 11%-14% (again with large errors) and which would be closer to the percentage found by BATSE.

If we consider only those GRBs in the sample of 35 GRBs which have been localized by the IPN and therefore which form an unbiased sample with regard to factors (1) and (2) above, the fraction of short, hard GRBs in this sample is 2/13, which corresponds to 15 (+11)(-8)% (1-sigma). This result is fully consistent with the BATSE results.

Consider now the GRBs in Table 1 which have been localized by the WXM. These bursts are affected by factor (1) but not by factor (2) (by definition, if the burst has been localized by the WXM, it occurred within the FREGATE FOV). However, these bursts are also affected by a third factor:

(3) Since short, hard GRBs are quite hard (by definition), some have relatively little emission in the WXM energy band. Consequently, they may not be localized, even though they occurred within the WXM FOV (and therefore within the FREGATE FOV). GRB 020113 in Table 1 is an example of such a burst.

That factors (1) and (3) are likely important can be demonstrated by examining the GRBs in Table 1 which were localized using the WXM. There are 26 of these, of which only 1 is a short, hard GRB. The probability of this happening by chance, assuming that short, hard GRBs are 20% of all GRBs, is $2.2 \times 10^{-2}$.

   
3.2 spectral fits

GRB photon spectra can in general be fit by the Band function (Band et al. 1993); which is two smoothly connected power laws. A typical GRB photon spectrum is thus described as follows:

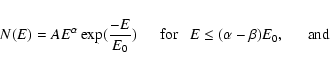
\begin{displaymath}N(E) = A E^\alpha \exp ({-E \over E_0}) ~~~~~~{\rm for}~~~ E \le (\alpha - \beta) E_0 , ~~~~~~{\rm and}~~~ \end{displaymath}


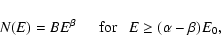\begin{displaymath}% N(E) = B E^\beta ~~~~~~{\rm for}~~~ E \geq (\alpha - \beta) E_0 , \end{displaymath} (1)


\begin{displaymath}{\rm where}~~~ B = A [(\alpha - \beta) \times E_0]^{(\alpha - \beta)} \times \exp (\beta - \alpha). \end{displaymath}

Here ${\alpha }$ is the photon index of the low energy power law, $\beta$is the photon index of the high energy power law, and E0 is the break energy. With this parametrization, the peak energy of the $\nu f_{\nu}$ spectrum is $E_{\rm p} = E_0 \times (2+\alpha)$. ${E_{\rm p}}$ is well defined for $\alpha \ge -2$ and $\beta < -2$.

The first step of our processing was the definition of the spectral range appropriate for the fitting procedure. On the low energy side the limit is set to 7 keV for instrumental reasons (the electronics threshold is not well modeled below 7 keV). On the high energy side, we computed the energy ${E_{{\rm max}}}$ such that the signal in the range [ ${E_{{\rm max}}}$ - 400] keV was only two sigmas above background. The spectral fit is done in the range [7 - ${E_{{\rm max}}}$] keV, ${E_{{\rm max}}}$ is given in Table 1.

Most of the time this energy range is not broad enough to allow the unambiguous determination of the 4 parameters of the Band function. Consequently, we decided to fit the observed spectra using only the low energy part of the Band function and the spectral break. The definition of ${E_{\rm p}}$ is not affected by the choice of this model. In the following, this model is called the cutoff power law model, and it is defined as

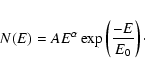
\begin{eqnarray*}N(E) = A E^\alpha \exp \left({-E \over E_0}\right)\cdot \end{eqnarray*}


The spectral deconvolution is done with XSPEC, using gain corrected spectra (allowing us to co-add the 4 detectors) and response matrices constructed from a detailed Monte Carlo simulation of the instrument. We include systematic errors at a level of 2% in the fitting procedure. This level of systematic errors is required to correctly fit a very bright burst from SGR 1900+14 with a smooth spectral shape (Olive et al. 2002b).

The parameters resulting from the fit and their 90% errors are given in Table 1. The cutoff power law model provides a good fit to our data as seen by reduced $\chi ^2$ values close to unity (see however Sect. 3.3 below). Examples of spectral fits are given in Fig. 2.

It is noted that the cutoff energy E0 is well constrained for only 19 GRBs (out of 35). These events are identified in Table 1 by their names in boldface. In the following we call these GRBs group A, and group B the 16 GRBs whose ${E_{\rm0}}$ is not constrained. Group B bursts are either faint bursts with not enough counts at high energy to constrain ${E_{\rm0}}$  or GRBs which have their ${E_{\rm0}}$ outside the energy range of FREGATE. It is tempting to fit the spectra of group B bursts with a simple power law (since we have no constraint on the cutoff energy) which would give stronger constraints on ${\alpha }$. It is not a good idea, however, to use a different model for one part of the sample because this introduces a bias in the measured values of the spectral parameters (see also Band et al. 1993). We thus keep the cutoff power law model, even when we have no constraint on ${E_{\rm0}}$, and indicate in Table 1 the best fit parameters and their errors for this model. We now discuss the distribution of the spectral parameters obtained with this procedure.


  \begin{figure} \par\includegraphics[width=8cm,clip]{2820_GRB010612papier.ps}\includegraphics[width=8cm,clip]{2820_GRB010613papier.ps}\end{figure} Figure 2: Spectral fits of GRB 010612 and GRB 010613 with a power law with a cut-off at 592 keV and 176 keV respectively.
Open with DEXTER

   
3.3 Peculiar bursts

We discuss here a few bursts which required special care in their spectral analysis.

3.3.1 GRB 020113 and GRB 020531

As mentioned in Sect. 3.1, GRB 020113 and GRB 020531 are Short/Hard GRBs. We provide their spectral parameters in Table 1, but we do not consider them further in the rest of the analysis.

3.3.2 GRB 001225 and GRB 020813

GRB 001225 and GRB 020813 are the two strongest GRBs detected by FREGATE. The spectra of these two bursts are adequately fit by a cutoff power law, except for a deficit of photons between 30 and 55 keV (see Appendix A available on-line at EDP Sciences), which is responsible for the high $\chi ^2$ values given in Table 1. When we exclude the region 30-55 keV for the spectral analysis we obtain a reduced $\chi ^2$of 1.24 for 96 d.o.f. for GRB 001225 and a reduced $\chi ^2$ of 1.20 for 97 d.o.f. for GRB 020813. The origin of this feature in the spectra of these two bright bursts is being investigated with a great care due to its proximity with the k-edge of iodine. The exclusion of this region doesn't change the global parameters for these two spectra.

3.3.3 GRB 021104

This burst cannot be fit with a single power law and requires a break. The break energy is too close to the low energy threshold of FREGATE to allow a reliable estimate of the low energy spectral index ${\alpha }$. We thus decided to freeze ${\alpha }$ to -1.0in the spectral fit.


   
Table 1: GRB list. This table gives the best fit parameters, the reduced $\chi ^2$ of the fit and the error bars on the spectral parameters. The names in bold indicate the events of group A (see text).
Name Time Durationa Angle Loc.b Emax ${\chi}^2/{\rm d.o.f.}^{{\rm c}}$ $- \alpha$ errors E0 errors ${E_{\rm p}}$ Sx d ${S}_{\gamma} ^{e}$ $S_x / S_{\gamma}$
  SOD s deg.   keV       keV          
001225 25759 32.3 37 I 400 1.78 /112 1.17 [1.16; 1.18] 283 [271-296] 235 190 1140 .17
010126 33162 7.7 50 I 220 1.11 /84 1.06 [0.82; 1.26] 115 [72-218] 108 7.7 29.9 .26
010213 45332 20.9 14 W 250 1.11 /89 2.14 [1.83; 2.55] 10000 [370-104] <20 1.8 2.4 .75
010225 60733 7.2 23 W 70 1.16 /42 .89 [-1.8; 2.14] 22 [5-104] 24 1.1 0.66 1.7
010326A 11701 23.0 60 I 250 .67 /89 .894 [0.66; 1.09] 260 [167-484] 287 16 160 .10
010326B 30792 3.2 17 W 120 .97 /58 1.12 [0.31; 1.71] 69 [25-104] 61 1.5 3.1 .48
010612 9194 74.1 14 W 250 .85 /89 1.22 [1.07; 1.31] 592 [274-104] 462 6.8 49 .14
010613 27235 152. 36 W 250 1.29 /89 1.40 [1.33; 1.47] 176 [139-235] 106 70 203 .34
010629 44468 15.1 28 W/I 200 .91 /81 1.17 [1.03; 1.31] 59 [48-75] 49 16 26 .62
010921 18950 24.6 45 W/I 200 1.20 /81 1.49 [1.43; 1.56] 206 [158-287] 105 38 102 .37
010923 33870 3.8 58 I 250 1.06 /89 1.74 [1.49; 2.04] 10000 [347-104] 2600 10 30 .33
010928 60826 48.3 31 W 400 1.17 /112 .623 [.561; .68] 260 [220-315] 358 11 210 .05
011019 31370 25.4 25 W 80 .76 /45 1.75 [0.04; 2.47] 87 [10-104] 22 1.7 1.7 1.0
011130 22775 83.2 26 W 70 .97 /42 1.08 [-0.5; 2.51] 32 [16-104] 29 .79 0.68 1.16
011212 14642 84.4 10 W 150 .53 /67 1.28 [-3.0; 2.24] 34 [3-104] 25 2.3 1.7 1.35
011216 10524 31.8 47 I 100 1.33 /52 1.82 [1.54; 2.11] 10000 [420-104] 1800 4.7 12.0 .39
020113 7452 1.31 34 I 400 1.15 /112 0.46 [0.05; 0.78] 239 [126-666] 368 .54 13.3 .04
020124 38475 78.6 33 W 250 .91 /89 1.10 [0.98; 1.21] 133 [101-186] 120 17 68 .25
020127 75444 9.3 22 W 200 .92 /81 1.19 [1.00; 1.36] 156 [97-330] 126 2.3 9.1 .25
020201 65828 241. 55 W 80 .95 /45 1.67 [0.71; 2.16] 99 [18-104] 33 23 28 .82
020214 67778 27.4 66 I 400 1.31 /112 .256 [.059; .439] 176 [145-219] 307 32 930 .03
020305 42925 250. 35 W 250 1.15 /89 .861 [.748; .968] 143 [113-192] 163 15 104 .14
020317 65731 3.3 23 W 150 1.08 /67 1.01 [-.78; 1.95] 44 [11-104] 44 1.2 1.7 .71
020331 59548 56.5 16 W 400 1.09 /112 .922 [.812; 1.02] 120 [97-153] 129 8.6 45 .19
020418 63789 7.54 64 I 400 .92 /112 1.10 [.78; 1.37] 240 [150-470] 216 22 139 .16
020531 1578 1.15 26 W/I 300 1.16 /97 1.10 [0.77; 1.30] 810 [200-104] 729 1.1 11.5 .10
020801 46721 336. 33 W 300 .90 /97 1.32 [1.09; 1.53] 116 [70-252] 79 66 163 .40
020812 38503 27.5 19 W 300 .98 /97 1.03 [.72; 1.31] 125 [71-316] 121 5.2 23 .23
020813 9859 90. 4 W 300 1.49 /112 1.05 [1.02; 1.07] 223 [205-238] 212 152 1020 .15
020819 53855 33.6 28 W 300 1.06 /97 1.03 [.93; 1.12] 94 [78-116] 91 16 54 .30
021004 43573 57.7 13 W 300 1.11 /97 1.64 [1.32; 1.74] 3000 [1500-104] 1080 6.4 23 .28
021014 23513 39.3 56 I 300 1.06 /97 1.16 [.77; 1.43] 504 [127-104] 423 9.2 71 .13
021016 37740 81.6 36 W/I 230 1.12 /86 .98 [.81; 1.13] 132 [92-211] 135 22 113 .19
021104 25262 19.7 31 W 60 1.18 /39 1 [-3.0; 1.29] 27 [16-51] 27 3.9 2.9 1.34
021112 12495 7.1 30 W 200 1.04 /81 1.47 [.89; 1.88] 186 [48-104] 99 .93 2.5 .37
a Duration T90 in the 7-400 keV energy range.
b This column indicates whether the burst has been localized by the WXM (W) or by the IPN (I).
c $\chi ^2$ is the reduced chi square.
d Sx is the fluence in the energy range 7-30 keV, in units of 10-7 erg cm-2.
e $S_{\gamma}$ is the fluence in the energy range 30-400 keV, in units of 10-7 erg cm-2.

   
4 Discussion

   
4.1 The distribution of E0 and ${\alpha }$

Figure 3 displays ${\alpha }$ as a function of the cutoff energy E0for the 35 GRBs studied here. We have also plotted for comparison 9 GRBs/XRFs discussed in Kippen et al. 2001 and 12 GRBs described in Amati et al. (2002). This figure shows a good agreement between the values measured by BeppoSAX and FREGATE. We note two features which we will discuss more extensively in the next sections: most values of ${\alpha }$ are compatible with the predictions of the synchrotron shock model and there is a tail of GRBs with ${E_{\rm0}}$ extending well below 100 keV.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2820_alpha_Eo.ps}\end{figure} Figure 3: Spectral parameters of 31 GRBs detected by FREGATE (dark symbols). As in the following plots group A GRBs (see text) are shown with dark triangles, group B GRBs with dark squares and the two short/hard GRBs with dark circles. A typical error bar (on ${\alpha }$ and E0) is also shown. Four GRBs with ${E_{\rm0}}$ above the FREGATE energy range upper limit are not shown in this plot. For comparison we also display 9 GRBs/XRFs discussed by Kippen et al. (2001) (empty squares) and 12 GRBs discussed in Amati et al. (2002) (crosses). The dotted horizontal lines delimit the range of ${\alpha }$ predicted by the synchrotron shock model (Lloyd & Petrosian 2000).
Open with DEXTER

   
4.1.1 The distribution of ${\alpha }$

Table 1 and Fig. 4 show that, with the exception of GRB 010213 ( $\alpha = -2.14$, but see discussion below), and GRB 020214 ( $\alpha = -.256$), the GRBs in our sample have ${\alpha }$ in the range -3/2 to -2/3, compatible with the values expected from radiation produced by synchrotron emission from shock accelerated electrons (Katz 1994; Cohen et al. 1997; Lloyd & Petrosian 2000).

GRB 010213 has the softest spectrum of our sample; its steep spectral index suggests a GRB having a very low ${E_{\rm p}}$, in any case below 20 keV. We consider that the spectral index which is measured by FREGATE in this case is probably NOT ${\alpha }$, but rather $\beta$. In fact a joint fit of the WXM and FREGATE data gives $\alpha = -1.37$, $\beta = -2.14$ and ${E_{\rm0}}$ = 4 keV ( ${E_{\rm p}}$ = 2.5 keV) for this burst (Kawai et al. 2003; Sakamoto et al. 2003).

GRB 020214 has a very hard spectrum, which is definitely not compatible with synchrotron radiation in its simple form (Lloyd 2002). We fit the spectrum of this GRB with the Band function, in order to check how the fit by a power law with a cutoff affected the value of ${\alpha }$. Because this GRB has many high energy photons, we were able to determine the 4 parameters of the Band function. We find $\alpha = -0.14 $, ${E_{\rm0}}$ = 140 keV and $\beta = -2.11 $ (with the errors [-0.42; +0.12], [104; 213], [-10; -1.75], respectively). The fit with the Band model tends to increase the value of ${\alpha }$, and therefore the difference with the canonical synchrotron values. We should keep in mind however that this GRB arrived on the detectors with a large off axis angle and that its spectral parameters can change quickly if we assume a slightly different angle of incidence (e.g. if we consider an angle of 68$^\circ$, the 90% error bar on ${\alpha }$ is [-0.72; 0], marginally consistent with the predictions of the synchrotron shock model).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2820_alpha.ps}\end{figure} Figure 4: Low energy spectral indices for 35 GRBs detected by FREGATE. The horizontal lines show the error bars on ${\alpha }$ for each of the 35 GRBs discussed in the paper. GRBs of group A (see text) have a positive ordinate. The two short/hard GRBs are indicated with dotted lines. The two vertical lines indicate the range of ${\alpha }$ expected for synchrotron radiation models (e.g. Lloyd & Petrosian 2000).
Open with DEXTER

   
4.1.2 The distribution of ${E_{\rm p}}$

In this section we again exclude the two short/hard GRBs. GRBs of group A have ${E_{\rm p}}$ which vary from 27 keV to 358 keV, with 2 events having ${E_{\rm p}}$ below 50 keV.

GRBs of group B can essentially be divided into 2 subgroups: a few hard bursts which have ${E_{\rm p}}$ above the upper energy limit of FREGATE (GRB 010612, GRB 010923, GRB 011216, GRB 021004, GRB 021014) and soft bursts with ${E_{\rm p}}$ in the range 20-60 keV (GRB 010213, GRB 010225, GRB 010326B, GRB 011019, GRB 011130, GRB 011212, GRB 020201, and GRB 020317). One event (GRB 021112) has ${E_{\rm p}}$ well within the FREGATE energy range but is so faint (two times fainter than the faintest event of group A) that it can adequately be fit by a simple power law.

Overall we thus have nine GRBs with ${E_{\rm p}}$ lower than 50 keV in a sample of 33 events (we define here soft GRBs as GRBs with ${E_{\rm p}}$ $\leq$ 50 keV, this is an arbitrary boundary but our conclusions do not depend on the choice of this number).

The low ${E_{\rm p}}$ values for GRBs of group B could be questioned however because the break energies of these bursts are not well constrained. We mentioned in Sect. 3.2 that these GRBs are fainter events with less counts than the GRBs of group A. We discuss below whether this lack of statistics can bias their spectral parameters. To this aim, we decreased the intensity of GRBs in the group A by a factor 6.5 to construct a new set, A', with the same number of photons as group B GRBs, and computed the spectral parameters of this new set. We characterize the spectral hardness of events in groups A, A' and B by two parameters: an average softness ratio $S_x / S_{\gamma}$ and the fraction r of events with ${E_{\rm p}}$ lower than 50 keV (even if ${E_{\rm0}}$ is not well constrained for samples A' and B). We find that log( $S_x / S_{\gamma}$) = -0.67 $\pm$ 0.08, -0.58 $\pm$ 0.11, and -0.28 $\pm$ 0.09 and r = 2/19, 2/19 and 7/14 for GRBs of group A, A' and B respectively. These numbers show that the spectral softness of GRBs in group B is not an artifact of their smaller number of photons. We are thus led to the conclusion that group B contains many intrinsically soft GRBs. These soft GRBs have few photons above 50 keV, and for them the effective energy range of FREGATE is significantly reduced explaining why their energy spectra can be fit with a single power law.

This analysis also shows that the ratio $S_x / S_{\gamma}$ is a robust estimator of the softness of FREGATE GRBs, and in the following we define soft GRBs as having ${E_{\rm p}}$ $\leq$ 50 keV or equivalently $S_x / S_{\gamma}$ greater than 0.60.

   
4.1.3 X-ray rich GRBs

The evidence for GRBs with low values of ${E_{\rm p}}$ ( ${E_{\rm p}}$ $\le$ 50 keV) has been accumulating over recent years. In 1998, Strohmayer et al. (1998) studied the X-ray to $\gamma$-ray spectra of 22 GRBs (they performed joint fits of the data recorded by a proportional counter and a scintillator spanning energies from 2 to 400 keV). They found 7 GRBs with ${E_{\rm p}}$ lower than 10 keV and 5 more with ${E_{\rm p}}$ lower than 50 keV, providing the first evidence for a population of soft GRBs. In the 1990's several authors studied the distribution of ${E_{\rm p}}$ for BATSE GRBs (e.g. Mallozzi et al. 1995; Brainerd et al. 2001). They reached the conclusion that ${E_{\rm p}}$ peaks around 200 keV with few GRBs having ${E_{\rm p}}$ below 50 keV. Recently Heise et al. (2001) discovered short transients in the Wide Field Cameras of BeppoSAX, which had little or no emission in the GRBM, at energies above 40 keV. These events were called X-Ray Flashes (XRFs). Kippen et al. (2001) found 9 of these events in the untriggered BATSE data and performed a joint fit of the WFC+BATSE data in order to derive ${E_{\rm p}}$ for these XRFs. They find values ranging from 4 to 90 keV, much lower than the average for BATSE triggered GRBs.

Based on the criterion ${E_{\rm p}}$ $\leq$ 50 keV, we find that our sample contains 9 soft bursts from a total of 33 long GRBs. While their ${E_{\rm p}}$ are not well constrained, we consider that these 9 events certainly have ${E_{\rm p}}$ lower than 50 keV. This percentage is comparable with 12 GRBs out of 22 with ${E_{\rm p}}$ $\le$ 50 keV in the GINGA sample (Strohmayer et al. 1998) and with 17 out of 66 GRBs in the BeppoSAX/WFC sample (Heise et al. 2001). Thus, following the lead of GINGA and BeppoSAX, HETE-2 confirms the existence of soft GRBs (with ${E_{\rm p}}$ lower than 50 keV). The connection of these soft GRBs with the population of "classical'' GRBs with ${E_{\rm p}}$ of a few hundred keV is discussed in the next section.

   
4.2 X-ray rich GRBs and the hardness-intensity correlation

Since FREGATE provides, for the first time, continuous coverage from 7 to 400 keV with a single instrument, it is ideally suited to study the question of whether events observed at low energies have the same properties as the classical GRBs observed at higher energies. In a first attempt to understand the possible connection between soft GRBs and classical GRBs, we use the fluence/fluence diagram plotted in Fig. 5. It is clear from this figure that there is no gap between the classical GRBs and the soft GRBs. Despite the small number of events, Fig. 5 suggests a continuous evolution of GRB hardness with intensity. This is the well known hardness-intensity correlation (hereafter HIC), but FREGATE shows that this correlation extends over 3 orders of magnitude in fluence.

In addition to FREGATE GRBs, Fig. 5 also displays two stars indicating the position of the two most X-ray rich GRBs detected by the GRBM on BeppoSAX: GRB981226 on the left (Frontera et al. 2000b) and GRB990704 (Feroci et al. 2001). Frontera et al. 2000b say that "GRB981226 has the weakest gamma-ray peak flux detected with the BeppoSAX GRBM''. Figure 5 shows that there is room for faint X-ray rich events which are too faint for the GRBM and could only be seen by the WFC. This confirms the results of Kippen et al. (2001) and clarifies the link between the X-ray rich GRBs detected by the GRBM+WFC on BeppoSAX and the XRFs detected only by the WFC.

Another way to display the hardness-intensity correlation is given in Fig. 6 which shows the inverse of the hardness (defined as the ratio of the fluence in the range 30-400 keV to the fluence in the range 7-30 keV) as a function of the total fluence (in the range 7-400 keV).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2820_fluence30400_630.ps}\end{figure} Figure 5: Fluence in the energy range 7-30 keV as a function of the fluence in the range 30-400 keV. Dark triangles show group A GRBs (see text) and empty triangles group B bursts. The solid line indicates events of constant hardness, the spectral hardness is higher below the line. The two stars indicate the position of the two most X-ray rich GRBs detected with the GRBM on BeppoSAX (see text).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2820_durete_l.ps}\end{figure} Figure 6: X-ray richness vs the total fluence. This plot shows the hardness-intensity correlation observed by FREGATE. The four lines indicate how GRB 020813, GRB 010921, GRB 020124, and GRB 021004 (from right to left) would evolve on this diagram if their redshifts were increased from the measured value (z = 1.25, 0.45, 3.2, and 2.31 respectively) to z= 10. For increasing redshifts, these GRBs move towards the upper left corner of the figure (their fluence decreases and their X-ray richness increases). Redshifts 1 and 5 are marked with crosses and redshifts 2 and 10 with empty diamonds.
Open with DEXTER

In order to give a more quantitative statement on the significance of this correlation we computed the average hardness ratio for the brightest 16 GRBs and the faintest 16 GRBs in our sample (excluding the two short/hard GRBs). Taking into account only the statistical errors (which are dominant) we find log( $S_x / S_{\gamma}$) = -0.79 $\pm$ 0.07 for the bright GRBs and log( $S_x / S_{\gamma}$) = -0.25 $\pm$ 0.07 for the faint GRBs. This difference is significant at the 5.5 sigma level, and it confirms the findings of other instruments (Atteia et al. 1994; Mallozzi et al. 1995; Dezalay et al. 1997; Atteia 2000). A linear fit of the correlation between the soft fluence (7-30 keV) and the hard fluence (30-400 keV) gives the following relation:

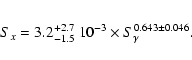
\begin{eqnarray*}S_x = 3.2^{+2.7}_{-1.5} ~10^{-3} \times S_{\gamma} ^{0.643 \pm 0.046}. \end{eqnarray*}


This fit should not however be taken too literally because the apparent deficit of faint hard GRBs could be a selection effect caused by the small number of photons of these bursts. The lack of bright X-ray rich GRBs is real.

In the past the origin of the hardness-intensity correlation in GRBs has been attributed to cosmological effects or to an intrinsic hardness-luminosity correlation. We now discuss these two interpretations using the FREGATE data.

Figure 6 plots the evolution of four GRBs with known redshift (GRB 010921 Ricker et al. 2002; GRB 020124 Hjorth et al. 2003; GRB 020813 Price et al. 2002; Fiore et al. 2002; and GRB 021004 Chornok & Filippenko 2002; Savaglio et al. 2002; Castro-Tirado et al. 2002b). with the redshift (up to z=10) on a fluence/hardness diagram. The spectra of these 4 GRBs were fit with a Band function having the same alpha and ${E_{\rm0}}$ as the cutoff power law fit and $\beta = -2.3$. For this study we used a Band function because it was not appropriate to neglect the high energy spectral index which plays an important role for GRBs at high redshift. We chose $\beta = -2.3$ because it is the average value found by Preece et al. (2000). For these computations we asssumed a flat universe with $\Omega_0$ = 0.7, $\Omega_\Lambda$ = 0.3 and H0 = 65 km s-1 Mpc-1.

Figure 6 shows that cosmological effects could in principle explain the observed correlation. In this case, however, we would also expect a significant time dilation of the soft GRBs. Figure 7 plots the duration T90 as a function of the total fluence. It shows that there is no significant time dilation of the faint GRBs. We note here that because the widths of the peaks in the time histories of GRBs - and the durations of GRBs - are shorter at higher energies (e.g., Fenimore et al. 1995 ), this partly (but only partly) compensates for the time dilation due to the cosmological redshift. GRB durations go approximately like E-0.4, so that this effect shortens the observed durations of GRBs at a redshift z = 10 relative to the durations of GRBs at a redshift z = 1 by a factor of about [(1+10)/(1+1)]0.4 = 2. Time dilation would be expected to increase the duration of the bursts by [(1+10)/(1+1)] = 5.5. Thus, overall, one expects bursts at high redshifts to be longer by a factor of only about 2.7. Still, Fig. 7 does not support such a dependence.

While it is always possible to invoke GRB evolution to produce intrinsically shorter GRBs at high redhifts, we consider that our observations do not favor the interpretation of the HIC purely in terms of cosmological effects. Finally, we note that Amati et al. (2002) find a correlation between the intrinsic (redshift corrected) ${E_{\rm p}}$ of 12 GRBs with known redshifts, and E52, their isotropic-equivalent energy radiated in gamma-rays, in units of 1052 ergs: ${E_{\rm p}}$ = 100  E520.52 keV. This correlation, if it extends over a sufficient range of redshifts could certainly explain the hardness-intensity correlation we observe. With this interpretation, the HIC would be the reflection of a more fundamental correlation between the radiated isotropic-equivalent energy and the spectral hardness in GRBs. Our observations suggest that this correlation could include the X-ray rich GRBs. If X-ray rich GRBs are intrinsically fainter, we should also expect them to be closer on average than bright GRBs. We discuss this issue in the next section.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2820_dure_l.ps}\end{figure} Figure 7: GRB duration (T90) as a function of the total fluence. This figure shows that faint GRBs are not significantly longer than bright events.
Open with DEXTER

   
4.3 The distance and nature of X-ray rich GRBs

A quick survey of the literature shows that X-ray rich GRBs have no or very faint optical afterglows. The only tentative identification of an optical afterglow is reported by Fruchter et al. (2002c) for GRB 020410: a faint source is seen with the STIS on the HST at V= 25.4 on May 8 and V= 26.9 on June 14. This identification is not certain however due to the possible confusion with a field supernova unrelated to the GRB.

X-ray rich GRBs, on the other hand, seem to have X-ray afterglows (e.g. GRB 981226, GRB 990704, GRB 011030, GRB 020410 or GRB 020427) and for some of them radio afterglows (GRB 981226, GRB 011030). Thanks to the good localization capabilities of Chandra, the host galaxies of GRB 981226, GRB 011030 and GRB 020427 have been identified (Frail et al. 1999; Fruchter et al. 2002a; Castro-Tirado et al. 2002a; Fruchter et al. 2002b), but their redshifts have not yet been measured. To summarize, we still have no measure of the distance of an X-ray rich GRB[*].

The nature of X-ray rich GRBs can be addressed from the theoretical or from an empirical point of view. From the theoretical point of view, we note that the model of internal shocks predicts that X-ray rich GRBs could be produced by fireballs with less efficient shocks (due to lower magnetic fields or to a lower contrast of the Lorentz factors within the ejecta) or by clean fireballs (with a low baryon load) (Zhang & Mészáros 2002; Daigne et al. 2002; Mochkovitch et al. 2003). In a clean fireball the initial Lorentz factor is higher but the internal shocks take place at larger distances from the central source where the density and the magnetic fields are smaller, leading to the emission of less energetic photons. Further theoretical studies are needed to assess whether one of these conditions can also explain the correlation found by Amati et al. (2002), the lack of bright optical afterglows and the unusual properties of the X-ray afterglows of X-ray rich GRBs (Frontera et al. 2000b; Feroci et al. 2001).

From the empirical point of view, if we combine the evidence in this paper that (a) X-ray rich GRBs are not a separate class of GRBs but represent an extension of the properties of "typical'' GRBs, and (b) the HIC correlation extends over three orders of magnitude in fluence and applies to X-ray rich GRBs with the conclusion of Frail et al. (2001) that the total energy of GRBs is roughly constant, we are led to the conclusion that the jet opening angle of X-ray rich GRBs are substantially larger than the jet opening angle of "typical'' GRBs. Additional observations are clearly required to understand the role of the progenitor and/or its environment in shaping the properties of the prompt GRB emission, particularly the peak energy.

   
5 Conclusions

Our observations have two interesting consequences: they confirm that the ${E_{\rm p}}$ distribution is broader than previously thought (Mallozzi et al. 1995; Preece et al. 2000; Brainerd et al. 2000) and they show that we do not see yet the faint end of the GRB distribution. If we assume that the correlation found by Amati et al. (2002) extends down to ${E_{\rm p}}$ as low as 20 keV, it would imply that the isotropic-equivalent energy radiated by a GRB with ${E_{\rm p}}$ = 20 keV is about 80 times smaller than the isotropic-equivalent energy radiated by a "typical'' GRB with ${E_{\rm p}}$ = 200 keV. Combined with the conclusion of Frail et al. (2000) that the total energy of GRBs is roughly constant, it implies that the jet opening angle of X-ray rich GRBs are substantially larger than the jet opening angle of "typical'' GRBs.

Future work with HETE-2 will bring several advances in this field and should contribute to our understanding of the population of soft/faint GRBs. The continuously growing GRB sample of FREGATE should provide better statistical evidence for the effects discussed in this paper and additional clues about the possible differences between bright and faint GRBs and about the nature of X-ray rich GRBs. Joint spectral analysis with the WXM will allow more precise determinations of ${\alpha }$ and ${E_{\rm0}}$ for X-ray rich GRBs. Finally, measuring the redshifts of a greater number of GRBs detected by HETE-2 will allow us to test the extent of the correlation between the spectral hardness of GRBs and their radiated energy in gamma-rays. X-ray rich GRBs also present an interesting challenge for future GRB missions and for observers on the ground. Future GRB missions will have to detect events which are much softer and fainter than the typical GRB population sampled by BATSE. Observers on the ground are faced with events which have fainter afterglows than the classical gamma-ray bursts.

To conclude we note that the joint detection of GRB 010213 (with ${E_{\rm p}}$ = 2.5 keV, Kawai et al. 2003; Sakamoto et al. 2003) by WXM and FREGATE and of GRB 020903 (with ${E_{\rm p}}$ = 3 keV, Kawai et al. 2003) by WXM only demonstrate the existence of events which are even softer than the bulk of the X-ray rich GRBs discussed in this paper.

Acknowledgements
The HETE-2 mission is supported in the US by NASA contract NASW-4690; in France by CNES contract 793-01-8479; and in Japan in part by the Minisitry of Education, Culture, Sports, Science and Technology Grant-in-Aid 13440063. KH is grateful for support under MIT contract SC-R-293291. GP aknowledges support by the Italian Space Agency (ASI) The authors acknowledge the support of the HETE-2 operation team. The authors acknowledge the use of J. Greiner GRB page at http://www.mpe.mpg.de/~jcg/grbgen.html.

References

 

Online material

6 Appendix: Spectra of the 35 GRBs


\begin{figure}\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB001225.ps}\vs... ... \includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB010213.ps} \end{figure}         \begin{figure}\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB010225.ps}\vs... ...\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB010612.ps} \end{figure}         \begin{figure}\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB010613.ps... ...\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB010923.ps} \end{figure}

\begin{figure}\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB010928.ps... ...\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB011212.ps} \end{figure}         \begin{figure}\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB011216.ps... ...\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB020127.ps} \end{figure}         \begin{figure}\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB020201.ps}\vs... ...\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB020317.ps} \end{figure}

\begin{figure}\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB020331.ps... ...\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB020801.ps} \end{figure}         \begin{figure}\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB020812.ps}\vs... ...\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB021004.ps} \end{figure}         \begin{figure}\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB021014.ps... ...\par\includegraphics[angle=-90,width=7.3cm,clip]{2820_GRB021112.ps} \end{figure}

Copyright ESO 2003