A&A 400, 811-821 (2003)
DOI: 10.1051/0004-6361:20021911
D. M. Neumann 1 - D. H. Lumb 2 - G. W. Pratt 1 - U. G. Briel 3
1 - CEA/DSM/DAPNIA Saclay, Service d'Astrophysique,
L'Orme des Merisiers, Bât. 709, 91191 Gif-sur-Yvette, France
2 -
Science Payloads Technology Division, Research and Science Support
Dept., ESTEC, Postbus 299 Keplerlaan 1, 2200AG Noordwijk, The Netherlands
3 -
Max-Planck Institut für extraterrestrische Physik,
Giessenbachstr.,
85740 Garching,
Germany
Received 19 June 2002 / Accepted 13 December 2002
Abstract
We present in this paper a substructure and spectroimaging study of the Coma
cluster of galaxies based on XMM-Newtondata. XMM-Newtonperformed a mosaic of observations of Coma
to ensure a large coverage of the cluster. We add the different
pointings together and fit elliptical beta-models to the data. We subtract
the cluster models from the data and look for residuals, which can be
interpreted as substructure. We find several
significant structures: the well-known subgroup connected to NGC 4839 in the
South-West of the cluster, and another substructure located between NGC 4839
and the centre of the Coma cluster. Constructing a hardness ratio image, which
can be used as a temperature map, we see that in front of this new structure
the temperature is significantly increased (higher or equal 10 keV). We
interpret this temperature
enhancement as the result of heating as this structure falls onto
the Coma cluster. We furthermore reconfirm the filament-like structure
South-East of the cluster centre. This region is significantly cooler than the
mean cluster temperature. We estimate the temperature of this structure to
be equal or below 1 keV.
A possible scenario to explain the observed features is
stripping caused by the infall of a small group of galaxies located around
the two galaxies NGC 4921 and NGC 4911 into the Coma cluster with a non-zero
impact parameter. We also see significant X-ray depressions North and
South-East of NGC 4921, which might either be linked to tidal forces due to
the merger with the Western structure or connected to an older cluster
merger.
Key words: galaxies: clusters: general - galaxies: intergalactic medium - galaxies: general - cosmology: miscellaneous - cosmology: large-scale structure of the Universe - X-rays: galaxies
The Coma cluster, also known as Abell 1656, is one of the best studied clusters in our Universe (see Biviano 1998 for a historical review). It has been explored in all wavelengths from radio to hard X-rays. However, despite the large number of observations, the physics of the Coma cluster and its dynamical state is not yet completely understood. The cluster hosts a powerful radio halo (Feretti & Giovannini 1998) and Beppo-Sax data recently revealed the existence of hard non-thermal X-ray emission (Fusco-Femiano et al. 1999).
Extensive work has been carried out to measure the velocity dispersion and
distribution of the galaxies located in the Coma cluster. Colless & Dunn
(1996) for example published a catalog of 552 redshifts and determined the
mean redshift of the cluster to be cz = 6853 km s-1 and a velocity dispersion
of
![]() km s-1. Colless & Dunn (1996) find and confirm
the presence of substructure in the galaxy distribution: there is a sub-group
located around NGC 4839, which lies to the South-West of the cluster. The
existence of this substructure was originally found by Mellier et al. (1988)
and Merritt & Trimbley (1994). Furthermore, it was noted by
Fitchett & Webster (1987) that the two
central galaxies, NGC 4889 and NGC 4874 have a significant difference in
velocity, which is indicative of a recent merger. It is probable that
NGC 4889 belonged
to a subgroup, which recently merged with the main
cluster and that NGC 4874 is the
central dominant galaxy of the main cluster.
km s-1. Colless & Dunn (1996) find and confirm
the presence of substructure in the galaxy distribution: there is a sub-group
located around NGC 4839, which lies to the South-West of the cluster. The
existence of this substructure was originally found by Mellier et al. (1988)
and Merritt & Trimbley (1994). Furthermore, it was noted by
Fitchett & Webster (1987) that the two
central galaxies, NGC 4889 and NGC 4874 have a significant difference in
velocity, which is indicative of a recent merger. It is probable that
NGC 4889 belonged
to a subgroup, which recently merged with the main
cluster and that NGC 4874 is the
central dominant galaxy of the main cluster.
There are a number of papers addressing the thermal X-ray emission of the Coma cluster which comes from the hot thermal intracluster medium (ICM). White et al. (1993) discussed substructures in the Coma cluster based on ROSAT-data. Briel et al. (1992) analyzed the ROSAT All-Sky-Survey data and determined the X-ray surface brightness profile of the cluster out to a radius of roughly 100 arcmin. Hughes (1989) performed an extensive mass analysis on the Coma cluster based on X-ray and optical data. Later work by Vikhlinin et al. (1997) revealed the existence of a filament-like substructure, which is most likely linked to NGC 4911, a bright spiral galaxy located South-East with respect to the centre of the cluster. Spectroimaging studies based on ASCA-data constrained the X-ray temperature distribution of the ICM. Honda et al. (1997) and Watanabe et al. (1999) presented temperature maps of the Coma cluster based on ASCA-data, which clearly showed that the ICM is not isothermal. Furthermore, Donnelly et al. (1999) saw indications for a hot spot North of the centre of the Coma cluster. Recently, first results of the Coma cluster based on XMM-Newton data were published: Briel et al. (2001) discussed the overall morphology of the cluster and showed the existence of several point-like sources, which are linked to individual galaxies in the cluster and which have not been accounted for in previous studies. Arnaud et al. (2001a) presented a temperature map of the central part of the cluster based on XMM-Newtondata with unprecedented spatial resolution. This map showed again variations of the X-ray temperature (see Jansen et al. 2001 for an overview of XMM-Newton and Turner et al. 2001 and Strueder et al. 2001 for an overview of the EPIC detectors). However, the previously found hot spot found by Donnelly et al. (1999) was not confirmed. Lastly, Neumann et al. (2001) presented strong evidence based on XMM-Newtondata that the substructure located around NGC 4839 (see above) is on its first infall onto the cluster from the South-West and has not yet passed its centre. This is in contradiction to previous work by Burns et al. (1994), who suggested that the group around NGC 4839 has already passed the centre of the Coma cluster once.
The aim of this paper is to perform a substructure and spectroimaging study of the Coma cluster based on XMM-Newtondata, to better understand the underlying physics. The work presented here is our first attempt to discuss the overall dynamics of the cluster, and is by no means exhaustive. It aims to show the large potential provided by the data obtained with XMM-Newton. The paper is organized as follows: after the introduction we present the observations in Sect. 2. This is followed by the description of our data treatment in Sect. 3. In Sect. 4 we present our spatial analysis and in Sect. 5 we describe our spectro-imaging results. In Sect. 6 we discuss our results and finish in Sect. 7 with the Conclusion.
Throughout this paper, we assume H0=50 km s-1 Mpc-1,
![]() and
q0 = 1/2. At a redshift of z=0.0232,
and
q0 = 1/2. At a redshift of z=0.0232, ![]() corresponds to 38.9 kpc.
The cluster is sufficiently close so that variations of the geometry of the Universe do not matter.
corresponds to 38.9 kpc.
The cluster is sufficiently close so that variations of the geometry of the Universe do not matter.
The size of the Coma cluster (roughly 3 degrees in diameter) greatly exceeds the field-of-view (FOV) of XMM-Newton. Therefore the observations of Coma were performed in mosaic mode with several exposures pointing at different regions of the cluster. The summary of all observations is shown in Table 1. The exposure times indicated are the effective observing times after flare rejection. We apply the same method and thresholds for flare rejection as described in Majerowicz et al. (2002) for the pn and MOS-cameras. During the observations the pn-camera was mostly operating in extended-full-frame mode. There was one additional Coma pointing, in which only the pn-camera was active (Coma 2), for which we were not able to run the pipeline processing at the time of the analysis. Thus we discard this observation in the following.
Our analysis presented here is based on SAS-version 5.1 and concerns only events in the field-of-view (FOV).
In order to correct for vignetting we apply the photon weighting method
described in Arnaud et al. (2001b). To outline it briefly: to each observed
event at energy E falling onto the detector position x,ywe attribute a correcting factor:
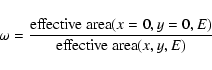 |
(1) |
All images presented in this study are vignetting corrected. For this we
create images by adding the different weight factors of the photons into
image pixels. The statistical uncertainty per image
pixel is calculated as
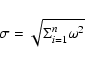 |
(2) |
While merging the data from different exposures we observed certain offsets of the order of a few arcseconds for which we corrected by looking at point sources, which were visible in two or more pointings. We shifted the pointings so that the same point source, visible in different exposures, appeared in each pointing at the same sky coordinate position. We estimate the remaining errors in the order of a few arcseconds.
Figure 1 shows the resulting countrate image in the energy band 0.5-2.0 keV after merging the different observations together (MOS and pn) and subtracting the background. For the background we used the Blank-Sky observations provided by D. Lumb and retrievable from the XMM-Newton web-pages. The background subtraction is not important for the construction of the countrate images, however, it is important for the determination of the hardness ratio map (see below).
In order to obtain Fig. 1 we perform the following data treatment:
We want to stress that the Coma pointings were performed in
medium filter mode while the data used for the background are compiled from
observations mainly using thin filter. However, since we only use
photons at energies above 0.5 keV we expect the difference of the different
filters to be negligible. Furthermore, at regions with high signal-to-noise
ratio we expect that the background subtraction is not important.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{neumann1.ps}
\end{figure}](/articles/aa/full/2003/12/aa2810/Timg11.gif) |
Figure 1:
The Coma cluster in the 0.5-2.0 keV band. The image is the sum of
all the different exposures (see Table 1) of the different MOS
and pn cameras (see text). The image is background and vignetting corrected.
We applied a small median filter to mask out effects caused by
detector gaps. Colour scale: dark blue regions correspond to countrates of 0.016 cts/s/arcmin2 and white regions to countrates |
| Open with DEXTER | |
Our aim in this study is to look for substructure and temperature variations in order to better understand the dynamical state of the Coma cluster.
For measuring substructure we fit an elliptical beta-model to the cluster images, which describes a relaxed cluster without substructure. Subsequently, we create a synthetic cluster image based on the best fit parameters of the beta-model. This model is subtracted from the data. The residuals remaining after subtraction, which indicate substructure, are examined for their significance. This method has been applied to useful effect in several other studies, e.g., Neumann & Böhringer (1997, 1999) and Neumann (1999).
In the following we describe the different steps of our substructure analysis in detail.
In fitting elliptical beta-models to the XMM-Newton data, we take as input the vignetting corrected images in the 0.5-2.0 keV energy band. This energy range was chosen since it provides the best signal-to-noise ratios (Scharf 2002). For this analysis we did not subtract the background, since we include it as fit parameter. We compare (see below and Table 2) the fitted background values with the countrate values observed in the background observations. This is a consistency check for the applied background subtraction.
We encounter small number Poisson statistics in the pixels located at the
outskirts of the cluster. This produces non-symmetric error bars for
the pixel values. Since we use ![]() statistics for our beta-model fitting,
which assumes a symmetric Gaussian probability distribution for the photons,
we have to correct for the asymmetry of the error bars. An easy
way to do this is to apply a Gaussian filter (
statistics for our beta-model fitting,
which assumes a symmetric Gaussian probability distribution for the photons,
we have to correct for the asymmetry of the error bars. An easy
way to do this is to apply a Gaussian filter (
![]() )
to the image before fitting the model. This procedure has proven to be valid
and gives good results as shown in previous studies (e.g. Neumann &
Böhringer 1997, 1999; Neumann 1999).
In order to account properly
for the vignetting, in our calculation of the error bars per pixel
we quadratically add the different weighting factors for each event in each
pixel before Gaussian filtering (Eq. (2)), and use this image as estimate
for the uncertainties in each pixel.
)
to the image before fitting the model. This procedure has proven to be valid
and gives good results as shown in previous studies (e.g. Neumann &
Böhringer 1997, 1999; Neumann 1999).
In order to account properly
for the vignetting, in our calculation of the error bars per pixel
we quadratically add the different weighting factors for each event in each
pixel before Gaussian filtering (Eq. (2)), and use this image as estimate
for the uncertainties in each pixel.
To check for possible instrument-dependent variations we treat the MOS- and the pn-data separately. The fit results are displayed in Table 3. They are in good agreement with each other and with previous studies, like Briel et al. (1992). Since we are only interested in the best-fit model in order to subtract it from the cluster data and check for residuals, we do not determine error bars on the fit parameters, which would be time consuming since the error bars would have to be estimated via a Monte-Carlo approach.
The centre of both the MOS and the pn-data fit coincide relatively well with
the position of the central galaxy NGC 4874, at:
![]() and
and
![]() .
The distance between the model centre and this
galaxy is less than 2 arcmin.
.
The distance between the model centre and this
galaxy is less than 2 arcmin.
We subtract the cluster model based on the best fit parameters of the
beta-model and calculate the corresponding significance of the
residuals for each instrument type independently. The exact method we use for
calculating
the significances is described in Neumann & Böhringer
(1997).
For our residual calculation we apply a Gaussian filter with
![]() .
We obtain two significance maps, one for the MOS-cameras, and the other
for the pn-camera. The residuals obtained for each type of camera are very
similar.
We quadratically add the two different significance maps
in order to obtain a residual image with better statistics. The result is
shown in Fig. 2. The image over which we
display the significance contours is the same as in Fig. 1.
.
We obtain two significance maps, one for the MOS-cameras, and the other
for the pn-camera. The residuals obtained for each type of camera are very
similar.
We quadratically add the two different significance maps
in order to obtain a residual image with better statistics. The result is
shown in Fig. 2. The image over which we
display the significance contours is the same as in Fig. 1.
We want to stress that the resulting residuals with a significance equal or
higher than +10 ![]() are extremely stable against changing the parameters
of the subtraced model.
are extremely stable against changing the parameters
of the subtraced model.
The residual map shown in Fig. 2 shows several significant structures:
| MOS | pn | |
| observed background |
|
|
| countrate in 10-4 counts/s/pixel | ||
fitted background |
1.2 | 3.8 |
| countrate in 10-4 counts/s/pixel |
| camera | S0 | x0 | y0 |
|
|
|
| cts s-1 arcmin-2 | in deg (J2000) | in deg (J2000) | in arcmin | in arcmin | ||
| MOS | 0.094 | 194.929 | 27.9586 | 11.1 | 9.0 | 0.72 |
| pn | 0.28 | 194.927 | 27.9597 | 12.1 | 11.2 | 0.85 |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{neumann2.ps}\end{figure}](/articles/aa/full/2003/12/aa2810/Timg25.gif) |
Figure 2:
The image is the same as in Fig. 1 only with different
image value cuts and a linear look-up-table (lut) instead of a logarithmic lut.
The contours are the significances of the residuals above main relaxed
cluster and background emission (see also text). The lowest contour and the
step width between two contours are each 5 |
| Open with DEXTER | |
In order to measure the temperature distribution of the ICM we determine the hardness ratio map for the Coma cluster. We make use of Fig. 1 and of the countrate image in the energy band 2-5 keV.
Both of these images are constructed as described in Sect. 3.2 and are fully background-subtracted. Background subtraction is crucial to the construction of the hardness ratio map; without this correction background-dependent variations would appear in the final image.
In order to
avoid artefacts due to photon statistics, we apply
a median filter to the images in the 0.5-2.0 keV and the 2.0-5.0 keV band.
We filter over a region of 12 by 12 pixels (pixel size is
![]() )
before we divide the image obtained in the higher
energy band by the image in the low energy band. Applying a median filter not
only helps for the statistics but also filters out the emission of
individual sources such as galaxies or AGN.
Since there are insufficient statistics in the outskirts of the cluster
to reliably constrain the hardness ratio,
we restrict ourselves to regions in which the countrate in the energy
band 2-5 keV band is above
)
before we divide the image obtained in the higher
energy band by the image in the low energy band. Applying a median filter not
only helps for the statistics but also filters out the emission of
individual sources such as galaxies or AGN.
Since there are insufficient statistics in the outskirts of the cluster
to reliably constrain the hardness ratio,
we restrict ourselves to regions in which the countrate in the energy
band 2-5 keV band is above
![]() cts/s/pixel.
This is a very
conservative limit (see below) which helps avoid artefacts
linked to imperfect background subtraction or to small number statistics.
cts/s/pixel.
This is a very
conservative limit (see below) which helps avoid artefacts
linked to imperfect background subtraction or to small number statistics.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{neumann3.eps}
\end{figure}](/articles/aa/full/2003/12/aa2810/Timg28.gif) |
Figure 3: The hardness ratio image obtained by dividing the image in the 2-5 keV band by the image in the 0.5-2 keV band (see also text). Assuming an isothermal spectrum, red regions correspond to parts of the cluster with temperatures below 8 keV, yellow regions correspond to kT>8 keV and white regions have temperatures above 10 keV. The contours are the significance of the residuals, see also Fig. 2. |
| Open with DEXTER | |
The hardness ratio image is shown in Fig. 3. The image is in three colours; red shows temperatures below 8 keV, yellow regions between 8-10 keV and white are regions with temperatures above 10 keV. Our results are in good agreement with those obtained by Arnaud et al. (2001a) and Briel et al. (2001).
Are the differences in hardness ratio significant or not? In order to evaluate the errors, we perform the following approximation.
We only look at regions in the hardness ratio image in
which the countrate in the 2-5 keV band is larger or equal to
![]() cts/s
per pixel (the pixel size is
cts/s
per pixel (the pixel size is
![]() ). Assuming a mean exposure of
20 ks per camera, we obtain 8 photons per pixel
). Assuming a mean exposure of
20 ks per camera, we obtain 8 photons per pixel![]() . Since the observed mean
hardness ratio is roughly 0.3 (which corresponds to a plasma temperature of
about 8 keV), the countrate in the 0.5-2 keV band is a
factor of about 3 higher than the countrate in the higher energy band. Thus,
we obtain roughly 24 photons per pixel in a 20 ks exposure. This calculation
takes only into account the source countrate. For the proper error calculation
we also have to include the background countrate which we subtracted via the
blank sky observations. The total background countrate in the 0.5-2.0 keV band
is
. Since the observed mean
hardness ratio is roughly 0.3 (which corresponds to a plasma temperature of
about 8 keV), the countrate in the 0.5-2 keV band is a
factor of about 3 higher than the countrate in the higher energy band. Thus,
we obtain roughly 24 photons per pixel in a 20 ks exposure. This calculation
takes only into account the source countrate. For the proper error calculation
we also have to include the background countrate which we subtracted via the
blank sky observations. The total background countrate in the 0.5-2.0 keV band
is
![]() cts/s/pixel and for the 2.0-5.0 keV band
cts/s/pixel and for the 2.0-5.0 keV band
![]() cts/s/pixel.
Furthermore, for the
hardness ratio image we applied a median filter derived from the
pixel values in a window of
cts/s/pixel.
Furthermore, for the
hardness ratio image we applied a median filter derived from the
pixel values in a window of
![]() image pixels.
If we assume that the median filter has the same error as if one averages over
all pixels, a good approximation, we can determine the
errors by calculating the total number of photons and using error propagation
including the background. We obtain a
image pixels.
If we assume that the median filter has the same error as if one averages over
all pixels, a good approximation, we can determine the
errors by calculating the total number of photons and using error propagation
including the background. We obtain a ![]() -error of 0.01 in the
hardness ratio. This corresponds to about 0.5 keV for temperatures below
10 keV. We want to stress that this
is the error estimate for the outer region. In the inner parts, where the
statistics are much better, the errors are much smaller. As an
example: from the outer parts from the cluster, to the centre, the increase of
X-ray intensity is of the order of a factor of 20.
-error of 0.01 in the
hardness ratio. This corresponds to about 0.5 keV for temperatures below
10 keV. We want to stress that this
is the error estimate for the outer region. In the inner parts, where the
statistics are much better, the errors are much smaller. As an
example: from the outer parts from the cluster, to the centre, the increase of
X-ray intensity is of the order of a factor of 20.
One final point concerning the results: the hardness ratio image shows two "hot spots'' to the South. The significance of these two points is very low since they lie both in pointing No. 4, which has an exceptionally low exposure time (see Table 1). It is thus quite likely that these features are statistical artefacts.
In Fig. 3, there is an obvious, large residual to the West of the cluster centre. The region lying between this structure and the Coma centre shows a temperature increase to temperatures equal to or above 10 keV. This suggests that it is heated via compression or via shock waves, which were created during the infall of this sub-structure onto the Coma centre. The creation of shock waves is observed in hydrodynamic simulations of galaxy cluster mergers (see for example Schindler & Müller 1993). It seems unlikely that the structure is a chance alignment in the line-of-sight.
The two maxima in this western structure could be caused by a disruption of a galaxy group during its infall onto the cluster centre into several smaller units. It is relatively unlikely that two galaxy groups are falling onto the Coma cluster at exactly the same time.
Previous work has shown that the galaxy group around NGC 4839 is falling onto
the Coma cluster (see for example Neumann et al. 2001 and
references therein). The infall direction
coincides with a filament which connects the Coma cluster with Abell 1367, and which is part of the
"Great Wall''. One may ask if the structure between NGC 4839 and the cluster centre is also falling in from the same direction. If a subcluster infalls from this direction, it will heat up the gas between it and the main cluster via compression. This will lead to an increase in the ram pressure encountered by the subcluster. Pressure increases linearly with temperature for an ideal gas (P=nkT): the relative difference in temperature between the hot region and the main cluster is ![]() 20%, indicating a similar increase in pressure, and which may be sufficient to slow down the infalling gas. It is possible that, due to inertia, the gas in the subcluster is not abruptly slowed down, but instead may move in a direction where there is no increase in pressure. This movement could be tangential from South to North. In this case, the hot region to the North can naturally be explained as due to compression of the remaining gas in the subcluster.
20%, indicating a similar increase in pressure, and which may be sufficient to slow down the infalling gas. It is possible that, due to inertia, the gas in the subcluster is not abruptly slowed down, but instead may move in a direction where there is no increase in pressure. This movement could be tangential from South to North. In this case, the hot region to the North can naturally be explained as due to compression of the remaining gas in the subcluster.
The increase of temperature towards the North has been seen in ASCA-data (Watanabe et al. 1999; Honda et al. 1996). It was interpreted as being due to heating by a shock wave created from a previous merger from a galaxy group located around NGC 4889, which is now one of the two main galaxies in the centre of the Coma cluster. It is not possible at present to distinguish between the two explanations.
Examination of DSS plates does not show any obvious overdensity of
galaxies coinciding with the Western residual structure. In this case, one might ask whether
this structure is the remaining gas from the subcluster which was once associated with NGC 4889. Ram pressure is known to act much more efficiently on gas than on galaxies, which would provide a natural explanation for the differences in location of the gas and the galaxy. The effectiveness of ram pressure stripping can be seen in the case of the subgroup around NGC 4839, in which the gas is clearly lagging behind the galaxies on the infall trajectory (Neumann et al. 2001). Taking the projected distance between NGC 4889 and the western substructure (![]() 1 Mpc) and a typical cluster merger or sound crossing timescale of 109 years, we can calculate the mean difference in velocity between the galaxy and
the gas. This value is close to the velocity dispersion of Coma (in the order of 1000 km s-1, Colless & Dunn 1996), which is not surprising given that typical cluster sizes are of order of a few Mpc. The feasibility of this scenario can only be assessed with high resolution hydrodynamic simulations, which take into account the differences of ram pressure between the galaxies and the gas of the merging subgroup.
1 Mpc) and a typical cluster merger or sound crossing timescale of 109 years, we can calculate the mean difference in velocity between the galaxy and
the gas. This value is close to the velocity dispersion of Coma (in the order of 1000 km s-1, Colless & Dunn 1996), which is not surprising given that typical cluster sizes are of order of a few Mpc. The feasibility of this scenario can only be assessed with high resolution hydrodynamic simulations, which take into account the differences of ram pressure between the galaxies and the gas of the merging subgroup.
This compact region clearly shows lower values in the hardness ratio image, indicating that this part of the cluster is cooler than the mean cluster temperature.
The filamentary form of the structure suggests that it may be linked to some sort of infall process in connection with ram pressure stripping. Since ram pressure stripping works efficiently only in the centre of the cluster, where the gas density is high, we suppose that this structure is relatively close to the centre of the cluster and not a projection effect. NGC 4911, a bright galaxy which lies in the region of the substructure, shows a relative difference in velocity with respect to the Coma cluster of 1000 km s-1, which is close to the velocity dispersion of the cluster as a whole.
To determine the origin of the filamentary Eastern structure, and more specifically to know whether the the observed stripped gas comes from an intragroup medium or from an interstellar medium linked to galaxies, we attempt to estimate the mass of gas of this structure. A high value for the mass would suggest that the gas comes from an intragroup medium, a low value would indicate that the origin of the gas is from gas located inside the galaxies.
The structure has a projected distance from the Coma
centre of roughly 1 Mpc and enhances the observed flux with respect to the
fitted beta-model by about 30%. Using a length of 1 Mpc, a diameter of
200 kpc, and assuming cylindrical symmetry (thus a thickness of the structure
in the line-of-sight of 200 kpc), the volume of the substructure
![]() .
.
In order to calculate the gas mass of this structure we have to determine the
contributions of the main cluster gas and the gas in the
substructure. The contribution of the main cluster gas has to
be integrated along the line-of-sight. For this we make use of the previously
determined beta-model parameters by Briel et al. (1992) (
![]() Mpc
Mpc
![]() cm-3). The determination of the gas mass of the substructure depends on its location with respect to the cluster. If located at a large distance to the cluster we can simply add the two X-ray contributions of main cluster and substructure. In this case we find an electron density of the subgroup of
cm-3). The determination of the gas mass of the substructure depends on its location with respect to the cluster. If located at a large distance to the cluster we can simply add the two X-ray contributions of main cluster and substructure. In this case we find an electron density of the subgroup of
![]() cm-3. Integrating this density over the previously calculated volume we find a total gas mass for the structure of
cm-3. Integrating this density over the previously calculated volume we find a total gas mass for the structure of
![]()
![]() .
If we assume that the structure is very close to the centre and that in fact the
physical distance towards the Coma centre is close to its projected distance
we need to take into account that the gas in the substructure is at the
same position than the gas of the main cluster, which enhances the X-ray emission in this region
.
If we assume that the structure is very close to the centre and that in fact the
physical distance towards the Coma centre is close to its projected distance
we need to take into account that the gas in the substructure is at the
same position than the gas of the main cluster, which enhances the X-ray emission in this region![]() .
In this case the required gas density for the subgroup is lower
than in the case of no physical connection between the two components. We
obtain in this case an electron density of
.
In this case the required gas density for the subgroup is lower
than in the case of no physical connection between the two components. We
obtain in this case an electron density of
![]() cm-3,
and a gas mass of
cm-3,
and a gas mass of
![]()
![]() .
Combining the two cases
as the two possible extremes we find that the gas mass of the substructure
lies between
.
Combining the two cases
as the two possible extremes we find that the gas mass of the substructure
lies between
![]()
![]() <
<
![]()
![]() .
This value for the gas mass is at the low end for a group of galaxies
(Mulchaey 2000) and
suggests that a part of the gas might also come
from the interstellar medium of galaxies themselves.
The obtained values are in very good agreement with the value obtained by Vikhlinen et al.
(1997) with
.
This value for the gas mass is at the low end for a group of galaxies
(Mulchaey 2000) and
suggests that a part of the gas might also come
from the interstellar medium of galaxies themselves.
The obtained values are in very good agreement with the value obtained by Vikhlinen et al.
(1997) with
![]()
![]() .
.
If we assume that the gas mass of the
substructure represents roughly
ten percent of the total mass of the substructure, which is of the order of
magnitude of what is typically found (see for example David et al. 1995),
then we obtain for
the total mass
![]()
![]() .
This is a few times larger than
the mass of a massive galaxy and again somewhat at the low end of the mass of
groups of
galaxies with typically a few 1013
.
This is a few times larger than
the mass of a massive galaxy and again somewhat at the low end of the mass of
groups of
galaxies with typically a few 1013 ![]() (e.g. Mulchaey 2000).
NGC 4911 and NGC 4921 lie in this
sub-structure and are by far the brightest galaxies (Fig. 4)
in this
region. Dow & White (1995) give a value for the optical luminosity of
NGC 4911 of
(e.g. Mulchaey 2000).
NGC 4911 and NGC 4921 lie in this
sub-structure and are by far the brightest galaxies (Fig. 4)
in this
region. Dow & White (1995) give a value for the optical luminosity of
NGC 4911 of
![]() (in
(in ![]() ) = 10.89. Since NGC 4921 has a similar magnitude
(see Doi et al. 1995), we can assume a similar
luminosity. Assuming a mass-to-optical light ratio
) = 10.89. Since NGC 4921 has a similar magnitude
(see Doi et al. 1995), we can assume a similar
luminosity. Assuming a mass-to-optical light ratio ![]() 10, we obtain
a total mass of NGC 4911 and NGC 4921 of
10, we obtain
a total mass of NGC 4911 and NGC 4921 of ![]() 1012
1012 ![]() ,
which is of
the same order of magnitude as the value required for the
entire filamentary substructure. This indicates that the
substructure is largely dominated by the two galaxies.
,
which is of
the same order of magnitude as the value required for the
entire filamentary substructure. This indicates that the
substructure is largely dominated by the two galaxies.
Matsushita (2001) recently presented a correlation between mass
of the hot interstellar medium and optical luminosity LB for late type
galaxies. Applying this correlation to NGC 4921 and NGC 4911 we find a mass
for the hot phase in the order of 1010 ![]() .
This is smaller
than the value of a few times 1011
.
This is smaller
than the value of a few times 1011 ![]() .
If correct, this implies that a
large fraction of the gas comes indeed from an intra-group medium.
.
If correct, this implies that a
large fraction of the gas comes indeed from an intra-group medium.
The X-ray structure we see likely originates from gas in the surrounding intra-group medium of a small group of galaxies plus, to some fraction, which we expect to be in the order of a few up to 10 or 20 per cent, from the stripped interstellar medium of the two galaxies, NGC 4911 and NGC 4921.
A cursory examination of Fig. 2 would suggest that the principal direction of motion is to the West with perhaps an additional component to the North. Figure 4 shows the X-ray residual over the optical image from the DSS, indicating that NGC 4921 is at the Eastern end of the structure and NGC 4911 is right at the position where the structure bends. The only way we can explain this alignment is by assuming a direction of motion to the East, with NGC 4921 at the head of the structure and NGC 4911 behind. The different directions of the stripped tails may indicate different velocity directions for the galaxies, with NGC 4911 only having a projected velocity component towards the East while NGC 4921 has an additional projected component to the North. This could indicate that the structure in which NGC 4911 and NGC 4921 are bound together changes its direction of velocity with time.
Are these two galaxies bound together? If they are, they should have similar measured velocities or redshifts. A combination of NASA Extragalactic Database (NED) and published data (Smith et al. 2000) indicates velocities of cz=7973 km-1 and cz=7560 km-1 for NGC 4911 and NGC 4921, respectively, suggesting that they are indeed gravitationally bound. (Note that the NED velocity for NGC 4921 is incorrect, having been superseded by the Smith et al. measurement.) Since the two galaxies have larger measured velocities than
the Coma cluster itself, it is reasonable to assume that the structure is
located between us and the Coma cluster, thus lying somewhat in front of
the Coma centre (although there is the small possibility that they are
background).
![\begin{figure}
\par\includegraphics[width=17cm,clip]{optik.ps}
\end{figure}](/articles/aa/full/2003/12/aa2810/Timg52.gif) |
Figure 4: The contours of the residuals superposed on the image of the DSS. The contours are the same as in Figs. 2 and 3. |
| Open with DEXTER | |
We can estimate the temperature of the sub-structure by assuming that it contributes about 30% to the total flux in the region, where it is located (see above). We perform simulations of spectra, assuming a main cluster temperature of 8 keV and a sub-group temperature of 1 keV and calculate the corresponding hardness ratio. We find a hardness ratio of 0.29, in agreement with the hardness ratio values in the region of the substructure. If interactions occur and are important for the emission mechanism, we expect the cold phase to be at a temperature close to or below 1 keV. Thus, 1 keV seems to be a good upper limit for the temperature of the structure. Temperatures around or below 1 keV were found to be typical values for compact groups of galaxies (see for example Helsdon & Ponman 2000).
In the scenario described above, the two galaxies must have a tangential component with respect to the centre of the main cluster, which implies that the merger is not a simple two-body encounter. The Coma cluster is surrounded by filamentary structures (see for example Huchra et al. 1990), and their gravitational pull could explain the non-zero impact parameter of the two galaxies on their infall onto the cluster.
Vikhlinin et al. (2001) have shown based on a study of Chandra data that the temperatures of the two dominant central galaxies NGC 4874 and NGC 4889 are significantly cooler than the surrounding gas. In our study we do not see a temperature drop in these regions, primarily because we average over a too wide area in our analysis to resolve this cooler gas.
The X-ray deficit in the South and East is difficult to explain. Comparing
the overall morphology of the gas and temperature distribution with recent
studies based on hydrodynamical simulations, such as Roettiger et al.
(1997) and Ricker & Sarazin (2001), we cannot find a
scenario which matches all observed features. We therefore think that this
decrement in X-ray emission is either due to tidal forces linked to the merger
with the Western structure![]() , or to an older merger,
possible connected to the Northern part of the
Western substructure. This might be the remnant of a sub group,
which already passed the core once. However, the physics of this deficit
in emission might be more complex. We want to stress, again, that this
decrement is
not an artefact of our beta-model fitting. Changing the
parameters for the model (position angle, core radius, centre position and
background) over a considerable range does not alter the result
(see above).
, or to an older merger,
possible connected to the Northern part of the
Western substructure. This might be the remnant of a sub group,
which already passed the core once. However, the physics of this deficit
in emission might be more complex. We want to stress, again, that this
decrement is
not an artefact of our beta-model fitting. Changing the
parameters for the model (position angle, core radius, centre position and
background) over a considerable range does not alter the result
(see above).
We performed a substructure and spectroimaging study based on the XMM-Newtondata of the Coma cluster. The data show the existence of substructures which are very likely interacting with the main cluster. The combination of spatial and spectral information based on data obtained with XMM-Newtonallows us to put global constraints on the dynamical state of the Coma cluster. These are important for our understanding of the physics of clusters. The results presented here show the large potential of future studies of clusters of galaxies observed with XMM-Newton.
Acknowledgements
We would like to thank the XMM-NewtonEPIC-team for support. In particular we are grateful to K. Dennerl, M. Freyberg and F. Haberl for fast and very competent replies to our questions. Furthermore we would like to thank J. Ballet for his help concerning the analysis based on the XMM-NewtonSAS software. We are grateful for the discussions with S. Schindler concerning cluster mergers and M. Arnaud in general. We would also like to thank J. Huchra, who acted as referee for the careful reading of the manuscript. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. We acknowledge the use of NASA's SkyView facility (http://skyview.gsfc.nasa.gov) located at NASA Goddard Space Flight Center. This research has made use of NASA's Astrophysics Data System Service. This work is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA).
| pointing | camera | exposure | RA | Dec | date |
| No. | in s | in deg | in deg | mm/yy | |
| 10 | m1 | 18576 | 194.910 | 28.1278 | 06/00 |
| m2 | 18584 | ||||
| pn | 17500 | ||||
| 11 | m1 | 13845 | 194.652 | 28.3989 | 06/00 |
| m2 | 15237 | ||||
| pn | 13754 | ||||
| 1 | m1 | 26559 | 194.199 | 27.4019 | 06/00 |
| m2 | 26594 | ||||
| pn | 23732 | ||||
| 2 | m1 | 26046 | 194.427 | 27.7272 | 12/00 |
| m2 | 26062 | ||||
| pn | 15000 | ||||
| 3 | m1 | 12519 | 194.634 | 27.4033 | 06/00 |
| m2 | 11523 | ||||
| pn | 11730 | ||||
| 4 | m1 | 476 | 195.019 | 27.5233 | 06/00 |
| m2 | 582 | ||||
| pn | 2970 | ||||
| 5 | m1 | 14977 | 194.865 | 27.7814 | 05/00 |
| m2 | 16485 | ||||
| pn | 14211 | ||||
| 6II | m1 | 14943 | 194.708 | 27.9811 | 12/00 |
| m2 | 14942 | ||||
| pn | 8874 | ||||
| 6 | m1 | 6548 | 194.708 | 27.9811 | 06/00 |
| m2 | 6744 | ||||
| pn | 3969 | ||||
| 7II | m1 | 23755 | 194.365 | 28.1447 | 12/00 |
| m2 | 23245 | ||||
| pn | 8874 | ||||
| 7 | m1 | 3153 | 194.365 | 28.1447 | 06/00 |
| m2 | 2960 | ||||
| pn | 358 | ||||
| 8 | m1 | 23455 | 195.357 | 27.7314 | 12/00 |
| m2 | 24172 | ||||
| pn | 18430 | ||||
| 9 | m1 | 19951 | 195.136 | 27.9497 | 06/00 |
| m2 | 20361 | ||||
| pn | 15443 | ||||
| bgd | m1 | 21145 | 195.404 | 27.3311 | 06/00 |
| m2 | 21563 | ||||
| pn | 17534 | ||||
| cen | m1 | 16103 | 194.945 | 27.9500 | 05/00 |
| m2 | 15894 | ||||
| pn | 14595 |