1 - Astrophysics Research Institute, Liverpool John Moores University, Twelve Quays House, Egerton Wharf, Birkenhead, CH41 1LD, UK
2 - South African Astronomical Observatory, PO Box 9, Observatory 7935, South Africa

Abstract
We present new $BV(RI)_{\rm C}$ photometry for a sample of 54 local G and K stars with accurate Hipparcos parallaxes in the metallicity range $-0.4 \leq {\rm [Fe/H]} \leq +0.3$ . We use this sample to develop a completely model-independent main sequence (MS) fitting method which we apply to 4 open clusters - the Hyades, Praesepe, the Pleiades and NGC 2516 - which all have direct Hipparcos parallax distance determinations. Comparison of our MS-fitting results with distances derived from Hipparcos parallaxes enables us to explore whether the discrepancy between the Hipparcos distance scale and other MS-fitting methods found for some clusters is a consequence of model assumptions. We find good agreement between our results and the Hipparcos ones for the Hyades and Praesepe. For the Pleiades and NGC 2516, when adopting the solar abundance determined from spectroscopy, we find significant disagreement at a level similar to that found by other MS-fitting studies. However, the colour-colour relationship for both these clusters suggests that their metallicity is significantly subsolar. Since the MS-fitting method relies on matching the cluster colours to a template MS, we argue that, when applying this method, the appropriate metallicity to adopt is the photometric subsolar one, not the solar abundance indicated by spectroscopy. Adopting photometric metallicities for all 4 clusters, we find complete agreement with the Hipparcos results and hence we conclude that the mismatch between the spectroscopic and photometric abundances for the Pleiades and NGC 2516 is responsible for the discrepancies in distance estimates found by previous studies. The origin of this mismatch in abundance scales remains an unsolved problem and some possible causes are discussed.

Key words: stars: abundances - stars: distances - open clusters and associations: individual: Hyades, Pleiades

The results of the Hipparcos astrometric mission (European Space Agency 1997) have recently provided the distances to several open clusters derived from their directly measured trigonometric parallaxes. These distances have, in turn, been used to test theoretical stellar models and investigate the evolutionary status of open cluster stars, by comparing theoretical isochrones with cluster Colour-Magnitude-Diagrams (CMDs) (see e.g., Castellani et al. 2002 and references therein).

It was very soon realized that the distances obtained by fitting the Main Sequence (MS) of isochrones with the appropriate metallicity to the corresponding cluster sequence (MS-fitting) do not always agree with the Hipparcos parallax distances. This was first shown by Pinsonneault et al. (1998, hereafter P98), whose theoretical isochrones, and their isochrones calibrated on the Hyades shape, provide MS-fitting distances in agreement, within the associated 1 $\sigma$ errors, with Hipparcos results for the cases of Hyades, Praesepe and $\alpha$ -Persei. However the Pleiades MS-fitting result is significantly longer than the Hipparcos value, whilst that of Coma Ber is significantly shorter. The case of the Pleiades is particularly egregious, with a discrepancy of almost 0.3 mag in the distance modulus.

Subsequent work has been devoted to the comparison of the Pleiades CMD with local MS stars of comparable metallicity, and with accurate parallaxes, in order to avoid the use of any theoretical input in deriving the MS-fitting distance. Soderblom et al. (1998) selected a sample of "young'' (on the basis of their chromospheric activity) solar-type stars (therefore supposedly of solar metallicity, like the Pleiades), which should represent the local counterpart of Pleiades stars; they have hence shown that the location of this local sample is compatible with the longer MS-fitting distance, not with the Hipparcos one. Only supposedly more metal poor objects (based mainly on their space velocity, not on spectroscopic estimates) show a MS location in agreement with the Hipparcos distance.

Stello & Nissen (2001) considered a sample of local F-stars with accurate parallaxes and Strömgren photometry, and selected objects within $\sim$ $\pm$ 0.10 of the cluster [Fe/H] - the Strömgren photometry for both Pleiades and field stars being used to derive the relative [Fe/H] and reddening values. The observed magnitude distribution of these field stars at a fixed colour shows a large spread due to the convolution of observational errors, binary contamination and evolutionary distribution, since F-stars 1-2 Gyr old already depart from the Zero Age MS (ZAMS). However, the authors were able to determine statistically a ZAMS locus from the lower envelope of the MS distribution which, again, was shown to lie above the Pleiades MS if the Hipparcos distance is assumed for the cluster. For example, in the M_V/(b-y)₀ plane the discrepancy is $\sim$ 0.25 mag.

On the other hand, very recently Castellani et al. (2002) have been able to achieve a good fit of the Pleiades MS with their theoretical isochrones and the Hipparcos distance, employing a subsolar abundance, namely ${\rm [Fe/H]} \sim -0.15$ , but one which is still compatible with recent metallicity determinations. At the same time their models can fit the Hyades MS with the Hipparcos distance, unlike the case of P98 whose models reproduce the Hyades distance, but not that of the Pleiades. The difference between these 2 theoretical results may be due to different sensitivities of the isochrone colours to [Fe/H]; in fact, according to P98 one needs ${\rm [Fe/H]} < -0.20$ to solve the discrepancy.

These conflicting results about the open cluster Hipparcos and MS-fitting distance scales are disturbing for reasons with far-reaching consequences, beyond merely the testing of stellar evolution models. Various young clusters harbour Cepheid stars, whilst intermediate-age and old clusters have Red Clump stars, both classes of objects being widely employed as extragalactic distance indicators. Testing of the properties of these standard candles in order to determine accurate zero-point calibrations necessarily makes use of MS-fitting distances to their parent cluster, since they are located at distances too large to have accurate Hipparcos parallaxes. In addition, MS-fitting distances are used to tie the Galactic globular cluster distances (and hence the age of the Galaxy) to the Hipparcos parallaxes, due to the lack of a precise parallax calibration for the RR Lyrae star absolute brightness (Groenewegen & Salaris 1999, but see also recent parallax determination for RR Lyrae itself by Benedict et al. 2002). It is therefore paramount to assess the accuracy of MS-fitting distances based on field stars with accurate Hipparcos parallaxes, by using open clusters on which both techniques can be applied.

In this paper we further analyze the consistency between MS-fitting and direct Hipparcos parallax distances for the Hyades, Praesepe, Pleiades and NGC 2516 open clusters; these clusters have deep and accurate enough CMDs to apply with confidence the MS-fitting method. We employ a purely empirical approach, based on selecting a sample of 54 G-stars from the local field MS population which we use to construct a template MS, and for which we have secured homogeneous $BV(RI)_{\rm C}$ photometry. Strict selection criteria ensure that these stars are not binary, have accurate Hipparcos parallaxes, and populate a region of the lower MS completely unaffected by age differences between field and cluster stars.

The layout of the paper is as follows: in Sect. 2 we present the new field dwarf sample, detailing selection criteria and sample biases, Sect. 3 describes our method for determining [Fe/H] values for the sample stars, whilst Sect. 4 gives full details of our empirical MS-fitting method. In Sect. 5 we present our results for the Hyades, Praesepe, Pleiades and NGC 2516 and in Sect. 6 we summarize these results and discuss their implications.

2 The field dwarf sample

2.1 Selection criteria

Suitable field dwarfs were selected using the three basic criteria of parallax error, absolute magnitude and metallicity, as described below.

All the stars in the sample have Hipparcos parallaxes with errors < $12\%$ , enabling both an accurate determination of their absolute magnitudes and an assessment of the Lutz-Kelker bias in the sample (see Sect. 2.3).

Absolute magnitudes are limited to stars with $M_{V} \geq 5.4$ to ensure they are unevolved and on the lower MS, and hence their position in a CMD does not depend on their age, which is not known.

Metallicities for the field dwarfs are determined from Strömgren indices available in the literature (Hauck & Mermilliod 1998). During the process of sample selection, the calibration of Schuster & Nissen (1989) (hereafter SN89) was used to calculate the field dwarf metallicities, and the range was limited to $-0.3 \leq {\rm [Fe/H]} \leq +0.3$ to be compatible with the range of abundances of the open clusters to be studied. However, in the early stages of this work it became apparent that the SN89 calibration for G dwarfs may not be reliable in this metallicity range. Twarog et al. (2002) find that the SN89 calibration systematically underestimates abundances for stars with ${\rm [Fe/H]} > \sim -0.2$ , and that the effect is strongly colour dependent. The issue of determining metallicities from the Strömgren indices will be addressed in Sect. 3.

The Hipparcos catalogue entries for all suitable candidates meeting the initial criteria were carefully checked to avoid the inclusion of any binaries or variable stars. From this selection process 54 suitable field dwarfs were identified and we have acquired new photometric $BV(RI)_{\rm C}$ data for all of them.

2.2 Observations and data reduction

Johnson-Cousins $BV(RI)_{\rm C}$ data for 54 field dwarfs were obtained at the Sutherland site of the South African Astronomical Observatory (SAAO) in 2002 February, March and June using the St Andrews Photometer on the 1-m telescope and, for a few of the brightest stars, the Modular Photometer on the 0.5-m telescope. Both photometers are of relatively conventional design and employ Hamamatsu R943-02 GaAs photomultipliers. All reductions were carried out using standard SAAO software and the data were transformed to the Cousins E-region system (see Menzies et al. 1989 for a compilation of standard stars). Four stars were observed on both telescopes and used to check for zero point differences; these were found to be $\leq$ 0.002 (and therefore insignificant) for all quantities except $(V-I)_{\rm C}$ where a mean difference of $0.005 \pm 0.005$ was found. This is hardly significant, but a correction of -0.005 was applied to the $(V-I)_{\rm C}$ data from the 0.5-m system to make the total data set as uniform as possible. The mean standard deviations of the data sample are $\pm$ 0.007, 0.004, 0.003 and 0.005 for V, (B-V), $(V-R)_{\rm C}$ and $(V-I)_{\rm C}$ respectively (126 observations of 54 stars) and we do not believe that any residual systematic errors in the data (arising from transformation errors) would be significantly larger than these values.

Table 1 presents the new data and lists Hipparcos number, observed V-magnitude, (B-V), $(V-R)_{\rm C}$ and $(V-I)_{\rm C}$ colours, standard deviations (in mmags), number of observations, parallax and parallax error (in mas) and [Fe/H] (calculated as described in Sect. 3). Our empirical MS-fitting method employs the (B-V) and $(V-I)_{\rm C}$ colour indices - the $(V-R)_{\rm C}$ observations are listed for information only.

Table 1: New photometry for field dwarf sample.
HIP V (B-V) $(V-R)_{\rm C}$ $(V-I)_{\rm C}$ $\sigma_{V}$ $\sigma_{BV}$ $\sigma_{VR}$ $\sigma_{VI}$    N $\pi$ $\Delta\pi$ [Fe/H]

39088 9.239 0.824 0.449 0.843 9 0 1 2    2 19.52 0.83 0.334

39342 7.166 0.889 0.480 0.896 2 3 5 4    2 57.88 0.58 -0.043

40051 8.778 0.897 0.502 0.937 6 3 3 4    4 29.86 0.82 0.090

40419 8.272 0.737 0.406 0.800 2 5 2 2    4 29.39 1.14 -0.483

42074 7.330 0.819 0.445 0.841 0 5 0 2    2 45.95 1.01 0.044

42281 8.688 0.883 0.484 0.901 1 5 3 3    4 27.02 1.18 0.310

42914 8.183 0.763 0.420 0.804 5 1 5 1    4 32.14 0.82 -0.095

44341 8.028 0.819 0.429 0.819 2 2 2 2    2 32.18 1.09 0.210

44719 8.410 0.772 0.421 0.813 4 4 2 7    2 25.83 0.91 0.034

46580 7.203 1.020 0.577 1.065 3 2 1 9    2 78.87 1.02 -0.110

46422 8.855 0.843 0.465 0.893 5 5 2 3    2 25.40 0.83 -0.204

48754 8.524 0.748 0.405 0.783 2 10 5 11    3 27.18 1.10 -0.321

50032 9.068 0.859 0.470 0.884 5 3 1 8    3 23.19 1.09 0.022

50274 8.966 0.790 0.428 0.827 4 3 0 2    2 22.42 0.82 -0.246

50713 9.360 0.781 0.423 0.807 11 3 1 4    3 17.30 1.26 0.134

50782 7.769 0.784 0.423 0.806 16 6 6 7    2 37.30 1.31 0.063

51297 8.859 0.818 0.449 0.861 4 2 1 3    3 29.83 1.03 -0.318

54538 9.738 0.785 0.437 0.845 3 2 4 8    3 16.39 1.24 -0.156

55210 7.275 0.747 0.413 0.788 7 4 1 1    2 45.48 1.00 -0.222

57321 9.370 0.783 0.429 0.814 0 5 3 3    2 18.94 1.33 -0.073

58536 8.411 0.760 0.416 0.793 2 1 4 2    2 27.81 1.05 0.033

58949 8.166 0.745 0.420 0.809 3 2 0 0    2 30.58 1.02 0.008

59572 7.918 0.800 0.426 0.791 3 6 2 0    2 32.30 1.02 0.374

59639 8.633 0.902 0.499 0.932 7 5 0 1    2 31.54 0.83 0.027

61291 7.143 0.848 0.480 0.896 0 4 0 0    2 61.83 0.63 -0.205

61998 8.441 0.726 0.403 0.770 3 2 1 2    2 27.45 1.13 -0.242

62942 8.247 0.861 0.475 0.903 8 2 0 3    2 38.12 1.44 -0.094

64103 9.668 0.696 0.385 0.746 7 3 6 8    2 14.41 1.48 -0.290

64125 9.402 0.816 0.459 0.878 6 0 1 0    2 19.08 1.28 -0.288

65121 8.594 0.949 0.524 0.969 2 2 2 1    2 32.83 1.08 0.142

65646 10.773 0.998 0.599 1.112 4 6 0 1    2 18.90 2.38 -0.401

67344 8.340 0.829 0.450 0.848 9 3 2 2    2 31.78 1.06 0.052

68936 8.356 0.833 0.443 0.824 0 7 1 5    2 26.14 1.18 0.444

69075 9.495 0.956 0.559 1.040 2 0 1 1    2 28.79 1.36 -0.490

69301 10.760 0.905 0.500 0.929 1 0 0 2    2 15.21 2.44 -0.208

69357 7.938 0.869 0.480 0.906 10 3 1 2    3 43.35 1.40 -0.081

69570 8.235 0.673 0.375 0.732 4 2 0 3    2 27.62 1.12 -0.557

71673 10.203 0.770 0.430 0.827 3 0 0 2    2 16.33 1.62 -0.182

72312 7.761 0.896 0.500 0.935 1 0 1 1    2 50.84 1.04 -0.123

72339 8.046 0.786 0.423 0.804 9 2 2 9    2 33.60 1.51 0.133

72577 9.073 0.972 0.553 1.030 9 2 0 7    2 32.53 1.56 -0.301

72688 7.804 1.014 0.583 1.069 2 4 0 3    2 58.96 1.05 -0.027

72703 8.380 0.702 0.381 0.746 4 2 0 6    2 25.68 1.29 -0.386

73547 7.736 0.719 0.397 0.768 0 4 1 4    2 36.84 0.98 -0.522

73963 10.343 0.898 0.503 0.943 10 2 5 6    3 13.57 1.91 -0.116

75266 8.281 0.993 0.542 0.990 12 2 1 5    3 39.35 1.37 0.155

80043 8.901 0.952 0.550 1.032 0 0 1 0    2 38.80 1.37 -0.456

80700 8.807 0.779 0.422 0.803 6 1 1 3    3 21.50 1.27 0.314

81237 8.756 0.773 0.426 0.812 13 0 1 3    3 25.32 1.15 -0.149

84164 9.186 0.852 0.504 0.953 2 2 0 4    2 17.74 1.51 -0.304

85425 7.879 0.692 0.390 0.745 1 2 2 0    2 32.04 1.24 -0.432

87089 8.912 0.823 0.474 0.898 10 9 9 12    2 26.16 1.16 -0.112

88553 8.460 0.718 0.403 0.766 3 0 0 2    2 26.99 1.19 -0.149

89497 8.545 0.760 0.421 0.806 9 3 2 0    2 27.11 1.20 -0.088

**Table 1:** New photometry for field dwarf sample.
HIP	V	(B-V)	$(V-R)_{\rm C}$	$(V-I)_{\rm C}$	$\sigma_{V}$	$\sigma_{BV}$	$\sigma_{VR}$	$\sigma_{VI}$	N	$\pi$	$\Delta\pi$	[Fe/H]
39088	9.239	0.824	0.449	0.843	9	0	1	2	2	19.52	0.83	0.334
39342	7.166	0.889	0.480	0.896	2	3	5	4	2	57.88	0.58	-0.043
40051	8.778	0.897	0.502	0.937	6	3	3	4	4	29.86	0.82	0.090
40419	8.272	0.737	0.406	0.800	2	5	2	2	4	29.39	1.14	-0.483
42074	7.330	0.819	0.445	0.841	0	5	0	2	2	45.95	1.01	0.044
42281	8.688	0.883	0.484	0.901	1	5	3	3	4	27.02	1.18	0.310
42914	8.183	0.763	0.420	0.804	5	1	5	1	4	32.14	0.82	-0.095
44341	8.028	0.819	0.429	0.819	2	2	2	2	2	32.18	1.09	0.210
44719	8.410	0.772	0.421	0.813	4	4	2	7	2	25.83	0.91	0.034
46580	7.203	1.020	0.577	1.065	3	2	1	9	2	78.87	1.02	-0.110
46422	8.855	0.843	0.465	0.893	5	5	2	3	2	25.40	0.83	-0.204
48754	8.524	0.748	0.405	0.783	2	10	5	11	3	27.18	1.10	-0.321
50032	9.068	0.859	0.470	0.884	5	3	1	8	3	23.19	1.09	0.022
50274	8.966	0.790	0.428	0.827	4	3	0	2	2	22.42	0.82	-0.246
50713	9.360	0.781	0.423	0.807	11	3	1	4	3	17.30	1.26	0.134
50782	7.769	0.784	0.423	0.806	16	6	6	7	2	37.30	1.31	0.063
51297	8.859	0.818	0.449	0.861	4	2	1	3	3	29.83	1.03	-0.318
54538	9.738	0.785	0.437	0.845	3	2	4	8	3	16.39	1.24	-0.156
55210	7.275	0.747	0.413	0.788	7	4	1	1	2	45.48	1.00	-0.222
57321	9.370	0.783	0.429	0.814	0	5	3	3	2	18.94	1.33	-0.073
58536	8.411	0.760	0.416	0.793	2	1	4	2	2	27.81	1.05	0.033
58949	8.166	0.745	0.420	0.809	3	2	0	0	2	30.58	1.02	0.008
59572	7.918	0.800	0.426	0.791	3	6	2	0	2	32.30	1.02	0.374
59639	8.633	0.902	0.499	0.932	7	5	0	1	2	31.54	0.83	0.027
61291	7.143	0.848	0.480	0.896	0	4	0	0	2	61.83	0.63	-0.205
61998	8.441	0.726	0.403	0.770	3	2	1	2	2	27.45	1.13	-0.242
62942	8.247	0.861	0.475	0.903	8	2	0	3	2	38.12	1.44	-0.094
64103	9.668	0.696	0.385	0.746	7	3	6	8	2	14.41	1.48	-0.290
64125	9.402	0.816	0.459	0.878	6	0	1	0	2	19.08	1.28	-0.288
65121	8.594	0.949	0.524	0.969	2	2	2	1	2	32.83	1.08	0.142
65646	10.773	0.998	0.599	1.112	4	6	0	1	2	18.90	2.38	-0.401
67344	8.340	0.829	0.450	0.848	9	3	2	2	2	31.78	1.06	0.052
68936	8.356	0.833	0.443	0.824	0	7	1	5	2	26.14	1.18	0.444
69075	9.495	0.956	0.559	1.040	2	0	1	1	2	28.79	1.36	-0.490
69301	10.760	0.905	0.500	0.929	1	0	0	2	2	15.21	2.44	-0.208
69357	7.938	0.869	0.480	0.906	10	3	1	2	3	43.35	1.40	-0.081
69570	8.235	0.673	0.375	0.732	4	2	0	3	2	27.62	1.12	-0.557
71673	10.203	0.770	0.430	0.827	3	0	0	2	2	16.33	1.62	-0.182
72312	7.761	0.896	0.500	0.935	1	0	1	1	2	50.84	1.04	-0.123
72339	8.046	0.786	0.423	0.804	9	2	2	9	2	33.60	1.51	0.133
72577	9.073	0.972	0.553	1.030	9	2	0	7	2	32.53	1.56	-0.301
72688	7.804	1.014	0.583	1.069	2	4	0	3	2	58.96	1.05	-0.027
72703	8.380	0.702	0.381	0.746	4	2	0	6	2	25.68	1.29	-0.386
73547	7.736	0.719	0.397	0.768	0	4	1	4	2	36.84	0.98	-0.522
73963	10.343	0.898	0.503	0.943	10	2	5	6	3	13.57	1.91	-0.116
75266	8.281	0.993	0.542	0.990	12	2	1	5	3	39.35	1.37	0.155
80043	8.901	0.952	0.550	1.032	0	0	1	0	2	38.80	1.37	-0.456
80700	8.807	0.779	0.422	0.803	6	1	1	3	3	21.50	1.27	0.314
81237	8.756	0.773	0.426	0.812	13	0	1	3	3	25.32	1.15	-0.149
84164	9.186	0.852	0.504	0.953	2	2	0	4	2	17.74	1.51	-0.304
85425	7.879	0.692	0.390	0.745	1	2	2	0	2	32.04	1.24	-0.432
87089	8.912	0.823	0.474	0.898	10	9	9	12	2	26.16	1.16	-0.112
88553	8.460	0.718	0.403	0.766	3	0	0	2	2	26.99	1.19	-0.149
89497	8.545	0.760	0.421	0.806	9	3	2	0	2	27.11	1.20	-0.088

2.3 Lutz-Kelker corrections, reddening and metallicity bias

Since the field dwarf sample was selected on parallax error, their absolute magnitudes are subject to Lutz-Kelker bias which has the effect of systematically underestimating their distances (Lutz & Kelker 1973). Following the procedures of Hanson (1979), Lutz-Kelker corrections were derived based on the distribution of proper motions of the sample stars, which were taken from the Hipparcos database. Hence, absolute magnitudes were corrected using the relation:

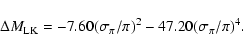
Reddening for the field dwarfs was neglected since all the stars in the sample lie well within 75 pc of the Sun (the average distance being 35.9 pc), a region in which several authors have concluded that reddening effects are negligible (see discussion in Percival et al. 2002, hereafter Paper I).

We made no attempt to correct for any metallicity bias in the sample since our previous investigation showed that any effect on the derived cluster distances is very small, even when working in a lower metallicity regime (see discussion in Paper I). For the current sample, the peak of the metallicity distribution falls roughly between ${\rm [Fe/H]} = -0.2$ and solar, which reflects the distribution of the parent population in the solar neighbourhood and so any biases are likely to be negligible.

3 Metallicity calibration

The MS-fitting method relies crucially on determining, on an homogeneous scale, the metallicities of a) the clusters being studied and b) the field dwarf sample, which is used to construct a template main sequence. In our earlier study of the Galactic Globular Cluster 47 Tucanae (Paper I), we used Strömgren data and the G-star calibration of SN89 to calculate abundances for a sample of local subdwarfs in the range $-1.0 < {\rm [Fe/H]} < -0.3$ - a procedure adopted by many other authors for deriving abundances of sub-solar metallicity stars. However, Twarog et al. (2002) find a discrepancy in this G-star calibration which came to light when analyzing cool dwarfs of late spectral type in the Hyades, for which the abundance is known to be super-solar. The effect appears to be systematic and strongly colour dependent and can lead to an underestimate of the abundance of solar or super-solar abundance stars by as much as 0.4 dex. This problem may begin to affect stars with abundances greater than ${\rm [Fe/H]} \sim -0.2$ and is most pronounced when b-y is larger than $\sim$ 0.47. Since in our study we are using exclusively unevolved, lower MS stars at roughly solar metallicity, these are the very stars which are most strongly affected.

Twarog et al. (2002) suggest that at least one of the sources of the problem lies in the metallicity dependence of the Strömgren c₁ index, which has previously been underestimated for more metal-rich stars. This results in some main-sequence stars with high metallicities (above the Hyades value) being classified as giants because of their high c₁ index, which in turn can lead to systematic discrepancies when these indices are used to derive abundances. The original SN89 calibration was intended to apply across a large metallicity range, $-2.6 < {\rm [Fe/H]} < 0.4$ , and accounted for the fact that some stars have started to evolve off the main sequence. Hence, it has a complicated functional form with many cross terms, making it virtually impossible to disentangle the metallicity dependence of one particular term (c₁ in this case). In an attempt to address this problem, Haywood (2002, hereafter H02) has provided an updated version of the SN89 calibration, using more recent spectroscopic data for the calibrating stars, which keeps the same functional form and redetermines the coefficients of the various terms. Again, this calibration is valid over a wide metallicity range, $-2.0 < {\rm [Fe/H]} < 0.5$ , and accounts for evolving stars. Both the SN89 and the H02 calibrations require the metallicity of the Hyades to be specified as an input parameter, specifically, Hyades stars are included in the fitting procedure with an assumed Hyades metallicity, and given double weighting to force the fit at the high metallicity end of the scale. SN89 assumed ${\rm [Fe/H]_{Hyades}}=0.13$ , whilst H02 adopts a value of 0.14.

Since all the field dwarfs in our MS-fitting sample are specifically chosen to be unevolved stars (ensured by the requirement that $M_{V} \geq 5.4$ ) and should all be within $\sim$ 0.4 dex of solar metallicity (specifically, they are not low metallicity halo stars, but rather local disk stars) the metallicity calibration from Strömgren indices can potentially be a lot simpler. The most important element in any attempted metallicity calibration is to have an homogeneous sample of spectroscopically determined abundances for stars for which there are also Strömgren data. It is also vital to be able to tie the abundance scale of any particular sample to some known zero-point, so that useful comparisons can be made.

For this purpose, we chose to use the sample of Favata et al. (1997) (hereafter FMS97), who present [Fe/H] determinations from homogeneous spectroscopic data for a volume limited sample of G and K dwarfs from the Gliese catalogue of nearby stars. FMS97 compare their abundance scale with the catalogue of Taylor (1995, and references therein), in which literature [Fe/H] values for cool stars are converted to a coherent temperature scale (the same temperature scale as that adopted by FMS97). They find almost one-to-one correspondence for the stars in common between the 2 samples, the slope of the mean relationship being 1.028 with a RMS scatter of 0.09, and negligible offset (see FMS97, their Fig. 2). Taylor (1994) finds ${\rm [Fe/H]} = 0.107 \pm0.01$ for the Hyades, a value which is consistent with the scale of Gratton (2000, hereafter G00) for open clusters, which we will use in this work. G00 consists of a self-consistent set of abundance determinations for open clusters compiled from values in the literature, and calibrated against high resolution spectroscopic data, the listed value for the Hyades being ${\rm [Fe/H]} = 0.13 \pm 0.06$ . Hence we adopt the metallicity scale of FMS97 for our calibrating sample without any change in zero-point.

We identified all the stars in the FMS97 sample which met the same basic criteria as our field dwarf sample and had Strömgren data in the Hauck & Mermilliod (1998) catalogue. Hence a cut in magnitude was made at $M_{V} \geq 5.4$ (derived from Hipparcos parallaxes and photometry in the literature) to ensure that the calibrating stars were unevolved, and the metallicity range was limited to $-0.45 \leq {\rm [Fe/H]} \leq +0.35$ . This resulted in a subset of 18 stars. We then took all the Hyades members listed as single and non-variable in Perryman et al. (1998) with Strömgren indices in the Hauck & Mermilliod catalogue and made a cut in b-y of $0.31 \leq b-y \leq 0.79$ ; this corresponds roughly to an absolute magnitude cut of 3.5 < M_V < 8.0 and yielded a subset of 41 stars. We then examined the relationship between the Strömgren b-y, c₁ and m₁ indices and the spectroscopic metallicities for the FMS97 sample, by comparing them with the Hyades main sequence relationships. As suggested by Twarog et al. (2002), we found that the principal metallicity indicator for these unevolved stars is the c₁ index. We then proceeded as follows:

The Hyades main sequence in c₁ vs. m₁ was fitted with a 4th order polynomial via a least-squares fitting routine. The best-fit relationship was found to be:

Applying these relationships to the individual stars in the FMS97 sample to "predict'' their metallicities, and comparing these values with their spectroscopic determinations, we find that

A comparison of our predicted metallicities with those of H02 is rather good - for our full field dwarf sample, and including the 41 Hyads used in our calibration, the line of best-fit is ${\rm [Fe/H]_{us}} = 0.946{\rm [Fe/H]_{Haywood}} + 0.006$ , with a dispersion of 0.13 dex.

3.1 Cluster abundances

In order to ensure that we are working with a self-consistent set of abundances for the field dwarf sample and the cluster sample, we adopted for reference the abundance scale of G00 for the clusters in this study; as previously discussed, the Hyades [Fe/H] listed by G00 agrees well with the result from our Strömgren calibration for the field dwarfs. Table 2 lists the cluster abundances from G00, along with cluster ages taken from Pinsonneault et al. (2000).

4 Empirical MS-fitting technique

The basic MS-fitting method consists of using the field dwarf sample defined above to construct a template main sequence for comparison with the main sequence of the cluster in question. This necessitates "shifting'' each sample star in colour to account for the differences in metallicity between the individual stars (which all have different abundances, within the specified range) and the cluster. Then the shift in V-magnitude required to match the template MS to the cluster main line (after cluster reddening is accounted for) represents the distance modulus, (m-M)₀.

**Table 2:** Reference metallicities and ages of open clusters.
Cluster	${\rm [Fe/H]_{G00}}$	Age (Myr)
Hyades	$+0.13\pm0.06$	650
Praesepe	$+0.04\pm0.06$	600
Pleiades	$-0.03\pm0.06$	100
NGC 2516	$-0.16\pm0.11$	140

We note here that, to be physically correct, the procedure of shifting the field dwarfs to match the metallicity of a particular cluster should preserve mass (Reid 1997). This implies that adjustments to both magnitude and colour would be necessary to match each field dwarf to a star of equivalent mass, at the metallicity of the cluster. However, since mass also evolves along the MS, at a given colour, luminosity and metallicity, the mass of a star also depends on its age. Since in general we do not have reliable ages for local stars it is not usually possible to apply these magnitude shifts in a physically correct way. In Paper I, we tested the effect of applying colour and magnitude corrections to the subdwarf sample (for which $-1.0 < {\rm [Fe/H]} < -0.3$ ) assuming an arbitrary fixed age of 10 Gyr. The resulting template MS covered a different range of magnitudes than the one which included colour shifts only, as shifting a star of fixed mass to a lower metallicity increases its luminosity, and vice-versa. However, since the shape of the isochrones is essentially the same across the metallicity range we are using (see Sect. 4.1), the shape of the resulting template is not changed and, consequently, fits to these revised templates yield the same distance moduli as the templates constructed using colour shifts only.

Colour-magnitude diagrams for the field dwarf sample, before any shifts have been applied, are displayed in Fig. 2. The (B-V) and (V-I) colours are the observed values, as listed in Table 1, and the M_V values are the LK-corrected absolute magnitudes.

Since one of the aims of this work is to explore whether discrepancies between Hipparcos parallax distances and MS-fitting distances for some clusters are due to model dependencies in MS-fitting methods, we want to derive the metallicity dependent colour shifts empirically i.e. we do not want to rely on model isochrones at any stage in the procedure, so that our results will not be model dependent.

4.1 Method

We make only one assumption, which is that the shape of the isochrones is the same for the portion of the lower MS that we use in the fits, across the narrow metallicity range we have defined. All the field dwarfs which are used to construct the template MS lie in the absolute magnitude range $5.4 \leq M_{V} \leq 7.0$ , where M_V is the LK corrected magnitude, and the metallicity range is as defined by the subset of the FMS97 sample used in the metallicity calibration, namely $-0.45 \leq {\rm [Fe/H]} \leq 0.35$ . The theoretical models of Girardi et al. (2000) show that the isochrones should be parallel in this range in both colour planes. Also, if we combine the local field dwarfs used in this study with those in Paper I (which are in the range $-1.0 < {\rm [Fe/H]} < -0.3$ ), there is no measurable change in slope when the data are binned by metallicity, in either colour plane.

Using this assumption of similarity of shape for isochrones of different metallicities, the metallicity dependent colour shifts are calculated by first determining the colour that each field dwarf would have at a fixed absolute magnitude of M_V=6, which we label (B-V)_{M_V=6} or (V-I)_{M_V=6}. We then look at the relationship between (B-V)_{M_V=6}(or (V-I)_{M_V=6}) and metallicity, [Fe/H], to calculate $\Delta (B-V)$ (or $\Delta (V-I)$ ) as a function of $\Delta {\rm [Fe/H]}$ . The observed colours of the field dwarfs were "corrected'' to their appropriate values at M_V=6 using the slope of the Hyades main sequence, effectively as an empirical isochrone. The Hyades slope was derived using only single stars as defined by Perryman et al. (1998), at their absolute V-magnitudes, as determined from the improved Hipparcos parallaxes of Madsen et al. (2002). Fits were made in the V/(B-V) and V/(V-I) planes, using the $V_{\rm J}$ magnitudes and $(B-V)_{\rm J}$ and $(V-I)_{\rm C}$ colours as listed in the Hipparcos catalogue (fields H5, H37 and H40 respectively). The derived metallicity dependencies were:
$\Delta(B-V) = 0.154 \Delta {\rm [Fe/H]}$ and $\Delta(V-I) = 0.103 \Delta {\rm [Fe/H]}$ . It is important to note that neither the assumed metallicity nor the parallax distance of the Hyades play a part in this process, we are merely using the shape of the Hyades MS. In fact, the derived dependencies are rather insensitive to the exact slope assumed for the main sequence. In the procedure employed above, the Hyades MS was fitted to a cubic function, but the relevant portion in the V/(B-V) plane is actually almost linear, with a gradient of $\sim$ 5. As a quick check, we tested the effect of assuming a MS gradient of 8, a value far outside the expected range of MS slopes. With this assumed slope, the metallicity dependence in (B-V) becomes $\Delta(B-V) = 0.132 \Delta {\rm [Fe/H]}$ , and the change in the distance moduli we ultimately derive is no more than 0.03 mag.

Using the above relationships, the appropriate colour shifts are applied to each field dwarf in the sample, at their absolute magnitudes, to build up a template MS at the metallicity of each cluster to be studied. The template MS corresponding to each particular cluster is then shifted in V-magnitude to match the main line of the cluster in question, the shift in V being equal to the distance modulus, m-M, and the best-fit to the cluster main line is found by using a least-squares fitting routine. Weighted errors are used for the field dwarfs and include both photometry errors and magnitude errors due to errors on the parallax, where $\Delta M_{V} = 2.17(\Delta \pi/\pi)$ . Errors on the metallicities of both the field dwarfs and the cluster are also accounted for and the best-fit distance modulus is found by minimizing $\chi^{2}$ .

We note here that HIP 84164 is an obvious outlier in the CMD and may either be evolved or an unidentified binary. A further 7 stars in the sample have predicted metallicities which fall outside the range used in our calibration. These 8 stars have therefore been omitted from all our subsequent analyses, leaving a total sample of 46 field dwarfs. Details of the fits for each cluster are presented in the next section.

5 Cluster by cluster analysis

Main lines for each of the open clusters were derived from archive data, as detailed below, by fitting to a polynomial using a least-squares fitting routine and minimizing $\chi^{2}$ . Reddening values were taken from the literature and the cluster metallicities of G00 were used, unless otherwise stated.

5.1 Hyades

$V_{\rm J}$ , $(B-V)_{\rm J}$ and $(V-I)_{\rm C}$ data for the Hyades were taken directly from the Hipparcos catalogue (fields H5, H37 and H40, respectively). Most of the data for the Hyades listed in these fields are taken from ground-based photoelectric observations, and a few of the $(V-I)_{\rm C}$ values are transformations from other indices e.g. $(V-I)_{\rm J}$ or $(R-I)_{\rm C}$ .

Shifting the whole field dwarf sample to ${\rm [Fe/H]} = 0.13$ and fitting to the derived cluster main lines results in distance moduli of $(m-M)_{0} = 3.33 \pm 0.06$ from the (B-V) index and $(m-M)_{0} = 3.32 \pm 0.04$ from $(V-I)_{\rm C}$ . Thus we reproduce precisely the Hipparcos parallax distance modulus of $(m-M)_{0} = 3.33 \pm 0.01$ (Perryman et al. 1998).

As a consistency check, we performed the fits using the subset of 9 stars with [Fe/H] values within $\pm$ 0.08 of the Hyades metallicity (with an average of ${\rm [Fe/H]}=0.122$ , coincidentally). Since these stars have, within the errors, the same metallicity as the cluster, no shifts in colour were applied. The resulting distance moduli were: $(m-M)_{0} = 3.33 \pm 0.09$ from (B-V) and $(m-M)_{0} = 3.29 \pm 0.07$ from $(V-I)_{\rm C}$ , thus we are sure there are no systematic effects arising from our derived metallicity dependencies. Figures 3 and 4 show the Hyades main line shifted to its best-fit distance in, respectively, the V/(B-V) and $V/(V-I)_{\rm C}$ planes. In each case, the fit to the full "shifted'' field dwarf sample is shown in the left panel, whilst the fit to the "unshifted'' subset is shown on the right.

5.2 Praesepe

Data for Praesepe were taken from the WEBDA data base at http://obswww.unige.ch/webda/. All the available (B-V) and (V-I) photoelectric data were used to minimize the effect of systematic offsets between the various data sets and averages were taken for stars with multiple observations. The $(B-V)_{\rm J}$ data are principally made up of samples taken from Johnson (1952), Mendoza (1967), Upgren et al. (1979), Weis (1981), Stauffer (1982) and Mermilliod et al. (1990). All the archive (V-I) data for Praesepe are either on the Johnson or the Kron systems, rather than Cousins. $(V-I)_{\rm J}$ data are from Mendoza (1967) whilst the $(V-I)_{\rm K}$ data are made up of the samples from Upgren (1979), Weis (1981) and Stauffer (1982). The (V-I) data were converted to the $(V-I)_{\rm C}$ system using the transformations of Bessell (1979) and Bessell & Weis (1987), where $(V-I)_{\rm C} = 0.778(V-I)_{\rm J}$ and $(V-I)_{\rm C} = 0.227 + 0.9567(V-I)_{\rm K} + 0.0128(V-I)_{\rm K}^{2} -0.0053(V-I)_{\rm K}^{3}$ . Known binaries from Bouvier et al. (2001) were removed and initial cuts were made at 0.4 < (B-V) < 1.4 and $0.45 < (V-I)_{\rm C} < 1.8$ . The cluster main lines were found by successively fitting to a function, making 1 $\sigma$ cuts and then re-fitting, until the solutions converged. This effectively removes any field contamination and unidentified binaries from the sample.

Assuming zero cluster reddening and shifting the field dwarf sample to the G00 metallicity value of ${\rm [Fe/H]} = 0.04 \pm 0.06$ results in distance moduli of $(m-M)_{0} = 6.19 \pm 0.06$ from the (B-V) fits and $(m-M)_{0} = 6.24 \pm 0.04$ from $(V-I)_{\rm C}$ . These results are just consistent, within the 1 $\sigma$ errors, with the Hipparcos parallax distance found by van Leeuwen (1999) of $(m-M)_{0} = 6.37 \pm 0.15$ . A recent study of cluster reddenings by Taylor & Joner (2002) has found an average reddening of E(B-V) = 0.022 for Praesepe. If this reddening is assumed, the cluster distance modulus increases by $\sim$ 0.05 mag, making it more consistent with the Hipparcos result. Figure 5 shows the best-fits to the Praesepe main line in V/(B-V) (left panel) and V/(V-I) (right panel) assuming ${\rm [Fe/H]} = 0.04$ and zero reddening.

5.3 Pleiades

Photoelectric data for the Pleiades were also taken from WEBDA and treated in a similar manner to those for Praesepe. $(B-V)_{\rm J}$ data are principally from Johnson & Mitchell (1958), Mendoza (1967), Landolt (1979) and Stauffer (1984). The available (V-I) data have been transformed onto the Cousins system (see Sect. 5.2) - the $(V-I)_{\rm J}$ sample being from Mendoza (1967) and $(V-I)_{\rm K}$ principally from Stauffer (1984). Averages were taken for stars with multiple observations and initial cuts made at 0.4 < (B-V) < 1.4 and $0.45 < (V-I)_{\rm C} < 1.8$ . Known binaries from Bouvier et al. (1997) and Raboud & Mermilliod (1998) were removed from the samples. The Pleiades is known to have patchy reddening and so individual stars were dereddened and extinction corrected using the values from Breger (1986). For stars with no reddening listed by Breger, an average value of E(B-V) = 0.04 was assumed. The main lines were derived as for Praesepe, by making successive fits and 1 $\sigma$ cuts, until the solution converged.

Using the G00 metallicity value of ${\rm [Fe/H]} = -0.03 \pm 0.06$ leads to a dereddened distance modulus of $(m-M)_{0} = 5.76 \pm 0.06$ from the (B-V) fits and $(m-M)_{0} = 5.58 \pm 0.04$ from $(V-I)_{\rm C}$ (see Fig. 6). These two distance moduli are mutually inconsistent and significantly longer than the Hipparcos parallax distance of $(m-M)_{0} = 5.37 \pm 0.07$ (van Leeuwen 1999).

Performing fits using just the subset of stars with abundances within $\pm$ 0.1 dex of the assumed cluster metallicity, and not applying any colour shifts, produces exactly the same distance moduli in both colour planes and so there do not appear to be any systematic effects arising from our derived metallicity dependencies. We also note here that our dereddened Pleiades main line in V/(B-V) exactly matches that derived by Turner (1979), who, assuming solar abundance for the Pleiades, finds a distance modulus of 5.56, assuming 3.15 for the Hyades i.e. a difference of 2.41 mag. This compares well with our difference of 2.43 mag from these fits at ${\rm [Fe/H]} = -0.03$ .

5.4 NGC 2516

6 Discussion

Employing our empirical MS-fitting method, we derive distance moduli for the Hyades and Praesepe which are in agreement with the Hipparcos parallax distances, when using the cluster spectroscopic metallicity scale by G00. However, for both the Pleiades and NGC 2516 the distance moduli we find are discrepant with respect to those from Hipparcos, in qualitative agreement with the findings by P98 (in the case of the Pleiades) and Terndrup et al. (2002, in the case of NGC 2516). These results are shown in the left panel of Fig. 8, where we display the difference between our derived distance moduli and those from Hipparcos, $\Delta (m-M)^{\rm MSF}_{\rm Hip}$ (where $\Delta (m-M)^{\rm MSF}_{\rm Hip} = (m-M)_{\rm This~paper} - (m-M)_{\rm Hipparcos}$ ) against the age of the cluster (taken from Pinsonneault et al. 2000, see Table 2). Note that in the case of the Pleiades and NGC 2516 we have taken the average of the distance moduli in V/(B-V) and $V/(V-I)_{\rm C}$ . The error bars represent the 1 $\sigma$ errors from this paper and from van Leeuwen (1999), added in quadrature.

These discrepancies in the Pleiades and NGC 2516 distances have already been interpreted as an indication of systematic errors in the Hipparcos parallaxes for these two clusters; these (hypothetical) errors would amount to $\sim$ 1-2 mas (P98) in case of the Pleiades, and only $\sim$ 0.3 mas in case of NGC 2516 (Terndrup et al. 2002). Systematic errors in the Hipparcos parallaxes have however been ruled out by van Leeuwen (1999) and more recently by Makarov (2001).

There is another possible explanation for this mismatch, related to the possibility that the colours of the Pleiades and NGC 2516 MS stars are too blue for their nominal spectroscopic [Fe/H]. When applying the MS-fitting technique, the field dwarf colours have in principle to be shifted to the intrinsic colours of the cluster MS, so that the vertical shift necessary to superimpose the two sequences is a true measure of the cluster distance modulus. It is therefore paramount that the spectroscopic [Fe/H] scale for the clusters is consistent with both the subdwarf and cluster colours. We are in a position to test this concurrence by using the $(B-V)-(V-I)_{\rm C}$ colour-colour diagrams. Once the cluster reddening is accounted for, the position of a cluster main line (or field dwarf sequence) in this colour-colour diagram is a function of its metallicity, and can be compared with the sequence of subdwarfs shifted to the nominal cluster spectroscopic metallicity.

In Fig. 9 we show, as an example, the dereddened colours for the Hyades and Pleiades MS plotted together with the colours of the whole field dwarf sample shifted in metallicity to ${\rm [Fe/H]} = 0.13$ and ${\rm [Fe/H]} = -0.4$ , respectively. Whereas the Hyades line nicely agrees with the field dwarf colours at the Hyades metallicity, the Pleiades colours are consistent with the cluster abundance being significantly subsolar at ${\rm [Fe/H]} \sim -0.4$ , rather than the near solar abundance indicated from spectroscopy. For reference, we show in Fig. 10 the Hyades and Pleiades colour-colour relations, as plotted in Fig. 9, along with the main line for the old open cluster M67 which has approximately solar abundance from high resolution spectroscopy (G00 gives ${\rm [Fe/H]} = +0.02$ ). Data for M67 are from Montgomery et al. (1993) and the reddening value of E(B-V)=0.04 is taken from Twarog et al. (1997).

This mismatch between the Pleiades spectroscopic and photometric metallicity fully explains the discrepancy between the MS-fitting distance moduli in V/(B-V) and $V/(V-I)_{\rm C}$ , and with the Hipparcos distance. In fact, assuming a value ${\rm [Fe/H]} = -0.4 \pm 0.1$ appropriate to the Pleiades intrinsic colours and rederiving the MS-fitting distance, we obtain $(m-M)_{0} = 5.46 \pm 0.09$ from the (B-V) colour and $(m-M)_{0} = 5.39 \pm 0.06$ from $(V-I)_{\rm C}$ . These results are now mutually consistent and also in agreement with the Hipparcos parallax distance of $(m-M)_{0} = 5.37 \pm 0.07$ (van Leeuwen 1999).

We repeated the same analysis for NGC 2516 and Praesepe. In the first case we obtain a metallicity slightly lower than the Pleiades one, that is ${\rm [Fe/H]} = -0.5$ , which again provides consistent distances. If we adopt ${\rm [Fe/H]} = -0.5 \pm 0.1$ and redo the fits, the best-fit distance moduli are: $(m-M)_{0} = 7.95 \pm 0.10$ from (B-V) and $(m-M)_{0} = 7.79 \pm 0.07$ from $(V-I)_{\rm C}$ . These results are also in agreement, within their 1 $\sigma$ errors, with the Hipparcos parallax distance of (m-M)₀ = 7.70^+0.16_-0.15 (Robichon et al. 1999).

In the case of Praesepe the photometric metallicity happens to be the same as that of the Hyades, a result also in agreement with the spectroscopic analysis by Boesgaard et al. (1988), and in any case not dramatically different from the G00 result. At the Hyades metallicity the derived distance moduli become: $(m-M)_{0} = 6.26 \pm 0.06$ from (B-V) and $(m-M)_{0} = 6.28 \pm 0.04$ from $(V-I)_{\rm C}$ (assuming a zero reddening; they are increased by 0.05 mag if we use E(B-V)=0.022). Both results are completely consistent with the Hipparcos distance $(m-M)_{0} = 6.37 \pm 0.15$ (van Leeuwen 1999).

The right panel of Fig. 8 summarizes these results obtained from the photometric metallicities; the previous discrepancies with respect to the Hipparcos parallaxes have now disappeared. We conclude that our analysis does not support any discrepancy between MS-fitting and Hipparcos distances, at least for the clusters we have studied. The key point is the realization that the colours of the MS of the Pleiades and NGC 2516 are not appropriate for their spectroscopic metallicities. It is important to stress that this occurrence is not invoked as an hypothetical explanation for the distance mismatch obtained using the spectroscopic metallicities, but it is demonstrated by comparing the cluster and subdwarf colour-colour diagrams. A MS-fitting based distance is meaningful only if the colours of the reference MS are consistent with the cluster ones, and this is clearly not the case for the Pleiades and NGC 2516 when the G00 [Fe/H] values are used. It is the photometric metallicity based on the colour indices used in the MS-fitting procedure that has to be used in order to get a meaningful MS-fitting distance, not the spectroscopic one, if this is different. Therefore the widely discussed discrepancy between MS-fitting and Hipparcos distances for these two clusters is just an artifact due to the clusters' colours which are inconsistent with their spectroscopic metallicity.

A possible explanation for this colour mismatch would be that the field dwarf [Fe/H] scale (and hence colours) is inconsistent with the cluster one. However, we have already seen that the field dwarf [Fe/H] scale predicts the G00 Hyades metallicity, which is also confirmed by many independent spectroscopic analyses. It is therefore not possible to claim a zero point offset between our field dwarf metallicity scale and that of G00. The case of Praesepe, whose metallicity based on the MS colours is only slightly different from the G00 one and in agreement with independent spectroscopic estimates, further confirms the absence of any substantial offset.

Another possibility is a much higher helium content for the Pleiades and NGC 2516 than for the local field dwarfs. P98 and Stello & Nissen (2001) discuss the possibility that anomalous results for the Pleiades may be caused by a higher than expected He abundance. Both authors conclude that this is unlikely because the over-abundance required would be very large, although this cannot be entirely ruled out without further spectroscopic studies of both the Pleiades and other young clusters.

It is not easy to find an explanation for this discrepancy between spectroscopic and photometric [Fe/H] for Pleiades and NGC 2516. Unless a combination of errors in the spectroscopic metallicity, photometry and reddening conspire to produce the observed mismatch, one can only speculate on the origin of this problem. It is interesting to note that it affects the two younger clusters which should contain faster rotators and have higher chromospheric activity levels on average. P98 suggest that the colour-temperature relation may be different for fast and slow rotators - their Fig. 10 appears to show that Pleiades fast rotators lie below the cluster main line in the V(B-V) CMD for colours redder than $(B-V) \sim 0.9$ , but that the same stars lie on the main line in V/(V-I). Also NGC 2516 members may have a pattern of rotation rates similar to the Pleiades stars (see Terndrup 2002, their Fig. 5).

It should be noted however, that predictions from theory do not necessarily agree with the trend suggested by the empirical data. For solar metallicity stars with masses greater than 1.5 $M_{\odot}$ , Hernández et al. (1999) find that the predicted colours are redder for the faster rotators, whilst for low metallicity stars ([Fe/H] $< \sim -1.0$ ) on the MS and around the turnoff, Deliyannis et al. (1989) find no significant difference between their standard and rotational models. Evidently, this disparity between theory and observation requires a more detailed investigation, which is well beyond the scope of the present work. It is clear however, that rotation may well be a factor contributing to the apparently anomalous colours in young clusters, which could potentially lead to a discrepancy between the spectroscopic and photometric abundance estimates.

Sung et al. (2002) have discussed the possibility that chromospheric activity produces a blue excess in NGC 2516 G- and K-star colours, an occurrence dismissed by Terndrup et al. (2002), who however find blue excesses for late-K dwarfs in the Pleiades. In a very recent study of active binary stars, Katz et al. (2003) find that, when deriving effective temperatures from colour indices for these active stars, the (V-I) index gives significantly cooler estimates than the (B-V) index. This offset is in the same sense that we find for the 2 young clusters i.e. at fixed (B-V), the (V-I) colours are too red for their spectroscopic abundance. In an attempt to further test this possibility we have considered the chromospheric activity study by Henry et al. (1996), and selected stars with either very low or very high activity, in order to test if their (B-V)-(V-I) colour-colour relationship is a function of the level of chromospheric activity. Unfortunately the low number of objects with both colours available prevented us from drawing any meaningful conclusions on this issue, which in our opinion needs a deeper analysis.

The open cluster distance scale

A new empirical approach

1 Introduction