A&A 400, 769-778 (2003)
DOI: 10.1051/0004-6361:20021822

Kinetic simulations of the solar wind from the subsonic to the supersonic regime

S. Landi1 - F. Pantellini2


1 - Dipartimento di Astronomia e Scienza dello Spazio, Largo Enrico Fermi 2, 50125 Firenze, Italy
2 - Observatoire de Paris, LESIA, 5 Place Jules Janssen, 92195 Meudon, France

Received 30 August 2001 / Accepted 9 December 2002

Abstract
We present and discuss a completely self-consistent kinetic simulation of a steady state transonic solar type wind. The equations of motion of an equal number of protons and electrons plunged in a central gravitational field and a self-consistent electric field are integrated numerically. Particles are allowed to make binary collisions with a Coulombian scattering cross-section. The velocity distributions of the particles injected at the boundaries of the simulation domain are taken to be Maxwellian. As anticipated by previous authors we find that the transonic solution implies the existence of a peak in the proton equivalent potential at some distance above the sonic critical point. Collisions appear to be the fundamental ingredient in the process of accelerating the wind to supersonic velocities. For a given temperature at the base of the simulation domain the acceleration efficiency decreases with decreasing density. The reason is that the plasma has to be sufficiently collisional for the heat flux to be converted efficiently into plasma bulk velocity. Concerning the heat flux we find that even when in the vicinity of the sonic point the collisional mean free path of a thermal particle is significantly smaller than the typical scales of variation of the density or the temperature, the electron heat flux cannot be described conveniently by the classical Spitzer-Härm conduction law; not even in most of the subsonic region. Indeed, in the simulations where a transonic wind forms the heat flux has been found to strongly exceed the Spitzer-Härm flux, in opposition to recently published results from multi-moment models. We emphasize that given the high coronal temperatures we use in our simulations (3 times the typical solar values) we do not expect the results presented in this report to be uncritically transposable to the case of the "real'' solar wind. In particular, the quantitative aspects of our results must be handled with some care.

Key words: Sun: solar wind - stars: winds, outflows - plasmas - conduction - methods: numerical


1 Introduction

At all heights, from the bottom of the corona up into the interplanetary space, the solar atmosphere is a permanently expanding, out of thermodynamic equilibrium and fully ionized plasma. During the 1950's the recognition of the weak collisionality of the solar wind conveyed some doubts concerning the ability of fluid models to describe the solar atmosphere conveniently. As a consequence Chamberlain (1960), largely influenced by the theories on gas evaporation from planetary atmospheres, published the first kinetic model of the solar wind. In Chamberlain's evaporation model the wind is subsonic at the Earth's orbit in clear opposition with the supersonic solution of the fluid equations proposed a few years earlier by Parker (1958). During the early 1960's in situ measurements confirmed the supersonic nature of the solar wind and kinetic models just fell in disuse for some time. In the early 1970's it became clear that Chamberlain's erroneous prediction of a subsonic wind was the consequence of having mistakenly assumed that the charge neutralizing electric field was the Pannekoek-Rosseland field (e.g., Rosseland 1924). The latter is based on the assumption of a static solar atmosphere which has been a privileged working hypothesis since Laplace's Traité de mécanique céleste, published in the early years of the nineteenth century, but has been shown to be completely at odds with observations. After the definitive relaxation of the static approximation for the electric field, kinetic models of the solar wind were back on stage again (Jockers 1970).

The simplest, and most widely used kinetic models are the so called exospheric models (e.g., Lemaire & Sherer 1971). In these models the solar atmosphere is assumed to change from fully collisional to collisionless at a sharply defined level called the exobase. Above the exobase, conventional exospheric models assume a monotonically decreasing equivalent proton potential $\Psi_{\rm p}$ (cf. Eq. (4)) and no protons coming into the system from infinity, so that, by construction, all protons have anti sunward directed velocities. For non pathological distribution functions this means that the plasma bulk velocity at the exobase is of the order of the proton thermal velocity, i.e. of the order of the sound velocity. For example, $\langle v\rangle = v_{\rm p}/\sqrt{\pi}$ is the mean velocity of a proton population with Maxwellian velocity distribution $f_{\rm M}= n_0(\pi v_{\rm p}^2)^{-3/2}\exp[(v_\parallel^2+v_\perp^2)/v_{\rm p}^2]$ truncated for $v_\parallel<0$ (subscripts $\parallel$ and $\perp$ refer to the radial direction with respect to the center of the Sun). Since the typical velocity of a proton at the exobase is by construction of the order of the radial bulk velocity, it follows that the exobase is located at a heliocentric distance comparable to the distance r* where the subsonic-supersonic transition is located (the sonic critical point). However, as demonstrated graphically by Jockers (1970), the proton potential cannot be monotonic from deep inside the corona, where the bulk velocity is supposed to be small compared to sound speed and where static approximation may apply, out to infinity, where the wind is supersonic. Jockers anticipated that on its way from the corona to infinity a transonic wind must overcome a maximum in the proton potential $\Psi_{\rm p}$ such that $\Psi_{\rm p}(r_\psi) > \Psi_{\rm p}(\infty)$, where $r_\psi$ is the location of the maximum. In two recent papers Scudder (Scudder 1996a,b) pushes a step farther by identifying the critical point of Parker's fluid model with the location of the maximum of the proton potential energy $\Psi_{\rm p}$. Based on that assumption he derives a number of constraints on the possible radial variations of both the proton and the electron temperatures near the sonic point. However, even though the existence of a transonic wind seems to be intimately related to the existence of a peak of the potential $\Psi_{\rm p}$, there is no reason for $r_\psi$ to coincide with the sonic point of fluid theories unless very special, and therefore unlikely, conditions are met there. For example, in the simulations presented in this paper we do always find $r_\psi > r_*$. It can be shown analytically that this is indeed the normal case for radially decreasing temperature profiles provided T decreases more slowly than r-1 (Meyer-Vernet et al. 2002).

In this paper we present self-consistent kinetic simulations of a stationary solar type wind, where we concentrate on those aspects which cannot be addressed by fluid theories such as the electric field, the heat flux and the collisionality of the plasma. We deliberately treat only the most simple case of Maxwellian boundary conditions for the particles' velocity distribution function. The effects of plasma instabilities and waves are also not included in the model. Such additional "complications'' may hide part of the fundamental physics of the acceleration process and shall be discussed elsewhere. In this respect we do merely mention that the effect of resonant waves on a hybrid (fluid + kinetic) solar wind model has been discussed by Tam & Chang (1999) who conclude that ions may well be accelerated more efficiently by resonant waves rather than by the radial electric field. A similar model has been used by Lie-Svendsen & Leer (2000) to show that the two temperature electron velocity distribution functions often observed in the solar wind can be generated by Coulomb collisions without the need of assuming the presence of non-Maxwellain distribution in the corona. Olsen & Leer (1999) and Li (1999) use a closed system of transport equations based on an anisotropic bi-Maxwellian approximation for the velocity distribution functions to simulate the solar wind from the lower corona outward. Lie-Svendsen et al. (2001) extend the model down to the chromosphere based on the argument that chromosphere, transition region, corona and solar wind constitute a coupled system. The system of equations used by these authors is known as the 16-moment approximation (e.g., Demars & Schunk 1979) is a fluid-type model including transport effects such as heat flow and viscosity and even Coulomb collisions between interacting species. The main purpose of the above authors was to reproduce as good as possible the characteristics of the coronal plasma by including ad-hoc heating functions supposed to mimic the local deposit of energy due to plasma waves. If suitably chosen the heating functions can reproduce the temperature profile and temperature anisotropies which observations suggest to prevail in the solar corona (e.g., Esser et al. 1999). In many respects, our model is much more limited than the above multi-moment models which include most of the ingredients (e.g. radiation, plasma heating through waves, collisions, etc.). However, these models are fundamentally fluid models and many ingredients are not self-consistent. Our model is kinetic and fully self-consistent, but neither waves nor radiation and not even the lower layers of the corona are taken into account. In addition, because of computational limitations, we use an artificially low proton to electron mass ratio, and an exceedingly high coronal temperature, so that transposition of our results to the case of the real Sun must be done critically. One substantial difference between our results and the results from the mentioned multi-moment models is that we find that the electron heat flux in the corona is one order of magnitude larger than the classical value predicted by the Spitzer-Härm formula (Spitzer & Härm 1953), whereas the multi-moment models find it to be of the same order. Of course, both models are subject to their own limitations so that the question of whether the heat flux in the solar wind is classical or not appears to remain an open question.

Even though the physical parameters characterizing the wind simulated in the following section do not correspond exactly to those observed for the Sun, we shall refer to the simulated wind as the solar wind and to the central star as the Sun.

2 The model

Details of the simulation model have been given in two previous papers (Pantellini 2000; Landi & Pantellini 2001) and shall not be repeated here to full extent. The model is spatially one dimensional, i.e. all fields depend on the heliocentric distance r only. An equal number of protons and electrons are allowed to move freely in the domain $r_0<r<r_{\rm max}$, where r0 is the solar radius and $r_{\rm max}$ is the outer boundary of the system located several solar radii beyond the sonic point. The equations of motion are those of a particle of mass m and charge q in a central gravitational field produced by a star of mass M and a radial, charge neutralizing electric field, $\mathcal{E}(r)$, i.e.

  
                       $\displaystyle {{{\rm d}^2r}\over{{\rm d}t^2}} = -{{G M}\over r^2} + {{L^2}\over{m^2 r^3}} +{q\over m} \mathcal{E}(r).$ (1)
    $\displaystyle \vec{L} \equiv m \vec{r}\times\vec{v}_\perp ={\rm constant}$ (2)

where G is gravitational constant, $\vec{L}$ the angular momentum of the particle and $\vec{v}_\perp$ its velocity component perpendicular to the radial direction. Two particles finding themselves simultaneously at the same radial distance rdo either make an isotropic elastic collision with a probability $\propto u^{-4} r^{-2}$ or just go through each other as if they were transparent. The u-4 dependence of the collision probability mimics velocity dependence of the scattering cross section for Coulomb collisions whereas the r-2 dependence accounts for the spherical geometry of the problem. The transport properties of such a plasma have been shown to be very much the same as those of a Fokker-Planck plasma (Pantellini & Landi 2001; Landi & Pantellini 2001).

3 Defining the simulation

The physical state of the solar corona at heliocentric distance r0 (the lower boundary of our simulation domain) is characterized by the dimensionless parameter $\gamma$ defined as ($k_{\rm B}$ is the Boltzmann constant)

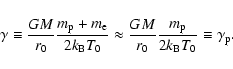\begin{displaymath}% \gamma\equiv {{GM}\over{r_0}} {{m_{\rm p}+m_{\rm e}}\over... ..._0}} {{m_{\rm p}}\over{2k_{\rm B}T_0}}\equiv \gamma_{\rm p}. \end{displaymath} (3)

The parameter $\gamma$ is half the ratio of the escape velocity squared to the protons thermal velocity squared $v_{\rm p0}^2\equiv 2k_{\rm B}T_0/m_{\rm p}$. For a typical solar coronal temperature $T_0=10^6~{\rm K}$ one has $\gamma=11.6$. The fact that $\gamma$ is larger than unity means that a typical coronal proton is too slow to escape to infinity. On the other hand, for coronal electrons at the same temperature one has $\gamma_{\rm e} = 6.3 \times 10^{-3}\ll 1$, meaning that the vast majority of the electrons would easily escape to infinity if gravity was the only force field. The solar corona is thus characterized by $\gamma\gtrsim 1$ and  $\gamma_{\rm e} \ll 1$. In order to reduce the required computational time to an acceptable level we choose $\gamma_{\rm p}=4$ and $\gamma_{\rm e}=10^{-2}$, instead of the above values of the real Sun. This, means that we adopt a rather high coronal temperature of $2.9 \times 10^6~{\rm K}$ and an artificially low proton to electron mass ratio $m_{\rm p}/m_{\rm e}=400$. However, since the two important constraints for a solar type atmosphere $\gamma_{\rm p}\gtrsim 1$, $\gamma_{\rm e} \ll 1$ are satisfied we expect the simulations to provide a fair approximation of the solar case.

The equations of motion Eqs. (1) and (2) are integrated for N protons, and an N electrons in the radial distance range between r=r0 and $r=r_{\rm top}\equiv 51r_0$. The number N is determined by the requirement of the collision frequency of an electron in the system (near r=r0) being roughly equal to the Fokker-Planck collision frequency of a plasma with an electron number density $n_{\rm e}\approx 10^8~{\rm cm}^{-3}$, which is a typical figure in the solar corona. The so calculated number N turns out to be of the order 103 (Landi & Pantellini 2001). Each time a proton or an electron hits the boundary at r=r0 it is injected back into the system according to a non drifting isotropic Maxwellian velocity distributions with a temperature T0. Given that the protons reaching the top boundary at $r=r_{\rm top}$ are generally either supersonic or nearly supersonic most of it must be re-injected into the system at r=r0. On the other hand, electrons reaching the $r=r_{\rm top}$ boundary are injected back into the system either at r=r0 or at $r=r_{\rm top}$ depending on what is needed to make the electron flux to be equal to the proton flux (zero charge current condition). The injection method ensures that there are always N protons and N electrons in the system. The velocity distribution of the electrons injected at the top boundary is chosen to be a drifting bi-Maxwellian with radial and perpendicular temperatures equal to the radial and perpendicular temperature of the outgoing electrons. Finally, the drift velocity of the electrons at  $r=r_{\rm top}$ is taken to be equal to the drift velocity of the protons measured at $r=r_{\rm top}$. In case of a supersonic wind this is just the average velocity of the protons escaping from the top of the system. In a subsonic wind some protons have to be re-injected into the system from the top. The temperature and the number of the re-injected protons is then adjusted iteratively until a coherent solution is obtained, in a manner similar to the one used by Landi & Pantellini (2001) to simulate the static corona. The electric field profile is adjusted iteratively, during an initialization phase, until zero charge flux and local charge neutrality is achieved in all points of the system.

4 Results

4.1 Effect of varying the coronal density

The number density n and the collisionality of the simulated plasma is dependent on the number of particles N used in the model. Figure 1 shows the results of 4 simulations which only differ in the number N of simulated particles, i.e. N=400, 784, 1600, 6400, the N=400 run being the one with the most tenuous (i.e. less collisional) atmosphere. The corresponding number densities at the base of the system are $n_0 [10^8~{\rm cm}^{-3}]=0.8, 1.5, 3.6$ and 13.4, respectively. The differences between the 4 simulations are substantial in many respects. The most evident difference is that the wind acceleration is much more efficient in the high density case, even though the thermal Knudsen number $K_T\equiv \overline\lambda_{\rm ep} \vert \partial \ln T_{\rm e\parallel}(r)/\partial r \vert$ (where $\overline\lambda_{\rm ep}\equiv v_{\rm e\parallel}/ \overline\nu_{\rm ep}$ is the electron-proton collisional mean free path based on the electron-proton rate of momentum exchange $\overline\nu_{\rm ep}$ (Landi & Pantellini 2001, Appendix B), and where $v_{\rm e\parallel}\equiv (2k_{\rm B}T_{\rm e\parallel}/m_{\rm e})^{1/2}$ is the radial thermal electron velocity) is much smaller than unity for all runs, ranging from 10-3, for the densest case, to 10-2 for the most tenuous case. From the figure it appears that the two more tenuous cases do not even become supersonic with respect to radial proton thermal velocity $v_{\rm p\parallel }\equiv (2k_{\rm B}T_{\rm p\parallel }/m_{\rm p})^{1/2}$ (which coincides with the fluid isothermal sound speed when $T_{\rm p\parallel}=T_{\rm e\parallel}$). The curves on the bottom panel of Fig. 1 illustrate the effect of collisions on the proton potential energy $\Psi_{\rm p}$. The latter results from the sum of the gravitational potential and a charge neutralizing electrostatic potential $\phi$:

 \begin{displaymath}% \Psi_{\rm p} = -{{GMm_{\rm p}}\over{r_0}}\left({{r_0}\over{r}}-1\right) + e\phi(r) \end{displaymath} (4)


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3906f1.eps}\end{figure} Figure 1: Flow velocity, Mach number and proton potential energy profiles for four different values of the number of particles N in the system. From bottom to top the velocity profiles correspond to N=400, 784, 1600, 6400, respectively. In all runs $\gamma =4$ and $m_{\rm p}/m_{\rm e}=400$. The normalizing velocity v0 is the proton thermal velocity $v_{\rm p}(r_0)$. TheMach number is defined as the ratio of the radial bulk velocity ofthe plasma divided by the proton thermal speed $v_{\rm p\parallel }\equiv (2k_{\rm B}T_{\rm p\parallel }/m_{\rm p})^{1/2}$. The normalizing energy $\Psi _0$ is given by $\Psi _0=GMm_{\rm p}/r_0$. Thus, as a reference, if the charge and current neutralizing electric field was the Pannekoek-Rosseland potential $\Psi _{\rm p}/\Psi _0 \approx 0.5$ for $r\gg r_0$.
Open with DEXTER

where e is the absolute value of the electron charge and where, because of the finite extent of the simulation domain we choose the level r=r0 to be the reference level for both the gravitational potential and the electrostatic potential, rather than $r=\infty$. Thus $\Psi_j(r_0)=0$ by construction. The decreasing height of the potential barrier the protons have to overcome as the plasma collisionality increases is evident. In the least collisional case (dash-dot profiles in Fig. 1) the potential $\Psi_{\rm p}$ is a monotonically growing function of r. However, increasing the system's collisionality beyond a given threshold makes the potential $\Psi_{\rm p}$ become non monotonic, with the peculiar formation of a maximum a few solar radii above the bottom boundary at $r=r_\psi$. As already stated in the introduction the existence of a maximum in the proton potential has been suggested some time ago by Jockers (1970). Scudder (1996a) pushed a step farther by postulating $r_\psi$ to coincide with the position of the isothermal sonic point of Parker's fluid theory. Figure 1 shows that when a maximum of $\Psi_{\rm p}$ exists, it is located above the sonic point, in agreement with the theoretical predictions (Meyer-Vernet et al. 2002). Figure 1 also shows that the low density cases do neither produce a maximum in the proton potential nor a supersonic wind, at least if terms of the parallel temperature based Mach number. One may suspect that if the Mach number was defined with respect to the mean temperature $T\equiv (T_\parallel+2 T_\perp)/3$ the flow would more easily become supersonic at large distances because of the $T_\perp \propto r^{-2}$ dependence implied by the conservation of angular momentum in a collisionless plasma with negligible heat flux. In the end, however, given that in the collisionless limit and for $r \rightarrow \infty$, one has $T_\parallel \rightarrow {\rm const.}$ (e.g., Meyer-Vernet & Issautier 1998), so that $T\rightarrow T_\parallel$, asymptotically. As a consequence, the distant Mach number does not depend on which of the two above definitions has been used.

In summary, the main consequence of increasing the plasma density beyond some threshold appears to be a reduction of the potential barrier the protons have to overcome in order to escape to infinity, accompanied by the formation of a local maximum in the $\Psi_{\rm p}(r)$ profile. As we shall see below the formation of the maximum in the proton potential energy is intimately related to the existence of both an outward directed, and radially decreasing heat flux, and a radially decreasing temperature profile. Both contribute in strengthening the outward directed electric field $\mathcal{E}=-\partial\phi/\partial r$, thus facilitating the extraction of the protons. In this context we shall remember that if the plasma was static (impermeable boundaries) with equal electron and proton temperatures, the charge neutralizing potential $\phi$ would be the celebrated Pannekoek-Rosseland potential (e.g., Rosseland 1924)

 \begin{displaymath}% \phi(r)=\phi_{\rm PR}(r)\equiv {{GM}\over{r_0}}~{{m_{\rm p... ...{\rm e}}\over{m_{\rm p}}}\right) \left({r_0\over{r}}-1\right) \end{displaymath} (5)

and the total potential energy of a proton would be a monotonically increasing function of r
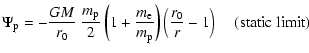$\displaystyle \Psi_{\rm p}= -{{GM}\over{r_0}}~{{m_{\rm p}}\over 2} \left(1+{{m_... ..._{\rm p}}}\right) \left({{r_0}\over r}-1 \right)\;\;\;\; {\rm (static\; limit)}$      

asymptotically reaching the value $GM m_{\rm p}/(2 r_0)$ which is much higher than the values observed in the simulations (cf. bottom panel of Fig. 1).

4.2 Wind acceleration

Let us now address the question of the wind acceleration mechanism. In order to do so we write the energy equation for the species j for the case of a steady state and purely radial wind. Indeed, the second moment of Boltzmann's equation (e.g., Endeve & Leer 2001) leads to the following expression

 \begin{displaymath}% E_j={1\over 2} m_j v_j^2 + h_j(r)+\Psi_j + {{q_j}\over{n_j v_j}} \end{displaymath} (6)

where qj, nj, vj are the heat flux, density and bulk velocity of the corresponding species and where we have defined the enthalpy per particle of the species j

 \begin{displaymath}% h_j(r)\equiv {3\over 2}k_{\rm B} T_{j\parallel}+k_{\rm B} T_{j\perp}. \end{displaymath} (7)

We note in passing that the first moment of Boltzmann's equation leads to Jockers's Eq. (1.1) (Jockers 1970)

 \begin{displaymath}% m_j v_j {{\partial v_j}\over{\partial r}}= - {1\over n}{{\... ...T_{j\perp}\right) - {{\partial \Psi_j}\over{\partial r}}\cdot \end{displaymath} (8)

When applied to the electrons one may neglect the small terms proportional to the electron mass $m_{\rm e}$ in Eq. (8) which then reduces to the usual expression for the electric field $\mathcal{E}$

 \begin{displaymath}% e\mathcal{E} = -\frac{1}{n_{\rm e}}\frac{\partial}{\partial... ...r}k_{\rm B}\left(T_{{\rm e}\parallel}-T_{{\rm e}\perp}\right). \end{displaymath} (9)

But let us come back to Eq. (6). In all simulations $E_{\rm e}$ and $E_{\rm p}$ are separately approximately constant over the whole simulation domain (excepted for a small region near the r=r0 boundary). This is shown in Fig. 2 for the N=6400 case.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3906f2.eps}\end{figure} Figure 2: Proton and electron energy profiles obtained by evaluating Eq. (6) for the N=6400 simulation. Note how both, $E_{\rm e}$ and $E_{\rm p}$ are separately constant over most of the simulation domain. The electrostatic profile $-e\phi $ is plotted as a reference.
Open with DEXTER

At first, this seems to indicate that the net energy exchanges between protons and electrons are quantitatively small. This is not necessarily correct. Indeed, it appears that the system does merely organize itself in order to ensure a spatially constant proton to electron energy density ratio throughout the system. The ratio can be constant even if interspecies energy exchanges via collisions are strong. A simple example of such a system consists of a collisional proton-electron plasma under the effect a constant gravitational acceleration field g. In this case the temperatures of both, electrons and protons, must be equal, isotropic and spatially constant. Further, the heat flux must vanish and the charge neutralizing electric field is just the Pannekoek-Rosseland field $g(m_{\rm p}-m_{\rm e})/(2e)$ so that $E_{\rm p}=E_{\rm e} = (5/2)k_{\rm B} T + g(m_{\rm p}+m_{\rm e})z/2$, i.e. $E_{\rm p}/E_{\rm e}=1$, independently of the height z. On the other hand, as we shall see below, in the spherically symmetric case the heat flux (mainly conveyed by the electrons) is the dominant source of energy for the acceleration of the wind. In order to proof this affirmation it is useful to evaluate the mean energy per particle  $\langle E\rangle$ as a function of r. Averaging the contribution of electrons and protons according to Eq. (6) leads to

 \begin{displaymath}% \langle E\rangle \approx {1\over 2}\left[ {1\over 2} m_{\r... ...{r_0}}\left(1- {{r_0}\over r}\right) + {{q}\over{nv}}\right] \end{displaymath} (10)

where the enthalpy term h(r) includes the temperature terms from all species (electrons and protons). In order to obtain Eq. (10) we made use of the fact that ${m_{\rm p}} \gg{m_{\rm e}}$ and that the proton and electron number fluxes are equal, i.e. $n_{\rm p} v_{\rm p}=n_{\rm e} v_{\rm e}\equiv nv$. As a reference, the number flux nv has been found to be of the order $10^{-2} v_{\rm e 0} n_0$ in all runs. In particular for the N=6400 case we find $nv=1.2 \times 10^{-2}~ n_0 v_{\rm e 0}$. The energy flux $F_{\rm E}$ conveyed by the wind through the spherical shell located at a distance r is the product of the particles mean energy at that distance (after deduction of their gravitational energy) times the number of particles crossing the shell per time unit. Since the total number density is equal to twice the number density of either species the particle flux is a constant given by $8\pi r^2 nv$ and the energy flux becomes

\begin{displaymath}% F_{\rm E}(r) =8\pi r^2 nv\left[\langle E\rangle - {{GM m_{\rm p}}\over{2r_0}}\left(1- {{r_0}\over r}\right) \right]\cdot \end{displaymath} (11)


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3906f3.eps}\end{figure} Figure 3: Relative importance of each term in Eq. (10) for the most dense case N=6400 (top panel) and the most tenuous case N=400 (lower panel). The dense case supports a transonic wind (the vertical line in the top panel gives the position of the sonic point r*) while the tenuous case does not. From the comparison of the two figures it appears that the wind acceleration is primarily driven by the heat flux term q/(nv).
Open with DEXTER

Figure 3 illustrates the relative importance of each of the 4 terms in Eq. (10) as a function of the radial distance r for the N=6400 (top) and the N=400 (bottom) run. Since the gravity term vanishes at r=r0 and the bulk velocity v is much smaller than the sound speed, only the enthalpy and the heat flux term contribute to the total energy there. The reason for the total energy being slightly larger in the low density case arises from the heat flux term q/(nv) being stronger in that case. This is because at r=r0 we do not have control over this term as we do for the enthalpy, which only depends on the temperature imposed at the boundary. Interestingly the run characterized by the largest heat flux term q/(nv)(which does not necessarily mean that the heat flux q, or the specific heat flux q/n are largest) is precisely the one where the wind remains subsonic. This is particularly surprising in the light of the fact that the velocity of the wind is clearly boosted by the heat flux term given that the enthalpy profile is seemingly identical for the two cases. However, a strong heat flux term near the bottom does not guarantee that the wind will be accelerated to supersonic velocities. A sufficient amount of collisions is needed to efficiently transform the energy transported outward by the electron heat flux into bulk plasma kinetic energy.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3906f4.eps}\end{figure} Figure 4: Radial and perpendicular temperature profiles for 4 different values of the N. Note the log-log axis of the top two panels.
Open with DEXTER

Figure 4 shows that the radial electron temperature profile  $T_{\rm e\parallel}$ is essentially insensitive to the density while $T_{\rm e\perp}$ is not. Indeed, in the collisionless limit the parallel and perpendicular temperatures are independent of each other and one should observe $T_{\rm e\perp} \propto r^{-2}$ in order to satisfy to the angular momentum conservation law of individual particles (cf. Eq. (2)). As a consequence, in the rigorously collisionless case, $T_{\rm e\perp}$ should decrease by a factor 502 from bottom to top of the simulation domain. Collisions do significantly contribute in limiting this bottom to top perpendicular electron temperature gradient which ranges from 10 to 30 depending on the value of N. On the other hand, for all four cases the parallel temperature only drops by a factor 3 from bottom to top, leading to strong temperature anisotropies $T_{\rm e\parallel}/T_{\rm e\perp}$ (bottom panel in Fig. 4). This is not particularly surprising as in the collisionless limit the parallel temperature of a plasma plunged in a potential field is constant as long as the velocity distribution function is close to Maxwellian.

We can now summarize the wind acceleration scenario from a kinetic point of view. The natural decrease of the temperature with distance (essentially due to the fact that in the collisionless limit $T_\perp \propto r^{-2}$) implies the existence of a radial heat flux predominantly conveyed by the electrons. The heat flux is transfered from the electrons to the protons which become accelerated in the outward direction. Since the momentum of the wind is mainly carried by the heavy protons (rather than by the light electrons) the plasma as a whole becomes accelerated in this way. This mechanism must be particularly efficient in the region located inside the spherical shell $r=r_\Psi$ (location of the maximum of $\Psi_{\rm p}$) where the protons have to climb uphill in order to escape from the potential energy well (cf. Fig. 1). As already stated above, collisions contribute in increasing the electric field strength. Since the electric field is directed outward, increasing the electric field favors the extraction of the protons from the gravitational well by reducing the height of the maximum in the proton potential $\Psi_{\rm p}$. The fluid estimate of the macroscopic electric field $\mathcal{E}$ for a spherically symmetric electro-proton plasma can be obtained by differentiating Eq. (6) for the electrons. Neglecting the small terms proportional to $m_{\rm e}$ and taking advantage of the fact that $E_{\rm e}$ is approximately constant (in particular if one compares it to the $\phi(r)$ profile shown in Fig. 2) we then obtain

 \begin{displaymath}% e\mathcal{E} \approx -k_{\rm B}{{\partial}\over{\partial r... ...-{{\partial}\over{\partial r}}\left({{q}\over{nv}}\right)\cdot \end{displaymath} (12)

This estimate is not as rigorous as the standard estimate based on Eq. (8) since it is based on the assumption of a constant  $E_{\rm e}(r)$ profile. The equation has the advantage of highlighting the role of the heat flux in the shaping of the electric field profile. For radially decreasing temperature profiles the first two terms on the right hand side of Eq. (12) are positive and favor the outward acceleration of the protons. They are reminiscent of the thermoelectric effect (e.g., Pantellini & Landi 2001). Given that q/nv has been seen to decrease with distance for the two extreme cases shown in Fig. 3 it follows that the third term on the right hand side of Eq. (12) is also positive for all simulation. However, the contribution of the latter to the acceleration is significantly stronger in the N=6400 case than in the N=400 case, where the radial dependence of q/nv is seemingly weak.

It is instructive to apply Eq. (12) to a a weakly collisional system. In such a case the parallel temperature $T_{\rm e\parallel}$ is roughly constant and the perpendicular temperature $T_{\rm e\perp} \propto r^{-2}$. This leads to the collisionless approximation

 \begin{displaymath}% e\mathcal{E} \propto {{\rm constant}\over{r^3}} - {{\partial}\over{\partial r}}\left({{q}\over{nv}}\right) \end{displaymath} (13)

where the constant is positive. From Eq. (13) it appears that when the heat flux term is constant, or only weakly spatially dependent, such that the first term on the right hand side of the equation dominates over the second term, the electric field decreases faster than the gravitational field (i.e. $ \mathcal{E} \propto r^{-3}$). This is the reason for the proton potential energy $\Psi_{\rm p}$ to be a monotonically growing function of distance r in the N=400 case shown in Fig. 1. Increasing the number of particles in the system makes the plasma more collisional and forces the perpendicular temperature $T_{\rm e\perp}$ to fall off more slowly than r-2 (see Fig. 4) making it harder for the gravitational force acting on a proton to overcome the electric force. Eventually, if $T_{\rm e\perp}$ decreases more slowly than r-1, there must be a minimum distance beyond which the electric force on a proton overcomes the gravitational force and $\Psi_{\rm p}$ has a maximum. This is clearly the case for the N=6400 case shown in Fig. 4 where $T_{\rm e\perp}\propto r^{-0.6}$. For the N=400 case the temperature profile is steeper, with an average radial dependence given by $T_{\rm e\perp}\propto r^{-0.9}$. Thus, even though all profiles can be described by a power law which decreases more slowly than r-1 (on average over the simulation domain) all profiles tend to steepen at large distances because of the plasma tendency to become less collisional. Eventually beyond some N-dependent threshold distance the $T_{\rm e\perp}$ profiles becomes steeper than r-1 so that the formation of a maximum of $\Psi_{\rm p}$ becomes impossible beyond this point. This is the case for the N=400 run. In the other three runs a maximum forms below the point where the $T_{\rm e\perp}$ profile becomes steeper than r-1. We can now reexamine Fig. 3 in the light of Eq. (12). Figure 3 already told us that the enthalpy profile is not very sensitive on the plasma collisionality even though it contributes significantly in strengthening the electric field according to Eq. (12). The determinant contribution in accelerating the wind to supersonic velocities comes from the heat flux term q/(nv) which has been seen to be much more sensitive on the plasma collisionality. As demonstrated by Eq. (12), the heat flux term contributes to the strengthening of the outward directed electric field, provided it decrease with distance. Figure 3 shows that the heat flux term decreases for both simulations represented on the figure with the steepest profile being associated with the high density case which therefore produces the strongest electric field, according to the last term on the right-hand side of Eq. (12).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3906f5.eps}\end{figure} Figure 5: Parallel electron velocity distribution functions (solid lines) in arbitrary units at two different positions in the system, near the base and in the supersonic region. Shown are results of the N=6400 simulation. The dashed lines represent Maxwellian distributions for which the first three moments (density, mean velocity and temperature) are those of the measured distributions. Velocities are normalized to the electron thermal velocity $v_{\rm e0}=v_{\rm e}(r_0)$.
Open with DEXTER

For the N=6400 simulation the parallel electron velocity distribution functions at the base of the system at r=r0, and in the supersonic region at r=45 r0 are shown in Fig. 5. Since the collisional mean free path $\lambda$ is proportional to v4 high energy electrons are nearly unaffected by collisions on their journey through the system. Thus, the velocity distribution of the high energy electrons flowing downward is the imprint of the upper boundary condition whereas the velocity distribution of the high energy electrons flowing upward is the imprint of the lower boundary at r=r0. On the other hand, the low energy electrons, which populate the core of the velocity distribution function, are strongly affected by collisions. As a consequence, at low velocities, the electron velocity distributions are approximately isotropic Maxwellians which do not carry any heat flux. Instead, the heat flux is carried by the high energy electrons which are responsible for the asymmetry of the distribution function. As illustrated by the profiles in Fig. 5 the heat flux is due to a deficiency of downward flowing high energy electrons near the lower boundary and to an excess of upward flowing particles in the supersonic region.

4.3 Comments on the electron heat flux


  \begin{figure} \par\includegraphics[width=7.3cm,clip]{h3906f6.eps}\end{figure} Figure 6: Electron heat flux profile (solid line) and thermal Knudsen number $K_T\equiv \overline\lambda_{\rm ep} \vert \partial \ln T_{\rm e\parallel}(r)/\partial r \vert$ (dashed line) for the most strongly collisional case N=6400 normalized to $q_0\equiv n_0 m_{\rm e} v_{\rm e0}^3$, where $v_{\rm e0}$ is the electron thermal velocity at the base of the system at r=r0. The triangle on the heat flux axis indicates the heat flux expected near the base of the system using the Spitzer-Härm formula (Spitzer & Härm 1953). The dot-dash line shows the $-T_{\rm e\parallel }^{5/2} \partial T_{\rm e\parallel }/\partial r$ law normalized to the measured flux at r=r0.
Open with DEXTER

Figure 6 shows the heat flux and the thermal Knudsen number KT measured in the N=6400 run. One observes that while it remains approximately constant in the supersonic region above the $r\approx10 r_0$ level, KT grows steeply in the subsonic region, where it increases from 10-3 to 10-2. Since $K_T \lesssim 2 \times 10^{-2}$ in whole simulation domain, it is not particularly surprising that the heat flux closely follows a $T_{\rm e\parallel}^{5/2} \partial T_{\rm e\parallel}/\partial r$ dependence (dot-dash curve) as in the case of the classical Spitzer-Härm heat conduction formula (Spitzer & Härm 1953). This conclusion is misleading, since, despite the smallness of the Knudsen number, the heat flux is strongly non classical. As already pointed out by several authors in the past the classical heat conduction formulation breaks down either because the heat flux intensity exceeds a value of the order 10-2q0 (Gray & Kilkenny 1980), or because the Knudsen number is larger than 10-3 (Shoub 1983), or because the flow velocity is a significant fraction of the sound speed (Hollweg 1974; Alexander 1993), or even because the electric field in the system is of the order of the Dreicer field $\mathcal{E}_{D}\equiv kT_{\rm e} /(e\overline\lambda_{\rm ep})$ (Scudder 1996b). Indeed, in the N=6400 simulation the electric field at the sonic point is $\mathcal{E}\approx \mathcal{E}_{D}$, reaching an intensity $\mathcal{E} \approx 8 \mathcal{E}_{D}$ in the N=1600 case. Concerning the heat flux intensity, Fig. 6 shows that it is small enough for the the low heat flux intensity condition established by Gray & Kilkenny (1980) to be satisfied. One can therefore conclude that the heat flux intensity is low enough for the plasma to be capable to support a Spitzer-Härm flux. Let us now address the problem of the heat flux in a flowing, and weakly collisional plasma. As discussed by Hollweg (1974) and Alexander (1993) a non negligible fraction of the of the energy is carried by a collisionless term of the form $q_{\rm NC}=(3/2)\alpha nv k_{\rm B}T_{\rm e}$ where $\alpha$ is a positive numerical factor of order unity (note that the electron temperature has been supposed to be isotropic by these authors). Given that collisions are still relatively important in our simulations we make the ansatz that the observed electron heat flux is made of the sum of a classical (collisional) term (e.g., Braginskii 1965) $q_{\rm SH}$ and a collisionless term $q_{\rm NC}$

 
                     $\displaystyle % q_{\rm e}$ = $\displaystyle q_{\rm SH} + q_{\rm NC}$  
  = $\displaystyle -3.16~{ {n k_{\rm B}^2 T_{\rm e}}\over { m_{\rm e}{\overline\nu_{... ...{\partial T_{\rm e}}\over{\partial r}} +{3\over 2}~\alpha~nv k_{\rm B}T_{\rm e}$ (14)

where $\alpha$ is a positive constant of order unity whose numerical value depends on the assumptions of the specific heat flux model (Hollweg 1974; Alexander 1993). As a guide, Hollweg's estimate of $\alpha$ for the solar wind are in the range 2.0 to 7.0 (Hollweg 1974). Equation (14) shows that the two heat conduction terms have an extremely different dependence on the macroscopic moments of the plasma. The Spitzer-Härm heat conduction does only depend on the temperature, and its radial variation, while the collisionless term $q_{\rm NC}$ depends on both the electron number flux and the temperature (but not on the temperature gradient). This situation is reminiscent of the heat conduction in a plasma confined to the space between two parallel plates separated by a distance L at temperatures T0 and $T_{\rm L}$, respectively (Landi & Pantellini 2001). If the plasma is dominated by collisions the heat conduction between the two plates just equal to $q_{\rm SH}$. However, if the plasma is sufficiently diluted for a non negligible number of electrons to be able to proceed from one plate to the other without colliding with other particles in the system, the heat flux is best described by the collisionless approximation $q_{\rm NC} \propto n(T_0 T_{\rm L}^{1/2}-T_{\rm L}T_0^{1/2})$ which (unlike $q_{\rm SH}$) is a function of the number density n.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3906f7.eps}\end{figure} Figure 7: Electron heat flux calculated using the collisionless approximation $q_{\rm NC}=(3/2)\alpha nv T_{\rm e\parallel }$ (top panel), the classical Spitzer-Härm approximation $q_{\rm SH}= -{\rm constant}\times T_{\rm e\parallel }^{5/2}{{\partial T_{\rm e\parallel }}/{\partial r}}$ (middle panel). The lower panel shows the heat flux profiles effectively measured in the simulations. Fluxes are in arbitrary units, but the same normalization has been used for all simulations.
Open with DEXTER

Figure 7 compares the Spitzer-Härm estimate and the collisionless estimates of the electron heat flux with the observed heat flux for the four simulations. All profiles in the figure have been obtained using $T_{\rm e\parallel}$ in place of the temperature $T_{\rm e}$ which appears in Eq. (14). Even though Hollweg's collisionless approximation is not expected to provide an accurate approximation of the heat flux in the simulated systems, it appears that the measured heat flux varies significantly from one simulation to the other, in good qualitative agreement with the non collisional flux $q_{\rm NC}$ obtained using Alexander's model (Alexander 1993) to compute $\alpha$ in Eq. (14) after replacing $T_{\rm e}$ by $T_{\rm e\parallel}$. The Spitzer-Härm prediction of an equal heat flux intensity for all four simulations (based on the fact that the radial profiles of $T_{\rm e\parallel}$ are very similar cf. Fig. 4) is completely at odds with the measured intensities. But why is this so, despite the smallness of the Knudsen number? The answer is hidden in Eq. (14). Indeed, from Eq. (14), after replacing $T_{\rm e}$ by $T_{\rm e\parallel}$, it follows that the ratio of the two contributions to the total heat flux is given by

 \begin{displaymath}% {{q_{\rm NC}}\over{q_{\rm SH}}} = {{3\alpha}\over{3.16}}~ {{v}\over{v_{\rm e\parallel}}}~ {{1}\over{K_T}}\cdot \end{displaymath} (15)

From Eq. (15) it follows that the condition for the heat flux in the system to be dominated by the classical term $q_{\rm SH}$ one must have $K_T \gg \alpha v/v_{\rm e\parallel}$. For example, at the sonic point one has $v/v_{\rm e\parallel}=(m_{\rm e}/m_{\rm p})^{1/2}=1/20$ and $K_T\approx 10^{-2}$ from where one can estimate $q_{\rm NC}/q_{\rm SH}\approx 5\alpha$, which is substantially larger that unity for any reasonable value of $\alpha$. Thus, for the heat flux to be of the Spitzer-Härm type in the vicinity the sonic point requires the thermal Knudsen number to be larger than $(m_{\rm e}/m_{\rm p})^{1/2}$. The simulations suggest that this is not easily achievable because the driving of the wind to supersonic velocities does precisely requires the plasma to be sufficiently collisional at the sonic point. As already stated, the way around this restriction may be the presence of an additional scattering mechanism (e.g. waves) in the plasma. However, in that case the Spitzer-Härm formulation of the heat transport would not be the relevant one anyway. As already pointed out in the introduction recent multi-moment simulations of the solar wind yield a close to classical electron heat flux (e.g. Olsen & Leer 1999; Li 1999; Lie-Svendsen et al. 2001). The discrepancy may be due to the fact that physical conditions of the wind we simulate are quite different from those used in these multi-moment simulations or, eventually, to the fact that the heat flow equations in the multi-moment models are affected by the closure scheme. The simplified version of the Coulomb collision operator used in our model or even the one-dimensionality of the model may also contribute to the observed discrepancy. The reason for the radial dependence of the heat flux measured in the simulation (cf. Fig. 6) to be roughly of the Spitzer-Härm type stems from the fact that the radial dependences of both terms in Eq. (14) are quite similar for the given temperature profiles. Indeed, if we replace $T_{\rm e}$ by $T_{\rm e\parallel}$ in Eq. (14) and use the fair approximation $T_{\rm e}\propto r^{-0.4}$ (from Fig. 4) it follows that both $q_{\rm SH}$ and $q_{\rm NC}$ vary approximately as r-2.4.

4.4 Effects of varying the proton to electron mass ratio

Given the artificially low mass ratio in our simulations there is a concern about the sensitivity of the results on the value of  $m_{\rm p}/m_{\rm e}$. In order to address this question we show the same simulation for two different values of $m_{\rm p}/m_{\rm e}$ in Fig. 8. The other parameters are identical for both simulations , i.e. $\gamma_{\rm p}=4$ and N=6400. In both cases the formation of a transonic wind occurs, in association with the formation of a maximum in the proton potential. However, the maximum's amplitude is substantially higher, and less peaked, in the low mass ratio simulation. The discrepancy is likely due to the fact that in the high mass ratio case the scattering of the electrons in velocity space by the protons is more efficient than in the low mass ratio case. Indeed, the temperature ratio $T_{\rm e\parallel}/T_{\rm e\perp}$ reaches a value of 3 at the upper boundary in the $m_{\rm p}/m_{\rm e}=400$ case (cf. Fig. 4) and a value of 4 in the $m_{\rm p}/m_{\rm e}=100$case. As a result the absolute value of second term on the right hand side of Eq. (9) is significantly smaller in the high mass ratio case than in the low mass ratio case. Since the sign of this term is negative it contributes in reducing the the strength of the overall positive electric field. From Fig. 4 one may argue that a similar argument applies to the observation that the electric field strength increases with increasing plasma density (i.e. with increasing collisionality) as does effectively show Fig. 1.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3906f8.eps}\end{figure} Figure 8: Dependence of the Mach number and the proton potential energy on the proton to electron mass ratio for the simulation with N=6400. Even though the qualitative behavior is similar it appears that a high mass ratio is in favor of a stronger acceleration of the wind. The definitions for the Mach number and the normalizing energy $\Psi _0$ are the same as in Fig. 1.
Open with DEXTER

Extrapolating these observations to $m_{\rm p}/m_{\rm e}=1836$ and N=6400 one therefore expects the maximum of the proton potential to drop to an even lower level. The peak is expected to be at least as marked as for the $m_{\rm p}/m_{\rm e}=400$ case.

5 Conclusion

From self-consistent kinetic simulation of a solar type wind we find that, unless an efficient isotropization mechanism for the electron velocity distribution (e.g. wave-particle interaction), or some source of suprathermal electron distributions are invoked (e.g. shock produced), the formation of a transonic wind is only compatible with a sufficiently high collisionality in the vicinity of the sonic point r=r*. In oder words, the coronal density must exceed a threshold density for the wind acceleration to be sufficiently strong to become supersonic. Given the admittedly oversimplifications in our model, combined with the fact that the parameters we use are rather unrealistic (excessively high coronal temperature and low $m_{\rm p}/m_{\rm e}$ ratio) makes it impossible for us to specify an upper limit for the thermal Knudsen number at the sonic point r*. We do merely show that the number cannot be arbitrarily large, the limiting value most likely being of the order unity, or less. As already stated, non Maxwellian boundary conditions, feeding an excess of suprathermal particles into the system (e.g. kappa distributions) may help overcoming the low Knudsen number condition. However, the existence of non thermal particle distributions rises the question of their origin. We chose not to address this question and assume Maxwellian boundary conditions which have the advantage of not requiring the introduction of additional ad hoc parameters into the model. Thus, in the absence of any electron scattering mechanism (apart from collisions), and unless special boundary conditions are imposed at the base of the simulation domain, collisions appear to be the essential ingredient for the wind to become accelerated to supersonic velocities, mainly because collisions are necessary to convert the electron heat flux into bulk energy of the plasma. The enthalpy gradient does also contribute to the acceleration of the wind. However, the acceleration associated with the radially decreasing enthalpy is found to be weakly dependent on the plasma collisionality and doesn't seem to be the discriminating factor in the acceleration of the wind to supersonic velocities.

In simulations where a transonic wind forms we find that the proton potential has a maximum near (but above) the sonic point. Typical values of the electric field near the sonic point r* are found to be of the order of Dreicer's field, or larger. The presence of such strong electric field intensities may contribute in making the electron heat flux depart from the classical Spitzer-Härm formula (which requires the electric field being much weaker than Dreicer) but the main reason for the observed heat flux to depart from the Spitzer-Härm prediction is due to the presence of a strong "non collisional'' heat flux  $q_{{\rm NC}} \propto nvT_{\rm e}$. The latter appears to contribute significantly to the total electron heat flux, even in the region where the wind velocity is much smaller than the sound speed. We are aware of the fact that extrapolating the above results to the "real'' Sun is a perilous exercise. However, we do not expect the qualitative behavior of a system with real coronal temperature and real proton to electron mass-ratio to behave in a substantially different way from the high density case discussed in this paper. In particular, increasing the proton to electron mass ratio from 400 to 1836 implies a factor two increase in the electron thermal velocity, only. Given that the electron thermal velocity at the base of the system is already one order of magnitude larger than the escape velocity for the $m_{\rm p}/m_{\rm e}=400$ case, not much difference is expected in a system with twice this thermal velocity. The skeptical reader may also argue that using a realistic mass ratio would substantially modify the transport properties of the plasma. This is certainly true, but we expect the modifications to be small, essentially because neither the classical electron heat flux  $q_{\rm SH}$ nor the collisionless heat flux  $q_{\rm NC}$ depend on the mass ratio, at least as long as $m_{\rm p}/m_{\rm e}\gg 1$. We expect the excessively high coronal temperature used in our simulations to be a more crucial limitation in the process of transposing the above results to the solar case just because the proton thermal velocity and the escape velocity are of the same order, i.e.  $\sqrt{\gamma_{\rm p}}=O(1)$. Indeed, the coronal temperature of the real Sun is roughly 3 times smaller that the value we use here. This implies a factor $\sqrt{3}$ difference for the order unity quantity $\gamma_{\rm p}$. The impact is certainly non negligible from a quantitative point of view but there aren't any reasons for us to believe that the qualitative aspects of our results do not apply to the solar case. For instance, whether or not the collisionless heat flux near the solar sonic point is really one order of magnitude stronger that the classical Spitzer-Härm flux remains an open question since this finding discords with recent results from multi-moment models.

Acknowledgements
We thank the referee for the detailed comments which very much helped us during the revision of the paper.

References

 

Copyright ESO 2003