2 Description of the strategy

Since this research includes an iterative process, one has to be very careful not to introduce (and so to propagate) any errors. The strategy in its entirety therefore encompasses a number of steps, including (1.) a spectral coverage of standard infrared sources from A0 to M8, (2.) a homogeneous data reduction, (3.) a detailed literature study, (4.) a detailed knowledge of the impact of the various parameters on the spectral signature, (5.) a statistical method to test the goodness-of-fit (Kolmogorov-Smirnov test) and (6.) high-resolution observations with two independent instruments. Some points (in particular, points 4 and 5) have already been demonstrated in the case of $\alpha$ Tau in Paper I. Points 1, 2 and 6 will be elaborated on in Sects. 3, 4 and 5 respectively.

In its totality, the general method of analysis - based on these 6 points - may be summarised as follows:
a large set of standard stars (A0-M8) has been observed with ISO-SWS (Sect. 3). The observational data first have been subjected to a homogeneous data-reduction procedure (Sect. 4). Thereafter, the carefully reduced ISO-SWS data of one warm and one cool star were compared with the observational data of two independent instruments (FTS-KP and FTS-ATMOS, see Sect. 5). This step is very crucial, since this is the only secure and decisive way to point out calibration problems with the detectors of ISO-SWS. The complete observational data-set, covering a broad parameter space, was then compared with theoretical predictions. By knowing already some problematic points in the calibration of ISO-SWS, these comparisons led both to a refinement of our knowledge on the calibration problems and to a determination of theoretical modelling problems (Sect. 6).

The knowledge on the relative importance of the different molecules - displaying their characteristic absorption pattern somewhere in the broad ISO-SWS wavelength-range - and on the impact of the various stellar parameters on the infrared spectrum enabled us also to determine the fundamental stellar parameters for the cool giants in our sample Paper I. Due to severe calibration problems with the band-2 data (see Sect. 4), only band-1 data were used for this part of the process. Once a high-level of agreement between observed and synthetic data was reached, a statistical test was needed to objectively judge on the different synthetic spectra. A choice was made for the Kolmogorov-Smirnov test Paper I. This statistical test globally checks the goodness-of-fit of the observed and synthetic spectra by computing a deviation estimating parameter $\beta$ (see Eq. (5) in Paper I). The lower the $\beta$-value, the better the accordance between the observed data and the synthetic spectrum.

Using this method, the effective temperature, gravity, metallicity, microturbulent velocity together with the abundance of C, N and O and the ${\rm ^{12}C/^{13}C}$-ratio were estimated for the cool stars. From the energy distribution of the synthetic spectrum between 2.38 and 4.08 $\mu$m and the absolute flux-values in this wavelength range of the ISO-SWS spectrum, the angular diameter was deduced. We therefore have minimised the residual sum of squares

$$\sum\limits_{i~=~1}^{n} (f(i) - g(i))^2, \nonumber$$

with f(i) and g(i) representing respectively an observational and a synthetic data point at the ith wavelength point.

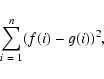The error bars on the atmospheric parameters were estimated from 1. the intrinsic uncertainty on the synthetic spectrum (i.e. the possibility to distinguish different synthetic spectra at a specific resolution, i.e. there should be a significant difference in $\beta$-values) which is thus dependent on both the resolving power of the observation and the specific values of the fundamental parameters, 2. the uncertainty on the ISO-SWS spectrum which is directly related to the S/N of the ISO-SWS observation, 3. the value of the $\beta$-parameters in the Kolmogorov-Smirnov test and 4. the still remaining discrepancies between observed and synthetic spectra.

It should be noted that an error on the effective temperature introduces an error on the angular diameter. The IR flux of the cool giants does not follow the Rayleigh-Jeans law for a black-body, and we can write ${\cal{F}}_{{\rm obs}}^{\lambda} \propto {T_{\rm eff}}^q \cdot \theta_{\rm d}^2$. Thus, with $\theta_{\rm d} \propto {{\cal{F}}_{{\rm obs}}^{\lambda}}^{1/2} \cdot {T_{\rm eff}}^{-q/2}$ and $\sigma_{<{\cal{F}}>} = 0.10 {\cal{F}}$, one obtains

$$\frac{\sigma_{<\theta_{\rm d}>}}{\theta_{\rm d}} = \sqrt{\fra... ...2_{<{T_{\rm eff}}>}}{{T_{\rm eff}}^2} + \sigma^2_{{\rm int}}},$$ (1)

with $\sigma^2_{{\rm int}}$ being the intrinsic uncertainty on the angular diameter (i.e. the amount by which one may change the angular diameter without significant difference in the residual sum of squares). The uncertainty on the angular diameter (Eq. (2)) is mainly determined by the uncertainty in the absolute flux (the first term in Eq. (2)), resulting in almost the same percentage errors in $\theta_{\rm d}$. Using the ISO-SWS observational data of these cool giants, we could demonstrate that $q \approx 1.3 \pm 0.1$ for 3600  ${\rm K} \le \mbox{$T_{{\rm eff}}$ }\le 4400$ K (Decin 2000). With $q \approx 1.3$, $\sigma_{<{T_{\rm eff}}>} = 70$ K and $\mbox{$T_{{\rm eff}}$ }= 3850$ K, the uncertainty increases with a factor 1.008 compared to the q = 1situation.

From the angular diameter and the parallax measurements (mas) from Hipparcos (with an exception being $\alpha$ Cen A, for which a more accurate parallax by Pourbaix et al. 1999, is available), the stellar radius was derived. This radius, together with the gravity - determined from the ISO-SWS spectrum - then yielded the gravity-inferred mass. From the radius and the effective temperature, the stellar luminosity could be extracted.

This method of analysis could however not be applied to the warm stars of the sample. Absorption by atoms determines the spectrum of these stars. It turned out to be unfeasible to determine the effective temperature, gravity, microturbulence, metallicity and abundances of the chemical elements from the ISO-SWS spectra of these warm stars, due to

• problems with atomic oscillator strengths in the infrared (see Sect. 6.1);
• the small dependence of the IR continuum on the fundamental parameters (when changed within their uncertainty);
• the small dependence of the observed atomic line strength on the fundamental parameters, and
• the absence of molecules, which are each of them specifically dependent on the various stellar parameters.

Therefore, good-quality published stellar parameters were used to compute the theoretical model and corresponding synthetic spectrum. The angular diameter was deduced directly from the ISO-SWS spectrum, which then yielded - in conjunction with the assumed parallax, gravity and effective temperature - the stellar radius, mass and luminosity.