A&A 400, 679-694 (2003)
DOI: 10.1051/0004-6361:20021793

ISO-SWS calibration and the accurate modelling
of cool-star atmospheres[*]

II. General results[*]

L. Decin1,[*] - B. Vandenbussche1 - C. Waelkens1 - K. Eriksson2 - B. Gustafsson2 - B. Plez3 -
A. J. Sauval4 - K. Hinkle5


1 - Instituut voor Sterrenkunde, KULeuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
2 - Institute for Astronomy and Space Physics, Box 515, 75120 Uppsala, Sweden
3 - GRAAL - CC72, Université de Montpellier II, 34095 Montpellier Cedex 5, France
4 - Observatoire Royal de Belgique, Avenue Circulaire 3, 1180 Bruxelles, Belgium
5 - National Optical Astronomy Observatory[*], PO Box 26732, Tucson, Arizona 85726, USA

Received 22 November 2001 / Accepted 2 December 2002

Abstract
The fine calibration of the ISO-SWS detectors (Infrared Space Observatory - Short Wavelength Spectrometer) has proven to be a delicate problem. We therefore present a detailed spectroscopic study in the 2.38-12 $\mu $m wavelength range of a sample of 16 A0-M2 stars used for the calibration of ISO-SWS. By investigating the discrepancies between the ISO-SWS data of these sources, the theoretical predictions of their spectra, the high-resolution FTS-KP (Kitt Peak) spectrum of $\alpha $ Boo and the solar FTS-ATMOS (Atmospheric Trace Molecule Spectroscopy) spectrum, both calibration problems and problems in computing the theoretical models and the synthetic spectra are revealed. The underlying reasons for these problems are sought for and the impact on the further calibration of ISO-SWS and on the theoretical modelling is discussed extensively.

Key words: instrumentation: spectrographs - methods: data analysis - infrared: stars - stars: atmospheres - stars: late-type - stars: fundamental parameters


  
1 Introduction

For the astronomical community analysing ISO-SWS data (Infrared Space Observatory, Short-Wavelength Spectrometer, de Graauw et al. 1996), a first point to assess when judging and qualifying their data concerns the flux calibration accuracy. Since the calibration process is not straightforward, knowledge on the full calibration process and on the still remaining calibration problems is crucial when processing the data.

One way to detect calibration problems is by comparing observed data with theoretical predictions of a whole sample of standard calibration sources. But, as explained in Decin et al. (2000) (hereafter referred to as Paper I) a full exploitation of the ISO-SWS data may only result from an iterative process in which both new theoretical developments on the computation of stellar spectra - based on the MARCS and TURBOSPECTRUM code (Gustafsson et al. 1975; Plez et al. 1992; Plez et al. 1993), version May 1998 - and more accurate instrumental calibration are involved.

Precisely because this research entails an iterative process, one has to be extremely careful not to confuse technical detector problems with astrophysical issues. Therefore, the analysis in its entirety encloses several steps. Some steps have already been demonstrated in the case of $\alpha $ Tau in Paper I. They will be summarised in Sect. 2. Other points will be introduced in Sect. 2 and will be elaborated in the first sections of this article (Sects. 3-5). Having described the method of analysis, the general discrepancies between observed and synthetic spectra are subjected to a careful scrutiny in order to elucidate their origin. At this point, a distinction can be made between discrepancies typically for warm stars and those typical for cool stars. For this research, warm stars are defined as being hotter than the Sun ( $T_{{\rm eff},\odot} = 5770$ K) and their infrared spectra are mainly dominated by atomic lines, while molecular lines are characteristic of cool star spectra. A description on the general trends in the discrepancies for warm and cool stars will be made in this paper, while each star of the sample will be discussed individually in two forthcoming papers in which also an overview of other published stellar parameters will be given.

As stated in Paper I, the detailed spectroscopic analysis of the ISO-SWS data has till now been restricted to the wavelength region from 2.38 to 12 $\mu $m. So, if not specified, the wavelength range under research is limited to band 1 (2.38-4.08 $\mu $m) and band 2 (4.08-12.00 $\mu $m). Band 3 (12.00-29.00 $\mu $m) will be elaborated on by van Malderen (van Malderen et al. 2001, in prep.).

This paper is organised as follows: in Sect. 2 the general method of analysis is summarised. The sample of ISO-SWS observations is described in Sect. 3, while the data reduction procedure is discussed in Sect. 4. The observations of two independent instruments are introduced in Sect. 5. In Sect. 6, the results are elaborated on. In the last section, Sect. 7, the impact on the calibration of ISO-SWS and on the theoretical modelling is given.

The appendix of this article is published electronically. Most of the grey-scale plots in the printed version of the article are printed in colour in the appendix, in order to better distinguish the different spectra.

  
2 Description of the strategy

Since this research includes an iterative process, one has to be very careful not to introduce (and so to propagate) any errors. The strategy in its entirety therefore encompasses a number of steps, including (1.) a spectral coverage of standard infrared sources from A0 to M8, (2.) a homogeneous data reduction, (3.) a detailed literature study, (4.) a detailed knowledge of the impact of the various parameters on the spectral signature, (5.) a statistical method to test the goodness-of-fit (Kolmogorov-Smirnov test) and (6.) high-resolution observations with two independent instruments. Some points (in particular, points 4 and 5) have already been demonstrated in the case of $\alpha $ Tau in Paper I. Points 1, 2 and 6 will be elaborated on in Sects. 3, 4 and 5 respectively.

In its totality, the general method of analysis - based on these 6 points - may be summarised as follows:
a large set of standard stars (A0-M8) has been observed with ISO-SWS (Sect. 3). The observational data first have been subjected to a homogeneous data-reduction procedure (Sect. 4). Thereafter, the carefully reduced ISO-SWS data of one warm and one cool star were compared with the observational data of two independent instruments (FTS-KP and FTS-ATMOS, see Sect. 5). This step is very crucial, since this is the only secure and decisive way to point out calibration problems with the detectors of ISO-SWS. The complete observational data-set, covering a broad parameter space, was then compared with theoretical predictions. By knowing already some problematic points in the calibration of ISO-SWS, these comparisons led both to a refinement of our knowledge on the calibration problems and to a determination of theoretical modelling problems (Sect. 6).

The knowledge on the relative importance of the different molecules[*] - displaying their characteristic absorption pattern somewhere in the broad ISO-SWS wavelength-range - and on the impact of the various stellar parameters on the infrared spectrum enabled us also to determine the fundamental stellar parameters for the cool giants in our sample Paper I. Due to severe calibration problems with the band-2 data (see Sect. 4), only band-1 data were used for this part of the process. Once a high-level of agreement between observed and synthetic data was reached, a statistical test was needed to objectively judge on the different synthetic spectra. A choice was made for the Kolmogorov-Smirnov test Paper I. This statistical test globally checks the goodness-of-fit of the observed and synthetic spectra by computing a deviation estimating parameter $\beta $ (see Eq. (5) in Paper I). The lower the $\beta $-value, the better the accordance between the observed data and the synthetic spectrum.

Using this method, the effective temperature, gravity, metallicity, microturbulent velocity together with the abundance of C, N and O and the ${\rm ^{12}C/^{13}C}$-ratio were estimated for the cool stars. From the energy distribution of the synthetic spectrum between 2.38 and 4.08 $\mu $m and the absolute flux-values in this wavelength range of the ISO-SWS spectrum, the angular diameter was deduced. We therefore have minimised the residual sum of squares

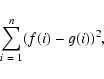\begin{displaymath}\sum\limits_{i~=~1}^{n} (f(i) - g(i))^2, \nonumber \end{displaymath}  

with f(i) and g(i) representing respectively an observational and a synthetic data point at the ith wavelength point.

The error bars on the atmospheric parameters were estimated from 1. the intrinsic uncertainty on the synthetic spectrum (i.e. the possibility to distinguish different synthetic spectra at a specific resolution, i.e. there should be a significant difference in $\beta $-values) which is thus dependent on both the resolving power of the observation and the specific values of the fundamental parameters, 2. the uncertainty on the ISO-SWS spectrum which is directly related to the S/N of the ISO-SWS observation, 3. the value of the $\beta $-parameters in the Kolmogorov-Smirnov test and 4. the still remaining discrepancies between observed and synthetic spectra.

It should be noted that an error on the effective temperature introduces an error on the angular diameter. The IR flux of the cool giants does not follow the Rayleigh-Jeans law for a black-body, and we can write ${\cal{F}}_{{\rm obs}}^{\lambda} \propto {T_{\rm eff}}^q \cdot \theta_{\rm d}^2$. Thus, with $\theta_{\rm d} \propto {{\cal{F}}_{{\rm obs}}^{\lambda}}^{1/2} \cdot {T_{\rm eff}}^{-q/2}$ and $\sigma_{<{\cal{F}}>} = 0.10 {\cal{F}}$, one obtains

 \begin{displaymath}\frac{\sigma_{<\theta_{\rm d}>}}{\theta_{\rm d}} = \sqrt{\fra... ...2_{<{T_{\rm eff}}>}}{{T_{\rm eff}}^2} + \sigma^2_{{\rm int}}}, \end{displaymath} (1)

with $\sigma^2_{{\rm int}}$ being the intrinsic uncertainty on the angular diameter (i.e. the amount by which one may change the angular diameter without significant difference in the residual sum of squares). The uncertainty on the angular diameter (Eq. (2)) is mainly determined by the uncertainty in the absolute flux (the first term in Eq. (2)), resulting in almost the same percentage errors in $\theta_{\rm d}$. Using the ISO-SWS observational data of these cool giants, we could demonstrate that $q \approx 1.3 \pm 0.1$ for 3600  ${\rm K} \le \mbox{$T_{{\rm eff}}$ }\le 4400$ K (Decin 2000). With $q \approx 1.3$, $\sigma_{<{T_{\rm eff}}>} = 70$ K and $\mbox{$T_{{\rm eff}}$ }= 3850$ K, the uncertainty increases with a factor 1.008 compared to the q = 1situation.

From the angular diameter and the parallax measurements (mas) from Hipparcos (with an exception being $\alpha $ Cen A, for which a more accurate parallax by Pourbaix et al. 1999, is available), the stellar radius was derived. This radius, together with the gravity - determined from the ISO-SWS spectrum - then yielded the gravity-inferred mass. From the radius and the effective temperature, the stellar luminosity could be extracted.

This method of analysis could however not be applied to the warm stars of the sample. Absorption by atoms determines the spectrum of these stars. It turned out to be unfeasible to determine the effective temperature, gravity, microturbulence, metallicity and abundances of the chemical elements from the ISO-SWS spectra of these warm stars, due to

Therefore, good-quality published stellar parameters were used to compute the theoretical model and corresponding synthetic spectrum. The angular diameter was deduced directly from the ISO-SWS spectrum, which then yielded - in conjunction with the assumed parallax, gravity and effective temperature - the stellar radius, mass and luminosity.

  
3 Description of the sample

It seems important to cover a broad parameter space in order to be able to distinguish between calibration problems and problems related to the computation of a theoretical model and/or to the generation of a synthetic spectrum. Therefore, stellar standard candles spanning the spectral types A0-M8 were observed. The observations were obtained in the context of two ISO-SWS proposals. Some calibration data were also provided by the SIDT (SWS Instrument Dedicated Team) in the framework of a quick-feedback refining of the model SEDs used for the SWS calibration. In total, full-resolution SWS scans of 20 standard stars, covering the full A0-M8 spectral range were obtained. Stars with an earlier spectral type were included in the proposals of S. Price. An overview of the objects, observing dates and integration times ( $t_{{\rm int}}$) can be found in Tables 1 and 2. Stars indicated by a "$\bullet$'' are stars which have been scrutinised more carefully than stars indicated by a "$\circ$''. We first focused on $\alpha $ Bootes (K2 IIIp), because of its well-known stellar parameters and the high quality of the ISO-SWS data for this object (Decin et al. 1997). From then on, we have gone, step by step, towards both higher and lower temperatures. Why the two warmest stars in our sample (being Vega and Sirius) have been considered, but have not been studied into all detail, will be explained in Sect. 6.1. The other "$\circ$''-stars in Table 2 are stars cooler than an M2 giant - i.e. cooler than $\sim $3500 K. Calibration problems with $\gamma $ Cru, variability (Monnier et al. 1998), the possible presence of a circumstellar envelope, stellar winds or a warm molecular envelope above the photosphere (Tsuji et al. 1997) made the use of hydrostatic models for these stars inappropriate and have led to the decision to postpone the modelling of the coolest stars in the sample.


 

 
Table 1: The logbook of the ISO-SWS observations used for this study. The observing date can be calculated from the revolution number which is the number of days after 17 November 1995. Sub-bands of bands 1 and 2 observed completely or partially during an AOT06 observation are given underneath the table. The wavelength ranges for the different sub-bands can be found in Table 3.
name HD HR HIC Spectral AOT mode $t_{{\rm int}}$ revo-
        Type (speed) [sec] lution
$\circ$ $\alpha $ Lyr 172167 7001 91262 A0V AOT01 (3) 3462 178
Vega         AOT06 5642 650*1
          AOT06 4354 678*2
$\circ$ $\alpha $ CMa 48915 2491 32349 A1V AOT01 (4) 6538 689
Sirius         AOT01 (1) 1140 868
$\bullet$ $\beta $ Leo 102647 4534 57632 A3Vv AOT01 (3) 3462 189
Denebola         AOT01 (1) 1096 040
$\bullet$ $\alpha $ Car              
Canopus [0pt]45348 [0pt]2326 [0pt]30438 [0pt]F0II [0pt]AOT01 (4) [0pt]6538 [0pt]729
$\bullet$ $\alpha $ Cen A 128620 5459 71683 G2V AOT01 (4) 6538 607
          AOT01 (1) 1140 294
$\bullet$ $\delta$ Dra 180711 7310 94376 G9III AOT1 (4) 6538 206
          AOT01 (4) 6528 072
$\bullet$ $\xi$ Dra 163588 6688 87585 K2III AOT01 (3) 3454 314
          AOT01 (1) 1044 068
$\bullet$ $\alpha $ Boo 124897 5340 69673 K2IIIp AOT01 (4) 6538 452
Arcturus         AOT01 (4) 6528 071
          AOT01 (1) 1140 275
          AOT01 (1) 1094 056
          AOT06 3904 583*3
          AOT06 4720 601*4
          AOT06 4510 608*5
$\bullet$ $\alpha $ Tuc 211416 8502 110130 K3III AOT01 (4) 6539 866
$\bullet$ $\beta $ UMi 131873 5563 72607 K4III AOT01 (4) 6546 182
Kochab         AOT01 (2) 1816 079


*1: 1A, 1B, 1D, 1E, 2A, 2B, 2C; *2: 1A, 1D, 1E, 2A; *3: 1A, 1B, 1D, 2A, 2C; *4: 1A, 1B, 1D, 1E, 2A, 2B, 2C; *5: 1A, 1B, 1D, 1E, 2A, 2B, 2C.



 

 
Table 2: Logbook of the ISO-SWS observations: continuation of Table 1.
name HD HR HIC Spectral AOT mode $T_{{\rm int}}$ revo-
        Type (speed) [sec] lution
$\bullet$ $\gamma $ Dra 164058 6705 87833 K5III AOT01 (4) 6538 377
Etamin         AOT01 (4) 6542 040
          AOT01 (2) 1912 811
          AOT01 (1) 1140 496
          AOT01 (1) 1062 126
          AOT06 4568 501*6
          AOT06 5676 559*7
$\bullet$ $\alpha $ Tau 29139 1457 21421 K5III AOT01(4) 6538 636
Aldebaran         AOT06*8 3700 681
$\bullet$ H Sco 149447 6166 81304 K6III AOT01(4) 6538 847
$\bullet$ $\beta $ And 6860 337 5447 M0III AOT01 (4) 6538 795
Mirach         AOT01 (3) 3454 440
          AOT01 (2) 1912 423
$\bullet$ $\alpha $ Cet 18884 911 14135 M2III AOT01 (4) 6538 797
Menkar         AOT01 (4) 6538 806
$\bullet$ $\beta $ Peg 217906 8775 113881 M2.5III AOT01(4) 6538 551
Scheat         AOT01 (3) 3454 206
          AOT01 (1) 1140 206
          AOT01 (1) 1096 056
$\circ$ $\gamma $ Cru 108903 4763 61084 M4III AOT01(4) 6538 609
          AOT01 (2) 1912 258
          AOT01 (2) 1816 079
          AOT06 5630 643*9
$\circ$ $\beta $ Gru 214952 8636 112122 M5III AOT01 (3) 3454 538
$\circ$ g Her 148783 6146 80704 M6III AOT01 (4) 6538 800
$\circ$ T Mic 194676   100935 M7/8III AOT01 (4) 6538 872


*6: 1D, 1E, 2A, 2B, 2C; *7: 1A, 1B, 1D, 1E, 2A, 2B, 2C; *8: 1A, 1B, 1D, 1E, 2C; *9: 1A, 1B, 1D, 1E, 2A, 2B, 2C.


  
4 Data reduction

In order to reveal calibration problems, the ISO-SWS data have to be reduced in a homogeneous way. For all the stars in our sample, at least one AOT01 observation[*] (AOT = Astronomical Observation Template; AOT01 = a single up-down scan for each aperture with four possible scan speeds at degraded resolution) is available, some stars have also been observed using the AOT06 mode (=long up-down scan at full instrumental resolution). Since these AOT01 observations form a complete and consistent set, they were used as the basis for the research. In order to check potential calibration problems, the AOT06 data are used. The scanner speed of the highest-quality AOT01 observations was 3 or 4, resulting in a resolving power $\simeq$870 or $\simeq$1500, respectively (Leech et al. 2002). The appropriate resolving power of each sub-band was taken to be the most conservative theoretical resolving power as determined by Lorente in Leech et al. (2002), with the exception being band 1A for which this value has been changed from 1500 to 1300, as will be discussed in Sect. 6.2.

The ISO-SWS data were processed to a calibrated spectrum by using the same procedure as described in Paper I using the calibration files available in OLP6.0.

The band 2 (Si:Ga) detectors used in SWS "remember'' their previous illumination history. Going from low to high illumination, or vice versa, results in detectors asymptotically reaching their new output value. These are referred to as memory effects or transients. For sources with fluxes greater than about 100 Jy, memory effects cause the up and down scans in the SPD (=Standard Processed Data) to differ in response by up to 20% in band 2. Since an adapted version of the Fouks-Schubert model to correct for these memory effects in band 2 was still in development (Leech et al. 2002), this method could not be applied during our reduction procedure. Instead, we have used the down-scan data of our observation as a reference to do a correction of the flux level of the first scan (up-scan). This is justified since the memory effects appear to be less severe in the down-scan measurements, suggesting a more stabilised response to the flux level for the down-scan data.

Also the band 2 dark current subtraction is closely tied to the band 2 memory effect correction. The memory effect for Si:Ga detectors as described by the Fouks-Schubert model is an additive effect. As such, its proper correction will take place during the dark current subtraction. Since this correction tool was still not available, all dark currents were checked individually. When a dark current was corrupted too much by memory effects, its value was replaced by the value of a preceding or following dark-current not being affected. In this way, a small error can occur, which is, however, negligible due to the high flux level of our stellar sources.


 

 
Table 3: Factors used to multiply the sub-bands for the highest-quality AOT01 observation (denoted by its revolution number) of the selected stars in our sample are given. For each band the wavelength range $\lambda _{\rm b}$ - $\lambda _{\rm e}$ (in $\mu $m) and the (constant) resolving power for a speed-4 AOT01 observation are also noted. For a speed-3 AOT01 observation one has to multiply the average resolving power by $\sim $0.58. In the last two columns the pointing offset as estimated from known imperfections in the satellite attitude control system is given in arcsec, where the y-axis denotes the cross-dispersion direction for SWS and the z-axis the dispersion direction.
  1A 1B 1D 1E 2A 2B 2C rev. dy dz
$\lambda / \Delta \lambda $ 1300 1200 1500 1000 1200 800 800      
$\lambda _{\rm b}$ [$\mu $m] 2.38 2.60 3.02 3.52 4.08 5.30 7.00      
$\lambda _{\rm e}$ [$\mu $m] 2.60 3.02 3.52 4.08 5.30 7.00 12.00      
$\alpha $ Lyr 1.06 1.06 1.00 1.00 1.00 0.97 +12Jy 178 -0.608 -1.179
$\alpha $ CMa 1.00 1.00 1.00 0.995 1.12 1.23 1.00 689 0.034 0.003
$\beta $ Leo 0.99 0.99 1.00 1.00 1.16 1.27 +3.5Jy 189 0.478 0.556
$\alpha $ Car 0.97 0.98 1.00 1.00 0.98 1.10 0.91 729 0.024 0.072
$\alpha $ Cen A 1.01 1.02 1.00 1.01 0.985 1.06 0.91 607 0.000 0.000
$\delta$ Dra 0.97 0.98 1.00 1.015 1.03 1.02 1.10 206 -0.422 1.480
$\xi$ Dra 0.99 0.99 1.00 0.99 1.12 1.15 1.05 314 1.286 -0.282
$\alpha $ Boo 0.995 1.01 1.00 1.005 0.95 1.05 1.00 452 0.000 0.000
$\alpha $ Tuc 1.005 1.02 1.00 1.01 1.05 1.00 1.00 866 0.000 0.000
$\beta $ UMi 1.00 1.015 1.00 1.01 0.91 0.885 1.00 182 -1.062 0.045
$\gamma $ Dra 0.995 1.005 1.00 1.005 0.935 0.98 0.91 377 -0.304 0.181
$\alpha $ Tau 1.00 1.01 1.00 1.00 1.00 1.045 1.00 636 0.000 0.000
H Sco 1.00 1.015 1.00 1.00 1.13 1.05 1.15 847 0.000 0.000
$\beta $ And 1.00 1.00 1.00 1.005 1.00 1.10 0.95 795 0.000 0.000
$\alpha $ Cet 0.985 1.00 1.00 1.01 0.935 1.03 0.91 797 0.000 0.000
$\beta $ Peg 1.00 1.015 1.00 1.005 0.935 1.03 0.935 551 0.017 0.095


Since the different sub-band spectra can show jumps in flux at the band-edges, several sub-bands had to be multiplied by a small factor to construct a smooth spectrum. Three causes for the observed shift factors between different sub-bands of an observation and between different observations of a given stellar source can be reported: 1. pointing errors, 2. problems with the RSRF correction, and 3. a problematic dark current subtraction, from which the pointing errors are believed to have the largest impact. The pointing errors as well as the RSRF correction causes a decrease in flux by a gain factor, while the dark current subtraction can lower the flux level by an offset. As the effects of the pointing errors are estimated to have the biggest effect, and since the stars in our sample have a high flux level so that the dark current subtraction only plays a marginal role, the individual sub-bands were multiplied with a factor - rather than shifted with an offset - in order to obtain a smooth spectrum. These factors (see Table 3) were determined by using the overlap regions of the different sub-bands and by studying the other SWS observations. The band-1D data were taken as reference data, due to the absence of strong molecular absorption in this wavelength range which may cause a higher standard deviation in the bins obtained when rebinning the oversampled spectrum, and - most importantly - due to the low systematic errors in this band, caused by e.g. errors in the curve of the RSRF, detector noise, uncertainties in the conversion factors from $\mu $V/s to Jy, ... (Leech et al. 2002). Using the total absolute uncertainty values - which have accumulated factors from each of the calibration steps plus estimated contributions from processes which were unprobed or uncorrected - as given in Table 5.3 in Leech et al. (2002), the estimated 1 $\sigma$ uncertainty on these factors is 10%. As is clearly visible from Table 3, these factors do not show any trend with spectral type or flux-level. This is displayed in Fig. 1, where the band-border ratios between 1A-1B, 1B-1D and 1D-1E are plotted in function of the flux at 2.60, 3.02 and 3.52 $\mu $m respectively. For this plot, all the observations of the cool stars in our sample, discussed in the Appendix of Paper IV of this series, are used. In band 1, the band-border ratios of 1A-1B and 1D-1E are from bands within the same aperture. Going from band 1B to band 1D, the aperture changes. Satellite mispointings can have a pernicious impact on this band-border ratio: the mean deviation of the band-border ratios w.r.t. 1 is significantly larger for 1B-1D (=0.015) than for 1A-1B and 1D-1E (being respectively 0.009 and 0.005). Due to the problems with memory effects in band 2 (4.08-12 $\mu $m), the factors of each sub-band of band 2 were determined by use of the corresponding spectral data of Cohen (Cohen et al. 1992, 1995, 1996; Witteborn et al. 1999): for Vega and Sirius Cohen has constructed a calibrated model spectrum; a composite spectrum (i.e. various observed spectra have been spliced to each other using photometric data) is available for $\alpha $ Cen A, $\alpha $ Boo, $\gamma $ Dra, $\alpha $ Tau, $\beta $ And, $\alpha $ Cet, and $\beta $ Peg; a template spectrum (i.e. a spectrum made by using photometric data of the star itself and the shape of a "template'' star) is built for $\delta$ Dra (template: $\beta $ Gem: K0 III), $\xi$ Dra (template: $\alpha $ Boo: K2 IIIp), $\alpha $ Tuc (template: $\alpha $ Hya: K3 II-III) and H Sco (template: $\alpha $ Tau: K5 III). When no template was available (for $\beta $ Leo, $\alpha $ Car and $\beta $ UMi), the synthetic spectrum showing the best agreement with the band-1 data was used as reference. This does not imply that we are trapped in a circular argument, since the stellar parameters for the synthetic spectrum were determined from the band-1 data only. Moreover, the maximum difference in the correction factors for band 2 obtained when using the synthetic spectra instead of a Cohen template for the 13 stars common in the sample is 7%, which is well within the photometric absolute flux uncertainties claimed by Leech et al. (2002). Note that all shift factors are in within the AOT01 band border ratios as derived in Figs. 5.33 and 5.34 in Leech et al. (2002). Using the overlap regions in band 2 can have quite a big effect on the final composed spectrum: focussing on $\beta $ UMi, we note that by using these overlap regions band 2A (and consequently bands 2B and 2C) should be shifted downwards by a factor 1.04; in order then to match the shifted band 2B and band 2C, band 2C should be once more shifted downwards by a factor 1.12. In general, the error in the absolute flux could increase to $\sim $20% at the end of band 2C when this method would be used.

For a more elaborate discussion on the SWS error budget, we would like to refer to Leech et al. (2002).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3317f1_bw.ps} \end{figure} Figure 1: Flux ratios between the different sub-bands of band 1 at the wavelengths of overlap. The mean deviation w.r.t. 1 is given for the different band borders at the right corner of the figure.
Open with DEXTER

  
5 Verification of the results with FTS-KP and FTS-ATMOS spectra

To test our findings - indicating either a calibration problem or a theoretical modelling problem - with data taken with an independent instrument, a high-resolution observation of both one warm and one cool star were included. The high-resolution Fourier Transform Spectrometer (FTS) spectrum of $\alpha $ Boo (Hinkle et al. 1995b) and the Atmospheric Trace Molecule Spectroscopy (ATMOS) spectrum of the Sun (Farmer & Norton 1989; Geller 1992) are used as external control to the process.

The Arcturus observations were obtained with the FTS at the Kitt Peak (KP) 4 m Mayall telescope mainly in 1993 and 1994 and are described in Hinkle et al. (1995a); Hinkle et al. (1995b). The entirety of the 1 to 5 $\mu $m Arcturus spectrum detectable from the ground was observed twice at opposite heliocentric velocities, allowing the removal of many telluric lines. We refer to these two spectra as the winter and summer observations. The data were obtained at a resolving power ($\lambda$/ $\Delta\lambda$) near 100 000. Spectra of the Earth's atmosphere, derived from high resolution solar spectra, have been ratioed to the Arcturus spectra to largely remove the telluric lines. Most telluric lines less than 30% deep are cleanly removed but as the optical depth of the telluric lines increases more information is lost and lines over 50% deep can not be removed. Gaps in the plots appear at these spectral regions. A typical example of the Arcturus spectra is shown in Fig. 16 on page [*]. In the upper panel of Fig. 16, some CO lines of the first overtone are plotted. In the lower panel of Fig. 16, one can clearly distinguish atomic and OH lines.

During the period from November 3 to November 14, 1994, the Atmospheric Trace Molecule Spectroscopy (ATMOS) experiment operated as part of the ATLAS-3 payload of the shuttle Atlantis (Gunson et al. 1996). The principal purpose of this experiment was to study the distribution of the atmosphere's trace molecular components. The instrument, a modified Michelson interferometer, covering the frequency range from 625 to 4800 cm-1 at a spectral resolution of 0.01 cm-1, also recorded high-resolution infrared spectra of the Sun. A small part of the intensity spectrum is shown in Fig. 2. The Holweger-Müller model (Holweger & Müller 1974) was used as input for the computation of the synthetic spectrum of the Sun. A microturbulent velocity of 1 km s-1 was assumed.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f2_bw.ps} \end{figure} Figure 2: FTS-ATMOS intensity spectrum of the Sun (black) at a resolving power $\lambda / \Delta \lambda $ of 60 000. The synthetic spectrum (grey) has been computed using the Holweger-Müller model (Holweger & Müller 1974) with $\mbox{$\xi_{\rm t}$ }= 1$ km s-1.
Open with DEXTER

In the case of $\alpha $ Boo, a high-resolution synthetic spectrum was first generated with the stellar parameters of Kjærgaard et al. (1982) as input parameters ( $\mbox{$T_{{\rm eff}}$ }= 4350$ K, $\log g = 1.80$, [Fe/H] = -0.50, $\varepsilon $(C) = 7.89, $\varepsilon $(N) = 7.61, $\varepsilon $(O) = 8.68). For the microturbulence $\xi_{\rm t}$ a velocity of 1.7 km s-1 was assumed as being the mean for red giants (Gustafsson et al. 1974). Since both Mäckle et al. (1975) and Bell et al. (1985) found a Si and Mg abundance depleted with respect to the solar values, $\varepsilon $(Mg) was taken to be 7.33 and $\varepsilon $(Si) to be 7.20. For the anisotropic macroturbulence $\Gamma_{\rm t}$, a radial-tangential profile was assumed (Gray 1975) with FWHM of 3 km s-1. This synthetic spectrum was then convolved with the beam-profile function (i.e. a sinc-function). Both observed FTS-KP and synthetic spectrum were rebinned to a resolving power of 60 000, since the resolving power of the FTS-KP was not constant over the whole wavelength range. Using this set of input-parameters, the high-excitation CO ( $\Delta v = 1$ and $\Delta v = 2$) and SiO ( $\Delta v = 2$) lines were predicted as being too weak. This was confirmed from both the FTS-KP and the ISO-SWS spectrum. Especially from the ISO-SWS spectrum - and more specifically from the slope in bands 1B and 1D - it became clear that the gravity should be lowered. Using then the FTS-KP-spectra, the input parameters were improved until an optimal fit was obtained (see Fig. 16 on page [*]). This resulted in the following parameters: $\mbox{$T_{{\rm eff}}$ }= 4350$ K, $\log g = 1.50$, [Fe/H] = -0.50, $\mbox{$\xi_{\rm t}$ }= 1.7$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }= 7$, $\varepsilon $(C) = 7.96, $\varepsilon $(N) = 7.61, $\varepsilon $(O) = 8.68, $\varepsilon $(Mg) = 7.33 and $\varepsilon $(Si) = 7.20.

Discrepancies appearing from the confrontation of the synthetic spectrum with both the FTS-KP and the ISO-SWS spectra, may be clearly attributed to problems in constructing the model or generating the synthetic spectrum. Other discrepancies in the ISO-SWS versus synthetic spectrum are the ones caused by calibration problems.

For the warm stars in the sample, an analogous comparison was performed with the help of the FTS-ATMOS intensity spectrum of the Sun. Discrepancies between the ISO-SWS and synthetic spectra of $\alpha $ Cen A (G2V) were compared with the discrepancies found in the comparison between the FTS-ATMOS spectrum of the Sun and its synthetic spectrum (Fig. 2).

Inspecting Figs. 2 and 16, some discrepancies become immediately visible, e.g. the CO 2-0 and 3-1 are predicted too weak in both figures. The reason for this and other discrepancies will be explained in the next section.

  
6 Results

Computing synthetic spectra is one step, distilling useful information from it is a second - and far more difficult - one. Fundamental stellar parameters for this sample of bright stars are a first direct result which can be deduced from this comparison between ISO-SWS data and synthetic spectra. In Papers III and IV of this series, these parameters will be discussed and confronted with other published stellar parameters.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f3_col.ps} \end{figure} Figure 3: Comparison between the ISO-SWS data of $\alpha $ Cen A (black) and the synthetic spectrum (grey) with stellar parameters $\mbox{$T_{{\rm eff}}$ }= 5830$ K, $\log g = 4.35$, M = 1.3 $M_{\odot }$, [Fe/H] = 0.25, $\mbox{$\xi_{\rm t}$ }= 1.0$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }~\!\! =~\!\! 89$, $\varepsilon $(C) = 8.74, $\varepsilon $(N) = 8.26, $\varepsilon $(O) = 9.13 and $\mbox{$\theta_{\rm d}$ }= 8.80$ mas. Some of the most prominent discrepancies between these two spectra are indicated by an arrow. A coloured version of this plot is available in the appendix as Fig. .1.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{aah3317new/h3317f4_col.eps} \end{figure} Figure 4: Comparison between band 1 and band 2 of the ISO-SWS data of $\gamma $ Dra (black) and the synthetic spectrum (grey) with stellar parameters $\mbox{$T_{{\rm eff}}$ }= 3960$ K, $\log g = 1.30$, M = 1.7 $M_{\odot }$, [Fe/H] = 0.00, $\mbox{$\xi_{\rm t}$ }= 2.0$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }= 10$, $\varepsilon $(C) = 8.15, $\varepsilon $(N) = 8.26, $\varepsilon $(O) = 8.93 and $\mbox{$\theta_{\rm d}$ }= 9.98$ mas. A coloured version of this plot is available in the appendix as Fig. .2.
Open with DEXTER

A typical example of both a warm and cool star is given in Figs. 3 and 4 respectively. Different types of discrepancies do emerge. The size of the discrepancies between ISO-SWS observations and theoretical predictions varies a lot. Both for the warm and for the cool stars we see a general good agreement in shape between the ISO-SWS and theoretical data in band 1, with however (local) error peaks up to $\sim $8%. An exception is $\beta $ Peg for which the shape is wrong by $\sim $6% and local error peaks may go up to $\sim $15%. The agreement between observational and synthetic data is worse in band 2: a general mismatch by up to $\sim $15% may occur.

By scrutinising carefully the various discrepancies between the ISO-SWS data and the synthetic spectra of the standard stars in our sample, the origin of the different discrepancies was elucidated. First of all, a description on the general trends in discrepancies for the warm stars will be made, after which the cool stars will be discussed.

  
6.1 Warm stars: A0-G2

1.
Especially when concentrating on $\alpha $ Cen A (G2 V), one notifies quite a few spectral features which appear in the ISO-SWS spectrum, but are absent in the synthetic spectrum. By comparing the spectra of the other warm stars ($\beta $ Leo, $\alpha $ Car, $\alpha $ Lyr and $\alpha $ CMa) with each other, corresponding spectral features can be recognised in their ISO-SWS spectra, although this is somewhat more difficult for $\beta $ Leo due to the lower resolving power and lower signal-to-noise ratio. Also for the cooler stars in the sample, these spectral features are (weakly) present. Some of the most prominent ones are indicated by arrows in the spectrum of $\alpha $ Cen A in Fig. 3. Molecular absorption can not be a possible cause of/ contribution to e.g. the 3.9 $\mu $m feature, since this feature is seen for the warm stars in the sample, where no molecular absorption occurs at these wavelength ranges. The solar FTS-ATMOS spectrum proved to be extremely useful for the determination of the origin of these features. All spectral features, indicated by an arrow in Fig. 3, turned out to be caused by - strong - atomic lines (Mg, Si, Fe, Al, C, ...). This is illustrated for the wavelength range from 3.85 to 3.92 $\mu $m in Fig. 5. In panel a of Fig. 5, the high-resolution FTS-ATMOS spectrum of the Sun is compared with its synthetic spectrum in the wavelength range from 3.853 to 3.917 $\mu $m. The strongest lines are identified by using the line list of Geller (1992). At the ISO resolving power of 1000 in band 1E, these atomic lines are reduced to the features indicated in panel b. The same features can be recognised in the ISO-SWS spectrum of $\alpha $ Cen A in panel c. It is clear that these atomic features are not well calculated for the synthetic spectra of the Sun and $\alpha $ Cen A.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f5_bw.ps} \end{figure} Figure 5: In panel a) the high-resolution FTS-ATMOS spectrum of the Sun is compared with its synthetic spectrum based on the Holweger-Müller model (1974) and computed by using the atomic line list of Hirata & Horaguchi (1995). Panel  b) shows the same comparison as panel  a), but now at a resolving power of 1000 for the wavelength range going from 3.52-4.08 $\mu $m (band 1E). The data of band 1E of the ISO-SWS spectrum of $\alpha $ Cen A (at a resolving power of 1000) are plotted in panel  c).
Open with DEXTER

For Fig. 5, the atomic line list of Hirata & Horaguchi (1995) was used to generate the synthetic spectrum. This line list has as starting files the compilation by Kurucz & Peytremann (1975) and Kurucz (1989) who lists the semi-empirical gf-values for many ions. Energy levels were adopted from recent compilations (Sugar & Corliss 1985) or individual works. The line list of Kelly (1983) was merged into the file. The gf-values are taken from several compilations (e.g. Fuhr et al. 1988a, 1988b; Reader et al. 1980; Wiese et al. 1966, 1969; Morton 1991, 1992). Published results of the Opacity Project (Seaton 1995) were also included. Comparing the atomic line list of Hirata & Horaguchi (1995) with the identifications as given by Geller (1992) made clear that quite some lines are misidentified or not included in the IR atomic line list of Hirata & Horaguchi (1995).

The usage of VALD (Vienna Atomic Line Database: Piskunov et al. 1995; Ryabchikova et al. 1997; Kupka et al. 1999)[*] and the line list of van Hoof (1998) did not solve the problem. Obviously, the oscillator strengths of the atomic lines in the infrared are not known sufficiently well.

In order to test this hypothesis, Sauval (2002, priv. comm.) has constructed a new atomic line list by deducing new oscillator strengths from the high-resolution ATMOS spectra of the Sun (625-4800 cm-1). A preliminary comparison using this new linelist is given in Fig. 6 (which should be compared with Fig. 5). The contents, nature, limitations, uncertainties, ... of this new line list will be discussed in a forthcoming paper. But it is already obvious from a confrontation between Figs. 5 and 6 that these new oscillator strengths from Sauval are more accurate.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f6_bw.ps} \end{figure} Figure 6: In panel a) the high-resolution ATMOS spectrum of the Sun is compared with its synthetic spectrum based on the Holweger-Müller model (1974) and computed by using the atomic line list of Sauval (2002, priv. comm.). Panel  b) shows the same comparison as panel  a), but now at a resolving power of 1000 for the wavelength range going from 3.52-4.08 $\mu $m (band 1E). The data of band 1E of the ISO-SWS spectrum of $\alpha $ Cen A (at a resolving power of 1000) are plotted in panel  c).
Open with DEXTER

It is plausible that the same reason, i.e. wrong and missing oscillator strengths of atomic lines in the infrared, together with noise, is the origin of the observed discrepancies between the ISO-SWS and synthetic spectra for the other warm stars in the sample, because

The lack of reliable atomic data rendered the determination of the fundamental stellar parameters for the warm stars from the ISO-SWS data impossible. Another consequence concerns the continuum, which was very difficult to determine. Therefore, the uncertainty on the angular diameter of these warm stars is more pronounced.

2.
Secondly, the hydrogen lines are conspicuous. For example, the synthetic hydrogen Pfund lines are almost always predicted as being too strong for main-sequence stars, while they are predicted as being too weak for the supergiant $\alpha $ Car. This indicates a problem with the generation of the synthetic hydrogen lines, which is corroborated when the high-resolution FTS-ATMOS spectrum of the Sun is compared with its synthetic spectrum (see Fig. 7). In the TURBOSPECTRUM program (Plez et al. 1992; Plez et al. 1993) the hydrogen line-profile calculation, adopted from the SYNTHE code of Kurucz, includes the Stark, the Doppler, the van der Waals and the resonance broadening. For the first four lines in every series, the fine structure is also included for the core calculations. The problematic computation of the self broadening of hydrogen lines (Barklem et al. 2000) and the unproper treatment of the convection by using the mixing-length theory (see, e.g., Asplund et al. 2000 where realistic ab-initio 3D radiative-hydrodynamical convection simulations have been used) may account for part of this discrepancy.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f7_bw.ps} \end{figure} Figure 7: FTS-ATMOS intensity spectrum of the Sun (black) at a resolving power $\lambda / \Delta \lambda $ of 60 000. The synthetic spectrum (grey) has been computed using the Holweger-Müller model (Holweger & Müller 1974) with $\mbox{$\xi_{\rm t}$ }= 1$ km s-1. The Bracket $\beta $ line is indicated by an arrow. Most of the other features are CO $\Delta v = 2$ lines, some are atomic lines.
Open with DEXTER

3.
Compared to the ISO-SWS data, the synthetic spectra of warm stars display a higher synthetic flux between the H5-9 and H5-8 hydrogen line (see Fig. 8). From other SWS observations available in the ISO data-archive, we could deduce that this "pseudo-continuum'' starts arising for stars hotter than K2 ($\sim $4500 K). Since this effect is systematically seen for all warm stars in the sample, the origin of this discrepancy can not be a wrong multiplication factor. Note that band 1D and band 1E overlap each other over quite a large wavelength range, so that the multiplication factor of band 1E can be accurately determined. Moreover such an effect was not seen for the cooler K and M giants, the spectrum of which is dominated by OH features in this wavelength range, so we could reduce the problem as having an atomic origin. A scrutiny on the hydrogen lines shows that the high-excitation Humphreys-lines (from H6-18 on) - and Pfund-lines - are always calculated as too weak. Moreover, the Humphreys ionisation edge occurs at 3.2823 $\mu $m. Since the discrepancy does not appear above the limit (i.e. at shorter wavelengths) and is disappearing beyond the Brackett-$\alpha $ line, the conclusion is reached that a problem with the computation of the complex line profile of the crowded Humphreys hydrogen lines towards the series limit causes this discrepancy. The higher the transition, i.e. going from H6-18 to H6-93, the more the $\log gf$-value should be increased in order to get a good match between observations and theoretical computations: increasing $\log gf$ with +0.3 dex gives us a good match for the H6-18 line in $\alpha $ Car, while we should increase $\log gf$ with +1.0 dex for the H6-16 line in $\alpha $ Car. We may conclude that a complex problem with the computation of the pressure broadening will be on the origin of the discussed discrepancy.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f8_bw.ps} \end{figure} Figure 8: Comparison between the observed ISO-SWS spectrum of $\alpha $ Car and its synthetic spectrum in the wavelength region from 3.20 to 4.08 $\mu $m. The Brackett-$\alpha $, two Pfund-lines (H5-8 and H5-9) and a number of Humphreys-lines are identified. The dashed line indicates the Humphreys ionisation edge.
Open with DEXTER

4.
From 3.48 $\mu $m on, fringes at the end of band 1D affect the ISO-SWS spectra of almost all stars in the sample.

5.
A clear discrepancy is visible at the beginning of band 1A. For the warm stars, the H5-22 and H5-23 lines emerge in that part of the spectrum. An analogous discrepancy is also seen for the cool stars, though it is somewhat more difficult to recognise due to the presence of many CO features (Fig. 9). Being present in the continuum of both warm and cool stars, this discrepancy is attributed to problems with the Relative Spectral Response Function (RSRF). A broad-band correction was already applied at the short-wavelength edge of band 1A (Vandenbussche et al. 2001), but the problem seems not to be fully removed. At the band edges, the system response is always small. Since the data are divided by the RSRF, a small problem with the RSRF at these places may introduce a pronounced error at the band edge.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f9_bw.ps} \end{figure} Figure 9: Band 1A of Vega (A0 V), $\alpha $ Car (F0 II) and $\alpha $ Tau (K5 III) are displayed. The ISO-SWS spectrum is plotted in black, the synthetic spectrum in grey. A clear discrepancy is visible at the beginning of this band ( $\lambda \protect \la 2.407$ $\mu $m).
Open with DEXTER

6.
Memory effects of the detectors make the calibration of band 2 for all the stars very difficult. These memory effects are more severe for the cool stars, since the CO and SiO absorptions cause a steep increase (decrease) in flux for the up (down) scan (Fig. 10). Band-border ratios are determined from the composite SEDs by Cohen or from the synthetic spectrum. The RSRFs for the sub-bands will therefore only be modelled well once there is a fool-proof method to correct SWS data for detector memory effects. Two other examples of this problematic RSRF modelling are visible in band 2B and band 2C. For almost all warm and cool stars, there is a "dip'' around 6 $\mu $m and a jump in flux level around 9.3 $\mu $m (Fig. 10). This latter problem is a residue of the correction for an instrumental absorption feature, documented by Vandenbussche et al. (2001). The short-wavelength part of band 2A (where the CO $\Delta v = 1$absorption starts) and of band 2C (with SiO $\Delta v = 1$) are thus useless for passing a quantitative judgement upon the parameters influencing the observed spectrum in this wavelength range, like $T_{{\rm eff}}$, $\varepsilon $(C), $\varepsilon $(O), ... From the longer wavelength parts of these same bands, one will not be able to estimate directly fundamental stellar parameters, but these data enable us to see if there are no contradictions between this part of the ISO-SWS spectrum and the synthetic spectrum generated using the parameters adopted from literature or estimated from the ISO-SWS data in band 1.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f10_col.ps} \end{figure} Figure 10: Band 2 for Sirius (A1 V) and $\gamma $ Dra (K5 III) are displayed. The ISO-SWS spectrum is plotted in black, the synthetic spectrum in grey. Problems with the RSRF are indicated by an arrow. A coloured version of this plot is available in the appendix as Fig. .3.
Open with DEXTER

  
6.2 Cool stars: G2-M2

1.
The situation changes completely when going to the cool stars of the sample. While the spectrum of the warm stars is dominated by atomic-line features, molecules determine the spectral signature of the cool stars. A few of the - problematic - atomic features (see Sect. 6.1) can still be identified in these cool stars, e.g. the Mg-Si-Al-Ti-Fe spectral feature around 3.97 $\mu $m (Fig. 5) remains visible for the whole sample, even in $\beta $ Peg.

2.
One of the most prominent molecular features in band 1 is the first-overtone band of carbon monoxide (CO, $\Delta v = 2$) around 2.4 $\mu $m. Already from $\alpha $ Cen A on, CO lines emerge in band 1A, although the atomic features are still more dominant for this star. It is striking that for all stars in the sample with spectral type later than G2, the strongest CO features (=band heads of $^{12}{\rm {CO}}$ 5-3, 6-4, 7-5, 8-6, and of $^{13}{\rm {CO}}$ 4-2, 5-3, 6-4 and 7-5) are always predicted too strong compared to the ISO-SWS observation (see, e.g., band 1A of $\gamma $ Dra in Fig. 11, where both SWS and theoretical data are rebinned to a resolving power of 1500, being the most conservative theoretical resolution for band 1A, Leech et al. 2002). The only exception is seen for the band head of $^{13}{\rm {CO}}$ 4-2 since the problem with the RSRF at the beginning of band 1A (see point 5. in previous section) dominates in this wavelength range.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f11_col.ps} \end{figure} Figure 11: Comparison between the ISO-SWS observation and the synthetic spectrum of $\gamma $ Dra at a resolving power of 1500 (being the most conservative theoretical resolution for band 1A Leech et al. 2002). A coloured version of this plot is available in the appendix as Fig. .4.
Open with DEXTER

In these oxygen-rich stars, the CO lines are a direct measure of the C abundance. From the present spectra, this carbon abundance can be estimated in two ways:

Computing a synthetic spectrum with the carbon abundance determined from this last criterion, results however in the (strongest) computed CO spectral features being too strong compared to the ISO-SWS observation, most visible in the strong bandheads (2-4%). It has to be noted that this mismatch occurs in band 1A, where the standard deviation of the rebinned spectrum is larger than for the other sub-bands (see Fig. 6 in Paper I) and that the error is within the quoted accuracy of ISO-SWS in band 1A (Leech et al. 2002). However, this mismatch is not random, in the sense that the observed CO features are always weaker than the synthetic ones.

A first step towards solving this problem was the use of the high-resolution FTS-KP spectrum of $\alpha $ Boo (see Sect. 5). As was explained in Sect. 5 a high-resolution synthetic spectrum was generated for $\alpha $ Boo and rebinned to a resolution of 60 000. The agreement between the observed FTS-KP and synthetic spectrum is extremely good! One example was already shown in Fig. 16, another one is depicted in Fig. 17 on page [*]. In this latter figure, the problematic subtraction of the atmospheric contribution causes the spurious features around 2.46700 $\mu $m for the summer FTS-KP spectrum and around 2.46735 $\mu $m for the winter FTS-KP spectrum[*]. When scrutinising carefully the first-overtone CO lines in the FTS-KP spectrum, it is obvious that all the 12CO 2-0 lines, and almost all the 12CO 3-1 lines, are predicted as too weak (by 1-2%) and not as too strong as was suggested in previous paragraph from the comparison between ISO-SWS and synthetic spectra! Also the fundamental CO lines are predicted as being a few percent too weak. For a better judgement of the KP-SWS-synthetic correspondence, the FTS-KP spectrum was rebinned to the ISO resolving power. This was not so straightforward due to the presence of the spurious features originating from the problematic subtraction of the atmospheric contribution. In order to conserve the flux, these spurious features were replaced by the flux value of the synthetic spectrum. This adaptation is acceptable for the following reasons:

Figure 18 on page [*] shows the comparison between the ISO-SWS, the FTS-KP and the synthetic spectrum for $\alpha $ Boo at a resolving power of 1500. It is clear that the differences between the strength of the CO features in the ISO-SWS and FTS-KP spectrum are significant. This is a strong indication for problems in the calibration process. The question now arises where this calibration problem originates from.

Firstly, it has to be noted that the flux values are unreliable in the wavelength region from 2.38 to 2.40 $\mu $m due to problems with the RSRF of band 1A; main features here include the CO 2-0 P18 and the CO 2-0 P21 lines.

Secondly, no correlation is found with the local minima and maxima in the RSRF of band 1A.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f12_col.ps} \end{figure} Figure 12: Comparison between the AOT06 observation (revolution 538, black) and the AOT01 speed-4 observation (grey) of $\gamma $ Dra. Both are rebinned to a resolving power of 1500. A coloured version of this plot is available in the appendix as Fig. .5.
Open with DEXTER

Defining the spectral resolution and instrumental profile for the ISO-SWS grating spectrometers, is not straightforward (Lorente 1998; Lutz et al. 1999). Only for an AOT02 observation has the instrumental profile now been derived quite accurately (Lutz et al. 1999). The AOT01 mode introduces an additional smoothing which, due to the intricacies of SWS-data acquisition, is different from a simple boxcar smooth. The simulation of SWS-AOT01 scans gives non-gaussian profiles, as can be seen in Fig. 6 by Lorente (1998). Nevertheless, the theoretical profile of a speed-4 observation approximates a gaussian profile very closely. Therefore, since the instrumental profile of an AOT01 is still not exactly known, the synthetic data were convolved with a gaussian with ${FWHM}=\lambda$/resolution. This incorrect gaussian instrumental profile introduces an error which will be most visible on the strongest lines.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f13_col.ps} \end{figure} Figure 13: Top: Comparison between the AOT01 speed-4 observation of $\gamma $ Dra rebinned at 1) a resolving power of 1500 (black) and 2) a resolving power of 1300 (grey). Bottom: Comparison between the ISO-SWS AOT01 observation in band 1A (black) and its synthetic spectrum (grey) at a resolving power of 1300. A coloured version of this plot is available in the appendix as Fig. .6.
Open with DEXTER

Only for $\gamma $ Dra an AOT06 observation, scanning this wavelength range, was available in the ISO data-archive. The comparison between the AOT01 speed-4 and AOT06 observation, both rebinned to a resolving power of 1500, is an indication that the resolving power of an AOT01 speed-4 observation in band 1A is lower than 1500 (Fig. 12). The theoretical resolving power for an AOT01 speed-4 observation in band 1A is $\ge$1500. Figure 5 in Lorente (1998) shows, however, a large deviation from this value, attributed to the fainter continuum of the source used for measuring the instrumental profile and the less accurate fitting in this band. The use of a resolving power of 1300 - instead of the theoretical resolving power of 1500 - for band 1A yields a) almost no difference from the AOT01 SWS data at a resolving power of 1500 and b) a better match between the SWS and synthetic data for the strongest CO features (Fig. 13). This observational resolving power of 1300 is also in good agreement with the observational value given by Lorente (1998) in her Fig. 5.

The incorrect use of a Gaussian instrumental profile, together with too high a - theoretical - resolving power of 1500 form the origin of the discrepancy seen for the strongest CO features. Therefore, the resolving power of band 1A was taken to be 1300 instead of 1500. Part of the other discrepancies seen in band 1A may be explained by problems with 1. the accuracy of the oscillator strengths of atomic transitions in the near-IR (see point 1. in this section) or 2. the RSRF in the beginning of band 1A (see point 5. in previous section).


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f14_col.ps} \end{figure} Figure 14: Summer and winter FTS-KP spectra of $\alpha $ Boo at a resolving power $\lambda / \Delta \lambda $ of 60 000. They are compared with the synthetic spectrum for $\alpha $ Boo with stellar parameters $\mbox{$T_{{\rm eff}}$ }= 4350$ K, $\log g = 1.50$, M = 0.75 $M_{\odot }$, [Fe/H] = -0.50, $\mbox{$\xi_{\rm t}$ }= 1.7$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }= 7$, $\varepsilon $(C) = 7.96, $\varepsilon $(N) = 7.61, $\varepsilon $(O) = 8.68, $\varepsilon $(Mg) = 7.33 and $\Gamma _{\rm t} = 3$ km s-1. The OH 1-0 lines are predicted as too weak. A coloured version of this plot is available in the appendix as Fig. .7.
Open with DEXTER

3.
Concentrating in the OH-lines, we see that for both the high-resolution FTS-KP (Figs. 14 and 16) and the medium-resolution SWS spectra (Fig. 19), the strongest lines (OH 1-0 and OH 2-1 lines) are predicted as too weak, while the other OH lines match very well. Since the same effect occurs for these two different observations, it is plausible to assume that the origin of the problem is situated in the theoretical model or in the synthetic-spectrum computation. Wrong oscillator strengths for the OH lines could, e.g., cause that kind of problems. Being based on different electric dipole moment functions (EDMFs), the OH-line lists of Sauval (Mélen et al. 1995), Partridge & Schwenke (1997) and Goldman et al. (1998), do however all show the same trend. The difference in $\log gf$-value for the main branches is small (<0.01) between Goldman and Sauval, and is somewhat larger (<0.05) between Schwenke and Sauval. Thus, no systematic error seems to occur in the oscillator strenghts. Since a similar discrepancy was also noted for the low-excitation CO lines, some assumptions on which the models are based, e.g. homogeneity, hydrostatic equilibrium, are cleary questionable for these stars.

4.
From 3.48 $\mu $m on, fringes at the end of band 1D affect the ISO-SWS spectra of almost all stars in the sample.

5.
Also for the cool stars, the same remark as given in point 6 for the warm stars concerning the memory effects applies. Clearly, the fundamental bands of CO and SiO are present for almost all cool stars, though no accurate quantitative scientific interpretation can be made due to these memory effects.

  
7 Implications on calibration and modelling

The results of this detailed comparison between observed ISO-SWS data and synthetic spectra have an impact both on the calibration of the ISO-SWS data and on the theoretical description of stellar atmospheres.

From the calibration point of view, a first conclusion is reached that the broad-band shape of the relative spectral response function is at the moment already quite accurate, although some improvements can be made at the beginning of band 1A (see Fig. 15) and band 2. Also, a fringe pattern is recognised at the end of band 1D. Inaccuracies in the adopted instrumental profile used to convolve the synthetic spectra with, together with too high a resolving power, may cause the strongest CO $\Delta v = 2$ band heads in the observed ISO-SWS spectrum to be weaker than the predicted line strength.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f15_bw.ps} \end{figure} Figure 15: The observed ISO-SWS spectra of some stars with different spectral types are divided by their synthetic spectrum calculated by using the atomic line list of Hirata & Horaguchi (1995). The ratio is rebinned to a resolving power of 250. Only at the beginning of band 1A the same trend is visible in all stars, indicating that the broad-band shape of the relative spectral-response functions is already quite accurately known for the different sub-bands of band 1, with the only exception being at the beginning of band 1A. The feature arising around 3.85 $\mu $m for the cool stars is an atomic feature discussed is Sect. 6.1.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{h3317f16_col.eps} \end{figure} Figure 16: Summer (red) and winter (green) FTS-KP spectrum of $\alpha $ Boo at a resolving power of 60 000. The differences between the summer and winter FTS-KP spectrum of $\alpha $ Boo are mainly the result of noise resulting from the removal of the telluric spectrum. Due to the opposite heliocentric shifts of the spectra, the spectrum of Arcturus is fully recovered in spite of the telluric lines. The Arcturus spectra are compared with the synthetic spectrum (black) for $\alpha $ Boo with stellar parameters $\mbox{$T_{{\rm eff}}$ }= 4350$ K, $\log g = 1.50$, M = 0.75 $M_{\odot }$, [Fe/H] = -0.50, $\mbox{$\xi_{\rm t}$ }= 1.7$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }= 7$, $\varepsilon $(C) = 7.96, $\varepsilon $(N) = 7.61, $\varepsilon $(O) = 8.68, $\varepsilon $(Mg) = 7.33, $\varepsilon $(Si) = 7.20 and $\Gamma _{\rm t} = 3$ km s-1.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{h3317f17_col.eps} \end{figure} Figure 17: Summer (red) and winter (green) FTS-KP spectra of $\alpha $ Boo at a resolving power $\lambda / \Delta \lambda $ of 60 000. They are compared with the synthetic spectrum (black) for $\alpha $ Boo with stellar parameters $\mbox{$T_{{\rm eff}}$ }= 4350$ K, $\log g = 1.50$, M = 0.75 $M_{\odot }$, [Fe/H] = -0.50, $\mbox{$\xi_{\rm t}$ }= 1.7$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }= 7$, $\varepsilon $(C) = 7.96, $\varepsilon $(N) = 7.61, $\varepsilon $(O) = 8.68, $\varepsilon $(Mg) = 7.33 and $\Gamma _{\rm t} = 3$ km s-1.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f18_col.eps} \end{figure} Figure 18: Comparison between CO spectral features of the ISO-SWS spectrum of $\alpha $ Boo (black), the summer FTS-KP spectrum (red), the winter FTS-KP spectrum (green) and the synthetic spectrum (blue) at a resolving power of 1500.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{h3317f19_col.eps} \end{figure} Figure 19: Comparison between OH spectral features of the ISO-SWS spectrum of $\alpha $ Boo (black), the summer FTS-KP spectrum (red), the winter FTS-KP spectrum (green) and the synthetic spectrum (blue) at a resolving power of 1500. The strong atomic feature around 3.87 $\mu $m is discussed in Sect. 6.1.
Open with DEXTER

Concerning the modelling part, problems with the construction of the theoretical model and the computation of the synthetic spectra are pointed out. The comparison between the high-resolution FTS-KP spectrum of $\alpha $ Boo and the corresponding synthetic spectrum revealed that the low-excitation first-overtone (and fundamental) CO lines and fundamental OH lines are predicted as being a few percent too weak, indicating that some assumptions, on which the models are based, are questionable for cool stars. This is not surprising: in the MARCS-code radiative equilibrium is assumed, also for the outermost layers, implying that a temperature bifurcation, caused by e.g. effects of convection and convective overshoot with inhomogeneities in the upper photosphere, can not be allowed for. Consequently, the cores of e.g. CO lines - or the saturated CO lines in general - are not described with full success. Noting however the high level of accordance between observations and theoretical predictions for many molecular lines, we may conclude that the oscillator strengths for these molecular transitions are now already accurate enough in order to use these lines to test some of the assumptions made in the mathematical stellar atmosphere code: e.g. the temperature distribution can be disturbed in order to simulate a chromosphere, convection, a change in opacity, ... The complex computation of the hydrogen lines, together with the inaccurate atomic oscillator strengths in the infrared rendered the computation of the synthetic spectra for warm stars difficult. Therefore, one of us (J. S.) has derived empirical oscillator strengths from the high-resolution FTS-ATMOS spectrum of the Sun (for more details, we refer to Paper V of this series and to Sauval 2002).

Although it was impossible to perform a detailed comparison between observed and synthetic data in band 2, we may conclude that the continua of the synthetic spectra in this wavelength range are reliable, but that strong molecular lines (e.g. band heads of CO $\Delta v = 1$ and SiO $\Delta v = 1$) may be predicted a few percent too weak. Nevertheless, combining the synthetic spectra of both warm and cool stars, allowed us to test the recently developed method for memory effect correction (Kester et al. 2001) and to re-derive the relative spectral response function for bands 1 and 2 for OLP10 (Vandenbussche et al. 2001). The results of these tests are described in Vandenbussche et al. (2001), Leech et al. (2002). In conjunction with photometric data, this same input data-set was used for the re-calibration of the absolute flux-level of the spectra observed with ISO-SWS (Shipman et al. 2001). In this way, both consistency and integrity were implemented. Moreover, the synthetic spectra of the standard sources of our sample are not only used to improve the flux calibration of the observations taken during the nominal phase, but they are also an excellent tool to characterise instabilities of the SWS spectrometers during the post-helium mission.

Although we have mainly concentrated on the discrepancies between the ISO-SWS and synthetic spectra - since this was the main task of this research - we would like to emphasise the good agreement between observed ISO-SWS data and theoretical spectra. The small discrepancies still remaining in band 1 are at the 1-2% level for the giants, proving not only that the calibration of the (high-flux) sources has already reached a good level of accuracy, but also that the description of cool star atmospheres and molecular line lists is quite accurate.

Acknowledgements
LD acknowledges support from the Science Foundation of Flanders. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France and of the VALD database, operated at Vienna, Austria. It is a pleasure to thank the referees, J. Hron and F. Kupka, for their careful reading of the manuscript and for their valuable suggestions.

References

 

Online Material

Appendix A: Comparison between different observational and synthetic data (coloured plots)

In this section, Figs. 3, 4, Figs. 10-14 of the accompanying article are plotted in colour in order to better distinguish the different observational or synthetic spectra.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{a3317f1_col.ps} \end{figure} Figure A.1: Comparison between the ISO-SWS data of $\alpha $ Cen A (black) and the synthetic spectrum (red) with stellar parameters $\mbox{$T_{{\rm eff}}$ }= 5830$ K, $\log g = 4.35$, M = 1.3 $M_{\odot }$, [Fe/H] = 0.25, $\mbox{$\xi_{\rm t}$ }= 1.0$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }~\!\! =~\!\! 89$, $\varepsilon $(C) = 8.74, $\varepsilon $(N) = 8.26, $\varepsilon $(O) = 9.13 and $\mbox{$\theta_{\rm d}$ }= 8.80$ mas. Some of the most prominent discrepancies between these two spectra are indicated by an arrow.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{a3317f2_col.ps} \end{figure} Figure A.2: Comparison between band 1 and band 2 of the ISO-SWS data of $\gamma $ Dra (black) and the synthetic spectrum (red) with stellar parameters $\mbox{$T_{{\rm eff}}$ }= 3960$ K, $\log g = 1.30$, M = 1.7 $M_{\odot }$, [Fe/H] = 0.00, $\mbox{$\xi_{\rm t}$ }= 2.0$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }= 10$, $\varepsilon $(C) = 8.15, $\varepsilon $(N) = 8.26, $\varepsilon $(O) = 8.93 and $\mbox{$\theta_{\rm d}$ }= 9.98$ mas.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{a3317f3_col.ps} \end{figure} Figure A.3: Band 2 for Sirius (A1 V) and $\gamma $ Dra (K5 III) are displayed. The ISO-SWS spectrum is plotted in black, the synthetic spectrum in red. Problems with the RSRF are indicated by an arrow.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{a3317f4_col.ps} \end{figure} Figure A.4: Comparison between the ISO-SWS observation and the synthetic spectrum of $\gamma $ Dra at a resolving power of 1500 (being the most conservative theoretical resolution for band 1A Leech et al. 2002).


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{a3317f5_col.ps} \end{figure} Figure A.5: Comparison between the AOT06 observation (revolution 538, black) and the AOT01 speed-4 observation (red) of $\gamma $ Dra. Both are rebinned to a resolving power of 1500.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{a3317f6_col.ps} \end{figure} Figure A.6: Top: Comparison between the AOT01 speed-4 observation of $\gamma $ Dra rebinned at 1) a resolving power of 1500 (black) and 2) a resolving power of 1300 (red). Bottom: Comparison between the ISO-SWS AOT01 observation in band 1A (black) and its synthetic spectrum (red) at a resolving power of 1300.


  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{a3317f7_col.ps} \end{figure} Figure A.7: Summer (red) and winter (green) FTS-KP spectra of $\alpha $ Boo at a resolving power $\lambda / \Delta \lambda $ of 60 000. They are compared with the synthetic spectrum (black) for $\alpha $ Boo with stellar parameters $\mbox{$T_{{\rm eff}}$ }= 4350$ K, $\log g = 1.50$, M = 0.75 $M_{\odot }$, [Fe/H] = -0.50, $\mbox{$\xi_{\rm t}$ }= 1.7$ km s-1, $\mbox{${\rm ^{12}C/^{13}C}$ }= 7$, $\varepsilon $(C) = 7.96, $\varepsilon $(N) = 7.61, $\varepsilon $(O) = 8.68, $\varepsilon $(Mg) = 7.33 and $\Gamma _{\rm t} = 3$ km s-1. The OH 1-0 lines are predicted as too weak.
Copyright ESO 2003