A&A 400, 161-183 (2003)
DOI: 10.1051/0004-6361:20021690
S. Benetti1 - E. Cappellaro2 - R. Ragazzoni3 - F. Sabbadin1 - M. Turatto1
1 - INAF - Osservatorio Astronomico di Padova, vicolo dell'Osservatorio 5,
35122 Padova, Italy
2 - INAF - Osservatorio Astronomico di Capodimonte, via Moiariello 11, 80131 Napoli, Italy
3 - INAF - Osservatorio
Astrofisico di Arcetri, Largo E. Fermi 5, 50125, Italy
Received 24 September 2002 / Accepted 11 November 2002
Abstract
Long-slit NTT+EMMI echellograms of NGC 6818 (the
Little Gem) at nine equally spaced position angles, reduced
according to the 3-D methodology introduced by Sabbadin et al. (2000a,b), allowed us to derive: the expansion law, the
diagnostics and ionic radial profiles, the distance and the central
star parameters, the nebular photo-ionization model, the 3-D
reconstruction in He II, [O III] and [N II], the multicolor
projection and a series of movies. The Little Gem results to be a
young (3500 years), optically thin (quasi-thin in some directions)
double shell (
![]() )
at a distance of 1.7
kpc, seen almost equatorial on: a tenuous and patchy spherical
envelope (
)
at a distance of 1.7
kpc, seen almost equatorial on: a tenuous and patchy spherical
envelope (
![]() pc) encircles a dense and inhomogeneous
tri-axial ellipsoid (
pc) encircles a dense and inhomogeneous
tri-axial ellipsoid (
![]() pc,
pc,
![]() ,
,
![]() )
characterized by a hole along the major axis and a
pair of equatorial, thick moustaches. NGC 6818 is at the start of
the recombination phase following the luminosity decline of the
0.625
)
characterized by a hole along the major axis and a
pair of equatorial, thick moustaches. NGC 6818 is at the start of
the recombination phase following the luminosity decline of the
0.625 ![]() central star, which has recently exhausted the
hydrogen shell nuclear burning and is rapidly moving toward the
white dwarf domain (log
central star, which has recently exhausted the
hydrogen shell nuclear burning and is rapidly moving toward the
white dwarf domain (log
![]() K;
K;
![]() ). The nebula is destined to become thicker
and thicker, with an increasing fraction of neutral, dusty gas in
the outermost layers. Only over some hundreds of years the plasma
rarefaction due to the expansion will prevail against the slower and
slower stellar decline, leading to a gradual re-growing of the
ionization front. The exciting star of NGC 6818 (
). The nebula is destined to become thicker
and thicker, with an increasing fraction of neutral, dusty gas in
the outermost layers. Only over some hundreds of years the plasma
rarefaction due to the expansion will prevail against the slower and
slower stellar decline, leading to a gradual re-growing of the
ionization front. The exciting star of NGC 6818 (
![]() 17.06)
is a visual binary: a faint, red companion (
17.06)
is a visual binary: a faint, red companion (
![]() 17.73)
appears at 0.09 arcsec in PA
17.73)
appears at 0.09 arcsec in PA
![]() ,
corresponding to a
separation
,
corresponding to a
separation ![]() 150 AU and to an orbital period
150 AU and to an orbital period ![]() 1500 years.
1500 years.
Key words: planetary nebulae: individual: NGC 6818 - ISM: kinematics and dynamics
It is widely accepted that an "aged'' star of low to medium mass
(
![]() )
which is evolving toward the white
dwarf region of the H-R diagram, first expels and then ionizes
the surface layers, thus generating the Planetary Nebula (PN)
phenomenology (Paczynski 1970; Aller 1984; Pottasch 1984; Osterbrock
1989).
)
which is evolving toward the white
dwarf region of the H-R diagram, first expels and then ionizes
the surface layers, thus generating the Planetary Nebula (PN)
phenomenology (Paczynski 1970; Aller 1984; Pottasch 1984; Osterbrock
1989).
![\begin{figure}
\par\includegraphics[width=14.9cm,clip]{H4002F1.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg38.gif) |
Figure 1: WFPC2 archive images of NGC 6818 in [O III] (left) and [N II] (right). The binary nature of the central star is shown in the enlargement at the bottom. North is up and East to the left. |
| Open with DEXTER | |
Thanks to the advent of sophisticate photo-ionization codes
(Harrington 1989; Pequignot 1997; Ferland et al. 1998), we now know in
detail the physical effects produced by any UV flux on any gas
distribution and composition. Conversely, the situation is quite
disappointing for a true nebula, due to projection limitations: on the
one hand the HST imagery has strongly enhanced the ground-based
evidences of the PNe complexity, on the other hand the observational
data are still interpreted in terms of approximate structures and
unrealistic assumptions for the physical conditions, like
![]() and
and ![]() constant all over the object (more comments are
in Aller 1984, 1990, 1994).
constant all over the object (more comments are
in Aller 1984, 1990, 1994).
In order to overcome the wide gap between theory and practice, the apparent, bi-dimensional nebular image should be de-projected, and the accurate spatial distribution of the gas recovered.
To this end we have developed an original procedure based on high dispersion spectra: the PN being an extended and expanding plasma, the position, thickness and density of each elementary volume can be, in principle, obtained from the radial velocity, width and flux of the corresponding emission. We first apply a tomographic analysis, which reconstructs the ionic distribution in the nebular slices covered by the spectrograph slit, and then assemble all the tomographic maps by means of a 3-D rendering procedure for studying the morphology, physical conditions, ionization, spatial structure and evolutionary status.
The rationale of the method and the earliest, rough results based on plate echellograms go back to
Sabbadin et al. (1985, 1987). More recent, "quantitative'' observations (i.e. using a linear detector)
concern NGC 40 and NGC 1501, both objects covered at moderate spectral resolution,
![]() ,
with the Echelle + 1.82 m telescope of Padua Observatory at Asiago, Cima Ekar (Sabbadin et al. 2000a,b;
Ragazzoni et al. 2001; hereafter Papers I to III, respectively).
,
with the Echelle + 1.82 m telescope of Padua Observatory at Asiago, Cima Ekar (Sabbadin et al. 2000a,b;
Ragazzoni et al. 2001; hereafter Papers I to III, respectively).
At the same time we have carried out a survey of two dozen
PNe and proto-PNe in both hemispheres with ESO NTT+EMMI (spectral range
![]() 3900-7900 Å, R=60 000, spatial resolution
3900-7900 Å, R=60 000, spatial resolution ![]() 1.0 arcsec) and the Telescopio Nazionale
Galileo (TNG)+SARG (spectral range
1.0 arcsec) and the Telescopio Nazionale
Galileo (TNG)+SARG (spectral range
![]() 4600-8000 Å, R=115 000, spatial resolution
4600-8000 Å, R=115 000, spatial resolution ![]() 0.7 arcsec).
The observed sample covers a variety of morphologies, kinematics and evolutionary phases, including
NGC 2392 (the Eskimo nebula), NGC 3132 (the Eight-Burst n.), NGC 3242 (the Ghost of Jupiter n.), NGC 6210 (the Turtle n.),
NGC 6543 (the Cat's Eye n.), NGC 6751 (the Glowing Eye n.),
NGC 6826 (the Blinking n.), NGC 7009 (the Saturn n.),
NGC 7662 (the Blue Snowball n.), IC 418 (the Spirograph n.), He 2-47 (the Starfish n.), MyCn 18
(the Hourglass n.),
MZ 3 (the Ant n.), and as many un-dubbed, but equally exciting targets.
0.7 arcsec).
The observed sample covers a variety of morphologies, kinematics and evolutionary phases, including
NGC 2392 (the Eskimo nebula), NGC 3132 (the Eight-Burst n.), NGC 3242 (the Ghost of Jupiter n.), NGC 6210 (the Turtle n.),
NGC 6543 (the Cat's Eye n.), NGC 6751 (the Glowing Eye n.),
NGC 6826 (the Blinking n.), NGC 7009 (the Saturn n.),
NGC 7662 (the Blue Snowball n.), IC 418 (the Spirograph n.), He 2-47 (the Starfish n.), MyCn 18
(the Hourglass n.),
MZ 3 (the Ant n.), and as many un-dubbed, but equally exciting targets.
The 3-D ionization structure of NGC 6565 has been presented by Turatto et al. (2002, Paper IV); here we discuss the case of NGC 6818 (PNG 025.8-17.9, Acker et al. 1992).
The paper is structured as follows: Sect. 2 introduces the nebula, Sect. 3 presents the observational material and the reduction procedure, Sect. 4 is dedicated to the gas kinematics, Sect. 5 concerns the radial profile of the physical conditions (electron temperature and electron density from forbidden line ratios), in Sect. 6 the ionization structure and the overall gas distribution are discussed, in Sect. 7 we derive the nebular distance, mass and age, in Sect. 8 the central star parameters are given, Sect. 9 contains the application of the photo-ionization model (CLOUDY), Sect. 10 describes the 3-D structure of the nebula in different ions, and Sect. 11 presents a short discussion and the conclusions.
The [N II] emission mainly occurs in two irregular equatorial "moustaches'' and in a multitude of condensations (in some cases presenting a sort of radially arranged cometary tail), which are brighter in the southern part of the nebula.
The striking HST multicolor reproduction by Arsen Hajian & Yervant Terzian (http://ad.usno.navy.mil/pne/gallery.html) highlights the composite envelope structure and the large stratification of the radiation within NGC 6818.
Rubin et al. (1998) reported the presence of two faint stars, roughly 2-4 arcsec N and NE of
the central star, which could be physically associated to it. A careful analysis of the WFPC2 frames
allowed us to unveil the true binary nature of the central star: the red, faint companion is at a distance
of 0.093(![]() 0.004) arcsec in position angle (PA)
0.004) arcsec in position angle (PA)
![]() (see the enlargement at the bottom of Fig. 1).
(see the enlargement at the bottom of Fig. 1).
Following Weedman (1968) our nebula is a prolate spheroid (an ellipse rotated about the major axis) of moderate ellipticity (axial ratio 3:2) observed perpendicular to the major axis, whereas Sabbadin (1984) suggests a somewhat optically thick prolate spheroid in a early evolutionary phase, seen almost pole-on. According to Hyung et al. (1999), a definitive statement on the geometry must wait for more adequate kinematical data, due to the complexity of NGC 6818.
To this end we have secured a series of long-slit, radially arranged echellograms. They were analysed with the 3-D methodology described in Papers I to IV.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{H4002F2.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg46.gif) |
Figure 2:
Detailed structure (in logarithmic scale) of some representative emissions
at the nine observed PA of NGC 6818. The blue-shifted gas is to the left.
The slit orientation at each PA is indicated
in the corresponding [O I] frame. The |
| Open with DEXTER | |
Nine echellograms of NGC 6818 (exposure time 600 s; spectral
resolution 60 000 with a slit 1.0 arcsec wide) have been obtained on
July 29, 2000 at the ESO NTT in photometric sky conditions and seeing between 0.7 and 1.0 arcsec. We have used a
40 arcsec long slit centered on the exciting star for all the selected PA,
ranging from 10
![]() to 170
to 170
![]() with a constant step of 20
with a constant step of 20
![]() .
Since we do not insert an interference filter (as normally done by the other observers to isolate a single order),
each spectrum covers 80 echelle orders (
.
Since we do not insert an interference filter (as normally done by the other observers to isolate a single order),
each spectrum covers 80 echelle orders (![]() 3967 Å of [Ne III] to
3967 Å of [Ne III] to ![]() 7751 Å of [Ar III]),
and provides the
spatio-kinematical structure of a good two dozen nebular emissions, representing all the main ionic species.
7751 Å of [Ar III]),
and provides the
spatio-kinematical structure of a good two dozen nebular emissions, representing all the main ionic species.
The reduction method follows conceptually the standard procedure, including bias, flat field, distortion correction, wavelength and flux calibration, and is carefully described in Paper IV.
Figure 2 illustrates the detailed structure in [O I] (![]() 6300 Å), [N II] (
6300 Å), [N II] (![]() 6584 Å), H I
(
6584 Å), H I
(![]() 6563 Å), [O III] (
6563 Å), [O III] (![]() 5007 Å) and He II (
5007 Å) and He II (![]() 4686 Å) at the
observed PA. NGC 6818 exhibits a complex ionization structure:
4686 Å) at the
observed PA. NGC 6818 exhibits a complex ionization structure:
- [O I] is only seen
in the outermost regions, in the form of distinct condensations, which in some cases are
symmetrically arranged (the moustaches), otherwise single (like the cometary knot in PA
![]() ,
southern edge);
,
southern edge);
- the low ionization [N II] emission forms a double envelope of inhomogeneous
structure from PA
![]() to PA
to PA
![]() ,
and a single, elongated and distorted ring from
PA
,
and a single, elongated and distorted ring from
PA
![]() to
PA
to
PA
![]() .
The presence of FLIERS (fast, low ionization emitting regions), as introduced by
Balick et al. (1993, see also Corradi et al. 1996), is not confirmed here: although some isolated spikes present a
faint, high velocity
tail, the overall [N II] emission of NGC 6818 can be understood in terms of "normal''
nebular regions simply shadowed by some inner and dense layer causing the ionization drop in the
outer plasma;
.
The presence of FLIERS (fast, low ionization emitting regions), as introduced by
Balick et al. (1993, see also Corradi et al. 1996), is not confirmed here: although some isolated spikes present a
faint, high velocity
tail, the overall [N II] emission of NGC 6818 can be understood in terms of "normal''
nebular regions simply shadowed by some inner and dense layer causing the ionization drop in the
outer plasma;
- the H![]() line (central row in Fig. 2) is characterized by a very blurred appearance
(due to a combination of thermal motions plus fine structure plus expansion velocity gradient), masking the
detailed distribution of the ionized gas. The same effect is also present in He I and He II, but
it is particularly damaging for H
line (central row in Fig. 2) is characterized by a very blurred appearance
(due to a combination of thermal motions plus fine structure plus expansion velocity gradient), masking the
detailed distribution of the ionized gas. The same effect is also present in He I and He II, but
it is particularly damaging for H![]() ,
the reference emission in both the radial electron density
and ionization determinations (Paper IV);
,
the reference emission in both the radial electron density
and ionization determinations (Paper IV);
- ![]() 5007
5007 ![]() of [O III] (a mean-high excitation ion), by far the strongest line in the
optical region, highlights the double envelope structure of NGC 6818: the inner shell
(better seen between PA
of [O III] (a mean-high excitation ion), by far the strongest line in the
optical region, highlights the double envelope structure of NGC 6818: the inner shell
(better seen between PA
![]() and PA
and PA
![]() )
is an irregular ellipsoid broken along the
major axis (N-S direction) whose equatorial, denser regions are identified by the "moustaches''.
The line-tilt between PA
)
is an irregular ellipsoid broken along the
major axis (N-S direction) whose equatorial, denser regions are identified by the "moustaches''.
The line-tilt between PA
![]() and PA
and PA
![]() suggests that we are misaligned
with both the intermediate and the minor axes of the inner ellipsoid, and that the line of the nodes is at
PA
suggests that we are misaligned
with both the intermediate and the minor axes of the inner ellipsoid, and that the line of the nodes is at
PA
![]() .
The outer shell is almost un-tilted, spherical,
holed at North and South, and circumscribes the internal one;
.
The outer shell is almost un-tilted, spherical,
holed at North and South, and circumscribes the internal one;
- the He II emission (bottom row in Fig. 2) marks the highest excitation nebular regions,
mainly constituted by the inner shell. Note the blurred appearance of ![]() 4686 Å,
essentially due to the thirteen fine structure components.
4686 Å,
essentially due to the thirteen fine structure components.
The first, qualitative picture of the spatial structure coming from the echellograms confirms the
indications already obtained from the imaging (Sect. 2).
| Ion | IP (eV) | 2
|
||||
| Wilson (1950) | Sabbadin (1984) | Meatheringham et al. (1988) | Hyung et at. (1999) | this paper | ||
| [O I] | 0.0 | - | - | - | - | 72: |
| [S II] | 10.4 | - | - | - | 60.7 | 71 |
| [O II] | 13.6 | 60.2 | - | 59.1 | 58.9 | 69: |
| H I | 13.6 | 55.5 | 52 | - | 42.6 | 55 |
| [N II] | 14.5 | - | 64 | - | 61.8 | 70 |
| [S III] | 23.4 | - | - | - | 50.8 | 65: |
| He I | 24.6 | - | - | - | 57.3 | 66 |
| [Ar III] | 27.6 | - | - | - | 48.9 | 64 |
| [O III] | 35.1 | 56.2 | 54 | 55.1 | 51.3 | 62 |
| [Ar IV] | 40.7 | - | - | - | 30.7 | 48 |
| [Ne III] | 41.0 | 58.0 | - | - | 52.2 | 63 |
| N III | 47.4 | - | - | - | 41.5 | - |
| He II | 54.4 | 42.4 | - | 41.9 | 31.5 | 45 |
| [Ar V] | 59.8 | - | - | - | 20.2 | 36 |
| [Ne V] | 97.1 | 32.6 | - | - | - | - |
According to Papers I to IV,
the expansion velocity (
![]() )
of the ionized gas can be
derived from the analysis of the "central star pixel line'' (cspl) in the different ions. The cspl
is parallel to the dispersion, selects the nebular material
projected at the apparent position of the star (whose motion is purely radial) and is the same
in all the frames, the slit being radially arranged. Thus, in order to improve the S/N of the faintest
emissions, the nine echellograms have been combined.
)
of the ionized gas can be
derived from the analysis of the "central star pixel line'' (cspl) in the different ions. The cspl
is parallel to the dispersion, selects the nebular material
projected at the apparent position of the star (whose motion is purely radial) and is the same
in all the frames, the slit being radially arranged. Thus, in order to improve the S/N of the faintest
emissions, the nine echellograms have been combined.
The results are contained in the last column of Table 1, where the
ions are put in order of increasing ionization potential (IP). Typical
errors are 1.5 km s-1 for the strongest forbidden emissions (like
![]() 6584 Å of [N II] and
6584 Å of [N II] and ![]() 5007 Å of [O III])
to 3.0 km s-1 for the faintest ones (in particular:
5007 Å of [O III])
to 3.0 km s-1 for the faintest ones (in particular: ![]() 6300 Å of [O I], because of the knotty structure, and
6300 Å of [O I], because of the knotty structure, and
![]() 7319.87 Å of [O II], which is partially blended with
7319.87 Å of [O II], which is partially blended with
![]() 7318.79 Å also belonging to the O+ red
quartet). The corresponding uncertainties for the recombination lines
are: 2.5 km s-1 for
7318.79 Å also belonging to the O+ red
quartet). The corresponding uncertainties for the recombination lines
are: 2.5 km s-1 for ![]() 6563 Å (H I), and 2.0 km s-1 for
6563 Å (H I), and 2.0 km s-1 for ![]() 5876 Å (He I) and
5876 Å (He I) and ![]() 4686 Å (He II).
4686 Å (He II).
Columns 3 to 6 of Table 1 report the kinematical results from
the literature. In detail:
- Wilson (1950) obtained a single Coudè spectrum of NGC 6818 (without de-rotator)
at spectral resolution
![]() ;
;
- Sabbadin (1984) observed the nebula
at four PA (long-slit echellograms at
![]() );
);
- Meatheringham et al. (1988,
long-slit echellograms at unspecified position,
![]() )
also measured
the width at 10
)
also measured
the width at 10![]() maximum intensity of
maximum intensity of ![]() 5007 Å obtaining
5007 Å obtaining
![]() km s-1
(following Dopita et al. 1985, this corresponds to the largest expansion velocity of the gas);
km s-1
(following Dopita et al. 1985, this corresponds to the largest expansion velocity of the gas);
- Hyung et al. (1999,
![]() )
studied
four bright regions located along the apparent minor and major axes (4-5 arcsec
East and West, and 9-10 arcsec North and South of the central star); their
values represent lower limits to
)
studied
four bright regions located along the apparent minor and major axes (4-5 arcsec
East and West, and 9-10 arcsec North and South of the central star); their
values represent lower limits to
![]() (various ions), due to projection effects.
(various ions), due to projection effects.
In Table 1 the kinematical variety reported by the different authors is symptomatic of the difficulties connected to the analysis of the high dispersion spectra, and, according to Hyung et al. (1999), stresses the fact that only the detailed coverage at adequate spatial and spectral resolutions can provide a reliable information on the structure of a chaotic object like NGC 6818.
As cspl refers to the kinematical properties of the matter projected at the apparent position of the star, so the "zero velocity pixel column'' (zvpc), corresponding to the recession velocity of the whole nebula, gives the radial distribution of the ionized gas which is expanding perpendicularly to the line of sight (Paper IV and references therein).
The intensity peak separations, 2
![]() ,
in the different emissions at the nine PA of NGC 6818 are presented in Table 2.
Both Fig. 2 and Table 2 indicate complex zvpc profiles, often multi-peaked (inner and outer shell), fast
changing in direction, and variable (at a given PA) from ion to ion. The observed line structure
depends on the radial matter distribution, the ionization and the intensity of the emission (the same occurs
for the cspl assuming
,
in the different emissions at the nine PA of NGC 6818 are presented in Table 2.
Both Fig. 2 and Table 2 indicate complex zvpc profiles, often multi-peaked (inner and outer shell), fast
changing in direction, and variable (at a given PA) from ion to ion. The observed line structure
depends on the radial matter distribution, the ionization and the intensity of the emission (the same occurs
for the cspl assuming
![]() ,
as normally observed in PNe).
,
as normally observed in PNe).
To be noticed: the "relative'' spectral and spatial resolutions of our echellograms, as introduced
in Paper III, differ by a factor of two. The former is
given by
![]() ,
,
![]() being the spectral resolution, and the latter by
being the spectral resolution, and the latter by
![]() radius,
radius,
![]() ). In practice this means that the
spatial information of NGC 6818 is twice as detailed as the kinematical one.
). In practice this means that the
spatial information of NGC 6818 is twice as detailed as the kinematical one.
In order to assemble the kinematical and the spatial results (corresponding to a single radial direction and to nine tangential
directions, respectively) we must identify the PA at which
![]() .
The solution comes from the qualitative picture resulting from
both the imaging (Sect. 2) and the spectra (Sects. 3 and 4). Let's consider for the main component of NGC 6818 the most
general spatial structure, i.e. a tri-axial ellipsoid. The major axis, projected in PA
.
The solution comes from the qualitative picture resulting from
both the imaging (Sect. 2) and the spectra (Sects. 3 and 4). Let's consider for the main component of NGC 6818 the most
general spatial structure, i.e. a tri-axial ellipsoid. The major axis, projected in PA
![]() ,
is almost
perpendicular to the line of sight, since the emissions, although inhomogeneous and distorted by irregular motions,
appear un-tilted. The intermediate and the minor axes lie in PA
,
is almost
perpendicular to the line of sight, since the emissions, although inhomogeneous and distorted by irregular motions,
appear un-tilted. The intermediate and the minor axes lie in PA
![]() ,
and the line-tilt observed at PA
,
and the line-tilt observed at PA
![]() and 110
and 110
![]() indicates that we are misaligned with both these axes. Thus,
indicates that we are misaligned with both these axes. Thus,
![]() along the apparent minor axis of
the nebula, that is between PA
along the apparent minor axis of
the nebula, that is between PA
![]() and 110
and 110
![]() .
.
The cspl-zvpc connection for the inner and the outer shells is illustrated in Fig. 3, showing both
![]() (at PA
(at PA
![]() and 110
and 110
![]() )
and
)
and
![]() vs. IP. For reasons of
homogeneity each zvpc peak separation is normalized to the corresponding [O III] value.
vs. IP. For reasons of
homogeneity each zvpc peak separation is normalized to the corresponding [O III] value.
| Ion | 2
|
(arcsec) | |||||||
|
|
|
|
|
|
|
|
|
|
|
| [O I] | 23.5: | 23.0: | 22.0: | --; 22.5: | --; 22.5: | --; 22.5: | --; 22.0: | --; 22.5: | 22.3: |
| [S II] | 23.5 | 22.4 | 22.0 | 15.6; 22.4 | --; 22.3: | 15.8; 22.5 | 14.0; 22.0 | --; 22.4 | 22.6 |
| [O II] | 23.1: | 22.8: | 21.7: | --; 22.2: | --; 21.7: | --; 22.5: | --; 22.0: | --; 22.0: | 21.8: |
| HI | 19.2: | 16.7: | 16.4: | 14.0:; 21.0: | 12.8:; 19.5: | 13.0:; 21.0: | 13.1:; 20.5: | 14.7:; 21.0: | 20.2: |
| [N II] | 23.5 | 22.4 | 22.0 | 15.8; 22.4 | --; 22.2 | 15.6; 22.4 | 14.5; 22.4 | 16.0; 22.4 | 21.8 |
| [S III] | 21.3 | 20.5 | 18.4: | 15.3; -- | 15.5:; -- | 14.5:; -- | 13.4; 21.3: | 15.0; 20.5: | 19.9: |
| He I | 22.2 | 20.5 | 18.1 | 15.7; 22.2 | 14.5; 20.6 | 14.5:; 21.0 | 13.2:; 21.3 | --; 19.2: | 20.8 |
| [Ar III] | 22.5 | 19.8 | 17.6 | 15.4; 22.2 | 14.6; 20.5 | 14.7; 21.0 | 13.7; 21.4 | 15.4; 21.9 | 21.1 |
| [O III] | 20.7 | 20.0 | 18.5 | 15.3; 21.2 | 15.0; 20.2 | 15.0; 21.0 | 13.8; 20.0 | 15.9; 21.0 | 20.4 |
| [Ar IV] | 17.9: | 15.3 | 13.1: | 12.3; -- | 11.0; -- | 11.1; -- | 12.0; -- | 12.7; -- | 16.4 |
| [Ne III] | 21.7: | 20.9: | 20.0: | 15.3:; -- | 15.2:; 21.0: | 14.5; 21.0 | 14.3; 20.4 | --; 21.3: | 21.6 |
| He II | 19.0 | 15.2 | 12.3 | 11.8; -- | 11.0; -- | 11.0; -- | 12.1; -- | 12.6; -- | 16.6 |
| [Ar V] | 17.7: | 13.3: | 10.6: | 9.8; -- | 8.0:; -- | 8.5; -- | 9.9; -- | 10.9; -- | 13.7 |
![\begin{figure}
\par\includegraphics[angle=-90,width=12.7cm,clip]{H4002F3.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg79.gif) |
Figure 3:
Expansion velocity in the cspl (left) and peak separation
in the zvpc for the inner and the outer shells of NGC 6818 at PA
|
| Open with DEXTER | |
NGC 6818 is characterized by a large stratification of the radiation and of the kinematics, in agreement with
the Wilson's (1950) law. However,
![]() and
and
![]() of [Ar IV] and [Ne III]
considerably deviate from the sequence defined by the other ionic species.
This behavior, also noticed
in NGC 6565 (Paper IV), is typical of a PN powered by a high temperature central star (for
details, see the above-mentioned reference and Sect. 9).
Instead, the anomalous position of H I in Fig. 3 is the obvious consequence of the mono-electron atomic structure
of hydrogen.
of [Ar IV] and [Ne III]
considerably deviate from the sequence defined by the other ionic species.
This behavior, also noticed
in NGC 6565 (Paper IV), is typical of a PN powered by a high temperature central star (for
details, see the above-mentioned reference and Sect. 9).
Instead, the anomalous position of H I in Fig. 3 is the obvious consequence of the mono-electron atomic structure
of hydrogen.
The
![]() vs. IP relation being the same at all the observed PA
(from Table 2), we can assess that in NGC 6818 the expansion
velocity is proportional to the distance from the central star through
the relation:
vs. IP relation being the same at all the observed PA
(from Table 2), we can assess that in NGC 6818 the expansion
velocity is proportional to the distance from the central star through
the relation:
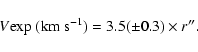 |
(1) |
Therefore in the following we will consider Eq. (1) as representative of the whole nebular kinematics.
All this is synthesized in Fig. 4, showing the position-velocity
(P-V) maps, i.e. the complete radial velocity field at the nine
observed PA. They are relative to the systemic heliocentric velocity
of the nebula,
![]() ) km s-1, corresponding
to
) km s-1, corresponding
to
![]() ) km s-1, and are scaled according to
Eq. (1). In other words, they reproduce the tomographic maps in the
nebular slices covered by the slit. We have selected He II, [O III]
and [N II] as representative of the high, medium and low ionization
regions, respectively.
) km s-1, and are scaled according to
Eq. (1). In other words, they reproduce the tomographic maps in the
nebular slices covered by the slit. We have selected He II, [O III]
and [N II] as representative of the high, medium and low ionization
regions, respectively.
These multicolor P-V maps highlight the large stratification of the radiation and the chaotic nebular structure.
NGC 6818 is optically thin in most directions. The low excitation [N II] emission is associated to the
presence of some inner and dense layer (see the moustaches, for example). The outermost, faint [N II] spikes detected
in PA
![]() ,
90
,
90
![]() ,
150
,
150
![]() and 170
and 170
![]() belong to the external shell.
belong to the external shell.
The existence of a prominent hole to the North and of a smaller one to the South, as suggested by Rubin et al.
(1998), is confirmed. The southern cavity is less evident in Fig. 4, being only grazed by our spectra at
PA
![]() and 10
and 10
![]() .
Further hollows are present (like at PA
.
Further hollows are present (like at PA
![]() and 90
and 90
![]() ,
in the approaching gas at West
of the central star position).
,
in the approaching gas at West
of the central star position).
The radial ionization structure of the S-SE edge at PA
![]() ,
corresponding to the region of the "cometary knot'' visible in
Fig. 1, is puzzling: [O III] is lacking, whereas He II and [N II] are
intense in the inner and the outer layers, respectively.
,
corresponding to the region of the "cometary knot'' visible in
Fig. 1, is puzzling: [O III] is lacking, whereas He II and [N II] are
intense in the inner and the outer layers, respectively.
In summary: although some spectral features of the northern and southern holes can be tentatively interpreted in terms of ionized gas moderately accelerated by some blowing-up agent (as suggested by Rubin et al. 1998), the linear expansion law here adopted represents a valid approximation of the overall nebular kinematics.
We can obtain the ![]() radial profile from the diagnostic line ratios
of ions in p2 or p4 configurations (like [O III] and [N II]), and the
radial profile from the diagnostic line ratios
of ions in p2 or p4 configurations (like [O III] and [N II]), and the ![]() radial distribution from both
the diagnostics of ions in p3 configuration (like [S II]) and the absolute H
radial distribution from both
the diagnostics of ions in p3 configuration (like [S II]) and the absolute H![]() flux. According to
Paper IV, the zvpc, which is independent on the expansion velocity field, must be used.
flux. According to
Paper IV, the zvpc, which is independent on the expansion velocity field, must be used.
In the specific case of NGC 6818 the large H![]() broadening
(due to thermal motions, fine structure and expansion velocity gradient) prevents the accurate determination of
F(H
broadening
(due to thermal motions, fine structure and expansion velocity gradient) prevents the accurate determination of
F(H![]() )
)
![]() (and then of
(and then of ![]() (H
(H![]() )).
Thus, in this section
)).
Thus, in this section ![]() [O III],
[O III], ![]() [N II] and
[N II] and ![]() [S II] are derived from the corresponding line intensity
ratios. Later on (Sect. 6.3) we will illustrate the adopted escamotage providing
F(H
[S II] are derived from the corresponding line intensity
ratios. Later on (Sect. 6.3) we will illustrate the adopted escamotage providing
F(H![]() )
)
![]() and
and ![]() (H
(H![]() )
from the observed radial ionization structure and the assumption
)
from the observed radial ionization structure and the assumption ![]() constant across the nebula.
constant across the nebula.
First of all the observed line intensities must be corrected for interstellar absorption according
to:
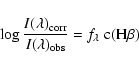 |
(2) |
Thanks to the excellent spatial and spectral accuracies achieved by the
superposition technique used (![]() 0.15 arcsec and
0.15 arcsec and ![]() 1.0 km s-1,
respectively) we can extend the H
1.0 km s-1,
respectively) we can extend the H![]() /H
/H![]() analysis to
the whole spectral image, as recently introduced (Paper IV) in the study of
NGC 6565, a compact, dust embedded PN exhibiting a complex c(H
analysis to
the whole spectral image, as recently introduced (Paper IV) in the study of
NGC 6565, a compact, dust embedded PN exhibiting a complex c(H![]() )
profile.
The results are less dramatic for NGC 6818, since the blurred appearance of both H
)
profile.
The results are less dramatic for NGC 6818, since the blurred appearance of both H![]() and H
and H![]() limits the resolution: besides some indications of a soft decline in the innermost regions (likely caused
by a local increase of
limits the resolution: besides some indications of a soft decline in the innermost regions (likely caused
by a local increase of ![]() ), the spectral maps appear quite homogeneous at
), the spectral maps appear quite homogeneous at
![]() ),
corresponding to
),
corresponding to
![]() )
(for the case B of Baker & Menzel 1938,
)
(for the case B of Baker & Menzel 1938,
![]() K and
log
K and
log
![]() ;
Brocklehurst 1971; Aller 1984; Hummer & Storey 1987).
;
Brocklehurst 1971; Aller 1984; Hummer & Storey 1987).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{H4002F4.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg98.gif) |
Figure 4:
Position-velocity maps at the nine observed PA for the high (He II, blue), medium ([O III],
green) and low ([N II], red) ionization regions of NGC 6818, scaled according to the relation
|
| Open with DEXTER | |
First we obtain ![]() [O III] from
[O III] from ![]() 5007 Å/
5007 Å/![]() 4363 Å, the line ratio being almost
independent on
4363 Å, the line ratio being almost
independent on ![]() for
for
![]() cm-3.
cm-3.
![]() [S II] is then derived from
[S II] is then derived from ![]() 6717 Å/
6717 Å/![]() 6731 Å (using
6731 Å (using ![]() [O III] to take into
account the weak dependence of the ratio on
[O III] to take into
account the weak dependence of the ratio on ![]() ).
Last,
).
Last, ![]() [N II] comes from
[N II] comes from ![]() 6584 Å/
6584 Å/![]() 5755 Å (adopting
5755 Å (adopting ![]() [S II] for its weak dependence
on the electron density).
[S II] for its weak dependence
on the electron density).
Although the resulting ![]() [O III],
[O III], ![]() [N II] and
[N II] and ![]() [S II] profiles rapidly change with PA,
as expected of the chaotic structure of NGC 6818, nevertheless there are some common features.
In order to highlight both the differences and the analogies we have selected two PA close to the apparent
major axis (PA
[S II] profiles rapidly change with PA,
as expected of the chaotic structure of NGC 6818, nevertheless there are some common features.
In order to highlight both the differences and the analogies we have selected two PA close to the apparent
major axis (PA
![]() and PA
and PA
![]() )
and two PA close to the apparent minor axis
(PA
)
and two PA close to the apparent minor axis
(PA
![]() and PA
and PA
![]() )
as representative of the whole nebular phenomenology.
)
as representative of the whole nebular phenomenology.
The results are shown in Fig. 5; their main limitation is evident: due to the weakness of the [N II] auroral
line and of the [S II] doublet, ![]() [N II] and
[N II] and ![]() [S II] can be obtained only at the
corresponding intensity peaks (in the best case).
[S II] can be obtained only at the
corresponding intensity peaks (in the best case).
![]() [O III] presents a well-defined radial profile common to all the PA: it is
[O III] presents a well-defined radial profile common to all the PA: it is ![]() 15 000 K in the
tenuous, innermost regions, it gradually decreases outward down to 12 000-12 500 K in the densest layers, and
later it remains more or less constant (the last statement is weakened by the auroral line faintness). Such a radial
trend is in quantitative agreement with the results by Rubin et al. (1998), based on
15 000 K in the
tenuous, innermost regions, it gradually decreases outward down to 12 000-12 500 K in the densest layers, and
later it remains more or less constant (the last statement is weakened by the auroral line faintness). Such a radial
trend is in quantitative agreement with the results by Rubin et al. (1998), based on ![]() 4363 Å
and
4363 Å
and ![]() 5007 Å HST/WFPC2 imagery. The presence of a
5007 Å HST/WFPC2 imagery. The presence of a ![]() gradient across
the nebula is also suggested by Hyung et al. (1999). Previous ground-based
gradient across
the nebula is also suggested by Hyung et al. (1999). Previous ground-based ![]() [O III] determinations are mean values
for the brightest (i.e. densest) regions and span the range 11400 K (de Freitas Pacheco et al.
1991) to
12 770 K (Mathis et al. 1998).
[O III] determinations are mean values
for the brightest (i.e. densest) regions and span the range 11400 K (de Freitas Pacheco et al.
1991) to
12 770 K (Mathis et al. 1998).
In Fig. 5 ![]() [N II] refers to the intensity peaks of the low ionization regions and is systematically below
[N II] refers to the intensity peaks of the low ionization regions and is systematically below ![]() [O III],
in agreement with both the previous reports for NGC 6818 (9500 K, Hyung et al. 1999, to 11 280 K, McKenna et al. 1996)
and the general results for PNe (see Aller 1990; Gruenwald & Viegas 1995; Mathis et al. 1998).
More
[O III],
in agreement with both the previous reports for NGC 6818 (9500 K, Hyung et al. 1999, to 11 280 K, McKenna et al. 1996)
and the general results for PNe (see Aller 1990; Gruenwald & Viegas 1995; Mathis et al. 1998).
More ![]() values for NGC 6818 are: 11 500 K (C III], Kaler 1986), 12 700 K and 13 800 K ([Ne V] and [O IV],
respectively, Rowlands et al. 1989), 14 700 K (Balmer discontinuity, Liu & Danziger 1993), 12 500 K (C III], Mathis et al. 1998), 13 000 K ([Cl IV], Hyung et al. 1999) and 19 000 K ([O II], Keenan et al. 1999).
values for NGC 6818 are: 11 500 K (C III], Kaler 1986), 12 700 K and 13 800 K ([Ne V] and [O IV],
respectively, Rowlands et al. 1989), 14 700 K (Balmer discontinuity, Liu & Danziger 1993), 12 500 K (C III], Mathis et al. 1998), 13 000 K ([Cl IV], Hyung et al. 1999) and 19 000 K ([O II], Keenan et al. 1999).
In summary, the mean kinetic energy of the free electrons in NGC 6818 is quite large. This on the one hand
explains both the H![]() broadening and the strength of the forbidden lines (in particular,
broadening and the strength of the forbidden lines (in particular,
![]() 5007 Å of
[O III]), on the other hand is indicative of a very hot central star
(
5007 Å of
[O III]), on the other hand is indicative of a very hot central star
(
![]() K, also supported by the presence of high excitation emissions, up to [Ne V],
IP =97.1 eV; see Table 1).
K, also supported by the presence of high excitation emissions, up to [Ne V],
IP =97.1 eV; see Table 1).
Concerning the [S II] electron densities in the zvpc (Fig. 5), they are limited to the brightest parts of the external,
low ionization layers and show peaks up to
![]() ) cm-3.
Previously Hyung et al. (1999) obtained
) cm-3.
Previously Hyung et al. (1999) obtained
![]() cm-3 (they also report
cm-3 (they also report
![]() cm-3 from the improved calculations for 3 equivalent p-electrons by Keenan et al. 1996).
cm-3 from the improved calculations for 3 equivalent p-electrons by Keenan et al. 1996).
Besides the zvpc, we have extended the ![]() 6717 Å/
6717 Å/![]() 6731 Å analysis to the prominent
knots of the entire [S II] spectral images. The resulting
6731 Å analysis to the prominent
knots of the entire [S II] spectral images. The resulting ![]() [S II] values span the range
[S II] values span the range
![]() )
to
)
to
![]() ) cm-3, the equatorial moustaches being the densest regions of NGC 6818.
) cm-3, the equatorial moustaches being the densest regions of NGC 6818.
In the next section we will derive the local filling factor,
![]() ,
by combining
,
by combining ![]() [S II] and
[S II] and ![]() (H
(H
![]() ,
since
,
since ![]() [S II]
[S II]![]()
![]() (H
(H
![]() (Aller 1984;
Osterbrock 1989).
(Aller 1984;
Osterbrock 1989).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4002F5.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg109.gif) |
Figure 5:
The diagnostics radial profile at PA
|
| Open with DEXTER | |
All the main ionic species are present in the echellograms, with the usual, dreadful handicap for hydrogen:
due to the large H![]() broadening, the deconvolution for
instrumental resolution plus thermal motions plus fine structure appears inadequate, and
the detailed F(H
broadening, the deconvolution for
instrumental resolution plus thermal motions plus fine structure appears inadequate, and
the detailed F(H
![]() profile cannot be determined. Moreover:
profile cannot be determined. Moreover:
- the principal O+ emissions
(![]() 3726
3726 ![]() and
and ![]() 3729 Å) fall outside our
spectral range. We have considered the much weaker
3729 Å) fall outside our
spectral range. We have considered the much weaker ![]() 7319.87 Å
the strongest line of the red O+ quartet;
7319.87 Å
the strongest line of the red O+ quartet;
- ![]() 3967 Å of [Ne III] being at the extreme blue edge
of the frame, the quantitative Ne++ analysis appears quite uncertain.
3967 Å of [Ne III] being at the extreme blue edge
of the frame, the quantitative Ne++ analysis appears quite uncertain.
In absence of H![]() we are forced to adopt
we are forced to adopt ![]() 5007 Å as reference line, thus
obtaining the radial ionization structure relative to O++ according to:
5007 Å as reference line, thus
obtaining the radial ionization structure relative to O++ according to:
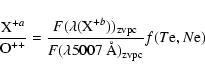 |
(3) |
The radial profiles of
![]() at the four selected PA of NGC 6818, shown in Fig. 6, contain
a number of interesting features:
at the four selected PA of NGC 6818, shown in Fig. 6, contain
a number of interesting features:
- the weakness of the low excitation emissions in PA
![]() northern sector, PA
northern sector, PA
![]() both sectors and
PA
both sectors and
PA
![]() both sectors indicates that the nebula is optically thin in these directions. It is almost thick in PA
both sectors indicates that the nebula is optically thin in these directions. It is almost thick in PA
![]() southern sector and PA
southern sector and PA
![]() both sectors;
both sectors;
- as expected, He++/O++ decreases outward and He+/ O++ increases. They cross for
![]() ,
implying that
,
implying that
![]() .
Since in these internal regions
.
Since in these internal regions
![]() (see Eqs. (10) and (11) in Sect. 6.3) we derive
(see Eqs. (10) and (11) in Sect. 6.3) we derive
![]() ;
;
- from similar considerations we infer
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
These chemical abundances (relative to oxygen) must be compared with the corresponding values (relative to hydrogen) obtained from the conventional method, as illustrated in the next Section.
According to the critical analysis by Alexander & Balick (1997) we consider the total line fluxes (i.e. integrated over the whole spatial profile and the expansion velocity field). The resulting ionic abundances must be multiplied for the corresponding ICFs, the correcting factors for the unobserved ionic stages. These were obtained both empirically (Barker 1983, 1986) and from interpolation of theoretical nebular models (Shields et al. 1981; Aller & Czyzak 1983; Aller 1984; Osterbrock 1989).
The final mean chemical abundances of NGC 6818, presented in Table 3 (last column), are in reasonable
agreement with the previous
estimates reported in the literature (also listed in the Table), and in excellent agreement with the
indications of Sect. 6.1.
![\begin{figure}
\par\includegraphics[width=15.1cm,clip]{H4002F6.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg123.gif) |
Figure 6:
The radial ionization structure (relative to O++) at PA
|
| Open with DEXTER | |
As emphasized in Paper IV, the H![]() flux distribution in the zvpc,
F(H
flux distribution in the zvpc,
F(H![]() )
)
![]() ,
is the fundamental
parameter linking
,
is the fundamental
parameter linking ![]() with both the spatial and the
kinematical properties of the expanding plasma through the relation:
with both the spatial and the
kinematical properties of the expanding plasma through the relation:
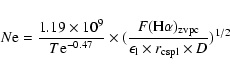 |
(4) |
In order to recover F(H![]() )
)
![]() we start assuming
we start assuming
![]() ,
constant across the nebula.
At each radial position:
,
constant across the nebula.
At each radial position:
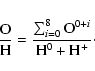 |
(5) |
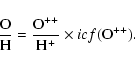 |
(6) |
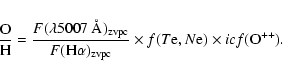 |
(7) |
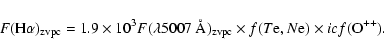 |
(8) |
Equation (8) provides the H![]() flux distribution in the zvpc (and
flux distribution in the zvpc (and
![]() (H
(H![]() )
through Eq. (4)) once the ionization correcting factor
)
through Eq. (4)) once the ionization correcting factor
![]() is known. The complex structure of NGC 6818 implies that
is known. The complex structure of NGC 6818 implies that
![]() strongly changes across the nebula. In the innermost
regions we have: O0/O++<<1, O+/O++<<1 and
H0/H+<<1. Thus
strongly changes across the nebula. In the innermost
regions we have: O0/O++<<1, O+/O++<<1 and
H0/H+<<1. Thus
![]() becomes:
becomes:
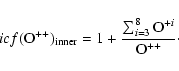 |
(9) |
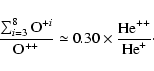 |
(10) |
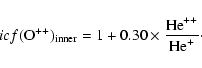 |
(11) |
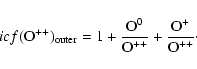 |
(12) |
Figure 7 evidences the basic advantage of using
![]() in the determination of the electron density
radial distribution:
in the determination of the electron density
radial distribution: ![]() (H
(H![]() )
extends
all over the nebular image, whereas
)
extends
all over the nebular image, whereas ![]() [S II] is limited to the peaks of the low excitation regions.
[S II] is limited to the peaks of the low excitation regions.
| Element | Aller & Czyzak | de Freitas Pacheco et al. | Liu & Danziger | Hyung et al. | This paper |
| (1983) | (1991) | (1993) | (1999) | ||
| He | 0.107 | 0.126 | 0.114 | 0.105 | 0.106( |
| C | 4.47 |
- | - | 8.0 |
- |
| N | 1.41 |
1.1 |
- | 4.0 |
1.4( |
| O | 5.50 |
5.25 |
6.37 |
7.0 |
5.5( |
| Ne | 1.23 |
- | - | 1.0 |
9.0( |
| Na | 3.09 |
- | - | 3.0 |
- |
| Mg | - | - | - | 3.0 |
- |
| Si | - | - | - | 9.0 |
- |
| S | 8.9 |
1.2 |
- | 7.0 |
6.2( |
| Cl | 1.9 |
- | - | 3.0 |
- |
| Ar | 3.8 |
- | - | 4.0 |
4.0( |
| K | 1.02 |
- | - | 2.0 |
- |
| Ca | 1.15 |
- | - | 1.5 |
- |
In detail:
- at PA
![]() (along the apparent major axis),
(along the apparent major axis), ![]() (H
(H![]() )
presents a single, broad and asymmetric (i.e. steeper
outwards) bell-shaped profile;
)
presents a single, broad and asymmetric (i.e. steeper
outwards) bell-shaped profile;
- the double-peak structure is very subtle at PA
![]() (close to the apparent major axis), the
inner peaks being predominant;
(close to the apparent major axis), the
inner peaks being predominant;
- at both PA
![]() and 110
and 110
![]() (close to the apparent minor axis) the two-shell
distribution clearly appears; the
(close to the apparent minor axis) the two-shell
distribution clearly appears; the ![]() (H
(H![]() )
top corresponds to the inner peaks at PA
)
top corresponds to the inner peaks at PA
![]() ,
whereas at
PA
,
whereas at
PA
![]() the peaks are almost equivalent;
the peaks are almost equivalent;
- an outward, low density tail is present at all directions, extending up to about 15 arcsec from the star.
Note in Fig. 7 the match between ![]() (H
(H![]() )
and
)
and ![]() [S II] for
[S II] for
![]() 9.5(
9.5(![]() 1) arcsec kpc, implying that
1) arcsec kpc, implying that
![]() ) kpc (see Table 2 and Sect. 4).
Although the assumption
) kpc (see Table 2 and Sect. 4).
Although the assumption
![]() provides a lower limit of 0.9 kpc
for the nebular distance, we can no longer delay a better quantification of this fundamental parameter.
provides a lower limit of 0.9 kpc
for the nebular distance, we can no longer delay a better quantification of this fundamental parameter.
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{H4002F7.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg143.gif) |
Figure 7:
The |
| Open with DEXTER | |
The only individual distance reported in the literature (based on rough parameters for the star and the nebula)
goes back to Gurzadyan (1970), who derived an indicative value of 2.2 kpc from the observed to expected size of
the He++ zone.
| Author | Distance (kpc) | Method |
| O'Dell (1962) | 1.7 | Shklovsky (1956), i.e. ionized mass = const. |
| Cahn & Kaler (1971) | 1.82-2.38 | Shklovsky |
| Cudworth (1974) | 1.95 | proper motions |
| Milne & Aller (1975) | 2.07 | Shklovsky (radio) |
| Cahn (1976) | 2.2 | Shklovsky |
| Acker (1978) | 1.6 | published statistical distance scales re-calibrated with individual distances |
| Maciel & Pottasch (1980) | 1.46 | ionized mass-radius relation |
| Daub (1982) | 1.29 | ionized mass-radio surface brightness relation |
| Phillips & Pottasch (1984) | 4.45 | observed vs. predicted radio fluxes |
| Maciel (1984) | 1.5 | ionized mass-radius relation |
| Amnuel et al. (1984) | 0.95 | radio surface brightness-radius relation |
| Kingsburgh et al. (1992) | 2.46 | Shklovsky |
| Cahn et al. (1992) | 1.87 | ionized mass-surface brightness relation |
| van de Steene & Zijlstra (1995) | 1.58 | radio continuum surface brightness temperature-radius relation |
| Zhang (1995) | 1.68 | ionized mass-radius and radio cont. surface bright. temp.-radius relations |
| Gorny et al. (1997) | 2.1 | theoretical evolutionary tracks vs. observed nebular and stellar parameters |
| Mal'kov (1997) | 2.5 | theoretical evolutionary age vs. observed dynamical age |
| Cazetta & Maciel (2000) | >2.9 | Peimbert & Torres-Peimbert (1983)
|
| temperature |
||
| Bensby & Lundström (2001) | 2.23 | ionized mass-radius relation |
| Phillips (2002) | 0.63 | radio surface brightness-radius relation |
As compensation the nebula is present in a good 20 catalogues of statistical distances (listed in Table 4). They provide the following mean values:
In order to derive the dynamical parallax we have analysed the first and second epoch (1998.30 and 2000.45, respectively) HST images of NGC 6818, searching for the angular expansion of the ionized gas; when combined with Eq. (1), it provides a reliable nebular distance (Reed et al. 1999; Palen et al. 2002). Since the target is at the centre of the planetary camera (PC) chip in the 2000.45 images, whereas it is quite off-axis in the 1998.30 ones, the correction for optical camera distortions was performed with the IRAF/STSDAS task "drizzle'' (see Fruchter & Hook 2002) using the Trauger coefficients.
No apparent shift is obtained from the couples of [O III] and [N II] frames.
According to Reed et al. (1999), we infer that the
angular expansion of the gas is <1.2![]() 10-2 arcsec, that is
10-2 arcsec, that is
![]() arcsec yr-1.
Since
arcsec yr-1.
Since
![]() (km s-1)/
(km s-1)/
![]() (arcsec yr-1)], we derive
(arcsec yr-1)], we derive
![]() pc.
pc.
We have attempted a better quantification of D(NGC 6818) through the
interstellar absorption-distance relation (Lutz 1973; Gathier et al. 1986;
Saurer 1995) given by the field stars with accurate mV,
mB, spectral type and luminosity class. They were selected using
the SIMBAD facilities of the CDS, Strasbourg Astronomical Observatory.
The resulting ![]() -distance law is presented in Fig. 8, where the small cluster of data at the right
edge refers to the super-giant stars of NGC 6822 (Barnard's galaxy), a nearby Ir galaxy projected at about 40
arcmin S-SE of our nebula.
-distance law is presented in Fig. 8, where the small cluster of data at the right
edge refers to the super-giant stars of NGC 6822 (Barnard's galaxy), a nearby Ir galaxy projected at about 40
arcmin S-SE of our nebula.
Figure 8 indicates that:
- the galactic absorption rapidly changes in direction (note the spread of the
low-weight points). This is confirmed by the inspection of both the ESO/SERC and the Palomar
Schmidt surveys, showing a variable background crossed by a series of extended, broad and faint emitting filaments;
- close to the nebula direction (high-weight data), ![]() quickly increases up to
quickly increases up to
![]() -1.5 kpc,
and later is constant (as expected of the large galactic latitude of the field,
-1.5 kpc,
and later is constant (as expected of the large galactic latitude of the field,
![]() ). Note that
for the super-giant stars of the nearby galaxy NGC 6822 we have
). Note that
for the super-giant stars of the nearby galaxy NGC 6822 we have
![]() (galactic)
(galactic)
![]() (NGC 6822), where
(NGC 6822), where
![]() (NGC 6822) changes from star to star, and
(NGC 6822) changes from star to star, and ![]() (galactic) = const. For
(galactic) = const. For ![]() (NGC 6822) = 0 we infer
(NGC 6822) = 0 we infer
![]() ), in excellent agreement with the literature reports (see Gallart et al. 1996; Bianchi et al. 2001);
), in excellent agreement with the literature reports (see Gallart et al. 1996; Bianchi et al. 2001);
- from
![]() )
(Acker 1978) we have
)
(Acker 1978) we have
![]()
![]() )
and D(NGC 6818)
)
and D(NGC 6818)
![]() 1.5 kpc.
1.5 kpc.
Although in Fig. 8 all the solutions for
![]() kpc appear legitimate, both the large galactic latitude
of the nebula (
kpc appear legitimate, both the large galactic latitude
of the nebula (
![]() )
and the low radial velocity relative to the Local Standard of Rest,
)
and the low radial velocity relative to the Local Standard of Rest,
![]() km s-1 (Sect. 4),
decidedly favour the lowest values, i.e.
km s-1 (Sect. 4),
decidedly favour the lowest values, i.e.
![]() kpc (in agreement with the information
previously obtained from the statistical distance scales).
kpc (in agreement with the information
previously obtained from the statistical distance scales).
In the following we will adopt
![]() ) kpc,
corresponding to a distance from the galactic plane
) kpc,
corresponding to a distance from the galactic plane ![]() 0.5 kpc.
0.5 kpc.
The local filling factor in the nebula is
![]() .
The ionized mass (obtained in different ways: from the H
.
The ionized mass (obtained in different ways: from the H![]() flux, the radio flux and the observed
flux, the radio flux and the observed ![]() distribution;
Aller 1984; Pottasch 1984; Osterbrock 1989 and
Paper IV) results to be
distribution;
Aller 1984; Pottasch 1984; Osterbrock 1989 and
Paper IV) results to be
![]() ,
and the kinematical age
,
and the kinematical age
![]() ) yr.
) yr.
![]() is close to the total nebular mass, NGC 6818 being an optically thin (almost thin in
some directions) PN, whereas
is close to the total nebular mass, NGC 6818 being an optically thin (almost thin in
some directions) PN, whereas
![]() represents a lower limit to the actual age,
represents a lower limit to the actual age,
![]() ,
since the dynamical history of the gas is unknown.
We can obtain a reliable estimate of
,
since the dynamical history of the gas is unknown.
We can obtain a reliable estimate of
![]() by assuming a nebular ejection at
by assuming a nebular ejection at
![]()
![]()
![]()
![]() ,
followed by a constant acceleration up to
,
followed by a constant acceleration up to
![]()
![]() .
.
![]()
![]() comes from the OH/IR sources, commonly regarded as the PNe precursors
(Habing 1996). For
comes from the OH/IR sources, commonly regarded as the PNe precursors
(Habing 1996). For
![]()
![]() km s-1 (Chengalur et al. 1993; David et al. 1993; Sjouwerman et al. 1998) we derive
km s-1 (Chengalur et al. 1993; David et al. 1993; Sjouwerman et al. 1998) we derive
![]() ) yr, i.e. our nebula is rather young.
) yr, i.e. our nebula is rather young.
As mentioned in Sect. 2, the exciting star of NGC 6818 is the northern component
of a visual binary system.
The WFPC2 frames taken through the broad-band filter
F555W (
![]() Å,
Å,
![]() Å) give mV = 17.06(
Å) give mV = 17.06(![]() )
for the central star and
)
for the central star and
![]() )
for the southern red
companion, where the unknown star colors are the main source of inaccuracy.
Please note that for D = 1.7 kpc we have (MV)0(red companion)
)
for the southern red
companion, where the unknown star colors are the main source of inaccuracy.
Please note that for D = 1.7 kpc we have (MV)0(red companion) ![]() +5.75, as expected of a late spectral
type (G8 to K0) Main Sequence star: a further, although weak, sign in favour of the adopted distance.
+5.75, as expected of a late spectral
type (G8 to K0) Main Sequence star: a further, although weak, sign in favour of the adopted distance.
According to Tylenda et al. (1993) and Feibelman (1994), the exciting
star of NGC 6818 presents a weak emission line spectrum in both the UV
and the optical regions. In order to derive the H I and He II Zanstra
temperatures, ![]() H I and
H I and ![]() He II respectively, we have
obtained the total H
He II respectively, we have
obtained the total H![]() and
and ![]() 4686 Å nebular fluxes
from the overall line profile at each PA, assuming a circular symmetry
of the spectral image. We find log
4686 Å nebular fluxes
from the overall line profile at each PA, assuming a circular symmetry
of the spectral image. We find log
![]() ) mW m-2 and
) mW m-2 and
![]() ), in excellent agreement with the
values reported by Aller & Czyzak (1979), Kohoutek & Martin (1981),
Webster (1983), Acker et al. (1991), and Hyung et al. (1999).
), in excellent agreement with the
values reported by Aller & Czyzak (1979), Kohoutek & Martin (1981),
Webster (1983), Acker et al. (1991), and Hyung et al. (1999).
The resulting Zanstra temperatures are log(
![]() )
and
log(
)
and
log(
![]() ).
We note in passing that
).
We note in passing that
![]() He II; this is quite surprising for a high excitation, optically
thin (almost thin in some directions) PN.
Previous determinations (Harman & Seaton 1966; Martin 1981; Gathier & Pottasch 1988; Mal'kov 1997) span the range
4.82 to 5.20 for log(
He II; this is quite surprising for a high excitation, optically
thin (almost thin in some directions) PN.
Previous determinations (Harman & Seaton 1966; Martin 1981; Gathier & Pottasch 1988; Mal'kov 1997) span the range
4.82 to 5.20 for log(![]() H I), and 5.03 to 5.30 for log(
H I), and 5.03 to 5.30 for log(![]() He II). Moreover Pottasch & Preite-Martinez
(1983) and Preite-Martinez et al. (1991) find log T*=4.93 and 5.02-5.05, respectively, from the energy
balance of the nebula.
He II). Moreover Pottasch & Preite-Martinez
(1983) and Preite-Martinez et al. (1991) find log T*=4.93 and 5.02-5.05, respectively, from the energy
balance of the nebula.
The stellar luminosities are log
![]() )
and
)
and
![]() )
(using the bolometric
corrections by Schönberner 1981, and adopting D = 1.7 kpc).
)
(using the bolometric
corrections by Schönberner 1981, and adopting D = 1.7 kpc).
NGC 6818 results to be a rather young PN surrounding a very hot star of relatively low luminosity.
This suggests that:
- the central star is a hydrogen-burning post-AGB star (the helium-burning ones evolve too slowly);
- the stellar mass, M*, is larger than
the average value (![]() 0.60
0.60 ![]() )
of the PNe nuclei (Blöcker 1995 and references therein).
)
of the PNe nuclei (Blöcker 1995 and references therein).
The detailed comparison with the theoretical evolutionary tracks by Schönberner (1981, 1983), Iben (1984),
Wood & Faulkner (1986), Blöcker & Schönberner (1990), Vassiliadis & Wood (1994) and Blöcker (1995) confirms
that no solutions are possible for the He-burning post-AGB stars (they are too slow), whereas the H-burning nuclei
give
![]() .
.
Moreover, the position of the central star of NGC 6818 in the log L-log T diagram coincides with
the beginning of the luminosity decline at the end of the shell nuclear burning. In this evolutionary phase all
models present a large luminosity gradient with a deep minimum at
![]() ,
i.e. the value
obtained for the central star of NGC 6818.
For example the 0.625
,
i.e. the value
obtained for the central star of NGC 6818.
For example the 0.625 ![]() H-burning nucleus by Blöcker (1995) (showing an astonishing resemblance with
our star) has
H-burning nucleus by Blöcker (1995) (showing an astonishing resemblance with
our star) has
![]() at t=3457 yr, and
at t=3457 yr, and
![]() at t=3585 yr, i.e. it drops in
luminosity by a factor of 3.5 in 128 yr.
at t=3585 yr, i.e. it drops in
luminosity by a factor of 3.5 in 128 yr.
And indeed, the central star of NGC 6818 is clearly visible in the earliest photographic reproduction of the nebula (Pease 1917; plate
taken on July 12,
1912 with the Mount Wilson 60-inch reflector); the rough
photometric sequence defined by the field stars gives
![]() ).
More stellar magnitude estimates reported in the literature are:
).
More stellar magnitude estimates reported in the literature are:
![]() (Curtis 1918),
(Curtis 1918),
![]() (Berman 1937),
(Berman 1937),
![]() (Cudworth 1974),
(Cudworth 1974),
![]() (Martin 1981), mB> 15 (Shaw & Kaler 1985),
mB=16.97 and
mV=17.02 (Gathier & Pottasch 1988), and
mV=17.06 (this paper, referring to the epoch 1998-2000).
(Martin 1981), mB> 15 (Shaw & Kaler 1985),
mB=16.97 and
mV=17.02 (Gathier & Pottasch 1988), and
mV=17.06 (this paper, referring to the epoch 1998-2000).
In addition, the first spectroscopic observation of NGC 6818
(star+nebula, Palmer 1903, referring to 1901) indicates "a pretty
strong continuum spectrum extending out to ![]() 372, with the
following bright lines: H
372, with the
following bright lines: H![]() ,
H
,
H![]() ,
H
,
H![]() ...''. Palmer
observed a large sample of nebulae with the Crossley reflector+plate
spectrograph, reporting that "the faintest continuum spectrum
photographed was that of a fifteenth magnitude star''.
...''. Palmer
observed a large sample of nebulae with the Crossley reflector+plate
spectrograph, reporting that "the faintest continuum spectrum
photographed was that of a fifteenth magnitude star''.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H4002F8.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg198.gif) |
Figure 8: The interstellar absorption-distance relation for the field stars of NGC 6818. Three symbols are used, referring to stars at different angular separation from the nebula. |
| Open with DEXTER | |
In spite of the photometric heterogeneity of these data, the suspicion of a "historical'' decline for the nucleus
of NGC 6818 appears legitimate (and robust).
Also note that the magnitudes of the star just before the luminosity drop were:
![]() and
and
![]() (for D=1.7 kpc and
(for D=1.7 kpc and
![]() ).
).
In summary, all the evidence is that:
- the quite massive central star is rapidly fading,
- the thin-thick transition is hanging over the nebula.
Within this scenario the following caveat is in order: because of the luminosity drop of the fast evolving star, the
ionization and thermal structure of NGC 6818 are out of equilibrium. The recombination
processes prevail, being faster in the high ionized species (Tylenda 1986; Marten & Szczerba 1997);
this qualitatively explains the observed, unexpected closeness of the H I and He II Zanstra temperatures: the nebula is
still optically thin (almost thin in some directions), but H![]() maintains a "longer memory'' than
maintains a "longer memory'' than
![]() 4686 Å of the past stellar luminosity.
Although the large
4686 Å of the past stellar luminosity.
Although the large ![]() of the gas implies a short "time lag'' of the main nebula
(a few dozen years), nevertheless both
of the gas implies a short "time lag'' of the main nebula
(a few dozen years), nevertheless both ![]() He II and, even more,
He II and, even more, ![]() H I are slightly over-valued.
In other words: NGC 6818 is over-luminous with respect to the present UV stellar flux.
H I are slightly over-valued.
In other words: NGC 6818 is over-luminous with respect to the present UV stellar flux.
The overall picture of our nebula shows a remarkable series of analogies with NGC 6565.
According to
Paper IV, NGC 6565 is a young (2300 yr), optically thick ellipsoid embedded in a large
cocoon of neutral, dusty gas. It is in a deep recombination phase (started about 400 yr ago), caused by the
luminosity drop of the massive powering star (
![]() ), which has almost reached the white
dwarf locus (
), which has almost reached the white
dwarf locus (
![]() ,
,
![]() ).
).
All this suggests the evolutive contiguity of the two PNe, NGC 6818 being a bit older, but also a bit less "mature'' than NGC 6565, i.e. the central star of the latter is more massive. No doubt NGC 6818 will develop in the near future most of the observational characteristics already present in NGC 6565 (and in the other recombining PNe contained in Tylenda 1986 and Corradi et al. 2000).
We have also carried out a search for other PNe in the peculiar evolutionary phase of NGC 6818 (e.g. at the very beginning of the thin-thick transition) adopting the following criteria: high temperature and quite low luminosity of the star, different [O III] and [N II] nebular morphology, high excitation class and relatively weak low ionization emissions. Among the dozen or so candidates we identified, the most promising are NGC 6326, NGC 6884, NGC 7354 and IC 4663.
In this section the photo-ionization code CLOUDY (Ferland et al. 1998) is applied to a PN having the same distance, matter distribution and chemical composition of NGC 6818.
We immediately point out that CLOUDY is a "steady-state'' model (a constant UV flux hits the nebula), whereas we argued that the ionization and thermal structure of NGC 6818 are out of equilibrium, because of the fast luminosity drop of the star. A similar, but less dramatic situation occurs in the recombining PN NGC 6565, which is in quasi-equilibrium, since the stellar evolution slows down and the luminosity gradient rapidly decreases while approaching the white dwarf domain (Paper IV).
In absence of an "evolving'' photo-ionization code, which takes into account the gas reactions
to a fast changing UV flux, at the moment we apply CLOUDY to the present nebula, (NGC 6818)(t0), as well to
(NGC 6818)(t0-100 yr) and (NGC 6818)(t0+100 yr).
Both the past and the future "snapshots'' come from a homologous expansion
(i.e.
![]() and N(H)
and N(H)
![]() ), being the dynamical time t0= 2300 yr and
), being the dynamical time t0= 2300 yr and
![]() .
Moreover, the
evolutionary track of the 0.625
.
Moreover, the
evolutionary track of the 0.625 ![]() H-burning post-AGB star by Blöcker (1995) was adopted for the stellar parameters. Last, we have
selected the quite thin East sector at PA
H-burning post-AGB star by Blöcker (1995) was adopted for the stellar parameters. Last, we have
selected the quite thin East sector at PA
![]() as "mean'' density radial profile of (NGC 6818)(t0).
The input data are contained in Table 5. The results, shown in Fig. 9, can be synthesized as follows:
as "mean'' density radial profile of (NGC 6818)(t0).
The input data are contained in Table 5. The results, shown in Fig. 9, can be synthesized as follows:
- at (t0-100 yr) (upper row) the intense UV flux of the luminous and hot star completely ionizes the nebula, which
appears as
a very high excitation object at large ![]() ,
optically thin in all the directions;
,
optically thin in all the directions;
- at (t0) (central row) the stellar luminosity is hardly sufficient for ionizing the gas, and the high excitation
nebula is
almost thick in some directions, where the low ionization emissions emerge;
- at (t0+100 yr) (bottom row) the UV flux is far inadequate: the innermost plasma maintains
a high degree of excitation, but the external layers are thick, with prominent [O I], [O II], [N II] and [S II]
lines. Note that the outermost parts of the "steady'' photo-ionization model are neutral, whereas
are recombining in a "true'' evolving nebula (they create a faint halo embedding the main object).
Although these results call for caution due to the photo-ionization model limitations, nevertheless they support the evolutive scenario of the previous sections: NGC 6818 is a PN at the very beginning of the recombination phase.
A direct confirmation is expected of the detailed analysis of the equatorial moustaches, representing the densest and brightest (i.e. thickest) regions of NGC 6818 (Sect. 5.3). To this end we have first de-projected the spectral images through Eq. (1), and then repeated the complete procedure already applied to the zvpc.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{H4002F9.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg208.gif) |
Figure 9:
"Steady'' photo-ionization model of NGC 6818, East sector in PA
|
| Open with DEXTER | |
Let's consider the southern, approaching moustache in PA
![]() .
The de-projected radial profiles of the main emissions, the
diagnostics and the
.
The de-projected radial profiles of the main emissions, the
diagnostics and the
![]() ionic abundances are shown in Fig. 10.
ionic abundances are shown in Fig. 10.
We are particularly interested to ![]() 6300 Å of [O I],
marking the neutral (or almost neutral) nebular layers, where the
efficiency of the resonant charge-exchange reaction
6300 Å of [O I],
marking the neutral (or almost neutral) nebular layers, where the
efficiency of the resonant charge-exchange reaction
![]() largely increases (Williams 1973). Note
that on the one hand the [O I] line is very sensitive to the physical
conditions, on the other hand no precise information is yet available
for the electron temperature of the external, neutral (or almost
neutral) gas dominated by the recombination and cooling processes. We
arbitrarily adopt
largely increases (Williams 1973). Note
that on the one hand the [O I] line is very sensitive to the physical
conditions, on the other hand no precise information is yet available
for the electron temperature of the external, neutral (or almost
neutral) gas dominated by the recombination and cooling processes. We
arbitrarily adopt
![]() K, which is lower than
K, which is lower than
![]() (ionized gas), but not enough low to compromise the [O I]
emissivity (a choice supported by the large kinetic energy of the free
electrons in NGC 6818; see Sect. 5.3).
(ionized gas), but not enough low to compromise the [O I]
emissivity (a choice supported by the large kinetic energy of the free
electrons in NGC 6818; see Sect. 5.3).
Moreover, referring to the ionization correcting factor
![]() of Sect. 6.3, it includes H0, whose
contribution comes from the equilibrium condition
of Sect. 6.3, it includes H0, whose
contribution comes from the equilibrium condition
![]() ), valid for
), valid for
![]() ,
i.e. in
the nebular regions affected by the
,
i.e. in
the nebular regions affected by the
![]() reaction (Williams 1973; Stancil et al. 1999).
reaction (Williams 1973; Stancil et al. 1999).
The observational results of Fig. 10 must be compared with the "steady'' photo-ionization model of the moustache presented in Fig. 11 (the stellar parameters obviously refer to time t0 of Table 5).
Besides the general features common to all the directions (i.e. the decreasing ![]() [O III] radial profile,
[O III] radial profile,
![]() [O III],
[O III],
![]() ,
,
![]() [S II] for (
[S II] for (
![]() 9.5 arcsec kpc, and so on), the moustache of NGC 6818 (Fig. 10) exhibits a remarkable peculiarity: the external layers are partially
neutral, and the outward ionization decline is very smooth, as expected of a recombining region. On the contrary, the
"steady'' photo-ionization model in Fig. 11 predicts an abrupt ionization fall (to be noticed: the photo-ionization model
at (t0-100 yr), not shown here, indicates that a century ago the moustache was optically thin to the UV stellar flux).
9.5 arcsec kpc, and so on), the moustache of NGC 6818 (Fig. 10) exhibits a remarkable peculiarity: the external layers are partially
neutral, and the outward ionization decline is very smooth, as expected of a recombining region. On the contrary, the
"steady'' photo-ionization model in Fig. 11 predicts an abrupt ionization fall (to be noticed: the photo-ionization model
at (t0-100 yr), not shown here, indicates that a century ago the moustache was optically thin to the UV stellar flux).
The ![]() depletion rate for recombination is given by:
depletion rate for recombination is given by:
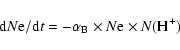 |
(13) |
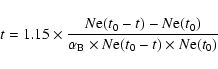 |
(14) |
The application of Eq. (14) to the external parts of the "true''
moustache (Fig. 10) furnishes t=30-60 yr (t = 60-120 yr and 20-40 yr
for ![]() (almost neutral gas) = 5000 K and 12 000 K, respectively). In
spite of the heavy assumptions, this agrees with all the previous
evidences suggesting that the recombination phase has just begun in
NGC 6818.
(almost neutral gas) = 5000 K and 12 000 K, respectively). In
spite of the heavy assumptions, this agrees with all the previous
evidences suggesting that the recombination phase has just begun in
NGC 6818.
The spectral images of the forbidden lines have been de-convolved for
seeing, spectral resolution and thermal motions, while also fine
structure has been taken into account for ![]() 4686 Å of He II. They all were de-projected through
Eq. (1), and assembled by means
of the 3-D rendering procedure described in Paper III.
4686 Å of He II. They all were de-projected through
Eq. (1), and assembled by means
of the 3-D rendering procedure described in Paper III.
In order to reproduce the spatial structure on the paper we adopt the usual method: a series of
opaque reconstructions of the nebula seen from different directions, separated by 15
![]() .
Each couple forms a stereoscopic
pair providing a 3-D view of NGC 6818.
.
Each couple forms a stereoscopic
pair providing a 3-D view of NGC 6818.
The novelties are represented by the multicolor projection and the movies.
For reasons of space we only present the opaque reconstruction in He II, [O III] and [N II] for a rotation of
180
![]() around the East-West axis (close to the minor axis). This is shown in Figs. 12 to 16,
where the upper-right panel corresponds to
the nebula seen from the Earth (West is up and North to the left, to allow the reader the stereo-view).
around the East-West axis (close to the minor axis). This is shown in Figs. 12 to 16,
where the upper-right panel corresponds to
the nebula seen from the Earth (West is up and North to the left, to allow the reader the stereo-view).
The high excitation layers of NGC 6818 (Fig. 12) form an inhomogeneous shell seen almost equatorial on, open-ended at
North and South; it merges in a closed ellipsoid at lower ![]() 4686 Å fluxes.
4686 Å fluxes.
The opaque reconstruction in [O III] is given for two absolute flux cuts: log
![]() erg s-1 cm-3 (Fig. 13), and
-17.75 erg s-1 cm-3 (Fig. 14).
Since
erg s-1 cm-3 (Fig. 13), and
-17.75 erg s-1 cm-3 (Fig. 14).
Since
![]() and
and
![]() ), they correspond to
), they correspond to
![]() cm-3 (Fig. 13), and
cm-3 (Fig. 13), and
![]() cm-3 (Fig. 14) (for
cm-3 (Fig. 14) (for
![]() K and
K and
![]() ).
The [O III] high cut represents the densest regions of the inner shell, mainly constituted by the equatorial moustaches and
by an extended cup in the southern part, whereas the external, inhomogeneous shell appears in the low cut frames, characterized
by the large hole at North (along the major axis).
).
The [O III] high cut represents the densest regions of the inner shell, mainly constituted by the equatorial moustaches and
by an extended cup in the southern part, whereas the external, inhomogeneous shell appears in the low cut frames, characterized
by the large hole at North (along the major axis).
| Radial density profile | right panels of Fig. 9 (cf. Sects. 6.3 and 9) |
| Chemical abundances: | |
| C, Na, Mg, Si, Cl, K, Ca | Hyung et al. (1999) |
| He, N, O, Ne, S, Ar | this paper |
| other elements | PN (CLOUDY default) |
| Dust | PN (CLOUDY default) |
| Filling factor | 0.5 |
| at time (t0-100 yr): blackbody with
T*=170 000 K and
|
|
| Exciting star | at time (t0): blackbody with
T*=160 000 K and
|
| at time (t0+100 yr): blackbody with
T*=140 000 K and
|
The brightest and the faintest [N II] regions refer to ![]() 6584 Å at the cuts
6584 Å at the cuts
![]() erg s-1 cm-3 (Fig. 15), and -18.80 erg s-1 cm-3 (Fig. 16). The [N II] (high cut) distribution mimics the corresponding [O III] one,
whereas at lower fluxes the outermost, knotty structure emerges. Note the general weakness of the low ionization layers for
erg s-1 cm-3 (Fig. 15), and -18.80 erg s-1 cm-3 (Fig. 16). The [N II] (high cut) distribution mimics the corresponding [O III] one,
whereas at lower fluxes the outermost, knotty structure emerges. Note the general weakness of the low ionization layers for
![]() .
.
These stereo-reconstructions confirm that NGC 6818 consists of a double shell projected almost equatorial on; the external
one is spherical (
![]() pc),
faint and patchy. It circumscribes a dense and inhomogeneous tri-axial ellipsoid (
pc),
faint and patchy. It circumscribes a dense and inhomogeneous tri-axial ellipsoid (
![]() pc,
pc,
![]() ,
,
![]() )
characterized by a large hole along the major axis and a couple of thick equatorial regions (the moustaches).
)
characterized by a large hole along the major axis and a couple of thick equatorial regions (the moustaches).
These "almost'' true color reproductions highlight the variety of looks exhibited by the Little Gem: roundish to elliptical, to quasi-bipolar (according to the current morphological classifications; Greig 1972; Stanghellini et al. 1993; Corradi & Schwarz 1995; Gorny et al. 1997). NGC 6818 resembles NGC 6153, Hu 1-1 and NGC 4071 when seen from (0,60), K 3-57 and M 2-51 from (0,90), A 70 from (90,0), IC 4663 from (0,30) and NGC 7354 from (150,0) (see the imagery catalogues of PNe by Acker et al. 1992; Schwarz et al. 1992; Manchado et al. 1996; Gorny et al. 1999).
A number of limitations are implicit when showing the 3-D structure on the paper. They are both objective (space, choice of the rotation axes, the nebular parameters, the cuts etc.), and subjective (difficulty in the stereo view). In order to overcome all these handicaps, we have decided to introduce a series of movies as integral and functional part of each PN analysis.
Such an "in fieri'' film library, providing the multicolor
projection, the opaque recovery in different ions and at various cuts,
some slices and radial profiles etc. (suggestions are welcome), can be
found at http://web.pd. astro.it/sabbadin (where the acronym
"sabbadin'' stands for "stratigraphy and best boundary analytic
determination in nebulae'', sic!).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4002F10.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg232.gif) |
Figure 10:
The observed radial properties of the southern, approaching moustache of NGC 6818 in PA
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4002F11.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg233.gif) |
Figure 11:
"Steady'' photo-ionization model for the southern, approaching
moustache of NGC 6818 in PA
|
| Open with DEXTER | |
We are also exploring new graphical solutions, rendering at best the (present) spatial reconstruction and the (forthcoming) spatio-temporal one. In particular, we are sounding the wide potential of the virtual reality.
In the previous sections of this paper dedicated to the Little Gem we have (partially) extracted and interpreted the huge amount of physical information contained in the ESO NTT+EMMI echellograms by means of the 3-D procedure developed in Papers I to IV for all types of extended, expanding nebulae.
NGC 6818 results to be a young (3500 yr), optically thin (quasi-thin
in some directions) double-shell at a distance of 1.7 kpc, projected
almost equatorial-on: a tenuous, patchy spheroid (
![]() pc)
encircles an inner, dense, inhomogeneous ellipsoid (
pc)
encircles an inner, dense, inhomogeneous ellipsoid (
![]() pc,
pc,
![]() ,
,
![]() )
empty along the major axis and
optically thick in a pair of equatorial moustaches.
)
empty along the major axis and
optically thick in a pair of equatorial moustaches.
We recall that outer attached shells have been found in both the 1D and 2D hydrodynamical models (see e.g. Mellema 1995; Corradi et al. 2000; Villaver et al. 2002), due to a D-type ionization front in the early evolution of the PN. However, all these models fail to reproduce the smooth, innermost radial density profile observed in NGC 6818 (Fig. 7); they predict an empty region (the hot bubble) and a quick density rise (the gas compression is provided by the thermal energy of the hot bubble formed by the adiabatic shock at the interaction region between the high velocity stellar wind and the material ejected during the superwind phase).
The central star of NGC 6818 is a visual binary: a faint, red
companion appears at 0.09 arcsec in PA
![]() ,
corresponding to a
separation
,
corresponding to a
separation ![]() 150 AU. For an orbit of low eccentricity the Kepler's
third law provides a period
150 AU. For an orbit of low eccentricity the Kepler's
third law provides a period ![]() 1500 yr. Note that (by chance?) the
two stellar components appear aligned with the major axis of the
nebula.
1500 yr. Note that (by chance?) the
two stellar components appear aligned with the major axis of the
nebula.
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{H4002F12.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg234.gif) |
Figure 12:
The structure of NGC 6818 for a rotation around the
East-West axis centered on the exciting star. Opaque reconstruction at |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=14.8cm,clip]{H4002F13.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg235.gif) |
Figure 13:
Same as Fig. 12, but for [O III] at the flux
cut log
E( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H4002F14.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg237.gif) |
Figure 14:
Same as Fig. 13, but for the [O III] flux cut log
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H4002F15.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg239.gif) |
Figure 15:
Same as Figs. 12 to 14, but for [N II] at
the flux cut log
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H4002F16.eps}
\end{figure}](/articles/aa/full/2003/10/aah4002/Timg241.gif) |
Figure 16:
Same as Fig. 15, but for the [N II]
flux cut
|
| Open with DEXTER | |
| |
Figure 17:
Multicolor appearance of NGC 6818 (
|
| Open with DEXTER | |
| |
Figure 18: Same as Fig. 17, but for a rotation around the E -W axis. |
| Open with DEXTER | |
Despite some pioneering studies, the physical effects produced by a
wide binary system on the PN ejection and shaping are still poorly
known. Following Soker (1994), an orbital period comparable or longer
than the mass-loss episode generating the nebula causes a density
enhancement in the equatorial plane and/or spiral structures. Soker
(2001) suggests that in wide binary systems (final orbital periods in
the range 40 to 104 yr) an outer, spherical structure is formed by
the early AGB wind. Toward the end of the AGB phase, the increased
mass-loss rate creates an accretion disk around the companion. If
this blows jets or a collimated fast wind, two lobes appear in the
inner nebula (a multi-lobed structure in the case of a precessing
accretion disk). Always according to Soker (2001), a fraction of 5![]() to 20
to 20![]() of all PNe originate in such wide binary systems.
Curiously, the same author (Soker 1997) includes (with a high degree
of confidence) NGC 6818 among the PNe resulting from the common
envelope evolution with a sub-stellar companion (planet(s) and/or a
brown dwarf). It is evident that the argument deserves further
attention.
of all PNe originate in such wide binary systems.
Curiously, the same author (Soker 1997) includes (with a high degree
of confidence) NGC 6818 among the PNe resulting from the common
envelope evolution with a sub-stellar companion (planet(s) and/or a
brown dwarf). It is evident that the argument deserves further
attention.
The Little Gem is in a peculiar evolutionary phase, i.e. at the very
beginning of the recombination process.
This is caused by the
luminosity decline of the 0.625 ![]() central star (
central star (
![]() K;
K;
![]() ), which has
recently exhausted the nuclear shell burning and is rapidly moving towards the white dwarf region.
The stellar drop being
fated to continue, NGC 6818 will become thicker and thicker, and the amount of neutral, dusty gas in the outermost layers will
increase with time. The ionization front will re-grow only in some hundreds years, when the gas dilution due to
the expansion will overcome the slower and slower luminosity decline.
), which has
recently exhausted the nuclear shell burning and is rapidly moving towards the white dwarf region.
The stellar drop being
fated to continue, NGC 6818 will become thicker and thicker, and the amount of neutral, dusty gas in the outermost layers will
increase with time. The ionization front will re-grow only in some hundreds years, when the gas dilution due to
the expansion will overcome the slower and slower luminosity decline.
Concerning the observational analogies between NGC 6818 (this paper) and NGC 6565 (Paper IV), in Sect. 8 we have pointed out the probable evolutive contiguity of the two nebulae. We stress here a more facet of the affair, e.g. the importance of the temporal factor: thanks to the excellent spatial and spectral resolutions achieved by the 3-D analysis applied to high quality spectra, we can no longer regard a PN as a static, uniform and un-changeable object; it is a dynamical, inhomogeneous and evolving plasma.
Ironically, this quite reverses the gap between theory and practice outlined in the Introduction: now the existing "steady'' photo-ionization models appear inadequate to interprete the observational data. A 3-D "evolving'' code is highly desired, providing for the gas reactions to the changing UV flux of the central star.
In summary: we have inferred a self-consistent picture of the Little
Gem by means of ESO NTT+EMMI echellograms. Deeper observations at
even higher spatial and spectral resolutions will disentangle the
still unresolved problems, like the accurate ![]() [N II] and
[N II] and ![]() [S II]
radial profiles (Sect. 5), the intriguing ionization structure
of the cometary knot in PA
[S II]
radial profiles (Sect. 5), the intriguing ionization structure
of the cometary knot in PA
![]() (Sect. 4) and the possible
blowing of the gas in the Northern and Southern holes (Sect. 4).
Moreover, a gradual change of the [N II]/[O III] morphology is
expected in the future HST imagery, due to the peculiar evolutionary
phase of the nebula.
Concerning the exciting star, a painstaking search in the world-wide
archives (both spectroscopic and photometric), and new, deep, UV to IR
spectra of the stellar system (hot central star + cold companion) are
needed.
(Sect. 4) and the possible
blowing of the gas in the Northern and Southern holes (Sect. 4).
Moreover, a gradual change of the [N II]/[O III] morphology is
expected in the future HST imagery, due to the peculiar evolutionary
phase of the nebula.
Concerning the exciting star, a painstaking search in the world-wide
archives (both spectroscopic and photometric), and new, deep, UV to IR
spectra of the stellar system (hot central star + cold companion) are
needed.
At last, the "vexata quaestio'': which are the mechanisms and the physical processes ejecting and shaping a PN like NGC 6818? In our opinion the question appears premature, and the answer is beyond the aims of the paper, given the "forest'' of proposed models (see Icke et al. 1992; Mellema 1997; Dwarkadas & Balick 1998; Garcia-Segura et al. 1999; Frank 1999; Blackman et al. 2001; Soker & Rappaport 2001; Balick & Frank 2002), and the "desert'' of carefully studied true nebulae. We are confident that new, reliable and deep insights on each object and on the whole class will come out of the comparative analysis of a representative sample of PNe and proto-PNe.
This is the final goal of our survey carried out with ESO NTT+EMMI and TNG+SARG. Indeed, the superb quality of these echellograms constitutes a powerful tool for unveiling the evolutional secrets of the PNe (as well for masking the cultural gaps of the authors).
Acknowledgements
It is a pleasure to thank Gary Ferland, Arsen Hajian, Garrelt Mellema (the referee), Detlef Schönberner and Noam Soker for their suggestions, comments, encouragements and criticisms.This paper has been financied by the grant Cofin MM02905817 of the Italian Ministry of Education (MIUR) and partially supported by the grant ASI (Agenzia Spaziale Italiana) I/R/70/00.