A&A 400, 95-118 (2003)
DOI: 10.1051/0004-6361:20021861
R-band imaging of the host galaxies of RGB BL Lacertae objects
K. Nilsson1 - T. Pursimo1 - J. Heidt2 - L. O. Takalo1
- A. Sillanpää1 - W. Brinkmann3
1 - Tuorla Observatory, Väisäläntie 20, 21500 Piikkiö, Finland
2 - Landessternwarte Heidelberg, Königstuhl, 69117 Heidelberg, Germany
3 - Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstrasse,
85740 Garching, Germany
Received 23 August 2002 / Accepted 16 December 2002
Abstract
We present optical R-band images of 100 BL Lacertae objects
in the ROSAT-Green Bank (RGB) sample obtained at the Nordic Optical
Telescope (NOT). For 62 objects we could not find any previously
published images in the literature, of these 35 are new BL Lacs
discovered during the RGB BL Lac survey. We were able to resolve the
host galaxy in 62% of the objects. We analyze the host galaxies using
a two-dimensional fitting procedure and tabulate the best-fit core
magnitude and host galaxy parameters (magnitude, effective radius,
ellipticity, position angle and shape parameter  )
for each
object. With two exceptions, all objects are better fit by a model
representing an elliptical galaxy (
)
for each
object. With two exceptions, all objects are better fit by a model
representing an elliptical galaxy (
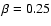 )
than by a disk
galaxy model (
)
than by a disk
galaxy model (
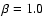 ). In the two exceptions the disk
host fit is only marginally better than the elliptical host fit,
however, and we do not find a single clear example of a disk-dominated
host galaxy. The host galaxies have an average brightness
). In the two exceptions the disk
host fit is only marginally better than the elliptical host fit,
however, and we do not find a single clear example of a disk-dominated
host galaxy. The host galaxies have an average brightness
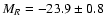 and average effective radius
and average effective radius
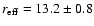 kpc. Their bulk properties are indistinguishable from normal
elliptical and radio galaxies. The median
kpc. Their bulk properties are indistinguishable from normal
elliptical and radio galaxies. The median  is 0.18, well below
the value 0.25 that is normally used to describe ellipticals. However,
the difference may be caused by a selection effect due to the
dependence of
is 0.18, well below
the value 0.25 that is normally used to describe ellipticals. However,
the difference may be caused by a selection effect due to the
dependence of  on host galaxy luminosity.
on host galaxy luminosity.
Key words: BL
Lacertae objects: general - galaxies: nuclei - galaxies: structure
BL Lacertae objects (BL Lacs) are a subclass of active galactic nuclei
characterized by almost featureless optical continuum, high optical
polarization (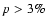 )
and variability over the whole
electromagnetic spectrum. These properties are believed to be caused
by a relativistic jet aligned close to the line of sight. Doppler
boosting and relativistic beaming enhance the nuclear radiation
considerably and make the detection of the host galaxy and the line
emission very difficult.
)
and variability over the whole
electromagnetic spectrum. These properties are believed to be caused
by a relativistic jet aligned close to the line of sight. Doppler
boosting and relativistic beaming enhance the nuclear radiation
considerably and make the detection of the host galaxy and the line
emission very difficult.
Previous studies (e.g. Abraham et al. 1991; Stickel et al. 1993; Wurtz et al. 1996; Falomo & Kotilainen
1999; Scarpa et al. 2000a; Urry et
al. 2000; Pursimo et al. 2002) have shown that BL
Lacs lie in the nuclei of luminous (
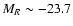 )
and large
(
)
and large
(
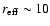 kpc) elliptical galaxies. Their bulk properties
appear to be indistinguishable from those of the host galaxies of
Fanaroff-Riley (FR) type I radio sources (Fanaroff & Riley
1974), supporting the unifying view that BL Lacs are FR I
radio sources seen almost along the direction of the jet (Urry &
Padovani 1995). Further support for the unifying view comes
from the fact that the extended radio luminosities and emission line
luminosities seem to be similar in both types of objects (see Urry &
Padovani 1995).
kpc) elliptical galaxies. Their bulk properties
appear to be indistinguishable from those of the host galaxies of
Fanaroff-Riley (FR) type I radio sources (Fanaroff & Riley
1974), supporting the unifying view that BL Lacs are FR I
radio sources seen almost along the direction of the jet (Urry &
Padovani 1995). Further support for the unifying view comes
from the fact that the extended radio luminosities and emission line
luminosities seem to be similar in both types of objects (see Urry &
Padovani 1995).
So far any possible connection between the nuclear properties and the
host galaxy properties has remained elusive. Wurtz et
al. (1996) found no difference between the host galaxies of
X-ray and radio selected BL Lacs. A similar conclusion was reached by
Urry et al. (2000), who found no difference between the host
galaxies of "red'' and "blue'' (i.e. low frequency peaked and high
frequency peaked) BL Lacs in their HST study of 110 objects. On the
other hand, the broad emission line AGN studied by Schade et
al. (2000) showed a weak but significant correlation between
the nuclear brightness and the host galaxy brightness. A similar weak
correlation was found for X-ray selected BL Lacs by Falomo &
Kotilainen (1999) and for the radio selected 1 Jy BL Lacs by
Pursimo et al. (2002), although in both papers it was noted
that this correlation may be a result of selection effects,
e.g. missing faint nuclei in very luminous hosts.
Since the central black hole is ultimately responsible for the
production of nuclear activity, the possibility of a nucleus-host
galaxy connection has become more appealing recently with the findings
that many global properties of galaxies seem to correlate with the
central black hole mass. Firstly, Magorrian et al. (1998)
found that the kinematic data of 36 nearby galaxies indicate the
presence of a massive dark object in the center of the galaxies and
that the mass of the dark object correlates with the bulge luminosity
and mass. Recent studies of this relationship obtain
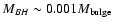 (McLure & Dunlop 2002; Merritt &
Ferrarese 2001). Secondly, the central velocity dispersion
of the bulge
(McLure & Dunlop 2002; Merritt &
Ferrarese 2001). Secondly, the central velocity dispersion
of the bulge 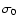 has been found to exhibit a tight correlation
with the central black hole mass (Ferrarese & Merritt 2000,
Gebhardt et al. 2000). Falomo et al. (2002) have
recently applied this correlation to 7 BL Lacs and found the black
hole masses to be in the range
of
has been found to exhibit a tight correlation
with the central black hole mass (Ferrarese & Merritt 2000,
Gebhardt et al. 2000). Falomo et al. (2002) have
recently applied this correlation to 7 BL Lacs and found the black
hole masses to be in the range
of
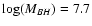 -
-
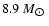 .
Furthermore, Wu et al. (2002) estimated
.
Furthermore, Wu et al. (2002) estimated
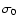 for 92 AGN with elliptical hosts using the fundamental
plane and found a range of masses of
for 92 AGN with elliptical hosts using the fundamental
plane and found a range of masses of
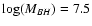 -
-
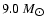 .
Finally, Graham et al. (2001) discovered a
correlation between the bulge light profile and the central black hole
mass that appears to be even tighter than the correlation with central
velocity dispersion. Fitting Sérsic (1968) 1/n light
profiles to the bulge light distributions they found
.
Finally, Graham et al. (2001) discovered a
correlation between the bulge light profile and the central black hole
mass that appears to be even tighter than the correlation with central
velocity dispersion. Fitting Sérsic (1968) 1/n light
profiles to the bulge light distributions they found
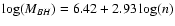 with a 0.32 dex scatter in
with a 0.32 dex scatter in
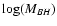 .
.
Given the above relations it seems that an accurate analysis of the
host galaxy light profile might provide a way to estimate the central
black hole masses in BL Lacs and to study the dependence of nuclear
parameters on the host galaxy parameters. This kind of analysis can
also be used to test the unified scheme, the relation between BL Lacs
and nonactive galaxies and the cosmological evolution of the BL Lac
population. With these goals in mind we started an observing program
of several BL Lac samples at the Nordic Optical Telescope (NOT). Part
of these observations have already been published (Heidt et
al. 1999a; Nilsson et al. 1999a; Pursimo et
al. 2002). Here we present the images and fitting results
for the RGB sample. A more detailed statistical analysis will follow
in a subsequent paper.
Throughout the paper we assume H0 = 50 km s-1 Mpc-1 and
q0 = 0.0 when computing absolute parameters.
2 The sample
The ROSAT-Green Bank (RGB) sample of BL Lacertae objects was formed by
Laurent-Muehleisen et al. (1999, hereafter LM99). The ROSAT
All-Sky Survey (Voges 1992) was first correlated with the 5 GHz
Green Bank radio survey (Gregory et al. 1996) by selecting
sources with
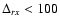 arcsec (Brinkmann et al.
1996). This initial catalog of 2127 sources was then
observed at the VLA for accurate radio positions, which produced a
list of 1567 reliable RASS-VLA matches. Optical identification was
made using the Automatic Plate Measuring (APM) scans of the Palomar
Observatory Sky Survey (POSS) I plates (971 reliable RASS-VLA-POSS I
matches were found) after which optical spectroscopy was used to
classify the brightest (O
arcsec (Brinkmann et al.
1996). This initial catalog of 2127 sources was then
observed at the VLA for accurate radio positions, which produced a
list of 1567 reliable RASS-VLA matches. Optical identification was
made using the Automatic Plate Measuring (APM) scans of the Palomar
Observatory Sky Survey (POSS) I plates (971 reliable RASS-VLA-POSS I
matches were found) after which optical spectroscopy was used to
classify the brightest (O 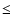 18.5) objects (Laurent-Muehleisen
et al. 1998, hereafter LM98). Of the 594 classified sources
53 turned out to be BL Lacs, of which 38 were new
discoveries. Combining these BL Lacs with previously known BL Lacs in
the RGB catalog yielded the final RGB BL Lac catalog of 127 objects.
18.5) objects (Laurent-Muehleisen
et al. 1998, hereafter LM98). Of the 594 classified sources
53 turned out to be BL Lacs, of which 38 were new
discoveries. Combining these BL Lacs with previously known BL Lacs in
the RGB catalog yielded the final RGB BL Lac catalog of 127 objects.
The catalog is triply limited (radio, optical, X-ray) but not
complete, although a complete subsample of 33 objects was drawn
from the sample (LM99). The flux limits in the three different bands
depend on various factors: the radio limit is  15 mJy for
declinations above 30
15 mJy for
declinations above 30 and
and  24 mJy below. The X-ray
limit is set by the RASS to a few times 10-13 erg cm-2 s-1 in the
0.1 - 2.4 keV band depending on spectral shape and
amount of galactic absorption. The optical limit is less well
defined. The complete sample has the limit O < 18.0 mag, but the
rest of the sample has no clearly defined optical limit. Given the
above limits, the completeness of the sample is hard to assess (LM99).
24 mJy below. The X-ray
limit is set by the RASS to a few times 10-13 erg cm-2 s-1 in the
0.1 - 2.4 keV band depending on spectral shape and
amount of galactic absorption. The optical limit is less well
defined. The complete sample has the limit O < 18.0 mag, but the
rest of the sample has no clearly defined optical limit. Given the
above limits, the completeness of the sample is hard to assess (LM99).
In the
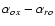 color-color diagram the RGB BL Lacs
cover a larger area than previous samples made using a single
selection frequency. Given this wide scatter in broadband nuclear
properties the RGB catalog provides an excellent sample to study the
nucleus - host galaxy connection. Another interesting feature of the
RGB sample is the inclusion of borderline objects, termed as BL Lac
"candidates'' in LM99. These objects do not adhere to the rather
strict definition used by Stocke et al. (1991), namely that
all emission lines must have
color-color diagram the RGB BL Lacs
cover a larger area than previous samples made using a single
selection frequency. Given this wide scatter in broadband nuclear
properties the RGB catalog provides an excellent sample to study the
nucleus - host galaxy connection. Another interesting feature of the
RGB sample is the inclusion of borderline objects, termed as BL Lac
"candidates'' in LM99. These objects do not adhere to the rather
strict definition used by Stocke et al. (1991), namely that
all emission lines must have
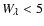 Å and the spectral
drop at the Ca H&K lines near 4000 Å (Br
Å and the spectral
drop at the Ca H&K lines near 4000 Å (Br
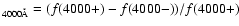 )
is smaller than 25%. In addition to
objects satisfying these criteria LM99 included also objects with 25%
< Br
)
is smaller than 25%. In addition to
objects satisfying these criteria LM99 included also objects with 25%
< Br
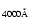 < 40% as candidate BL Lacs. The candidate
objects were also allowed to have
< 40% as candidate BL Lacs. The candidate
objects were also allowed to have
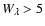 Å if it was
smaller than a Br
Å if it was
smaller than a Br
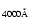 -dependent limit prescribed by
Marchã et al. (1996). The latter criterion is still
somewhat arbitrary, but it is less dependent of the dilution of
nuclear light by the host galaxy and thus includes objects with
optically fainter nuclei with BL Lac type characteristics.
Additionally, any object denoted as candidate by previous authors or
objects whose classification was based on a low resolution (80 Å)
spectrum was termed as candidate. There are altogether 27 candidates
in the RGB BL Lac sample, 21 of which were observed during this study.
-dependent limit prescribed by
Marchã et al. (1996). The latter criterion is still
somewhat arbitrary, but it is less dependent of the dilution of
nuclear light by the host galaxy and thus includes objects with
optically fainter nuclei with BL Lac type characteristics.
Additionally, any object denoted as candidate by previous authors or
objects whose classification was based on a low resolution (80 Å)
spectrum was termed as candidate. There are altogether 27 candidates
in the RGB BL Lac sample, 21 of which were observed during this study.
One unfortunate deficit of the RGB BL Lac sample is that the
redshifts are known for only 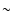 50% of the sample and some
redshifts are highly uncertain. Since the determination of the
redshift requires detection of nuclear emission lines or absorption
lines of the host galaxy, it is possible that objects with strong
emission lines (for a BL Lac object) and/or bright host galaxies are
preferred among the objects with known z. Given the possibility of
these biases one should thus be careful when interpreting the results.
50% of the sample and some
redshifts are highly uncertain. Since the determination of the
redshift requires detection of nuclear emission lines or absorption
lines of the host galaxy, it is possible that objects with strong
emission lines (for a BL Lac object) and/or bright host galaxies are
preferred among the objects with known z. Given the possibility of
these biases one should thus be careful when interpreting the results.
The observations were carried out at the Nordic Optical Telescope
(NOT)![[*]](/icons/foot_motif.gif) on La Palma, Spain during several observing
runs in 1995-2002. We used three different instruments, whose
characteristics are listed in Table 1. HiRAC and StanCam are
direct imaging cameras with field of view of
on La Palma, Spain during several observing
runs in 1995-2002. We used three different instruments, whose
characteristics are listed in Table 1. HiRAC and StanCam are
direct imaging cameras with field of view of
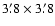 and
and
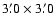 ,
respectively, whereas ALFOSC
is a focal reducer giving a field of view of
,
respectively, whereas ALFOSC
is a focal reducer giving a field of view of
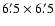 .
.
Table 1:
The instruments used in this study.
| Instrument |
pixels |
pix. scale |
gain |
RON |
| |
|
[
 pix.-1] pix.-1] |
[e-/ADU] |
[e-] |
| HiRAC |
20482 |
0.11 |
1.3 |
6.2 |
| StanCam |
10242 |
0.176 |
1.7 |
6.5 |
| ALFOSC |
20522 |
0.189 |
1.0 |
6.5 |
We obtained (Cousins) R-band images for 100 objects, and additional B,
V or I-band images for  40 objects. Here we discuss the R-band
images only. The individual exposures of the BL Lacs were kept short
enough as not to saturate the nucleus. For bright objects (R < 15)
we obtained several exposures of 15-150 s, which were then
combined. For fainter objects a few exposures of 300-900 s were
sufficient. The total exposure times vary from 90 to 6000 s depending
on the relative prominence of the host galaxy. Table 3
gives the log of observations. Columns 1 and 2 give the RGB name and
the name in other catalogs, Col. 3 indicates whether the object is a
BL Lac candidate in LM98, Col. 4 whether the object was a new BL Lac
in LM98, Col. 5 gives the galactic extinction in the R-band from
Schlegel et al. (1998), obtained through NED
40 objects. Here we discuss the R-band
images only. The individual exposures of the BL Lacs were kept short
enough as not to saturate the nucleus. For bright objects (R < 15)
we obtained several exposures of 15-150 s, which were then
combined. For fainter objects a few exposures of 300-900 s were
sufficient. The total exposure times vary from 90 to 6000 s depending
on the relative prominence of the host galaxy. Table 3
gives the log of observations. Columns 1 and 2 give the RGB name and
the name in other catalogs, Col. 3 indicates whether the object is a
BL Lac candidate in LM98, Col. 4 whether the object was a new BL Lac
in LM98, Col. 5 gives the galactic extinction in the R-band from
Schlegel et al. (1998), obtained through NED![[*]](/icons/foot_motif.gif) , Col. 6 the observing date, Col. 7 the
instrument, Col. 8 the total integration time, Col. 9 the seeing
and Col. 10 gives references to previous observations that have been
published since 1990.
, Col. 6 the observing date, Col. 7 the
instrument, Col. 8 the total integration time, Col. 9 the seeing
and Col. 10 gives references to previous observations that have been
published since 1990.
We have already published data for 14 BL Lac objects in Table 3. Pursimo et al. (2002) analyzed the host
galaxies of 1 Jy BL Lacs. Of the 9 objects common to this study 8 are
re-analyzed here with our 2-dimensional decomposition procedure. We
excluded 0721+713 from this study due to the fact that no suitable PSF
stars were available in the frame. Images of 1745+398 and 1806+468
have been published before by Nilsson et al. (1997,
1999b), but no host galaxy analysis was made. The images and
fitting results for 1104+382, 1442+120, 1653+397, 1743+195 and
2039+523 are reproduced here from our previous studies for
completeness (Heidt et al. 1999a, 1999b; Nilsson et
al. 1999a). We have indicated in Table 3 the
objects for which we have published data before with the reference
to the original publication.
The images were reduced in a standard way by subtracting the bias,
dividing by twilight flat-fields and removing the cosmic ray hits
using IRAF procedures. For ALFOSC we used flat-fields obtained at
different position angles of the instrument to remove the background
nonuniformity caused by scattered light. Generally a better than 1%
uniformity of the sky background over the entire field was
achieved. The photometric calibration was made by observing several
photometric standard stars in Landolt (1992) during the
night. When the weather conditions were not photometric we used
calibrated comparison stars in the same field as the object (Fiorucci
& Tosti 1996; Fiorucci et al. 1998; Villata et
al. 1998).
4.1 PSF variability
It is well known that an accurate determination of the PSF is crucial
to the nucleus/host galaxy separation, especially for marginally
resolved objects. The best results are obtained by using observed
stars in the same field as the BL Lac under study. In this way one can
circumvent problems associated with changing seeing conditions and/or
tracking errors. However, aberrations in the imaging system can
introduce PSF changes over the field of view and thus degrade the
results.
We made an examination of the PSF shape (FWHM, ellipticity and PA)
over the field of all three instruments. This examination revealed
that in HiRAC and StanCam the PSF is very stable over the field of
view. In ALFOSC, however, the PSF shape is changing considerably: in
typical frames the FWHM changes 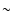 7%, the ellipticity by
7%, the ellipticity by 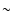 0.04 and the position angle more than 90 degrees over the field of
view. These changes are caused by the re-imaging optics of ALFOSC that
introduce a curved focal plane and astigmatism (Rasmussen
1996; Andersen, priv. comm.).
0.04 and the position angle more than 90 degrees over the field of
view. These changes are caused by the re-imaging optics of ALFOSC that
introduce a curved focal plane and astigmatism (Rasmussen
1996; Andersen, priv. comm.).
We investigated whether the PSF changes could be modeled such that
they could be used in our simulations (Sect. 4.3). We
decided to concentrate on the lowest order aberrations that cause the
change of FWHM, 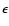 and PA over the field. The star images
contain also higher order aberrations (e.g. coma) but to model these
would complicate the task considerably with little gain since the
low-order aberrations usually dominate. ALFOSC produces also ghost
images that may contribute to the PSF variability, but their
brightness is very low (<0.05% of peak intensity).
and PA over the field. The star images
contain also higher order aberrations (e.g. coma) but to model these
would complicate the task considerably with little gain since the
low-order aberrations usually dominate. ALFOSC produces also ghost
images that may contribute to the PSF variability, but their
brightness is very low (<0.05% of peak intensity).
We experimented with different ways to model the PSF and ended up with
a model that consists of two parts, an atmospheric part and an
aberration part. The atmospheric part is modeled with an azimuthally
symmetric Moffat profile described by three parameters, the magnitude,
Moffat  and FWHM. This part represents the atmospheric smearing
and it is assumed to be constant over the field. The aberration part
is described via the 6 lowest order Zernike polynomials
and FWHM. This part represents the atmospheric smearing
and it is assumed to be constant over the field. The aberration part
is described via the 6 lowest order Zernike polynomials
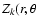 ),
k = 1...6, of which the first 3 terms Z1..3 (the "piston'', tip
and tilt terms, respectively) have no effect on the PSF shape. The
Z4-term is associated with defocus and Z5 and Z6 with
astigmatism. We first compute the phase error
),
k = 1...6, of which the first 3 terms Z1..3 (the "piston'', tip
and tilt terms, respectively) have no effect on the PSF shape. The
Z4-term is associated with defocus and Z5 and Z6 with
astigmatism. We first compute the phase error 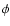 at the pupil
from
at the pupil
from
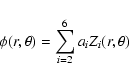 |
(1) |
parametrized by the Zernike coefficients a2...6 (a1 = 0),
multiply it with a mask containing the secondary mirror and secondary
support and finally Fourier transform to produce the aberrated image
corresponding to a2...6. The computations are made assuming that
the light is monochromatic with
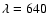 nm. The aberrated
image is then convolved with the atmospheric part and rebinned to the
instrument resolution to yield the final model image. Using an
iterative Levenberg-Marquardt loop we fit this model to each star in
the field by
nm. The aberrated
image is then convolved with the atmospheric part and rebinned to the
instrument resolution to yield the final model image. Using an
iterative Levenberg-Marquardt loop we fit this model to each star in
the field by 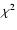 minimization. To improve the convergence to the
global minimum we use a pyramidal recursive algorithm similar to
Iglesias (1998). We make two passes through the stars in
each field. During the first pass the Moffat
minimization. To improve the convergence to the
global minimum we use a pyramidal recursive algorithm similar to
Iglesias (1998). We make two passes through the stars in
each field. During the first pass the Moffat  and FWHM of the
atmospheric profile are free parameters and during the second pass,
they are held constant at the median values from the first pass. The
total number of free parameters is 8 during the first pass and 6
(magnitude, a2 - a6) during the second pass. From 5 to 60
(typically 10-15) stars per field were fit with the above fitting
procedure depending on the number of suitable stars.
and FWHM of the
atmospheric profile are free parameters and during the second pass,
they are held constant at the median values from the first pass. The
total number of free parameters is 8 during the first pass and 6
(magnitude, a2 - a6) during the second pass. From 5 to 60
(typically 10-15) stars per field were fit with the above fitting
procedure depending on the number of suitable stars.
In Fig. 1 we show two examples of the results obtained
with this fitting procedure. Each circle/line pair corresponds to a
star in the two particular BL Lac fields shown here as an
example. Since the NOT is an alt-az telescope, the alignment of the
telescope optics changes with respect to the instrument from object to
object and each field gives slightly different results. The two cases
in Fig. 1 are typical, however, and illustrate the
difference of PSF variability in HiRAC and ALFOSC.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F1u.eps}\par\includegraphics[width=8.8cm,clip]{h3941F1l.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg36.gif) |
Figure 1:
Two examples of the PSF variability over the
field of view in HiRAC (upper panel) and ALFOSC (lower panel). Each
symbol corresponds to a star in the field. The diameter of the symbol
is proportional to the fitted a4 (defocus) coefficient. The
direction and length of the lines are proportional to the a5 and
a6 (astigmatism) coefficients. Note the difference in PSF
variations across the field of view of the two instruments. |
| Open with DEXTER |
Our analysis of the PSF changes across the field of view confirms our
initial finding that the PSF variations are more severe in
ALFOSC than in HiRAC and StanCam. The focal planes of HiRAC and
StanCam are flat but slightly tilted with the direction of the tilt
changing from object to object. In ALFOSC the focal plane is curved
with possible tapering in the edges, and relatively constant from
object to object. It is qualitatively similar to the focal plane map
given in Rasmussen (1996). The average peak-to-peak
variation in a4 is 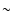 1.7, which corresponds to a 0.54
1.7, which corresponds to a 0.54
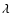 phase error or
phase error or
in the focal plane, where F is the focal ratio (6.4 for
ALFOSC). This is slightly smaller than the value 150 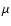 m quoted in
Rasmussen (1996), but reasonable given the number of
assumptions in the model and possible color effects and a tilt of the
focal plane.
m quoted in
Rasmussen (1996), but reasonable given the number of
assumptions in the model and possible color effects and a tilt of the
focal plane.
This procedure works reasonably well when the aberrations are roughly
constant, i.e. when the observations have been made during a short
interval and/or when the instrument has not rotated strongly.
Occasionally, bad results are obtained even though the optical
alignment should have been stable during the exposures. These may be
cases where tracking errors or higher order aberrations contribute
significantly to the PSF shape. It was also found that a good S/N is
required for optimal results and thus the noise in a4 - a6 is
higher in fields populated mostly by faint stars.
4.2 Method of analysis
The host galaxy fitting procedure is described in detail in Nilsson et
al. (1999a). A 2-dimensional model is fitted to the observed
image via 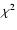 minimization using a Levenberg-Marquardt loop. The
model consists of two components, the BL Lac core and the host
galaxy. The core is parametrized by its position (
minimization using a Levenberg-Marquardt loop. The
model consists of two components, the BL Lac core and the host
galaxy. The core is parametrized by its position (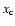 ,
,
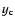 )
and
magnitude
)
and
magnitude 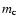 ,
whereas the host galaxy is parametrized by position
(
,
whereas the host galaxy is parametrized by position
(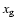 ,
,
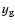 ), total magnitude
), total magnitude 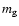 ,
effective radius
,
effective radius
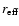 ,
ellipticity
,
ellipticity 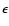 ,
position angle PA and shape parameter
,
position angle PA and shape parameter  (equal to 1/n in the Sérsic (1968) model). The surface
brightness of the galaxy is obtained from
(equal to 1/n in the Sérsic (1968) model). The surface
brightness of the galaxy is obtained from
![\begin{displaymath}I(r) = I({r}_{\rm e}){\rm dex} \left\{ -b_{\beta} \left[ \lef...
...rac{{r}}{{r}_{\rm e}} \right) ^{\beta} - 1 \right] \right\}\ ,
\end{displaymath}](/articles/aa/full/2003/10/aah3941/img47.gif) |
(2) |
where 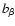 is a
is a  -dependent constant defined such
that
-dependent constant defined such
that
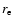 always encircles half of the total light.
always encircles half of the total light.
The model is convolved with the PSF determined by averaging 2-3 stars
in the field, that were comparable in brightness to the BL Lac. In a
few cases bright enough stars were not available, which resulted in a
lower S/N PSF. This may have caused a failure to detect a weak host
galaxy or resulted in less accurate host galaxy parameters in some
cases. However, our error simulations (Sect. 5)
take into account the effect of the noisy PSF, so cases where this
effect might be significant can be recognized. We also tried to
improve the PSF using our modeling of the PSF changes across the field
in the previous section. In principle, if sufficiently many stars in
the field could be modeled, one could predict the shape of the PSF at
the object's location. Tests on several fields showed that the PSF can
be improved when the exposures have been made over a short time
period, i.e. when the optical aberrations are almost constant, and
when sufficient number of stars (15-20) are available in the field.
Since these conditions are not always met, we decided not to correct
the PSF in order to treat all objects in the same way.
Before fitting, the background level was estimated by averaging
measurements made in rectangular areas around the BL Lac and
subtracted. In cases where a background gradient was present a
low-order surface was fit to the background pixels and subtracted.
All overlapping objects were masked out prior to fitting. In some
cases we iterated between fitting the BL Lac and a nearby object and
subtracting either of the objects before fitting the other. Sometimes
it was not possible to completely mask a nearby source because it
extended over the BL Lac core. We note in Sect. 5.2
the cases where we suspect that nearby sources have affected the
results. The fit was limited to a circular region with such a radius
that the minimum surface brightness of the object was 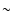 3-5 times higher than the uncertainty of the background level,
(typically
3-5 times higher than the uncertainty of the background level,
(typically
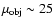 mag/sq arcsec at the outer
radius).
mag/sq arcsec at the outer
radius).
The amount of information obtainable of the host galaxies depends on
the distance of the object and on the nuclear dominance
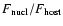 ,
both of which vary considerably over the sample.
The minimum we wanted to achieve is to get an estimate of the
magnitude and size of the host galaxy. Therefore we made two types of
fits depending on the relative brightness of the host galaxy. When the
host galaxy was reasonably strong compared to the nucleus, we fitted
three galaxy models with
,
both of which vary considerably over the sample.
The minimum we wanted to achieve is to get an estimate of the
magnitude and size of the host galaxy. Therefore we made two types of
fits depending on the relative brightness of the host galaxy. When the
host galaxy was reasonably strong compared to the nucleus, we fitted
three galaxy models with
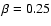 (de Vaucouleurs profile),
(de Vaucouleurs profile),
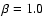 (exponential profile) and
(exponential profile) and  as a free
parameter. The total number of free parameters was 9 or 10. If the
host galaxy was very weak (more than
as a free
parameter. The total number of free parameters was 9 or 10. If the
host galaxy was very weak (more than 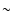 2 mag fainter than the
nucleus), we fitted only two models (
2 mag fainter than the
nucleus), we fitted only two models (
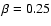 and 1.0) keeping
the core and host galaxy position fixed and
and 1.0) keeping
the core and host galaxy position fixed and 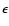 = PA = 0. The
number of free parameters was three (
= PA = 0. The
number of free parameters was three (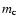 ,
,
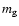 and
and 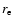 )
in these
cases. There were 7 such cases in the sample. The effective radii
obtained with these two methods are not directly comparable, but they
can be made such by multiplying the effective radii of the first type
fits by
)
in these
cases. There were 7 such cases in the sample. The effective radii
obtained with these two methods are not directly comparable, but they
can be made such by multiplying the effective radii of the first type
fits by
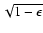 .
.
4.3 Simulations
We have made simulations to test the modeling algorithm and its
sensitivity to different noise sources, including photon and readout
noise, PSF variability and background determination error. We made 14
simulation runs corresponding to different contributions of the above
noise sources. In each run we created six sets of 30 simulated images
of an adopted "standard'' BL Lac + host galaxy (elliptical,
MR = -23.7 and
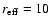 kpc). The six sets corresponded to
two cases of nuclear brightness,
kpc). The six sets corresponded to
two cases of nuclear brightness,
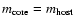 and
and
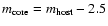 and three redshifts z = 0.15,
0.3 and 0.5. We added the effect of galactic extinction (
AR
= 0.1 was assumed), K-correction and passive evolution to the apparent
magnitudes of the host galaxy. All simulated images corresponded to a
900 s exposure with the HiRAC at 0
and three redshifts z = 0.15,
0.3 and 0.5. We added the effect of galactic extinction (
AR
= 0.1 was assumed), K-correction and passive evolution to the apparent
magnitudes of the host galaxy. All simulated images corresponded to a
900 s exposure with the HiRAC at 0
 7 seeing and a sky
background of 21.5 mag/sq arcsec.
7 seeing and a sky
background of 21.5 mag/sq arcsec.
Each simulated image was constructed as follows: first a noise-free
core + host galaxy image was made. Then a4 - a6 in
Eq. (1) were drawn from an uniform distribution and
the corresponding PSF was created, after which the model was convolved
with this PSF. Then photon and readout noise plus a small offset from
a zero-mean Gaussian distribution that represents the sky
determination error were added to the simulated image. Prior to the
fitting the defocus coefficient a4 was changed by a small amount
and a second PSF was created. Photon and readout noise were added to
this second PSF, after which it was used as the PSF model in the fit.
Each simulated image was thus convolved with a different PSF and
fitted with a another PSF that differed from the first PSF with
respect to the defocus coefficient a4. This simple approach
produced residuals that closely resemble the "quadrupole-like''
residuals seen in the data (see e.g. 0929+502 in
Fig. 10). For the simulated fits we used the same
procedure as for the real data (Sect. 4.2). After each
fit the mean values and standard deviations we logged.
In the noiseless case the program found the correct parameters to a
high accuracy. As expected, the more noise was added the higher the
scatter in the fitted parameters became. The most significant finding
was that noise in the PSF biases the results if the host galaxy is
apparently small (i.e. at z > 0.3). One obtains too small and too
faint host galaxies from the fits when using a low S/N PSF star. To
avoid this bias one should use a PSF star that is 1 to 2 magnitudes
brighter than the object or, alternatively, average several stars in
the field. Noise in the BL Lac image also biases the results in a
similar way, but in this case the bias is <10% for
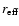 and <0.05 mag for
and <0.05 mag for 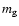 at
at 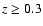 for an exposure of 900
s. Well-resolved sources (z = 0.15) are virtually free from the above
biases. PSF or background determination errors increase the scatter
in parameter distributions, but do not bias the average results.
for an exposure of 900
s. Well-resolved sources (z = 0.15) are virtually free from the above
biases. PSF or background determination errors increase the scatter
in parameter distributions, but do not bias the average results.
5 Results
The results of the host galaxy fits are given in Tables 4 and 5. Table 4 gives the fit results for the de Vaucouleurs
model and for the unresolved objects. Table 5
gives the results for the free  model. As explained above, the
free
model. As explained above, the
free  model was fitted only to objects that were subjectively
judged to be resolved well enough (55 objects).
model was fitted only to objects that were subjectively
judged to be resolved well enough (55 objects).
The errors of the fitted parameters were estimated via
simulations. For each object we created 30-50 simulated images that
corresponded to the best-fitting parameters and performed the fits in
a way similar to the actual fits. To the simulated images we added
photon and readout noise, background uncertainty and PSF noise in a
way similar to the test simulations (Sect. 4.3). The
amount of defocus needed to introduce the PSF errors was determined by
examining the residuals of the actual fits and adjusting the defocus
to match the observed residuals. It is clear that this simple approach
does not take into account all elements of the PSF variability, but in
most cases the residuals are very similar to the residuals seen in the
actual data. The residuals are more complex in cases where the
exposures have been taken over the course of several hours or during
different nights. In these cases the defocus was adjusted to obtain
the right amplitude of residuals although their exact shape is not
correct.
The errors in Tables 4 and 5
give the standard deviation of each parameter in the simulations. To
the magnitude errors we have added in square the error of photometric
calibration, which is 0.03-0.05 mag in most cases. Although we have
included most noise sources into our simulations, the errors should
still be treated as lower limits, since they do not include systematic
errors. The latter may arise e.g. when a de Vaucouleurs model does not
adequately describe the surface brightness distribution of the host
galaxy (and in many host galaxies it clearly does not).
The columns in Table 4 give:
(1) Object name in the RGB list.
(2) Redshift.
(3) Resolved or unresolved? Via simulations we determined that the
fitting program converges either towards
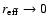 or
or
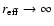 when the host galaxy is below the
noise level. Any object producing this kind of result is denoted as
"unresolved'' in Table 4. For the rest we require
that
when the host galaxy is below the
noise level. Any object producing this kind of result is denoted as
"unresolved'' in Table 4. For the rest we require
that
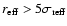 for the object to be resolved,
where
for the object to be resolved,
where
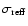 comes from the error simulations. Given that
the error bars are lower limits we decided to use this rather strict
limit.
comes from the error simulations. Given that
the error bars are lower limits we decided to use this rather strict
limit.
(4) R-band magnitude of the BL Lac nucleus. For unresolved objects this
comes from a fit with a core component only. The magnitudes are observed
magnitudes with no corrections applied.
(5) R-band magnitude of the host galaxy. These are, again,
observed magnitudes with no corrections applied.
(6) Effective (half-light) radius of the host galaxy in arcsec
along the major axis.
(7) Surface brightness at the effective radius of the host galaxy
in mag/sq arcsec.
(8) Ellipticity of the host galaxy. A dash indicates that the
ellipticity was held constant (0.0) during the fit.
(9) Position angle of the host galaxy, measured anticlockwise from the
north. A dash indicates that the PA was held constant (0.0) during
the fit.
(10) Reduced chi squared of the fit.
(11) The ratio between the 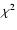 of the exponential model (
of the exponential model (
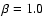 )
and the
)
and the 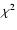 of the de Vaucouleurs model (
of the de Vaucouleurs model (
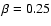 ).
).
(12) This column is marked with a Y if a new host galaxy detection has been
made in this paper.
The same parameters for the free  model are given in Table 5 in addition to the best-fitting
model are given in Table 5 in addition to the best-fitting  in
Col. 8.
in
Col. 8.
In Fig. 2 we show the 1-dim. radial profiles of the 37 objects where we have made a new host galaxy detection. The profiles
were extracted from the 2-dim. images using the ellipse task in
IRAF. In addition to the observed points (marked with asterisks) we
show the seeing-convolved core + host galaxy model (solid line), host
galaxy model (dashed line) and the core model (dotted line). In
Fig. 10 we show four examples of BL Lac images before and
after subtracting the best-fitting 2-dim. model. The field size,
lowest contour level (in mag/sq arcsec) and the host galaxy model
used in the subtraction are given below each image. Contour interval
is 1 mag/sq arcsec. In Fig. 11 we show similar images of four
interesting objects.
Table 6 gives the intrinsic parameters of the host galaxies for
objects with known redshift. The meaning of the Cols. is:
(1) RGB name.
(2) The K-correction in the R-band from Fukugita et al. (1995).
(3) Core absolute magnitude for the de Vaucouleurs model. For
unresolved objects the core magnitude comes from a fit with
the core component only. The magnitudes have been corrected for galactic
absorption, but no K-correction has been applied (i.e. we have assumed
a power law spectrum of the form
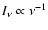 ).
).
(4) Host galaxy absolute magnitude for the de Vaucouleurs model. The
magnitudes have been corrected for galactic absorption and a
K-correction from Fukugita et al. (1995) has been applied.
(5) Host galaxy effective radius in kpc. The values have been
multiplied by
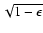 ,
where
,
where 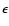 is the host galaxy
ellipticity.
is the host galaxy
ellipticity.
(6)-(8) Same as (3)-(5), but for the free  model.
model.
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{0110prof.eps}\hfill
...
...prof.eps}\hfill
\includegraphics[width=4.3cm,clip]{1341prof.eps} }\end{figure}](/articles/aa/full/2003/10/aah3941/Timg63.gif) |
Figure 2:
Radial profiles of the new host galaxy
detections. The x-axis shows the major axis distance from the nucleus
in arcsec and the y-axis the R-band surface brightness in mag
arcsec-2. Asterisks mark the observed points, the solid line the
core + host galaxy model, dashed line the host galaxy model and the
dotted line the core model. The  used in the host galaxy model
is also given, except when a de Vaucoulerus model (
used in the host galaxy model
is also given, except when a de Vaucoulerus model (
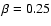 )
has
been used. )
has
been used. |
| Open with DEXTER |
There are 5 objects in the sample that have a spectroscopically
measured redshift, but no host galaxy was detected. We have estimated
an upper limit for their host galaxy luminosity using sets of
simulated BL Lac images. Each set consisted of 30 simulations and the
brightness of the host galaxy was changed by 0.3 mag between the
sets. In all sets we used
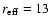 kpc (the average value of
the whole sample) and
kpc (the average value of
the whole sample) and
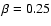 for the host galaxy. The core
magnitude was obtained from the fits with a core component only. We
fitted the 30 simulated images with a core + host galaxy model and
computed the average fitted effective radius
for the host galaxy. The core
magnitude was obtained from the fits with a core component only. We
fitted the 30 simulated images with a core + host galaxy model and
computed the average fitted effective radius
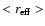 and the
rms scatter
and the
rms scatter
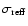 for each simulation set. We then
plotted
for each simulation set. We then
plotted
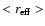 /
/
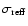 against the host galaxy
magnitude and the point where this curve fell below
against the host galaxy
magnitude and the point where this curve fell below
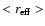 /
/
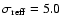 was adopted as the upper limit for
the host galaxy magnitude. This upper limit and the corresponding
upper limit for the host galaxy luminosity are given in Tables
4 and 6, respectively.
was adopted as the upper limit for
the host galaxy magnitude. This upper limit and the corresponding
upper limit for the host galaxy luminosity are given in Tables
4 and 6, respectively.
In Fig. 3 we compare the fitted host galaxy parameters
(magnitude and effective radius) to those found in the literature. We
found 26 objects common in three studies. All have used a de
Vaucouleurs model for the host galaxy. Two of the studies (Falomo &
Kotilainen 1999; hereafter FK99 and Pursimo et al. 2002; hereafter P02) have obtained their data with the
NOT, the P02 data are the same as used in this study. Any differences
between our results and the P02 results should thus reflect
differences in the analysis method. The third dataset comes from the
HST study of Scarpa et al. (2000a; hereafter SU00). All
comparison sets have been analyzed with the same 1-dim analysis
package, whereas we have used a 2-dim method. To facilitate the
comparison we have multiplied our effective radii by
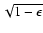 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F3u.eps}\par\includegraphics[width=8.8cm,clip]{h3941F3l.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg68.gif) |
Figure 3:
The comparison of the fitted a) magnitude
and b) effective radius with previous results (this work - comparison
work). Filled triangles: Falomo & Kotilainen (1999); open
circles: Scarpa et al. (2000a); filled circles: Pursimo et
al. (2002). |
| Open with DEXTER |
For the host galaxy magnitudes we do not find any systematic
differences (Fig. 3a). The average difference between
our magnitudes and the comparison magnitudes is
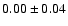 mag
with a rms scatter of 0.23 mag. The latter is clearly larger than most
of the quoted error bars, which is most likely due to systematic
errors not accounted for in the error analyses. The average difference
to the P02, who used the same data as we did, is
mag
with a rms scatter of 0.23 mag. The latter is clearly larger than most
of the quoted error bars, which is most likely due to systematic
errors not accounted for in the error analyses. The average difference
to the P02, who used the same data as we did, is
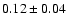 mag
(6 data points) with a 0.09 mag rms scatter. The effective radius
seems to be less well determined, especially for large
mag
(6 data points) with a 0.09 mag rms scatter. The effective radius
seems to be less well determined, especially for large
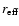 ,
as can be seen in 3b. For objects with
,
as can be seen in 3b. For objects with
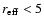 arcsec the rms scatter is 1.5 arcsec, i.e.
arcsec the rms scatter is 1.5 arcsec, i.e.  50% in most of the
sources. For large host galaxies (
50% in most of the
sources. For large host galaxies (
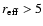 arcsec) a
systematic difference is seen with respect to the HST data, which seem
to indicate systematically smaller galaxies than our ground-based
images.
arcsec) a
systematic difference is seen with respect to the HST data, which seem
to indicate systematically smaller galaxies than our ground-based
images.
The reason for these differences lies probably in the difficulty of
accurately determining the scale length in the presence of a bright
nucleus. One source of discrepancy could be that host galaxies do not
always follow closely the de Vaucouleurs law. If one tries to fit a de
Vaucouleurs model to a host galaxy that deviates from such law,
different analysis methods may produce different results. We
correlated the difference of
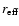 in Fig. 3b
with
in Fig. 3b
with  ,
but did not find an increasing difference of
,
but did not find an increasing difference of
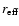 with increasing deviation from
with increasing deviation from
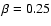 as might be
expected if the above effect were strong. It was also noted by P02,
that the fitted effective radius depends on the outer radius of
the fit region, which might contribute to the scatter.
as might be
expected if the above effect were strong. It was also noted by P02,
that the fitted effective radius depends on the outer radius of
the fit region, which might contribute to the scatter.
5.2 Notes on individual objects
0007+472: This object is unresolved, but our upper limit for the
host galaxy luminosity (
MR > -22.4) indicates that the host
galaxy should have been easily detected at z = 0.280 (see also
Fig. 4) . The redshift is from Kock et al. (1996),
who report two possible absorption features (G-band and NaD) at
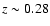 in a "partially reduced spectrum''. The redshift clearly
needs to be checked.
in a "partially reduced spectrum''. The redshift clearly
needs to be checked.
0035+598: This object consists of two point sources separated by
1.6 arcsec (Scarpa et al. 1999a, FK99). Of these, the eastern
object (object B in Scarpa et al. 1999a) is the likely BL Lac
candidate. Gravitational lensing seems to be ruled out by the color
difference of the two components. FK99 found the object resolved but
noted the possibility of contaminating light from a nearby bright
star. Our fit for this object was made by iterating between the object
and the nearby companion and subtracting either of the objects before
fitting the other. We find both objects to be unresolved and
subtracting both of them leaves no significant residuals, except the
faint galaxy (galaxy G in Scarpa et al. 1999a) 1.4 arcsec
south of the BL Lac.
0040+408: This BL Lac candidate is located towards M 31.
The background is peppered with stars of M 31 and a correct determination
of the background is impossible. Thus we did not attempt to fit a host
galaxy model to this object. Subtraction of a point source reveals a
faint object 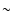 0.9 arcsec away at PA
0.9 arcsec away at PA
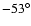 .
It is not
clear whether the nearby companion belongs to M 31 or is associated
with the BL Lac object.
.
It is not
clear whether the nearby companion belongs to M 31 or is associated
with the BL Lac object.
0109+182: Bauer et al. (2000) give z = 0.145 for this
object. A weak nebulosity is observed after subtracting the core (Fig. 10). This nebulosity corresponds to a host galaxy with
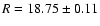 and
and
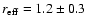 arcsec. The
error in the effective radius does not satisfy our criterion for a
resolved object, thus this object is denoted unresolved in Table 4. With the above values the host galaxy would be
rather faint (
MR = -22.0) and small (
arcsec. The
error in the effective radius does not satisfy our criterion for a
resolved object, thus this object is denoted unresolved in Table 4. With the above values the host galaxy would be
rather faint (
MR = -22.0) and small (
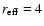 kpc).
kpc).
0250+172: Bauer et al. (2000) give z = 1.10 for this
BL Lac. The object is clearly resolved, and at z = 1.10 the host
galaxy would be exceedingly bright (
MR < -29.0) and large
(
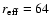 kpc). Thus the redshift is most likely too high.
There is a faint (R = 22.0) object 0.9 arcsec away from the nucleus at
PA
kpc). Thus the redshift is most likely too high.
There is a faint (R = 22.0) object 0.9 arcsec away from the nucleus at
PA 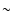 90
90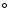 .
We could not determine if this object is
resolved or not, but it could be a distant star-forming galaxy giving
rise to the high redshift in Bauer et al. (2000).
.
We could not determine if this object is
resolved or not, but it could be a distant star-forming galaxy giving
rise to the high redshift in Bauer et al. (2000).
0314+247: A dust lane is visible crossing the host galaxy
SE of the nucleus. A second, fainter dust lane is visible south
of the nucleus. In the log(
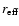 )-
)-
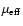 projection
of the fundamental plane (Fig. 9) this object lies below
the general trend, probably due to the absorption by dust in the host
galaxy.
projection
of the fundamental plane (Fig. 9) this object lies below
the general trend, probably due to the absorption by dust in the host
galaxy.
0326+024: Falomo (1996) noted the two nearby
companions roughly west of the nucleus. The outer one seems to be
severely distorted, possibly due to interaction with the BL Lac host
galaxy. It could also consist of two overlapping galaxies.
0416+010: This BL Lac has been previously imaged extensively
(see Table 3). The host galaxy parameters have been
determined by 7 studies with the host magnitude and effective radius
ranging from 17.45 to 17.80 and from 0.8 to 6.1 arcsec, respectively.
Our values (17.73 and 2.9 arcsec) lie within this range.
0424+006: This object was found to be resolved by Abraham et al.
(1991) and Falomo (1996) and unresolved by Wright et al. (1998b). We find the object unresolved, which may be due
to the fact that the nucleus was very bright (R = 13.7) during our
observations.
0505+072: Bauer et al. (2000) give
z = 0.0272, but they
note that the spectrum is of poor quality. At this redshift the host galaxy
would be very faint (
MR = -18.3) and small (
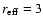 kpc).
The redshift probably needs to be checked.
kpc).
The redshift probably needs to be checked.
0650+250: As in all previous studies, this object remains
unresolved. FK99 note that the tentative redshift 0.203 would lead to
a relatively faint host galaxy.
0757+099: All previous authors find this object barely resolved.
Falomo (1996) gives R = 18.9 and
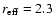 arcsec for
the host galaxy and SU00 R = 19.2 and
arcsec for
the host galaxy and SU00 R = 19.2 and
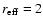 arcsec. Our
results indicate a slightly brighter (R = 18.55) and smaller (
arcsec. Our
results indicate a slightly brighter (R = 18.55) and smaller (
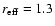 arcsec) host galaxy. This object has a tentative redshift
z = 0.66, but this would lead to a very bright host galaxy (SU00). The
galaxy 14 arcsec NE of 0757+099 has a redshift z = 0.270 (Pesce et al. 1995). At this redshift our results would indicate
MR = -23.2, and
arcsec) host galaxy. This object has a tentative redshift
z = 0.66, but this would lead to a very bright host galaxy (SU00). The
galaxy 14 arcsec NE of 0757+099 has a redshift z = 0.270 (Pesce et al. 1995). At this redshift our results would indicate
MR = -23.2, and
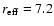 kpc.
kpc.
Table 3:
The observing log.
| RGB |
Other name |
C |
N |
AR |
Date |
Instr.1 |
Exp. |
FWHM |
Prev. obs. |
| |
|
|
|
|
dd/mm/yy |
|
[s] |
[arcsec] |
|
| |
|
|
|
|
|
|
|
|
|
| 0007+472 |
RXJ 00079+4711 |
|
|
0.26 |
18/07/98 |
A |
1200 |
1.1 |
|
| 0035+598 |
1ES 0033+595 |
|
|
2.35 |
19/07/98 |
A |
900 |
1.1 |
20,27,34,36 |
| 0040+408 |
B3 0037+405 |
y |
|
0.17 |
25/7/98 |
A |
1800 |
1.1 |
|
| 0109+182 |
RXJ 01090+1815 |
|
|
0.16 |
04/08/00 |
A |
1200 |
1.7 |
|
| 0110+418 |
RXJ 01100+4149 |
y |
y |
0.19 |
04/07/97 |
A |
240 |
0.9 |
|
| |
|
|
|
|
02/09/98 |
A |
|
|
|
| 0112+227 |
S2 0109+22 |
|
|
0.10 |
15/12/98 |
A |
2070 |
1.2 |
10,18 |
| 0115+253 |
RXJ 01157+2519 |
y |
|
0.20 |
01/09/98 |
A |
720 |
0.8 |
|
| 0123+343 |
1ES 0120+340 |
|
|
0.16 |
18/01/02 |
A |
1200 |
1.0 |
20 |
| 0136+391 |
B3 0133+388 |
|
y |
0.21 |
14/12/98 |
A |
1200 |
1.0 |
|
| 0152+017 |
PMNJ 0152+0146 |
y |
y |
0.09 |
14/12/98 |
A |
540 |
0.8 |
|
| 0153+712 |
8C 0149+710 |
|
|
1.63 |
01/09/98 |
A |
150 |
0.7 |
|
| 0202+088 |
PMNJ 0202+0848 |
y |
|
0.23 |
15/12/98 |
A |
1800 |
1.0 |
|
| 0214+517 |
RXJ 02142+5144 |
|
|
0.47 |
01/09/98 |
A |
150 |
0.8 |
|
| 0227+020 |
RXJ 02272+0201 |
y |
|
0.08 |
15/12/98 |
A |
1800 |
1.2 |
|
| 0250+172 |
RXJ 02506+1712 |
|
y |
0.40 |
14/12/98 |
A |
1500 |
0.9 |
|
| 0314+247 |
RXJ 03140+2445 |
y |
y |
0.45 |
14/12/98 |
A |
1200 |
1.0 |
|
| 0316+090 |
RXJ 03161+0904 |
|
|
0.95 |
18/01/02 |
A |
900 |
1.1 |
|
| 0321+236 |
RXJ 03219+2336 |
|
y |
0.50 |
14/12/98 |
A |
1500 |
1.0 |
|
| 0326+024 |
1H 0323+022 |
|
|
0.30 |
14/12/98 |
A |
1600 |
1.1 |
10,11 |
| 0416+010 |
1H 0414+009 |
|
|
0.32 |
15/12/98 |
A |
1200 |
0.9 |
1,3,4,10,11,20,23,34,36 |
| 0424+006 |
PKSJ 0424+0036 |
|
|
0.27 |
14/12/98 |
A |
660 |
1.1 |
2,10,18 |
| 0505+042 |
PMNJ 0505+0416 |
|
y |
0.21 |
14/12/98 |
A |
2400 |
1.0 |
|
| 0650+250 |
1ES 0647+250 |
|
|
0.26 |
14/12/98 |
A |
900 |
1.0 |
20,34,36 |
| 0654+427 |
B3 0651+428 |
|
|
0.26 |
14/12/98 |
A |
1500 |
1.0 |
|
| 0656+426 |
4C +42.22 |
y |
y |
0.30 |
15/12/98 |
A |
600 |
0.9 |
|
| 0710+591 |
1H 0658+595 |
|
y |
0.10 |
14/12/98 |
A |
1200 |
1.0 |
30,34,35,36 |
| 0757+099 |
PKSJ 0757+0956 |
|
|
0.06 |
14/12/98 |
A |
1600 |
1.0 |
2,10,18,34,36 |
| 0806+595 |
RXJ 08063+5931 |
|
y |
0.14 |
15/12/98 |
A |
1800 |
1.0 |
|
| 0814+296 |
EXO 0811.2+2949 |
|
|
0.10 |
15/12/98 |
A |
1800 |
0.9 |
|
| 0831+044 |
OJ 49 |
|
|
0.09 |
14/12/98 |
A |
1050 |
1.0 |
2,10,18,30,34,36 |
| 0854+441 |
B3 0850+443 |
|
|
0.07 |
15/12/98 |
A |
1800 |
1.0 |
|
| 0854+2012 |
OJ 287 |
|
|
0.08 |
04/01/98 |
S |
5160 |
0.6 |
7,9,11,16,19,23,34,35,36,373 |
| 0915+295 |
B2 0912+29 |
|
|
0.06 |
15/12/98 |
A |
1500 |
1.1 |
2 |
| 0916+526 |
RXJ 09168+5238 |
y |
|
0.04 |
15/12/98 |
A |
1200 |
1.1 |
|
| 0928+747 |
8C 0923+750 |
|
|
0.09 |
15/12/98 |
A |
1800 |
0.9 |
11,20,34,36 |
| 0929+502 |
RXJ 09292+5013 |
y |
|
0.04 |
14/12/98 |
A |
1500 |
0.9 |
|
| 0930+350 |
7C 0927+3516 |
|
|
0.03 |
16/12/98 |
A |
1800 |
1.1 |
|
| 0952+656 |
RXJ 09524+6538 |
|
y |
0.37 |
14/12/98 |
A |
1800 |
0.9 |
|
| 1000+225A |
4C +22.25 |
|
|
0.08 |
15/12/98 |
A |
1800 |
1.0 |
|
| 1012+424 |
B3 1009+427 |
y |
y |
0.04 |
16/12/98 |
A |
1200 |
1.1 |
|
| 1015+494 |
1H 1011+496 |
|
|
0.03 |
16/12/98 |
A |
1200 |
1.0 |
20,34,36 |
| 1037+571 |
RXJ 10377+5711 |
|
|
0.01 |
16/12/98 |
A |
1500 |
0.9 |
|
| 1053+494 |
MS 1050.7+4946 |
|
|
0.06 |
06/05/02 |
A |
600 |
1.0 |
|
| 1104+3822 |
Mkn 421 |
|
|
0.04 |
05/01/98 |
S |
600 |
0.5 |
11,253,30,31,32,33,34,36 |
| 1136+676 |
RXJ 11365+6737 |
|
|
0.02 |
14/12/98 |
A |
1200 |
1.0 |
|
| 1136+701 |
Mkn 180 |
|
|
0.04 |
05/07/97 |
A |
90 |
1.2 |
2,30,34,36 |
| 1149+246 |
EXO 1149.9+2455 |
|
|
0.08 |
16/12/98 |
A |
1200 |
0.9 |
|
| 1151+589 |
8C 1148+592 |
|
|
0.08 |
05/07/97 |
A |
120 |
1.8 |
|
| 1217+301 |
1ES 1215+303 |
|
|
0.06 |
15/12/98 |
A |
600 |
1.1 |
2,34,36 |
| 1221+282 |
W Comae |
|
|
0.06 |
23/01/01 |
S |
1280 |
0.6 |
11 |
| 1230+253 |
RXJ 12302+2517 |
|
|
0.05 |
05/07/97 |
A |
120 |
1.4 |
|
| 1248+583 |
PG 1246+586 |
|
|
0.03 |
05/07/97 |
A |
120 |
1.2 |
34,36 |
| 1310+3232 |
AU CVn |
|
|
0.04 |
08&11/07/96 |
S |
6000 |
0.9 |
7,29,373 |
| 1341+399 |
RXJ 13410+3959 |
y |
|
0.02 |
06/05/02 |
A |
600 |
1.0 |
|
| 1415+485 |
RXJ 14155+4830 |
|
y |
0.04 |
16/06/96 |
H |
600 |
1.2 |
|
| 1419+5432 |
OQ 530 |
|
|
0.04 |
08,11& |
S |
6000 |
0.6 |
2,7,11,30,34,35,36,373 |
| |
|
|
|
|
12/07/96 |
|
|
|
|
Table 3:
Continued.
|
RGB |
Other name |
C |
N |
AR |
Date |
Instr.1 |
Exp. |
FWHM |
Prev. obs. |
| |
|
|
|
|
dd/mm/yy |
|
[s] |
[arcsec] |
|
| 1427+541 |
RXJ 14274+5409 |
y |
y |
0.03 |
18/06/96 |
S |
600 |
0.5 |
|
| 1428+426 |
1H 1430+423 |
|
|
0.03 |
19/06/96 |
H |
900 |
0.8 |
30,34,36 |
| 1439+395 |
PG 1437+398 |
|
|
0.03 |
05/07/97 |
A |
120 |
1.2 |
34,36 |
| 1442+1202 |
1ES 1440+122 |
|
|
0.08 |
12/07/96 |
S |
1200 |
0.6 |
213,27,30,34,36 |
| 1448+361 |
RXJ 14479+3608 |
|
y |
0.03 |
17/06/96 |
H |
600 |
0.6 |
|
| 1454+514 |
RXJ 14544+5124 |
y |
y |
0.04 |
17/06/96 |
H |
600 |
0.7 |
|
| 1516+293 |
RXJ 15166+2917 |
y |
y |
0.07 |
18/06/96 |
S |
900 |
0.6 |
|
| 1517+654B |
1H 1515+660 |
|
|
0.07 |
17/06/96 |
H |
600 |
0.8 |
20,27,34,36 |
| 1532+302 |
RXJ 15319+3016 |
y |
y |
0.08 |
18/06/96 |
S |
900 |
0.5 |
|
| 1533+342 |
RXJ 15333+3416 |
|
y |
0.06 |
16/06/96 |
H |
600 |
0.7 |
|
| 1534+372 |
RXJ 15347+3716 |
y |
y |
0.05 |
18/06/96 |
S |
600 |
0.6 |
|
| 1540+1472 |
4C +14.60 |
|
|
0.15 |
09/07/96 |
S |
4380 |
0.8 |
7,11,17,29,34,36,373 |
| 1554+201 |
MS 1552.1+2020 |
|
|
0.13 |
04/07/97 |
A |
120 |
1.6 |
11,20 |
| 1602+308 |
RXJ 16022+3050 |
|
|
0.07 |
16/06/96 |
H |
600 |
0.6 |
|
| 1626+352 |
RXJ 16264+3513 |
|
|
0.06 |
01/09/98 |
A |
150 |
0.9 |
|
| 1644+457 |
B3 1642+458 |
|
|
0.04 |
31/08/98 |
A |
150 |
1.0 |
|
| 1652+403 |
RXJ 16527+4023 |
|
y |
0.05 |
16/06/96 |
H |
600 |
0.6 |
|
| 1653+3972 |
Mkn 501 |
|
|
0.05 |
08&11/07/96 |
S |
2670 |
0.7 |
2,6,7,8,11,253,31,37 |
| 1704+716 |
RXJ 17047+7138 |
|
|
0.09 |
17/06/96 |
H |
600 |
0.8 |
|
| 1719+177 |
PKSJ 1719+1745 |
|
|
0.18 |
01/09/98 |
A |
360 |
0.9 |
2 |
| 1728+502 |
1H 1727+502 |
|
|
0.08 |
06/07/97 |
A |
60 |
1.8 |
11,30,34,36 |
| 1742+597 |
RXJ 17424+5945 |
|
y |
0.12 |
17/06/96 |
H |
600 |
0.7 |
|
| 1743+1952 |
1ES 1741+196 |
|
|
0.24 |
13/07/96 |
S |
840 |
0.8 |
223 |
| 1745+3982 |
B3 1743+398B |
|
y |
0.11 |
16/06/96 |
H |
1800 |
0.7 |
263 |
| 1748+7002 |
S5 1749+70 |
|
|
0.08 |
21/10/95 |
S |
5460 |
0.6 |
7,34,36,373 |
| 1749+433 |
B3 1747+433 |
|
|
0.09 |
31/08/98 |
A |
150 |
0.8 |
|
| 1750+470 |
B3 1748+470 |
y |
y |
0.09 |
17/06/96 |
H |
900 |
0.7 |
|
| 1756+553 |
RXJ 17561+5522 |
|
y |
0.10 |
17/06/96 |
H |
600 |
0.8 |
|
| 1806+6982 |
3C 371 |
|
|
0.10 |
13/07/96 |
S |
1530 |
0.6 |
7,11,153,24,28,30,34,36,37 |
| 1808+468 |
RXJ 18079+4648 |
|
y |
0.10 |
17/06/96 |
H |
600 |
0.8 |
|
| 1811+442 |
RXJ 18118+4416 |
|
y |
0.21 |
17/06/96 |
H |
900 |
0.8 |
|
| 1813+317 |
EXO 1811.7+3143 |
|
|
0.13 |
19/07/98 |
A |
900 |
0.9 |
|
| 1824+5682 |
4C +56.27 |
|
|
0.16 |
11/07/96 |
S |
2400 |
0.8 |
7,12,29,34,36,373 |
| 1829+540 |
RXJ 18293+5403 |
|
y |
0.09 |
17/06/96 |
H |
600 |
0.7 |
|
| 1838+480 |
RXJ 18387+4802 |
|
y |
0.15 |
19/06/96 |
H |
1200 |
0.6 |
|
| 1841+591 |
RXJ 18412+5906 |
|
y |
0.12 |
18/06/96 |
S |
600 |
0.6 |
|
| 1848+427 |
RXJ 18487+4245 |
|
y |
0.21 |
17/06/96 |
H |
900 |
0.8 |
|
| 2039+5232 |
1ES 2037+521 |
y |
|
2.44 |
11/07/96 |
S |
1500 |
1.0 |
20,213,34,36 |
| 2145+073 |
MS 2143.4+0704 |
|
|
0.20 |
05&06/07/97 |
A |
180 |
1.0 |
11,14,17,20,29,34,35,36 |
| 2202+4222 |
BL Lacertae |
|
|
0.88 |
20/10/95 |
S |
5400 |
0.8 |
7,11,30,34,36,373 |
| 2243+203 |
RXJ 22438+2020 |
|
y |
0.13 |
19/06/96 |
H |
300 |
0.6 |
|
| 2250+384 |
B3 2247+381 |
y |
y |
0.40 |
19/06/96 |
H |
600 |
0.6 |
|
| 2319+161 |
RXJ 23196+1611 |
|
y |
0.12 |
15/12/98 |
A |
800 |
1.2 |
|
| 2322+346 |
RXJ 23226+3436 |
y |
y |
0.32 |
17/07/98 |
A |
1200 |
1.1 |
|
1 A = ALFOSC, S = StanCam, H = HiRAC.
2 Data published before, reanalysis is made in this paper.
3 Reference to the original publication.
References :
1. Falomo et al. (1990);
2. Abraham et al. (1991);
3. Falomo & Tanzi (1991);
4. McHardy et al. (1992);
5. Romanishin (1992);
6. Kotilainen et al. (1993);
7. Stickel et al. (1993);
8. Kotilainen & Ward (1994);
9. Benítez et al. (1996);
10. Falomo (1996);
11. Wurtz et al. (1996);
12. Falomo et al. (1997);
13. Gladders et al. (1997);
14. Jannuzi et al. (1997);
15. Nilsson et al. (1997);
16. Yanny et al. (1997);
17. Kotilainen et al. (1998);
18. Wright et al. (1998b);
19. Wright et al. (1998a);
20. Falomo & Kotilainen (1999);
21. Heidt et al. (1999a);
22. Heidt et al. (1999b);
23. Heidt et al. (1999c);
24. Martel et al. (1999);
25. Nilsson et al. (1999a);
26. Nilsson et al. (1999b);
27. Scarpa et al. (1999a);
28. Scarpa et al. (1999b);
29. Urry et al. (1999);
30. Falomo et al. (2000);
31. Gonzáles-Serrano & Carballo (2000);
32. Gorham et al. (2000);
33. Jansen et al. (2000);
34. Scarpa et al. (2000a);
35. Scarpa et al. (2000b);
36. Urry et al. (2000);
37. Pursimo et al. (2002).
|
0814+296: Two faint objects are seen close to the object after
subtracting the nucleus. The brighter one (
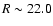 )
is 2.2 arcsec
away at PA
)
is 2.2 arcsec
away at PA
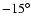 and the fainter one (
and the fainter one (
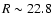 )
1.3 arcsec
away at PA 67
)
1.3 arcsec
away at PA 67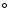 .
No redshift information is available for the
BL Lac or the nearby objects.
.
No redshift information is available for the
BL Lac or the nearby objects.
0854+441: A weak nebulosity is seen SE of the nucleus after
point source subtraction. This nebulosity could be due to PSF
subtraction errors.
0854+201: This object is one of the most studied in the sample,
yet the host galaxy parameters are still poorly determined. SU00 found
0854+201 to be unresolved. P02 found the object marginally resolved
using the same dataset as in the present paper and a 1-dim. analysis
method. The best-fitting host galaxy parameters corresponded to R =
18.9 and
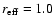 arcsec. The object remains unresolved
with the 2-dim. analysis method used in this study. We derive an
upper limit
MR> -24.0 for the host galaxy. A weak
nebulosity is seen around the nucleus after PSF subtraction extending
a bit further towards S and SE. No redshift information is available
for the close companion at 3.6 arcsec distance and PA
arcsec. The object remains unresolved
with the 2-dim. analysis method used in this study. We derive an
upper limit
MR> -24.0 for the host galaxy. A weak
nebulosity is seen around the nucleus after PSF subtraction extending
a bit further towards S and SE. No redshift information is available
for the close companion at 3.6 arcsec distance and PA
 .
Our optical spectra obtained at the William Herschel
Telescope (WHT) show that the diffuse galaxy 10 arcsec away at PA
.
Our optical spectra obtained at the William Herschel
Telescope (WHT) show that the diffuse galaxy 10 arcsec away at PA
 has a narrow emission line at 7200 Å (Nilsson et al.
1995).
has a narrow emission line at 7200 Å (Nilsson et al.
1995).
0915+295: Abraham et al. (1991) found the object
unresolved. A faint nebulosity is seen SW of the nucleus after PSF
subtraction (Fig. 11). We cannot determine if this nebulosity
is due to an intervening galaxy or a nearby companion. The fits have
been made under the assumption that it is a companion and the SW part
of the object was masked out from the fit. However, an equally good
fit can be achieved assuming a decentered host. In this case the host
galaxy would have R = 16.02 and
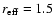 arcsec with a 0.2
arcsec decentering between the nucleus and the host. Higher resolution
images are clearly needed to resolve the issue.
arcsec with a 0.2
arcsec decentering between the nucleus and the host. Higher resolution
images are clearly needed to resolve the issue.
0928+747: This is one of the highest redshift objects resolved
in this study (z = 0.638). Our results agree well with the those
obtained with the HST (SU00).
1104+382: This object is discussed in more detail by Nilsson et al. (1999a). The bright companion galaxy was masked from the
fit, but its outer parts may still be affecting the results. Gorham et al. (2000) find the companion to be a spiral with an
unresolved nucleus.
1136+676: The host galaxy is clearly elongated towards a
nearby galaxy, possibly due to interaction with it and the ellipticity
of the host galaxy increases monotonically from 2 to 16 arcsec distance.
Due to this increase our constant ellipticity model underestimates
the flux at large distances from the nucleus (Fig. 2).
1136+701: The bright star (R = 15.16) 6.3 arcsec away from the
nucleus at PA 174 was iteratively removed before final
fitting.
was iteratively removed before final
fitting.
1149+246: The redshift (z = 0.402) is from Beckmann et al. (2002, priv. comm.).
1217+301: The nearby companion galaxy SW of the nucleus may
affect the fit results.
1221+282: There is a companion galaxy (
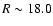 )
SW of the
nucleus. The companion appears distorted and a weak bridge of
emission extends towards the BL Lac nucleus from it. The bright
nucleus made the determination of host galaxy parameters difficult,
hence the large error in
)
SW of the
nucleus. The companion appears distorted and a weak bridge of
emission extends towards the BL Lac nucleus from it. The bright
nucleus made the determination of host galaxy parameters difficult,
hence the large error in  .
.
1310+323: This is the highest redshift object in the sample (z =
0.996). We have a very deep exposure (6000 s) taken under good seeing
conditions (0.9 arcsec), yet no sign of the host galaxy is seen.
Urry et al. (1999) found the object also unresolved in their
deep HST exposure. Stickel et al. (1993) noted that the
outer isophotes are extended more to the west than to the east. There
is a very faint galaxy (
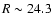 )
at 3.8 arcsec distance and PA
)
at 3.8 arcsec distance and PA
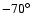 that could be the cause of the isophote asymmetry.
that could be the cause of the isophote asymmetry.
1419+543: This is one of the two objects in the sample for which
a formally better fit is obtained when using a disk model (
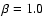 )
than when using the de Vaucouleurs model (
)
than when using the de Vaucouleurs model (
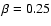 ). It has
also the highest fitted
). It has
also the highest fitted  (0.57) of the sample. Previous authors
have alternatively described 1419+543 as a disk galaxy (Abraham et al. 1991; Wurtz et al. 1996) or an elliptical
galaxy (SU00, P02). Stickel et al. (1993) noted that the
outer parts of the host (r > 5 arcsec) follow
(0.57) of the sample. Previous authors
have alternatively described 1419+543 as a disk galaxy (Abraham et al. 1991; Wurtz et al. 1996) or an elliptical
galaxy (SU00, P02). Stickel et al. (1993) noted that the
outer parts of the host (r > 5 arcsec) follow
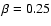 closely, whereas in the inner part there is an additional component
that showed up after subtraction of the elliptical model. This object
is discussed in more detail in Sect. 6.
closely, whereas in the inner part there is an additional component
that showed up after subtraction of the elliptical model. This object
is discussed in more detail in Sect. 6.
1427+541: After subtracting the model a pattern resembling
spiral arms is seen (Fig. 11). This BL Lac candidate could
thus be hosted by a galaxy with a considerable disk component. The
fitted  is also among the highest (0.32) in the
sample. However, the nucleus is very weak, and an almost equally good
fit can be obtained without any nuclear component. The 4000 Å break
is also very close to the limit (39%) set by LM99. It is therefore
not clear if this object really has a BL Lac nucleus.
is also among the highest (0.32) in the
sample. However, the nucleus is very weak, and an almost equally good
fit can be obtained without any nuclear component. The 4000 Å break
is also very close to the limit (39%) set by LM99. It is therefore
not clear if this object really has a BL Lac nucleus.
1442+541: This object was discussed in more detail in Heidt et
al. (1999a). There is a very bright companion galaxy only 2.5
arcsec away whose physical association with 1442+120 is confirmed by
spectroscopy (Heidt, priv. comm.). Scarpa et al. (1999a)
found a pointlike object 0.29 arcsec East of the BL Lac nucleus and
discuss a possible lensing scenario. We do not detect this point
source due to much lower resolution.
1516+293: This object has several bright companions that could
not be masked out completely, and thus may affect the fit.
1517+654: Scarpa et al. (1999a) found three arclets and
two bright spots surrounding the object, indicative of gravitational
lensing. We barely detect the spots, and with a priori knowledge
of their location also very faint trails of the arcs can be seen. The
object remains unresolved as in FK99 and Scarpa et al. (1999a).
1540+147: Our result agrees well with the recent HST results for
this high-redshift (z = 0.605) BL Lac. Urry et al. (1999)
found R = 19.0 and
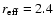 arcsec for the host galaxy and
SU00 R = 20.2 and
arcsec for the host galaxy and
SU00 R = 20.2 and
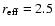 arcsec, whereas we find R = 19.9and
arcsec, whereas we find R = 19.9and
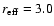 arcsec. P02 found R = 19.9 and
arcsec. P02 found R = 19.9 and
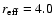 arcsec using the same data as in this study. This object is one of
the two objects for which an exponential host galaxy profile gives a
better fit than a de Vaucouleurs profile. The
arcsec using the same data as in this study. This object is one of
the two objects for which an exponential host galaxy profile gives a
better fit than a de Vaucouleurs profile. The 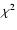 is almost the
same for both models, however. Urry et al. (1999) also found
1540+147 equally well fitted by the two models
is almost the
same for both models, however. Urry et al. (1999) also found
1540+147 equally well fitted by the two models
1626+352: The core plus a de Vaucouleurs fit for this object
gives
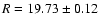 and
and
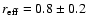 arcsec
for the host galaxy. Because of the errors in
arcsec
for the host galaxy. Because of the errors in
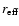 this
object is denoted as unresolved in Table 4. At
redshift z = 0.500 the above values would indicate
MR = -24.1and
this
object is denoted as unresolved in Table 4. At
redshift z = 0.500 the above values would indicate
MR = -24.1and
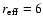 kpc.
kpc.
1653+397: This object is discussed in more detail in Nilsson et
al. (1999a). Fairly large residuals are seen in the inner
part of the object after subtracting the best-fitting free  model. Gonzáles-Serrano & Carballo (2000) report 1653+397
to have disky isophotes.
model. Gonzáles-Serrano & Carballo (2000) report 1653+397
to have disky isophotes.
1719+177: Abraham et al. (1991) found the object
resolved, but could no determine the host galaxy type. We find the
object unresolved, but our exposure time is relatively short (360 s).
1743+195: See Heidt et al. (1999b) for a detailed
discussion of the object. The two nearby companions are at the same
redshift as the BL Lac object.
1745+398: Nilsson et al. (1999b) discuss the arclike
structure 8 arcsec SE of the BL Lac nucleus (z = 0.267) and show it to
be a lensed image of a background galaxy at z = 1.057. Assuming that
the arc lies on the Einstein ring one obtains
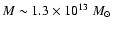 and
and
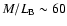 inside a radius of 40
kpc. Like in 1136+676, the ellipticity of the host galaxy
increases outwards and our model underestimates the flux at large
distances from the nucleus.
inside a radius of 40
kpc. Like in 1136+676, the ellipticity of the host galaxy
increases outwards and our model underestimates the flux at large
distances from the nucleus.
1748+700: This distant BL Lac (z = 0.770) was not resolved by
the HST (SU00) and it remains unresolved in the deep NOT exposure
(P02, this study).
1750+470: The bright nearby companion may be affecting the fit.
1806+698: Nilsson et al. (1997) discovered the optical
jet roughly SW of the nucleus. This jet has also been imaged with HST
(Martel et al. 1999; Scarpa et al. 1999b). There is
a bridge of emission connecting the host galaxy of 1806+698 to a pair
of companion galaxies SW of the BL Lac. The radio structure of
1806+698 is atypical, resembling more an FR II radio galaxy than an FR
I radio galaxy (Wrobel & Lind 1990).
1813+317: This object lies below the general trend in the
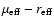 plot (the object at log
plot (the object at log
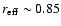 and with larger errorbars in Fig. 9). There is
no clear reason (bad PSF, bright companions, bad convergence of the
fit) why the fit for 1813+371 should be significantly worse than for
the rest of the sample. The redshift (0.117) is from Giommi et
al. (1991), and at this redshift the host galaxy would be
rather faint (
MR = -21.7) and small (
and with larger errorbars in Fig. 9). There is
no clear reason (bad PSF, bright companions, bad convergence of the
fit) why the fit for 1813+371 should be significantly worse than for
the rest of the sample. The redshift (0.117) is from Giommi et
al. (1991), and at this redshift the host galaxy would be
rather faint (
MR = -21.7) and small (
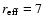 kpc). The redshift of 1813+317 could thus be actually higher than
0.117, in which case it would move up and towards the right in
Fig. 9.
kpc). The redshift of 1813+317 could thus be actually higher than
0.117, in which case it would move up and towards the right in
Fig. 9.
1824+568: This is the highest redshift (z = 0.664) resolved
object in the sample. We use the same data as P02 and our results
agree well with each other (
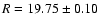 ,
,
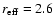 arcsec and
arcsec and
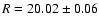 ,
,
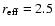 arcsec in P02 and
this study, respectively). The two HST studies (Urry et al.
1999, SU00) find similar host magnitudes, but smaller host
galaxy (
arcsec in P02 and
this study, respectively). The two HST studies (Urry et al.
1999, SU00) find similar host magnitudes, but smaller host
galaxy ( 1 arcsec).
1 arcsec).
1838+480: The nearby bright companion may be affecting the fit.
1848+427: The object remains unresolved, but faint emission is
seen between the object and a nearby companion.
2039+523: The redshift (z = 0.053) is from our own observations
at the Calar Alto 2.2 m telescope (Rector et al., in preparation). The
nearby star was iteratively removed before final fitting. SU00 report
a faint companion galaxy at 0.6 arcsec distance and PA 135 .
.
2202+422: The analysis of this object is complicated by the
presence of numerous overlapping stars and galaxies, a nearby bright
star, and diffuse galactic emission. Most of the Eastern side of the
object was masked from the fit. There are higher than usual residuals
in the inner part of the object, which could be due to an inner
component or an artifact due to insufficient masking of the
overlapping objects.
2319+161: Like 0035+598 this object consists of two point
sources close to each other (Fig. 11). An astrometric solution
to 17 APM stars in the field pinpoints the radio coordinates to the NW
object. The accuracy of this solution is  0.5 arcsec. The nearby
object is 3.3 arcsec away at PA 124
0.5 arcsec. The nearby
object is 3.3 arcsec away at PA 124 .
The spectra obtained at
the Calar Alto 2.2 m telescope (Rector et al., in preparation) show
the companion to be a galactic M class star.
.
The spectra obtained at
the Calar Alto 2.2 m telescope (Rector et al., in preparation) show
the companion to be a galactic M class star.
6 Discussion
In this section we discuss briefly the general properties of the
objects. A more detailed analysis will be given in a forthcoming
paper.
In Fig. 4 we show the dependence of the host galaxy absolute
magnitudes on redshift for the de Vaucouleurs model. Candidate objects
are denoted with open symbols and confirmed BL Lacs with filled
symbols. The solid line gives the behavior of an object with R = 19.0assuming
AR = 0.1, the K-correction from Fukugita et al. (1995) and no evolution. The R = 19 line seems to
determine the bottom envelope of the data pretty well indicating an
optical cutoff for the host galaxies at roughly this magnitude. As a
result of this cutoff an increase of average absolute magnitude with
redshift is seen.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F4.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg115.gif) |
Figure 4:
The dependence of the host galaxy luminosity on
redshift. Open symbols refer to BL Lac candidates, filled symbols to
confirmed BL Lacs. Arrows mark the objects for which only an
upper limit could be determined. The line gives the absolute magnitude
of an object with R = 19.0. |
| Open with DEXTER |
At z < 0.2, where the above selection effect is not yet serious, the
candidate host galaxies appear slightly brighter (
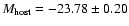 )
than the hosts of the confirmed BL Lacs (
)
than the hosts of the confirmed BL Lacs (
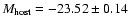 ), but using the K-S test the null hypothesis
that both samples are drawn from the same distribution can be rejected
at only 9% level. The average host absolute magnitude for the
whole sample is -23.86 with a 0.75 mag scatter which is in good
agreement with recent studies, e.g.
), but using the K-S test the null hypothesis
that both samples are drawn from the same distribution can be rejected
at only 9% level. The average host absolute magnitude for the
whole sample is -23.86 with a 0.75 mag scatter which is in good
agreement with recent studies, e.g.
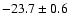 (Urry et al.
2000) and
(Urry et al.
2000) and
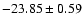 (FK99). The redshift
distributions of the three samples (Fig. 5) differ
slightly: the average redshift of resolved objects is lower in the
present sample (
(FK99). The redshift
distributions of the three samples (Fig. 5) differ
slightly: the average redshift of resolved objects is lower in the
present sample (
 )
than the two comparison samples
(
)
than the two comparison samples
(
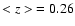 and 0.24 in FK99 and Urry et al. 2000,
respectively). However, none of the three studies detected host
galaxies above z = 0.7 and all of them detected only a handful of
hosts above z = 0.4, so one would not expect large differences of
average
and 0.24 in FK99 and Urry et al. 2000,
respectively). However, none of the three studies detected host
galaxies above z = 0.7 and all of them detected only a handful of
hosts above z = 0.4, so one would not expect large differences of
average
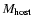 between the samples. The effective radii are
also very similar to what has been found previously. The average
effective radius of the RGB hosts is
between the samples. The effective radii are
also very similar to what has been found previously. The average
effective radius of the RGB hosts is
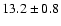 kpc for the de
Vaucouleurs model and
kpc for the de
Vaucouleurs model and
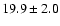 kpc for the free
kpc for the free  model.
model.
At z < 0.2 the nuclei of the BL Lac candidates seem to have
systematically fainter nuclei than the confirmed BL Lacs. The average
nuclear brightness is
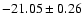 for the candidate objects
compared to
for the candidate objects
compared to
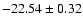 of the certain BL Lacs. This difference
is not surprising since the candidate objects have mostly 25% <Br
of the certain BL Lacs. This difference
is not surprising since the candidate objects have mostly 25% <Br
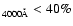 indicative of weak nuclear activity and/or
low nucleus/host galaxy flux ratios. The candidate nuclei are also
fainter than the nuclei of the 1 Jy BL Lacs studied in P02 that are
all brighter than
MR = -22.0. However, in the EMSS sample
studied by FK99, many nuclei have
-22 <MR< -20,
i.e. the candidate nuclei are not unprecedentedly faint. The nuclear
brightnesses of the candidates and certain BL Lacs seem to form a
homogeneous distribution with no gap between them. This further
supports the view that the candidates represent the low-luminosity end
of the RGB BL Lacs.
indicative of weak nuclear activity and/or
low nucleus/host galaxy flux ratios. The candidate nuclei are also
fainter than the nuclei of the 1 Jy BL Lacs studied in P02 that are
all brighter than
MR = -22.0. However, in the EMSS sample
studied by FK99, many nuclei have
-22 <MR< -20,
i.e. the candidate nuclei are not unprecedentedly faint. The nuclear
brightnesses of the candidates and certain BL Lacs seem to form a
homogeneous distribution with no gap between them. This further
supports the view that the candidates represent the low-luminosity end
of the RGB BL Lacs.
As Table 4 shows, our model fits favor almost
exclusively the de Vaucouleurs model (
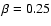 )
over the
exponential disk model (
)
over the
exponential disk model (
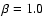 ). Only in two cases (1419+543
and 1540+147) among the 62 resolved objects one obtains a smaller
). Only in two cases (1419+543
and 1540+147) among the 62 resolved objects one obtains a smaller
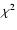 for the disk model than for the elliptical model. In
1540+147 the difference is small and the overall fit is not very good
(
for the disk model than for the elliptical model. In
1540+147 the difference is small and the overall fit is not very good
(
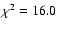 for the disk model and 16.1 for the elliptical
model). Thus we do not believe that the difference is significant.
for the disk model and 16.1 for the elliptical
model). Thus we do not believe that the difference is significant.
In 1419+543 there is evidence of an inner component in the host galaxy
(see individual notes on the objects). In addition to the core +
bulge fits we also fitted a core + bulge + disk model to this
object. The disk component was defined by four parameters, magnitude
(
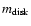 ), effective radius (
), effective radius (
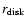 ), ellipticity
(
), ellipticity
(
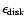 )
and position angle (PA
)
and position angle (PA
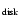 ). We used
). We used
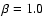 for the disk component and the disk and bulge were
assumed to be cocentric. The total number of free parameters was
thus 14 (3 for the core, 7 for the bulge and 4 for the disk). In
Fig. 6 we show the two models and the corresponding model
components. With the core + bulge + disk model we obtain a slightly
better fit (
for the disk component and the disk and bulge were
assumed to be cocentric. The total number of free parameters was
thus 14 (3 for the core, 7 for the bulge and 4 for the disk). In
Fig. 6 we show the two models and the corresponding model
components. With the core + bulge + disk model we obtain a slightly
better fit (
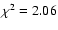 )
than with the core + bulge model
(
)
than with the core + bulge model
(
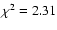 ). The disk is fainter than the bulge (
). The disk is fainter than the bulge (
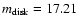 and
and
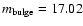 ), but larger (
), but larger (
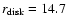 kpc and
kpc and
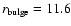 kpc) and its ellipticity is higher
(
kpc) and its ellipticity is higher
(
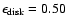 and
and
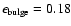 ). For
the bulge we obtain
). For
the bulge we obtain
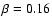 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F5u.eps}\par\includeg...
...]{h3941F5m.eps}\par\includegraphics[width=8.8cm,clip]{h3941F5l.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg142.gif) |
Figure 5:
The redshift distribution of the resolved
objects in the RGB sample (upper panel). For comparison the redshift
distribution of resolved objects in Urry et al. (2000;
middle panel) and Falomo & Kotilainen (1999; lower panel)
are shown. |
| Open with DEXTER |
We also performed an isophote analysis using the ellipse task in
IRAF. This analysis shows that there is a peak in both ellipticity
and in the b4 Fourier coefficient (as defined in Jedrzejewski
1987) at  3 to 8 arcsec distance from the nucleus
(Fig. 6). Positive values of b4 indicate disky isophotes
thus supporting the presence of a disk component 1419+543. We also
subtracted the disk component from the 2-dim. images and performed the
isophote analysis on the subtracted image. Both the ellipticity and
the b4 coefficient were considerably reduced by the subtraction of
the disk component (Fig. 6). There is thus evidence of a
significant disk component in 1419+543. Given the large size of the
disk and high disk to bulge luminosity ratio
(D/B) = 0.84) and the
host galaxy of 1419+543 should probably be classified as an S0 galaxy,
or maybe even an Sb0 galaxy given the appearance of the residuals in
Fig. 11.
3 to 8 arcsec distance from the nucleus
(Fig. 6). Positive values of b4 indicate disky isophotes
thus supporting the presence of a disk component 1419+543. We also
subtracted the disk component from the 2-dim. images and performed the
isophote analysis on the subtracted image. Both the ellipticity and
the b4 coefficient were considerably reduced by the subtraction of
the disk component (Fig. 6). There is thus evidence of a
significant disk component in 1419+543. Given the large size of the
disk and high disk to bulge luminosity ratio
(D/B) = 0.84) and the
host galaxy of 1419+543 should probably be classified as an S0 galaxy,
or maybe even an Sb0 galaxy given the appearance of the residuals in
Fig. 11.
We have not determined for each object whether the de Vaucouleurs
model is significantly (in a statistical sense) better than the disk
model, but the
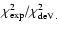 values in
Table 4 and the fact that not a single clear case
of a disk host was detected strongly support the view that BL Lac
objects are almost exclusively found in elliptical galaxies. Urry et al. (1999) found that for 58 objects among the 72 that were
resolved the de Vaucouleurs model was preferred over the disk model
with a high statistical significance and concluded that at most 8% of
the BL Lacs are hosted by disk type galaxies.
values in
Table 4 and the fact that not a single clear case
of a disk host was detected strongly support the view that BL Lac
objects are almost exclusively found in elliptical galaxies. Urry et al. (1999) found that for 58 objects among the 72 that were
resolved the de Vaucouleurs model was preferred over the disk model
with a high statistical significance and concluded that at most 8% of
the BL Lacs are hosted by disk type galaxies.
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{h3941f6.ps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg145.gif) |
Figure 6:
Surface brightness analysis of 1419+543. The
upper panels show the observed surface brightness (asterisks) and two
models (solid lines): the core+ bulge model (left) and the core +
bulge + disk model (right). The core model (dotted line), bulge model
(dashed line) and disk model(dot-dashed line) are also shown. The
lower panels show the ellipticity and b4 Fourier
coefficient. Asterisks mark observer values and filled symbols the
values after subtraction of the disk component. |
| Open with DEXTER |
In Fig. 7 we show the distribution of the fitted  values for the 55 objects that were judged to be well enough resolved
for such a fit. The median
values for the 55 objects that were judged to be well enough resolved
for such a fit. The median  is 0.18, well below
is 0.18, well below
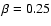 typically used to describe elliptical galaxy profiles. It is well
known, that not all ellipticals follow strictly the
typically used to describe elliptical galaxy profiles. It is well
known, that not all ellipticals follow strictly the
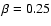 intensity profile (e.g. Caon et al. 1993). It is therefore
interesting to ask whether the deviation in Fig. 7 is
significant. This is currently very difficult to answer given the
uncertainties in the determination of
intensity profile (e.g. Caon et al. 1993). It is therefore
interesting to ask whether the deviation in Fig. 7 is
significant. This is currently very difficult to answer given the
uncertainties in the determination of  .
There is also a
selection effect at work here: only objects that were judged well
enough resolved were fit with the free
.
There is also a
selection effect at work here: only objects that were judged well
enough resolved were fit with the free  model, which means that
bright and/or large host galaxies are favored. Caon et al.
(1993) have shown that in normal E and S0 galaxies brighter
and larger galaxies have also higher Sérsic n, i.e. smaller
model, which means that
bright and/or large host galaxies are favored. Caon et al.
(1993) have shown that in normal E and S0 galaxies brighter
and larger galaxies have also higher Sérsic n, i.e. smaller
 (= 1/n). We also see a correlation of this type in
our data (Fig. 8), albeit with high scatter. The median size
of the free
(= 1/n). We also see a correlation of this type in
our data (Fig. 8), albeit with high scatter. The median size
of the free  fitted galaxies is 15.5 kpc which, applying the
relationship log n = 0.28 + 0.52 log
fitted galaxies is 15.5 kpc which, applying the
relationship log n = 0.28 + 0.52 log  in Caon et
al. (1993), would translate to
in Caon et
al. (1993), would translate to
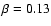 ,
i.e. significantly lower than 0.25.
,
i.e. significantly lower than 0.25.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F8.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg148.gif) |
Figure 8:
The dependence of  on effective
radius. The solid line gives the relationship in Caon et
al. (1993) for normal E and S0 galaxies.
on effective
radius. The solid line gives the relationship in Caon et
al. (1993) for normal E and S0 galaxies. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F9.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg149.gif) |
Figure 9:
The Kormendy relation for the host
galaxies when the de Vaucouleurs model is used. The solid line gives
the fitted slope for the data, the dashed line gives the relationship
for normal ellipticals from Hamabe & Kormendy (1987). |
| Open with DEXTER |
There could also be factors related to the fitting process that affect
the  distribution. First, since the free
distribution. First, since the free  model has more
freedom, it is harder to separate the host galaxy contribution from
the nuclear contribution than with the more rigid de Vaucouleurs
model, especially in the areas close to the nucleus. We have compared
the fitted
model has more
freedom, it is harder to separate the host galaxy contribution from
the nuclear contribution than with the more rigid de Vaucouleurs
model, especially in the areas close to the nucleus. We have compared
the fitted  in our error simulations
(Sect. 5) to the input values and found no strong
bias with respect to
in our error simulations
(Sect. 5) to the input values and found no strong
bias with respect to  .
The median difference
.
The median difference
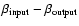 is -0.01 with a 0.02 rms deviation i.e. if there
is any bias, it is actually making the fitted
is -0.01 with a 0.02 rms deviation i.e. if there
is any bias, it is actually making the fitted  larger
than the "correct''
larger
than the "correct''  .
.
Secondly, there is the possibility that the companion galaxies that
are commonly seen around these BL Lacs could somehow decrease
 .
Lower
.
Lower  means that there is more light in the outer
parts of the galaxy. This light could partially be light from nearby
companions that we cannot mask out completely. To study the effect of
the companions we made an examination of the BL Lac images and divided
them into two groups: those that seemed to possess at least one
relatively bright companion inside the fitting radius and those that
did not. Of the 55 objects fitted with the free
means that there is more light in the outer
parts of the galaxy. This light could partially be light from nearby
companions that we cannot mask out completely. To study the effect of
the companions we made an examination of the BL Lac images and divided
them into two groups: those that seemed to possess at least one
relatively bright companion inside the fitting radius and those that
did not. Of the 55 objects fitted with the free  model 23 were
judged to belong to the first group and 32 to the second. We found the
median
model 23 were
judged to belong to the first group and 32 to the second. We found the
median  to be 0.18 in both groups, i.e. the same as for the
whole sample. This simple test thus suggests, that we are able to
mask the companions sufficiently to not seriously affect the fitted
to be 0.18 in both groups, i.e. the same as for the
whole sample. This simple test thus suggests, that we are able to
mask the companions sufficiently to not seriously affect the fitted
 .
A better solution than just mask the companions might be to
fit and remove them iteratively. Recently McLure et
al. (1999) fitted free
.
A better solution than just mask the companions might be to
fit and remove them iteratively. Recently McLure et
al. (1999) fitted free  models to a sample of radio
galaxies, radio-quiet quasars and radio-loud quasars observed with the
HST. They found the
models to a sample of radio
galaxies, radio-quiet quasars and radio-loud quasars observed with the
HST. They found the  values to be concentrated around
values to be concentrated around
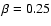 .
The luminosities and sizes of the host galaxies studied by
McLure et al. (1999) are similar to ours, so the difference
in the average values of
.
The luminosities and sizes of the host galaxies studied by
McLure et al. (1999) are similar to ours, so the difference
in the average values of  remains unexplained.
remains unexplained.
![\begin{figure}
\par\includegraphics[width=10.6cm,clip]{h3941F10.eps}
\par\end{figure}](/articles/aa/full/2003/10/aah3941/Timg151.gif) |
Figure 10:
Examples of objects in the RGB BL Lac
sample. The upper panel for each object shows the observed image and
the lower panel the model subtracted image. North is up and east is
to the left in all images. Between the panels (from left to right) the
field of view in arcsec, surface brightness of the lowest contour
(mag/sq arcsec) and the galaxy model used in the subtraction are
given. Contour interval is 1 mag/sq arcsec. If no galaxy model is
given, only a point source has been subtracted from the observed
image. The upper two objects are unresolved leaving either no
residuals or PSF residuals due to the different focus of the object
and the PSF star (see the text) after PSF subtraction. The lower left
panel shows an object with faint emission around the nucleus, but this
object is still unresolved according to the criteria used in this
paper. The lower right panel shows a clearly resolved object. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=10.7cm,clip]{h3941F11.eps} %\end{figure}](/articles/aa/full/2003/10/aah3941/Timg152.gif) |
Figure 11:
Examples of unusual objects : in 0915+295 a very nearby
companion or an intervening galaxy is seen, 1419+253 has unusual
residuals, 1427+541 has spiral arms and 2319+161 has a nearby
companion point source, shown to be an M-star by spectroscopy. |
| Open with DEXTER |
Many objects show considerable residuals in the inner parts of the
host galaxy that can not be attributed to PSF errors or complications
arising from nearby bright companions alone (e.g. 0152+017, 0656+426,
1419+543). In these objects there is probably an inner component,
possibly a disk, and a two-component model for the host galaxy would
be better. However, a three-component model (core + bulge + disk)
would complicate the task even further and, given the small apparent
size of many of the objects, it is not clear if the model parameters
could be sufficiently constrained.
In Fig. 9 we show the
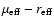 projection of the fundamental plane (the Kormendy relation) for the
resolved BL Lacs with known redshifts when the de Vaucouleurs
model is used for the host galaxy. The values of
projection of the fundamental plane (the Kormendy relation) for the
resolved BL Lacs with known redshifts when the de Vaucouleurs
model is used for the host galaxy. The values of
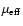 in
Tables 4 and 5 have been
corrected for the galactic extinction, K-correction and the
cosmological surface brightness dimming. For the de Vaucouleurs model
(Fig. 9) the best-fitting line is given by
in
Tables 4 and 5 have been
corrected for the galactic extinction, K-correction and the
cosmological surface brightness dimming. For the de Vaucouleurs model
(Fig. 9) the best-fitting line is given by
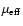 = (18.85
= (18.85 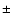 0.33) + (2.48
0.33) + (2.48 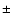 0.27) log(
0.27) log(
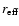 )
and
for the free
)
and
for the free  model
model
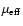 = (17.50
= (17.50 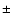 0.49) +
(3.91
0.49) +
(3.91 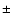 0.38) log(
0.38) log(
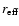 ). The former relationship is
similar to the relationship in Hamabe & Kormendy (1987),
who fitted the de Vaucouleurs model to a sample of nonactive
elliptical and early-type disk galaxies. The slope for the free
). The former relationship is
similar to the relationship in Hamabe & Kormendy (1987),
who fitted the de Vaucouleurs model to a sample of nonactive
elliptical and early-type disk galaxies. The slope for the free
 model is somewhat steeper, but within the range found for
other BL Lacs samples. FK99 found
model is somewhat steeper, but within the range found for
other BL Lacs samples. FK99 found
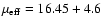 log(
log(
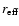 ), Urry et al. (2000)
), Urry et al. (2000)
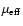 =
(17.2
=
(17.2 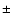 0.7) + (3.9
0.7) + (3.9 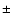 0.9) log(
0.9) log(
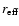 )
and P02
)
and P02
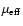 = (17.85
= (17.85 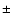 0.68) + (3.27
0.68) + (3.27 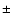 0.59) log(
0.59) log(
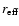 ). Moreover, the combined sample of FR I and II radio galaxies
studied by Govoni et al. (2000) gave
). Moreover, the combined sample of FR I and II radio galaxies
studied by Govoni et al. (2000) gave
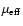 =
(18.44
=
(18.44 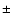 0.35) + (2.58
0.35) + (2.58 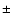 0.29) log(
0.29) log(
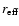 ). All these
relationships are very similar and, like many previous authors, we can
conclude that in the
). All these
relationships are very similar and, like many previous authors, we can
conclude that in the
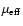 -
-
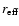 plane the BL Lac
host galaxies are indistinguishable from normal ellipticals and radio
galaxies.
plane the BL Lac
host galaxies are indistinguishable from normal ellipticals and radio
galaxies.
There are a few objects above or below the general trend in
Fig. 9. The two objects below the main part at
log(
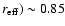 are 1813+317 (the object with larger
error bars) and 0314+247. Both objects have been discussed in
Sect. 5.2. The redshift of 1813+317 could be actually
higher than what is quoted in the literature and 0314+247 is clearly
affected by dust which probably lowers its
are 1813+317 (the object with larger
error bars) and 0314+247. Both objects have been discussed in
Sect. 5.2. The redshift of 1813+317 could be actually
higher than what is quoted in the literature and 0314+247 is clearly
affected by dust which probably lowers its
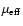 .
The four
objects clearly above the main part in Fig. 9 are all
high-redshift objects: these are 1149+246 (z = 0.402), 0928+747 (z =
0.638), 1841+591 (z = 0.530) and 1824+568 (z = 0.664) from upper left
to lower right. All are intrinsically very bright and may thus not be
representative of the whole elliptical galaxy class. Their large
K-corrections (0.6-1.5) lift them above other objects and if their
SEDs are not similar to elliptical galaxy SEDs, as we have assumed,
our correction would be incorrect and they could actually lie lower in
Fig. 9. We also do not correct for passive evolution of
the host galaxies, which, if applied, would bring them lower in
Fig. 9.
.
The four
objects clearly above the main part in Fig. 9 are all
high-redshift objects: these are 1149+246 (z = 0.402), 0928+747 (z =
0.638), 1841+591 (z = 0.530) and 1824+568 (z = 0.664) from upper left
to lower right. All are intrinsically very bright and may thus not be
representative of the whole elliptical galaxy class. Their large
K-corrections (0.6-1.5) lift them above other objects and if their
SEDs are not similar to elliptical galaxy SEDs, as we have assumed,
our correction would be incorrect and they could actually lie lower in
Fig. 9. We also do not correct for passive evolution of
the host galaxies, which, if applied, would bring them lower in
Fig. 9.
There are a handful of objects that are promising lensing
candidates. The two double sources (0035+598 and 2319+161) are
probably not lensed: there is no sign of the lensing galaxy in either
object. In 0035+598 the colors of the two point objects are very
different (FK99) and our spectrum shows the nearby object of 2319+161
to be a galactic star. In 0814+296 there are two very nearby objects
and in 0915+295 our resolution is not sufficient to determine whether
there is a nearby companion or a decentered host. In 0250+172 there is
a faint object very close to the nucleus but the nature of this
objects is unclear.
Finally, as was noted in Sect. 2, only 50% of the
RGB BL Lacs have a spectroscopically determined redshift, and in some
cases the redshift is uncertain. During this study we found
altogether 14 resolved objects that do not currently have a
redshift. We have started a program to determine the redshifts of
these objects and for one object (2039+523, z = 0.053) a redshift has
already been obtained. In Table 2 we show the estimated
redshifts for the remaining 13 objects. We used the fitted host
magnitude, effective radius and ellipticity to plot the object's
location in the log(
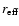 )-
)-
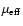 plane as a function
of redshift. At some point this curve intersects with the fitted
Kormendy relation in Fig. 9 and in Table 2 we
give the redshift corresponding to this intersect point for each
object. We tested this method with 13 objects with known redshifts
between 0.1-0.6 and found the estimated redshifts to be accurate to
within
plane as a function
of redshift. At some point this curve intersects with the fitted
Kormendy relation in Fig. 9 and in Table 2 we
give the redshift corresponding to this intersect point for each
object. We tested this method with 13 objects with known redshifts
between 0.1-0.6 and found the estimated redshifts to be accurate to
within 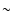 0.05, except for two high-z objects that lie above the
main part in Fig. 9. Thus some objects in Table
2 may have redshifts higher than indicated if their host
galaxies are somehow unusual. Finally, we note that the objects in
Table 2 have relatively high redshifts and if they are added
to our sample, the redshift distibution of the resolved objects
becomes more similar to that of Urry et al. (2000) and
Falomo & Kotilainen (1999).
0.05, except for two high-z objects that lie above the
main part in Fig. 9. Thus some objects in Table
2 may have redshifts higher than indicated if their host
galaxies are somehow unusual. Finally, we note that the objects in
Table 2 have relatively high redshifts and if they are added
to our sample, the redshift distibution of the resolved objects
becomes more similar to that of Urry et al. (2000) and
Falomo & Kotilainen (1999).
We have obtained new R-band images of 86 BL Lacertae objects in the
ROSAT-Green Bank (RGB) sample. Combining the data from our previous
studies we present here the optical images and host galaxy analysis of
100 objects. For 62 objects in the sample we did not find previously
published data in the literature, 35 of these were new BL Lacs
discovered during the RGB BL Lac survey. We were able to resolve the
host galaxy in 62% of the objects. We analyze the host galaxies using
a two-dimensional fitting procedure and give the best-fit core
magnitude and host galaxy parameters (magnitude, effective radius,
ellipticity, position angle and  )
for each object.
)
for each object.
With two exceptions, all objects are formally better fit by a
model representing an elliptical galaxy (
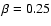 )
than by a
disk galaxy model (
)
than by a
disk galaxy model (
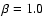 ). However, the disk host fit is only
marginally better in the two exceptions. One of them (1419+543) has a
very large disk component, and should probably be classified as an S0
or Sb0 galaxy. Thus we do not find a single clear case of a
disk-dominated host galaxy in our sample.
). However, the disk host fit is only
marginally better in the two exceptions. One of them (1419+543) has a
very large disk component, and should probably be classified as an S0
or Sb0 galaxy. Thus we do not find a single clear case of a
disk-dominated host galaxy in our sample.
The host galaxies have an average brightness
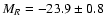 and effective radius
and effective radius
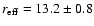 kpc and their bulk properties are indistinguishable from normal
ellipticals and radio galaxies. The median
kpc and their bulk properties are indistinguishable from normal
ellipticals and radio galaxies. The median  is 0.18, well below
the value of 0.25 that is normally used to describe
ellipticals. However, the difference may be due to a selection effect
caused by the
is 0.18, well below
the value of 0.25 that is normally used to describe
ellipticals. However, the difference may be due to a selection effect
caused by the
 correlation (Caon et al. 1993).
correlation (Caon et al. 1993).
In a subsequent paper (Nilsson et al., in preparation) we will present
a more detailed statistical study of the relationship between BL Lac
host galaxies and other ellipticals and the host galaxy - BL Lac
nucleus connection.
Acknowledgements
This work has been supported by the Academy of Finland through project
42697 (KN) and through SFB 328 and 439 (JH). KN thanks
Prof. I. Appenzeller, Prof. H. Jørgesen, Prof. N. H. Andersen and
the staff of Landessternwarte Heidelberg, Copenhagen University
Observatory and Risø National Laboratory for support and pleasant
working environment during this work. We also thank R. Rekola and
P. Keinänen for the help during the observations. The data presented
here have been partly taken using ALFOSC, which is owned by the
Instituto de Astrofisica de Andalucia (IAA) and operated at the Nordic
Optical Telescope under agreement between IAA and the NBIfAFG of the
Astronomical Observatory of Copenhagen.
-
Abraham, R. G., McHardy, I. M., & Crawford, C. S. 1991, MNRAS, 252, 482
In the text
NASA ADS
-
Bauer, F. E., Condon, J. J., Thuan, T. X., & Broderick, J. J. 2000,
ApJS, 129, 547
In the text
NASA ADS
-
Beckmann, V., Bade, N., & Wucknitz, O. 1999, A&A, 352, 395
NASA ADS
-
Benítez, E., Dultzin-Hacyan, D., Heidt, J., et al. 1996, ApJ, 464, L47
NASA ADS
-
Brinkmann, W., Siebert, J., Reich, W., et al. 1995, A&AS, 109, 147
In the text
NASA ADS
-
Caon, N., Capaccioli, M., & D'Onofrio, M. 1993, MNRAS, 265, 1013
In the text
NASA ADS
-
Falomo, R. 1996, MNRAS, 283, 241
In the text
NASA ADS
-
Falomo, R., & Kotilainen, J. K. 1999, A&A, 352, 85 (FK99)
In the text
NASA ADS
-
Falomo, R., Kotilainen, J. K., & Treves, A. 2002, ApJ, 569, L35
In the text
NASA ADS
-
Falomo, R., Melnick, J., & Tanzi, E. G. 1990, Nature, 345, 692
NASA ADS
-
Falomo, R., Scarpa, R., Treves, A., & Urry, C. M. 2000, ApJ, 542, 731
In the text
NASA ADS
-
Falomo, T., & Tanzi, E. G. 1991, AJ, 102, 1294
In the text
NASA ADS
-
Falomo, R., Urry, C. M., Pesce, J. E., et al. 1997, ApJ, 476, 113
In the text
NASA ADS
-
Fanaroff, B., & Riley, J. M. 1974, MNRAS, 167, 31
In the text
-
Fiorucci, M., & Tosti, G. 1996, A&AS, 116, 403
In the text
NASA ADS
-
Fiorucci, M., Tosti, G., & Rizzi, N. 1998, PASP, 110, 105
In the text
NASA ADS
-
Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9
In the text
NASA ADS
-
Fukugita, M., Shimasaku, & K., Ichikawa, T. 1995, PASP, 107, 945
In the text
NASA ADS
-
Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13
In the text
NASA ADS
- Giommi, P., Tagliaferri, G., Beuermann, K.,
et al. 1991, ApJ, 378, 77
In the text
NASA ADS
-
Gladders, M. D., Abraham, R. G., McHardy, I. M., et al. 1997, MNRAS, 284, 27
NASA ADS
-
González-Serrano, J. I., & Carballo, R. 2000, A&AS, 142, 353
In the text
NASA ADS
-
Gorham, P. W., van Zee, L., Unwin, S. C., & Jacobs, C. 2000, AJ, 119, 1677
In the text
NASA ADS
-
Govoni, F., Falomo, R., Fasano, G., & Scarpa, R. 2000, A&A, 353, 507
In the text
NASA ADS
-
Graham, A. W., Erwin, P., Caon, N., & Trujillo, I. 2001, ApJ, 563, L11
In the text
NASA ADS
- Gregory, P. C., Scott, W. K., Douglas, K., &
Condon, J. J. 1996, ApJS, 103, 427
In the text
NASA ADS
-
Hamabe, M., & Kormendy, J. 1987, in Structure and Dynamics of Elliptical
Galaxies, ed. P. T. de Zeeuw (Dordrecht: Kluwer), IAU Symp., 127, 379
In the text
-
Heidt, J., Nilsson, K., Sillanpää, A., Takalo, L. O., & Pursimo, T.
1999a, A&A, 341, 683
In the text
NASA ADS
-
Heidt, J., Nilsson, K., Fried, J. W., Takalo, L. O., & Sillanpää, A.
1999b, A&A, 348, 113
In the text
NASA ADS
-
Heidt, J., Nilsson, K., Appenzeller, I., et al. 1999c, A&A, 352, L11
NASA ADS
-
Iglesias, I. 1998, Appl. Opt., 37, 5427
In the text
NASA ADS
-
Jannuzi, B. T., Yanny, B., & Impey, C. 1997, ApJ, 491, 146
NASA ADS
-
Jansen, R. A., Franx, M., Fabricant, D., & Caldwell, N. 2000, ApJS, 126, 271
NASA ADS
-
Jedrzejewski, R. I. 1987, MNRAS, 226, 747
In the text
NASA ADS
-
Kock, A., Meisenheimer, K., Brinkmann, W., Neumann, M., & Siebert, J. 1996,
A&A, 307, 745
In the text
NASA ADS
-
Kotilainen, J. K., Falomo, R., & Scarpa, R. 1998, A&A, 336, 479
NASA ADS
-
Kotilainen, J. K., & Ward, M. J. 1994, MNRAS, 266, 953
NASA ADS
-
Kotilainen, J. K., Ward, M. J., & Williger, G. M. 1993, MNRAS, 263, 655
NASA ADS
-
Landolt, A. U. 1992, AJ, 104, 340
In the text
NASA ADS
- Laurent-Muehleisen, S. A., Kollgaard, R. I.,
Ciardullo, R., et al. 1998, ApJS, 118, 127 (LM98)
In the text
NASA ADS
-
Laurent-Muehleisen, S. A., Kollgaard, R. I., Feigelson, E. D., Brinkmann,
W., & Siebert, J. 1999, ApJ, 525, 127 (LM99)
In the text
NASA ADS
-
Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285
In the text
NASA ADS
-
Marchã, M. J. M., Browne, I. W. A., Impey, C. D., & Smith, P. S. 1996,
MNRAS, 281, 425
In the text
NASA ADS
-
Martel, A. R., Baum, S. A., Sparks, W. B., et al. 1999, ApJS, 122, 81
In the text
NASA ADS
-
McHardy, I. M., Luppino, G. A., George, I. M., Abraham, R. G.,
& Cooke, B. A. 1992, MNRAS, 256, 655
NASA ADS
-
McLure, R. J., & Dunlop, J. S. 2001, MNRAS, 327, 199
NASA ADS
-
McLure, R. J., & Dunlop, J. S. 2002, MNRAS, 331, 795
In the text
NASA ADS
-
McLure, R. J., Kukula, M. J., Dunlop, J. S., et al. 1999, MNRAS, 308, 377
In the text
NASA ADS
-
Merritt, D., & Ferrarese, L. 2001, MNRAS, 320, L30
In the text
NASA ADS
-
Nilsson, K., Heidt, J., Pursimo, T., Sillanpää, A., & Takalo, L. O.
1997, ApJ, 484, L107
In the text
NASA ADS
-
Nilsson, K., Pursimo, T., Takalo, L. O., et al. 1999a, PASP, 111, 1223
In the text
NASA ADS
-
Nilsson, K., Sillanpää, A., & Takalo, L. O. 1995, in Workshop of
two years of intensive monitoring of OJ 287 and 3C 66A,
ed. L. O. Takalo, Tuorla Observatory Reports, No. 176, 80
In the text
-
Nilsson, K., Takalo, L. O., Pursimo, T., et al. 1999b, A&A, 343, 81
In the text
NASA ADS
-
Pesce, J. E., Falomo, R., & Treves, A. 1995, AJ, 110, 1554
In the text
NASA ADS
-
Pursimo, T., Nilsson, K., Takalo, L. O., et al. 2002, A&A, 381, 810 (P02)
In the text
NASA ADS
-
Rasmussen, P. K. 1996, ALFOSC installation report, p. 9, obtainable from
http://not.iac.es
In the text
-
Romanishin, W. 1992, ApJ, 401, 65
-
Scarpa, R., Urry, C. M., Falomo, R., Pesce, J. E., & Treves, A. 2000a,
ApJ, 532, 740 (SU00)
In the text
NASA ADS
-
Scarpa, R., Urry, C. M., Falomo, R., et al. 1999a, ApJ, 521, 134
In the text
NASA ADS
-
Scarpa, R., Urry, C. M., Falomo, R., & Treves, A. 1999b, ApJ, 526, 643
In the text
NASA ADS
- Scarpa, R., Urry, C. M., Padovani, P.,
Calzetti, D., & O'Dowd, M. 2000b, ApJ, 544, 258
NASA ADS
-
Schade, D. J., Boyle, B. J., & Letawsky, M. 2000, MNRAS, 315, 498
In the text
NASA ADS
-
Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525
In the text
NASA ADS
-
Sérsic, J.-L. 1968, Atlas de Galaxias Australes (Cordoba: Obs. Astron.)
In the text
-
Stickel, M., Fried, J. W., & Kühr, H. 1993, A&AS, 98, 393
In the text
NASA ADS
-
Stocke, J. T., Morris, S. L., Gioia, J. M., et al. 1991, ApJS, 76, 813
In the text
NASA ADS
-
Trujillo, I., Graham, A. W., & Caon, N. 2001, MNRAS, 326, 869
NASA ADS
-
Urry, C. M., Falomo, R., Scarpa, R., et al. 1999, ApJ, 512, 88
In the text
NASA ADS
-
Urry, C. M., & Padovani, P. 1995, PASP, 107, 803
In the text
NASA ADS
-
Urry, C. M., Scarpa, R., O'Dowd, M., et al. 2000, ApJ, 532, 816
In the text
NASA ADS
- Villata, M., Raiteri, C. M., Lanteri, L.,
Sobrito, G., & Cavallone, M. 1998, ApJS, 130, 305
In the text
-
Voges, W. 1992, in Proc. of the ISY Conference Space Science,
ESA ISY-3 (ESA Publications), 9
In the text
-
Wright, S. C., McHardy, I. M., & Abraham, R. G. 1998a, MNRAS, 295, 799
NASA ADS
-
Wright, S. C., McHardy, I. M., Abraham, R. G., & Crawford, C. S. 1998b,
MNRAS, 296, 961
In the text
NASA ADS
-
Wrobel, J. M., & Lind, K. R. 1990, ApJ, 348, 135
In the text
NASA ADS
-
Wu, X.-B., Liu, F. K., & Zhang, T. Z. 2002, A&A, 389, 742
In the text
NASA ADS
-
Wurtz, R., Stocke, J. T., & Yee, H. K. C. 1996, ApJS, 103, 109
In the text
NASA ADS
-
Yanny, B., Jannuzi, B. T., & Impey, C. 1997, ApJ, 484, L113
NASA ADS
Copyright ESO 2003
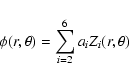
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F1u.eps}\par\includegraphics[width=8.8cm,clip]{h3941F1l.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg36.gif)
![\begin{displaymath}I(r) = I({r}_{\rm e}){\rm dex} \left\{ -b_{\beta} \left[ \lef...
...rac{{r}}{{r}_{\rm e}} \right) ^{\beta} - 1 \right] \right\}\ ,
\end{displaymath}](/articles/aa/full/2003/10/aah3941/img47.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{0110prof.eps}\hfill
...
...prof.eps}\hfill
\includegraphics[width=4.3cm,clip]{1341prof.eps} }\end{figure}](/articles/aa/full/2003/10/aah3941/Timg63.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{1415prof.eps}\hfill
...
...udegraphics[width=4.3cm,clip]{2322prof.eps}\hspace*{13.7cm} \hfill\end{figure}](/articles/aa/full/2003/10/aah3941/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F3u.eps}\par\includegraphics[width=8.8cm,clip]{h3941F3l.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg68.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F4.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg115.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F5u.eps}\par\includeg...
...]{h3941F5m.eps}\par\includegraphics[width=8.8cm,clip]{h3941F5l.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg142.gif)
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{h3941f6.ps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg145.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F7.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg147.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F8.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg148.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3941F9.eps}
\end{figure}](/articles/aa/full/2003/10/aah3941/Timg149.gif)
![\begin{figure}
\par\includegraphics[width=10.6cm,clip]{h3941F10.eps}
\par\end{figure}](/articles/aa/full/2003/10/aah3941/Timg151.gif)
![\begin{figure}
\par\includegraphics[width=10.7cm,clip]{h3941F11.eps} %\end{figure}](/articles/aa/full/2003/10/aah3941/Timg152.gif)